Significance
The hippocampus is thought to store a large number of experiences that, despite their similarity, can be individually retrieved with minimal interference. Studies have shown that place cells in hippocampal area CA3 form statistically independent representations of pairs of environments. It has remained unclear, however, whether CA3 place cells maintain this independence when the number of environments is increased. We recorded activity from CA3 in 11 environments with nearly identical geometric features. Spatial firing patterns remained uncorrelated across all 55 pairs of environments, with minimal overlap in the populations of active cells. The data suggest that the capacity of the CA3 network is large and speak against extensive recurrence of spatial motifs across experiences.
Keywords: memory, hippocampus, place cells, space
Abstract
The contribution of hippocampal circuits to high-capacity episodic memory is often attributed to the large number of orthogonal activity patterns that may be stored in these networks. Evidence for high-capacity storage in the hippocampus is missing, however. When animals are tested in pairs of environments, different combinations of place cells are recruited, consistent with the notion of independent representations. However, the extent to which representations remain independent across larger numbers of environments has not been determined. To investigate whether spatial firing patterns recur when animals are exposed to multiple environments, we tested rats in 11 recording boxes, each in a different room, allowing for 55 comparisons of place maps in each animal. In each environment, activity was recorded from neuronal ensembles in hippocampal area CA3, with an average of 30 active cells per animal. Representations were highly correlated between repeated tests in the same room but remained orthogonal across all combinations of different rooms, with minimal overlap in the active cell samples from each environment. A low proportion of cells had activity in many rooms but the firing locations of these cells were completely uncorrelated. Taken together, the results suggest that the number of independent spatial representations stored in hippocampal area CA3 is large, with minimal recurrence of spatial firing patterns across environments.
Episodic memory is characterized by an apparently astronomical storage capacity. Thousands of new experiences are encoded every day. Days, months, or years later we may be able to retrieve details of those experiences, such as where the event took place, who was present, and what the attendees did. The ability to store large numbers of experiences with minimal interference is thought to depend on neural network properties of the hippocampus, particularly those of the CA3 system, which can be described as an autoassociative network with strong intrinsic connectivity (1–3). Memories may be stored in this network by strengthening connections between cells that were active at the encoding stage. These cells are then thought to be reactivated during memory retrieval following stimulation of a subset of the ensemble.
The ability to retrieve memories from inputs that are only partly similar to the original comes at the risk of activating a different neuronal ensemble. The hippocampus is thought to embody several mechanisms for preventing such interference, all ensuring that new representations overlap minimally with preexisting ones (2, 4, 5). By orthogonalizing representations, hippocampal networks are thought not only to minimize interference but also to maximize the number of experiences that can be stored in the same network. Evidence for these ideas is provided by the fact that when animals are tested in environments with common features, representations of these environments in hippocampal place cells, in CA3, are often no more similar than expected by chance (6). Place cells are hippocampal cells that fire specifically when the animal is at a certain location (7). Each place in an environment is defined by a unique combination of active place cells (8, 9). When a key property of the environment is changed, such as the shape of the recording box or the nature of the experimental task, a completely new firing pattern may be elicited (10–12). This replacement of the active ensemble is referred to as “remapping.” The formation of orthogonal place maps in a single room location, following only minor changes in properties of the environment, is thought to reflect mechanisms similar to those used to disambiguate places and events in hippocampal memory (13).
In a network where new ensembles can be formed from any arbitrary combination of active cells, the storage capacity would be very large (14). Recent observations suggest, however, that hippocampal network activity is to some extent preconfigured. The hippocampus contains cell populations with distinct developmental histories that interconnect selectively within as well as between hippocampal subfields (15, 16). Such clusters of interconnected neurons may limit the number and variability of place-cell ensembles that can be formed when animals encounter new environments. Functional evidence for constraints on place-cell ensemble formation is provided by studies reporting that the sequence of firing among a set of place cells during running on a linear track is expressed in the resting state even before the animal runs down the track for the first time (17). The existence of predictive firing points to prewired networks as a possible determinant of place-cell recruitment during formation of new spatial representations. Developmental constraints like these would be in agreement with early theoretical work suggesting that the basis of a spatial map is embedded in the hippocampal circuit, ahead of experience (18, 19). The extent to which new representations are shaped by genetic or developmental mechanisms for ensemble formation is not known, however, nor is the impact that such mechanisms might have upon the storage capacity of the hippocampal network.
The capacity of hippocampal networks can be probed by comparing spatial representations across large numbers of environments with overlapping sensory features. Here we trained rats to forage in a total of 11 square boxes, each placed in a different room. Boxes and rooms had similar shape and size. Activity was recorded from the same ensembles of CA3 place cells in each room to determine whether elements of the place-cell representation were reused across environments when the number of room combinations was increased.
Results
CA3 pyramidal cells were recorded over two consecutive days in the dorsal hippocampus of seven rats while the rats chased food crumbles in square boxes. Activity was recorded successively in 11 different recording rooms (Fig. 1 and Fig. S1). One room was highly familiar to the rat; the remaining 10 were novel. Five new rooms were introduced each day. Two 15-min recording sessions were preceded and succeeded by 15-min blocks of rest on a pedestal near the recording box. Each room had a black 1-m-wide square recording box placed centrally at the back end of the room, with experimenter and recording equipment placed between the recording box and the room entrance (Fig. 1). The recording equipment was wheeled between rooms to ensure identical filtering and amplification. One novel room and the familiar room were repeated each day to check for stability. Repeated rooms were placed at the beginning and the end of the daily trial sequence (Fig. 1A).
Fig. 1.
Experimental setup and procedure. (A) Test protocol. On the first test day (DAY1), rats were transported into the familiar room (F), where they rested for 15 min next to the recording arena (REST F) before foraging started in the recording box. Foraging in the familiar environment lasted for 15 min (F). After a second 15-min rest trial (REST F), the rat was moved with the mobile recording rig to novel room 1 (N1) for 15 min of rest (rest N1) followed by 2 × 15 min of foraging (N1) and another rest trial (REST N1). The procedure was repeated across all novel rooms (day 1: N1–N5; day 2: N6–N10). Each day, the recordings in the novel environments were succeeded by a second test in the familiar environment to check for stability. (B) Photographs of all 11 rooms. White squares indicate room number. The mobile recording rig including the red crane (present in all pictures) enabled continuous recording. Different 1- × 1-m recording boxes were used in each of room. Position and location of cue card also varied across rooms.
A total of 342 well-isolated cells were accepted for analysis. All accepted cells were from CA3. Interneurons were excluded. On average, 49 CA3 place cells were collected per animal, including “silent” cells that fired only during rest or sleep. With an activity threshold Θ = 0.10 Hz (90 spikes over 15 min), the mean number of active CA3 cells per animal was 30. Among the total of 342 accepted cells, 210 were active in at least one environment. The average number of active place cells per room, summed over rats, was 46.1 ± 8.6 (mean ± SEM; average per rat: 6.62 ± 0.7). Electrodes were located across the entire proximodistal axis of the CA3 subfield (Fig. 2 A and B). Cells had stable firing fields across days as indicated by high spatial correlation between trials in the same familiar room on different days (mean ± SEM: 0.67 ± 0.08). This correlation was not significantly lower than between consecutive recordings in the same room (first vs. second half of trial: 0.73 ± 0.04; t(6) = 1.1, P = 0.30). High spatial correlation was also observed between dispersed tests in the same room (N1 and N6, r = 0.59 and r = 0.78, respectively; both P < 0.01).
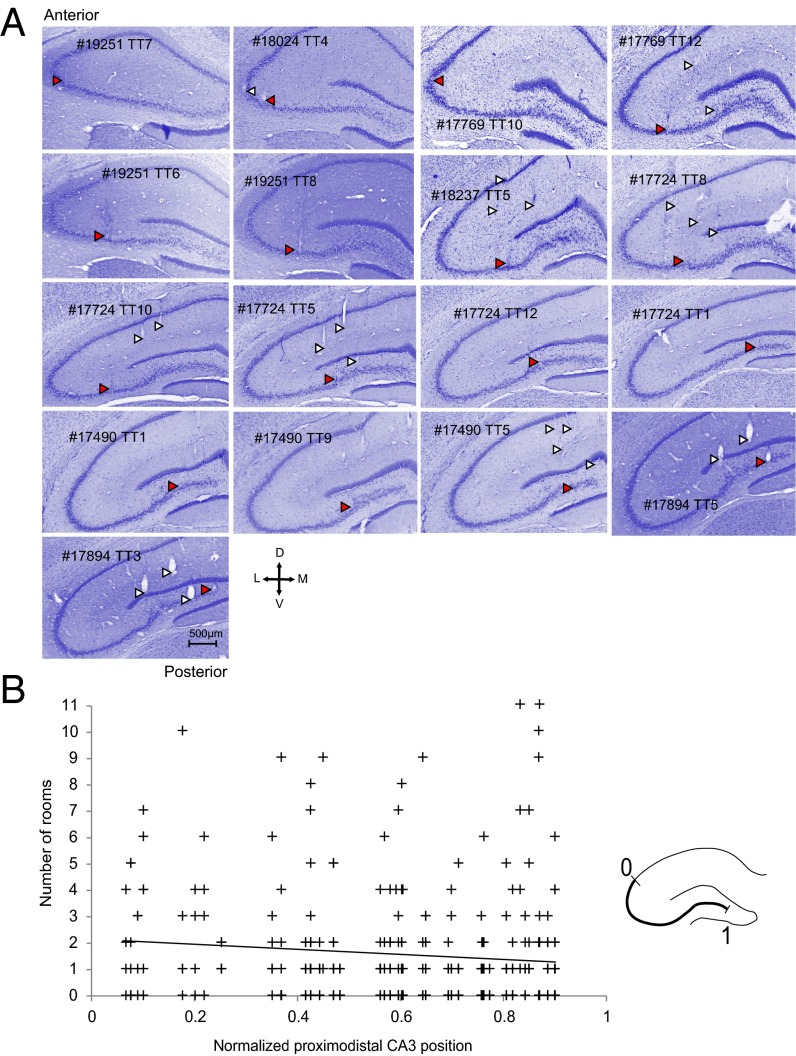
Fig. 2.
Tetrode locations of each animal. (A) Individual panels show Nissl-stained coronal sections through the hippocampus. Rat numbers (five digits) and tetrode numbers (TT) are indicated. Tetrode traces are indicated with arrowheads. Red arrowheads indicate tetrodes with cells that were active in more than five rooms. (Scale bar for all images, 500 µm.) (B) Scatterplot showing number of rooms that a cell was active in as a function of position along the proximodistal axis of CA3. Each cross corresponds to one cell. (Inset) Schematic showing proximodistal axis scaled from 0 to 1. Cells active in multiple rooms were not confined to a specific location on the proximodistal axis (r = −0.09, P > 0.05).
Nearly all cells that were active in any given environment had spatially confined firing fields (Fig. 3A). However, in most cells, the activity was limited to one or two of the 11 environments (Fig. 3 A and B). At Θ = 0.10 Hz, 39% of the identified cells were silent, 30% were active in just one room, and 13% were active in two rooms (Fig. 3B). Only 6% (21/342) of all cells were active in six or more rooms and fewer than 3% (10/342) were active in eight or more rooms (Fig. S2). The probability for a cell to be active in a given room (λ) was 0.14 (the average number of active rooms per cell was 1.49). Mean activation probabilities with Θ = 0.10 Hz were similar across all 10 novel rooms (range across rooms and rats: 0.03–0.32) and only slightly higher in the familiar room (mean across rats, 0.18; range, 0.07–0.25). There was no significant correlation between λ and the position of the room in the test sequence (r = −0.16, P = 0.64; mean ± SEM for novel rooms on day 1: 0.13 ± 0.10; day 2: 0.14 ± 0.10). Lowering the activity threshold to Θ = 0.05 Hz (45 spikes over 15 min) increased the percentage of cells with activity in six or more rooms to 11%. With a threshold of Θ = 0.01Hz (nine spikes over 15 min) this percentage increased to 27% (Fig. 3B).
Fig. 3.
Activity of three representative CA3 place cells in 11 recording rooms. (A) First row and every second subsequent row: color-coded rate maps showing distribution of firing rate within and between environments (blue, no firing; red, peak firing). Color is scaled to the peak rate (bottom right). Remaining rows: trajectory of the animal with spikes superimposed as red dots on the path. Animal number (five digits) and tetrode number (TT) are indicated. n = novel, F = familiar. The majority of the cells, such as TT9_6 and TT3_3, fire in one or two rooms. A small number of cells, such as TT7_2, fire in many or most rooms. (B) Frequency distribution showing number of cells with activity in successive numbers of rooms (1–11). Number of cells as a function of number of rooms in which the cells were active. Distributions are shown for different rate thresholds (Θ). Most CA3 place cells were silent or active in only 1 or 2 of the 11 rooms when Θ = 0.05 Hz or 0.10 Hz.
We next asked whether the distribution of active cells was different from the distribution expected if all cells had the same activation probability in each room, independently of each other and independently across rooms. Denoting with λ(Θ) the probability that a neuron be active in a given room, the null hypothesis was therefore that all neurons could be assigned the same value λ (which would depend on Θ). There were C cells (C = 342) and N rooms (N = 11). The equation
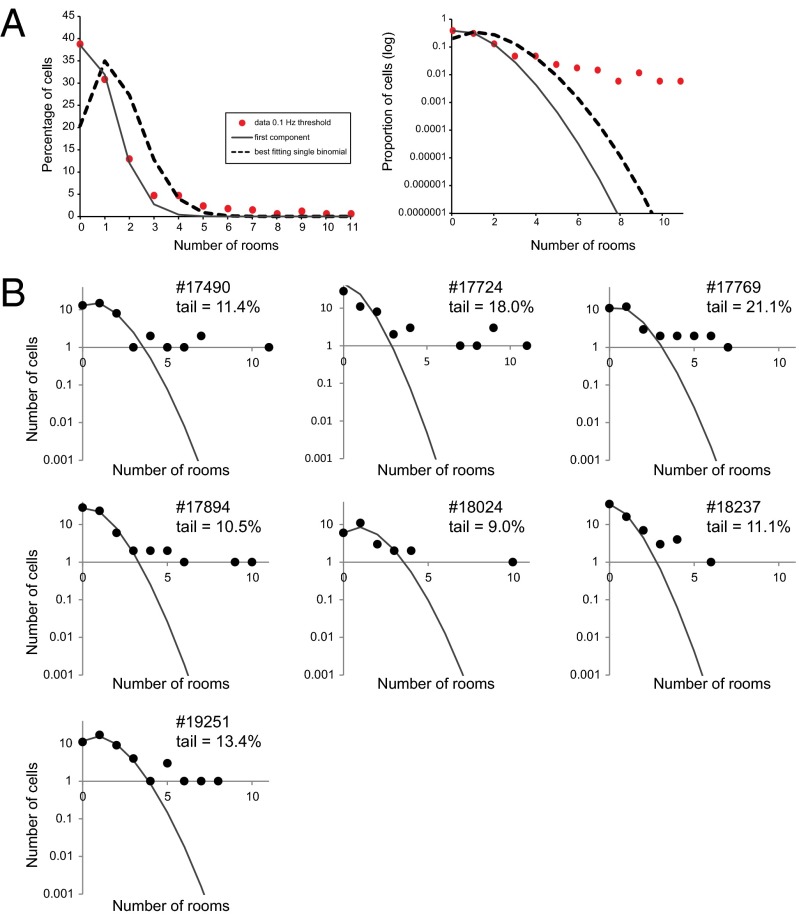
gives the binomial distribution expected for the number Cq(n) of neurons active in 0, 1, .., n, …, N rooms. One can set λ(Θ) equal to the observed average fraction of rooms in which cells are active but this model does not fit the observed numbers (Fig. 4A). Alternatively, one can set λ(Θ) to fit the first few data points for n = 0,1,…, but then the fit for large n becomes even worse. The lack of fit at the high end of the distribution was expressed in every single animal (Fig. 4B). Thus, a model using a single binomial parameter λ is not right and the hypothesis that all cells have similar activation probabilities can be rejected (χ2 = 364.8, P < 0.001).
Fig. 4.
The number of cells that were active in any number of rooms does not follow the binomial distribution expected if all cells had the same a priori probability λ of being active in a room. (A) Entire data sample. The dashed curve is the binomial distribution with λ = 0.14. The first few data points are much better fit by a binomial with λ = 0.07 (solid curve), which accounts for a fraction a0 = 85% of the cells, leaving the remaining 15% in the tail extending to high n values. The semilog scale to the right emphasizes this tail. Data and fits are for the 0.10-Hz threshold, but similar results hold for other threshold values. (B) The same data for individual animals, showing that a tail of overactive cells is present in all cases. Each panel shows for one animal the distribution of the number of cells active in any number n of rooms, on a semilog scale and with a 0.10-Hz activity threshold. The solid curve is the best binomial fit to the first three data points, those for n = 0, 1, and 2, and the fraction of cells not accounted for by these fits is indicated. Proportions of cells in tail are indicated.
The main deviation from the binomial distribution is evident in the small but highly significant number of cells that were active in several rooms. For example, setting a Θ = 0.10 Hz, with λ = 0.14, the null hypothesis would predict roughly half a cell to be active in 6 or more rooms, instead of the observed 21, and none to be active in 8 or more, instead of the observed 10 (Fig. 4A and Fig. S2). This discrepancy indicates that some of the cells have a much higher probability of participating in the representation of an environment than others. Given recent reports that the distribution of firing rates in some cell populations is approximately log-normal, with a heavy tail toward high values (20), and that the “propensity” of different CA1 cells to show place fields along a 48-m track is approximately gamma-distributed (21), we asked whether the number of cells active in n rooms could be described by the convolution of a specific distribution P(λ) with the binomial distribution, i.e.
The log-normal and the gamma distributions extend from 0 to infinity and cannot serve as a model for P(λ), where λ ranges from 0 to 1 only. We thus considered a few alternative models for P(λ) but could not identify a continuous analytical form for P(λ), defined by only a few free parameters, that would describe the observed distribution satisfactorily (Materials and Methods). A simple description, both of the overall data and for individual animals, can be obtained instead by just separating an extended tail from the main distribution describing most of the cells. The latter is itself very close to a binomial specified by the single parameter λ0; that is, we write the form
where the form of the Tail is left unspecified, and the parameters a0 and λ0 are those that best describe most of the cells (those active in zero, one, or two rooms; Materials and Methods). The fraction (1 − a0) is a measure of how significant is the tail of overactive cells. Across different animals this fraction ranged from 9.0% to 21.1%, and was on average 13.5 ± 4.1% (mean ± SD; Fig. 4B).
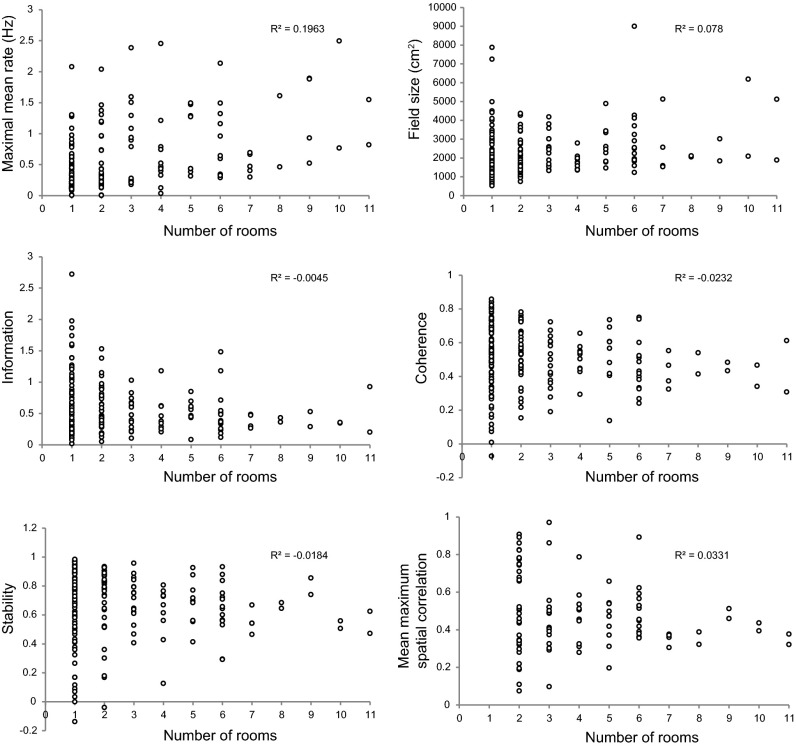
The “overactive” cells differed in several ways from the rest of the population. The mean firing rate of these cells was higher (correlation between mean rate in the most-active room and the number of rooms in which the cell passed threshold: r = 0.44, P < 0.01), the place field was larger (r = 0.28 P < 0.01), the spatial coherence was slightly weaker (r = −0.15, P = 0.03), and the place field was less stable across repeated tests in the same room (r = −0.14, P = 0.05; Fig. 5). There was no significant correlation between the number of rooms that the cell was active in and the cell’s spatial information value (r = −0.07, P = 0.34). There was also no significant relationship between the locations of the firing fields of the overactive cells in different rooms (maximum spatial correlation between room pairs vs. number of rooms that the cell was active in: r = −0.18, P = 0.7; Fig. 5). Cells that were active in many rooms were scattered across the entire CA3, from the distal to the proximal end. The correlation between the number of rooms that a cell was active in and its location along the axis from proximal to distal CA3 was negligible (r = −0.10, P > 0.05; Fig. 2B).
Fig. 5.
Place-cell characteristics for all CA3 cells that were active in at least one room (N = 210). Mean firing rate, field size, spatial information, spatial coherence, stability within rooms and maximal spatial correlation across rooms are plotted against the number of rooms a cell was active in. Mean firing rate is the maximum of room-specific mean rates across all rooms. Field size, information, coherence, and stability, in contrast, are averaged over all rooms in which the cell passed a rate threshold of Θ = 0.10 Hz. For spatial correlation across rooms, only cell pairs that passed the 0.10-Hz threshold in both rooms were used (N = 99). Maximal correlation was determined by rotating each map in steps of 90° and selecting the maximum correlation value.
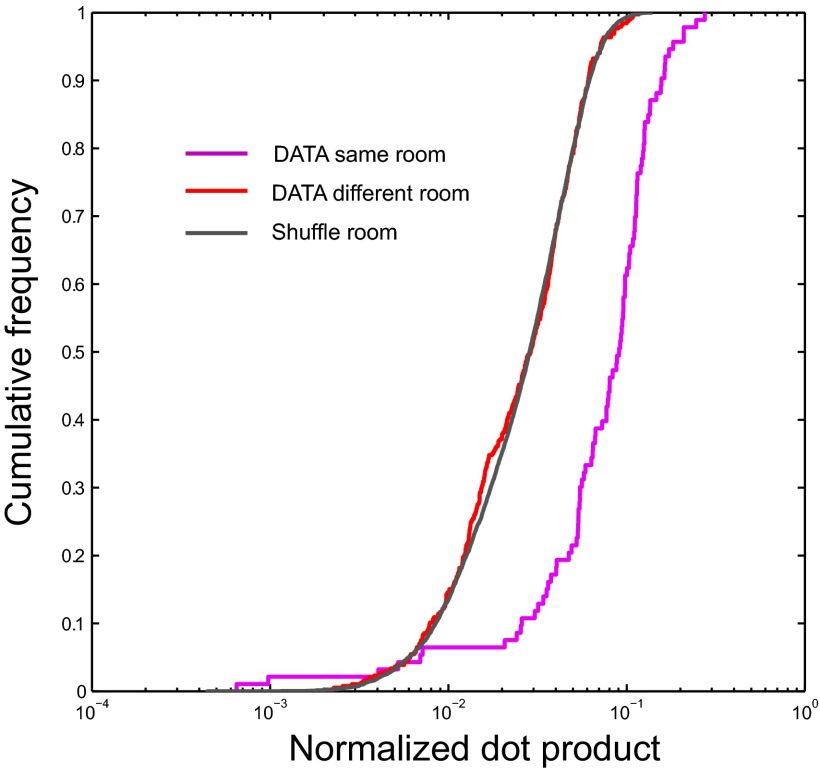
To determine whether ensembles of active place cells were more similar across rooms than expected by chance, we measured the overlap of normalized firing rates between each combination of rooms. Overlap was defined as the mean product, across cells, of the mean firing rates of each cell in the two rooms, and rates were normalized in that they were expressed as the ratio of the cell’s mean firing rate to the maximal mean rate of that cell across all rooms (6). The distribution of overlap values across 55 room pairs and seven animals (385 values in all) was similar to the distribution obtained by shuffling the rate of each cell across rooms (Mann–Whitney u test, Z = 0.51, df = 7,383, P = 0.61; Fig. 6). Both distributions were close to log-normal, so that their cumulative density functions (CDFs) took a characteristic sigmoid shape when plotted on a semilogarithmic scale. In contrast, the overlap between ensembles activated on successive visits to the same room was distributed toward higher values, as shown by a CDF shifted to the right (Z = 10.4, df = 477, P < 0.001; Fig. 6).
Fig. 6.
Similarity of firing rates between each of the 55 combinations of rooms. For each pair of rooms, the overlap of activity was defined as the mean product, across cells, of the mean firing rates of each cell in the two rooms, divided by the maximal mean rate of that cell across all rooms. Overlaps between different rooms (red line) are contrasted to overlaps between repeated exposures to the same room (pink line). Note the strong similarity between observed data across rooms and distributions of shuffled data where each rate map is assigned randomly to one of the 11 rooms (black line), suggesting that the distribution of active cells across rooms is close to orthogonal.
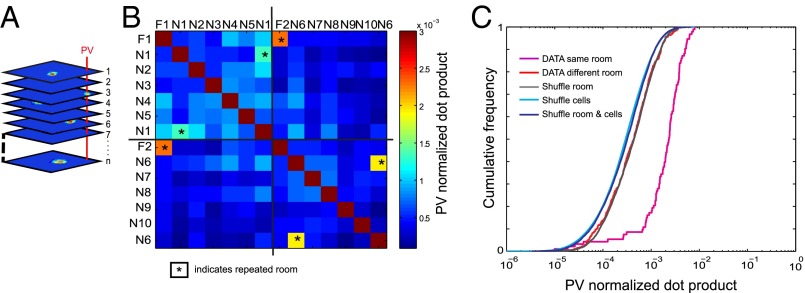
Orthogonalization can be achieved not only by recruitment of unique cell assemblies but also by randomization of firing locations among cells that fire in multiple environments. To investigate whether place-cell maps were spatially uncorrelated, or whether spatial patterns were preserved across subsets of rooms, we binned the rate maps of each cell in a given room into 5- × 5-cm bins and stacked the maps on top of each other into a 3D matrix. Population vectors were defined for each 5- × 5-cm bin (4, 22). The procedure allowed for 55 map comparisons (Fig. 7B and Fig. S3). Population vectors were not much correlated across combinations of different rooms (Fig. S3; mean population vector correlation for all combinations of novel rooms: r = 0.08 ± 0.005). In contrast, on successive trials in the same room the vectors were highly correlated (all rooms; average with SEM for all rats r = 0.65 ± 0.02). High correlations were also observed between repeated trials in the same room when these trials were separated by multiple trials in other rooms (familiar room, room 1, and room 6: r = 0.49 ± 0.05, Fig. S3). Correlations in the same room were significantly larger than correlations across different rooms (successive trials: t(100) = 3.4, P < 0.001; nonsuccessive trials: t(89) = 3.4, P < 0.001).
Fig. 7.
Dot product between population vectors across all combinations of test rooms. (A) Definition of population vectors. The rates of all recorded CA3 cells were stacked into 400 composite population vectors (PVs), one for each of the 20 × 20 pixels of the recording box. Population vectors with the local rates of each neuron were defined for each pixel. (B) Color-coded matrix showing average dot product values for population vectors between rooms (all 55 room pairs), including repeated exposures to the familiar room (F) and rooms N1 and N6, which were presented twice. Repeated trials are indicated by asterisks. (C) Distributions of shuffled data obtained either by random assignment of rate maps across rooms (shuffle room) or by shuffling of cell identities within rooms (shuffle cells) or by combining the two procedures (shuffle room and cells). Note the low dot product between all different pairs of rooms but significantly higher dot products between repeated trials in the same environment (DATA same room; first and second half of recording).
We finally assessed whether the entire distribution of 7 × 55 = 385 map comparisons was different from the distribution expected by chance (see Fig. 7B for all data and Fig. S4 for individual animals). For this test, we used the average dot product between population vectors at corresponding locations as a measure of similarity rather than the Pearson correlation. The average dot product is equivalent to the overlap measure extended to the spatial dimension. We compared the observed data with the distributions obtained through distinct shuffling procedures (Fig. 7C). First, shuffling was performed by randomly assigning the spatial map of each cell to a different room and then calculating new population vectors, resulting in a new combination of active and inactive cells at each location in the recording box. The procedure was repeated 1,000 times. Cells with activity below 0.10 Hz in all rooms were not included in these analyses. The distribution of the observed data for different rooms was again close to log-normal, matching the shuffled data almost perfectly (Z = −0.70, df = 7,383, P = 0.44; Fig. 7C) and suggesting that similarity between the spatial patterns of activity in two different rooms occurs no more frequently than expected by chance. Similar distributions were found across individual animals (Fig. S5B). The mean observed dot product for different rooms was significantly smaller than the mean observed dot product for repeated trials in the same room (Z = −10.8, df = 476, P < 0.001; CDF shifted to the right in Fig. 7C and Fig. S5B).
Can the lack of correlation between population vector maps across rooms be summarized by the simple model that each neuron is randomly recruited to participate in the representation of a novel room? To address this issue, we finally shuffled spatial maps both between rooms and between cells, again 1,000 times. Now, the cumulative distribution function of the similarity values was skewed slightly but significantly to the left compared with the observed data and the distribution after shuffling only across rooms (Z = 4.8, df = 13,998, P < 0.001; Fig. 7C). The median dot product between rooms was 4.37 × 10−4 in the observed data and 4.40 × 10−4 when shuffling only across rooms, whereas it decreased to 3.08 × 10−4 when shuffling across rooms and cells. This difference shows that the random recruitment model is not quite correct (i.e., not all cells were recruited with the same probability λ). Shuffling only across cells yields roughly the same cumulative distribution of similarity as shuffling both rooms and cells (Z = 1.7, df = 391,998, P = 0.07; Fig. 7C). We also asked whether the maps of different room pairs might be more similar after rotating one map relative to the other, because rats may lose their absolute compass orientation when they are carried from one room to the next. However, rotating the rate maps in steps of 90°, in the way that generated the largest correlation, did not lead to a distribution of similarity values that was significantly different from the distribution obtained by applying similar rotation on the shuffled data (Z = 0.39, df = 7,383, P = 0.70).
To determine whether the left-shift of the cell-shuffled distribution was caused by the unequal activation probabilities of the recorded cells, we finally performed a separate shuffling procedure where the subsets of overactive cells (defined as cells that were active in three rooms or more) and the subset of more sparsely active cells (one or two rooms) were shuffled only within their own subset. This simple partition into two subsets, still heterogeneous in terms of activation probability, yielded a less left-shifted distribution than when cell identities were shuffled across the entire sample (Fig. S5A). The median value for the distribution with shuffling within subsets was 3.93 × 10−4, significantly higher than when cells were shuffled across the entire sample (Z = −12.6, df = 13,998, P < 0.001; Fig. S5A). Taken together these analyses indicate that the discrepancy between cell-shuffled data and observed data is due to the nonuniform probability of activation in the data, where a proportion of the cells is much more active than the rest of the population.
Discussion
The key finding of this study is that when representational capacity was challenged by exposing animals to a range of rooms with similar sensory features, CA3 place cells continued to form unique representations for every single environment. Unique representations were formed within a single trial. The spatial discharge pattern never carried over from one environment to another. The findings are consistent with previous work showing that CA3 place cells form independent maps for pairs of environments (6) but extend it by demonstrating that no recurrence of spatial firing patterns occurs when the number of environments is increased from 2 to 11 and the number of combinations from 1 to 55. The unique firing patterns of the individual environments were stored in memory such that when the animal was introduced to one of the rooms a second time the spatial map from the first exposure was reactivated.
The complete lack of overlap between spatial maps suggests that the capacity of the CA3 network is large, despite recent indications suggesting that hippocampal cells are not randomly connected. Developmental studies indicate that, through direct or indirect connections, hippocampal cells form synapses preferentially with cells from the same clone (15, 16). Clustering of connectivity might point to an architecture of discrete subpopulations that have different functional properties. A discrete organization of the CA3 network may give rise to preconfigured spatial maps (18, 19), although such maps would likely serve only as a scaffold for further refinement following experience (23, 24). Evidence for preconfigured activity includes the report that the sequence of place fields expressed when an animal runs along a linear track for the first time is expressed during rest already before the experience (17), which suggests that new representations to some extent may be based on sequence relationships already encoded in the circuit. The present work suggests that such preconfigured spatial or temporal relationships, to the extent that they exist, do not constrain the discreteness of CA3 representations for multiple environments with overlapping sensory features. The orthogonal nature of the representations may be unique to the CA3 subfield of the hippocampus; CA1 representations are known from previous work to exhibit more overlap than expected by chance (25), although remarkable context specificity has also been demonstrated (26). The lack of correlation between CA3 representations may help preserve the large storage capacity estimated for this network with mathematical network models based on the orthogonalization assumption (14). Our study verifies that the storage capacity of CA3 is extensive, although the capacity bound remains to be determined.
The skewed nature of the distribution of active cells across rooms, with many cells firing in one or few rooms and few cells firing in many rooms, is reminiscent of the gamma-Poisson distribution of firing fields for individual CA1 place cells in a continuous environment (21) as well as the more general log-normal nature of firing-rate distributions in a variety of systems (20). Here we observed a nearly log-normal distribution of overlap or dot product values, with a slightly larger shift to the right than would be expected with strict orthogonality, reflecting the small and distributed subset of neurons that fired in many environments. The tendency for some place cells to fire in multiple environments is reminiscent of the similarity in ensemble activity reported for subsets of hippocampal cells during equivalent experiences in different environments (27–30). The function of the overactive cells remains to be determined, but the recruitment of a small number of cells to fire nonselectively across rooms, at different locations, may enable the encoding of common elements among spatial environments, over and above the orthogonalization emerging as a consequence of the use of nonoverlapping cellular subpopulations for separation of spatial environments in memory.
Materials and Methods
Subjects.
Seven male Long Evans rats (∼600 g and 4–5 mo old at implantation) were housed in a humidity and temperature-controlled environment on a 12-h light/12-h dark cycle in individual transparent Plexiglas cages (45 × 30 × 35 cm). Rats were kept at 95% of free-feeding body weight during the test phase. All experiments and surgery were performed in accordance with the Norwegian Animal Welfare Act and the European Convention for the Protection of Vertebrate Animals used for Experimental and Other Scientific Purposes.
Surgery, Electrode Preparation, and Implantation.
Before surgery, the rats were anesthetized with isoflurane [4% (vol/vol) in the induction chamber, which was gradually lowered to 0.5–3% (vol/vol) over the course of the surgery]. Airflow was 1.4 mL⋅min−1. The rats were given analgesic (Temgesic and Metacam) and received local anesthetic (xylocaine) under the skin (s.c. injection) before the incision was made. The animal was placed in a Kopf stereotaxic frame and ear bars were fixed to stabilize the head during surgery. A “hyperdrive” with 14 independently movable tetrodes was implanted above the right hippocampus at coordinates anteroposterior 3.8 and mediolateral 3.0 relative to bregma. The implant was secured with jewelers’ screws and dental cement. Tetrodes were constructed by twisting together four 17-µm polymide-coated platinium-iridium wires (90–100%; California Fine Wire) plated with platinum to lower the impedance of the electrode tip to between 120–250 kΩ at 1 kHz before implantation. After the animal woke up, it was treated orally with Metacam (Meloxicam, 0.1 mg/300 g; Boehringer Ingelheim) for 3 d. On the surgery day, after the animal woke up, the tetrodes were turned about 1,000 µm to make sure they were in the brain.
During the following 4–5 wk the tetrodes were gradually lowered in small increments (of 50 µm or less) to reach the CA3 area. Turning was performed while the rat rested on a towel in a flowerpot placed on a pedestal next to the recording arena. EEG and spiking events were used as visual references for the position of the tetrodes inside the brain, together with the depth of the tetrodes. Two tetrodes were used to record a reference signal from the corpus callosum and an EEG signal from the stratum lacunosum-moleculare. Increasing amplitude of theta as well as phenotype of sharp waves was monitored as indicators of distance from the CA3 pyramidal layer. Turning stopped when large-amplitude waveforms appeared at depths near 3.0 mm. On the days of the experiment the tetrodes were not moved at all to ensure stable recordings and to later verify the position of the tetrodes with histological procedures.
The hyperdrive was connected to a multichannel, impedance-matching, unity-gain headstage (HS-54; Neuralynx). The output of the headstage was conducted via a lightweight multiwire tether cable through an 82-channel slip-ring commutator to a digital data acquisition system with 64 programmable amplifiers (Neuralynx). Unit activity was amplified 3,000–5,000 times and band-pass–filtered from 600 to 6,000 Hz. Spike waveforms were time-stamped and digitized at 32 kHz. Spike thresholds set by the experimenter ranged from 50 to 90 µV for individual tetrodes. EEG signals were amplified by a factor of 1,000 and recorded continuously between 0 and 475 Hz. The animal’s movement was tracked with light-emitting diodes at a sampling rate of 50 Hz.
Behavioral Procedures.
While tetrode positions were optimized rats were trained to forage for chocolate sprinkles in the familiar room for up to 1 h each day in a black square box (100 × 100 × 50 cm) with a white cue card on the north wall of the box. During the test stage of the experiment, with 10 novel rooms, a different recording box was used in each room (all boxes 100 × 100 × 50 cm except for one whose dimensions were 100 × 100 × 80 cm). The position and the size of the cue card varied across boxes. The sequence of novel rooms did not follow a spatial pattern (Fig. 1 and Fig. S1). Each day comprised about 8 h of continuous recording. The rats were given access to a water bottle between trials to prevent dehydration and to encourage further foraging.
A mobile recording system on wheels was put together to allow continuous recording of spike activity across trials in different rooms (Fig. 1B). The recording cable was connected to a commutator and a tracking camera on a mobile crane. When stable firing responses and potential CA3 place cells had been identified the animal rested for 1 d. The experiment started on day 1 by exposing the animals first to the familiar environment then to five novel rooms, and then again to the familiar room (Fig. 1A). On day 2 they were tested in five other novel rooms, in addition to the familiar room, which again was presented at the beginning and end of the sequence. On each day the rats were introduced twice to one of the five novel rooms (N1 on day 1; N6 on day 2) to determine whether firing patterns were maintained. In each room activity was recorded while the animal foraged food crumbles in a 100- × 100-cm square black box for two consecutive blocks of 15 min. Data were also recorded during rest on the pedestal for 15 min before the first trial and for 5 min after the second trial in each room. After the second rest period the experimenter transported the mobile recording system and the rat to the next room while recording was paused. The rat was not disconnected from the headstage at any time during the day of the experiment, but the tether was disconnected from the commutator to ease transportation between the rooms.
Data Analysis.
Spikes were sorted offline using SpikeSort 3D (Neuralynx) mainly in 2D projections using waveform energies and amplitudes to separate out putative place cells from noise. Putative interneurons were separated from putative place cells based on differences in average firing rate and spike width. Interneurons were excluded from further analysis. Owing to the continuous nature of the recording, all running trials and rest trials from five novel rooms and the familiar room were clustered together. Rate maps were constructed from well-isolated cells by summing the total number of spikes that occurred in a location bin (5 × 5 cm) divided by the time the animal spent in that bin. The rate map was smoothed with a Gaussian kernel centered on each bin. All of the data were speed-filtered; periods with running speeds below 5 cm/s were excluded.
A place field was defined as an area of nine or more (5 × 5 cm) adjacent bins with firing rates exceeding 20% of the peak firing rate of the rate map. Spatial information content in bits per spike was calculated as
where λi is the mean firing rate in the i-th bin, λ is the overall mean firing rate, and pi is the probability of the animal’s being in the i-th bin, as described previously (31, 32). Spatial coherence was estimated as the first-order spatial autocorrelation of the unsmoothed place field map, that is, the mean correlation between firing rate of each bin and the averaged firing rate in the eight adjacent bins (33). Spatial correlation was calculated by binning maps in a linearized fashion before cell pairs above threshold were correlated across rooms or between trials from the same room. Filtered or unvisited bins were set to NaN values, which were removed from both linearized maps before the correlation. Spatial stability was defined as the spatial correlation between the first and second day of testing in the familiar room, or between dispersed tests in the same room (N1 and N6). To check whether the maximal correlation increases as a function of number of rooms, one map was kept constant while the other map was rotated in steps of 90° because place fields tend to orient themselves according to the walls of the box (34). The mean of the maximum spatial correlation across rooms was reported.
Fitting with Binomials.
A specific hypothesis H about the distribution P(λ) across cells of the probability to be active in any one room leads to a model for the distribution of the number of cells active in n rooms. The model q(n) is given, if the representation of each room is independent of that of others, by the convolution of P(λ) with the binomial distribution, that is,
To assess the relative plausibility of two “nested” hypotheses H1 and H2, where H1 is simpler and can be obtained by imposing constraints on the free parameters of H2, one can use Wilks’ (1938) theorem (35), which states that the difference of their log-likelihoods, multiplied by 2, has an approximate χ2 distribution, with degrees of freedom the number of constraints imposed. In our case, H2 can be taken to be the true H generating the empirically observed distribution p(n), which has n = 11 “free parameters.”
The likelihood that the observed numbers of units Cp(n) for each of the N + 1 values of n have been produced by a model with degrees of freedom, expressing hypothesis H, can be roughly estimated as the product over n of the Poisson factor for the probability of Cp(n) events, given expectation Cq(n):
once one disregards the constraint that Σn p(n) = 1, and also that the values of n are ordered rather than nominal categories, so the probability of Cp(n) events would in fact be influenced by neighboring expectations, e.g., Cq(n − 1), Cq(n + 1).
The log likelihood is then simply a sum over bins
Comparing a model H to H, which reproduces the data exactly, requires computing (twice) the difference:
that is, 2C times the Kullback–Leibler divergence KL between the p and q distributions. The divergence is a positive number, approximately χ2-distributed with 11 df.
Note that P(λ) extends from 0 to 1, unlike the log-normal distribution of firing rates and the gamma distribution of place field propensities of related studies (20, 21), and that to serve as a model it should have few free parameters. If written as a sum of discrete components, for example,
with six components it has already df = 11 free parameters and it should reproduce the data exactly.
When trying a model P(λ) with fewer discrete components, we found a marginally acceptable fit with three components (df = 5) for the overall data, which however did not fit adequately all individual animals. A P(λ) with only two components would not fit the overall data. A continuous P(λ) requires a minimum of five free parameters to effectively reproduce those of the three-component discrete P(λ), the position and height of three peaks; and the additional parameters describing the width of the continuous function around each peak therefore do not further improve the fit.
Overlap, Population Vector Similarity, and Shuffling.
To compute overlaps between representations, the mean activation of each cell in any particular room was expressed as a ratio of its mean firing rate to the maximal mean rate of that cell across all rooms. This was considered as the component of a mean activation vector, of length the total number of cells recorded in that session. The overlap was then calculated as the normalized dot product between the activation vectors in two rooms (i.e., the sum of the products of corresponding components divided by the number of components).
To compute location-specific population vectors instead, the activation of each cell in any one location (one of the 20 × 20 spatial bins) of any particular room was expressed as a ratio of its firing rate to the maximal rate of that cell across rooms and locations. A full population representation of each room by the recorded neurons was then expressed by a 3D matrix in which one index indicates the neuron and the two others the spatial location (5 × 5 cm bins) (6). Each matrix element was in the range from 0 to 1. The similarity between population vectors was calculated as the normalized dot product of the matrices (i.e., the average across locations and neurons of the product of the corresponding matrix elements). The distribution of similarity values was accumulated for the entire set of 7 × 55 = 385 within-animal pairs of both mean activation vectors and location-specific population vectors. The observed distribution was then compared with distributions obtained through three different shuffling procedures, one in which the rate maps of any individual cell were shuffled across rooms, a second in which rate maps in any individual room were shuffled across cells (either across all cells or across the cells of a predefined subset of either sparsely active or overactive cells), and the third one combining the two first procedures. Shuffling was always repeated 1,000 times. An activity threshold (e.g., of 0.10 Hz) was used to exclude cells that were not active in any of the rooms.
Similarity values were also computed, for each room pair, by rotating the map of one of the rooms in steps of 90° relative to the other map and keeping the largest similarity value among the four comparisons thus obtained. This rotation procedure was performed both for the observed data and the shuffled data.
Histology and Tetrode Location.
Rats were give an overdose of pentobarbital and perfused intracardially with saline (saline 0.9 sodium chloride) followed by 4% (vol/vol) formaldehyde. Brains were extracted and placed in formaldehyde for at least 1 wk before 30-µm frozen coronal sections of the hippocampal area were cut on a cryostat and stained with cresyl violet. Images were collected with a Zeiss Axoimager-Z1 microscope equipped with a digital camera. Tetrode positions were reconstructed and tetrode tip location determined based on the position of the hyperdrive on the animal’s head and by comparison with adjacent sections. Position of the tetrode tip along the proximal–distal axis of CA3 was determined by defining its position on a line through the cell layer on a coronal section (proximal end = 0; distal end = 1).
Supplementary Material
Acknowledgments
We thank A. M. Amundsgård, K. Haugen, E. Henriksen, K. Jenssen, E. Kråkvik, H. Waade, and V. Frolov for technical assistance. The work was supported by an Advanced Investigator Grant from the European Research Council (ENSEMBLE Grant 268598), the Kavli Foundation, the Centre of Excellence scheme of the Research Council of Norway (Centre for the Biology of Memory and Centre for Neural Computation), and the Charles University Research Fund PRVOUK P36.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1421056111/-/DCSupplemental.
References
- 1.Marr D. Simple memory: A theory for archicortex. Philos Trans R Soc Lond B Biol Sci. 1971;262(841):23–81. doi: 10.1098/rstb.1971.0078. [DOI] [PubMed] [Google Scholar]
- 2.McNaughton BL, Morris RG. Hippocampal synaptic enhancement and information storage within a distributed memory system. Trends Neurosci. 1987;10:408–415. [Google Scholar]
- 3.Treves A, Rolls ET. Computational analysis of the role of the hippocampus in memory. Hippocampus. 1994;4(3):374–391. doi: 10.1002/hipo.450040319. [DOI] [PubMed] [Google Scholar]
- 4.Leutgeb JK, Leutgeb S, Moser MB, Moser EI. Pattern separation in the dentate gyrus and CA3 of the hippocampus. Science. 2007;315(5814):961–966. doi: 10.1126/science.1135801. [DOI] [PubMed] [Google Scholar]
- 5.Treves A, Rolls ET. Computational constraints suggest the need for two distinct input systems to the hippocampal CA3 network. Hippocampus. 1992;2(2):189–199. doi: 10.1002/hipo.450020209. [DOI] [PubMed] [Google Scholar]
- 6.Leutgeb S, Leutgeb JK, Treves A, Moser MB, Moser EI. Distinct ensemble codes in hippocampal areas CA3 and CA1. Science. 2004;305(5688):1295–1298. doi: 10.1126/science.1100265. [DOI] [PubMed] [Google Scholar]
- 7.O’Keefe J, Dostrovsky J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971;34(1):171–175. doi: 10.1016/0006-8993(71)90358-1. [DOI] [PubMed] [Google Scholar]
- 8.O'Keefe J, Nadel L. The Hippocampus As a Cognitive Map. Oxford Univ Press; Oxford: 1978. [Google Scholar]
- 9.Wilson MA, McNaughton BL. Dynamics of the hippocampal ensemble code for space. Science. 1993;261(5124):1055–1058. doi: 10.1126/science.8351520. [DOI] [PubMed] [Google Scholar]
- 10.Muller RU, Kubie JL. The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. J Neurosci. 1987;7(7):1951–1968. doi: 10.1523/JNEUROSCI.07-07-01951.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bostock E, Muller RU, Kubie JL. Experience-dependent modifications of hippocampal place cell firing. Hippocampus. 1991;1(2):193–205. doi: 10.1002/hipo.450010207. [DOI] [PubMed] [Google Scholar]
- 12.Markus EJ, et al. Interactions between location and task affect the spatial and directional firing of hippocampal neurons. J Neurosci. 1995;15(11):7079–7094. doi: 10.1523/JNEUROSCI.15-11-07079.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Colgin LL, Moser EI, Moser MB. Understanding memory through hippocampal remapping. Trends Neurosci. 2008;31(9):469–477. doi: 10.1016/j.tins.2008.06.008. [DOI] [PubMed] [Google Scholar]
- 14.Battaglia FP, Treves A. Stable and rapid recurrent processing in realistic autoassociative memories. Neural Comput. 1998;10(2):431–450. doi: 10.1162/089976698300017827. [DOI] [PubMed] [Google Scholar]
- 15.Deguchi Y, Donato F, Galimberti I, Cabuy E, Caroni P. Temporally matched subpopulations of selectively interconnected principal neurons in the hippocampus. Nat Neurosci. 2011;14(4):495–504. doi: 10.1038/nn.2768. [DOI] [PubMed] [Google Scholar]
- 16.Xu HT, et al. Distinct lineage-dependent structural and functional organization of the hippocampus. Cell. 2014;157(7):1552–1564. doi: 10.1016/j.cell.2014.03.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dragoi G, Tonegawa S. Preplay of future place cell sequences by hippocampal cellular assemblies. Nature. 2011;469(7330):397–401. doi: 10.1038/nature09633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.McNaughton BL, et al. Deciphering the hippocampal polyglot: The hippocampus as a path integration system. J Exp Biol. 1996;199(Pt 1):173–185. doi: 10.1242/jeb.199.1.173. [DOI] [PubMed] [Google Scholar]
- 19.Samsonovich A, McNaughton BL. Path integration and cognitive mapping in a continuous attractor neural network model. J Neurosci. 1997;17(15):5900–5920. doi: 10.1523/JNEUROSCI.17-15-05900.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Buzsáki G, Mizuseki K. The log-dynamic brain: How skewed distributions affect network operations. Nat Rev Neurosci. 2014;15(4):264–278. doi: 10.1038/nrn3687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rich PD, Liaw HP, Lee AK. Place cells. Large environments reveal the statistical structure governing hippocampal representations. Science. 2014;345(6198):814–817. doi: 10.1126/science.1255635. [DOI] [PubMed] [Google Scholar]
- 22.Jezek K, Henriksen EJ, Treves A, Moser EI, Moser MB. Theta-paced flickering between place-cell maps in the hippocampus. Nature. 2011;478(7368):246–249. doi: 10.1038/nature10439. [DOI] [PubMed] [Google Scholar]
- 23.Wilson MA, McNaughton BL. Reactivation of hippocampal ensemble memories during sleep. Science. 1994;265(5172):676–679. doi: 10.1126/science.8036517. [DOI] [PubMed] [Google Scholar]
- 24.Claiborne BJ, Amaral DG, Cowan WM. A light and electron microscopic analysis of the mossy fibers of the rat dentate gyrus. J Comp Neurol. 1986;246(4):435–458. doi: 10.1002/cne.902460403. [DOI] [PubMed] [Google Scholar]
- 25.Leutgeb JK, et al. Progressive transformation of hippocampal neuronal representations in “morphed” environments. Neuron. 2005;48(2):345–358. doi: 10.1016/j.neuron.2005.09.007. [DOI] [PubMed] [Google Scholar]
- 26.Hayman RM, Chakraborty S, Anderson MI, Jeffery KJ. Context-specific acquisition of location discrimination by hippocampal place cells. Eur J Neurosci. 2003;18(10):2825–2834. doi: 10.1111/j.1460-9568.2003.03035.x. [DOI] [PubMed] [Google Scholar]
- 27.Wood ER, Dudchenko PA, Eichenbaum H. The global record of memory in hippocampal neuronal activity. Nature. 1999;397(6720):613–616. doi: 10.1038/17605. [DOI] [PubMed] [Google Scholar]
- 28.Singer AC, Karlsson MP, Nathe AR, Carr MF, Frank LM. Experience-dependent development of coordinated hippocampal spatial activity representing the similarity of related locations. J Neurosci. 2010;30(35):11586–11604. doi: 10.1523/JNEUROSCI.0926-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.McKenzie S, et al. Hippocampal representation of related and opposing memories develop within distinct, hierarchically organized neural schemas. Neuron. 2014;83(1):202–215. doi: 10.1016/j.neuron.2014.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McKenzie S, Robinson NT, Herrera L, Churchill JC, Eichenbaum H. Learning causes reorganization of neuronal firing patterns to represent related experiences within a hippocampal schema. J Neurosci. 2013;33(25):10243–10256. doi: 10.1523/JNEUROSCI.0879-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Skaggs WE, McNaughton BL, Wilson MA, Barnes CA. Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus. 1996;6(2):149–172. doi: 10.1002/(SICI)1098-1063(1996)6:2<149::AID-HIPO6>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 32.Henriksen EJ, et al. Spatial representation along the proximodistal axis of CA1. Neuron. 2010;68(1):127–137. doi: 10.1016/j.neuron.2010.08.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Muller RU, Kubie JL. The firing of hippocampal place cells predicts the future position of freely moving rats. J Neurosci. 1989;9(12):4101–4110. doi: 10.1523/JNEUROSCI.09-12-04101.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.O’Keefe J, Burgess N. Geometric determinants of the place fields of hippocampal neurons. Nature. 1996;381(6581):425–428. doi: 10.1038/381425a0. [DOI] [PubMed] [Google Scholar]
- 35.Wilks SS. Weighting systems for linear functions of correlated variables when there is no dependent variable. Psychometrica. 1938;(3):23–40. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.