van der Waals interactions at the nanoscale: The effects of nonlocality

Significance

The van der Waals interaction is a ubiquitous but subtle force between particles mediated by quantum fluctuations of charge. It is the most long-range force acting between particles and influences a range of phenomena such as surface adhesion, friction, and colloid stability. Calculations of the force between parallel surfaces >10 nm apart is a simple task, but when the geometry is more complex, e.g., a pair of nanospheres <5 nm apart, the task is more difficult. Furthermore a macroscopic description of the dielectric properties no longer suffices, and we must consider the diffuse nonlocal nature of the electron polarization cloud. In this paper, we propose a simple analytic treatment of the problem.

Abstract

Calculated using classical electromagnetism, the van der Waals force increases without limit as two surfaces approach. In reality, the force saturates because the electrons cannot respond to fields of very short wavelength: polarization charges are always smeared out to some degree and in consequence the response is nonlocal. Nonlocality also plays an important role in the optical spectrum and distribution of the modes but introduces complexity into calculations, hindering an analytical solution for interactions at the nanometer scale. Here, taking as an example the case of two touching nanospheres, we show for the first time, to our knowledge, that nonlocality in 3D plasmonic systems can be accurately analyzed using the transformation optics approach. The effects of nonlocality are found to dramatically weaken the field enhancement between the spheres and hence the van der Waals interaction and to modify the spectral shifts of plasmon modes.

The van der Waals force is an electromagnetic interaction between correlated fluctuating charges on two electrically neutral surfaces (1–4). As the surfaces approach more closely, the force increases as fluctuations of shorter and shorter length scale come into play, but ultimately the force will saturate when the surfaces are so close that the even shortest wavelength charge fluctuations are included. It is this saturation with which we are concerned in this paper and to treat it, we need to go beyond the conventional description of a solid by a permittivity, $\epsilon \left(\omega \right)$, that depends only on the frequency, $\omega$. Here we recognize that the response of a solid depends on the length scale of the fluctuations and introduce a formalism using a generalized nonlocal permittivity, $\epsilon \left(\omega ,\mathbf{k}\right)$ (5–13), that also depends on the wave vector, $\mathbf{k}$, and hence takes into account the saturation. Neglect of nonlocality leads to an unphysical diverging van der Waals force at short distances. We apply the technique of transformation optics (14–16) to solve the difficult problem of including nonlocal effects when two nanoscale bodies interact and illustrate our theory with calculations for two closely spaced nanospheres.

Ultimately at a few tenths of a nanometer, just before the surfaces touch, direct contact of the charges will come into play through electron tunneling (17–25); in other words, chemical bonding will dominate the final approach. Here we are not concerned with chemical bonding, which is extensively treated elsewhere in the literature.

The van der Waals force is weaker than chemical bonding effects, but plays an important role in a broad range of areas, such as surface and colloidal science, nanoelectromechanical systems, and nanotechnology (2, 3, 26–28). In the classical electrodynamics picture where nonlocality is neglected, the fluctuating surface charges are located precisely on the surface and these infinitely compressed charges result in the unphysically divergent van der Waals force (1, 29). In a more realistic framework, considering the inherent quantum nature of electrons, the surface charges are intrinsically smeared across the boundary in a subnanometer layer (7, 20–22), which dramatically alters the van der Waals energy in the small gap limit (30–33). Due to the complexity introduced by nonlocality, its influence on the van der Waals force in 3D geometries has never been described appropriately. Esquivel-Sirvent and Schatz investigated the influence of nonlocality on the van der Waals force between two spherical gold nanoparticles (32). However, they used Hamaker's method (1), which has been widely recognized as an inaccurate method for such nanoparticle systems where the size and the separation are comparable.

We developed a theoretical approach to treat nonlocal problems, which is as accurate as other semiclassical nonlocal methods (such as the hydrodynamic model) but much more efficient in terms of both simulation time and memory consumption when implemented in numerical simulations (34). In this paper, we show that 3D nonlocal systems can be studied analytically by combining our nonlocal model with the technique of transformation optics.

Results and Discussion

We start by considering a dimer of nanospheres, a prototypical plasmonic system. Other structures such as a sharp metal tip (35–37) and two overlapping spheres (38–40) can be studied in a similar manner. Widely separated nanoparticles (of sizes larger than 10 nm) can be treated by neglecting nonlocality, and transformation optics provides an elegant analytical solution for the electromagnetic (EM) field (41). To calculate the van der Waals force, an analytic form of the permittivity is needed: metals can be described by a local permittivity, ${\epsilon }_{\text{M}}\left(\omega \right)={\epsilon }_b-{\omega }_p^2/\left[\omega \left(\omega +i\gamma \right)\right]$, where ${\epsilon }_b$ is usually expressed as a summation of several Lorentz models (see SI Text for details). As the particle separation is reduced to a nanometric scale, the nonlocal smearing of metallic electrons plays an important role, and the implementation of a spatially dispersive metal permittivity for longitudinal EM fields, ${\epsilon }_{\text{M}}\left(\omega ,\mathbf{k}\right)={\epsilon }_b-{\omega }_p^2/\left[\omega \left(\omega +i\gamma \right)-{\beta }^2{\left|\mathbf{k}\right|}^2\right]$, is required. The $\beta$ factor describes the degree of nonlocality and is proportional to the Fermi velocity.

Our recently proposed nonlocal model simplifies the theoretical treatment of this problem by avoiding the implementation of a k-dependent permittivity and replacing the spatial nonlocality with a thin dielectric layer decorating the metal surface (34). This effective local treatment of a nonlocal problem has been shown to the highly accurate. Using this model, the dimer of nanospheres can be represented by a pair of core-shell nanoparticles, as shown in Fig. 1A. The dielectric constant of the core is given by the normal metal permittivity ${\epsilon }_{\text{C}}={\epsilon }_{\text{M}}\left(\omega \right)$, whereas the dielectric function ${\epsilon }_{\text{S}}$ of the shell is approximately expressed by

$$\frac{{\epsilon }_{\text{S}}}{\mathrm{\Delta }{d}^{\prime }}=\frac{{\epsilon }_{\text{M}}\left(\omega \right)+1}{{\epsilon }_{\text{M}}\left(\omega \right){\lambda }_{\text{L}}\left(\omega \right)},$$ [1]

where $\mathrm{\Delta }{d}^{\prime }$ is the thickness of the shell; and ${\lambda }_{\text{L}}\left(\omega \right)$ denotes the penetration depth of the surface charges. It can be calculated as (5)

$${\lambda }_{\text{L}}=\sqrt{\frac{3}{5}}\frac{v_{\text{F}}}{\sqrt{{\omega }_p^2/{\epsilon }_{\text{M}}\left(\omega \to \infty \right)-\omega \left(\omega +i\gamma \right)}},$$ [2]

where $v_{\text{F}}$ and ${\omega }_p$ represent the Fermi velocity and the bulk plasma frequency of the metal, respectively. Eq. 1 only defines the ratio of the permittivity to the thickness of the dielectric shell. It indicates that we have a freedom to choose various combinations of ${\epsilon }_{\text{S}}$ and $\mathrm{\Delta }{d}^{\prime }$, corresponding to different configurations of the system. Here, two approaches are considered.

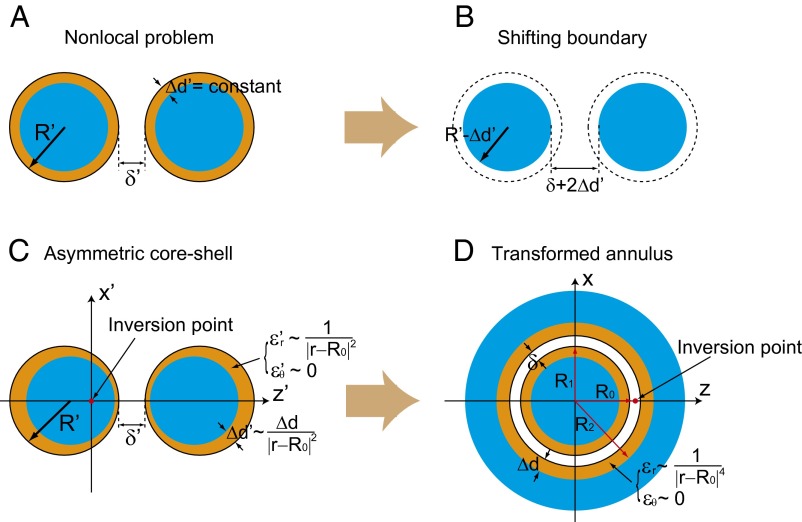
Fig. 1.

The schematic of the problem. A dimer of separated nanospheres where the surface charge smearing is described by an effective cover layer of (A) a constant thickness $\mathrm{\Delta }{d}^{\prime }$, (B) a constant permittivity, ${\epsilon }_{\text{S}}=1$ (shifting the metal boundary by $\mathrm{\Delta }{d}^{\prime }$), or (C) a variable thickness $\mathrm{\Delta }{d}^{\prime }$ and spatially dependent permittivity. Under an inverse transformation, the asymmetric core-shell structure in C can be mapped to a dielectric annulus (shown in D) defined by a dielectric-coated metal sphere and a dielectric-coated hollow sphere.

Shifting the Metal Boundary.

The simplest interpretation of the nonlocal effects is to describe the smearing of the induced polarization charge densities across the boundary as a shifting of the metal boundary (42). The amount of boundary shifting can be obtained by letting ${\epsilon }_{\text{S}}=1$ in Eq. 1;

$$\mathrm{\Delta }{d}^{\prime }\left(\omega \right)=\left[\frac{{\epsilon }_{\text{M}}\left(\omega \right)}{{\epsilon }_{\text{M}}\left(\omega \right)+1}\right]{\lambda }_{\text{L}}\left(\omega \right),$$ [3]

which is frequency dependent. Applying this shifting boundary approximation to the nanosphere dimer gives an effective geometry of spheres with a slightly increased separation and reduced radii of the two spheres, as shown in Fig. 1B. This effective local system can be analytically investigated using the transformation optics approach (41, 43).

Asymmetric Shell.

The shifting boundary approach is valid only at low frequencies, where $\mathrm{\Delta }{d}^{\prime }$ is much smaller than the penetration depth of surface plasmons (34). Keeping $\mathrm{\Delta }{d}^{\prime }$ to a sufficiently small value gives a more rigorous approach, which can also describe the optical responses of the structure in the higher frequency range. However, a dimer of core-shell nanoparticles with uniform shell thicknesses is difficult to study analytically. Alternatively, we can assume a nonuniform $\mathrm{\Delta }{d}^{\prime }\left({\mathbf{r}}^{\mathbf{\prime }}\right)$, which is proportional to ${r^{\prime }}^2$ ($r^{\mathbf{\prime }}$ is the distance to the origin in Fig. 1C). An inverse transformation, ${\mathbf{r}}^{\mathbf{\prime }}=R_{\text{T}}^2/\left(\mathbf{r}-{\mathbf{R}}_0\right)$, maps the asymmetric core-shell dimer structure in Fig. 1C to a concentric annulus as shown by Fig. 1D. Transformation optics theory requires the permittivity of the materials in the annulus geometry as

$${\epsilon }_{\text{B}}\left(\mathbf{r}\right)={\epsilon }_{\text{M}}{R}_{\text{T}}^2/{\left|\mathbf{r}-{\mathbf{R}}_0\right|}^2,$$ [4]

in the two blue regions

$${\epsilon }_{\text{W}}\left(\mathbf{r}\right)=R_{\text{T}}^2/{\left|\mathbf{r}-{\mathbf{R}}_0\right|}^2,$$ [5]

in the white region, and

$${\epsilon }_{\text{Y}}\left(\mathbf{r}\right)=\frac{{\epsilon }_{\text{M}}\mathrm{\Delta }d}{\left({\epsilon }_{\text{M}}-1\right){\lambda }_{\text{L}}}{\left(\frac{R_{\text{T}}}{\left|\mathbf{r}-{\mathbf{R}}_0\right|}\right)}^4,$$ [6]

in the yellow regions.

We can solve for the electrostatic potential $\varphi \left(r\right)$ in this annulus geometry by expanding it in spherical harmonics and solving a penta-diagonal scattering matrix. This procedure will in turn gives $\varphi \left(r^{\prime }\right)$ in the asymmetric core-shell dimer in Fig. 1C. Detailed derivations are provided in Materials and Methods.

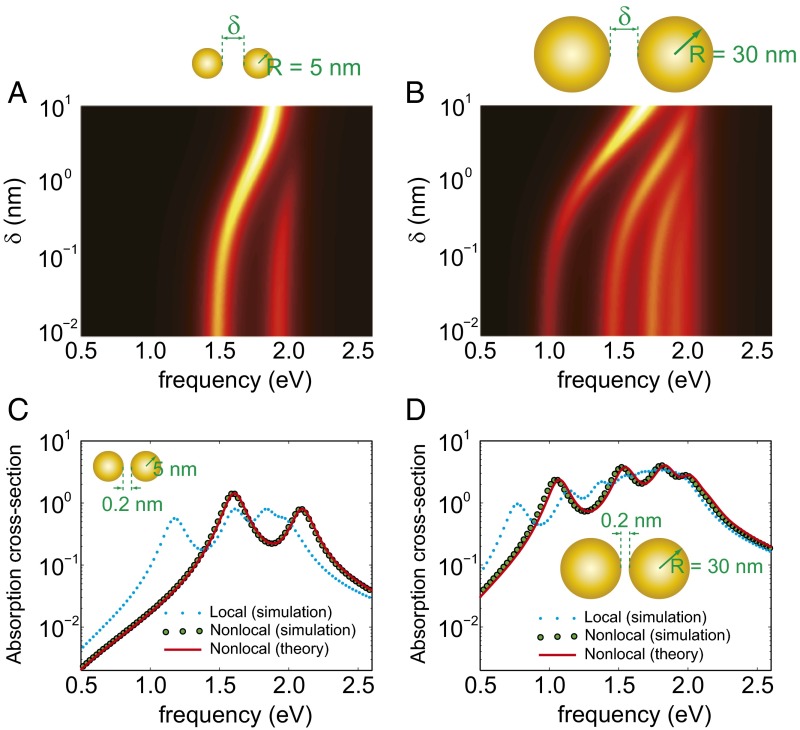
To verify our approach, we first apply our methodologies to calculating the optical spectra of two spherical dimers. Fig. 2 A and B displays the absorption efficiency (defined as the absorption cross section over the dimer physical size) contour plot for gold nanosphere dimers of 5 and 30 nm radii vs. the frequency and the gap size. As the gap narrows, the resonance shows a red shift, which saturates at the gap size $\delta \approx 0.2$ nm irrespective of the size of nanoparticles. However, the dimer of nanospheres with larger radius shows a more pronounced red shift (larger shifting frequency range) and therefore a broader plasmonic resonance band at small separations where nonlocal effects dominate. A similar result has been observed in the 2D case of nanowire dimer (8, 10). Fig. 2 C and D shows the numerical simulation results (using COMSOL Multiphysics) for the light absorption by spherical dimers of different sizes with (green dots) and without (cyan dashed curves) inclusion of the nonlocal effects. The red solid curves correspond to the absorption spectrums obtained with our analytical calculations, showing excellent agreement with the nonlocal numerical simulations.

Fig. 2.

The absorption spectrum for a dimer of spherical particles. The contour plot of the absorption cross section vs. the frequency and the separation for a pair of gold nanospheres with equal radii of (A) 5 and (B) 30 nm. Comparison of our analytical calculations with local and nonlocal numerical simulations for two closely separated ($\delta =0.2$ nm) gold spheres with equal radii of (C) 5 and (D) 30 nm.

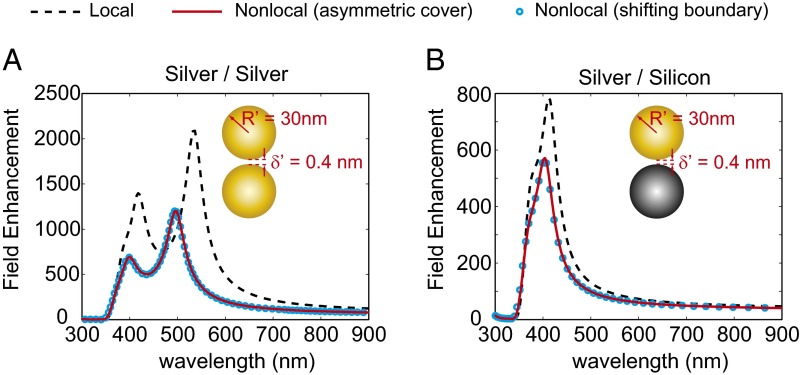
Recent experiments have shown that nonlocal effects set an upper limit for maximum field enhancement achievable with plasmonic nanoparticles (44, 45). Here, we investigate the field enhancement spectra at the center of the gap between two nanospheres. The separation between nanoparticles is 0.4 nm, above the quantum tunneling regime (17, 18). We consider first a dimer of two identical silver spheres ($R=30$ nm; the Johnson Christy data for silver are used) (46) and compare the classical calculation (black dashed curve) with our theoretical nonlocal calculations. Both the nonuniform coating assumption (red solid curve) and shifting boundary assumption (blue dots) are considered. In the nonlocal description, the spreading of the charge effectively smoothes the boundary at the gap, resulting in a reduction of the field enhancement with the peaks shifting toward smaller wavelengths compared with the local description. However, as depicted in Fig. 3A, considerable field enhancement can still be achieved with a maximum value larger than 1,000. The shifting-boundary calculation predicts the resonance shift and field enhancement in good agreement with the exact asymmetric-shell approach at frequencies below the bulk plasma frequency.

Fig. 3.

The field enhancements at the center of the gap between two spherical particles (A) between two silver spheres of equal radius 30 nm, separated by a 0.4-nm gap and (B) between a silver and a silicon spheres of equal radius 30 nm, separated by a 0.4-nm gap.

We next replace one silver sphere with a silicon sphere of the equal size and keep the separation between particles at 0.4 nm. The Palik data for silicon (47) are used. We neglect nonlocality in the silicon. At such a small separation, the fundamental mode in the silicon sphere hybridizes with the surface plasmon polaritons in the silver surface, allowing for a subwavelength confinement and large field enhancement. In this metal-dielectric hybrid system, more energy resides in the dielectric sphere, resulting in less energy confinement at the gap and smaller field enhancement compared with the silver sphere dimer system. However, as shown in Fig. 3B, the maximum field enhancement can still reach up to more than 500, and the frequency of the field enhancement peak is less sensitive to the nonlocal effect. Results for the sphere-plane configuration given in SI Text also confirm that extremely large field enhancements are possible even in the realistic nonlocal case.

It is worth pointing out that the field enhancement in the junction of two spheres also gives an indirect measurement of the van de Waals force. On one hand, the van de Waals force originates from the zero point energy of the modes, whose change is measured by the resonance shifts. On the other hand, the field enhancement is directly related to the coupling between the two particles, which is also measured by the amount of resonance shifts of the modes (44). Therefore, the reduction of the field enhancement in the nonlocal case indicates that the change of zero point energy, and hence the van de Waals force, is smaller than those in the local case.

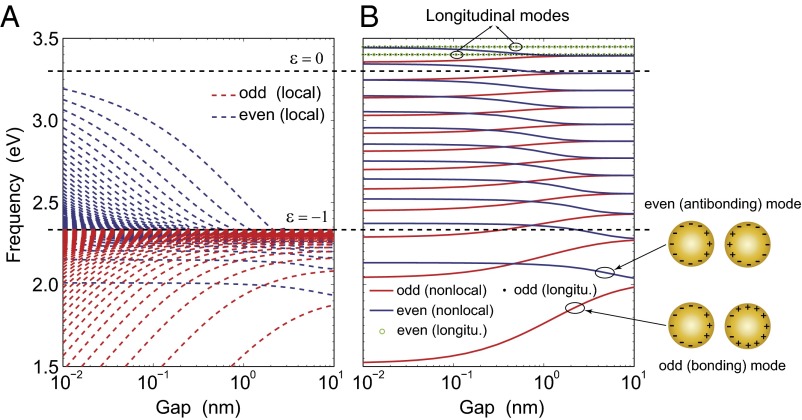
To illustrate this point, we first plot in Fig. 4 the shifts of resonances in terms of the gap size. The plasmonic system consists of two identical gold spheres of 5 nm radius. Both local (Fig. 4A) and nonlocal (Fig. 4B) cases are considered. Different from the study in Figs. 2 and 3, where we apply the plane wave incidence to excite only the bright modes, here we investigate all of the plasmonic modes (including the dark ones) by solving the characteristic equation (41, 43). For a simple test, the dielectric constant of gold is described by the Drude model, ${\epsilon }_{\text{M}}\left(\omega \right)=1-{\omega }_p^2/{\left(\omega +i\gamma \right)}^2$, with a bulk plasma frequency ${\omega }_p=3.3 \text{eV}$ and a damping frequency $\gamma =0$. The nonlocality is described by the parameter $\beta =0.0036c$. Here the loss is ignored to give a more critical test of our theory. In both local and nonlocal calculations, the odd modes tend to redshift and the even modes show a blue shift as the two spheres approach (see the inset of Fig. 4 for the definition of the odd and even modes). However, different from the local picture, all of the frequency shifts in the nonlocal case saturate at certain frequencies for small separations. As pointed out before, the van der Waals force results from the change of zero point motion of these modes, and saturation of the shifts indicates that the van der Waals force would be saturated in the touching limit.

Fig. 4.

Plots of plasmon resonance modes supported by a pair of 5-nm radius gold spheres vs. the separation. The permittivity of gold is ${\epsilon }_{\text{gold}}=1-{3.3}^2/{\omega }^2$. (A) In the local description, as the gap size decreases, the odd modes (red dashed lines) tend to zero frequency and the even modes (blue dashed lines) fall into two groups: one group of modes tends to the bulk plasma frequency ${\omega }_p=3.3\hspace{0.17em}\text{eV}$ ($\epsilon =0$) and another to discretized values below the surface plasmon frequency ${\omega }_{sp}=2.33\hspace{0.17em}\text{eV}$ ($\epsilon =-1$). (B) In the nonlocal description with $\beta =0.0036c$, only one group of even modes is observed. Moreover, the longitudinal plasmon modes (black dots for odd modes and green circles for even modes) emerge above ${\omega }_p$, and they remain nearly constant for various particle separations. The inset on the right plots the surface charge distributions for the odd (bonding) and even (antibonding) dipolar modes (49).

Nonlocality also results in the odd modes shifting above the surface plasmon frequency toward the bulk plasmon frequency ${\omega }_p$. It is worth noting that the bulk longitudinal plasmon modes (black dots/green circles in Fig. 4B) also emerge in the nonlocal case. However, the shifts of these modes are considerably smaller than the shifts of the surface modes. Therefore, the longitudinal plasmon modes have relatively small contribution to the van de Waals force.

To study the van de Waals interaction quantitatively, we fit the experimental data for gold using one Drude and ten Lorentz terms

$$\epsilon \left(\omega \right)=1-\underset{\text{free electrons}}{\underbrace{\frac{{\omega }_0^2}{\omega \left(\omega +i{\gamma }_0\right)}}}-\underset{\text{core electrons}}{\underbrace{{\displaystyle \sum _{j=1}^{10}\frac{f_j{\omega }_j^2}{{\omega }^2-{\omega }_j^2+i{\gamma }_j\omega }}}}.$$ [7]

Generally speaking, both free electrons and core electrons contribute to the dielectric response of metal. The Drude term in Eq. 7 corresponds to the free electrons, which show a divergent polarizability at the zero frequency (48). The core electrons, on the other hand, are bonded by the nuclei. They exhibit the strongest responses at finite resonance frequencies, and their contribution can be approximately described by Lorentizians. The fitting parameters in Eq. 7 are given in SI Text.

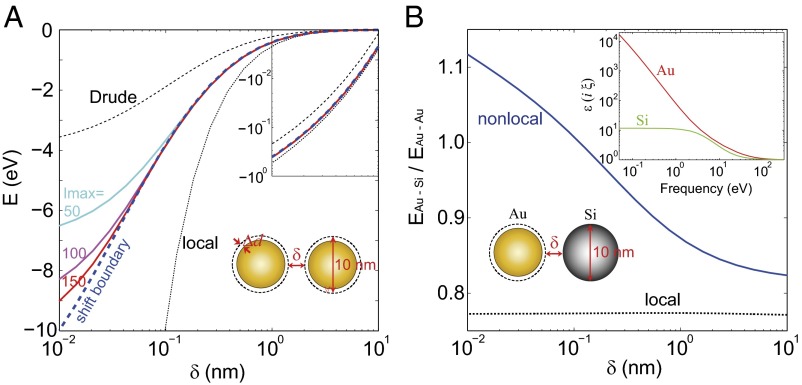
Using the aforementioned shifting boundary method, the van der Waals energy can be directly calculated within the local picture with an effective separation $\delta +2\mathrm{\Delta }d$ and an effective diameter $D-2\mathrm{\Delta }d$, as shown by the inset sketch in Fig. 5A. Using our previous procedure in (43), the van der Waals energy, taking into account the nonlocal effect, can easily be obtained. It is shown by the blue dashed line in Fig. 5A. Although the calculation in the local picture is exact, the shifting boundary approach itself is intrinsically an approximate procedure. To check its accuracy, we used the multipole expansion method (50) (see Materials and Methods for details). In the multipole expansion calculation, the nonlocal effect is exactly considered as long as enough terms in the series are included. The results become more accurate if more terms are used. As shown in Fig. 5A, we truncated the series at $\mathit{l=}{\mathit{l}}_{\max }-\left|m\right|$ for each $m$($\left|m\right|\le {\mathit{l}}_{\max }$), where ${\mathit{l}}_{\max }=50$ (cyan), $100$ (magenta), and $150$ (red). We found that the multipole expansion results converge to the shifting boundary one when increasing the truncating number ${\mathit{l}}_{\max }$. This phenomenon indicates that the shifting boundary method converges more rapidly than the multipole expansion method. It is also considerably more rapidly calculated.

Fig. 5.

van der Waals energy between two 10-nm-diameter nanospheres as a function of the separation. (A) Between two gold nanoparticles. For the blue dashed line, the nonlocal effect is considered by using the shifting boundary method as shown by the inset sketch, where the separation becomes $\delta +2\mathrm{\Delta }d$ and the diameter of each sphere decreases to $D-2\mathrm{\Delta }d$. For the solid lines, ${\mathit{l}}_{\max }=50$ (cyan), $100$ (magenta), and $150$ (red), the nonlocal van der Waals energies are calculated using the multipole expansion method, truncating the series at $\mathit{l=}{\mathit{l}}_{\max }-\left|m\right|$ for each $m$. The black dotted line shows the van der Waals energy calculated neglecting the nonlocal effect. The energy considering the nonlocal effect but neglecting the Lorentz terms in the permittivity is shown by the short dashed line. (Inset) Log-log plot in the separation range between 1 and 10 nm. (B) Between a gold and a silicon nanoparticle, normalized to that between two gold nanoparticles of the same size. Solid and dotted lines are nonlocal and local results, respectively. (Inset) Permittivities of gold and silicon at imaginary frequencies, fitted from the experimental data (SI Text).

For comparison, the van der Waals energy calculated neglecting the nonlocal effect is also shown in Fig. 5A by the black dotted line. It diverges as $-1/d$ in the small gap limit. However, the nonlocal results are eventually saturated at the touching limit. The magnitude of the nonlocal results is thus much smaller than the local one at subnanometer separations. We also study the van der Waals energy considering the nonlocal effect but neglecting the Lorentz terms (keeping the Drude term only) in the fitted permittivity formula. As shown by the black short dashed line, the magnitude of the van der Waals energy calculated neglecting the Lorentz terms is much smaller than the realistic nonlocal one. This result indicates that the core electrons make a significant contribution to the van der Waals forces at such a scale.

In Fig. 5B, the same method is used to study the van der Waals energy between gold and silicon nanospheres. The silicon as a dielectric is described in the local picture. Because the permittivity of silicon at imaginary frequencies is smaller than that of gold in the whole spectrum range (Fig. 5B, Inset), the van der Waals energy between gold and silicon nanospheres in the local picture is smaller than that between two gold spheres, as shown by the black dotted line.

In summary, we presented an analytical approach based on transformation optics to study the nonlocal effects in 3D plasmonic structures. As an example, nanosphere dimers with various separations are considered, and solutions for the optical spectrum, distribution of the modes, and van de Waals energy have been obtained. Our methodology not only makes feasible the analytical investigation of 3D nonlocal problems but also sheds insight into the understanding of nonlocal effects in plasmonic nanostructures.

Methods

Solution to the Concentric Annulus in Fig. 1D.

The core-shell structure in the physical space in Fig. 1C has an inhomogeneous thickness, which acquires an r-dependence

$$\mathrm{\Delta }{d^{\prime }}_{1\left(2\right)}=\frac{R_{\text{T}}^2}{{\left|{\mathbf{R}}_{1\left(2\right)}-{\mathbf{R}}_0\right|}^2}\mathrm{\Delta }d.$$ [8]

Then, the tangential and normal permittivity components of the dielectric material can be obtained as

$${{\epsilon }^{\prime }}_{\theta ,\phi }=\text{0},\hspace{0.17em}{{\epsilon }^{\prime }}_r^{1\left(2\right)}=\frac{{\epsilon }_{\text{b}}{\epsilon }_{\text{M}}{q}_{\text{L}}{i^{\prime }}_1\left(q_{\text{L}}{R^{\prime }}_{1\left(2\right)}\right)}{\left({\epsilon }_{\text{M}}-{\epsilon }_{\text{b}}\right)i_1\left(q_{\text{L}}{R^{\prime }}_{1\left(2\right)}\right)}\mathrm{\Delta }{d^{\prime }}_{1\left(2\right)}=C_{1\left(2\right)}\frac{\mathrm{\Delta }d}{{\left|{\mathbf{R}}_{1\left(2\right)}-{\mathbf{R}}_0\right|}^2},$$ [9]

where we introduced

$$C_{1\left(2\right)}=\frac{{\epsilon }_{\text{b}}{\epsilon }_{\text{M}}{q}_{\text{L}}{R}_{\text{T}}^2{i^{\prime }}_1\left(q_{\text{L}}{R^{\prime }}_{1\left(2\right)}\right)}{\left({\epsilon }_{\text{M}}-{\epsilon }_{\text{b}}\right)i_1\left(q_{\text{L}}{R^{\prime }}_{1\left(2\right)}\right)},$$ [10]

and the longitudinal plasmon normal wave vector $q_{\text{L}}=\sqrt{{\omega }_p^2/{\epsilon }_b-\omega \left(\omega +i\gamma \right)}/\beta$. $i_l(·)$ and ${i^{\prime }}_l(·)$ are the modified spherical Bessel function and its derivative. In the transformed annulus frame, the permittivity of virtual dielectric material can be calculated as

$${\epsilon }_{\theta ,\phi }=\text{0},\hspace{0.17em}{\epsilon }_r^{1\left(2\right)}=\frac{R_{\text{T}}^2}{{\left|{\mathbf{R}}_{1\left(2\right)}-{\mathbf{R}}_0\right|}^2}{{\epsilon }^{\prime }}_r^{1\left(2\right)}=C_{1\left(2\right)}\frac{R_{\text{T}}^2\mathrm{\Delta }d}{{\left|{\mathbf{R}}_{1\left(2\right)}-{\mathbf{R}}_0\right|}^4}.$$ [11]

The electrostatic potential in an anisotropic medium characterized by Eq. 10 must satisfy the following partial differential equation

$$\nabla \left(\mathbf{\epsilon }·\nabla \varphi \right)=0\Rightarrow \frac{1}{r^2}\frac{\partial }{\partial r}\left(\frac{r^2}{{\left|{\mathbf{R}}_{1\left(2\right)}-{\mathbf{R}}_0\right|}^4}\frac{\partial }{\partial r}\varphi \right)=0.$$ [12]

The general solution to Eq. 12 can be found as

$$\varphi =-b_1\left(\theta ,\phi \right)\left[{\left(\frac{R_{1\left(2\right)}^2}{R_0^2}+1\right)}^2-\frac{4R_{1\left(2\right)}}{R_0}\left(\frac{R_{1\left(2\right)}^2}{R_0^2}+1\right)\cos \theta +\frac{4R_{1\left(2\right)}^2{\cos }^2\theta }{R_0^2}\right]\frac{R_0}{r}+b_2\left(\theta ,\phi \right).$$ [13]

For the spherical dimer problem, we can write the electrostatic potential in the anisotropic dielectric region as

$$\begin{array}{l}\varphi ={\displaystyle \sum _{lm}\left\{-b_{lm}^{+}\left[\begin{array}{l}{\left(\frac{R_{1\left(2\right)}^2}{R_0^2}+1\right)}^2+\frac{4R_{1\left(2\right)}^2}{R_0^2}{\cos }^2\theta \\ -\frac{4R_{1\left(2\right)}}{R_0}\left(\frac{R_{1\left(2\right)}^2}{R_0^2}+1\right)\cos \theta \end{array}\right]\frac{R_0}{r}+b_{lm}^{-}\right\}\left|{\mathbf{R}}_{1\left(2\right)}-{\mathbf{R}}_0\right|Y_{lm}\left(\theta ,\phi \right)}\\ ={\displaystyle \sum _{lm}\frac{R_{1\left(2\right)}^2}{R_{0}r}\left\{\begin{array}{l}-\left[{\left(R_{1\left(2\right)}/R_0+R_0/R_{1\left(2\right)}\right)}^2+4\left(A_l^{m2}+A_{l+1}^{m2}\right)\right]b_{lm}^{+}\\ +4\left(R_{1\left(2\right)}/R_0+R_0/R_{1\left(2\right)}\right)\left(b_{l+1m}^{+}{A}_{l+1}^m+b_{l-1m}^{+}{A}_l^m\right)\\ -4\left(b_{l+2m}^{+}{A}_{l+2}^m{A}_{l+1}^m+b_{l-2m}^{+}{A}_{l-1}^m{A}_l^m\right)+b_{lm}^{-}{R}_{0}r/R_{1\left(2\right)}^2\end{array}\right\}\left|{\mathbf{R}}_{1\left(2\right)}-{\mathbf{R}}_0\right|Y_{lm}\left(\theta ,\phi \right)},\end{array}$$ [14]

where we introduced $A_l^m=\{\begin{array}{c}\sqrt{\left(l^2-m^2\right)/\left(4l^2-1\right)} if \left|m\right|<l,\\ \mathrm{ 0} if \left|m\right|\ge l,\end{array}$ and $\left|{\mathbf{R}}_{1\left(2\right)}-{\mathbf{R}}_0\right|=\sqrt{R_{1\left(2\right)}^2+R_0^2-2R_{1\left(2\right)}{R}_0\cos \theta }.$

Matching the boundary conditions (see SI Text for details), we can see that the presence of spatial nonlocality results in penta-diagonal matrices compared with the tridiagonal matrices (41) in the local case.

Multipole Expansion Method.

The total van der Waals energy between two spheres can be calculated in terms of the reflection amplitude of each sphere, cooperating with translation matrices that transfer a solution expressed in a basis appropriate to one sphere to a basis appropriate to the other

$$U=\frac{\hslash }{4\pi i}{\displaystyle \sum _{m=0}^{+\infty }{\displaystyle {\int }_{-\infty }^{+\infty }\ln \det \left(\mathbf{1}-\mathbf{M}\cdot {\mathbf{R}}_1\cdot \mathbf{N}\cdot {\mathbf{R}}_2\right)\mathit{d}}}\omega ,$$ [15]

where $\mathbf{M}$ and $\mathbf{N}$ are full matrices given by

$$M_{ll\prime }={(-1)}^{l\prime +m}\frac{(l+l\prime )!}{(l-m)!(l\prime +m)!},\hspace{1em}{N}_{ll\text{'}}={(-1)}^{\left|l-l\text{'}\right|}{M}_{ll\text{'}}..$$

${\mathbf{R}}_1$ and ${\mathbf{R}}_2$ are diagonal matrices given by

$$R_{1,ll\prime }={\delta }_{ll\prime }\left[\frac{-{\epsilon }_{\text{M}}+1+A_1}{{\epsilon }_{\text{M}}+\left(1+A_1\right)\left(1+l\right)/l}\right]{\left(\frac{{R^{\prime }}_1}{{R^{\prime }}_1+{R^{\prime }}_2+\delta }\right)}^{2l+1},$$

$$R_{2,ll\prime }={\delta }_{ll\prime }\left[\frac{-{\epsilon }_{\text{M}}+1+A_2}{{\epsilon }_{\text{M}}+\left(1+A_2\right)\left(1+l\right)/l}\right]{\left(\frac{{R^{\prime }}_2}{{R^{\prime }}_1+{R^{\prime }}_2+\delta }\right)}^{2l+1},$$

where ${R^{\prime }}_1$ and ${R^{\prime }}_2$ are the radii of each sphere in the physical space; $\delta$ is the separation between them; and $A_1$ and $A_2$ are the parameters where the nonlocal effect enters and given by

$$A_1=\frac{l\left({\epsilon }_{\text{M}}-1\right)}{q_L{R}_1}\frac{i_l\left(q_L{R}_1\right)}{{i^{\prime }}_l\left(q_L{R}_1\right)},\hspace{1em}{A}_2=\frac{l\left({\epsilon }_{\text{M}}-1\right)}{q_L{R}_2}\frac{i_l\left(q_L{R}_2\right)}{{i^{\prime }}_l\left(q_L{R}_2\right)},$$ [16]

where ${\epsilon }_{\text{M}}$ is the permittivity of each sphere. If $q_L\to \infty$, $A_{1,2}=0$, which goes to the local case.