Estimating the Causal Effect of Conduct Disorder on the Time from First Substance Use to Substance Use Disorders Using G-estimation

Abstract

Background

The effect of conduct disorder (CD) as a major risk factor of substance use disorder (SUD), controlling for other psychiatric problems, has been well established in literature. However other psychiatric problems are associated with (as confounders) an increased risk of SUD. When confounding exists, the use of the standard survival analysis approach would lead to a biased estimate of the effect of a time-varying exposure on the time to event.

Method

The authors used a G-estimation approach and estimated the causal effect of CD while controlling for time-varying confounders.

Results

The present study with N=1,420 found substantial difference in the estimated hazard ratio of CD (4.49 vs. 1.93) when the results from G-estimation and Cox regression were compared.

Conclusions

G-estimation fixed the problem of under estimating hazard ratio of CD controlling for all measured covariates.

Introduction

In this paper, we examine the causal effect of conduct disorder on the timing of substance use disorders. A large literature reports conduct problems as one of the major risk factors associated with drug use and abuse (1-6). The study by Sung et al. (7) showed a strong effect of conduct disorder (CD) on the transition from substance use to disorder. CD continued to be a major risk factor for substance use disorder (SUD) even after controlling for comorbidity with other psychiatric disorders. Here, we use prospective data and investigate if the association between the history of CD and the risk of SUD has a causal interpretation.

When confounding exists in assessing the effect of CD on the development of SUD, a causal relationship is difficult to assess, because the effect of time-varying exposure can change in relation to other time-varying covariates in a time-to-event model. Here, other psychiatric problems, such as depression (DEP), anxiety, and oppositional defiant disorder (ODD), some of which are highly comorbid with CD, are treated as potential confounders of the causal relationship between CD and SUD. In dealing with confounders, Robins (8) points out that standard regression models fail to control confounding.

The authors have adopted a survival modeling framework to address these issues. However, a fundamental assumption of a standard survival model, such as the time-dependent Cox proportional hazard regression, is that the change in exposure occurs in a random fashion. When subjects change exposure level due to other measures, i.e., not randomly, the results can be misleading. For example, a study using a Cox regression model with time dependent covariates to assess the effect of CD on time to SUD could not properly control for confounders, because confounders directly affect both CD and SUD, and past history of CD may affect confounders. The Cox regression model would only assess the direct effect of CD controlling for direct effect of other covariates in the model, which may lead to underestimating the effect of CD. In order to properly control the time dependent confounders, we use the G-estimation approach (9). This allows us to estimate the “causal” effect of CD on the risk of SUD. We compare the results from the G-estimation with those from the standard time-dependent Cox proportional hazard regression.

Methods

Study population

The authors use the data (N=1,420) from the Great Smoky Mountains Study (GSMS), which is a longitudinal study of the development of psychiatric disorder and substance use and abuse, conducted in a predominantly rural area of the southeastern United States. Full details of the study design and instruments used can be found elsewhere (7,10). Briefly, a representative sample of 9, 11, and 13 year olds was recruited from 11 counties in western North Carolina, using a household equal probability design. A two-phase sampling procedure was used, based on the first-phase sample of 4,500 subjects, out of which subsets were retained for the second phase. Youth with behavior problems and American Indian youth were over-sampled, relative to white youth with low levels of behavior problems. Participants were given a weight inversely proportional to their probability of selection; thus, the results presented are representative of the population from which the sample was drawn. Participants have been interviewed on average 6 times since the study began, with an average response rate of 83%. Before the interview process began, the parent and the child signed informed-consent forms. Approval for research protocol of Great Smoky Mountains Study (GSMS) was obtained from the Duke University Medical Center Institutional Review Boardo

Measures

The areas of interest in this study include substance use, abuse, and dependence, and the DSM-IV (11) psychiatric symptoms and disorders identified by the Child and Adolescent Psychiatric Assessment (CAPA) (12). The CAPA focuses on the 3 months immediately preceding the interview.

For substance use, abuse, and dependence, the CAPA asks the child or parent about any use of tobacco (cigarettes, snuff, and chewing tobacco), alcohol (without adult permission), and other substances, including cannabis, cocaine, crack, amphetamines, ice, inhalants, heroin, other opiod, LSD, PCP, psilocybin, sedatives, “club drugs” and steroids. In data analyses, we grouped the data into three classes of substance use: tobacco, alcohol, and other drugs.

We defined a substance use disorder (SUD) as use accompanied by significant impairment, i.e., “failure to fulfill major role obligations at work, school, or home” ((11), p.182) with or without dependence.

G-Estimation

Among the sample of 1,420 subjects, we use a subset of those who reported use of any substances (n= 1,031), contributed 6 waves (for those 13 at entry) or 7 waves (for those 9 and 11 at entry) of data. The exposure in this study is CD, and we considered other psychiatric disorders as possible confounders. The exposure and confounder status may change over time. The values of the variables, known to occur on or before the first interview, are considered baseline measures. The time to SUD is the number of years between the age at the reported onset of substance use and the age when the first SUD was diagnosed. The data values missing at random were ignored; however, we needed to have complete data of the exposure history of subjects for the use of G-estimation using a semi-parametric modeling approach, which is discussed later. When the intermediate exposure status between two time points was missing, the missing values were replaced with the values from the closest previous interview. To account for the over-sampling of children with behavior problems we obtained weighted parameter estimates and variances. All reported descriptive statistics and proportions in this study are appropriately weighted, but sample sizes (N) refer to actual numbers of participants.

Detailed discussion of the G-estimation approach is provided in (9, 13, 14). In G-estimation, it is crucial to assume the existence of latent counterfactual failure time using the language of Robins(15). The counterfactual failure time is defined as the time that would have occurred if the subject had been unexposed throughout follow-up. Each subject is assumed to have a set of unobserved failure times, termed counterfactual and denoted as U_i, in that these may not have actually occurred. We assume that each subject i has an underlying counterfactual failure time U_i, which is the time to SUD from the onset of substance use, provided there was no previous exposure. This is counterfactual, as it is unobservable for those who had exposure at any time. Then we introduced an unknown parameter ψ that needs to be estimated; the exposure, CD, accelerates time to SUD by a factor exp(−ψ). The time to SUD will be increased if ψ < 0, and decreased when ψ >0. Using the Cox accelerated failure time model (16), the counterfactual failure time is given by

$$U_i\left(\psi \right)=k_i+\sum _{t=1}^{T_i}\exp \{\psi \times C{D}_{it}\},\mathrm{t}=1,\dots ,T_{\mathrm{i}}$$ 1

where k_i is the number of years from the onset of substance use to the first interview, if the onset of use for subject i was before the first interview, otherwise k_i = 0; CD_it indicates the status of CD at time t for subject i; t=1,..., T_i. {T_i + k_i} is the observed time to SUD from the onset of substance use for subject i. For example, if ψ₀ = 0.3, T_i=3, k_i = 0 and CD_it ={1,0,1} for t=1,...,3, then, U_i = exp(0.3×1) + exp(0.3× 0) + exp(0.3×1)=3.70 years.

Thus, if the subject never had the exposure (i.e., CD), his time from first use to SUD would have been 3.7 years, instead of the actual 3 years (T_i=3).

Basically, G-estimation is the process of estimating ψ so that the assumption of no unmeasured confounders is satisfied (8). Under the assumption of no unmeasured confounders, counterfactual time to SUD is independent of current exposure, CD_t, given the past history of exposure up to time t-1 and the past and present time dependent covariates up to t. Thus, given the history of exposure and confounders, the current status of exposure is randomly assigned, regardless of counterfactual time to SUD. The assumption of no unmeasured confounders is not possible in an observational study, and knowing that there is an unmeasured confounder, which predicts both outcome and exposure, a causal inference is thus not possible. We deal with this by considering all past and current covariates that predict the outcome and exposure at time t. The assumption of no unmeasured confounder is also referred to as the assumption of strong treatment ignorability (17).

In summary, the fundamental idea of the G-estimation process in this study is as follows. The G-estimation of testing if ψ=0 is equivalent to testing the null hypothesis of no causal effect of CD on the observable time to SUD; i.e., that the observable time to SUD for subject i, denoted by T_i is equal to the counterfactual time to SUD, denoted by U_i. Also, if the assumption of no unmeasured confounder is satisfied, the null hypothesis of no causal effect would imply that the observable time to SUD {T_i + k_i} would be independent of current exposure, given past history of CD and past and current covariates because {T_i + k_i} =U_i(ψ) under the null of causal effect. The inference procedure for ψ is discussed in Appendix. The estimation procedure of counterfactual time for censored data is also described in Appendix.

In addition, Generalized Estimating Equation (GEE) model and Cox proportional hazard model were used to identify time varying confounders. All data analyses were implemented by SAS version 9.1.

RESULTS

Prevalence rates of SUD by substance types

Table 1 summarizes the reported rates of substance use and SUD, for three different types of substances: tobacco, alcohol, and drugs. Alcohol was the most commonly used substance (82%). Similar proportions of youth reported use of tobacco (53%) and other drugs (59%). Overall, the SUD prevalence rate among substance users was 34%. When drugs were involved in use, the SUD rate was higher (53%) than when alcohol (40%) and tobacco (45%) were involved. When two or more types were involved, the prevalence of SUD was higher than when participants only used a single substance (55% compared with 34% for two substances 62% compared with 53% for all three types of substances). The SUD rates were computed by using the number of specific substance users in the denominator and weighted to correct over sampling of high risk subjects.

Table 1.

Descriptive prevalence rate (weighted %) and unweighted count (in ()) of substance use by type and SUD among total 1,031 substance users

	Any	Tobacco	Alcohol	Drug	Tobacco+ Alcohol	Tobacco+ Drug	Alcohol+ Drug	Tobacco+Alcohol+Drug
Users	100 (1031)	53 (660)	82 (788)	59 (673)	42 (513)	39 (497)	53 (549)	35 (428)
SUD	34 (394)	45 (318)	40 (360)	53 (367)	55 (288)	59 (303)	57 (337)	62 (276)

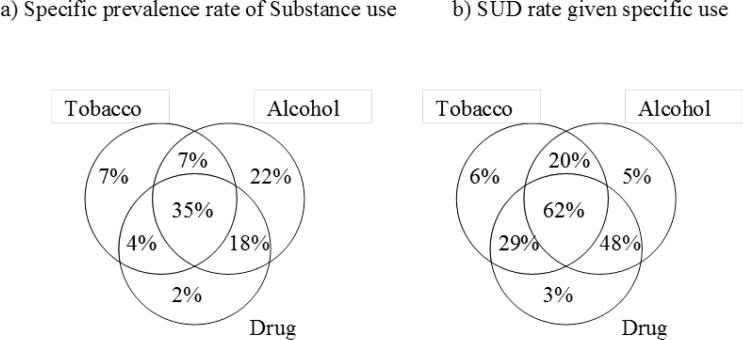
Figure 1 illustrates specific rates of use and SUD by substance type. While alcohol-only users accounted for 22% of cases, tobacco-only users (7%) and drug-only users (2%) were rare. Most users were multiple substance users, including both alcohol and drugs (22%) or all three types (35%). When only one type of substance was involved, the SUD rate was very low, ranging from 3% to 6%, but the SUD rate increased above 20% for two or more types of substance uses. Almost half (48%) of alcohol and drug users had SUD, and when all three types were used, SUD rates increased to 62%.

Figure 1.

Specific prevalence rates of a) substance use, and b) SUD by types of substances

The average age at onset of substance use was 15.1 for alcohol, 14.9 for tobacco, and 15.1 for drugs. Average time to SUD was 2.58 years from the onset of alcohol use, 2.75 for tobacco use, and 2.84 for drug use.

Test for time varying confounders

Knowing that SUD rates were different by types of substances used, we considered the effect of CD, controlling for confounding, on time from use to SUD by substance type. A covariate is a time-varying confounder (14) if the following are true: 1) a subset of the time-dependent covariates predict current CD given past CD and baseline covariates; and 2) a subset of the time-dependent covariates are predictors of the risk of SUD at any time t, controlling for a past history of CD and baseline covariates. We fitted a GEE model to assess 1), and a time-dependent Cox proportional hazard model to assess 2). The time-varying covariates considered as potential confounders in this study were the most common psychiatric disorders in this sample: oppositional defiant disorder (ODD), depression (DEP), generalized anxiety (GA), and separation anxiety (SEP). Those four psychiatric disorders were considered because the pilot study did not support other disorders as confounders.

To identify-time varying confounders, the relationship between the exposure, CD, and time varying covariates, given baseline covariate status and previous exposure, was examined using the GEE model as:

$$U_i=\exp (0.3\times 1)+\exp (0.3\times 0)+\exp (0.3\times 1)=3.70\text{years}.$$

where X̄_it is a vector of time dependent covariates up to t, including baseline, and ${\overline{CD}}_{i,t-1}$ is a vector consisting of history of CD up to t-1. The baseline covariate includes covariates known on or before the first interview. Separate GEE models were fitted to assess the effect of each of the potential confounders on CD. For example, to assess the association between current CD and ODD, controlling for past CD and baseline covariates, the independent variables included current and previous ODD, as well as baseline ODD, age, and sex.

Table 2 shows the relationship between CD and the current, past, and baseline of each covariate, separately controlling for age and previous CD status. Current CD was strongly associated with current ODD (OR:8.63), DEP (OR: 6.44), and GA (OR: 6.63), and previous DEP (OR: 4.46), GA (OR: 5.26), and SEP (OR: 3.63). SEP (OR: 0.26) was the only baseline comorbid conditions which had significant association with CD.

Table 2.

Association between current, previous and baseline values of each covariate and CD given age and past CD (cumulative): Odds ratio (2 sided P-value)

	ODD	DEP	GA	SEP
Current	8.63 (<0.0001)	6.44 (<0.0001)	6.63 (0.01)	3.06 (0.10)
Previous	1.68 (0.23)	4.46 (0.02)	5.26 (0.005)	3.63 (0.02)
Baseline	0.63 (0.19)	0.65 (0.40)	1.24 (0.65)	0.26 (0.004)

Next, the weighted, time-dependent Cox proportional hazard model was fitted to examine the predictors of time to SUD, using a SAS macro ROBPHREG (18) that fits proportional hazards regression models with a robust covariance matrix. Table 3 shows the hazard ratio of SUD for any substance users. Other highly insignificant covariates were dropped out of the model. Here, time to SUD was measured from the onset of any substance use. Among the baseline covariates, age (HR=0.74), GA (HR=4.32), ODD (HR=3.44) and DEP (HR=2.54) status, known at the time of first interview, were significantly associated with the time to SUD. The effect of CD on the transition to SUD diminished with age (HR: 0.74). Boys and girls did not have significantly different risk of developing SUD, given all other covariates. Some of the past or current covariates appeared to be protective factors: current GA (HR: 0.35) and history of GA (HR: 0.32) and history of ODD (HR: 0.50). This may be due to the high multi-colinearity with the same covariates, measured at different points in time. Controlling for baseline covariates, current CD significantly increased the risk of developing SUD (HR=1.93).

Table 3.

Hazard ratio^* of SUD for any of substance users

	Hazard ratio	2 sided P-value
Age	0.74	<0.0001
SEX (0=Girl, 1=Boy)	1.05	0.68
Conduct Disorder (CD)
Current CD	1.93	0.00
History of CD	1.65	0.02
Baseline CD	0.80	0.36
Generalized Anxiety (GA)
Current GA	0.35	0.01
History of GA	0.32	0.00
Baseline GA	4.32	0.00
Oppositional Defiant Disorder (ODD)
Current ODD	1.16	0.57
History of ODD	0.50	0.02
Baseline ODD	3.44	0.00
Depression (DEP)
Current DEP	1.00	0.98
History of DEP	0.95	0.84
Baseline DEP	2.54	0.00

^*Time from the onset of any substance use to SUD

Table 4 presents the results from the G-estimation. The causal factor, ψ, was obtained by the G-test discussed above. Fractional decrease, 1-exp(-ψ), in time to SUD, due to continuous exposure to CD, may be of more interest to researchers than the estimated value of ψ. If the Weibull distribution is assumed for counterfactual time to SUD, the Weibull shape parameter can be used to obtain the G-estimated causal ratio as a hazard ratio for CD. The shape parameter of the Weibull distribution was obtained by using the maximum likelihood method, and the G-estimated causal ratio was computed by taking exp(shape parameter× ψ). The causal ratio can be interpreted as SUD rate, if all subjects were exposed to CD up to time of SUD, divided by the rate when all subjects were unexposed throughout (14).

Table 4.

Cox proportional hazard ratio (2 sided P-value), and G-estimated causal ratio

Substance type	Cox HR (P-value)	Est. Causal factor ψ, (95% CI)	Fractional decrease* (95% CI)	Causal Ratio**, (95% CI)
At least one+	1.93 (0.00)	1.22 (0.68, 1.51)	0.70 (0.49, 0.78)	4.16 (2.21, 5.85)
Tobacco+	1.60 (0.05)	1.22 (0.52,1.34)	0.70 (0.41, 0.74)	3.16 (1.63, 3.52)
Alcohol+	1.03 (0.90)	1.37 (0.52,1.51)	0.75 (0.41, 0.78)	6.32 (2.01, 7.63)
Other Drugs+	0.89 (0.58)	0.69 (−0.09,0.99)	0.50 (1.09, 0.63)	2.60 (0.88, 3.94)
Tobacco+Alcohol++	0.94 (0.83)	1.19 (0.28, 1.34)	0.70 (0.24, 0.74)	4.06 (1.39, 4.84)
Tobacco+Drug++	1.03 (0.90)	0.40 (−0.21,0.99)	0.33 (1.23, 0.63)	1.77 (0.74, 4.11)
Drug+Alcohol++	0.78 (0.36)	0.28 (−0.13, 1.19)	0.24 (1.14, 0.30)	1.55 (0.82, 6.43)
All three++	0.70 (0.28)	−0.04 (−0.85, 0.95)	1.04 (2.33, 0.61)	0.94 (0.27, 4.34)

⁺Time to SUD from the onset of use

⁺⁺Time to SUD from the onset of use of later used substance

^*fractional decrease in time from the onset of use to SUD due to continuous exposure to CD

^**SUD rate if all subjects were exposed up to time of SUD divided by the rate when all subjects were unexposed throughout.

In Table 4, the hazard ratios from time dependent Cox proportional models were compared with the G-estimated causal ratios. CD had the strongest causal effect on time from the onset of alcohol use to SUD, with a fractional decrease of 75%, which means that the time to SUD would decrease by 75% if the subjects had CD continuously up to the onset of SUD. CD would have almost as strong as effect on time to SUD from the onset of any substance use (70% reduction) and of tobacco use (70% reduction). The causal ratio was also highest for alcohol use. CD did not appear to be as a strong cause of SUD when multiple substances were used.

When the G-estimated causal ratios were compared with the Cox regression hazard ratios, hazard ratios from Cox models were considerably smaller than causal ratios from G-estimation, which implies that the standard Cox model underestimated the effect of CD and that the underestimate was due to confounding. The biggest discrepancies were found between two methods for the effect of CD on time from the onset of alcohol use to SUD (Cox HR=1.03 Vs. G-est'd. CR=6.32). G-estimation showed an insignificant effect of CD, if the time to SUD was measured from the onset of drug use when other drug use was involved. When other drugs were involved, alone or in combination with alcohol or tobacco, the effect of CD on time to SUD was not significant.

DISCUSSION

When confounding exists, the use of the standard survival analysis approach can lead to biased estimates of the effect of a time-varying exposure on the time to event, by not adequately controlling for time varying covariates. When we fit the time-dependent Cox proportional hazard model with CD, controlling for other time varying covariates as well as baseline covariates, the estimated hazard ratio of CD on the time to SUD was 1.93, as shown in Table 3. However, the same modeling approach, without controlling for other covariates, produced an estimated hazard ratio of 4.49 (table not provided). This substantial difference in the estimated hazard ratio occurred because the Cox proportional hazard regression model controlled for the time-varying covariates, which were on the causal pathway, leading to the reduction in estimated hazard ratio of CD. The G-estimation approach fixes this problem, and allows us to estimate the effect of CD on time to SUD controlling for all measured covariates.

The effect of CD as a major risk factor of SUD has been well established in the literature (1-7). The authors used G-estimation to estimate the effect of CD on time to SUD from onset of various types of substances use, separately and in combination. In comparison with the results from Cox's proportional hazard regression models, G-estimated causal ratios were considerably higher, implying substantial confounding.

It is worth noting that CD did not have a significant effect on the time from first use of ‘other drugs’ to SUD. This was the case whether other drugs were used alone or in combination with alcohol and/or tobacco. This may be the result of two things: 1) onset of other drugs (mean age=18.23) was later than onset of alcohol (mean age=15.36) and tobacco (mean age= 15.44) ; and 2) the effect of CD on the transition to SUD diminished with age (Table 3). Thus, by the time the participants started using other drugs they were past the age at which CD has a strong impact on the speed of transition.

The validity of finding in the present study is limited in that the G-estimation approach is crucially dependent on the assumption of ‘no unmeasured confounder’. However, we recognize that this is an untestable assumption in an observational study. Even with the limitation, the present study contributes to the literature in that causal effects, beyond the associative effects, of CD on SUD was assessed using new methodology.

Appendix

Inference about unknown G-estimation parameter ψ

Inferences about ψ are made by a logistic regression in a general form of

$$Logit\left[p(C{D}_{it}=1)\right]={\beta }_1+{\beta }_2{\overline{X}}_{it}+{\beta }_3{\overline{CD}}_{i,t-1},$$

is a vector of time-dependent are unknown parameter vectors, , , , where β₁, β₂, β₁, θ are unknown parameter vectors, X̄_it is a vector of time-dependent covariates up to t including baseline, and ${\overline{CD}}_{i,t-1}$ is vector consisting of the history of CD up to t-1. Under the assumption that there are no unmeasured confounders, θ = 0 in equation A.1. Then, the G-estimated value of ψ is the value of ψ when θ =0. We fit a Generalized Estimating Equation (GEE) model with an independent covariance matrix (19) to test θ =0. The point estimate of ψ is the value of ψ for which the p-value of the θ =0 test is 1, and the 95% confidence interval of ψ is the value for which the p-value of θ =0 test is 0.05. The model in equation A.1 was fitted using the GEE approach with an independent covariance matrix, and obtained the point estimate and 95% intervals from the hypothesis testing if θ =0. By assuming the independent covariance matrix, the effect of covariate up to t is controlled, but the parameter estimates are independent of the covariate effect subsequent to t.

Censored data

The counterfactual time to SUD, U_i(ψ), in equation 1 can only be obtained for those who had first SUD before the end of the study period. Censoring occurred if SUD had not occurred by the last interview; the counterfactual failure time cannot be obtained for these subjects. For that reason, Mark and Robins (13), and Witteman et al. (14) replaced U_i(ψ) with Δ_i(ψ) in equation A.1 defined as:

$$Logit\left[p(C{D}_{it}=1)\right]={\beta }_1+{\beta }_2{\overline{X}}_{it}+{\beta }_3{\overline{CD}}_{i,t-1}+\theta U_i\left(\psi \right),t=1,\dots T_i,$$ A.1

where C_i (ψ) = {time from the onset of substance use to the last interview} if ψ ≥ 0 C_i (ψ) = {time from the onset of substance use to the last interview}×exp (ψ) if ψ < 0. Then, Δ_i (ψ) is a function of U_i (ψ) and {time from the onset of substance use to the last interview}; thus the value can always be obtained. While U_i (ψ) is the counterfactual time to SUD from the onset of substance use if the subject i never had CD, Δ_i (ψ) indicates if SUD would have been observed if the subject i never had CD.

We modified the SAS macro provided by (14) for our data, and implemented G-estimation in two steps: a) we obtained U_i(ψ) in equation 1 and Δ_i (ψ) by various values of ψ; and b) we ran GEE models of the equation of A.1 to obtain G-estimated values of ψ.