Estimation of Treatment Effects in Matched-Pair Cluster Randomized Trials by Calibrating Covariate Imbalance between Clusters

Abstract

Summary

We address estimation of intervention effects in experimental designs in which (a) interventions are assigned at the cluster level; (b) clusters are selected to form pairs, matched on observed characteristics; and (c) intervention is assigned to one cluster at random within each pair. One goal of policy interest is to estimate the average outcome if all clusters in all pairs are assigned control versus if all clusters in all pairs are assigned to intervention. In such designs, inference that ignores individual level covariates can be imprecise because cluster-level assignment can leave substantial imbalance in the covariate distribution between experimental arms within each pair. However, most existing methods that adjust for covariates have estimands that are not of policy interest. We propose a methodology that explicitly balances the observed covariates among clusters in a pair, and retains the original estimand of interest. We demonstrate our approach through the evaluation of the Guided Care program.

1. Introduction

Experimental designs often have the following three features: interventions are assigned at the cluster level; clusters are selected to form pairs, matched on observed covariates; and interventions are assigned to one cluster at random within each pair. One goal ofpolicy interest is to estimate the average outcome if all clusters in all pairs are assigned control versus if all clusters in all pairs are assigned to intervention. The effect of such a policy is easy to understand, because its definition or estimation does not have to depend on models. Such designs are useful when individual-level randomization is not feasible due to practical constraints, and when cluster assignment also reflects how the assignment would scale in practice.

The Guided Care program is a recent example of such a study (Boult et al., 2013). The study's goal was to assess the effect of Guided Care versus a control condition on functional health and other patient outcomes among clinical practices serving chronically ill older adults. In Guided Care, a trained nurse works closely with patients and their physicians to provide coordinated care. The control group does not have access to such a nurse. To assess the effect of the Guided Care intervention, the study recruited 14 clinical practices and matched them in 7 pairs using clinical practice and patient characteristics, and within each pair assigned randomly one clinical practice to Guided Care and the other to control.

A problem with cluster-level assignment is that it can leave substantial imbalances in the covariates within pairs. However, existing methods to estimate effects in such designs rarely use covariates in order to adjust for these imbalances. As a consequence, such methods, including nonparametric as well as hierarchical (meta-analysis) approaches, although useful in other ways (Imai, King, and Nall, 2009), can leave large uncertainty in the results. Methods that do use covariates usually estimate effects conditionally on covariates and cluster-specific random effects (Thompson, Pyke, and Hardy, 1997; Feng et al., 2001; Hill and Scott, 2009). With such methods, the estimands are no longer of policy interest and lack meaning when the modeling assumptions are misspecified.

We propose an approach that explicitly balances the observed covariates between clusters in a pair and still estimates causal effects of policy interest. In Section 2, we formulate the matched-pair cluster randomized design through potential outcomes. We then characterize in Section 3 the existing approaches to causal effects estimation and their complications. In Section 4, we propose a covariate-calibration approach and develop inferences with and without the need for assumptions for a hierarchical second level. Throughout these sections, the arguments are demonstrated through the evaluation of the recent Guided Care program. Section 5 concludes with discussion.

2. The Goal and Design Using Potential Outcomes

Consider a design that operates in pairs p = 1,...,n of clusters. In each pair p, the design recruits two clusters (e.g., clinical practices) indexed by i = 1, 2, matched on qualitative and quantitative characteristics, such as percentage of patients with private insurance, and where each clinical practice serves a community, say with a large number of N_p,i patients. The design then assigns to each clinic one of two treatments, namely control (t = 1) or intervention (t = 2). If clinical practice i of pair p is assigned treatment t, then potential outcomes Y_p,i,k(t) (Rubin, 1974, 1978) are to be measured on a random sample of k = 1 ,...,n _p,i patients from the N _p,i patients served in that clinical practice. We label F _p,i(y; t), μ_p,j(t), and ${\sigma }_{p,i}^2\left(2\right)$ the distribution (at value y), mean and variance of the potential outcome Y_p,i,k(t) within clinical practice i of pair p. The average outcomes in pair p are

$${\mu }_p\left(t\right)≔{\mu }_{p,i=1}\left(t\right){\pi }_{p,i=1}+{\mu }_{p,i=2}\left(t\right){\pi }_{p,i=2},$$ (1)

where “ := ” means “define,” π_p,i=1 is the fraction of patients served by clinic i = 1, that is, N_p,i=1/(N_p,i=1 + N_p,i=2), and similarly for π_p,i=2. One goal of policy interest is to estimate the average outcome if all clinical practices in all pairs are assigned control versus if all clinical practices in all pairs are assigned intervention. In terms of the model, the goal is to estimate a contrast between

$$\mu \left(1\right)≔E\left\{{\mu }_p(t=1)\right\}\text{and}\mu \left(2\right)≔E\left\{{\mu }_p(t=2)\right\},\text{for example}{\delta }^{\text{effect}}≔\mu \left(1\right)-\mu \left(2\right),$$ (2)

which is the average outcome if all clusters had been assigned treatment 1 versus if all clusters had been assigned treatment 2. Here, the expectations are taken over a larger population P of pairs from which p = 1,...,n can be considered a random sample. Alternative estimands (e.g., conditionally on the sample of pairs, Imai et al., 2009) can be considered, although this does not change the main issues discussed here.

Within each pair, the design assigns at random the intervention to one clinical practice and the control to the other, independently across pairs. Because in this design the original ordering i is arbitrary, and in order to ease comparisons with the existing meta-analytic approach (e.g., Thompson et al., 1997), for each pair p we relabel by c = 1 the clinical practice that is assigned control, and by c = 2 the clinical practice that is assigned intervention. The quantities Y_p,c,k(t), F_p,c(y; t), μ_p,c(t) and ${\sigma }_{p,c}^2\left(t\right)$are then redefined based on this relabeling and the above definitions. Then, the paired cluster randomized design implies the following:

Condition 1. The potential outcomes under treatments 1 and 2 in clinical practice c, and the number of patients served by clinical practice c are exchangeable (in distribution over pairs) between clinical practices c = 1 and c = 2 , that is,

$$\begin{array}{cc}\hfill pr\{{\left(\underset{¯}{F_{p,c}(\cdot ;1),F_{p,c}(\cdot ;2),N_{p,c}}\right)}_{c=1},{(F_{p,c}(\cdot ;1),F_{p,c}(\cdot ;2),N_{p,c})}_{c=2}\}& \hfill \\ \hfill =pr\{{\left(\underset{¯}{F_{p,c}(\cdot ;1),F_{p,c}(\cdot ;2),N_{p,c}}\right)}_{c=2},{(F_{p,c}(\cdot ;1),F_{p,c}(\cdot ;2),N_{p,c})}_{c=1}\}& \hfill \end{array}$$

where the arrows connect equal entries in arguments, and distribution pr is over pairs p in the larger population P of pairs.

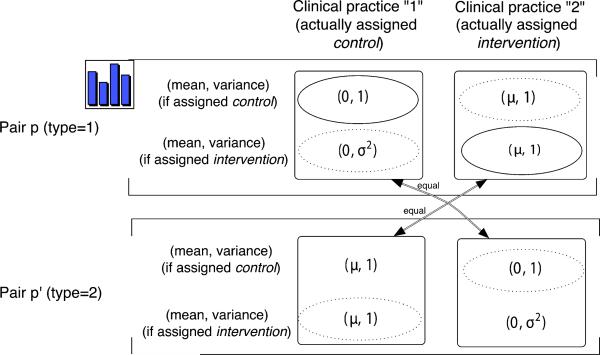
Condition 1 implies, for example, over population of pairs, the joint distribution of the “means and variances of potential outcomes under exposure to intervention (t = 1)” is the same for the clinical practices that are actually assigned the intervention (c = 2) as it is for the clinical practices that are actually assigned the control (c = 1). Figure 1 illustrates the structure of pairs, clinical practices, and assigned treatments in this paired cluster randomized design, along with means and variances of potential outcome distributions.

Figure 1.

The underlying structure of the paired-cluster randomized design. The top part (observed pair p) and bottom part (observed pair p’) are the two possible ways in which a single pair can be manifested in the design. Observed pair p has two clinical practices (represented by the two squares). For each clinical practice, the first row shows the mean and variance of patient outcomes if the clinical practice is assigned control and the second row shows the mean and variance if assigned intervention. The clinical practice actually assigned control is indicated by its placement in column “1”, and the clinical practice actually assigned intervention is in column “2”. The solid (nonsolid) ellipsoids show the means and variances that can (cannot) be estimated directly. Observed pair p’ shows how the same pair would be manifested in the design if the assignment of treatment to clinical practices were in reverse (a line with arrows connects the same clinical practice in these two different assignments). Condition 1 means that each of the two manifestations, p and p’ has the same probability.

Here we connect the observed data and existing methods to the above framework of potential outcomes, because this helps understand the meaning of the assumptions, explicit or implicit, required by the existing methods.

In order to estimate an effect such as δ^effect of (2), consider first a particular pair p: we can directly estimate the average potential outcome under control for the clinical practice assigned to the control, namely μ_p,c=1 (t = 1); and the average potential outcome under intervention for the clinical practice assigned to the intervention, namely μ_p,c=2 (t = 2). Specifically, for the control clinical practice (c = 1) of pair p, let ${\widehat{\mu }}_{p,c=1}(t=1)≔\frac{1}{n_{p,c=1}}{\sum }_{k=1}^{n_{p,c=1}}{Y}_{p,c=1,k(t=1)}$ denote the average of the observed outcomes, that is, the potential outcomes under t = 1; and for the intervention clinical practice (c = 2) of pair p, let ${\widehat{\mu }}_{p,c=2}(t=2)≔\frac{1}{n_{p,c=2}}{\sum }_{k=1}^{n_{p,c=2}}{Y}_{p,c=2,k(t=2)}$ denote the average of the observed outcomes, that is, the potential outcomes under t = 2. Then, letting ${\widehat{\delta }}_p^{\text{crude}}={\widehat{\mu }}_{p,1}\left(1\right)-{\widehat{\mu }}_{p,c}\left(2\right)$, and conditionally on pairs p whose clinical practices have particular values of $({\delta }_p^{\text{crude}},v_p^{\text{crude}})$, we have that

$$\mathrm{pr}({\widehat{\delta }}_p^{\text{crude}}\mid {\delta }_p^{\text{crude}},v_p^{\text{crude}})\stackrel{\cdot }{=}\text{Normal}({\delta }_p^{\text{crude}},v_p^{\text{crude}}),$$ (3)

where

$${\delta }_p^{\text{crude}}≔{\mu }_{p,1}\left(1\right)-{\mu }_{p,2}\left(2\right)\text{and}{v}_p^{\text{crude}}=\frac{{\sigma }_{p,1}^2\left(1\right)}{n_{p,1}}+\frac{{\sigma }_{p,1}^2\left(2\right)}{n_{p,2}}.$$

Here, “$\stackrel{\cdot }{=}$” means “approximately,” the notation pr(A_p | B_p) and E(A_p | B_p) means the distribution and expectation, respectively, of characteristic A_p among pairs in the larger population P that have characteristic B_p (if B_p is empty, the distribution and expectation are over all pairs).

Remark 1. In a pair p, the directly estimable (crude) contrast ${\delta }_p^{\text{crude}}$ is not a causal effect because it compares different clinical practices under different treatments (Thompson et al., 1997). However, the average, $E\left({\delta }_p^{\text{crude}}\right)$, over pairs is a causal effect, because the exchangeability of potential outcomes and between clinical practices 1 and 2 (Condition 1 above) implies (proof omitted) that

$$E\left({\delta }_p^{\text{crude}}\right)=E\left\{{\mu }_p(t=1)\right\}-E\left\{{\mu }_p(t=2)\right\}={\delta }^{\text{effect}}.$$ (4)

Thus, one can use the estimated differences, ${\widehat{\delta }}_p^{\text{crude}}$, within each pair as in (3), and expression (4), to estimate δ^effect, either with no additional assumptions (i.e., by simply averaging ${\widehat{\delta }}_p^{\text{crude}}$ over pairs), or under a hierarchical second level model.

Remark 2. The objective meaning that the potential outcomes assign to the terms in the model (3) implies the following, subtle fact: if the pair-specific ${\delta }_p^{\text{crude}}$ are to be eliminated (i.e., marginalized over) from the distribution (3), then Scrude should be first integrated out of (3) based on the conditional distribution $pr({\delta }_p^{\text{crude}}\mid v_p^{\text{crude}})$, that is,

$$pr({\widehat{\delta }}_p^{\text{crude}}\mid v_p^{\text{crude}})=\int pr({\widehat{\delta }}_p^{\text{crude}}\mid {\delta }_p^{\text{crude}},v_p^{\text{crude}})\cdot pr({\delta }_p^{\text{crude}}\mid v_p^{\text{crude}})\cdot \mathrm{d}\left({\delta }_p^{\text{crude}}\right).$$ (5)

This becomes relevant when examining the existing hierarchical modeling methods.

We next discuss complications of existing methods for estimating the effect of intervention δ^effect. We demonstrate the arguments by assessing the effect of the Guided Care intervention on the functional health outcome of the patients as measured by the physical component summary of the Short Form (SF)-36 version 2 (Ware and Kosinski, 2001).

3. Complications with Existing Methods

3.1. Consequences When Ignoring Covariates

Table 1 displays the observed average SF-36 scores for each of the seven pairs of practices in the Guided Care study (see outcome rows denoted as uncalibrated). Also displayed are the within pair differences in average SF-36 outcomes between control and intervention.

Table 1.

Summary of average SF36 outcomes for uncalibrated versus calibrated approaches. The first row block displays sample sizes; the second row block displays average outcomes that are uncalibrated and calibrated, respectively.

	Pair p
	1	2	3	4	5	6	7
Sample size
n p,c=1	17	16	42	23	52	23	28
n p,c=2	38	44	43	33	42	31	43
Outcome	Uncalibrated on covariates
${\widehat{\mu }}_{p,1}\left(1\right)$	36.4	36.5	39.6	39.1	39.7	33.8	39.6
${\widehat{\mu }}_{p,2}\left(2\right)$	37.3	36.6	39.3	35.3	35.2	36.4	40.9
${\widehat{\delta }}_p^{\text{crude}}$	−0.8	−0.1	0.3	3.8	4.5	−2.6	−1.3
${\left(v_p^{\text{crude}}\right)}^{1∕2}$	2.7	2.6	2.0	2.7	2.1	2.6	2.2
	Calibrated on covariates
* ${\widehat{\mu }}_{p,1}^{\text{calibr}}$	37.6	38.8	39.5	38.0	38.7	35.5	40.9
* ${\widehat{\mu }}_{p,2}^{\text{calibr}}$	36.7	35.8	39.4	36.0	36.4	35.1	40.0
${\widehat{\delta }}_p^{\text{calibr}}$	0.9	3.0	0.1	1.9	2.3	0.5	0.8
† ${\left(v_p^{\text{calibr}}\right)}^{1∕2}$	2.1	2.4	1.5	2.0	1.7	2.2	1.7

^*Calibration based on n_p,1 and n_p,2 observations in pair p.

^†$v_p^{\text{calibr}}$ is the pth diagonal element of ${\widehat{\Sigma }}_{{\widehat{\delta }}^{\text{calibr}}}$ in expression (14).

Using these outcome data and ignoring covariates, we first obtain the estimate of the overall effect δ^effect based only on the design-derived fact (4) that the average of ${\delta }_p^{\text{crude}}$ across pairs equals the effect of interest δ^effect (see Table 2, 1st level, “uncalibrated on covariates”). Because this first-level approach makes no further assumptions about the joint distribution of $pr({\delta }_p^{\text{crude}},v_p^{\text{crude}})$, the MLE of δ^effect is simply the unweighted sample average of ${\widehat{\delta }}_p^{\text{crude}}$, with its standard error estimated by the jackknife. Table 2 also reports the permutation test of no true effect for any person, by randomly permuting the labels of treatment within each pair.

Table 2.

Results from MLE, profile MLE, Bayes estimates and permutation test in the Guided Care program study. The covariates used for calibration are listed in the first column of Table 3; the outcome is the physical component summary of the Short Form 36 (SF36).

		${\widehat{\delta }}^{\text{effect}}$	95% CI	$s.e.\left({\widehat{\delta }}^{\text{effect}}\right)$	$\widehat{\mathrm{var}}\left({\delta }_p^{\ast }\right)$	p-Value (two-sided)
Uncalibrated on covariates	1st level
	MLE	0.5	(–1.4, 2.5)	1.0	–	0.59
	permutation	–	–	–	–	0.61
	1st+2nd level
	MLE	0.6	(–1.2, 2.5)	0.9	0.7	0.50
	pMLE	0.6	(–1.5, 2.7)	–	0.7	–
	Bayes	0.6	(–1.7, 3.0)	1.2	4.3	0.60
	permutation	–	–	–	–	0.60
Calibrated on covariates	1st level
	MLE	1.4	(0.5, 2.2)	0.4	–	<0.01
	permutation	–	–	–	–	0.02
	1st+2nd level
	MLE	1.2	(–0.2, 2.6)	0.7	0.0	0.08
	pMLE	1.2	(–0.2, 2.6)	–	0.0	–
	Bayes	1.3	(–0.4, 2.9)	0.9	1.5	0.13
	permutation	–	–	–	–	0.02

*represents ${\delta }_p^{\text{crude}}$ for the uncalibrated approach and ${\delta }_p^{\text{calibr}}$ for the calibrated approach.

For a hierarchical second-level (meta-analytic) inference, the current approach for paired-clustered designs (e.g., Thompson et al., 1997; Feng et al., 2001; Hill and Scott, 2009) is based on integrating the likelihood in (3) over the marginal distribution $pr\left({\delta }_p^{\text{crude}}\right)$, to obtain:

$$p{r}^{\ast }({\widehat{\delta }}_p^{\text{crude}}\mid v_p^{\text{crude}},{\delta }^{\text{effect}})=\int pr({\widehat{\delta }}_p^{\text{crude}}\mid {\delta }_p^{\text{crude}},v_p^{\text{crude}})\cdot pr\left({\delta }_p^{\text{crude}}\right)\cdot \mathrm{d}\left({\delta }_p^{\text{crude}}\right);$$ (6)

where $pr\left({\delta }_p^{\text{crude}}\right)=\text{Normal}({\delta }^{\text{effect}},v^2)$.

Table 2 (see 1st+2nd level, “uncalibrated on covariates”) shows inference for the effect δ^effect using the above likelihood (6), namely, the method of Thompson et al. (1997) with and without profiling out the variance v2 (see rows 3 and 4); and also inference based on the mean of the posterior distribution of δ^effect using the uniform shrinkage prior on v² as suggested by Daniels (1999) (see row 5). For comparison, we also obtained the two-sided tail probability from the distribution of the MLE from (6) as obtained from all the permutation possibilities of the intervention and control labels of clinical practices independently across pairs. None of these results suggest any substantial effect for the intervention.

In general, the hierarchical and non-hierarchical methods without covariates can be inaccurate for at least one of the following two reasons. First, any substantial covariate imbalances between clinical practices within a pair can result in substantial uncertainty, which is reflected in the variance of the estimators of the effect, and which may have influenced the point estimate. For the Guided Care study, Table 3 shows that a number of covariates show substantial imbalance between intervention and control groups. For example, the continuous covariate Chronic Illness Burden has severe imbalances between the clinical practices in pairs 2, 5, and 7, with t-statistics being −3.07, −4.81, and 2.52, respectively.

Table 3.

Checking covariate imbalances within each pair. For a continuous covariate (indicated by (a)), we calculate effect size as difference divided by pooled standard deviation. For a categorical covariate (indicated by (b)), odds ratio is calculated comparing rates of occurrence of each category between two clusters in a pair. To prevent infinite odds ratio, 0.5 is added to all the cells when calculating sample odds ratios.

	Pair
	1	2	3	4	5	6	7
age at interview(a)	0.3	-0.3	0.1	0.6	0.0	0.1	-0.1
Chronic Illness Burden(a)	0.5	-0.6	0.0	0.0	-1.1	0.1	0.6
SF36 Mental(a)	-0.3	0.1	0.3	0.2	0.3	-0.6	-0.5
SF36 Physical(a)	-0.1	-0.4	0.1	0.5	0.4	-0.6	-0.3
lives alone(b)	1.4	0.8	0.7	0.7	1.6	0.9	0.5
>high school education(b)	0.4	0.5	0.7	1.4	0.8	0.8	1.1
Female(b)	2.4	0.6	1.0	0.6	1.0	2.5	1.1
race(b)
Caucasian	0.5	0.2	0.9	0.8	1.5	0.5	0.7
African American	2.2	0.9	1.2	1.2	0.8	1.6	1.2
other	2.2	15.0	1.0	1.4	0.6	1.3	1.5
finances at end of month(b)
some money left over	0.0	0.7	1.4	0.7	1.5	0.7	0.6
just enough to make ends meet	8.9	1.0	0.3	1.3	0.6	1.2	1.4
not enough to make ends meet	18.2	8.4	7.0	1.0	1.2	2.0	1.6
self rated health(b)
≥very good	0.3	0.3	0.8	2.2	0.3	0.8	0.6
good	2.6	3.4	1.4	0.4	2.5	0.8	1.4
fair	0.9	0.9	0.4	0.3	2.5	4.2	0.5
poor	6.8	1.5	3.1	4.4	2.0	4.2	2.1

Second, the hierarchical model approach, in addition to its normality assumption, can be questioned for the following subtle reason. In order to integrate out ${\delta }_p^{\text{crude}}$ from the likelihood (3) to obtain a likelihood that, like (6), still depends on the variances $v_p^{\text{crude}}$, one must integrate ${\delta }_p^{\text{crude}}$ with respect to the conditional distribution of the estimand ${\delta }_p^{\text{crude}}$ given the variance $v_p^{\text{crude}}$, as in (5) of Remark 2, and not with respect to the marginal distribution $\mathrm{pr}\left({\delta }_p^{\text{crude}}\right)$ as in (6). The comparison of (6) to (5) shows that (6) implicitly assumes the following:

Condition 2. The estimand ${\delta }_p^{\text{crude}}$ and the variance $v_p^{\text{crude}}$ of ${\widehat{\delta }}_p^{\text{crude}}$ at the first level are independent across pairs p.

The motivation for using the likelihood (6) can be traced to Thompson et al. (1997, Section 5, Paragraph 2). There, inference for the paired-clustered design is assumed to have the same random-effects structure as that of DerSimonian and Laird (1986), who also assume Condition 2 but for a design that first randomly samples subjects from the population that a pair serves and then completely randomizes them, regardless of their clinical practice. We call this simpler design, a “paired-strata” design. We show below that violation of Condition 2 has more severe implications for the paired-clustered than for the paired-strata design.

In the paired-strata design, the observed difference, say ${\widehat{\delta }}_p^{\prime }$, in average outcomes between intervention and control individuals within a pair has mean, say ${\delta }_p^{\prime }$, equal to the causal effect μ_p(2) – μ_p(1) of (2). This means that, if the intervention has no effect in any pair, that is, the null hypotheses, μ_p(1) = μ_p(2) for all p, is correct, then ${\delta }_p^{\prime }$ is a constant (0) and so Condition 2 is satisfied. As a result, an approach based on (6) is valid for testing μ_p (1) = μ_p (2) for all p because Condition 2 is correct under the null hypothesis being tested in that design.

In the paired-clustered design, however, the mean, ${\delta }_p^{\text{crude}}$, of ${\widehat{\delta }}_p^{\text{crude}}$ is not a causal effect (see Remark 1 above) even if the intervention has no effect in any cluster, that is, even if the null hypotheses, μ_p,c(1) = μ_p,c(2) for all p and c, is correct. In particular, under this null, the mean ${\delta }_p^{\text{crude}}$ is μ_p,1 (1) – μ_p,2(1), that is, the difference between clinical practices 1 and 2 if they had both been assigned control. In practice, even after matching, the two clinical practices are expected to have imbalances in characteristics of the patients or the doctors, so that ${\delta }_p^{\text{crude}}$ is expectedly not zero, and, hence, Condition 2 can be violated. We then have the following result (proof in Appendix):

Result 1. If the intervention has no effect, μ(1) = μ(2), but Condition 2 is violated, then the MLE of the causal effect δ^effect based on (6) can converge to a non-zero value as the number of sampled pairs increases.

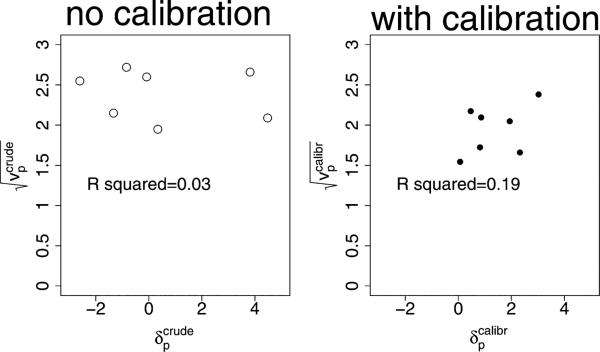
Therefore, it is important to try to assess the plausibility of Condition 2. For the Guided Care study, Figure 2 (left) plots the estimated values of $\sqrt{v_p^{\text{crude}}}$ against ${\delta }_p^{\text{crude}}$. Here there appear no noticeable warnings against independence. However, the covariate imbalances shown in Table 3 could still be contributing to inaccurate estimates through large variances as discussed earlier.

Figure 2.

Checking second level dependence. Left: estimates of $\sqrt{v_p^{\text{crude}}}$ versus ${\delta }_p^{\text{crude}}$; Right: estimates of $\sqrt{v_p^{\text{calibr}}}$ versus ${\delta }_p^{\text{calibr}}$, where $v_p^{\text{calibr}}$ are the diagonal elements of ${\Sigma }_{{\widehat{\delta }}^{\text{calibr}}}$.

3.2. Complications with Existing Covariate Methods

Some existing proposals do incorporate covariates into the model for $pr\left({\delta }_p^{\text{crude}}\right)$ on the right-hand side of likelihood (6). However, these approaches stop short of addressing the goal of estimating effects of policy interest. In particular, such existing approaches (e.g., Thompson et al., 1997, Section 5.5; Feng et al., 2001) define the treatment effect to be a contrast in the treatment coefficients of the posited model after conditioning on a particular value of the covariates and/or of random effects specific to the clusters. The first problem with such a treatment effect is that, its meaning is not objective: if, for example, the model is misspecified, then an effect set equal to a contrast of coefficients in the model does not have a well defined physical interpretation. The second problem is that, even if the model is correct, a treatment effect that is conditional on the covariates and/or the clusters is not usually equal to the overall effect.

4. Addressing the Problems

4.1. Calibration of Observed Covariate Differences between Clinical Practices

In order to use covariates to estimate the treatment effects in (2), we propose to first construct calibrated pair-specific averages, for each treatment t = 1, 2, in the sense that the distribution of the covariates reflected in the averages will be the same as the distribution of covariates combined from both clinical practices of the pair. Inference for these calibrated averages will then lead to inference for overall effects (2) with the gained precision of accounting for the difference in observed covariates between the matched clinical practices.

This section uses notation for the following additional structure for pair p:

• ○ X_p,c,k, for the measurement of a covariate vector before treatment administration, for the kth sampled patient of clinical practice c.

• ○ G_p,c(x), for the joint cumulative distribution function of the covariate vector X_p,c,k in clinical practice c, evaluated at value x; and Gp(x) for the joint cumulative distribution function (evaluated at x) of the covariate vector of a patient selected at random from pair p (i.e., from the two clinical practices of that pair, combined).

• ○ F_p,c (y | x; t), for the cumulative distribution function of the potential outcome Y_p,c,k (t) in clinical practice _c, evaluated at value y among covariate levels x, if clinical practice c is assigned treatment t; and let μ_p,c(x; t), for the mean of the latter distribution.

For pair p, consider now the estimable quantity, labeled as ${\mu }_p^{\text{calibr}}(t=1)$, that is constructed by, first, stratifying the average outcome into the covariate levels of the clinical practice c = 1 (assigned to treatment 1), namely μ_p,c=1(x; t = 1), and i then re-calibrating it with respect to the covariate distribution of the two clinical practices combined (and similarly for t = 2):

$$\begin{array}{cc}\hfill {\mu }_{p,c=1}^{\text{calibr}}≔& {\int }_x{\mu }_{p,c=1}(x;t=1)\mathrm{d}{G}_p\left(x\right),\hfill \\ \hfill {\mu }_{p,c=2}^{\text{calibr}}≔& {\int }_x{\mu }_{p,c=2}(x;t=2)\mathrm{d}{G}_p\left(x\right)\hfill \end{array}$$ (7)

To understand the above estimand, consider for example two clinical practices in a pair, that, although matched as closely as possible with respect to, say, the percentage of patients with a “low” or “high” risk covariate (x = low or high), the percentage of low risk in clinical practices 1 and 2 is 75% and 85%, respectively, that is, still differs appreciably between the clinical practices. Suppose also that clinical practice 2 serves twice as many patients as clinical practice 1. Ignoring covariates, the quantity that can be directly estimated from the data for representing the average outcome if both clinical practices are assigned treatment 1 is simply the average outcome within clinical practice 1, μ_p,c=1(1), which can be expressed in terms of the covariate as 0.75 · μ_p,c=1(x = low; t = 1) + 0.25 · μ_p,c=1(x = high; t = 1). When using covariates, the calibrated average ${\mu }_{p,c=1}^{\text{calibr}}$ is 0.82 · μ_p,c=1 (_x = low; t = 1) + 0.18 − μ_p,c=1(x = high; t = 1), because it generalizes the covariate-specific outcome averages under treatment 1 to the covariate distribution for both clinical practices in which $0.75\frac{1}{3}+0.85\frac{2}{3}=0.82$ have low risk.

More generally, one should expect that the calibrated contrasts ${\mu }_{p,c=1}^{\text{calibr}}-{\mu }_{p,c=2}^{\text{calibr}}$, though still not equal to the target causal effect μ_p(t = 1) – μ_p(t = 2) of (1) in each pair, should, (a) share the property with the uncalibrated estimands, that is, that their average over pairs equals the average causal effect δ^effect of (4); and (b) provide a basis for more efficient estimators than the uncalibrated contrasts. This is true if the design is more carefully formalized as follows:

Condition 3. The characteristics of a clinical practice, that is, the distribution of potential outcomes under treatments 1 and 2 conditionally on covariates, the distribution of covariates, and the number of people served by clinical practice c, namely the vector of functions [F_p,c(·|·,t = 1), F_p,c(·|· , t = 2), G_p,c(·), N_p,c], is exchangeable (in distribution over pairs) between clinical practices c = 1 and c = 2.

Then we have the following:

Result 2. (a) Under Condition 3, the average over pairs of the covariate-calibrations, ${\mu }_{p,c=1}^{\text{calibr}}$, that is, based on the clinical practice assigned to treatment 1 in each pair (see (8)) equals the average of the potential outcomes if the entire population had been assigned treatment 1 (similarly for treatment 2); hence the estimable contrast

$$E\left\{{\mu }_{p,c=1}^{\text{calibr}}\right\}vs.E\left\{{\mu }_{p,c=2}^{\text{calibr}}\right\}$$ (8)

equals the causal contrast (2); (b) if μ_p,c(x; t = c) are known, then the MLEs of $E\left\{{\mu }_{p,c=1}^{\text{calibr}}\right\}$ in (8) (and of the target estimands μ(t) in (2), due to (a) and the invariance property of the MLE) are the averages, over the observed pairs, of the empirical analogues of (8):

$$\int {\mu }_{p,c}(x;t=c)\mathrm{d}{\widehat{G}}_p\left(x\right),c=1,2,$$ (9)

where Ĝ_p is the weighted empirical distribution of covariates in pair p (the weight is determined by N_p,c).

Condition 3 implies Condition 1. The proof of Result 2 (a) follows by iterated expectations; the proof of (b) follows because the empirical distribution Ĝ_p (x) as defined above is, under no other assumptions, the MLE of G_p(x).

In practice, and simplifying the notation for the estimable averages μ_p,c(x; t = c)to μ_p,c(x), one can consider modeling μ_p,c(x) for each (pair p, cluster c), with μ_p,c(x; θ), where

$$h\left\{{\mu }_{p,c}(x,\theta )\right\}={\theta }_{p,c}+{\theta }_{cov}^{\prime }\cdot x\text{and}h\text{is a link function}.$$ (10)

Since these models condition on the pairs and clusters, the parameter θ can be estimated by weighted least squares estimator $\widehat{\theta }$ based on the first moment residuals Y_p,c,k – μ_p,c(X_p,c,k,θ), where approximately

$$\widehat{\theta }\mid \theta ,{\Sigma }_{\widehat{\theta }}\sim \text{Normal}(\theta ,{\Sigma }_{\widehat{\theta }}),$$ (11)

and where ${\Sigma }_{\widehat{\theta }}$ is the true variance-covariance matrix of $\widehat{\theta }$ which can be estimated by the robust variance-covariate matrix denoted by ${\widehat{\Sigma }}_{\widehat{\theta }}$.

Based on these, the calibrated estimands in (8) can be estimated within each pair and clinical practice, by

$$\widehat{{\mu }_{p,c}^{\text{calibr}}}=\int {\mu }_{p,c}(x,\widehat{\theta })\mathrm{d}{\widehat{G}}_p\left(x\right),\text{for all}p,c,$$ (12)

whose joint distribution can be approximated by the delta method as

$$\text{lvevel}1:\left[\begin{array}{cc}\hfill \widehat{{\mu }_{p=1,c=1}^{\text{calibr}}}\hfill & \hfill \widehat{{\mu }_{p=1,c=2}^{\text{calibr}}}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \widehat{{\mu }_{p=N,c=1}^{\text{calibr}}}\hfill & \hfill \widehat{{\mu }_{p=N,c=2}^{\text{calibr}}}\hfill \end{array}\right]\mid \theta ,{\Sigma }_{{\widehat{\mu }}^{\text{calibr}}}\sim \text{Normal}\left\{\left[\begin{array}{cc}\hfill {\mu }_{p=1,c=1}^{\text{calibr}}\hfill & \hfill {\mu }_{p=1,c=2}^{\text{calibr}}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\mu }_{p=N,c=1}^{\text{calibr}}\hfill & \hfill {\mu }_{p=N,c=2}^{\text{calibr}}\hfill \end{array}\right],{\Sigma }_{{\widehat{\mu }}^{\text{calibr}}}\right\},$$ (13)

and where ${\Sigma }_{{\widehat{\mu }}^{\text{calibr}}}$ can be estimated by ${\widehat{\Sigma }}_{{\widehat{\mu }}^{\text{calibr}}}$.

4.2. Estimation of Quantities of Original Interest

Expression (13) can be used for estimation of the causal contrast μ(1) vs. μ(2) (because of Result 2(a)); here we focus on δ^effect = μ(1) – μ(2). Specifically, setting ${\delta }_p^{\text{calibr}}={\mu }_{p,c=1}^{\text{calibr}}-{\mu }_{p,c=2}^{\text{calibr}}$ and ${\widehat{\delta }}_p^{\text{calibr}}=\widehat{{\mu }_{p,c=1}^{\text{calibr}}}-\widehat{{\mu }_{p,c=2}^{\text{calibr}}}$ we can consider the first or both levels of the following two-level model level 1’:

$$\text{level}1’:\left[\begin{array}{c}\hfill {\widehat{\delta }}_1^{\text{calibr}}\hfill \\ \hfill ⋮\hfill \\ \hfill {\widehat{\delta }}_N^{\text{calibr}}\hfill \end{array}\right]\mid \left[\begin{array}{c}\hfill {\delta }_1^{\text{calibr}}\hfill \\ \hfill ⋮\hfill \\ \hfill {\delta }_N^{\text{calibr}}\hfill \end{array}\right],\theta ,{\Sigma }_{{\widehat{\delta }}^{\text{calibr}}}\sim \text{Normal}\left\{\left[\begin{array}{c}\hfill {\delta }_1^{\text{calibr}}\hfill \\ \hfill ⋮\hfill \\ \hfill {\delta }_N^{\text{calibr}}\hfill \end{array}\right],{\Sigma }_{{\widehat{\delta }}^{\text{calibr}}}\right\},$$ (14)

$$\text{level}2’:{\delta }_p^{\text{calibr}}\mid {\delta }^{\text{effect}},{\tau }^2\sim \text{Normal}({\delta }^{\text{effect}},{\tau }^2),p=1,\dots ,N,$$ (15)

where expression (14) follows from (13), and the covariance matrix ${\Sigma }_{{\widehat{\delta }}^{\text{calibr}}}$, obtained by the delta method, can be estimated by ${\widehat{\Sigma }}_{{\widehat{\delta }}^{\text{calibr}}}$.

Table 1 shows the results for the calibrated estimates as derived from expressions (13) and (14) (see rows for outcome “calibrated on covariates”) for each of the seven pairs in the Guided Care study. The covariates that are involved in the calibration are listed in Table 3. It is notable that these calibrated differences, ${\widehat{\delta }}_p^{\text{calibr}}$, are positive, in favor of the control condition, for all pairs p.

Using these, Table 2 also reports the estimate of the overall effect δ^effect , first based only on the design-derived fact Result 2(a) that the average of ${\delta }_p^{\text{calibr}}$ over pairs equals the effect of interest δ^effect and ${\delta }_p^{\text{calibr}}$ can be estimated by ${\widehat{\delta }}_p^{\text{calibr}}$ as in (14) (see 1st level, “calibrated on covariates”). As with the uncalibrated first-level approach, this first-level calibrated approach makes no further assumptions about the joint distribution of $pr({\delta }_p^{\text{calibr}},{\Sigma }_{{\widehat{\delta }}^{\text{calibr}}})$, and the MLE of δ^effect is the unweighted sample average of ${\widehat{\delta }}_p^{\text{calibr}}$ (here, its standard error is estimated by the jackknife, although in general it is difficult to trust a confidence interval from a normal approximation with seven pairs). For this reason, we also calculated the significance level of the MLE by permutation of the treatment labels, thus testing the hypothesis of no true effect in any pair. In this case, and because all calibrated estimated differences have the same sign, the permutation based significance level is 2/(2⁷) = 0.016 in favor of the control condition.

For a two-level approach based on (14) and (15), one can estimate δ^effect, by first obtaining the marginalized likelihood, say, $L({\delta }^{\text{effect}},{\tau }^2,{\Sigma }_{{\widehat{\delta }}^{\text{calibr}}})$. After plugging in ${\widehat{\Sigma }}_{{\widehat{\delta }}^{\text{calibr}}}$ for ${\Sigma }_{{\widehat{\delta }}^{\text{calibr}}}$, we estimated δ^effect by three different methods: (i) the MLE; (ii) the MLE after profiling τ² out; and (iii) the posterior distribution of δ^effect using noninformative priors for τ² and δ^effect. We use a uniform shrinkage prior for the second-level variance τ² advocated by Daniels (1999). These results for the two-level approach are given in Table 2 (see rows 1st+ 2nd level, “calibrated on covariates”; MLE, pMLE, and Bayes, respectively).

As with the uncalibrated approach, the marginalized likelihood that uses (14) and (15) assumes that ${\delta }_p^{\text{calibr}}$ is independent of ${\Sigma }_{{\widehat{\delta }}^{\text{calibr}}}$. Figure 2, right panel, plots estimates of the square root of the diagonals of ${\Sigma }_{{\widehat{\delta }}^{\text{calibr}}}$, $\sqrt{v_p^{\text{calibr}}}$, versus estimates of ${\delta }_p^{\text{calibr}}$. Although the plot can be to some degree affected by measurement error, the R² of 0.20 suggests that some dependence exists. Although this dependence could be modeled in a modified second level, it is unclear how convincing such an approach would be as it would introduce even more modeling assumptions. To avoid this, we calculated instead the significance level of the two-level MLE estimate when evaluated from the permutation distribution of the treatment labels.

4.3. Assessment of the Hypothesis of No Effect

The proposed approach, in addition to being robust for hypothesis testing when evaluated by permutation, is likely to have a more general robustness property analogous to the one arising in a simpler design. Specifically, in the design of complete randomization of units (no pairing, no cluster-level randomization), Rosenblum and van der Laan (2010) have shown that a certain class of parametric models for covariates yield MLEs for the causal effect that are consistent for the null value if indeed there is no effect on any person, even if the models are incorrect. Shinohara, Frangakis, and Lyketsos (2012) showed that an extended class of models has this robustness property if the models satisfy an easy-to-check symmetry criterion.

For the matched-paired clustered-randomization design, analogous classes of models with such robustness property may also exist. Specifically, suppose that, more generally than model (10), we conceptualize a parametric model as one that allows distributions m_p,c(y | x) for the outcome at value y given covariate at value x for each (pair,cluster) labeled (p, c). Many flexible models m_p,c(·|·) (or, for brevity, m_p,c), including (10), have the property that if, for two pairs and their clusters

$$\left(\begin{array}{cc}\hfill p_1{c}_1\hfill & \hfill p_1{c}_2\hfill \\ \hfill p_2{c}_1\hfill & \hfill p_2{c}_2\hfill \end{array}\right)$$

the model allows the distributions

$$\left(\begin{array}{cc}\hfill m_{1,1}\hfill & \hfill m_{1,2}\hfill \\ \hfill m_{2,1}\hfill & \hfill m_{2,2}\hfill \end{array}\right),$$

then it also allows the distributions

$$\left(\begin{array}{cc}\hfill m_{2,2}\hfill & \hfill m_{1,2}\hfill \\ \hfill m_{1,2}\hfill & \hfill m_{2,2}\hfill \end{array}\right)\text{and}\left(\begin{array}{cc}\hfill m_{1,1}\hfill & \hfill m_{2,1}\hfill \\ \hfill m_{2,1}\hfill & \hfill m_{1,1}\hfill \end{array}\right).$$

The intuition of this property is that the model allows exchangeable distributions between any two observed pairs. Following a similar reasoning to that of Shinohara et al. (2012), we hypothesize that if (a) there is no effect of intervention in the distribution of any cluster, that is, in the true distributions defined in Condition 3, F_p,c(·|·; t = 1) = F_p,c(·|·; t = 2) for all p, c, and (b) a model that has the above symmetry property is used, then the limit of the MLE of the causal effect (8) is null even if the model is incorrect. A detailed treatment of this issue can allow for combining validity with increased efficiency in such designs as well.

5. Discussion

For the design that matches clusters of units and assigns interventions to clusters within pairs, we proposed an approach that estimates the average causal effect while also explicitly calibrating possibly covariate imbalance between the clusters. The approach can use only one level for inference, or can be used in a hierarchical model.

In the Guided Care study, a first-level inference with the new approach reports estimates of the causal effect with smaller estimated variance than that without using covariates (see Table 2). Although it is difficult to know if this is objectively true in this small sample of pairs, the results from the permutation tests between the two approaches are also consistent with this conclusion. A simple two-level approach, with or without covariates, makes an implicit assumption which can invalidate causal comparison of the interventions, and explicitly addressing the assumption would introduce additional modeling. The covariate-calibrated approach reports that the control condition leads to higher, albeit clinically insignificant, average overall SF36 score compared to that under Guided Care Nurse intervention, using either a single-level (approximate or permutation-based) analysis or a two-level permutation-based analysis (see Table 2).

The proposed approach is expected to be more generally robust to model misspecification when assessing the hypothesis of no effect, if the model (10) belongs in a relatively broad class. This expectation needs formal verification, but, if confirmed, can lead to more efficient estimation, and, hence, more efficient use of resources.

An alternative to the proposed approach can be to break the matching and then use regression-assisted (Donner, Taljaard, and Klar, 2007) or doubly robust estimators (Rosenblum and van der Laan, 2010) to estimate the treatment effect. Based on Rubin's (Rubin, 1978) theory, the matched design is still ignorable (and so the matching can be broken) if these variables that were used to create the matching are still available and are included in the outcomes model. In contrast, if these variables are not used in the model, then the design is not ignorable if the matching is broken, and this can generally lead to bias at least in the expression of the uncertainty in inference.

Appendix

Proof of Result 1

We show that the MLE of δ^effect based on the standard meta-analytic likelihood (6) is generally inconsistent. To do this, consider the simple but informative case of a population of pairs of practices as shown in Figure A.1, where μ follows the positive half of the standard normal distribution across such pairs. Because ${\delta }_p^{\text{crude}}$ is μ or – μ with probabilities $(\frac{1}{2},\frac{1}{2})$, marginally the normality of the distribution of ${\delta }_p^{\text{crude}}$ at the second level of (6) holds with ${\delta }^{\text{effect}}(=E\left({\delta }_p^{\text{crude}}\right))=0$ and with $\mathrm{var}\left({\delta }_p^{\text{crude}}\right)=1$. Consider also, for simplicity, that $\mathrm{var}\left({\delta }_p^{\text{crude}}\right)$ is known, and that within clinical practices, the number of patients sampled is a constant n and the variances ${\sigma }_{p,c}^2\left(t\right)$(t) are known and are as given in Figure A.1. Then, the maximizer ${\widehat{\delta }}^{\text{effect}}$ of the likelihood in (6) is ${\sum }_p{u}_p{\widehat{\delta }}_p^{\text{crude}}∕{\sum }_p{u}_p$, where ${\left(u_p\right)}^{-1}=\mathrm{var}\left({\delta }_p^{\text{crude}}\right)+v_p^{\text{crude}}$, and

$$v_p^{\text{crude}}=\{\begin{array}{cc}{w}_1=\frac{2}{n},\hfill & \text{it the practice}p{\text{is of type}}_p=1;\hfill \\ w_2=\frac{1+{\sigma }^2}{n},\hfill & \text{if the practice}p{\text{if of type}}_p=2.\hfill \end{array}\phantom{\}}$$

The probability limit of ${\widehat{\delta }}^{\text{effect}}$ is $E\left(u_p{\widehat{\delta }}_p^{\text{crude}}\right)∕E\left(u_p\right)$, and its sign will be the sign of $E\left(u_p{\widehat{\delta }}_p^{\text{crude}}\right)$. Here, although $E\left({\widehat{\delta }}_p^{\text{crude}}\right)=0$, Condition 2 fails because the sign of ${\delta }_p^{\text{crude}}$ depends on the magnitude of the variance v_p. In particular, $E\left(u_p{\widehat{\delta }}_p^{\text{crude}}\right)=E\left\{E(u_p{\widehat{\delta }}_p^{\text{crude}}\mid {\text{type}}_p)\right\}=\frac{\mu }{2}[{\{\mathrm{var}\left({\delta }_p^{\text{crude}}\right)+w_2\}}^{-1}-{\{\mathrm{var}\left({\delta }_p^{\text{crude}}\right)+w_1\}}^{-1}]$ which is non zero if δ² ≠ 1. This means that even if the null hypothesis of no intervention effect on the means is correct, the standard meta-analytic approach (6) is inappropriate if the intervention has an effect on the variance in at least one clinical practice.

Figure A.1.

Structure for the example used in the proof of Result 1 (Appendix). Shown is one true type of pair and the two types of observed pairs to which it can give rise, depending on which clinical practice is assigned control. In each parentheses shown are the mean and variance of the potential outcomes of patients of the corresponding clinical practice and under a give treatment, as denoted in Figure 1.