Characterizing the microstructures of biological tissues using Mueller matrix and transformed polarization parameters

Abstract

Mueller matrices can be used as a powerful tool to probe qualitatively the microstructures of biological tissues. Certain transformation processes can provide new sets of parameters which are functions of the Mueller matrix elements but represent more explicitly the characteristic features of the sample. In this paper, we take the backscattering Mueller matrices of a group of tissues with distinctive structural properties. Using both experiments and Monte Carlo simulations, we demonstrate qualitatively the characteristic features of Mueller matrices corresponding to different structural and optical properties. We also calculate two sets of transformed polarization parameters using the Mueller matrix transformation (MMT) and Mueller matrix polar decomposition (MMPD) techniques. We demonstrate that the new parameters can separate the effects due to sample orientation and present quantitatively certain characteristic features of these tissues. Finally, we apply the transformed polarization parameters to the unstained human cervix cancerous tissues. Preliminary results show that the transformed polarization parameters can provide characteristic information to distinguish the cancerous and healthy tissues.

1. Introduction

Polarization imaging techniques provide rich microstructural and optical information of samples, and have been tested in material, textiles and biomedical applications [1–5]. For biomedical tissues, many polarization parameters have been proposed to describe the distinctive pathological structures. For instance, the differential polarization (DP) [6] and the degree of polarization (DOP) [7,8] were used to detect human skin cancers. A Mueller matrix provides a comprehensive characterization of the polarization properties of the sample [9]. However, it describes only how the polarization state of light changes before and after the interaction with the media, but gives little information on the physics of the photon-tissue interactions and the microstructure of the scattering media. Moreover, for anisotropic media, many of the Mueller matrix elements vary with the orientation of the sample, making quantitative characterizations even more difficult [10,11]. Following certain transformation processes, one can derive new sets of polarization parameters which are functions of the Mueller matrix elements, but separate the effects due to sample orientation and present an explicit relationship to the structural and optical properties of the sample.

One of such processes is the Mueller matrix transformation (MMT) we proposed in previous works [12,13]. Both the experimental results of phantoms and the Monte Carlo simulation based on the sphere-cylinder scattering model confirm that the MMT parameters are not sensitive to the orientation of anisotropic sample, and are closely related to the characteristic features such as the alignment of the fibrous structure or density of the intracellular submicron organelles [13]. Another example of such transformation processes is the Mueller matrix polar decomposition (MMPD) technique proposed by Lu and Chipman [14], which converts a Mueller matrix into new parameters of clear physics meanings, such as: diattenuation, retardance (both linear retardance and circular retardance), and depolarization power. Again, these parameters separate effects due to the orientation angle and the microstructure of the sample [15–17].

In this paper, we select a group of tissue samples of distinctive structural properties and take the backscattering Mueller matrix measurements. Assisted by Monte Carlo simulations, we demonstrate the characteristic features in the experimental Mueller matrices for different tissues. Then we calculate the transformed polarization parameters following the MMT and MMPD procedures, and demonstrate again quantitatively the characteristic features. We apply these parameters to the unstained human cervix cancerous tissues to show the feasibility of cancer diagnosis. Experimental results indicate that the MMT and MMPD parameters can provide the microstructural information to differentiate the cancerous and healthy tissues.

2. Methods and materials

2.1 Mueller matrix imaging experimental setup

In this paper, we take the backscattering Mueller matrices using a dual rotating retarder configuration described by Azzam, Goldstein and Chipman [18–20]. As shown in Fig. 1 , the light from the LED (1 W, 633 nm) passes through the polarizer (P1, Thorlabs) and quarter-wave plate (QW1, Thorlabs). The photons backscattered from the sample pass through the analyzing quarter-wave plate (QW2, Thorlabs) and polarizer (P2, Thorlabs), and are recorded by a 12-bit CCD camera (QImaging 32-0122A). There is a 20 degree angle between the incident light and the CCD camera axis to avoid the surface reflection from the sample.

Fig. 1.

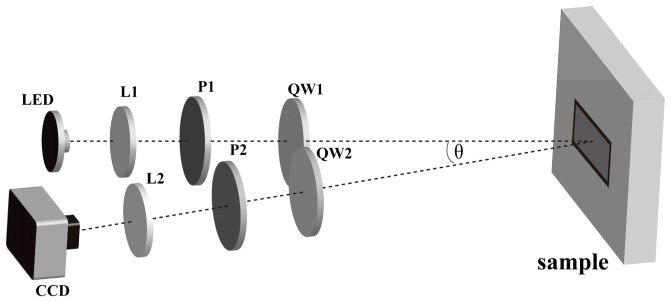
Schematic of experimental setup for the backscattering Mueller matrix measurement. P: polarizer; QW: quarter-wave plate; L: lens. The polarized light illuminates the sample at about 20 degree to the normal to eliminate the surface reflection. The diameter of the illumination area is about 1.8 cm.

During the measurements, the polarizers (P1, P2) are fixed in the horizontal direction, which is parallel to the source-sample-camera triangle plane. The two retarders (QW1, QW2) rotate with a fixed rate θ₁ = 5θ_{2 .} The Fourier series intensities are given by Eq. (1).

$$I={\alpha }_0+{\displaystyle \sum }_{n=1}^{12}\left({\alpha }_n\cos 2{\text{nθ}}_1+{\beta }_n\sin 2{\text{nθ}}_1\right)$$ (1)

where α_n and β_n are the Fourier coefficients, θ₁ is the rotation angle of the retarder QW1. The Mueller matrix elements can be calculated by using the Fourier coefficients according to [18]. More details on this Mueller matrix imaging method can be found in [19,20]. Before applied to tissue samples, the setup was calibrated with standard samples of known polarization properties. The maximum errors for the absolute values of the Mueller matrix elements are about 0.01.

2.2 Transformed polarization parameters

Apart from the Mueller matrix elements, we also use polarization parameters derived from certain transformation processes. One set of such parameters shown as Eq. (2) is extracted using the Mueller matrix transformation (MMT) technique proposed in our previous simulation and experimental studies on fibrous scattering samples [12]. Experiments and Monte Carlo simulation based on the sphere-cylinder scattering model [21–23] have shown that the Mueller matrix elements can be fitted to trigonometric functions, and there are several independent parameters can be extracted from the transformation process [12].

$$\begin{array}{l}A=\frac{2b\cdot t}{b^2+t^2}\in [0,1]\\ b=\frac{m22+m33}{2} \\ t=\frac{\sqrt{{(m22-m33)}^2+{(m23+m32)}^2}}{2}\\ \tan (2x)=\frac{m13}{m12}\end{array}$$ (2)

We have testified that the parameter A characterizes the order of alignments of the fibrous scatterers. There are signs indicating that A is also related to other factors which affect the anisotropy of the sample, such as birefringence. The parameter b is much more sensitive to the number density of the sub-wavelength “small” intracellular organelles than to those “large” cell nuclei [13]. The Mueller matrix transformation parameters A and b are extracted from the m22, m23, m32 and m33 elements, which have different physics meanings [10]. The parameter A shows the difference between the m22 and m33 elements, which is closely related to the aligned anisotropic structures. The parameter b is related to the diagonal m22, m33 elements, which are strongly correlated to the depolarization properties of the scattering media. For instance, for the backscattering Mueller matrices of scattering media, the smaller m22 and m33 (smaller parameter b) mean the larger depolarization [11]. The parameter x relates to the direction of fibrous structures [12]. Previous studies have shown that as the fibrous structures rotate, the m12 and m13 elements represent periodical intensity variations. Thus the m12 and m13 can be used to detect the orientation of fibrous scatterers shown as the parameter x [12].

We also adopt another set of transformed polarization parameters from the Mueller matrix polar decomposition (MMPD) technique [14]. The MMPD procedure transforms a Mueller matrix into a group of new parameters representing diattenuation D, retardance R (containing linear retardance δ and circular retardance Ψ), depolarization power Δ. All these parameters are insensitive to the orientation angle of the sample.

2.3 Biological tissue samples

We select tissue samples of distinctive structural and optical properties: chicken heart muscle Fig. 2(a) , bovine skeletal muscle Fig. 2(b), porcine liver Fig. 2(c) and porcine fat Fig. 2(d). Both the chicken heart and bovine skeletal muscle tissues are highly anisotropic due to the well aligned muscle fibers. Previous studies have shown that the anisotropy of tissues can originate from both scattering and optical birefringence. However, the anisotropy of scattering and of birefringence can hardly be distinguished by the Mueller matrix decomposition process quantitatively [22,23]. In the cross sectional area of chicken heart sample shown in Fig. 2(a), the muscle fibers are concentrically aligned around the ventricle. From the white light cross sectional image of the chicken heart sample we can observe that there are muscle fibers aligned parallel to the imaging X-Y plane in zone 1, whereas zone 2 contains randomly oriented muscle fibers. More detailed information of the heart muscle fiber orientations in different parts can be found in [24,25]. For the bovine skeletal muscle sample show in Fig. 2(b), the fibers are mostly distributed along a particular direction. The porcine liver and fat tissues on the other hand are both isotropic. The liver tissues contain much more complicated microstructure and stronger absorption than the fat tissues. Liver is a major vital organ and has hundreds of separate functions including glycogen storage, plasma protein synthesis, hormone production, and detoxification. The complicated microstructure of liver tissue and abundant organelles in liver cells are closely related to these physiology functions. Thus, a novel imaging method to accurately discrete the sub-wavelength structural information of unstained liver tissues can be helpful for the detection of many hepatic diseases with characteristic microstructural variations in the surface layer of the liver. During the imaging process, we keep the surface of the sample flat to avoid local over-exposure due to surface reflection.

Fig. 2.

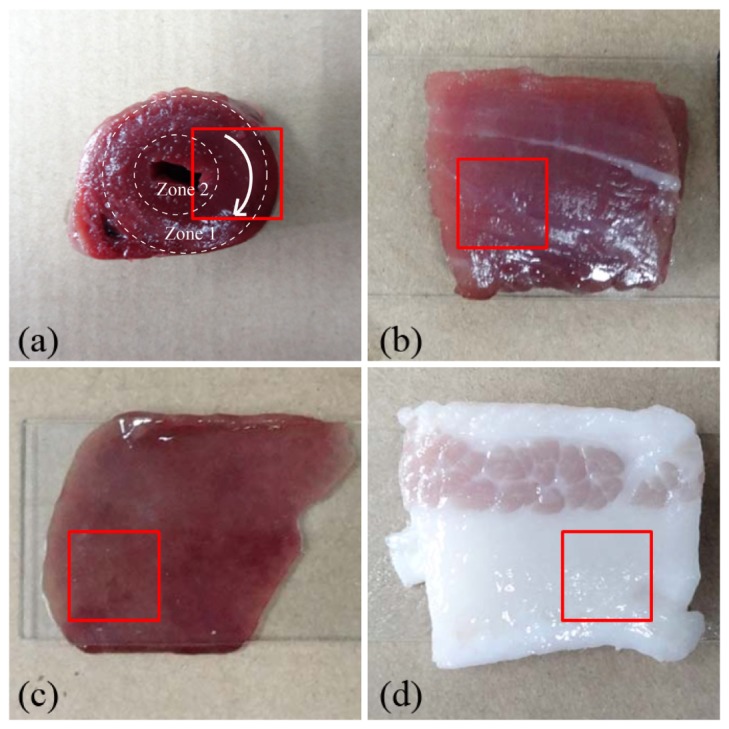
Photographs of the biological samples: (a) chicken heart tissue, (b) bovine skeletal muscle tissue, (c) porcine liver tissue, (d) porcine fat tissue. In order to show more structural details of the tissues, we choose 1 cm × 1 cm squares from the illumination areas as the imaging regions, which are marked by the red squares. For the chicken heart sample, zone 1 contains muscle fibers aligned parallel to the imaging X-Y plane, the white arrow line indicates the orientation of muscle fibers; zone 2 contains randomly oriented muscle fibers [24,25].

2.4 Human cervical cancer sample

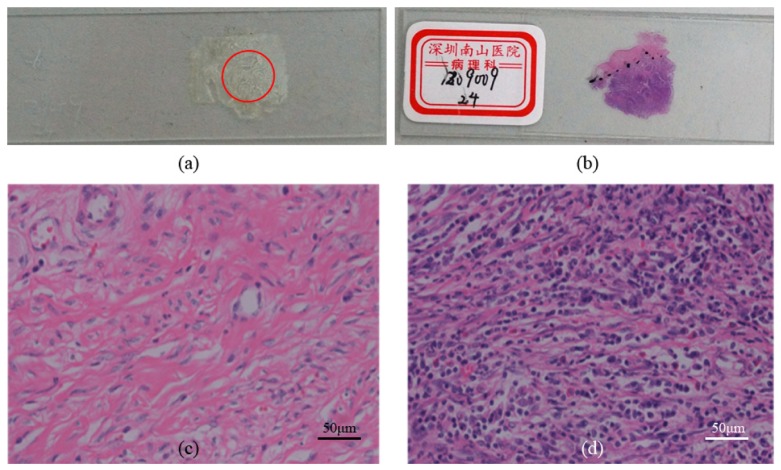
To testify the potential applications of polarization imaging techniques on biomedical diagnosis, we also apply the MMT and MMPD methods to some human cancerous tissue samples. We choose the anisotropic human cervix carcinoma tissue samples (Fig. 3 ). Most cervix carcinoma cases are originated from the infection of Human Papillomavirus (HPV), which can lead to cervical intraepithelial neoplasia (CIN) of the epithelium cells. As the CIN developing, when the carcinoma cells break the basal membrane of the epithelium layer the CIN converts to invasive cancer. Recently, polarization imaging techniques have shown possibilities to distinguish healthy and dysplastic cervical tissues. For instance, Pierangelo et al. measured the Mueller matrices of human cervix samples in different CIN stages, and reported that the healthy cervix tissues are highly anisotropic, resulting in different DOP imaging contrasts when the tissues were rotated [26]. They also found that the CIN lesions have smaller values of anisotropy, or MMPD parameter R than the healthy tissues. The samples used in this study are provided by Shenzhen Sixth People’s (Nanshan) Hospital. The sample for backscattering polarization imaging shown in Fig. 3(a) is an unstained 28 μm thick slice of the cervix tissue cut from the dehydrated paraffin. Previous studies have shown that comparing with the standard 4 μm thick slices of tissues, there are some multiple scattered photons from the 28 μm thick slices, which can be used for the backscattering Mueller matrix imaging studies [13]. For pathological comparisons, we also prepared the corresponding hematoxylin-eosin (H-E) stained 4 μm thick slice as shown in Fig. 3(b). The microscope images of the H-E stained slice shown in Fig. 3(c) and 3(d) show that the dysplastic region is with a darker stained color (denser and larger cell nuclei) than the healthy cervical region.

Fig. 3.

(a) Photograph of the 28 μm thick slice of unstained human cervix carcinoma tissue, the red circle indicates the imaging region, (b) photograph of the 4 μm thick slice of corresponding H-E stained human cervix carcinoma tissue, (c) microscope image of the H-E stained tissue of healthy region, (d) microscope image of the H-E stained tissue of cancerous region.

3. Results and discussion

3.1 Characteristic features in backscattering Mueller matrix elements

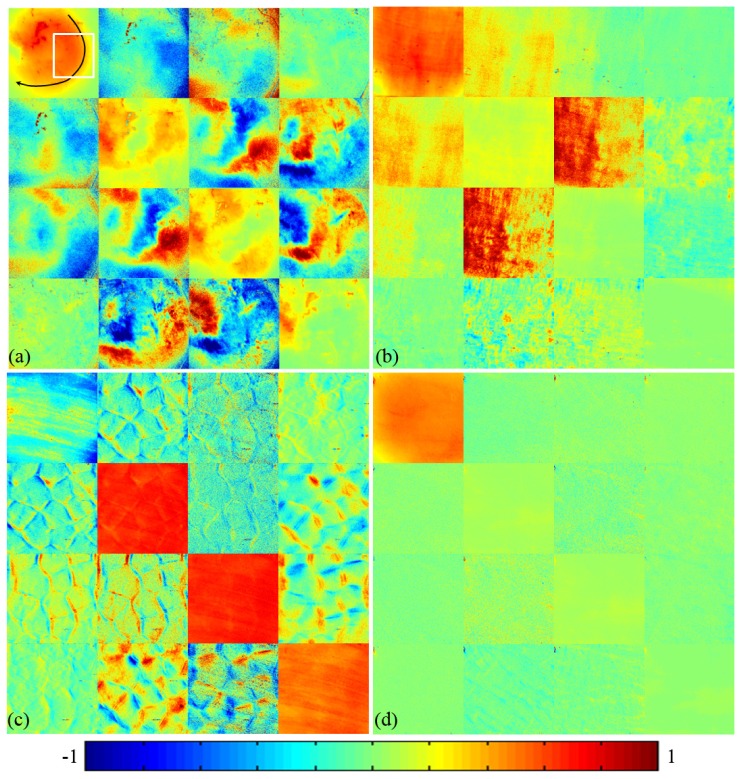
Figure 4 shows the experimental results of the backscattering Mueller matrices of different tissue samples. All the matrix elements are normalized by the m11. It can be observed from the Mueller matrices of chicken heart sample shown in Fig. 4(a) and bovine skeletal muscle sample shown in Fig. 4(b) that there are some prominent characteristic features of anisotropic media. Whereas the Mueller matrices of the liver sample shown in Fig. 4(c) and fat sample shown in Fig. 4(d) represent characteristic features of isotropic media. In previous experimental studies on phantoms and Monte Carlo simulations, we have learned that examining the characteristic behaviors of the Mueller matrix elements reveals very rich information on the structural or optical properties of samples, such as the depolarization power, the orientation and density of fibrous structures, the optical birefringence and absorption ability. First, the anisotropic and isotropic structures can be distinguished by the following characteristics. Mueller matrices of isotropic samples have diagonal elements only, and the magnitudes of the m22 and m33 elements are equal. Mueller matrices of anisotropic samples have both diagonal and non-diagonal elements. The m22 and m33 elements are different. The difference between the m22 and m33, and the magnitudes of non-diagonal elements will increase as the anisotropy of the sample increases [10]. Second, both the fibrous scatterers and optical birefringence can contribute to anisotropy [23]. However, the anisotropy originated from scattering on fibrous scatterers and from propagation in birefringent media show different features in the Mueller matrix: the fibrous scatterers induce periodical intensity variations in the m12, m21, m13, and m31 elements (m12 = m21, m13 = m31), while birefringence induces periodical intensity variations in the m24, m42, m34, and m43 elements (m24 = -m42, m34 = -m43). It is also found that the elements m22, m33, m23 and m32 are affected by both the scattering and optical anisotropy. The signs and intensities of these elements can be used to determine the directions of the aligned fibers or the birefringence [12]. Last, the intensities of diagonal elements m22, m33 and m44 are closely related to the depolarization and absorption capabilities of samples. Monte Carlo simulations have testified that, for isotropic samples higher number density of sub-wavelength small scatterers and larger absorption can both result in larger values of the normalized diagonal m22 and m33 elements for backscattering Mueller matrices, and also smaller depolarization [27]. It should be pointed out that, although the denser small scatterers and larger absorption have similar influence on the diagonal elements of normalized backscattering Mueller matrices, they can be distinguished if the Mueller matrices are not normalized.

Fig. 4.

Experimental results of backscattering Mueller matrices of biological samples: (a) chicken heart tissue (the black arrow line in m11 indicates the approximate orientation of muscle fibers. The white square indicates the approximate area chosen for the calculation of average values of Mueller matrix elements), (b) bovine skeletal muscle tissue, (c) porcine liver tissue, (d) porcine fat tissue. All the Mueller matrix elements are normalized by the m11. The color codes are from −1 to 1 for m11, m22, m33, and m44, and from −0.1 to 0.1 for other elements. The imaging area is about 1 cm × 1 cm.

The Mueller matrices of chicken heart shown in Fig. 4(a) and bovine skeletal muscle shown in Fig. 4(b) samples show prominent characteristic features of anisotropic media as discussed above. First, we can see that the Mueller matrices for heart and skeletal muscle samples are non-diagonal. Moreover, the magnitudes of the diagonal elements m22 and m33 are not equal. Figure 4(a) also shows that, as the orientation of the muscle fibers changes (indicated by the black arrow line), the Mueller matrix elements represent periodical intensity variations, which can be described by trigonometric functions [12]. The signs and values of the elements are correlated to the orientation and order of alignment of the fibers. For instance, in Fig. 4(b) the muscle fibers are mostly distributed along the x-axis, leading to a larger value of the m22 than m33, and also positive values of the m12 and m21 elements. We also notice that the m24, m34, m42 and m43 elements of chicken heart muscle sample are more prominent than bovine skeletal muscle sample, confirming that the birefringence effect of the former is stronger than that of the latter.

Meanwhile, the Mueller matrices shown in Fig. 4(c) and 4(d) reveal that the liver and fat tissues are mostly isotropic. For the fat and most parts of the liver tissues, their Mueller matrices are diagonal and their magnitudes satisfy the relation m22 = m33>m44. However, it can be observed in Fig. 4(c) that there are some hexagonal structures distributed around the isotropic liver tissues. At anatomic level, the hexagonal structures are supposed to be the boundaries of hepatic lobules, which are connective tissues. In order to confirm that the hexagonal structures are resulting from the hepatic lobules rather than the surface roughness, we measured several different liver tissue samples. During the measurements the surface of the sample was kept flat. The large values of the m24, m42, m34 and m43 elements and their characteristic relationships (m24 = -m42, m34 = -m43 as shown in Fig. 4) indicate that these connective tissues are highly birefringent. Considering the positive or negative signs of these elements we can extract both the magnitude and orientation of birefringence for tissues with complicated microstructure. Comparisons between Fig. 4(c) and 4(d) also reveal that although both tissues are mostly isotropic, there are still some distinctive differences between the liver and fat samples. For example, the fat tissue has smaller diagonal m22, m33 and m44 elements, showing a stronger depolarization power than the liver tissue. For the liver tissues, there are more metabolism related organelles such as mitochondria, lysosomes, and ribosomes (a few hundred nanometers in diameter) than fat tissues. The abundant organelles and notable absorption of the liver sample therefore lead to larger values of diagonal elements shown in Fig. 4(c) compared to the fat sample shown in Fig. 4(d) [13,27].

The overall characteristics features of different tissues are more clearly shown in Tab. 1 , which lists only the average values of the Mueller matrix elements for chicken heart, bovine muscle, porcine liver and fat tissues. For a direct comparison between the heart and skeletal muscle fibers, we choose an area of the chicken heart sample for calculation indicated by the white square in Fig. 4(a). For the turbid biological tissues with strong depolarization properties, their diagonal m22, m33 and m44 elements are larger than the others. The magnitudes of these averaged matrix elements can also distinguish tissues with different microstructure. For the isotropic liver and fat tissues their m22 and m33 elements are equal. For the anisotropic heart and skeletal muscle tissues, however, the m22 and m33 elements are different. When considering both the magnitudes and the signs of the non-diagonal elements, the orientation of the aligned fibrous scatterers can be approximately decided [12]. Table 1 also shows that the liver tissue has the largest diagonal m22, m33 and m44 elements, showing the smallest depolarization power and probably the existence of a large number density of sub-wavelength “small” scattering particles. The average values and signs of the m24, m42, m34 and m43 elements confirm that birefringence contributes to the anisotropy of the chicken heart tissue.

Table 1. Average values of Mueller matrix elements for different tissue samples.

	m12	m21	m13	m31	m22	m33	m23/32	m14/41	m24	m42	m34	m43	m44
heart*	−0.02	−0.01	0	−0.01	0.24	0.18	0.02	0	−0.02	0.02	0.03	−0.02	0.03
muscle	0.03	0.03	0	0	0.16	0.07	0.05	0	0.01	−0.01	−0.01	0.01	0.02
liver	−0.01	−0.01	0	0.01	0.67	0.67	0.01	0	0	0	0.01	−0.01	0.53
fat	0	0	0	0	0.07	0.07	0	0	0	0	0	0	0.02

*Average values of chicken heart are calculated from the area indicated as the white square shown in Fig. 4(a).

3.2 Characteristic features represented by the transformed polarization parameters

Although we can obtain very rich information on the structural or optical properties of the samples by examining the characteristic features of the Mueller matrix elements, such information is usually qualitative rather than quantitative. Also, both the experimental (see Fig. 4) and simulated results have testified that for anisotropic samples, most Mueller matrix elements are sensitive to the sample orientation [10,26]. Such a strong correlation with the orientation of samples will lead to serious influence on polarization measurements, making quantitative assessments even more difficult. Thus, separating the different effects due to the microstructure and orientation is crucial for quantitative characterization of biological tissues.

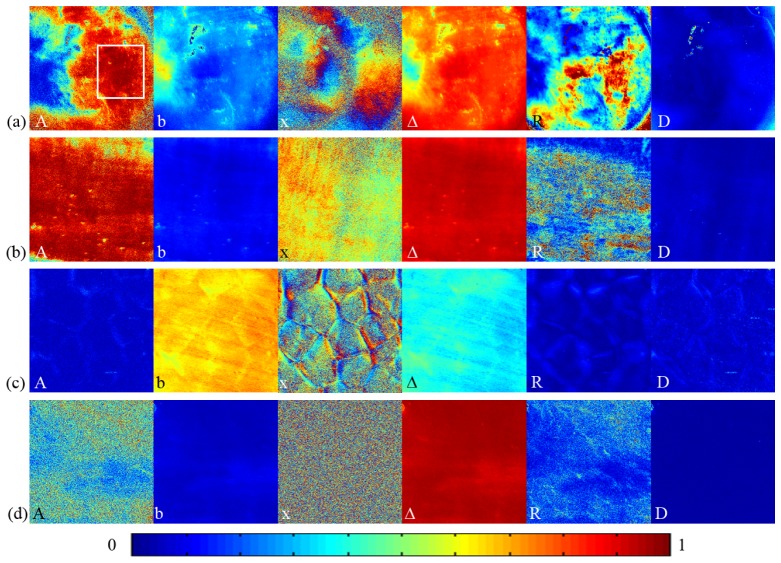
Using certain transformation processes, we can obtain new polarization parameters which are functions of Mueller matrix elements but have more explicit relationship with the intrinsic properties or orientations of the samples. Using Monte Carlo simulation based on a proper microscopic scattering model, we are able to find out the relationships between these parameters and the density, size, shape and orientations of the spherical or cylindrical scatterers, and the optical properties of the ambient media [21–23]. In this section we apply the MMT and MMPD parameters to the tissues. The imaging results of chicken heart sample shown in Fig. 5 confirm that the MMT parameters A, b and MMPD parameters depolarization Δ, retardance R, and diattenuation D are insensitive to the orientation of fibrous structures, while the MMT parameter x reveals the orientation angle of the aligned fibers. It can be observed from Fig. 4(a) that the orientation variation of chicken heart muscle fibers in the white square area induces intensity changes in the Mueller matrix elements. However, for the same white square area in Fig. 5(a), the values of the parameters A, b, Δ, R, and D are close to homogeneous. Moreover, the magnitudes of parameters A and R testify that the heart sample shown in Fig. 5(a) and skeletal muscle sample shown in Fig. 5(b) are anisotropic, the liver sample shown in Fig. 5(c) and fat sample shown in Fig. 5(d) are mostly isotropic. It can also be observed from Fig. 5 that the fat and skeletal muscle tissues are of larger values of depolarization Δ and smaller values of b. Previous studies using Monte Carlo simulations and experiments have shown that as the number density of small sub-wavelength particles increases, the diagonal elements m22 and m33 become larger, resulting in a larger value of the parameter b and a smaller value of the depolarization Δ [12,13]. From the images of these orientation independent polarization parameters we are able to identify finer details in the structure of tissues, such as the boundaries of hepatic lobules showing in A, R, and D images in Fig. 5(c).

Fig. 5.

2D images of MMT and MMPD parameters of biological samples: (a) chicken heart tissue (the white square indicates the approximate area chosen for the calculation of average values of MMT and MMPD parameters), (b) bovine skeletal muscle tissue, (c) porcine liver tissue, (d) porcine fat tissue. The color codes for MMT parameters A, b and MMPD parameters Δ and R are from 0 to 1, the color code for MMT parameter x is from 0 to 90 degree, the color code for MMPD parameter D is from 0 to 0.5.

We also calculate the average values of the MMT and MMPD parameters of tissue samples as presented in Tab. 2 . The biological samples often have a strong degree of heterogeneity, which cannot be reflected in the average values. However, the average values can help us to obtain the dominated features of the samples quickly. The average values of the MMT and MMPD parameters stay almost the same in repeat measurements with different sample orientations, and the measured values can be used as good indicators to distinguish microstructure of tissues, such as the alignment of fibers, or the densities of metabolism-related organelles [13]. For example, the well aligned fibers in heart and skeletal muscle samples lead to bigger values for the parameters A and R, both are correlated to the anisotropy of tissues and are related to some pathological features. It should be pointed out that the MMT parameter A contains contributions from both the birefringent medium and well aligned cylindrical scatterers. For the liver sample the average value of the depolarization is about 0.37, and for the fat and muscle samples their values are above 0.9. This is probably because that liver contains a large number of metabolism related organelles in cells (small scatterers), therefore is with the largest value of b and smallest value of Δ. Meanwhile, for adipocytes the smaller value of b indicates a lower metabolism level compared to other tissues. The experimental results in this section confirm that both the images and average values of the orientation independent transformed polarization parameters are good indicators for quantitative analysis of biological tissues.

Table 2. Average values of MMT and MMPD parameters for different tissue samples.

	A	b	Δ	R	D
heart*	0.91	0.21	0.84	0.69	0.04
muscle	0.88	0.11	0.92	0.42	0.03
liver	0.07	0.67	0.37	0.05	0.04
fat	0.40	0.07	0.95	0.19	0.01

*Average values of chicken heart are calculated from the area indicated as the white square shown in Fig. 5(a).

3.3 Characteristic features in human cervix cancerous tissues

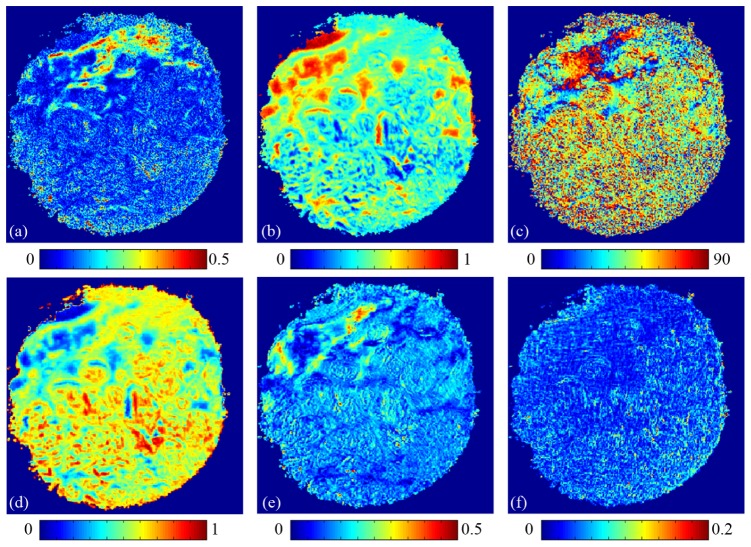
To test the potential applications of the orientation independent parameters on medical diagnosis, we measure the backscattering Mueller matrix of the unstained cervix sample shown in Fig. 3(a), and calculate the images of the MMT and MMPD parameters pixel by pixel as shown in Fig. 6 . It can be seen that for the healthy cervix tissues (upper parts of the images), the retardance R shown in Fig. 6(e) and the anisotropy A shown in Fig. 6(a) are with larger values, confirming that the healthy cervix tissues are highly anisotropic [26]. However, the values of the parameters R and A of the cancerous cervix tissues decrease significantly, indicating a breaking down of the well aligned fibrous structure which is a characteristic feature of cervical cancer [26]. The angle-related MMT parameter x shown in Fig. 6(c) also reveals the order of alignments of the healthy cervix tissues. Meanwhile, we notice that the cancerous regions have a smaller b shown in Fig. 6(b) and larger depolarization Δ shown in Fig. 6(d), which may also be resulted from the destruction of well aligned fibers. The diattenuation D shown in Fig. 6(f) represents no clear difference. Comparisons between microscope and polarization images of the H-E stained and unstained slices reveal that the orientation independent MMT and MMPD parameters can be used as potential tools to distinguish cancerous and normal regions for cervix tissues. In this paper we provide the early stage imaging results of a 28 μm thick slice section as a preliminary demonstration. However, the depolarization and absorption of full thickness tissue samples are larger than the slice sections. Thus, more statistical studies are still needed to show the effectiveness of applying the transformed Mueller matrix parameters to both the sectioned and full thickness samples including human cancerous tissues.

Fig. 6.

2D images of the MMT and MMPD parameters of cervix tissues shown in Fig. 3(a): (a) A, (b) b, (c) x, (d) depolarization Δ, (e) retardance R, (f) diattenuation D.

4. Conclusion

In this paper, we select a group of tissue samples of distinctive structural properties including chicken heart muscle, bovine skeletal muscle, porcine liver and porcine fat, and measure the backscattering Mueller matrices. By comparing the experimental results, we summarize the characteristic features of Mueller matrices of different microstructural and optical properties. First, the anisotropic and isotropic structures can be distinguished by the diagonal elements. Second, both the fibrous scatterers and optical birefringence can result in anisotropy. The anisotropy originated from scattering and birefringence can lead to different features in Mueller matrices. The signs and magnitudes of the matrix elements can be used to decide the directions of the aligned fibers or of the birefringence. Last, the intensities of diagonal elements are closely related to the depolarization and absorption abilities of samples. The experimental results show that using the backscattering Mueller matrices we can distinguish tissues with different characteristic features such as the anisotropy degree, orientation of anisotropic structures, depolarization and absorption abilities. To find out more quantitative and precise relations between the Mueller matrix parameters and microstructural properties of tissues, statistical studies on different tissue samples are still needed. Moreover, we calculate the MMT and MMPD parameters of the tissue samples, and demonstrate the characteristic features of these transformed polarization parameters. Experimental results of the unstained human cervix cancer tissues indicate that the MMT and MMPD parameters can provide rich microstructural information of cancerous and healthy tissues, and demonstrate the feasibility of using these parameters quantitatively for cancer diagnosis.