Three-dimensional motion correction using speckle and phase for in vivo computed optical interferometric tomography

Abstract

Over the years, many computed optical interferometric techniques have been developed to perform high-resolution volumetric tomography. By utilizing the phase and amplitude information provided with interferometric detection, post-acquisition corrections for defocus and optical aberrations can be performed. The introduction of the phase, though, can dramatically increase the sensitivity to motion (most prominently along the optical axis). In this paper, we present two algorithms which, together, can correct for motion in all three dimensions with enough accuracy for defocus and aberration correction in computed optical interferometric tomography. The first algorithm utilizes phase differences within the acquired data to correct for motion along the optical axis. The second algorithm utilizes the addition of a speckle tracking system using temporally- and spatially-coherent illumination to measure motion orthogonal to the optical axis. The use of coherent illumination allows for high-contrast speckle patterns even when imaging apparently uniform samples or when highly aberrated beams cannot be avoided.

1. Introduction

Motion in tissues has always been problematic for in vivo imaging in high-resolution optical systems [1–3]. From retinal to cardiac movements, these involuntary motions make it difficult to acquire and process artifact-free in vivo data. A number of approaches have been used to both correct and avoid motion. For cardiac and respiratory imaging, synchronization with the beating heart or imaging between breaths, respectively, is common in magnetic resonance imaging and ultrasound [3, 4]. When motion is involuntary and random in nature, though, the only options are to scan fast enough to avoid motion, compensate for motion during imaging, or correct the motion in post-processing. In optical coherence tomography (OCT), 2-D cross sections are easily acquired without motion artifacts, but full 3-D volumes often still require some amount of motion compensation or correction – especially for in vivo retinal imaging [5, 6].

For motion correction in post-processing, motion must be measured in some way. Depending on the application, the required precision of the measured motion will change. For traditional amplitude imaging, the required precision only depends on the resolution of the imaging system. Thus, for OCT, assuming features with sufficient contrast exist, separate incoherent imaging systems are often used in conjunction with the acquired data to rapidly track and correct for motion [6, 7]. For imaging modalities such as Doppler OCT, the required precision of axial motion tracking is well below the resolution of the system as it relies on the phase of backscattered light [8]. It is possible, though, to utilize spatial oversampling and the measured phase in depth to correct this motion [9]. Transverse motion correction in Doppler OCT requires the same precision as traditional OCT amplitude imaging, and thus can use similar tracking and correction techniques as other OCT imaging systems.

Interferometric Synthetic Aperture Microscopy (ISAM) [10], Computational Adaptive Optics (CAO) [11], Digital Adaptive Optics (DAO) [12], and Holoscopy [13] are all computed imaging techniques which can computationally correct defocus and optical aberrations, but are known to have especially high sensitivity to motion [14–16]. This is true for even the swept-source full-field techniques (DAO and Holoscopy). Even though the transverse phase relationship is preserved for each individual wavelength of light, the full spectrum, which is required for the reconstruction, is measured over time, and is therefore susceptible to motion. In addition, these techniques may actually be more susceptible to motion due to the long interrogation length of each point in the sample [15].

Axially, the stability requirements of computed optical interferometric techniques in general can be the strictest, as they utilize the phase of the measured data. This means that even motion on the order of the wavelength of light can interfere with the desired reconstruction.

For the transverse dimensions, defocus and aberration correction techniques are unique in that the tolerable level of motion can be well below the resolution of the imaging system [15, 16]. This occurs in the presence of aberrations where, when diffraction-limited performance is not achieved at the time of imaging, the stability requirements for correcting the aberrations actually increases due to a longer interrogation length [15]. Therefore, a separate incoherent imaging system with the same non-diffraction-limited performance cannot be used to measure motion with the required precision because of the lack of sharp high-contrast features.

In this paper, two motion correction techniques are presented. The first technique relies purely on the phase of the acquired OCT data to correct for small axial motion. This method is very general, is found to have few prior assumptions which need to be met, and does not require the use of a coverslip on the sample or tissue. The second technique requires additional hardware to track transverse motion. By illuminating the sample with a narrowband laser diode, and imaging the resulting speckle patterns onto a camera, motion can be tracked at high speeds and with high precision, even in the presence of aberrations. We show that combined, these techniques are sensitive enough to correct 3-D motion for in vivo numerical defocus and aberration correction. Previous work typically required either stable data at the time of imaging [17, 18], or a phase reference was used, such as a coverslip placed on the sample or tissue, to compensate for optical path length fluctuations [14]. Additionally, other efforts have shown that motion could be corrected by using only the acquired OCT data for numerical defocus correction and other phase-resolved techniques [19, 20]. Most of these techniques, though, are restricted to one- or two-dimensional motion correction.

2. Experimental setup

The experimental system used here was a 1,300 nm fiber-based SD-OCT system. A schematic is shown in Fig. 1 . Briefly, a superluminescent diode (SLD) with a bandwidth of 170 nm (FWHM) was used, giving a measured axial resolution of 6 µm (FWHM) in air. A 1024 pixel InGaAs line-scan camera (SU-LDH2, Goodrich) operated at 92 kHz line rate was used in the spectrometer (Bayspec, Inc.). The sample arm beam was collimated with an achromatic doublet with focal length of 30 mm (AC254-030-C, Thorlabs, Inc.). The objective lens was an achromatic doublet with focal length of 40 mm (AC254-040-C, Thorlabs, Inc.), resulting in a numerical aperture (NA) of 0.075 (1/e²). The software was developed in LabVIEW and the data was processed (standard OCT processing only) in real time through dynamic link library (DLL) function calls implemented in C (Microsoft Visual Studio 2008/2010 environment) with the compute unified device architecture (CUDA) extension v4.1 from NVIDIA, which was used for GPU kernel calls on the GPU (GeForce GTX 580, NVIDIA). The transverse field-of-view consisted of 600 x 600 pixels². Combined with a custom waveform (85% linear and 15% fly-back), the effective frame rate was 127.7 frames-per-second (FPS). Each OCT tomogram was acquired by raster-scanning a point across the sample. Thus, one transverse dimension defined a fast axis and the orthogonal transverse dimension defined a slow axis.

Fig. 1.

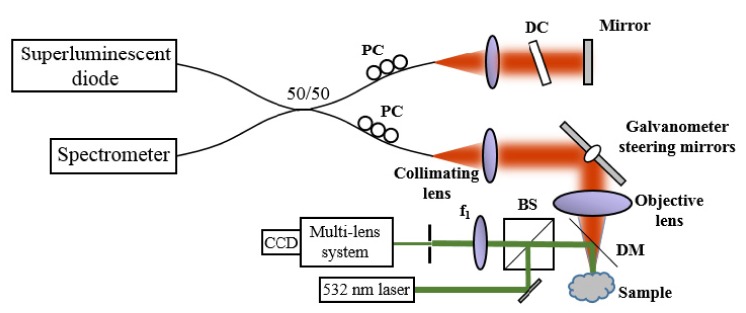
A schematic of the SD-OCT system with a speckle-tracking subsystem. PC: Polarization controllers, DC: Dispersion compensation, BS: Beamsplitter, DM: Dichroic mirror.

The speckle-tracking subsystem used a green (532 nm) laser (DJ532-10, Thorlabs, Inc.) which illuminated a small (~2 mm) region of the tissue via a dichroic beam splitter in the sample arm positioned between the sample and the objective lens. Although not ideal, this configuration was convenient to demonstrate the technique. As a result, astigmatism was introduced when the OCT sample light was focused through the dichroic plate. The reflected green light from the sample was imaged via a 40 mm focal length doublet (AC254-040-C, Thorlabs, Inc.) and a multi-element objective (PH6x8-II, Cannon) onto an 8.8 megapixel CCD USB3 camera (FL3-U3-88S2C-C, PointGrey). Before the multi-element objective, an iris was placed to control the NA of the system. The NA was adjusted until the average speckle size was slightly larger than a single pixel. A smaller NA was desirable to increase the oversampling of each speckle pattern, but the low intensity of light incident on the camera was the limiting factor. With a better dichroic mirror and properly coated optics, power should not be the limiting factor.

The actual speckle image took up a small area on the CCD (approximately 150 x 250 pixels²), and an even smaller subset was used for tracking (100 x 100 pixels²). The subsystem was synchronized with the SD-OCT system using an external trigger cable (ACC-01-3000, PointGrey). Although the camera is capable of capturing video at 60 frames-per-second (FPS), due to limitations of the camera firmware, it was only capable of externally triggering at 28 FPS. The camera was operated with an exposure time of 8.6 ms. The OCT system was then operated at 127.7 FPS. Most triggers from the OCT system were ignored by the camera due to the faster frame-rate of the OCT system. Therefore, 5 OCT frames were acquired for every one speckle image.

3. Three-dimensional motion correction

Motion along the optical axis was corrected utilizing phase differences between A-scans in the acquired OCT data and was similar to what has previously been used in Doppler OCT [9]. This method relies on the known phase statistics of speckle derived in [21]. A schematic of the algorithm is presented in the top of Fig. 2 and is similar to the phase stability assessment technique described in [16]. The key difference is that the stability assessment technique used previously specified a stationary (M-mode) imaging configuration. Here, we allowed the beam to scan and acquire a full OCT tomogram, then use the measured phase fluctuations to correct the phase data. The tradeoff of measurement sensitivity and spatial oversampling is discussed in Section 4.4.

Fig. 2.

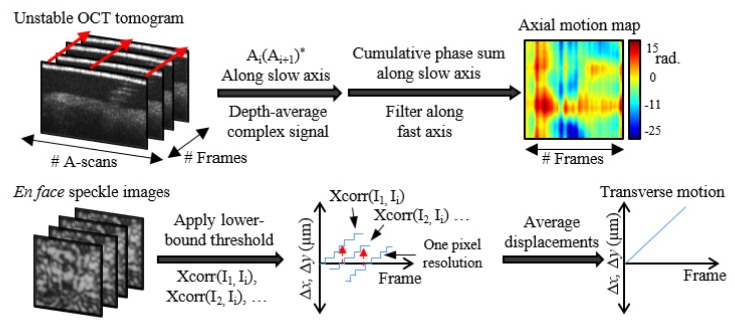
Three-dimensional motion tracking. The top row flowchart determines the axial motion from the OCT tomogram (no need for a coverslip), and the bottom row flowchart details sub-pixel speckle tracking using the speckle subsystem.

To step through the top of Fig. 2, phase differences between A-scans along the slow axis were calculated using complex conjugate multiplication, and then the complex data was averaged along depth. The complex data was used when averaging along depth to avoid phase unwrapping and to weight data voxels of larger SNR more than those with lower SNR. This was also discussed in more detail previously [16]. The resulting 2-D phase map was a measurement of any axial motion which occurred during imaging. The phase difference in the first fast axis line was then set to zero and a cumulative sum was performed along the slow axis to convert incremental phase changes to total phase changes. Finally, a mean filter along the fast axis was applied to smooth the phase map. The resulting phase map was then conjugated and applied to each depth in the OCT data. An example phase map is shown in the top right corner of Fig. 2.

Motion orthogonal to the optical axis was corrected using speckle images captured with the speckle-tracking subsystem. A custom sub-pixel 2-D cross-correlation algorithm was used to determine any motion displacements along each of the two dimensions. A schematic of this algorithm is presented in the bottom half of Fig. 2. First, all intensities below a chosen threshold were set to zero. This allowed only the bright speckle points to be tracked and suppressed some background noise. Next, each speckle frame was chosen and 2-D cross-correlated with the previous and future frames in time until the normalized cross-correlation coefficient dropped below a chosen value (we found that 0.3 provided reliable results). Thus, for each frame I_j, a cross-correlation was used to determine the 2-D movement with respect to each other frame, I_i. These traces along time are labeled as Xcorr(I_j, I_i) in Fig. 2 and only have single-pixel accuracy. Thus, many piecewise displacement traces were found, where each trace used a different speckle frame as zero reference and provided a resolution of one camera pixel as shown in the bottom center of Fig. 2. These traces were then aligned and averaged to compute the final sub-pixel displacements.

Using the sub-pixel displacements, movement along the fast axis could easily be corrected by shifting/interpolating the corresponding OCT frame by the necessary number of pixels using the interp1 function in MATLAB. Motion correction along the slow axis required a more involved algorithm. First, a blank volume of data was created in memory, which was twice as large as the original volume. Using the found displacements along the slow axis, the position of each fast-axis-corrected frame along the slow axis was calculated. Using these positions, the fast-axis frames were inserted into the blank volume by rounding to the nearest half-pixel. Any frames with duplicate positions were discarded. The data was then down-sampled using the interp1 function in MATLAB, which both attempted to fill in any missing data and to return the volume back to the original size.

The corrections in this paper first corrected for any transverse motion using the speckle tracking data (if available) and then applied the phase corrections described above for any motion along the optical axis.

Refocusing was performed by adjusting the z₄ Zernike polynomial as described in [11]. This is similar to the forward model derived in [22] and was chosen for its low computational complexity and avoidance of interpolations artifacts. To perform refocusing throughout all depths, two axially separated planes positioned at $z=z^1$ and $z=z^2$, were first manually refocused. Using these two z₄ values ( $z_4^1$ and $z_4^2$) as references, z₄ was varied linearly along depth to refocus the entire volume. Astigmatism introduced from the dichroic mirror was corrected using the z₆ Zernike coefficient, which was kept constant in depth. Mathematically, let $Z_4(k_x,k_y)$ and $Z_6(k_x,k_y)$ be the 4th and 6th Zernike polynomials which correct for defocus and astigmatism at 0° respectively. Then, for each depth, $z$, the volume was refocused according to the following.

$$S_{\text{AC}}(x,y,z)={ℱ}^{-1}\left\{{\tilde{S}}_{\text{OCT}}(k_x,k_y,z)\left((m_{4}z+b_4)\text{exp}(i{Z}_4)+z_6\text{exp}(i{Z}_6)\right)\right\}$$

Here, $S_{\text{AC}}$ is the refocused volume, $S_{\text{OCT}}$ is the original OCT volume, $m_4=(z_4^1-z_4^2)/(z^1-z^2)$, $b_4=z_4^1-m_4{z}^1$, and the arguments of the Zernike polynomials were omitted for brevity.

4. Experimental results

This section presents results which implemented the methods described above in a SD-OCT system. The utility of the motion correction algorithms is demonstrated via a tissue phantom and in vivo human skin. From previous studies [15, 16] we know that during refocusing and aberration correction, any uncorrected motion will manifest as smearing along the slow axis of the OCT system. In the following sections, figure images of the OCT en face planes are oriented such that the fast axis is vertical and the slow axis is horizontal.

4.1 Speckle results

As a first step, speckle movies were acquired from both scattering phantoms and in vivo samples to ensure that the speckle could be accurately tracked. Figure 3 shows the average of 121 frames from two sample videos ( Media 1 ^{(2.6MB, MOV)} and Media 2 ^{(2.4MB, MOV)} ). The phantom video was acquired with a tissue-mimicking phantom made from sub-resolution TiO₂ particles in a silicone PDMS gel. The concentration of particles allowed for sufficient scattering to produce speckle when imaged with the speckle-tracking subsystem. The phantom was placed on a 3-axis translation stage (PT3, Thorlabs, Inc.) and was moved along a single axis. After the sub-pixel tracking technique outlined in Section 3 was applied, the measured displacements were used to stabilize the speckle video and verify proper tracking. When compared to the tracked average, the untracked average in Fig. 3 shows very low contrast due to uncorrected motion.

Fig. 3.

Frames averages of two speckle-tracking videos. On left ( Media 1 ^{(2.6MB, MOV)} ), a static phantom was manually translated during imaging. On right ( Media 2 ^{(2.4MB, MOV)} ), a human finger was free to move in all dimensions during imaging. Tracked averages show noticeably higher contrast.

Next, an in vivo sample was chosen. Skin on the human finger was chosen as a convenient imaging site due to the space-restricted imaging space in the sample arm of our particular set-up, and because skin is a commonly-used tissue for in vivo optical imaging investigations. A similar result, as was shown for the tissue-mimicking phantom, is shown in Fig. 3 and Media 2 ^{(2.4MB, MOV)} for the human finger skin. The finger rested on a kinematic stage and was free to move in all dimensions. In addition to a significantly larger degree of motion, the speckle was observed to be of lower contrast and more dynamic than in the phantom case. We attribute this to sub-dermal blood flow which caused the speckle to move and partially wash out during imaging. Even so, there was sufficient stationary speckle to allow for reliable tracking. This is a key limiting factor for speckle tracking, and should be taken into consideration. In all the skin sites we were able to image, although the amount of dynamic speckle changed, there was still sufficient static speckle for tracking.

After confirming successful speckle tracking of tissue phantoms and in vivo skin, calibration between the speckle-tracking subsystem and the OCT system was necessary. To calibrate the system, a tissue phantom was used. The OCT system was set to repeatedly acquire the same frame while the speckle camera acquired images. The phantom was then moved along the fast axis. Two calibration parameters were found to be important. The first was pixel scaling: The number of pixels on the camera which correspond to one pixel in the OCT data. In our system, we found that one pixel of movement on the speckle camera was 1.9 pixels (3.8 µm) in the OCT data. The second parameter was time synchronization: The amount of time delay (measured in OCT frames) from the start of the OCT data to the start of the speckle data. We found that the speckle tracking data started 2.9 OCT frames (22.7 µs) after the start of the OCT tomogram.

We found the time delay parameter to be significant and should be measured to a fraction of an OCT frame. The speckle tracking movement was then interpolated to correct for the fractional time delay. Determination of these parameters was performed manually by iterating between them and viewing the stabilized OCT data until the performance was acceptable.

4.2 Phantom results

To test whether speckle tracking was reliable enough for defocus and aberration correction, the same tissue-mimicking phantom which was used in Section 4.1 was placed on a 3-axis piezoelectric stage (Thorlabs, Inc.) and moved in a controlled, sinusoidal manner. We note that although the phantom was only translated in the transverse dimensions, small axial vibrations can cause instabilities, and thus the full 3-D correction was used. Furthermore, this was the same phantom as used in Section 4.1, but with the axial-sectioning capability of OCT, the individual point scatterers can now be resolved.

Initially, the phantom was translated along the fast axis of the OCT system (top-to-bottom in Fig. 4 ). The amplitude of the motion was ~14.7 µm, and was limited by the piezoelectric stage. As a result of the motion, the OCT image (top left of Fig. 4) was distorted, resulting in poor refocusing (bottom left of Fig. 4). After speckle tracking and motion correction, the center column of Fig. 4 shows a less distorted OCT frame and better refocusing. This was confirmed by a control refocusing experiment where the phantom was not moved during imaging (far right column of Fig. 4). To show further detail, zoomed insets (2.5x) were included for each image in Fig. 4.

Fig. 4.

Refocused tissue phantom with 1-D motion. The phantom was translated in a sinusoidal manner along the fast axis (top-to-bottom). Scale bars represent 100 μm.

The next experiment induced sinusoidal motion along both the fast and slow axes. It is known that these computed imaging techniques are more sensitive to motion along the slow axis [15] and also that motion is more difficult to correct along the slow axis due to missing information [1, 2]. Therefore, the amplitude of motion along the slow axis was kept smaller (~9.4 µm) while the fast-axis motion was kept the same (~14.7 µm). The results are shown in Fig. 5 . The OCT images along the top row all appear very similar to the corresponding images in Fig. 4. When refocusing is applied, though, we see a noticeable difference. When refocusing is attempted with no motion correction (lower left, Fig. 5), the points appear elongated due to the addition motion along the slow axis. This is partially, but not completely removed after the motion correction (center column in Fig. 5). As a reference, the same control image (no motion during imaging) is again shown in the far right column of Fig. 5. Again, to show the improvements in more detail, zoomed insets (2.5x) for each image were included in Fig. 5.

Fig. 5.

Refocused tissue phantom with 2-D motion. The phantom was translated in a sinusoidal manner along both the fast (top-to-bottom) and slow (left-to-right) axes. When compared to Fig. 4, the refocusing is somewhat degraded. Scale bars represent 100 μm.

4.3 In vivo skin results

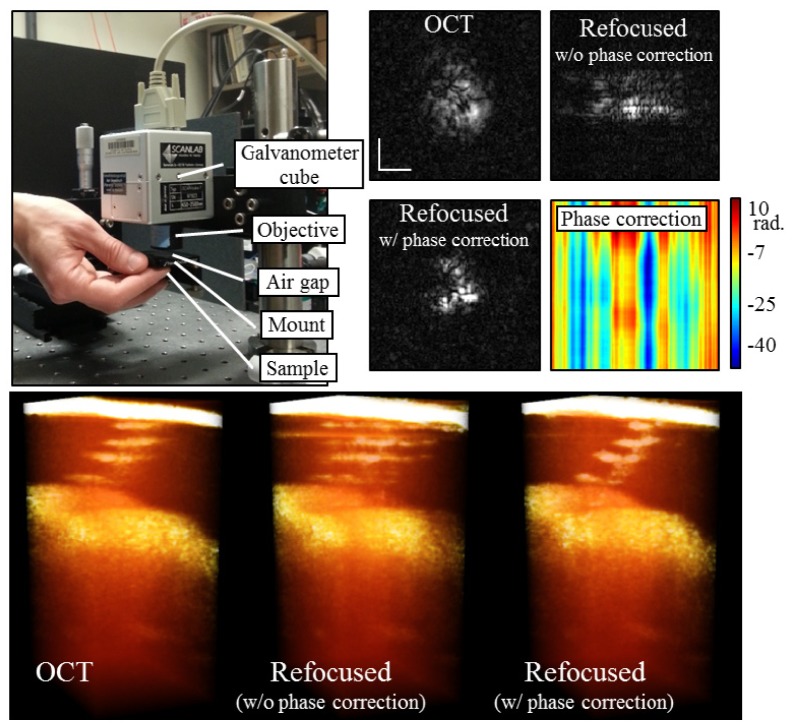
For the first experiment, a healthy human finger was gently pressed up against a kinematic optics mount (KM100T, Thorlabs) as shown in Fig. 6 . This mount was separate from the scanning optics and was cantilevered out from a 3-axis translation stage (PT3, Thorlabs). The direct contact with the skin tissue meant that transverse motion was minimal, while the cantilever was free to move up and down, allowing for motion along the optical axis. Thus, no speckle tracking was performed and only phase corrections were necessary. The OCT depths used for phase correction were cropped from mid-way through the sweat duct until the OCT signal fell off in depth (124 pixels in depth). We find that the strong reflection on the top surface should not be included. There was no coverslip to facilitate phase correction. Figure 6 shows the results from this experiment. The top row presents en face planes through a single sweat duct (cropped from a larger data set). From left-to-right, these planes show the original OCT data, the refocused data without phase correction, and the refocused data with phase correction. The refocused data without phase correction shows an elongation along the slow axis (left-to-right), which is indicative of motion artifacts. The phase-corrected refocused data shows a crescent profile which was expected from this slice through the spiral sweat duct. On the far right of Fig. 6, the 2-D phase map which was used for phase motion corrections is shown.

Fig. 6.

In vivo phase-only correction. Finger motion was restricted to the axial dimension as shown in the mounting schematic on the top left and used previously [16]. Top right shows en face images through a single sweat duct. Refocusing the OCT en face plane without phase correction results in smearing along the slow axis (left-to-right). With phase correction, though, the expected crescent shape of the sweat duct is recovered. A plot of the phase map used for correction is also shown. The bottom row shows 3-D renderings of the OCT and refocused tomograms. The sweat duct was cropped from a larger data set. Scale bars represent 50 µm.

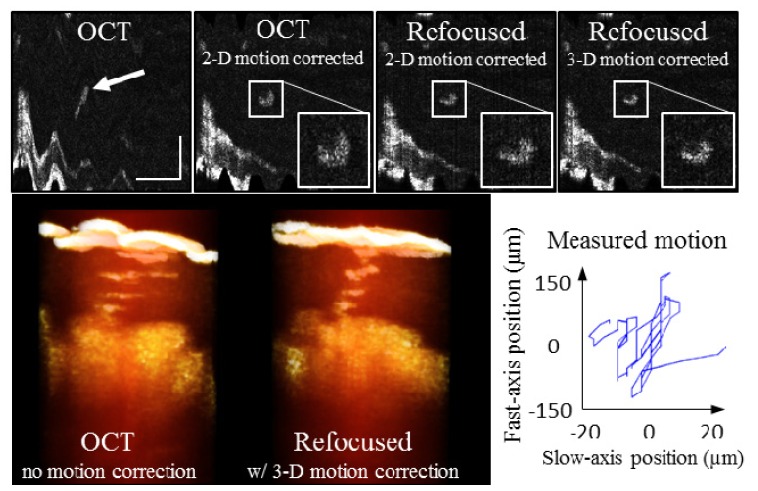
The second experiment corrected motion in all three dimensions. The same volunteer’s finger was now held in place on top of the same kinematic mount that was used in the first experiment. In reference to Fig. 6, the mount was translated down so that the volunteer’s finger fit between the mount and the objective. This then allowed for motion in all three dimensions. The volunteer was also asked to gently move his finger during imaging. Figure 7 shows the results. The top row shows a single en face plane. Visible in this en face section is the surface of the tissue (bottom left) and a single sweat duct (center, highlighted with arrow). On the far left is the original OCT data. One frame to the right is the same plane after using the speckle tracking for 2-D motion correction. The shape of the sweat duct is recovered. Next, refocusing was performed before phase correction. This plane shows improvement along the fast axis (top-to-bottom), but slight broadening along the slow axis (left-to-right), due to phase errors. Finally, the phase corrected refocused plane is shown on the far right of Fig. 7. Again, the crescent profile is visible. On the bottom row, 3-D renderings of the original OCT tomogram and the final refocused tomogram are shown, in addition to a plot of the 2-D tracked motion.

Fig. 7.

In vivo 3-D motion correction. The human volunteer was asked to gently move his finger during imaging. Using the acquired speckle video, 2-D transverse motion was corrected. When refocused, blurring along the slow axis occurred if only 2-D motion correction is performed. Including phase correction resulted in the best refocusing and the most well-defined crescent shape of the sweat duct in this en face plane (far right). The bottom row shows volume renderings (cropped from full tomogram) of the single sweat duct from the original OCT and the final refocused tomograms. Finally, the plot in the bottom right shows the 2-D motion tracked from the speckle video. Scale bars represent 300 µm.

4.4 Motion correction performance

It is important to attempt to determine the sensitivity of the motion correction techniques demonstrated here. In this article, we have shown that computational refocusing and aberration correction can be significantly improved with motion correction, and are comparable to controlled samples (no motion). Therefore, as a rough estimate, we can conclude that the sensitivity of the tracking and correction techniques approximately meet the stability requirements for defocus and aberration correction [15]. The following discussion continues in more detail.

We first investigate and discuss the sensitivity of the phase correction technique. To explore this, we imaged a layered tape phantom (Scotch brand Magic Tape) with the OCT system. The phantom had a coverslip on top and was placed on the 3-axis piezoelectric stage. During imaging, the sample was moved up and down. Recall that the phase correction algorithm used data which were scanned during imaging. Therefore, the sensitivity of the technique depends on the spatial oversampling factor. To explore this dependency, we acquired many tomograms at different oversampling factors. Three volumes of data were acquired at each oversampling factor. The scanned field-of-view along the slow axis was changed to vary the oversampling factor.

The phase motion was then measured using the technique described in Section 4. It was first measured by isolating just the OCT depths containing the tape, and then measured again by isolating just the depths containing the top of the coverslip. The coverslip provided a very reliable phase reference and was taken as the ground truth. The phase fluctuations measured from the depths containing the tape was compared to those measured from the coverslip. The root mean square (RMS) error as a function of oversampling factor is plotted in Fig. 8 (blue line). As the oversampling decreases (dy/ω₀ increases), the RMS error increases. Here, as previously used in [19], ω₀ is the 1/e radius of the diffraction-limited spot size at the Gaussian beam focus. The RMS error was compared to a Monte Carlo simulation. The simulation started with a volume of data consisting of all ones. Provided with the statistical properties of two sources of phase noise (one due to transverse motion and the other due to low SNR), the Monte Carlo simulation was performed in MATLAB by generating random numbers following the appropriate statistical distributions. In the simulation, phase changes due to transverse motion (scan noise) were modeled as additive noise to the phase of the simulated volume of data. The scan noise had a statistical distribution as provided in [21]. Phase noise due to SNR was modeled as an additive Rayleigh distribution on the real and imaginary parts of the simulated volume of data. The strength of the noise due to SNR was adjusted to match the SNR of the measured sample (~33 dB average along depth). The axial motion correction algorithm described in Section 3 was then applied to the simulated volume of data. Since the simulated data modeled no axial motion (only noise) any phase motion measured by it provided an indication of the sensitivity of the technique. The resulting standard deviation of the phase differences is shown in Fig. 8 (red line). These results show that the phase correction technique meets the stability requirements laid out in [15] for axial motion, even with dy/ω₀ = 2.

Fig. 8.

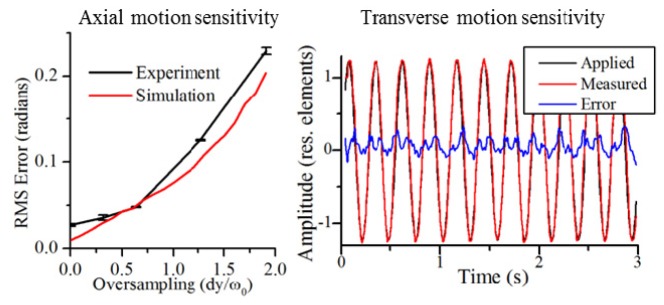
Sensitivity of axial and transverse motion correction. For axial motion correction, even with dy/ω₀ = 2, the RMS error satisfies the axial stability requirements [15]. For transverse motion, although the RMS error satisfied the stability requirements, residual sinusoidal motion was still present.

The sensitivity of the speckle-tracking system is more difficult to determine. It depends on many factors such as the frame-rate, NA, SNR, and magnification of the imaging system. The frame-rate of the camera is important because high-frequency motion can washout and blur the speckle image. In our system, 28 FPS was the maximum achievable frame rate due to firmware limitations, though 100 FPS would likely be ideal for in vivo imaging. The NA and magnification of the system will determine the size of the speckle on the camera. A smaller speckle size will result in more sharp edges and better tracking. Nyquist sampling of the speckle should be met, though, to ensure that the speckle contrast is adequate [23]. We also note that the purpose of this system is to track speckle and not necessarily resolve it. Therefore, highly over-sampled, low NA speckle will also provide good tracking (provided sufficient SNR). This means that the NA of the speckle-tracking system can be significantly lower than the NA of the OCT system. By considering the data used to calibrate the system (Section 4.1) (data not shown), we approximate that for our system, when using the tissue phantom, motion down to half an OCT pixel (~1 µm) can be measured. For in vivo tissue, this increased to a small number of pixels (~4 µm).

A more quantitative investigation is explained here. Included in Fig. 8 is the applied, measured, and residual error for the fast-axis motion from the experiment shown previously in Fig. 5. The amplitude of the motion was measured in normalized units (normalized to the diffraction-limited resolution) as previously described in [15]. The standard deviation of the differential error from Fig. 8 was calculated to be 0.018 s⁻¹ which is well below the stability requirements for Brownian motion along either the fast or slow axes [15]. The residual sinusoidal motion was then approximated by the peak-to-peak amplitude of the error signal. This was calculated to be 0.45 resolution elements which does not satisfy the stability requirements for sinusoidal motion, but is much smaller than 2.5 resolution elements which was the original strength of the motion. We believe much of the residual error to be a result of non-sinusoidal motion of the piezoelectric stage and not a limitation of the speckle-tracking.

5. Conclusion

The techniques demonstrated here were shown to correct for 3-D motion with enough sensitivity for computed optical interferometric techniques such as defocus and aberration correction. Axial motion correction used only the OCT data for phase correction without the use of a coverslip, and transverse motion correction used an additional speckle-tracking subsystem. The speckle-tracking subsystem is well-suited for general-purpose motion tracking, and has several benefits over incoherent imaging techniques. First, with even smooth, seemingly feature-less samples, coherent imaging will provide high-contrast speckle which can be tracked with high precision. In addition, even if the imaging system is imperfect, high-contrast speckle will still form on the camera. This is because, although optical defocus and aberrations will change the speckle, the statistical speckle size depends on the NA of the imaging system, which remains the same.