Quantitative elasticity measurement of urinary bladder wall using laser-induced surface acoustic waves

Abstract

The maintenance of urinary bladder elasticity is essential to its functions, including the storage and voiding phases of the micturition cycle. The bladder stiffness can be changed by various pathophysiological conditions. Quantitative measurement of bladder elasticity is an essential step toward understanding various urinary bladder disease processes and improving patient care. As a nondestructive, and noncontact method, laser-induced surface acoustic waves (SAWs) can accurately characterize the elastic properties of different layers of organs such as the urinary bladder. This initial investigation evaluates the feasibility of a noncontact, all-optical method of generating and measuring the elasticity of the urinary bladder. Quantitative elasticity measurements of ex vivo porcine urinary bladder were made using the laser-induced SAW technique. A pulsed laser was used to excite SAWs that propagated on the bladder wall surface. A dedicated phase-sensitive optical coherence tomography (PhS-OCT) system remotely recorded the SAWs, from which the elasticity properties of different layers of the bladder were estimated. During the experiments, series of measurements were performed under five precisely controlled bladder volumes using water to estimate changes in the elasticity in relation to various urinary bladder contents. The results, validated by optical coherence elastography, show that the laser-induced SAW technique combined with PhS-OCT can be a feasible method of quantitative estimation of biomechanical properties.

1. Introduction

The elasticity of the urinary bladder ensures its proper functioning during various phases of the micturition cycle [1, 2]. Alteration in bladder elasticity leads to bladder dysfunction, which manifests clinically as lower urinary tract symptoms including incontinence and high-pressure upper tract changes in some cases [2–6]. The elasticity of urinary bladder are attributed to relatively high proportions of connective tissue relative to smooth muscle in the urinary bladder wall [7–9]. As the amount of connective tissue increases compared to that of smooth muscle, the bladder becomes more rigid and is less able to expand during filling. This decreases the bladder capacity. Cystometry is the gold standard for measuring bladder compliance, but it is uncomfortable and carries the risk of infection [8, 10, 11]. Moreover, cystometry is a functional measurement technique that provides no information on structural alterations in the urinary bladder. Elastography has become an attractive topic in the biomedical field over the past decade; it employs different imaging modalities to evaluate tissue biomechanical properties from the tissue response generated by different mechanical stimulations, e.g., compression and vibration. Ultrasound-based elastography [12–16] and magnetic resonance imaging- (MRI-) based elastography [17–20] have been widely studied and applied for the diagnosis and evaluation of treatment responses in many diseases, e.g., breast cancer, cardiological disorders, and liver fibrosis staging. There have been preliminary studies of the application of ultrasound elastography and MR elastography to determining bladder elasticity [8, 21, 22]. These techniques have various disadvantages: 1) the resolution of ultrasound and MRI systems is relatively low. It is difficult for these methods to image the bladder diseases in early stage, e.g. early bladder cancer which is usually developing inside of the mucosa layer; 2) they require physical contact or a coupling material for stimulation and detection, which may not be desirable in clinical or surgical situations; 3) the techniques are generally designed assuming shear wave propagation in the bulk tissue and cannot reveal information on different layers in the bladder.

The application of laser-induced surface acoustic waves (SAWs) is a noncontact, nondestructive method that has been widely applied in industry, for example, to analyze the surface structure, plainness, coating layer thickness, and elastic properties of metallic specimens [23–29]. Laser-induced SAWs have started to attract attention for medical applications in the past decade. Wang et al. was the first to describe the application of laser-induced SAWs to clinical dental disease diagnosis [30, 31]. Our group pioneered the use of shaker- and laser-induced SAWs to evaluate the Young’s modulus of heterogeneous soft tissue and phantoms [32–37]. In the laser-induced SAW method, the deformation experienced by the target sample is less than 1 µm (typically ~100 nm) [37], which ensures linear behavior of the soft tissue. Our previous works proved that SAWs can be used to accurately evaluate the mechanical properties of layered viscoelastic soft tissues such as those in the skin, liver, and cornea [32–37]. On the other hand, optical coherence tomography (OCT) is a promising noninvasive, noncontact imaging technique capable of providing microstructural information on tissue with high resolution.

This paper explores the utility of phase-sensitive OCT (PhS-OCT) and the laser-induced SAW method for measuring bladder elasticity. The feasibility of the proposed noncontact, all-optical approach (i.e. to generate and detect SAW using optical methods) is tested on ex vivo porcine urinary bladder to estimate the change in elasticity under conditions of controlled incremental bladder contents. We used a Nd:YAG laser (532 nm) to induce the SAWs, which propagate on the bladder surface, and PhS-OCT to remotely record them. The SAW’s phase velocity curves were calculated using a signal processing procedure and yield the heterogeneous elasticity of different layers of the bladder under different volumes. The results show that PhS-OCT combined with laser-induced SAWs has great potential for functional assessment of the urinary bladder.

2. Material and methods

2.1 Theoretical background

Laser-generated mechanical waves have been widely used in industry for the nondestructive evaluation of layered materials. Here, we provide a brief background to facilitate our discussion in this paper. When a material is illuminated with an ultra-short high-energy laser pulse, the absorbed radiation causes a rapid localized increase in the temperature of the irradiated area. This increase in the temperature causes a rapid thermal expansion and results in the generation and propagation of mechanical waves. In the nondestructive thermoelastic regime, various ultrasonic waves can be generated including body waves, e.g., longitudinal waves (P-waves) and transverse waves (S-wave), and SAWs (also called Rayleigh waves). Body waves travel within the material, whereas SAWs travel along the surface of the material. The elasticity of the material is related to the propagation speed of these waves. However, the propagation of SAWs in a heterogeneous medium (i.e., layered materials or structures) shows a unique dispersive behavior [38–41], meaning that the different frequency components travel at different phase velocities within the material. The phase velocity (C_R) depends on the elastic and geometric properties of the material or structure through all the layers it penetrates [32–38]. In a single, isotropic homogeneous layer, the surface wave phase velocity can be approximated as:

$$C_R=\frac{0.87+1.12v}{1+v}\sqrt{\frac{E}{2\rho (1+v)}},$$ (1)

where E is the Young’s modulus, υ is the Poisson ratio, and ρ is the density of the material.

For a multi-layer medium, in which each layer has different elastic properties, the phase velocity of the surface wave is influenced by the mechanical properties of all the layers it penetrates. The elastic properties that affect the phase-velocity dispersion curve include not only the Young modulus, the Poisson's ratio and the density of each layer, but also the thickness of each layer. The surface waves with shorter wavelengths (higher frequency) penetrate shallow depths with the phase velocity depending on the superficial layers. The surface waves with longer wavelengths (lower frequency) penetrate deeper into the material, and the phase velocity tends to be mostly influenced by the elastic properties of the deeper layers.

The penetration depth z is approximately one wavelength (λ) of the associated SAWs, which is inversely related to the frequency of the wave [32]:

$$z\approx \lambda =\frac{C_R}{f}.$$ (2)

Thus, higher-frequency SAWs penetrate shallow depths, and their phase velocity depends on the superficial layers. On the other hand, lower-frequency SAWs penetrate deeper into the material, and their phase velocity tends to be influenced mostly by the elastic properties of the deeper layers.

2.2 Experimental setup

To test whether the proposed system can accurately measure changes in the bladder elasticity and to determine the relationship between the elasticity and the change in the bladder volume, we studied five fresh ex vivo porcine urinary bladders for two groups of experiments. The thickness of the bladder wall were measured as 7.3 mm (SD ± 1.6 mm). As can be seen in Fig. 1 , the bladder wall can be assumed as three layers: mucosa layer, detrusor muscle layer and adventitia layer. From histological photo of the porcine bladder wall, the thickness of different layers vary. The measured thickness of mucosa layer, detrusor muscle layer and adventitia layer were 1.4 mm (SD ± 0.5 mm), 5.4 mm (SD ± 0.76 mm) and 1.1 mm (SD ± 0.4 mm), respectively. Two of the bladder were opened up, and undertook elasticity testing from the luminal and serosal sides of the bladder wall. The results from this experiment act as a reference for the following bladder dynamic study. In bladder dynamic study, we used three bladders and each of the bladders was filled with five different incremental water volumes (0, 50, 100, 150, and 200 ml). Initially, the bladder was subjected to a loading force of pressure by increasing the water volume stepwise from 0 to 200 ml by a needle and sealed to maintain the content, followed by stepwise unloading back to 0 ml. The loading experimental protocol enabled us to study the dynamic response of the bladder to the contents and its influence on the bladder’s mechanical properties. The dynamic elasticity changes in both the bladder body and bladder neck were tested to study the effect of the volume on different areas of the urinary bladder.

Fig. 1.

(Left) an overview of porcine urinary bladder, (middle) a diagram of different layers of porcine urinary bladder wall and (right) histological photo of porcine uriniary bladder wall (the scale is 1 mm) [42].

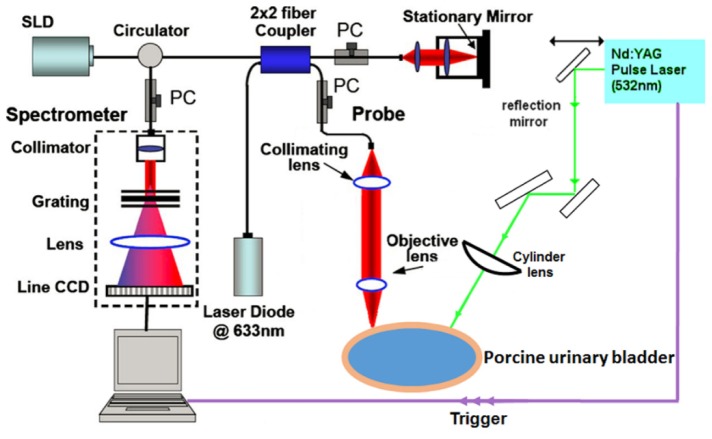
The system configuration used in this study is shown in Fig. 2 . It includes two main components: the laser-induced SAW generation component and PhS-OCT SAW detection component. A solid-state Nd:YAG laser (~532 nm central wavelength) (Continuum Surelite Laser) was used as the high-energy laser pulse source to generate SAWs on the surface of the urinary bladder from both the luminal and serosal sides. The short laser pulse was set to a duration of 6 ns (3 ns rise time) with an average energy of ~2–2.5 mJ and repetition rate of 1 Hz (1 s). Short laser pulse enables the generation of broad bandwidth of SAW signals, thus makes it possible to estimate the elasticity of superficial layer of the material. Before laser pulses were delivered to the sample, a cylindrical lens was employed to generate a line source with a line extent of ~2–2.5 mm impinging onto the bladder surface. Compared with the focused laser pulse, the line source significantly reduced the irradiated power density on the sample. Thus, a more affordable energy can be injected into the specimen without thermal damage, permitting an improved signal-to-noise ratio (SNR) for the measurement of surface waveforms compared with that of a circularly symmetric source [43–45]. A thin layer of black ink was applied to the irradiated area on the urinary bladder surface to improve the absorption of the laser and facilitate SAW generation. During the entire experiment, the sample irradiated area was monitored continuously to avoid any surface damage under the energy level used, and saline water drops were used every 30 s to avoid dehydration.

Fig. 2.

Schematic display of system setup.

The laser-induced SAWs were detected using a PhS-OCT system. The OCT imaging system can provide structural images of the samples as a function of depth, i.e., the thickness of each layer of the bladder wall. This system allows imaging of the tissue inner layer structures and simultaneously provides the elastic properties of the tissue. The PhS-OCT system employed a spectral-domain OCT system with a central wavelength of ~1310 nm and a bandwidth of approximately 83 nm from a superluminescent diode (SLD; Thorlabs) as the light source. It provided an axial resolution of approximately 8.9 µm in air. An optical circulator split the light from the SLD broadband light source into two paths in a 90/10 fiber-based Michelson interferometer. One beam was coupled onto a stationary reference mirror, and the second was focused onto the sample by an objective lens. The focal length of the objective lens was approximately 50 mm to provide a transverse resolution of approximately 15 µm. The coupler recombined the backscattered light from the sample arm and the reflected light from the reference arm into a home-made, high-speed spectrometer via the optical circulator. The spectrometer was equipped with a 14-bit, 1024-pixel InGaAs line scan camera with a maximum acquisition rate of approximately 47 kHz, which is sufficient to capture SAW signals in a frequency ranging up to 23.5 kHz with the maximum speed of 47m/s. Based on Eq. (1) we can assume that the system can measure the elasticity of materials up to 7 MPa. Since bladder is a typical soft tissue (elasticity range from few kPa to hundreds of kPa), the current setup is sufficient to fully analysis the elasticity behavior of urinary bladder. A computer was used to synchronously control the acquisition by the camera and the impulse excitation of the laser pulse. The minimum SAW velocity that the current system can measure is 0.022 m/s, determined by the time of SAW travelling between adjacent sampling locations (1mm), corresponding to a Young’s modulus 0.45 Pa, which represents the system sensitivity [32]. The system can detect SAW up to 23.5 kHz, assuming a material have SAW phase velocity of 5 m/s, the minimum depth that SAW probe can calculate is ~0.2 mm using Eq. (2).

In the SAW detection mode, we acquired 2000 lines over time at a sampling frequency of 47 kHz at each detection location; this imaging protocol is also known as M-mode acquisition. The scanner in the OCT system steered the probe beam in 1-mm steps to locations 2 to 6 mm from the excitation beam on the bladder surface. At each step, the probe beam was kept stationary for ~1 s while the OCT continuously captured the interference signals, which were then averaged and de-noised using the Hilbert–Huang method (to reduce the high-frequency random noise) to obtain the final SAW with an improved SNR. The system provides a phase sensitivity to the sample displacement of ~50 pm. A computer was used to synchronously control the acquisition of surface wave signals and the laser pulse excitation. The phase changes due to the SAWs on the bladder surface were evaluated. The SAW displacements were calculated using

$$\Delta z=\frac{\Delta \varphi \lambda }{4\pi n},$$ (3)

where Δφ is the detected phase change, λ is the central wavelength of the PhS-OCT system (1310 nm), and n is the index of refraction of the sample (~1.35). In the experiment, the averaged amplitude of the generated SAWs was typically ~50–100 nm.

2.3 Data processing

SAWs have a dispersion behavior that allows us to obtain the elasticity information for different layers of material as defined by different frequencies. The phase velocity dispersion curve, which can represent the elasticity of different layers, can be calculated from any two measured signals, y₁(t) and y₂(t), at selected locations x₁ and x₂. The phase difference Δφ between y₁(t) and y₂(t) was calculated using the phase of the cross-power spectrum Y₁₂(f):

$$Y_{12}(f)=Y_1(f)\cdot \overline{Y_2(f)}=A_1{A}_2{e}^{i({\phi }_2-{\phi }_1)},$$ (4)

where Y₁(f) and Y₂(f) are Fourier transforms of the measured signals y₁(t) and y₂(t), A₁ and A₂ are the amplitudes of the cross-power spectra, and Δφ = φ₁ − φ₂ is the phase difference. When the propagation wave has a wavelength equal to the distance ∆x, the measured phase difference will be 2π. In general, the ratio between the phase difference and 2π equals the ratio between the distance and the wavelength:

$$\Delta \phi /2\pi =(x1-x2)/\lambda .$$ (5)

Further, the phase velocity and frequency are related by

$$C_R(f)=(x1-x2)\cdot 2\pi \cdot f/\Delta \phi .$$ (6)

The final phase velocity dispersion curve was measured by averaging the phase velocities of every possible pair of signals.

3. Results

3.1 Bladder wall elasticity measurement

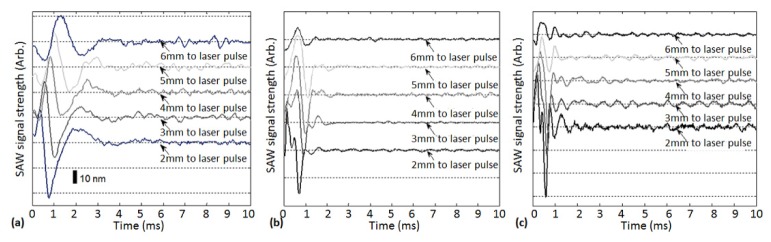
In the initial experiment, as mentioned, the bladder tissue was opened up to allow elasticity testing from the luminal and serosal sides of the bladder wall. The reason for this was to enable measurement of the pure bladder layer elastic properties without any pressure generated by changes in volume. Figure 3(a) and 3(b) show the typical SAWs recorded from the bladder surface from the serosal and luminal sides of the bladder wall, respectively. As mentioned before, the PhS-OCT sampled the SAWs first at a position about 2 mm from the pulse laser source, and then sequentially stepped to the required positions with a step size of 1 mm until it reached a position 6 mm from the pulse laser source. The laser-induced SAWs were clearly moving away from the excitation position because the arrival time of the surface wave became later when the detector was located farther away. The SAWs traveled faster on the luminal or mucosal layer of the bladder, demonstrating that the inner bladder wall is stiffer than the serosal side of the bladder wall. Note that some SAW signals do not begin at the base line, this phenomena is likely caused by the noise from thermal expansion when laser pulse was given.

Fig. 3.

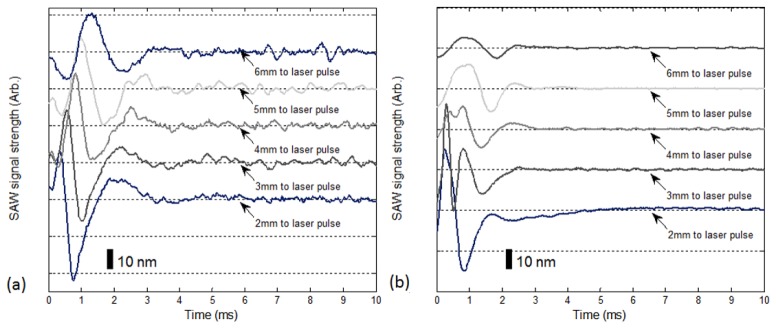
Typical laser-induced SAW recorded by PhS-OCT at the surface (a) via the serosal side of the bladder wall and (b) via the luminal side of the bladder wall. Each curve is shifted vertically by an equal distance to better illustrate the results captured at different positions. The horizontal dotted lines indicate the baseline. The bar indicates the estimated displacement of the surface wave. The similar dotted lines and bars also applies to Figs. 7 and 8.

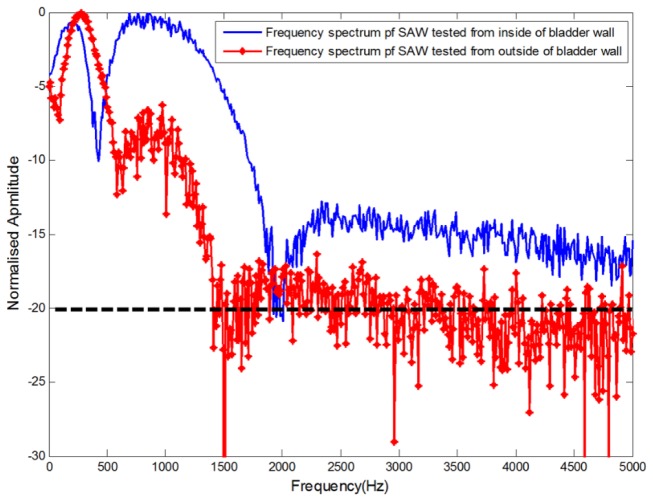
Both the autocorrelation spectra and phase velocity dispersion curves of the detected SAWs are key parameters for our analyses, as the former provide the available frequency range of the signals, whereas the latter provide the elastic and structural information for the samples. To analyze the phase velocity curve correctly, the frequency range of the SAWs has to be determined first. Figure 4 shows the frequency spectrum of SAWs tested from the luminal (blue line) and serosal (red line) sides of the bladder wall. The cut-off frequency for the surface waves was defined as −20 dB from the maximum of the autocorrelation spectrum, where the uncertainty of the dispersion curves starts to increase [30, 31]. According to this rule, the frequency range of the SAWs tested from the luminal side of the bladder wall ranges from 0 to 1800 Hz, and that of SAWs tested from the serosal side of the bladder wall ranges from 0 to 1400 Hz.

Fig. 4.

Frequency spectrum of SAWs tested from inside and outside of bladder wall.

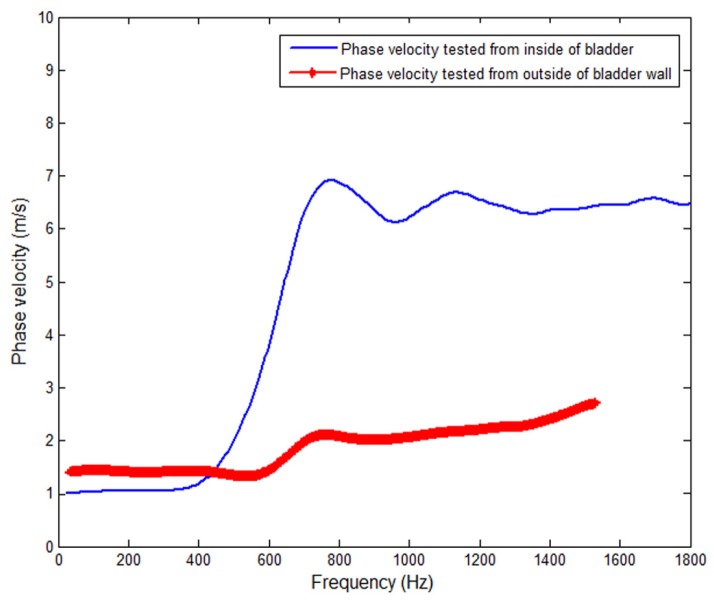
The corresponding phase velocity curves calculated from the acquired SAWs are shown in Fig. 5 . We use lowest mode in multiple SAW modes in this study as the signal energy is low in higher modes. Both phase velocity curves are not constant for all the frequencies. This indicates that the material under investigations is not homogeneous but is a layered material with elasticity differences between the superficial layer (mucosa and adventitia layers) and deep layer (detrusor muscle). The initial phase velocity tested from the mucosal side of the bladder wall (blue line) has a value of approximately 1 m/s; as the frequency increases, the phase velocity changes owing to the influence of the upper layer. The phase velocity increased and reached a plateau at approximately 6.5 m/s. The plateau value was selected when the value of the phase velocity curve reached 95% of the maximum value after the curve was smoothed. These results indicate that the bladder’s mucosal layer is much stiffer than the detrusor muscle. A frequency of less than 600 Hz indicates the mechanical properties of deeper tissue layers, whereas a frequency of greater than 800 Hz indicates the mechanical properties of the superficial layers. Similar phenomena can be found in the phase velocity curve obtained from the serosal side of the bladder wall (red line). The initial phase velocity has a value of approximately 1.4 m/s and increased to approximately 2.5 m/s as the frequency increased, which indicates that the adventitia layer is stiffer than the detrusor muscle. However, the elasticity difference is not as significant as that between the mucosa and detrusor muscle layers. The phase velocity curves tested from the luminal and serosal sides of the bladder wall differ significantly. This indicates a difference in the elasticity properties of the bladder mucosal and other layers. These estimated values suggest that the Young’s modulus of the mucosa layer is much higher than that of the peritoneal layer, and the mucosa layer is thicker than the adventitia layer, because the phase velocity curve reaches saturation at a lower frequency. Note that the phase velocity of bladder detrusor muscle layer (shown in low frequency) is different in the two phase velocity curves, it is because the data is captured from different area of the bladder wall.

Fig. 5.

Typical phase velocity curves from inside (blue line) and outside of bladder wall (red bold line with marks).

We measured the phase velocities for both the luminal and serosal sides of the bladder wall at 10 different locations. The Young’s modulus and layer thickness are summarized in Table 1 . To calculate the Young’s modulus, we chose the phase velocity value at the plateau around the frequency of 0–400 Hz for the detrusor muscle layers and the phase velocity of the frequency of plateau above 700 Hz for the mucosal and serosal layers. We can assume that the Poisson ratio and density of the soft tissue is approximately 0.5 and 1,100 kg/m³ in this study. Therefore, with these measured phase velocity values, we can calculate the Young’s modulus according to Eq. (1). On the other hand, the thickness of the mucosa and adventitia layers can be estimated from Eq. (2) using the phase velocity divided by the corresponding frequency of the turning point of the phase velocity curve. The turning point was defined when the phase velocity increased by 5% over the averaged phase velocity which represented detrusor muscle layer. The thickness assessment of different layers of bladder has potential to aid the diagnosis of bladder pathological conditions which related to layer thickness change.

Table 1. Phase velocity (averaged), estimated Young's modulus, and estimated layer thickness of 10 locations on bladder wall.

Location	Mucosa layer			Detrusor muscle layer		Adventitia layer
	Phase velocity (m/s)	Young’s modulus (kPa)	Layer thickn-ess (mm)	Phase velocity (m/s)	Young’s modulus (kPa)	Phase velocity (m/s)	Young’s modulus (kPa)	Layer thickn-ess (mm)
1	6.84 ± 0.68	160.76 ± 1.59	2.43	1.45 ± 0.26	7.22 ± 0.23	2.28 ± 0.95	17.86 ± 3.11	1.95
2	6.23 ± 0.26	133.36 ± 0.23	1.44	1.23 ± 0.37	5.20 ± 0.47	2.16 ± 0.87	16.03 ± 2.61	1.23
3	5.32 ± 0.76	97.25 ± 1.98	1.38	1.02 ± 0.12	3.57 ± 0.05	1.85 ± 0.69	11.76 ± 1.64	1.84
4	6.95 ± 1.52	165.97 ± 7.94	2.74	1.95 ± 0.61	13.07 ± 1.28	2.51 ± 0.84	21.64 ± 2.43	1.09
5	6.01 ± 1.28	124.11 ± 5.63	1.59	1.52 ± 0.33	7.94 ± 0.37	2.27 ± 0.54	17.71 ± 1.00	1.35
6	7.29 ± 0.69	182.61 ± 1.64	1.94	1.39 ± 0.24	6.64 ± 0.20	2.63 ± 0.61	23.77 ± 1.28	1.42
7	4.33 ± 0.36	64.42 ± 0.45	1.29	1.01 ± 0.36	3.51 ± 0.45	1.59 ± 0.85	8.69 ± 2.48	1.64
8	5.86 ± 0.94	117.99 ± 3.04	1.58	1.84 ± 0.15	11.63 ± 0.08	1.67 ± 0.73	9.58 ± 1.83	1.88
9	5.41 ± 0.55	100.57 ± 1.04	2.33	1.25 ± 0.27	5.37 ± 0.25	2.01 ± 0.63	13.88 ± 1.36	1.26
10	5.04 ± 1.21	87.28 ± 4.31	1.87	1.79 ± 0.19	11.01 ± 0.12	1.72 ± 0.57	10.17 ± 1.12	1.15

The results estimated from the phase velocity curves can be cross-validated using vibration optical coherence elastography (OCE) [46–49], as shown in Fig. 6(a) and 6(b). Vibration OCE is a qualitative method of determining the elasticity distribution of the tissue under investigation. Figure 6(a) and 6(b) show the elastography tested from the luminal and serosal sides of the bladder wall, respectively. High and low presented in the color bar indicates high stiffness and low stiffness of the material respectively. The modulation frequency was set at ~8 kHz, and the maximum actuator displacement applied to the specimens was:1 µm to ensure the generated strain was in pure linear-elastic regime. The vibration could be transmitted from the actuator to compress the specimens and trigger vibration in the axial direction. For the acquisition of a cross-sectional two dimensional (2D) elastography image, the PhS-OCT probe beam stayed for 512 repeat during A-line scan at every spatial location sequentially within the B-scan (total 512 locations) mode (as shown in Fig. 1) while the actuator repeatedly fired the stimulus. Thus, a complete B–scan consists of 512 × 512 A-scans. The elastography images show that the bladder mucosa and adventitia layers have higher stiffness than the detrusor muscle. A comparison of (a) and (b) shows that the bladder mucosa layer has a higher stiffness than the adventitia layer. In addition, the mucosa layer is thicker than the adventitia layer. The results obtained in Fig. 6 match the results of the SAW method.

Fig. 6.

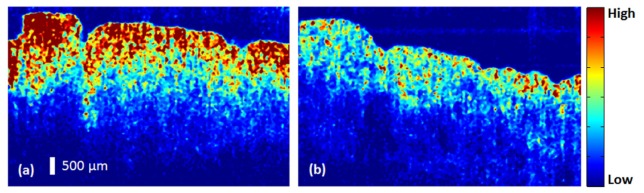
Elastography from (a) inside and (b) outside of bladder from vibration OCE.

3.2 Dynamic bladder wall elasticity change with bladder content

Figures 7 and 8 show typical SAWs recorded from the serosal side for the bladder body and bladder neck, respectively, for contents of 0 ml, 100 ml, and 200 ml. An increasing trend in the SAW velocity can be observed in the figures. The SAW travels fastest at a content of 200 ml and slowest at 0 ml, demonstrating that both the bladder body and neck become stiffer (a higher Young’s modulus) when the bladder is filled with water.

Fig. 7.

Typical laser-induced SAWs recorded by PhS-OCT at surface of bladder body with the contents controlled at (a) 0 ml, (b) 100 ml, and (c) 200 ml by loading.

Fig. 8.

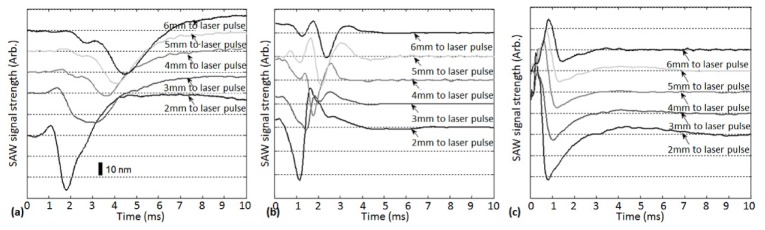
Typical laser-induced SAWs recorded by PhS-OCT at serosal side of bladder neck with contents controlled at (a) 0 ml, (b) 100 ml, and (c) 200 ml by loading.

To further strengthen these observations and subsequent statements, we analyzed the detected laser-induced SAWs group velocities and estimated the Young’s modulus of three ex vivo bladder body and bladder neck tissues under loading and unloading at these content values. The results are shown in Table 2 . SAWs group velocity is measured by taking the propagation time of the SAW at the minimal transmitted attenuation in the time domain. It can be calculated from the distance divided by the time delay as measured from the SAW energy peak of envelop of the SAW signal [46, 47]. Group velocity carry the general information about the material elasticity in time domain [35, 46–50]. Increasing in the bladder content will significantly increase the SAW group velocity, which reflect increase in the stiffness of all layers of bladder wall. Due to the increase in intravesical pressure during filling, the thickness of bladder wall become thinner. However, the total thickness of bladder wall is still exceed the imaging depth of OCT system, thus this issue is not discussed in this paper. Increasing of bladder content has a stronger effect on the bladder neck than on the bladder body at various contents ranging from 0 ml to 200 ml. The SAW group velocity increased by 89.3% in the bladder body and 317.8% in the bladder neck.

Table 2. SAW group velocities of ex vivo porcine urinary bladder during loading and unloading of water.

Content (ml)			0	50	100	150	200
SAW group velocity (m/s)	Load	Bladder body	6.54 ± 0.87	7.69 ± 0.61	8.35 ± 1.14	9.62 ± 1.18	12.38 ± 0.93
		Bladder neck	2.13 ± 0.41	3.34 ± 0.62	4.57 ± 0.57	6.79 ± 0.39	9.4 ± 0.45
	Unload	Bladder body	6.41 ± 0.93	7.55 ± 0.78	8.06 ± 0.79	9.42 ± 0.81	12.38 ± 0.93
		Bladder neck	2.25 ± 0.25	3.38 ± 0.34	4.26 ± 0.51	6.57 ± 0.48	9.40 ± 0.46
Young’s modulus (kPa)	Load	Bladder body	146.96 ± 2.60	203.19 ± 1.28	239.57 ± 4.47	317.98 ± 4.78	526.62 ± 2.97
		Bladder neck	15.59 ± 0.58	38.33 ± 1.32	71.76 ± 1.12	158.42 ± 0.52	303.61 ± 2.97
	Unload	Bladder body	141.18 ± 2.97	195.86 ± 2.09	223.22 ± 2.14	304.90 ± 2.25	526.62 ± 1.64
		Bladder neck	17.39 ± 0.21	39.25 ± 0.40	62.36 ± 0.89	148.32 ± 0.79	303.61 ± 1.64

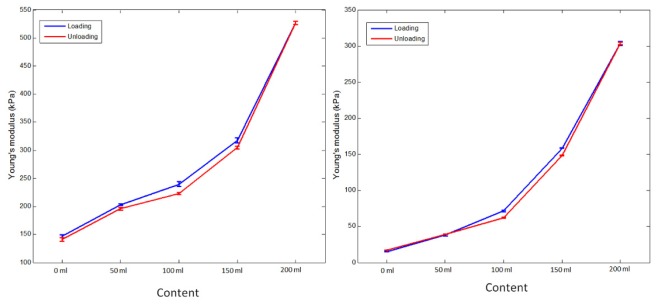
In Fig. 9 , we observe the estimated Young’s modulus of both the bladder body (left) and bladder neck (right) under five different incremental contents during loading and unloading. The curves show that the bladder exhibits nonlinear elastic behavior, as the estimated Young’s modus increases with increasing contents; this matched our expectation. Viscoelastic materials are well known to have both viscosity and elasticity; consequently, energy is dissipated by these materials when a stress is applied, and during the stress–strain cycle, hysteresis occurs. Because the bladder is a typical viscoelastic material, hysteresis can be observed in Fig. 9.

Fig. 9.

Estimated Young’s modulus under loading and unloading of bladder body (left) and bladder neck (right).

4. Discussion and conclusion

There are limited number of reports on the porcine bladder elasticity measurement using palpation device or ultrasound vibrometry. These studies treated bladder as a homogeneous material instead of layered material and reported the Young’s modulus ranging from 4 kPa to 260 kPa [8, 51, 52]. The large variety indicating there is no “gold standard” technology for bladder elasticity measurement. The main purpose of this proof of concept ex vivo study was to provide remote excitation and detection of mechanical waves (SAWs) in order to study the elasticity of different layers of the urinary bladder wall as well as their response to incremental changes in its contents. The proposed system can quantify the elastic modulus and geometrical parameters such as the bladder structure and thickness of different layers. In contrast to other investigated techniques, our method is a noncontact system and may thus be a useful tool for bladder diseases diagnosis.

We used the assumption of density and Poisson ratio to inverse the Young’s modulus of bladder tissue. On the basis of literature and previous studies, the Poisson ratio and density of soft tissue range from 0.49 to 0.5 and 1000-1200 kg/m³ respectively [57, 58]. The assumption of Poisson ratio and density is commonly used in quantitative elastography measurement techniques, i.e. MR elastography and ultrasound elastography. It is because these two parameters do not vary significantly in soft tissues. However, the assumption still brings the maximum error of 9%. The measurement error can be compensated if the real density and Poisson ratio are available, but it is usually ignored in the current quantitative elastography techniques. In addition, with the high sensitivity of current system, the quantitative data from our results are reliable.

SAWs phase velocity is not only dependent on the Young’s modulus of individual layers, but is considered as a combination of all depths travelled by the SAW. Thus, the phase velocity of deeper layer is influenced by superficial layers. To simply the complexity, we here assume that the phase velocity curve is depth-sectioning without the influence between each other in data analysis. Thus, the inversion procedure from phase velocity curve to final Young’s modulus of material was simplified in this study. We treated each plateau of the phase velocity curve as an individual layer of the bladder wall. The averaged values of plateau of the phase velocity curve were inversed to Young’s modulus using Eq. (1). We are currently developing a systematic inversion technique for the SAW method to mitigate this problem.

The hysteresis of bladder wall can be observed from Fig. 9, indicating its viscoelastic nature. The hysteresis of the wall of urinary bladder varies in different parts of the urinary bladder during loading and unloading. This in part can be explained by regional dependant distribution of elastin fibres both in amount and direction. Most of data informing our understanding of viscoelastic elements of urinary bladder comes from in vitro studies. Different studies have measured this using quasi-static loading protocols in experimental settings using strips of tissues removed from different parts of the bladder or on whole organ. Typically, bladder tissue has a “tri-phasic” elastic response to stretching or loading [63].Thus, the hysteresis presented in Fig. 9 cannot represent the full map of the whole bladder. It will be interesting to map the hysteresis of whole bladder and analyse different behaviours between different areas of bladder wall.

This experimental study describes a new application of measuring stiffness using a phase-sensitive OCT and SAW technique. The method does not rely on the measurement of pressure/volume characteristics, as done in routine clinical cystometry. The stiffness in turn represents the biomechanical properties of the urinary bladder wall. Different areas of the urinary bladder were shown to respond differently during filling and emptying of the bladder. This may be due to regional inhomogeneity in the trigone (bladder neck), midsection, and dome of the bladder, and may challenge the assumption that the urinary bladder is a homogeneous structure. Further in vivo validations of these findings are essential in order to apply these results for clinical benefits.

This technique could be applied in conjunction with conventional methods of cystometry to elucidate the structural and functional information from each layer of the urinary bladder wall, in particular the layers of thick luminal mucosa. Increasing the content of the urinary bladder resulted in a higher bladder wall tension and hence increased the stiffness, which is not unexpected [59–62].

The limitation of this study is that the system used a pulsed 532-nm light source to generate the SAWs. A thin layer of black ink was applied to the surface of the bladder because of the low absorption at 532 nm, which may not be an ideal wavelength for in vivo bladder studies. The issue may be resolvable by employing an infrared laser source (CO₂ laser with 10600nm wavelength or Er: YAG laser with 2960nm wavelength) or ultraviolet source (ArF laser with 193nm wavelength) such as those routinely used in clinical environments. These laser sources have high absorption coefficient in tissue, thus more laser energy can be absorbed to generate SAW with acceptable amplitude. Additional study should be conducted to analyse the thermal reactions of bladder tissue to these laser sources, which aims to avoid the thermal damage of tissue. In this case the radiant exposure value should be controlled no higher than maximum acceptable value defined by American National Standards Institute (ANSI) standard IEC 60825-1. Future integration and development of endoscopic [64] or needle based probes [65] of OCT detection beam could combine laser pulse stimulation thereby allowing the system to image deeper tissues. The OCT light from galvo-scanner is routed to a GRIN lens, which is fixed into a needle for side view. Laser pulse can be fibre coupled into the needle to generate surface acoustic wave. The laser pulse fibre is designed to be mounted on a translation stage before inserting into the needle probe, thus the laser pulse can move from near field to far field of OCT detection, i.e. with 6 mm distance presented in this paper. The design should allow the unobstructed movement of fibre in case of the damage during movement. A slot is needed in the probe for the placement of laser pulse to the bladder wall. The wave can be then be scanned by OCT needle probe. This design can overcome the limitation of deep tissue imaging associated with traditional OCT system.

In conclusion, we demonstrated that a combination of laser-induced SAWs and PhS-OCT can be successfully used to estimate the ex vivo porcine urinary bladder elasticity under static conditions and incremental changes in the contents. We estimated the Young’s modulus of different layers of the bladder wall and demonstrated that the elasticity of the bladder wall varies with the contents and exhibits hysteresis during the loading and unloading cycle. There is an inhomogeneous response to increasing contents, with greater stiffness in the bladder neck area than in the body of the urinary bladder. The proposed system can be used in the clinic when combined with urethral or cystometry catheters. Such integration may yield more accurate information and help in planning treatment for different conditions. The techniques and method described here may advance us toward the prospect of making it technically feasible to obtain differences in the bladder stiffness during different phases of the micturition cycle. Such systems with the potential of obtaining biomechanical information can also be used to assess pharmacological interventions in bladder conditions.