Blood vessel segmentation and width estimation in ultra-wide field scanning laser ophthalmoscopy

Abstract

Features of the retinal vasculature, such as vessel widths, are considered biomarkers for systemic disease. The aim of this work is to present a supervised approach to vessel segmentation in ultra-wide field of view scanning laser ophthalmoscope (UWFoV SLO) images and to evaluate its performance in terms of segmentation and vessel width estimation accuracy. The results of the proposed method are compared with ground truth measurements from human observers and with existing state-of-the-art techniques developed for fundus camera images that we optimized for UWFoV SLO images. Our algorithm is based on multi-scale matched filters, a neural network classifier and hysteresis thresholding. After spline-based refinement of the detected vessel contours, the vessel widths are estimated from the binary maps. Such analysis is performed on SLO images for the first time. The proposed method achieves the best results, both in vessel segmentation and in width estimation, in comparison to other automatic techniques.

1. Introduction

Evidence shows that changes in morphological features associated with retinal blood vessels such as widths, tortuosity and branching angles are biomarkers of systemic diseases such as hypertension, arteriosclerosis, stroke, myocardial infarction and cardiovascular disease [1–5]. The investigation of biomarkers has traditionally been confined to limited areas of the retina around the macula and the optic disc (OD). Examples are the Central Retinal Artery / Vein Equivalent [6] and Artery Vein Ratio [7], which are measured in an annulus that covers the surface from 1 to 1.5 optic disc diameters (ODD’s) around the center of the OD. Alternative devices such as the scanning laser ophthalmoscope (SLO) [8], with an ultra-wide field of view (UWFoV) of approximately 200° (compared to 30-60° with a fundus camera), can capture in a single image a larger part of the retina, allowing more extensive analysis of the associated vasculature. The automatic and objective quantification of morphometric vascular features is crucial, especially in population studies, where the manual annotation of large number of images would be an extremely time-consuming process. For this reason, since the work by Chaudhuri et al. [9], automatic tools for the segmentation of blood vessels and the estimation of their widths in fundus images have been extensively investigated and different approaches, such as [10–12] among others, have been presented in literature. To the best of our knowledge, the vast majority of these techniques have been developed for images acquired with fundus cameras and are less frequently applied to SLO images [13]. The task of vessel segmentation presents different challenges in UWFoV SLO images from conventional fundus images. For instance, the illumination is usually less uniform across such a large field of view. This leads to a lower contrast between the vessel edges and the background, especially in the periphery of the retina, and has to be taken into account.

The aim of this study is to present a supervised approach to vessel segmentation that is specifically tailored to UWFoV SLO images and to assess its performance in terms of segmentation accuracy and vessel width estimation error. We are the first group to investigate both tasks at the same time on this particular type of images. The proposed algorithm extends our previous unsupervised approach [14] based on Gaussian matched filters, morphological operations and hysteresis thresholding. This time multiple matched filters are adopted to take into account vessel width variations. The resulting maps, as well as information on vessel width and direction, are used as input to a neural network classifier. Segmentation results are evaluated using a ground truth set of images manually segmented by trained human observers.In addition, two well-known and publicly available segmentation techniques [15, 16], that give state-of-the-art results on fundus camera images, are adapted to work specifically on UWFoV SLO images and used for comparison. The performance of the proposed method is also evaluated in terms of accuracy of width estimation. The comparison is made, not only with the human observers and the two segmentation algorithms cited previously, but also with a version of the width estimation technique proposed by Lupascu et al. [17] that was adapted and modified for UWFoV SLO images.

No conclusions are drawn on associations between retinal vascular features and systemic disease but the method developed will enable future association studies.

2. Methods

This research followed the tenets of the Declaration of Helsinki and was approved by the Research Ethics Committee of the Universities of Dundee and Edinburgh, UK.

Informed consent was obtained by all the participants involved in the data collection.

2.1 Materials

For generality, the UWFoV SLO images (3900 x 3072 pixels) used in this study are acquired from a variety of volunteers with different medical histories. Ten images from volunteers (smokers and non-smokers, hypertensive and normotensive, mean age = 58.4 ± 17.5 years) involved in the SCOT-HEART Trial [18, 19], are captured using an Optos P200C SLO device. This non-mydriatic device makes use of a green laser source, operating at 532 nm, and of a red laser source, operating at 633 nm, to build a false color image of the retina and sub-retinal layers.

From each image [Fig. 1 ], 12 rectangular windows of size 2 x 1.5 ODD’s are extracted, manually segmented by two trained observers and used as ground truth to evaluate vessel segmentation. One window is centered on the OD. Four windows are located around the first one in order to capture the largest vessels usually visible in conventional fundus images with a narrower field of view. Three windows are located in the periphery of the image, avoiding eyelashes and other possible artifacts. Four additional windows are located in the area between the latest two groups. Apart from the one centered on the OD, the exact location of the other windows is different for each image, especially in the periphery, to ensure that windows not showing vessels are not selected.

Fig. 1.

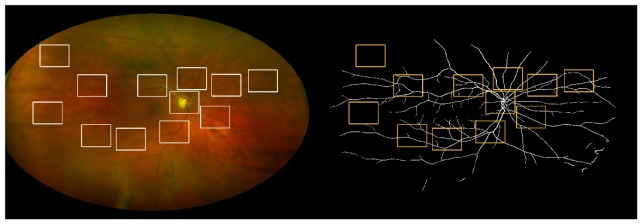
Original UWFoV SLO image (left) and binary map segmented using the proposed method (right). The windows used for the segmentation evaluation are also shown.

The choice of this 120-window data set is made so that the selected windows are representative of the range of vessel widths and background intensities that can be found in an UWFoV SLO at different distances from the OD. This is also a good trade-off between the portion of the area covered by the 12 windows and the time cost of the manual segmentation of an entire image. We have determined empirically that approximately 18 hours are needed for an observer to manually segment an entire UWFOV SLO image while only 4 hours are required for 12 windows.

In the same set of images, 32 vessel widths per image, for a total of 144 widths, are manually annotated by three trained observers (Obs 1, Obs 2, Obs 3) and used to assess the accuracy of width estimation. Every width is measured once by each observer at selected points along the blood vessel paths chosen by Obs 1. Respectively, 8 vessels are annotated in the annulus between 1.0 and 1.5 ODD’s from the OD center, called zone B [20], 8 vessels between 1.5 and 2.0 ODD’s, 8 vessels between 2.0 and 2.5 ODD’s and the last 8 vessels in the region outside the last annulus. In each region 4 arteries and 4 veins are selected. All the annotations are made using specific tools from the VAMPIRE [21] software suite.

2.2 Pre-processing steps, morphological cleaning and matched filtering

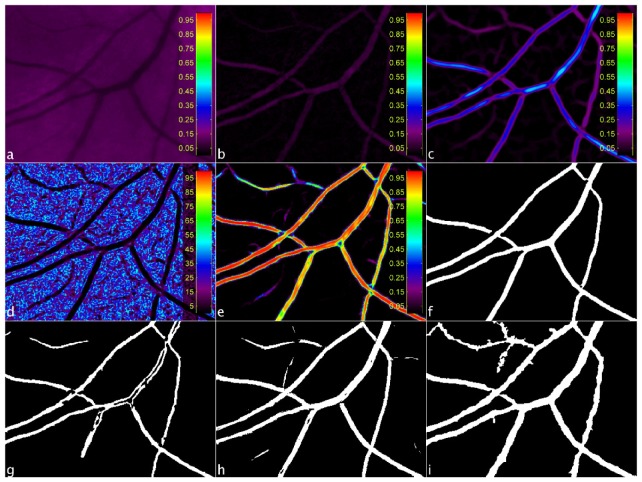
As reported in detail elsewhere [14], the green channel of the image [Fig. 2(a) ] undergoes a number of pre-processing steps to produce a map, M_m, where the background has been suppressed and the vascular network highlighted [Fig. 2(b)]. The retinal vasculature is further enhanced by convolving the map with a battery of orthogonally oriented Gaussian and Laplacian of Gaussian (LoG) kernels rotated in 15° steps to account for varying vessel orientation. The Gaussian filter is used to smooth the vessel along its direction while the LoG enhances the contrast of the vessel’s cross-sectional profile. The maximum intensity value at each pixel location is extracted to form a map [Fig. 2(c)], M_C. The process is repeated at four different scales using different values of standard deviation σ for the LoG and the Gaussian filters to accommodate for the range of vessel widths expected after a visual inspection of the UWFoV SLO images. In particular, σ = w/(2√2), where the width of vessels are w = [3 7 11 15] pixels for the LoG kernel and a value equal to 4σ is used for the respective Gaussian kernel.

Fig. 2.

Example of window extracted from an UWFoV SLO image at different stages of the segmentation process: green channel of the image (a), M_m (b), M_C (c), M_Sd (d), M_NN (e), M_B (f).Binary maps obtained by [14] (g), by [15] (h), by [16] (i).

A further step of morphological grayscale reconstruction is performed at this stage to recover small details lost during the process. A parametric map [22], M_W, encoding the width range from the set of four maps from the convolution stage is created by taking the maximum value at each pixel location. Two direction maps are computed by measuring the local orientation using eigenvalue analysis of the Hessian matrix [23] on two orthogonal versions of M_m. By computing the local standard deviation (SD) of each of these direction maps and taking the minimum value at each pixel location, a SD map [Fig. 2(d)], M_Sd, is created without large SD values.

2.3 Neural network classification and hysteresis thresholding

The six parameterized maps from the previous processing steps (four M_C’s, M_W and M_Sd) form the input vector to the neural network classifier. A fully connected, two-layer, feed-forward neural network with nine neurons in the hidden layer is used at this stage. The activation function for the hidden layer is the log-sigmoid function, logsig(n) = 1/(1 + e^-n), while the output layer has a softmax activation function, softmax(n) = eⁿ/∑eⁿ. The output is a map, M_NN [Fig. 2(e)], where the intensity, at each pixel location, is the likelihood estimated by the neural network of that pixel belonging to a vessel.

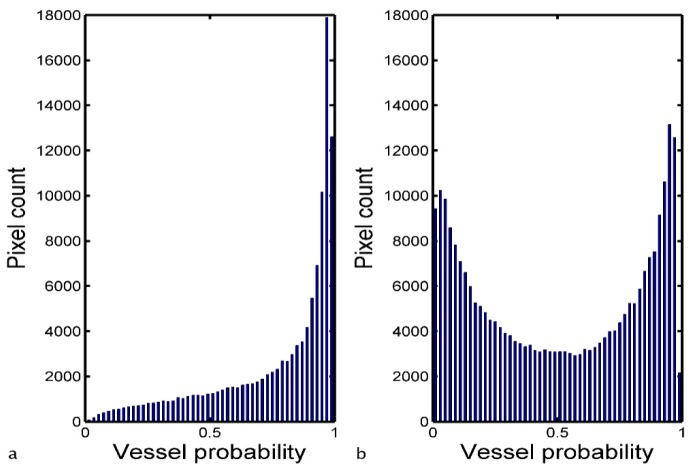
The final step in the processing towards the binary vessel map is to threshold M_NN. Hysteresis thresholding is chosen due to its ability to include vessel pixels of lower likelihood that could otherwise be lost with a single global threshold level. A lower and upper bounds are set and any pixels with intensity higher than the upper bound are considered vessels and set to 1 in the final binary map. All the pixels with intensity values between the two bounds and connected to those above the upper bound are considered vessels as well and set to 1. The rest of the pixels are considered background and set to 0 in the final binary map. To aid in the thresholding step, a binary map of estimated vessels, M_E, is obtained by setting all the pixels in M_Sd with intensity value ≤ 10 and connected to areas ≥ 1000 pixels (values determined by experiment) as vessel candidates and the rest as background. In the first instance, all pixel values in M_NN that falls in the vessel regions defined by M_E are identified and a vessel probability histogram is formed. Depending on the shape of this histogram one of two possible sets of hysteresis threshold bounds is chosen. If the histogram is well fitted (R² > 0.85) by a power function, f(x) = a + bx^c, with a single peak located between a vessel probability of 0.9 and 1, the lower and higher threshold bounds are fixed respectively at 0.50 and 0.65 [Fig. 3(a) ]. If the two conditions are not satisfied together, the threshold bounds are set respectively to M_h−0.15σ_h and M_h + 0.15σ_h, where M_h and σ_h are the mean value and the SD of the vessel probability histogram [Fig. 3(b)]. This second case occurs 20% of the times in our image set.

Fig. 3.

Examples of vessel probability histograms of all pixel values in M_NN that falls in the vessel regions defined by M_E: histogram well fitted by a power function with a single peek between 0.9 and 1 (a), histogram that does not satisfy the two conditions (b).

At this stage, M_E is skeletonized and added to the upper bound hysteresis map to connect potential vessel pixels of lower probability. This can be particularly effective in peripheral regions of UWFoV SLO images where contrast may be low but M_E can still predict vessel presence. Lastly, the binary map undergoes morphological cleaning to produce the final binary vessel map, M_B [Fig. 2(f)].

2.4 Adaptation of fundus-camera image segmentation techniques

Two fundus-camera image segmentation techniques are adapted to achieve the best segmentation performance on UWFoV SLO images and used for comparison. First, the supervised algorithm by Soares et al. [15] is re-trained on our data set (leave-one-image-out cross-validation) and the Gabor wavelet coefficients are re-scaled to fit the widths of blood vessels on UWFoV SLO images. Second, the algorithm by Bankhead et al. [16], in which the wavelet levels of the IUWT are rescaled and the threshold percentage yielding the binary map is lowered to account for the lower percentage of vessel pixels visible in the 200° field of view.

2.5 Width estimation

Four different binary maps are obtained from the segmentation of each image using the aforementioned techniques: proposed method, and our previous unsupervised approach, Robertson et al. [Fig. 2(g)], Soares et al. [Fig. 2(h)], Bankhead et al. [Fig. 2(i)]. After a step of spline-refinement of the vessel edges [24] is applied to the outputs of each segmentation algorithm, all the width of all the vessels annotated in the WE-Data set is measured. The width estimation algorithm by Lupascu et al. [17] is re-implemented adding a pre-processing step of contrast enhancement and adapting the Gaussian fit for the detection of the vessel boundaries. The algorithm is then re-trained on our data set (leave-one-image-out cross-validation).

2.6 Statistics

The inter-observer agreement between the trained annotators that manually segmented the vessels is evaluated in terms of Cohen’s Kappa coefficient [25]. With a k value equal to 0.83 the agreement is considered “almost perfect” according to the guidelines in [26].

To evaluate the performance of vessel segmentation algorithms, standard metrics are computed according to the guidelines in [20]. Mean values and SD of true positive rate (TPR), false positive rate (FPR), positive predictive value (PPV), negative predictive value (NPV), accuracy (Acc) and area under the curve (AUC) of the receiving operating characteristics of the segmentation techniques are calculated. Assuming the OD size to be constant and according to the number of pixels that a window covers, mean and SD are weighted to account for the variation of window size among images. The values achieved using the first observer as ground truth and those achieved using the second observer as ground truth are then averaged to obtain the final results reported in Section 3 [Table 1 ]. A McNemar’s test [27] is used to assess whether the difference in segmentation accuracy between the two best performing algorithms is statistically significant or not.

Table 1. Vessel segmentation results.

Segmentation Method	TPR	FPR	PPV	NPV	Acc	AUC
2nd Observer	0.833(0.026)	0.015(0.003)	0.833(0.026)	0.985(0.003)	0.972(0.003)	n. a.
Proposed method	0.702(0.059)	0.011(0.006)	0.865(0.048)	0.973(0.006)	0.965(0.006)	0.97
Robertson et al. [14]	0.593(0.073)	0.009(0.005)	0.858(0.062)	0.963(0.010)	0.957(0.008)	0.87
Soares et al. [15]	0.674(0.062)	0.017(0.004)	0.786(0.056)	0.970(0.006)	0.957(0.006)	0.96
Bankhead et al. [16]	0.819(0.038)	0.033(0.007)	0.697(0.049)	0.983(0.004)	0.954(0.006)	0.95

Values are expressed as average and (SD).

For every vessel width, the average of the values measured by the three observers (Obs average) is considered as ground truth. The set of vessel widths is divided in three subgroups. This choice is motivated by the fact that we are interested in assessing the algorithm performances in detail at different scales. Large vessels are those generally taken into account for the investigation of biomarkers in zone B. Medium vessels are the most numerous across the large field of view of the images in our data set. Small vessels could be relevant for the investigation of different types of biomarkers such as the fractal dimension of the retinal vasculature [28]. The choice of the thresholds (6.5 and 9.0 pixels) between the three subgroups is determined by visual inspection of the histogram of the manually annotated vessel widths so that the groups contain approximately the same number of samples. The smallest width measured in the data set is equal to 3.6 pixels while the largest one is equal to 14.4 pixels.

Since no statistically significant difference is found between the distributions of width estimation errors of arteries and veins (unpaired t-test, α = 0.05, p-value = 0.19), no further distinction is made in that sense in our analysis. We report width ranges and results [Table 2 ] using mean and SD of the ground truth, and mean and SD of the differences between estimated value and ground truth. The Pearson’s correlation coefficients (r) between the ground truth and the widths, either measured by the observers or estimated from the binary vessel maps, are also reported in the table. Lastly, paired t-tests are performed between the ground truth and the set of widths estimated from the binary maps obtained by the different segmentation techniques.

Table 2. Vessel width results.

Width range	Obs average	Differences with respect to the ground truth
		Obs 1	Obs 2	Obs 3	Robertson et al. [14]	Soares et al. [15]	Bankhead et al. [16]	Lupascu et al. [17]	Proposed method
Small 3.5-6.5	5.51 (0.72)	0.16 (0.51)	−0.04 (0.41)	−0.11 (0.63)	−0.40 (1.09)	−0.20 (1.52)	1.80 (1.41)	1.54 (1.08)	0.65 (0.94)
Medium 6.5-9.0	7.54 (0.73)	0.41 (0.63)	0.11 (0.55)	−0.53 (0.80)	−1.22 (1.65)	−0.40 (1.90)	2.00 (1.24)	0.84 (0.99)	0.16 (1.12)
Large 9.0-14.5	10.53 (1.23)	0.30 (0.75)	0.13 (0.51)	−0.44 (0.85)	−3.69 (2.64)	−2.18 (3.92)	1.36 (1.06)	−0.64 (1.64)	−0.55 (1.02)
Total 3.5-14.5	7.27 (1.94)	0.30 (0.62)	0.06 (0.50)	−0.35 (0.77)	−1.33 (2.03)	−0.63 (2.36)	1.81 (1.29)	0.85 (1.38)	0.22 (1.11)
Pearson’s r	1.00	0.96	0.97	0.92	0.42	0.49	0.81	0.71	0.82

Except from the last row, all values are expressed in pixels as average and (SD)

3. Results

The performance of the vessel segmentation algorithms are shown [Table 1]. From a McNemar’s test (α = 0.05, p-value < 0.001) we can infer that the proposed method achieves a significantly better segmentation accuracy with respect to the second best performing technique [15].

The evaluation of the vessel width estimation performance is shown [Table 2]. All figures are expressed in pixels. Given the UWFoV, the conversion pixel-µm depends on the location where the width is measured. This conversion can be calculated, following the instrument specifications provided by the manufacturers, after a stereographic projection (proprietary OPTOS software) of the image [29] that takes into account the gaze angle of the patient, determined by the location of the fovea. Based on a theoretical calculation on a subset of the annotated vessel widths, assuming a constant size of the eye bulb, we have determined that 1 pixel = 17.2 µm on average in zone B while at 4 ODD’s from the OD, where the farthest vessel width is measured, 1 pixel = 20.6 µm on average.

The proposed method is the only one that does not show a statistically significant difference (α = 0.05, p-value = 0.13) in the distribution of the estimated vessel widths with respect to the ground truth. Paired t-test between every other set of estimated widths and the ground truth result in a rejection of the null hypothesis (α = 0.05, p-value < 0.001 in all four cases).

4. Discussion

We presented a supervised vessel segmentation technique based on multi-scale matched filters, a neural network classifier and hysteresis thresholding. We addressed vessel segmentation in UWFoV SLO images as well as evaluated performance in terms of accuracy in vessel width estimation for the first time. The effectiveness of a segmentation algorithm in this second task is important since metrics based on vessel widths are considered biomarkers of systemic diseases. Therefore automatic segmentation algorithms producing inaccurate measures of widths could lead to erroneous conclusions in biomarker studies.

The proposed method achieves the best results in our comparison tests in vessel segmentation accuracy (Acc = 0.965 ± 0.006) and AUC (0.97). The low value of SD of the segmentation accuracy suggests that the method performs consistently on the entire set of windows. Windows located close to the OD are where largest vessels are the most visible. Thin vessels, instead, are more abundant in windows taken from the periphery of the image. A low SD in segmentation accuracy is therefore an indication of the goodness of the proposed technique in segmenting all possible scales of vessels. These results represent a considerable improvement with respect to our previous approach [14] and have proven to be significantly better than the performance achieved by the best of the techniques [15, 16] developed for fundus camera images that we adapted to UWFoV SLO images.

At the same time, the proposed method presents the lowest overall bias (0.22 pixels), which is comparable to those between human observers, and the lowest SD (1.11 pixels) in width estimation errors among the automatic algorithms [14–17] used for comparison. The results achieved by the proposed method are the only ones that do not show a statistically significant difference from the ground truth. Lastly, the values of Pearson’s r coefficients indicate that the widths estimated from the binary vessel maps automatically segmented with the proposed method are the most correlated (r = 0.82) to the ground truth.

It is worth noting that a good value of vessel segmentation accuracy does not necessarily imply good results in vessel width estimation. This is made explicit by the performance in the two tasks (see Table 1 and Table 2) of [14] and [15]. Both techniques show the second highest value of segmentation accuracy (Acc = 0.957) but at the same time the two lowest correlations (r respectively equal to 0.42 and 0.49) to the vessel width ground truth.

One known limitation of the proposed algorithm is its supervised nature that requires a tedious and time consuming step of manual segmentation of retinal images, necessary to train the neural network classifier. After the training phase, the time needed to process a whole UWFoV SLO image by our method is comparable (approximately 200 seconds) to the time required by the other supervised method [15] that has been tested. The unsupervised technique by Bankhead et al. [16] is considerably faster (10 seconds) given the same computer configuration (i5-3450 CPU @ 3.10 GHz, 8.00 GB of RAM).

A limitation of this study is that the OD dimension is assumed to be constant among participants as previously reported by other authors [7]. The study of the refraction of each subject is also beyond the scope of this work.

A more comprehensive investigation of the performance of the proposed method in conventional fundus camera images and the possible differences with respect to UWFoV SLO ones acquired from the same subject is currently being carried out.