Technical Note: PRESAGE three-dimensional dosimetry accurately measures Gamma Knife output factors

Abstract

Small-field output factor measurements are traditionally very difficult because of steep dose gradients, loss of lateral electronic equilibrium, and dose volume averaging in finitely sized detectors. Three-dimensional (3D) dosimetry is ideal for measuring small output factors and avoids many of these potential challenges of point and two-dimensional detectors. PRESAGE 3D polymer dosimeters were used to measure the output factors for the 4 mm and 8 mm collimators of the Leksell Perfexion Gamma Knife radiosurgery treatment system. Discrepancies between the planned and measured distance between shot centers were also investigated. A Gamma Knife head frame was mounted onto an anthropomorphic head phantom. Special inserts were machined to hold 60 mm diameter, 70 mm tall cylindrical PRESAGE dosimeters. The phantom was irradiated with one 16 mm shot and either one 4 mm or one 8 mm shot, to a prescribed dose of either 3 Gy or 4 Gy to the 50% isodose line. The two shots were spaced between 30 mm and 60 mm apart and aligned along the central axis of the cylinder. The Presage dosimeters were measured using the DMOS-RPC optical CT scanning system. Five independent 4 mm output factor measurements fell within 2% of the manufacturer’s Monte Carlo simulation-derived nominal value, as did two independent 8 mm output factor measurements. The measured distances between shot centers varied by ± 0.8 mm with respect to the planned shot displacements. On the basis of these results, we conclude that PRESAGE dosimetry is excellently suited to quantify the difficult-to-measure Gamma Knife output factors.

1. Introduction

Gamma Knife output factor measurements have traditionally been very difficult to perform because of the precise detector positioning requirements (Paskalev et al., 2003) and dose volume averaging effects from finitely sized detectors (Laub and Wong, 2003). However, measuring the 4 mm and 8 mm output relative to the 16 mm collimator output is important in quality assurance for the Gamma Knife system because these factors greatly impact the treatment dose accuracy. Three-dimensional (3D) dosimetry has the potential to be ideal for measuring small-field output factors. There are many examples of prior scientific studies measuring small field dosimetry with Presage and other 3D dosimeters including: Newton et al., (2011), Olding et al.,(2011), Clift et al., (2010), and Wang et al., (2010) among others. The volumetric nature of 3D dosimeters avoids the precise detector alignment requirements and the volume averaging issues of traditional dosimeters (Moutsatsos et al., 2009). Previous work by Ibbott et al. (1997) used 3D BANG polymer gel dosimeters to measure Gamma Knife dose distributions and compared them to the planned dose distributions using gamma analysis techniques, and Moutsatsos et al. (2009) used VIP polymer gel and a magnetic resonance imaging (MRI) scanner to measure Gamma Knife output factors. Ma et al. (2009) developed a relatively simple method to measure Gamma Knife output factors with 2D film measurments. Our work here uses analysis techniques similar to those of Moutsatsos et al. and Ma et al. but using commercially available PRESAGE (Heuris Inc., Skillman, NJ) 3D polymer dosimeters and an optical computed tomography (CT) readout system. PRESAGE is structurally solid and insensitive to oxygen contamination and therefore is more stable than many conventional gel dosimeters. PRESAGE dosimeters are nearly water equivalent (P. Y. Guo et al., 2006) and also yield quite linear changes in optical density versus absorbed dose (Yates et al., 2011) making them relatively convenient and easy to use.

2. Methods and Materials

2.1. Materials

PRESAGE 3D polymer dosimeters were used to measure the output factors for the 4 mm and 8 mm collimators for the Leksell Gamma Knife Perfexion system (Elekta AB, Stockholm, Sweden). PRESAGE is a radiochromic polymer dosimeter composed of solid, transparent polyurethane. The PRESAGE matrix contains a leuco-dye (Triarylmethane) that changes optical density when exposed to ionizing radiation (P. Guo et al., 2006). The PRESAGE dosimeters used for these experiments had a physical density of 1.08 g/cm³ and an effective atomic number (Z_eff) of 7.6 and therefore provided very little dose perturbation compared to ionization chambers (Das et al., 2008).

2.2. Experimental setup and irradiations

The relative PRESAGE dose distribution was measured on the Duke Midsized Optical-CT Scanner system developed for the Radiological Physics Center (DMOS-RPC) (Newton et al., 2010)(Thomas et al., 2011). Optical artifacts were reduced by optically scanning the dosimeters prior to irradiation and dividing the post-irradiation images by the pre-irradiation images. Any scratches or imperfections in the dosimeters prior to irradiation were imaged in the pre-irradiation images and therefore could be removed from the post-irradiation images. Each projection image was corrected for flood-field and dark-field response. The optical CT scans were created using a modified, filtered back-projection technique (Sakhalkar and Oldham, 2008). A typical scan was accomplished with 720 projection images spaced 0.5 degrees apart through one full revolution of the dosimeter in order to reconstruct a ~.5 mm x .5 mm x .5 mm dose grid. On the two experimental runs where a 1mm x 1mm x 1mm dose grid was reconstructed the original optical CT scan contained 360 projection images spaced at 1 degree intervals about the central axis. (table 1) A simple Ram-Lak filter was applied to the projection images used to construct the measured dose distribution in a filtered back-projection reconstruction algorithm.

Table 1.

Scanned PRESAGE dose resolution, output factor of interest, and 50% isodose prescription for the seven irradiations measured in this work

Measurement Number	Optical CT Resolution (mm x mm x mm)	Output Factor Evaluated	50% Isodose Prescription
1	1	4 mm	4 Gy
2	1	4 mm	4 Gy
3	0.5	4 mm	4 Gy
4	0.5	4 mm	4 Gy
5	0.5	4 mm	4 Gy
6	0.5	8 mm	3 Gy
7	0.5	8 mm	4 Gy

An anthropomorphic Cyberknife head phantom (Accuray, Sunnyvale, CA) was used for these experimental measurements. The standard Cyberknife film imaging insert was replaced with a custom-designed PRESAGE 3D dosimeter insert, which was composed of a polystyrene sleeve and keying mechanism that had been machined to hold 60 mm diameter x ~70 mm tall PRESAGE cylindrical dosimeters. This insert removed the air gaps surrounding the cylindrical dosimeter as well as determined its physical orientation within the head phantom (figure 1). The axial length of the PRESAGE dosimeters varied between experiments, ranging from 68 mm to 82 mm. The dosimeter length discrepancies were accounted for by inserting polyurethane spacers of appropriate thicknesses to remove any air gaps between the dosimeter and the head phantom. A Gamma Knife treatment head frame was mounted onto the phantom for treatment planning and irradiation. The head phantom was CT scanned following our standard Gamma Knife radiosurgery protocol of 1 mm slice thickness, 512 x 512 pixelization with a 25-cm field of view. Other than using the Elekta Gamma Knife head frame, our experimental measurements were made independently of any Elekta-designed measurement equipment.

Figure 1.

Head phantom shown mounted into a Gamma Knife halo assembly. Also shown are the green PRESAGE dosimeter, white polystyrene centering sleeve, and the black rotation bracket, which angularly aligns the keyed cylindrical dosimeter within the head phantom.

Five PRESAGE dosimeters were irradiated with two shots, one 4 mm and one 16 mm, spaced apart in order to measure the 4 mm output factor. Similarly, two PRESAGE dosimeters were irradiated with 8 mm and 16 mm shots in order to calculate the relative output for the 8 mm collimator. The Gamma Knife Perfexion has eight independent sectors that can be individually set to either the 4 mm, 8 mm, 16 mm, or blocked collimator positions. Each sector contains 24 separate ⁶⁰Co sources for a total of 192 beamlets that are symmetrically arranged about the shot center. In these measurements all eight sectors were opened to the appropriate collimator size for a given shot size. Our efforts were primarily focused upon on the 4 mm output factors (five of seven measurements) because they are traditionally more difficult to measure than the 8 mm output factors due to the smaller field sizes. The two shots were spaced between 30 mm and 60 mm apart and aligned along the central axis of the cylinder. In six of the total of seven measurements, 4 Gy was delivered to the 50% isodose line for both collimator shots. In the sixth measurement, 3 Gy was delivered to the 50% isodose line. The treatment planning system adjusted the individual shot delivery times based on the overall combined dose distribution. (table 1)

Two of the PRESAGE dosimeters were optically scanned and digitized to 1 mm x 1 mm x 1 mm dose voxels, and the remaining dosimeters were scanned and digitized to 0.5 mm x 0.5 mm x 0.5 mm dose voxels (table 1). The Gamma Knife treatment plans were created with the Leksell GammaPlan 10 software package using Elekta’s TMR 10 dose algorithm. The outer contour of the head phantom was directly derived from a CT scan of the phantom. Everything within the head structure was treated as water equivalent for the GammaPlan 10 dose calculations.

2.3. Experimental analysis

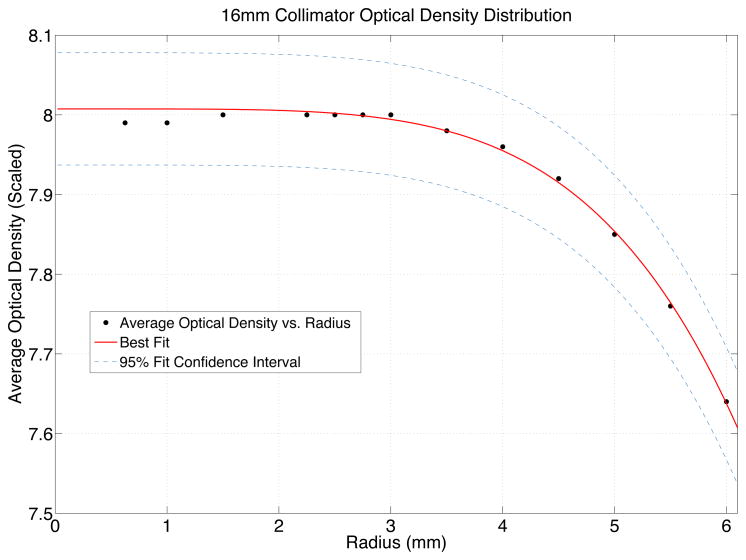
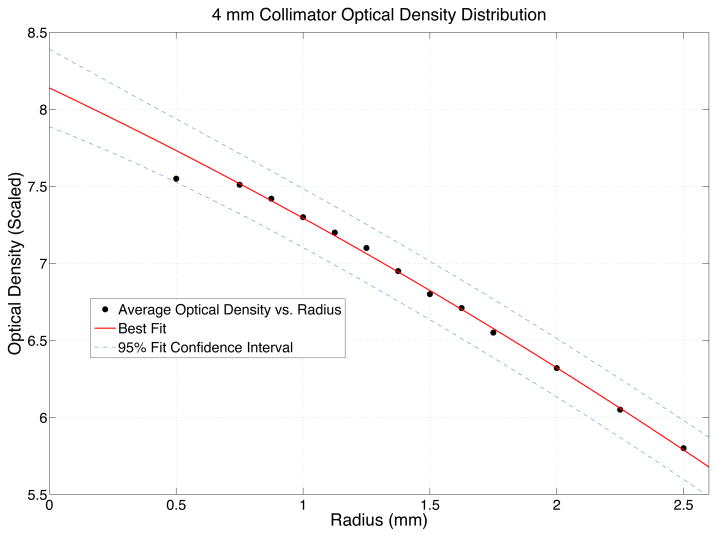
The procedure outlined by Ma et al. (2009) was followed to calculate the 4 mm and 8 mm output factors based on the peak dose delivered via the 4 mm and 8 mm collimators. The shutter, or timer error, for this Gamma Knife Perfexion was measured to be −0.13 seconds. The timer setting for the 16 mm shot irradiation was approximately 4 minutes to deliver 4 Gy @ 50% of dose to the dosimeter in this investigation. Therefore, the end effects were considered negligible and ignored for the rest of this analysis. These experimental measurements were compared against the manufacturer’s recently revised Monte Carlo simulation-based output factors of 0.814 for the 4 mm output factor and 0.900 for the 8 mm collimator for Perfexion (Elekta, 2011). To determine the shot centers for each of the nearly spherical dose shots, the “center of dose” was calculated in a manner similar to that used to calculate a center of mass of a 3D structure but based on voxel optical density values. The mean optical density was measured over spheres of smaller and smaller radii centered on the individual shot centers. This effectively allowed simulating measuring the dose response through a spectrum of different detector volumes and therefore extrapolate the distribution back to a theoretical “zero-volume” detector measurement to eliminate volume averaging effects. (table 2) (figure 2) (figure 3)

Table 2.

The mean optical densities for all voxels contained within spheres of specified radius representing dose responses from variously sized detectors, for one of the measured 16 mm collimator dose distributions. This data was used to fit and extrapolate the dose response down to the response of a theoretical zero-volume detector. Each data point was weighted proportionately to the square root of the number of voxels contained within that given spherical detector volume.

Radius (voxels)	Mean Optical Density (scaled)	Number of Voxels	√(Voxels)
12	7.64	7249	85.14
11	7.76	5583	74.72
10	7.85	4193	64.75
9	7.92	3055	55.27
8	7.96	2155	46.42
7	7.98	1441	37.96
6	8.00	907	30.12
5.5	8.00	696	26.38
5	8.00	529	23.00
4.5	8.00	379	19.47
3	8.00	118	10.86
2	7.99	35	5.92
1.25	7.99	7	2.65

Figure 2.

Starting with coordinates centered on the 16 mm dose distribution the average optical densities within spheres of smaller and smaller radii were measured. A power law function (equation 1) was fit to this data in order to globally scale the optical density distribution corresponding to the peak planned dose (8 Gy) for convenience and visualization of the dose distribution.

Figure 3.

After globally scaling the optical density distribution to the peak delivered dose a quadratic fit (equation 2) was found to best match the 4 mm dose distributions and a cubic equation (equation 3) was found to best match the 8 mm dose distributions. The best fit functions were used to extrapolate the dose response of a theoretical “zero volume detector” allowing accurate output factor measurements while avoiding the normal volume averaging issues found in finite point detector measurements.

For convenience the Presage optical density was first linearly scaled to match the treatment planning dose distribution, therefore scaling the maximum optical density measurement to “8,” corresponding to the maximum planned dose of 8 Gy at the shot centers. When extrapolating the 16 mm shot (optical density) back to simulate being measured by a zero-volume detector, a simple three-parameter power law function was found to best fit the dose distribution (equation 1).

The empirical, best-fit dose function was determined through trial and error by seeking to maximize the R-squared residuals (adjusted for degrees of freedom). The curve fitting was weighted proportionally to the square root of the number of voxels in each spherical volume and was performed in MATLAB (MathWorks, Natick, MA) using the curve fitting toolbox (equation 1) and (figure 2).

$$OD=A{(\mathit{radius})}^B+C$$ (1)

After re-scaling the overall optical density based on the 16 mm shot’s extrapolated zero-volume detector measurement, the maximum dose of the 4 mm shot was found by empirically fitting a quadratic function to the distribution (equation 2) and (figure 3).

$$OD=A{(\mathit{radius})}^2+B(\mathit{radius})+C$$ (2)

Similarly, for the 8 mm shot, a cubic polynomial was empirically found to be the best fit for this dose distribution (equation 3).

$$OD=A{(\mathit{radius})}^3+B{(\mathit{radius})}^2+C(\mathit{radius})+D$$ (3)

The uncertainty included in our output factor measurements came from the two separate curve fits applied in our analysis. First the 16 mm dose distribution was fit with a power law function (equation 1) and scaled the overall dose distribution so the peak-measured dose matched the delivered plan dose. This was done mostly for convenience and to allow us to compare the measured dose to the planned dose through gamma analysis techniques. The first uncertainty in our measurement was the 95% confidence limits on the C parameter in equation 1. Once the overall dose distribution was re-scaled based off of parameter C in equation 1, either a quadratic function (equation 2) was fit to the 4 mm dose peak or a cubic function (equation 3) was fit to the 8 mm peak. The second uncertainty in our output factor measurement was the 95% confidence limits on either the C parameter (equation 2) or the D parameter (equation 3). These two uncertainties were combined in quadrature to give us the overall 95% confidence interval for our final output factor measurement.

In addition to measuring the output factors for the 4 mm and 8 mm shots the difference in distance between the two measured shots and the irradiated dose plan were compared. The shot centers were manually estimated by looking at 2D dose slices of the measured Presage dose matrix. A weighted average of the dose distribution was calculated separately for all three dimensions within a small sphere centered on the manually estimated shot center in order to calculated the true shot center (x,y,z). The distance between the two measured shot centers in 3D space was then calculated. In order to estimate the positional error in the center of dose calculations a simply Monte Carlo simulation was performed in MATLAB. One experiment’s Presage pre-irradiation scan was chosen at random in order to estimate the voxel noise distribution (mean and standard deviation) and it was confirmed the other six experiments had similar noise characteristics. Each dosimeter’s voxel values were simulated with a mean value equal to that particular voxel’s post-scan value and adding a random number drawn from a randomized normal distribution matching our image noise characteristics. The center of the 16 mm shot was then calculated for this simulated data set (x₁₆, y₁₆, z₁₆) repeating the process thousands of times in order to determine the 95% uncertainty spread in calculating the center of dose with this technique (Δx₁₆, Δy₁₆, Δz₁₆). The 4 mm and 8 mm shot centers were similarly calculated as well as the distance between these two points propagating all positional uncertainties through the distance measurements.

3. Results

All seven independent experiments found that the measured Gamma Knife Perfexion output factors were within 2% of the manufacturer’s Monte Carlo simulation-based nominal values (table 3). The distance between the planned shot centers and the measured shot centers were also calculated. The measured shot separation distance varied from the planned displacement by ±0.8 mm between the seven dosimeter measurements (table 4). The calculated error in the measured center to center displacement was found to be ±0.003 mm at the 95% confidence interval.

Table 3.

Seven independent output factor measurements as well as the 95% confidence intervals (CIs) and the differences between the manufacturer’s accepted Monte Carlo-derived and the results based on the TMR 10 dose algorithm.

Measurement Number	Output Factor	Manufacturer’s Monte Carlo Accepted Output Factors	Average Measured Output Factors	Measured Output Factor 95% CI	Output Factor Difference
1	4 mm	0.814	0.827	[0.805, 0.849]	1.60%
2	4 mm	0.814	0.827	[0.805, 0.849]	1.60%
3	4 mm	0.814	0.814	[0.768, 0.860]	0.00%
4	4 mm	0.814	0.822	[0.806, 0.838]	0.98%
5	4 mm	0.814	0.799	[0.784, 0.814]	−1.84%
6	8 mm	0.900	0.882	[0.874, 0.890]	−2.00%
7	8 mm	0.900	0.906	[0.895, 0.917]	0.66%

Table 4.

Planned and measured shot displacements and offsets for all seven experiments. The uncertainty in the measured center-to-center displacement was simulated using Monte Carlo techniques to be ± 0.003 mm at the 95% confidence interval.

Measurement Number	Output Factor	Planned Shot Displacement (mm)	Measured Displacement (mm)	Center-to-Center Offset (mm)
1	4 mm	45.2	44.4	0.8
2	4 mm	55.9	56.6	−0.7
3	4 mm	45.1	45.9	−0.8
4	4 mm	32.0	32.5	−0.5
5	4 mm	32.0	31.5	0.5
6	8 mm	34.9	35.6	−0.7
7	8 mm	39.8	39.0	0.8

4. Discussion and Conclusions

The excellent agreement between the measured Gamma Knife Perfexion output factors and the manufacturer’s Monte Carlo-based values indicates great potential for PRESAGE dosimeters to accurately measure the notoriously difficult-to-measure 4 mm Gamma Knife output factor as well as the 8 mm output factor.

The manufacturer used Monte Carlo simulation to determine output factors in an ideal water sphere. The output factors are applied to calculate dose in the treatment planning system and are constant for each collimator size. We used the calculated total dose, in which the depth differences were accounted for, for each collimator size. The measurement in an anthropomorphic phantom is to validate the output factor in a near clinical situation accounted for the differences in depth and shape, rather than limit only to the simulated depth/geometry. The Cyberknife head phantom is composed of uniform, nearly water-equivalent plastic, with the addition of an anthropomorphically accurate skull. Clinically for Gamma Knife dose calculations we treat the skull as water equivalent. In addition our Gamma Knife calibrations are performed within water equivalent phantoms. Because our output factor measurements are relative we do not expect any significant errors in the output factors due to our small phantom inhomogeneities, especially when it is consistent with the clinical dose calculation in this regard. However, truly accounting for phantom inhomogeneities based on true CT number would be an interesting future step for this project.

A relatively large uncertainty of ± 0.8 mm was found when attempting to measure the distance between shot centers which is greater than the expected Gamma Knife mechanical precision of +/− 0.1 mm. The distance accuracy is expected to be similar to the Gamma Knife couch precision. The larger than expected discrepancy is likely from the asymmetric dose, and/or from the optical resolution of the dosimetry system. Although the treatment planning system took into account the dose distributions of the neighboring shots in adjusting the individual shot times, the dose influence of the neighboring shots could potentially skew the calculated shot center coordinates slightly (asymmetric dose). In our particular case the maximum spacing between shot centers was limited by our phantom and Presage detector dimensions. The further apart the two individual shots could be spaced would help reduce any errors introduced in finding the shot centers due to the second shot’s dose distribution. If greater shot-to-shot distance accuracy was desired, replacing the 16 mm shot with a second 4 mm shot would likely improve the positional uncertainty introduced by the flat and broad-peaked 16 mm shot. This could potentially serve as an additional quality assurance test for the Gamma Knife couch displacement.

3D dosimetry offers a solution to the volume averaging problems of ionization chambers and other finitely sized point source detectors and negates the requirement for precise mechanical alignment of the detector to the shot center. PRESAGE dosimetry is an accurate solution for measuring Gamma Knife output factors and performing quality assurance measurements for Gamma Knife treatment systems. The particular Presage formulation used in these experiments possessed a very linear relationship between optical density and irradiated dose within the dose ranges of these measurements (Yates et al., 2011). Absolute optical density to dose calibration of the Presage dosimeters was not performed for these measurements and Presage’s very linear dose response was relied upon. This does potentially introduce some small error in these measurements that was not directly accounted for here. (Ma et al., 2009) However, directly calibrating a Presage batch’s OD to dose response could potentially improve this technique further at the expense of complicating the procedure somewhat slightly.