Weighted Comparison of two Cumulative Incidence Functions with R-CIFsmry Package

Abstract

In this paper we propose a class of flexible weight functions for use in comparison of two cumulative incidence functions. The proposed weights allow the users to focus their comparison on an early or a late time period post treatment or to treat all time points with equal emphasis. These weight functions can be used to compare two cumulative incidence functions via their risk difference, their relative risk, or their odds ratio. The proposed method has been implemented in the R-CIFsmry package which is readily available for download and is easy to use as illustrated in the example.

1. Introduction

Competing risks data arise in medical studies where patients may experience failure from multiple causes, and failure from one cause precludes observation of failure from all other causes. For example, in cancer studies, two potential causes of failure are disease relapse and death in complete remission (without relapse). Since it is not possible for patients who died in remission to experience relapse and vice versa, death in remission and relapse are two competing risks. Evaluation of the effect of a treatment on a specific cause of failure must account for all other competing risks. One quantity of interest for competing risk data is the cumulative incidence function [1] which quantifies the probability of experiencing failure from a specific cause in the presence of other competing causes. The cumulative incidence function is a function of the cause-specific hazards from all causes of failure.

When there is only one cause of failure, i.e., no competing risks, treatment effects are often compared using the Kaplan and Meier [2] estimators, the log-rank test, and the hazard ratio of the Cox proportional hazards model [3]. A standard analysis approach for competing risks data is to model the treatment effect for each cause of failure, with the most common approach based on the Cox proportional hazards model [4, 5]. Although the Cox model can be applied to competing risks data, it models the treatment effect on the hazard function of a specific cause rather than modeling the treatment effect directly on the cumulative incidence of that cause.

Direct comparison of the cumulative incidence functions has also been considered. Gray [6] developed a log-rank type test and Fine and Gray [7] proposed a Cox type model for competing risks data. However, the interpretation of the Gray test and the Fine and Gray model is somewhat awkward and it is difficult to interpret the treatment effect directly on the cumulative incidence functions from these models.

Pepe [8] proposed a test based on the integrated difference between the weighted cumulative incidence functions. Lin [9] suggested a Kolmogorov-Smirnov type test based on the maximum difference between the cumulative incidence functions. Klein and Andersen [10] proposed a regression approach that models the cumulative incidence via the pseudovalues from a jackknife statistic computed from the cumulative incidence function. Scheike et al. [11] considered a class of flexible regression models based on the binomial regression modeling approach [12, 13, 14]. More recently, Zhang and Fine [15] proposed inferences based on the risk difference, the risk ratio, and the odds ratio of the cumulative incidence functions. Although these methods provide direct interpretation of the treatment effect on the cumulative incidence functions, they do not include weight functions that allow the researchers to focus on an early or a late treatment effect.

In a clinical study, a treatment may have a time-varying effect on the cumulative incidence of a specific cause of failure, that is, the treatment effect changes over time. For example, in a cancer study, the researchers may want to compare the outcomes after allogeneic stem cell transplantation to the outcomes after chemotherapy. It is well known that allogeneic stem cell transplantation has a higher early treatment-related mortality rate and a lower late relapse rate. This paper proposes a class of flexible weight functions that allows the investigators to focus on the treatment effect either in an early or a late period post treatment, or to evaluate the overall treatment effect treating all time periods post treatment with equal emphasis.

Specifically, this work extends the summary statistics of Zhang and Fine [15] to include a weight function with flexible parameters to emphasize the various post-treatment time periods. The weight functions proposed here were motivated by the class of flexible weights of Fleming and Harrington [16]. The cumulative incidence function is a subdistribution function, that is, the cumulative probability does not reach 1 at time infinity. The proposed weight functions adjust for this unique property of the cumulative incidence function to give the weights a relatively consistent interpretation.

This paper also introduces the R-CIFsmry package we developed to compute the summary statistics using the proposed weight functions. The R-CIFsmry package computes the estimates of the cumulative incidence for the cause of interest for each treatment group as well as the estimates of the weighted point-wise comparison between the two groups. It also constructs the confidence bands for the weighted comparison over the time interval starting from the earliest time point where both groups have experienced at least one failure from the cause of interest to the largest failure time for that cause. The R-CIFsmry package also provides the overall weighted summary statistics specified by the users.

Section 2 presents the summary statistics and the proposed weight functions. Section 3 gives the results of our simulation studies. The proposed method is applied to a real data example using the R-CIFsmry package in Section 4. The package is available from the Comprehensive R Archive Network at http://CRAN.P-project.org/package=CIFsmry.

Discussion of the proposed approach is given in Section 5.

2. Inferences for summary statistics and weight functions

2.1. Nonparametric estimate of cumulative incidence function

For subject j in group i, let T_ij be the event time and C_ij be the censoring time. Let X_ij = min (T_ij, C_ij), Δ_ij = I(T_ij ≤ C_ij), and let ε_ij be the cause of failure. For group i, assume that {X_ij, Δ_ij, Δ_ijε_ij} are independent and identically distributed for j = 1,···, n_i. Further assume that observations from the two treatment groups are independent. Let F_i1(t) be the cumulative incidence function of cause 1 for group i and be defined as

$$F_{i1}(t)=P(T_{ij}\le t,{\epsilon }_{ij}=1)={\int }_0^t{S}_i(u^{-})d{\mathrm{\Lambda }}_{i1}(u)$$

where S_i(u⁻) is the overall survival probability P (T_ij ≥ u) and Λ_i1(u) is the cumulative cause-specific hazard function of cause 1. Define the counting process $N_{ij}^1(t)=I\{X_{ij}\le t,{\mathrm{\Delta }}_{ij}{\epsilon }_{ij}=1\}$ and Y_ij(t) = I{X_ij ≥ t}. Let $N_{i•}^1(t)={\sum }_{j=1}^{n_i}{N}_{ij}^1(t)$ and $Y_{i•}(t)={\sum }_{j=1}^{n_i}{Y}_{ij}(t)$. The cumulative incidence function F_i1(t) is commonly estimated by the Aalen and Johansen [17] estimator

$${\widehat{F}}_{i1}(t)={\int }_0^t{\widehat{S}}_i(u^{-})d{\widehat{\mathrm{\Lambda }}}_{i1}(u)$$

where Ŝ_i(t) is the Kaplan-Meier estimator for all causes and ${\widehat{\mathrm{\Lambda }}}_{i1}(t)={\int }_0^t{\{Y_{•}(u)\}}^{-1}d{N}_{i•}^1(u)$ is the Nelson-Aalen estimator for cause 1. The asymptotic properties of F̂_i1(t) have been studied by Lin [9] and Andersen et al. [18] among others. Under regularity conditions (described in the Appendix of Zhang and Fine [15]), for i = 1, 2,

$$\sqrt{n_i}\left\{{\widehat{F}}_{i1}(t)-F_{i1}(t)\right\}=\frac{1}{\sqrt{n_i}}\sum _{j=1}^{n_i}{I}_{ij}^{F_1}(t)+o_p(1)$$

uniformly for t ∈ [0, τ] for a fixed τ where $I_{ij}^{F_1}(t)$ is called the influence function and its explicit expression can be found in [15]. Furthermore, $n_i^{1/2}\left\{{\widehat{F}}_{i1}(t)-F_{i1}(t)\right\}$ converges weakly to a Gaussian process. A consistent variance estimator for $n_i^{1/2}\left\{{\widehat{F}}_{i1}(t)-F_{i1}(t)\right\}$ can be obtained based on the influence function ${\widehat{\mathrm{\sum }}}_{i1}^{F_1}(t)={\sum }_j^{n_i}{\left\{{\widehat{I}}_{ij}^{F_1}(t)\right\}}^2/n_i$ where ${\widehat{I}}_{ij}^{F_1}(t)$ is a naive estimator for $I_{ij}^{F_1}(t)$ [15].

2.2. Summary statistics and weight functions

To assess the treatment effect, we are interested in testing the null hypothesis H₀: F₁₁(t) = F₂₁(t) for t ∈ [0, τ]. Pepe [8] proposed a summary statistic comparing two cumulative incidence functions defined as

$${\int }_0^{\tau }\{F_{11}(t)-F_{21}(t)\}W(t)dt$$ (1)

where W(t) is the weight function with ${\int }_0^{\tau }W(t)dt=1$. Zhang and Fine [15] considered some alternative summary statistics. Let G(u, v) be a transformation function maps from (D[0, τ], D[0, τ]) to ℜ, and G(u, v) has absolute continuous partial derivatives with respect to u and v. Three transformations have been considered and studied by Zhang and Fine [15]: G₁(u, v) = u − v; G₂(u, v) = u/v, for v > 0; and G₃(u, v) = {u/(1 − u)}/{v/(1 − v)}, for 0 < u, v < 1; which represent the risk difference, the risk ratio, and the odds ratio of two cumulative incidence functions, respectively. The proposed summary statistic has the form

$$\overline{G}={\int }_0^{\tau }G\{F_{11}(t),F_{21}(t)\}W(t)dt.$$

The statistic Ḡ when G = G₁ reduces to a Pepe’s test of Equation (1).

In biomedical research, it is common that the treatment effect changes over time and the researchers may be more interested in an early difference or a late difference instead of treating all time periods with equal interest. Pepe [8] and Zhang and Fine [15] among others proposed a weight function in their approaches. However, none of these approaches considered a specific weight function that puts emphasis on the treatment effect at an earlier or a later time period post treatment. For non-competing risks survival data, Fleming and Harrington [16] proposed a class of flexible weighted log-rank tests with weight function [S(t⁻)]^p[1 − S(t⁻)]^q where S(t) is the survival function from the pooled sample. When p > 0 and q = 0, this weight function gives more weight to the early time period, and when p = 0 and q > 0, it gives more weight to the late time period. The Fleming and Harrington weights are functions of S(t) which is directly related to the quantities being compared and it is also related to the size of the risk set at the comparison time points. Certain cases of Fleming and Harrington’s weighted log-rank statistics correspond to well known tests, e.g., (p = 0, q = 0) reduces to the log-rank test, (p = 1, q = 0) corresponds to the Prentice-Wilcoxon test. See Klein and Moeschberger [19] for a discussion and an illustration of various Fleming and Harrington weights.

Motivated by Fleming and Harrington [16], we propose a set of new weight functions to compare the cumulative incidence functions between two groups. The proposed weights are functions of the cumulative incidence of the cause of interest which are the quantities we want to compare. Since the cumulative incidence function is a subdistribution function which never goes to 1 as time goes to infinity, we propose rescaling the components of the weight function by dividing the cumulative incidence function by its value at the end of the study to give the components a numerical value ranging between 0 and 1. Having components with similar range of values gives the p and q parameters of the weight function a relatively consistent interpretation. The proposed weight function has the form

$$W(t)={\left\{1-\frac{F_1(t^{-})}{F_1(\tau )}\right\}}^p{\left\{\frac{F_1(t^{-})}{F_1(\tau )}\right\}}^q,t\in [0,\tau ]$$ (2)

where p ≥ 0 and q ≥ 0 and F₁(t) is the cumulative incidence function of cause 1 under the null hypothesis which can be estimated from the data using the pooled sample.

2.3. Inference for summary statistics with weight function

The summary statistic with the proposed weight can be estimated by

$$\widehat{\overline{G}}={\int }_0^{\tau }G\left\{{\widehat{F}}_{11}(t),{\widehat{F}}_{21}(t)\right\}\widehat{W}(t)dt,$$

where Ŵ (t) = {1 − F̂₁(t⁻)/F̂₁(τ)}^p {F̂₁(t⁻)/F̂₁(τ)}^q and F̂₁(t) is estimated from the pooled sample. Under regularity conditions, it can be shown that Ŵ (t) converges to W(t) uniformly for t ∈ [0, τ]. Zhang and Fine [15] showed that, for n = n₁ + n₂, $\sqrt{n}\left(\widehat{\overline{G}}-\overline{G}\right)$ converges in distribution to a normal random variable and the asymptotic variance can be consistently estimated by ${\widehat{\mathrm{\sum }}}_{\overline{G}}=n{\sum }_i{\sum }_j{\left\{{\widehat{I}}_{ij}^{\overline{G}}\right\}}^2$ where ${\widehat{I}}_{ij}^{\overline{G}}={\int }_0^{\tau }{G}^{(i)}\left\{{\widehat{F}}_{11}(t),{\widehat{F}}_{21}(t)\right\}{\widehat{I}}_{ij}^{F_1}(t)\widehat{W}(t)dt$ and G⁽¹⁾(u, v) = ∂G(u, v)/∂u and G⁽²⁾(u, v) = ∂G(u, v)/∂v.

Hypothesis tests and confidence intervals for the weighted point-wise comparison can be constructed based on the asymptotic normality. The confidence bands for the weighted summary can be constructed using the resampling technique described in details by Zhang and Fine [15] where the cut points for the (1 − α) × 100 percent confidence bands are the (1 − α) × 100^th percentile of a simulated process with independent standard normal variates.

3. Simulation Study

A simulation study was conducted to evaluate the performance of the proposed weight functions. Our simulation results indicate that the summary statistics based on the relative risk and the odds ratio are sensitive to the time period used for the comparison. The denominators of the relative risk and the odds ratio are functions of the cumulative incidence function F(t). Depending on the data, the cumulative incidence in the early time points may be close to zero causing instability when estimating the relative risk or the odds ratio at these early time points. The summary statistic based on the relative risk and the odds ratio can be stabilized by selecting a time interval for comparison where the cumulative incidences at the lower endpoint of the time interval are not too small.

Our simulation results suggest that the summary statistic based on the difference in cumulative incidence functions is the most stable. Therefore, only the results of the risk difference are shown in this section. We considerd several combinations of the parameters (p, q) for the weight function W(t) in Equation (2). Tables 1 – 4 show the results of five of these combinations: (i) heavy early weight (2,0), (ii) moderate early weight (1,0), (iii) even weight (0,0), (iv) moderate late weight (0,1), and (v) heavy late weight (0,2). Results for other combinations with larger values of p and q are discussed at the end of this section.

Table 1.

Type I error rates from simulation study for 20%, 30%, and 50% censoring

		(p, q): early → late
pc	ni	(2,0)	(1,0)	(0,0)	(0,1)	(0,2)	Gray
20%	50	0.0518	0.0528	0.0515	0.0526	0.0532	0.0514
	150	0.0481	0.0474	0.0467	0.0479	0.0478	0.0468
	250	0.0525	0.0523	0.0502	0.0504	0.0511	0.0515
30%	50	0.0522	0.0521	0.0532	0.0555	0.0588	0.0497
	150	0.0498	0.0496	0.0478	0.0491	0.0503	0.0475
	250	0.0513	0.0500	0.0507	0.0504	0.0499	0.0500
50%	50	0.0554	0.0574	0.0598	0.0612	0.0648	0.0520
	150	0.0522	0.0554	0.0562	0.0594	0.0614	0.0534
	250	0.0492	0.0498	0.0526	0.0508	0.0498	0.0494

Table 4.

Power under the late difference alternative with 30% censoring

		(p, q): early → late
ni	Curves	(2,0)	(1,0)	(0,0)	(0,1)	(0,2)	Gray
50	2 vs 3	0.0554	0.0849	0.1323	0.1487	0.1550	0.1878
	1 vs 3	0.0516	0.0680	0.2460	0.3044	0.3389	0.2754
150	2 vs 3	0.0642	0.1703	0.2928	0.3117	0.3140	0.4167
	1 vs 3	0.0564	0.1307	0.6842	0.7495	0.7756	0.6438
250	2 vs 3	0.0780	0.2815	0.4347	0.4466	0.4406	0.6023
	1 vs 3	0.0684	0.2240	0.8905	0.9118	0.9192	0.8506

Three total sample sizes of n = 100, 300, and 500 were considered for each scenario. Although the results for equal group sizes (n_i = 50, 150, 250) are shown here, similar results were observed from a simulation study with unequal group sizes. As expected, given the same total sample size, a balanced design with equal group sizes generally provides the best power. All simulations were performed using 10,000 replications.

The Type I error rate was evaluated under the null hypothesis with failure times for both groups generated from the cumulative incidence functions F₁(t) = p₁(1 − e^−t) for cause 1 (the cause of interest) and F₂(t) = (1 − p₁)(1−e^−t) for cause 2, where p₁ = F₁(∞) = 0.66 which means the maximum cumulative incidence of cause 1 was set to 66%. The null hypothesis was tested at the 95% confidence level with 20%, 30%, and 50% censoring. Table 1 shows the simulation results under the null hypothesis where p_c denotes the percentage of censoring. The type I error rates were consistently close to the nominal level for all weight functions and all sample sizes with 20% and 30% censoring. With 50% censoring, the type I error rates were slightly inflated with smaller sample sizes (n_i = 50, 150) but were close to the nominal level with larger sample size (n_i = 250).

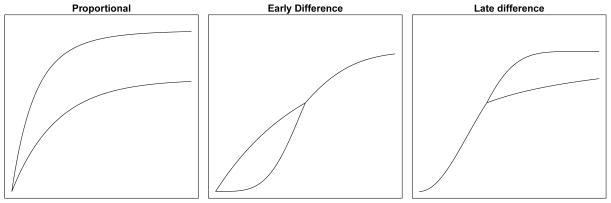
The power of the weighted comparisons was evaluated using three alternative scenarios for each weight function: (a) the first scenario assumes proportional subdistribution hazards between the two groups, (b) the second scenario assumes an early difference in the cumulative incidence functions, and (c) the third scenario assumes a late difference (see Figure 1). In this section, the powers are shown for simulation with 30% censoring. Similar results were observed for all alternative scenarios with 50% censoring.

Figure 1.

Three alternative scenarios considered in simulation study

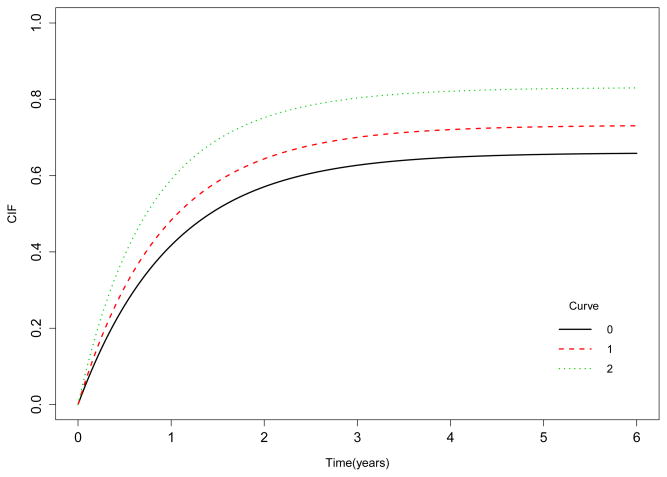
The failure times from cause 1 for the first scenario were generated from the cumulative incidence function F₁(t) = 1 − [1 − p₁(1 − e^−t)]^exp{βZ} where p₁ = 0.66 and Z is the indicator for group 2. In this scenario, the cumulative incidence of cause 1 for group 1 is the same as the cumulative incidence generated under the null hypothesis described above (Curve 0 of Figure 2). The subdistribution hazard of cause 1 for group 2 is exp(β) times the subdistribution hazard for group 1. The power was evaluated for two different values of β: 0.2 and 0.5 (Curves 1 and 2, respectively, of Figure 2). The failure times from cause 2 were generated from the cumulative incidence function F₂(t) = (1 − p₁)^exp{βZ}(1 − e^−texp{βZ}).

Figure 2.

Cumulative incidence curves for cause 1 under the proportional subdistribution hazards alternative

Table 2 shows the power for the five weight functions in this scenario. As expected, the power increases as the sample size increases and with a larger difference. Under the proportional subdistribution hazards alternative, the even weight function with (p = 0, q = 0) gives the best power and it is comparable to the Gray test [6]. However, the variation in power across all weight functions is small under this scenario.

Table 2.

Power under the proportional subdistribution hazards alternative with 30% censoring

		(p, q): early → late
ni	Curves	(2,0)	(1,0)	(0,0)	(0,1)	(0,2)	Gray
50	1 vs 0	0.1011	0.1121	0.1229	0.1218	0.1171	0.1143
	2 vs 0	0.3498	0.4048	0.4361	0.4217	0.4097	0.4395
150	1 vs 0	0.1809	0.2172	0.2352	0.2275	0.2221	0.2391
	2 vs 0	0.7671	0.8551	0.8744	0.8569	0.8445	0.8889
250	1 vs 0	0.2755	0.3328	0.3505	0.3386	0.3288	0.3606
	2 vs 0	0.9342	0.9755	0.9812	0.9760	0.9702	0.9848

The failure times for cause 1 with an early or a late difference were generated from cumulative incidence functions with piece-wise Weibull distributions of the form

$$F_1(t)=p_1\{1-exp(-{(t/2)}^A)\}$$ (3)

for both groups where the pieces were set at two years and p₁ = 0.66.

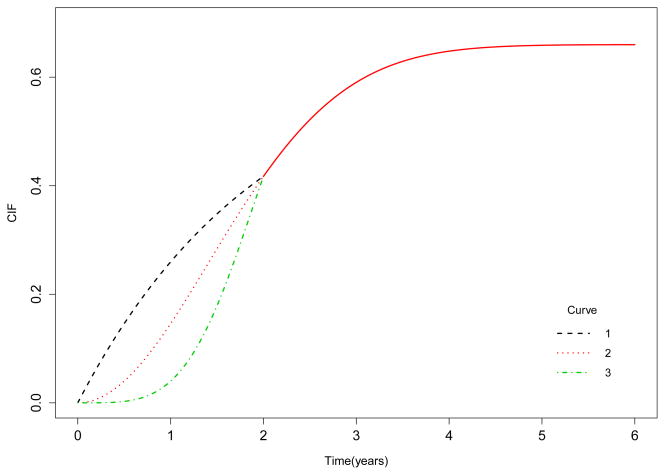
In the early difference alternative, the cumulative incidence functions for cause 1 in the first two years were generated for group 1 by setting A = 1, 2 (Curves 1 and 2, respectively, of Figure 3) and for group 2 A = 4 (Curve 3 of Figure 3). After two years, the failure times for both groups were generated by setting A = 2. The failure times for cause 2 were also generated from piece-wise Weibull distributions with the form F₂(t) = (1 − p₁){1 − exp(−(t/2)^A)} for both groups. Table 3 shows the power comparing the cumulative incidence functions between the two groups under these scenarios. The comparisons with early weights, (p = 2, q = 0) and (p = 1, q = 0), provide significantly more power than the comparisons with the even weight or with late weights. Even with a small sample size (50 per group), the power using a moderate early weight (p = 1, q = 0) increases three folds while using a heavy early weight (p = 2, q = 0) increases five folds compared to the power of the test with the even weight or that of the Gray test. The improvement in power is even more significant with larger sample sizes. For example, with n_i = 150, the power to detect the difference between Curves 1 and 3 using the Gray test was 27% and using the integrated difference with even weight was 21% whereas when using a moderate early weight, the power increased to 91% and to more than 99% with a heavy early weight.

Figure 3.

Cumulative incidence curves with difference in the first two years

Table 3.

Power under the early difference scenario with 30% censoring

		(p, q): early → late
ni	Curves	(2,0)	(1,0)	(0,0)	(0,1)	(0,2)	Gray
50	2 vs 3	0.2387	0.1527	0.0662	0.0586	0.0561	0.0714
	1 vs 3	0.5661	0.3571	0.0941	0.0633	0.0575	0.1247
150	2 vs 3	0.7512	0.4864	0.0953	0.0560	0.0529	0.1066
	1 vs 3	0.9929	0.9077	0.2108	0.0780	0.0544	0.2683
250	2 vs 3	0.9344	0.7213	0.1154	0.0536	0.0508	0.1344
	1 vs 3	1.0000	0.9930	0.3151	0.0871	0.0573	0.4196

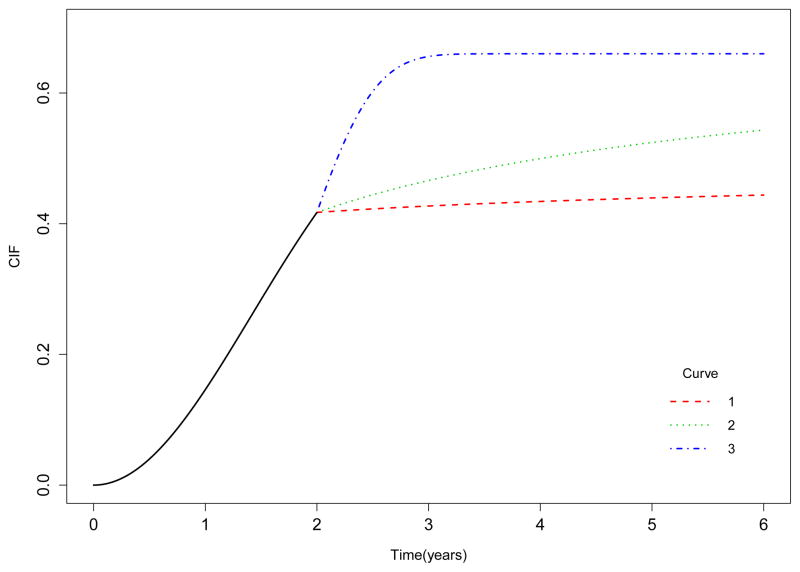
In the late difference scenario, the cumulative incidence functions for cause 1 before two years were generated with A = 2 for both groups. After the first two years, the cumulative incidence functions assume A = 0.1, 0.5 for group 1 (Curves 1 and 2, respectively, of Figure 4) and A = 4 for group 2 (Curve 3 of Figure 4). The failure times for cause 2 were also generated from piece-wise Weibull distributions with the form F₂(t) = (1 − p₁){1 − exp(−(t/2)^A)} for both groups. Table 4 shows the power when comparing the cumulative incidences under this scenario. The comparisons with late weights, (p = 0, q = 1) and (p = 0, q = 2), provide more power than the comparison with early weights. However, it is worth noting that the improvement in power using weight functions focusing on a late time period under the late difference alternative is more moderate than the improvement when using the early weight functions under the early difference scenario. This phenomenon can be explained by the large variance of the cumulative incidence estimate later in the time course.

Figure 4.

Cumulative incidence curves with difference after the first two years

Simulation results for the three alternative scenarios with 30% censoring were shown in this section. Simulation results with 50% censoring (not shown) lead to similar conclusions. Under the proportional subdistribution hazards alternative, the variation in power across all weight functions was small with the highest power achieved around the even weight function. Under the early difference alternative, the comparisons with early weights outperformed the comparisons with the even weight and the late weight functions. Under the late difference alternative, the comparisons with late weights provide more power than with other weight functions.

This section showed our simulation results for weight functions with the values of p and q ranging between 0 and 2. In practice, selection of the values for p and q depends on the cumulative incidence functions being compared. Although p and q can take much higher values, the improvement in power diminishes as p and q become too large. The larger the value of p the earlier the emphasis is on the treatment effect. In most cases, the difference between the cumulative incidences is very small in the very early time post treatment. Therefore, weighted comparison with very large p may show very small difference. In our simulation study, increasing the value of p from 2 to 5 lead to an increase of 10% – 20% in power under the early difference scenario for smaller sample sizes (n_i = 50, 150), however, the power only increased by less than 10% when p = 10 compared to when p = 5. The power barely increased when p was increased from 2 to 10 for larger sample size (n_i = 250). On the other hand, under the late difference alternative, the increase in power for the value of q = 10 compared to q = 2 was small when the difference was constant toward the end of the follow-up period (Curves 1 vs. 3 of Figure 4) and the power slightly decreased when the difference became smaller at the tail end (Curves 2 vs. 3 of Figure 4). It is important to note that the value of p and q must be selected prior to conducting the analysis. At the design stage, p and q can be selected by simulating data from the cumulative incidence functions hypothesized for the study and the p and q values from the weight function that gives the best power under this hypothesis can be selected for future analysis. The R-CIFsmry package described in the following section can be used for this type of design simulation.

4. R package and data example

4.1. Package CIFsmry

The proposed method has been implemented in an R package called CIF-smry. The package is available for download at http://CRAN.P-project.org/package=CIFsmry.

The CIFsm() function in the CIFsmry package provides point estimates and standard errors for the cumulative incidence functions separately for the two groups. The package also computes the weighted summary statistics for the risk difference, the relative risk, and the odds ratio of the cumulative incidence functions using the weight specified by the user. It also gives the confidence intervals and the confidence bands for the requested summary statistics. A simulated dataset called sim.dat is included in the package as an example.

The CIFsm() function requires an input data set consisting of three variables in the following order: event time, cause of failure, and treatment group. The cause of failure must be coded as 1 for the cause of interest, 2 for all other causes, and 0 for censored observations. (Note that the proposed weighted comparison and this package were developed to compare two cumulative incidence functions for a specific cause of failure. When there are more than two competing causes of failure, all causes of failure except for the cause of interest must be combined into one competing risk.) The treatment group must be coded as 1 for the treatment and 0 for the control. Other arguments for the CIFsm() function include:

• method: specify the summary statistic of interest. Options include “dif” (default), “rr”, and “or” for risk difference, relative risk, and odds ratio, respectively.

• pp, qq: specify the p and q values for the weight function. Even weight (pp = 0, qq = 0) is the default option.

• conf.bd: request confidence band for the summary statistic specified in the method argument. Options for this argument are TRUE (default) if confidence band is requested and FALSE if not needed. Setting the conf.bd = FALSE saves on computational time.

• n.sim: specify the number of simulations used to create the 95% confidence band (default is 500, not applicable if conf.bd = FALSE).

Calling the CIFsm() function produces the following values for each event time tjp:

• ny1, f1, f1.se, ny2, f2, f2.se which correspond to the number of patients at risk in group 1, the cumulative incidence estimate for cause 1 in group 1 and its standard error, the number of patients at risk in group 2, the cumulative incidence estimate for cause 1 in group 2 and its standard error, respectively, and

• dif, dif.se, dif.pv, rr, rr.se, rr.pv, or, or.se, or.pv correspond to the estimated risk difference, its standard error and p–value, the estimated relative risk, its standard error and p–value, and the estimated odds ratio, its standard error and p–value, respectively. Note that these are pointwise estimates for each event time tjp.

Calling the CIFsm() function also gives the following statistics for the time integrated weighted summary requested by the users:

• ave (the requested time integrated weighted summary statistic),

• avese (standard error of the time integrated weighted summary statistic),

• ci95 (95% confidence interval of the time integrated weighted summary),

• avepval (p–value of the time integrated weighted summary statistic),

• cbcut (95% confidence band cut points for the summary statistics), and

• region (time range of data used for comparison).

Other values given by CIFsm() include sample (total sample size from both groups), size (group sample size), njp (number of distinct event times), method (summary statistic specified), and weight (weight function used).

4.2. Bone marrow transplant example

In this section, we use a bone marrow transplant data set to illustrate the proposed weighted summary statistics and the CIFsmry package. The data came from a study by the Center for International Blood and Marrow Transplant Research (CIBMTR). The CIBMTR is comprised of clinical and basic scientists who confidentially share data on their blood and bone marrow transplant patients with the CIBMTR Data Collection Center located at the Medical College of Wisconsin. The CIBMTR is a repository of information about results of transplants at more than 450 transplant centers worldwide. The objective of this study was to identify factors that affect outcomes after transplantation for patients with myelodysplastic syndromes using bone marrow cells from a sibling with identical human leukocyte antigen [20]. The study showed that younger age and platelet cell count at the time of transplantation higher than 100 × 10⁹/L were associated with lower treatment-related mortality (TRM), higher disease-free survival as well as higher overall survival.

This illustrative example uses data from 408 patients with complete data to evaluate the effect of platelet cell count at transplant on treatment-related mortality. Patients were divided into two groups: platelets > 100 × 10⁹/L (treatment group, n = 128) versus platelets ≤ 100 × 10⁹/L (control group, n = 280). Treatment-related mortality is defined as death in remission with relapse as the competing risk. The example dataset is called bmt (data available in the R-timereg package) and consists of three variables time (failure or censoring time), cause (1 for TRM, 2 for relapse, and 0 for censored), and platelet (1 for platelets > 100 × 10⁹/L and 0 for platelets ≤ 100 × 10⁹/L).

To use the CIFsmry package, first download it to a local directory and then open R (version 3.0.1 or higher) and install the package. Load the package (library(CIFsmry)) and the data (data(bmt)). Frequency table of the variable cause shows that 161 patients (39%) died in remission, 87 (21%) experienced relapse, and 160 (39%) were alive and in remission at the last follow up.

table(bmt$cause)
> table(bmt$cause)
  0   1   2
160 161  87

Calling CIFsm() on the bmt dataset using the default options to compute the risk difference using the even weight function and to request the confidence band cutpoint from 1000 simultations

out <- CIFsm(bmt, n.sim = 1000)

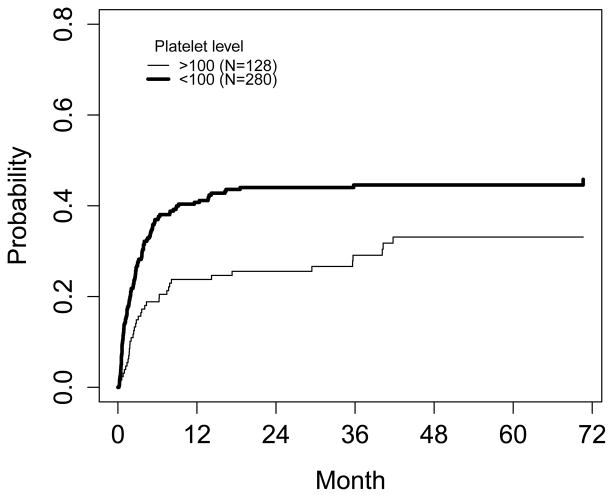
produces the estimates for the cumulative incidence of TRM for the two platelet groups and the integrated difference in TRM incidence using the even weight function (p = 0, q = 0). Plot of the cumulative incidence of TRM by treatment group (out$f1 and out$f2 for group 1 and 2, respectively) against time (out$tjp) in Figure 5 shows that higher platelet counts at transplantation (> 100 × 10⁹/L) was associated with lower non-relapse mortality.

Figure 5.

Cumulative incidence of treatment-related mortality for the two platelet groups

The following output

> out$method
[1] “dif”

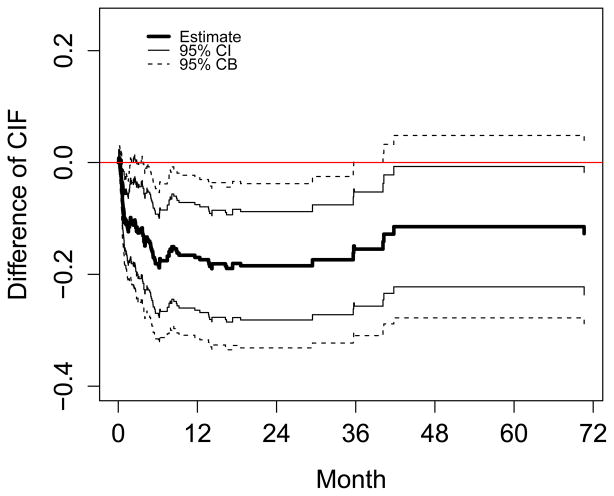
confirms that the comparison was based on the risk difference. Plot of the risk difference comparing high platelets to low platelets (out$dif) in Figure 6 suggests that the largest survival advantage associated with higher platelet counts occurred in the first 40 months post transplant. The 95% pointwise confidence intervals for the risk difference (solid lines in Figure 6, computed as out$dif ±1.96*out$dif.se) indicate that the pointwise differences in TRM were significantly lower than zero at all time points.

Figure 6.

Estimated TRM risk difference between high platelet group versus low platelet group

The comparison region and the confidence band cutpoints (for the risk difference, the relative risk, and the odds ratio, respectively) from 1000 simulations can be obtained by

> out$region
[1] 0.164 70.625
> out$cbcut
[1] 3.016650 2.953812 2.952391.

The 95% confidence bands (dashed lines in Figure 6, computed as out$dif ± out$cbcut[1] * out$dif.se) suggest that the survival advantage diminished and was no longer significant after 40 months post transplant.

The integrated difference in TRM between the platelet groups using even weight was estimated to be −0.14 with a 95% confidence interval of (−0.24, −0.05) and a p–value of 0.0023.

> summary(out)
Method: dif
Weight: 0 0
Summary statistics:
     est      se    ci95l     i95u    pval
-0.14467 0.04741 -0.23759 -0.05175 0.00228

However, the risk difference focusing on an early time period using the weight function (p = 2, q = 0) was more significant with a p–value < 0.0001 as expected due to a larger TRM difference in the early period.

out20 = CIFsm(bmt, method=“dif”, pp=2, qq=0)
> summary(out20)
Method: dif
Weight: 2 0
Summary statistics:
      est       se     ci95l     ci95u     pval
-1.16e-01 2.90e-02 -1.73e-01 -5.94e-02 6.05e-05

As noted at the end of Section 3, weight functions with much higher values of p focus the comparison on much earlier time post transplant. As seen in Figure 6, the risk difference in the first month or two post transplant was small. The p–value from the comparison with (p = 5, q = 0) was 0.0002 which was still significant but was larger than the p–value with (p = 2, q = 0) whereas the p–value in the comparison with (p = 10, q = 0) increased to 0.006.

Similar effects on non-relapse mortality were observed when the relative risk and the odds ratio were used as the summary statistics. The risk of TRM was lower in patients with platelet counts > 100 × 10⁹/L at the time of transplant. The risk and the odds of TRM using the even weight function were significantly lower in the high platelet group compared to the low platelet group. Similar results were observed for (p = 1, q = 0). However, the relative risk and the odds ratio became less significant in the comparisons with an early weight, (p = 2, q = 0). The p–values for the relative risk and the odds ratio were 0.031 and 0.025, respectively.

out.rr = CIFsm(bmt, method=“rr”)
> summary(out.rr)
Method: rr
Weight: 0 0
Summary statistics:
     est       se     ci95l    ci95u     pval
0.355580 0.099233 0.205772 0.614454 0.000211
out.or = CIFsm(bmt, method=“or”)
> summary(out.or)
Method: or
Weight: 0 0
Summary statistics:
    est      se    ci95l   ci95u    pval
0.27949 0.10841 0.13068 0.59778 0.00101

5. Discussion

In this work, we extended the summary statistics proposed by Zhang and Fine [15] to include a class of flexible weight functions. While the summary statistics allow direct comparison of the cumulative incidence functions between two treatment groups, the proposed weight functions allow the investigators to focus their comparison on an early or a late time period as relevant to their study. From our simulation study, we found that the summary statistics based on the relative risk and the odds ratio are sensitive to the time region of comparison. This sensitivity results from the cumulative incidences with values close to zero in the very early period post treatment. This sensitivity can be minimized by choosing the comparison time interval such that the cumulative incidences of interest are not too small. Unlike the relative risk and the odds ratio, the summary statistic based on the risk difference provides a more stable basis for comparison. Therefore, we recommend using the summary statistics based on the risk difference.

Our simulation study showed a large improvement in power when comparing cumulative incidence functions with an early difference using weight functions that focus on an early time period. However, the improvement in power was more moderate when the late weight functions were used to compare cumulative incidence functions with a late difference. An explanation for the moderate improvement with the late weight functions is due to the large variance of the cumulative incidence estimates later in the time course.

The proposed weighted summary statistics can be easily applied using the R-CIFsmry package. The CIFsmry package allows the users to specify the summary statistics and the weight functions of choice. As illustrated in Section 4, the cumulative incidence estimates, the risk difference, the relative risk, the odds ratio, the confidence intervals, the confidence bands, and the weighted integrated summary statistics can be obtained by simply calling the CIFsm() function. Implementation of the proposed approach in the R-CIFsmry package makes our method readily accessible to users.