Estimation of presynaptic calcium currents and endogenous calcium buffers at the frog neuromuscular junction with two different calcium fluorescent dyes

Abstract

At the frog neuromuscular junction, under physiological conditions, the direct measurement of calcium currents and of the concentration of intracellular calcium buffers—which determine the kinetics of calcium concentration and neurotransmitter release from the nerve terminal—has hitherto been technically impossible. With the aim of quantifying both Ca²⁺ currents and the intracellular calcium buffers, we measured fluorescence signals from nerve terminals loaded with the low-affinity calcium dye Magnesium Green or the high-affinity dye Oregon Green BAPTA-1, simultaneously with microelectrode recordings of nerve-action potentials and end-plate currents. The action-potential-induced fluorescence signals in the nerve terminals developed much more slowly than the postsynaptic response. To clarify the reasons for this observation and to define a spatiotemporal profile of intracellular calcium and of the concentration of mobile and fixed calcium buffers, mathematical modeling was employed. The best approximations of the experimental calcium transients for both calcium dyes were obtained when the calcium current had an amplitude of 1.6 ± 0.08 pA and a half-decay time of 1.2 ± 0.06 ms, and when the concentrations of mobile and fixed calcium buffers were 250 ± 13 μM and 8 ± 0.4 mM, respectively. High concentrations of endogenous buffers define the time course of calcium transients after an action potential in the axoplasm, and may modify synaptic plasticity.

Introduction

Calcium ions (Ca²⁺) play a leading role in the initiation, maintenance, and plasticity of neurotransmitter release at chemical synapses in both the central and peripheral nervous systems (Llinás et al., 1992; Chow et al., 1994; Augustine, 2001; Burnashev and Rozov, 2005; Schneggenburger and Neher, 2005; Pang and Südhof, 2010). The influx of Ca²⁺ into the nerve terminal following the action potential initiates the release of neurotransmitter and the subsequent postsynaptic potential. The properties of this potential reflect the magnitude of neurotransmitter release and the sensitivity of the postsynaptic membrane to the neurotransmitter.

In some synapses, the Ca²⁺ current can be measured directly (Borst and Sakmann, 1996, 1998; Yazejian et al., 1997), but such recordings from the frog neuromuscular junction are problematic because the small diameter (1–2 μm) and substantial length (100–500 μm) of the nerve terminal prohibits the use of the patch clamp and two-electrode voltage clamp techniques. Recordings with a loose macropatch clamp formed under the nerve perineurial sheath (Anderson et al., 1988), or with a macropatch electrode attached to the membrane as close as possible to a release site (Brigant and Mallart, 1982), have been accomplished only under non-physiological conditions, such as in the presence of K⁺-channel blockers.

Alternatively, optical methods may be employed to estimate the action-potential-induced Ca²⁺ influx and the subsequent distribution of Ca²⁺ ions in the axoplasm. The basis of these methods is the recordings of fluorescence transients which arise as a result of changes in the fluorescence intensity of specific calcium-sensitive dyes that interact with Ca²⁺ ions (DiGregorio and Vergara, 1997; Sabatini and Regehr, 1998; Suzuki et al., 2000; Sabatini et al., 2002; Luo et al., 2011).

The profile of intracellular Ca²⁺ distribution, and consequently the parameters of the fluorescence signal, is defined by the calcium influx and by the concentration of endogenous calcium-binding proteins (Ahmed and Connor, 1988; Burnashev and Rozov, 2005; Collin et al., 2005; Lin et al., 2005; Kreiner and Lee, 2006; Muller et al., 2007). After entering through voltage-gated channels, 95% of the Ca²⁺ ions bind to binding sites located within 10–50 nm of the site of entry (Neher, 1995). Mobile calcium buffers are represented by soluble Ca²⁺-binding proteins of the EF-hand family, including parvalbumins, calbindin-D9k, calbindin-D28k, calretinin, calmodulin, and proteins of the S100 family (Schwaller, 2010), or else by small molecules such as ATP and GTP which affect the diffusion of Ca²⁺ and define their operational distance (Feher et al., 1989; Zhou and Neher, 1993). Fixed endogenous Ca²⁺ buffers are associated with cellular organelles or elements of the cytoskeleton (Gabso et al., 1997; Muller et al., 2005). Fixed buffers slow the diffusion of Ca²⁺ and prolong the lifetime of high Ca²⁺ levels near the release zone (Zhou and Neher, 1993; Kits et al., 1999; Matveev et al., 2004). But for many peripheral synapses, including the frog neuromuscular junction, many of the details of the regulation of axoplasmic Ca²⁺ and of the properties of endogenous calcium buffers in terminals remain unknown.

In previous work, we have compared experimental and model-based approaches to show that the presence of endogenous fixed calcium buffers in the motor nerve terminal of frogs can explain the desynchronization of neurotransmitter release under conditions of low extracellular calcium and synchronization of quantal release in the presence of a mobile buffer (Samigullin et al., 2005; Bukharaeva et al., 2007; Gilmanov et al., 2008). In the present work, we measure fluorescence transients activated by a single nerve impulse in the motor nerve terminal of a frog using two calcium-sensitive fluorescent dyes with different affinities to calcium. We compare these fluorescence transients with the simultaneous measurement of the postsynaptic response of a muscular fiber. We then use mathematical modeling to estimate the parameters of the calcium current and the contribution of the endogenous calcium buffers of different mobilities to the spatial distribution of Ca²⁺ in the axoplasm.

Materials and methods

Preparation and solutions

The animals (frogs, Rana ridibunda) were anesthetized with ether prior to being decapitated in accordance with the European Communities Council Directive (November 24, 1986; 86/609/EEC). The protocol of the experiments was approved by the Animal Care and Use Committee of Kazan State Medical University. An isolated neuromuscular preparation of the musculus cutaneous pectoris was continuously perfused with Ringer solution (in mM): NaCl 113.0, KCl 2.5, CaCl₂ 1.8, and NaHCO₃ 3.0 (pH 7.2–7.4). The temperature was set at 20.0 ± 0.3°C. D-tubocurarine (5 μM) was added to the solution to prevent muscle contractions in response to nerve stimulation.

Calcium dye loading

Two fluorescent calcium dyes of different affinities were used: the low-affinity Magnesium Green (MG), which has dissociation constant K_d = 19 μM, and the high-affinity Oregon Green BAPTA-1 (OGB-1), whose dissociation constant is K_d = 0.17 μM (Maravall et al., 2000). The loading concentration of the fluorescent dyes was 50 mM. All dyes were obtained from Molecular Probes (Eugene, OR, USA).

The loading of the dyes was carried out through the nerve stump, as described by Peng and Zucker (1993) and Wu and Betz (1996). After this procedure, all terminals in the proximal part of the nerve trunk had sufficient basal levels of fluorescence. It has been established that the approximate intra-terminal concentration of dyes loaded into a nerve by this method is 40–150 μ M (Suzuki et al., 2000). The loading procedure does not have any appreciable influence on the amplitude of the postsynaptic response or on the frequency of the miniature end-plate potentials (Wu and Betz, 1996).

Recording of the fluorescent signals of the single action potentials

Fluorescence signals were monitored using a photometric system based on an Olympus BX-51 microscope with water immersion objective (40×, NA = 0.8) and a high-sensitivity photodiode (S1087, Hamamatsu, Japan) (Samigullin et al., 2010). To choose the area for recording the fluorescence, we used the optical viewfinder (Till Photonics, Munich, Germany). Light excitation at a wavelength of 488 nm was generated by Polychrome V (Till Photonics, Munich, Germany). To minimize bleaching of the dye and to the lower background fluorescence, the recording area of the nerve terminal was restricted using an iris diaphragm. Illumination was gated by a shutter with a typical exposure time of 400 μs and a delivery rate of 0.5 Hz. The signals from the photodiode were digitized with a Digidata 1200B analog-to-digital converter (Axon Instruments, California, USA). The recording of fluorescence and the synchronization of the illumination and stimulation was controlled by WinWCP software (Strathclyde University, Glasgow, UK). The change in fluorescence was represented as ΔF/F₀ (the change in fluorescence intensity relative to the background fluorescence as a percentage). For each experiment, about 60 fluorescent responses were recorded and averaged.

The time parameters of the fluorescence signals depend on the interaction of the dye with the calcium—specifically, on the speed of the forward and reverse reactions of the calcium–dye complex formation. The speeds of the forward reaction of the low-affinity (MG) and high-affinity (OGB-1) dyes differ (see Table 1). The dissociation rate of the calcium–dye complex is almost 30 times lower for OGB-1 than for MG, which explains the longer rise time and decay time observed with OGB-1.

Table 1.

Parameters of the model.

Parameter	Value	References
Intracellular concentration of calcium [Ca]in	0.05 μM	Helmchen et al., 1996
Calcium diffusion (DCa)	220 μm2 s−1	Albritton et al., 1992
Endogenous fixed buffer (kon)	100 μM−1 s−1	Xu et al., 1997
Endogenous fixed buffer (koff)	104 s−1	Xu et al., 1997
Endogenous fixed buffer concentration	2000–12000 μM	**
Endogenous mobile buffer (kon)	6 μM−1 s−1	Schwaller, 2010
Endogenous mobile buffer (koff)	1 s−1	Schwaller, 2010
Endogenous mobile buffer diffusion (DBmob)	43 μm2 s−1	Schmidt et al., 2003
Endogenous mobile buffer concentration	50–500 μM	**
Magnesium Green (kon)	90 μM−1 s−1	Zhao et al., 1996
Magnesium Green diffusion	15 μm2 s−1	Zhao et al., 1996
Magnesium Green dissociation constant	19 μM	Zhao et al., 1996
Magnesium Green concentration	100 μM	Suzuki et al., 2000
Oregon Green BAPTA-1 kon	400 μM−1 s−1	Saftenku, 2009
Oregon Green BAPTA dissociation constant	0.17 μM	Maravall et al., 2000
Oregon Green BAPTA diffusion	15 μm2 s−1	Saftenku, 2009
Oregon Green BAPTA concentration	100 μM	Suzuki et al., 2000
Maximum pump velocity (Vmax)	3.8.10−4 μM. cm−2 s−1	**
Pump dissociation constant (Kpm)	0.83 μM	Sala and Hernandez-Cruz, 1990
Leak rate (Kleak)	1.2 10−10 cm−2 s−1	**
Extracellular concentration of calcium [Ca]extra	1800 μM	Experimental conditions
Width of calcium current (σ)	0.0005 s	**
Amplitude of calcium current (iCa)	1.6 pA	**

^**Obtained from modeling parameters.

Electrophysiological recording of nerve-action potentials and end-plate currents

Suprathreshold stimuli of 0.2 ms duration were applied to the nerve at 0.5 Hz through a suction electrode. The nerve-action potentials and extracellular end-plate currents were recorded using heat-polished Ringer-filled extracellular pipettes with tip diameters of 20 μm and resistances of 1–3 MΩ. For optimal contact with the preparation, the pipette tip was beveled at 35° (Vyshedskiy and Lin, 2000). The calcium transients were recorded in the same region where the extracellular pipette was placed. The electrical and optical signals were sampled simultaneously at 3-μs intervals by a 12-bit analog–digital converter (Digidata 1200B, Axon Instruments, California, USA), stored on a computer, and processed in AxoScope (Axon Instruments, California, USA).

Computer modeling of intracellular calcium concentrations

Experimental and theoretical studies have shown that, in the frog nerve terminal, a presynaptic action potential only opens a few calcium channels, and that the interaction of calcium influxes through different channels is low (Wachman et al., 2004; Luo et al., 2011). Experiments in non-mammalian synapses indicate that calcium channels are tightly coupled to the sites where synaptic vesicles are docked; the opening of a single Ca²⁺ channel (producing a Ca²⁺ nanodomain; Yoshikami et al., 1989; Augustine, 1990; Stanley, 1991) is sufficient to initiate vesicular fusion. We therefore neglected non-linear interactions of currents through the channels and considered only one channel in the model of one active zone, with the assumption that the total Ca²⁺ current is the linear summation of currents through the individual channels. Such a presentation of the Ca²⁺ channel as a point source on the presynaptic membrane is common for modeling exocytotic release (Smith, 1996; Bauer, 2001; Gilmanov et al., 2008).

The terminal was modeled as a cylinder with height of 2 μm and a diameter of 2 μm, with the calcium channel as a point source in its center. The height of frog's neuromuscular terminal (the height of the cylinder in the model—Figure S1 in the Supplementary Materials) was taken from Birks et al. (1960) and Pawson et al. (1998). In addition to fluorescent dye molecules in the cytoplasm, the presence of mobile and fixed buffers was also assumed (Klingauf and Neher, 1997). The interaction of Ca²⁺ in the terminal with the fluorescent dye and endogenous Ca²⁺ buffers can be described by the equation:

$$Ca\text{\hspace{0.17em}+\hspace{0.17em}}{B}_n\begin{array}{c}{k}_{B_n}^{\text{on}}\\ \rightleftarrows \\ k_{B_n}^{\text{of}}\end{array}Ca{B}_n,$$ (1)

where k^on_Bn and k^of_Bn are the association and dissociation rate constants and B_n (where n = d, fix, mob, referring to the fluorescent dye, fixed endogenous buffer, and mobile endogenous buffer, respectively). Assuming mass action kinetics and Fickian diffusion, we established a system of seven partial differential equations (PDE):

$$\begin{array}{l}\frac{\partial [\text{Ca}]}{\partial t}=D_{Ca}·△\left[Ca\right]+i_{Ca}·\delta \left(x-x_0,y-y_0,z-z_0\right)\\ -k_{B_{fix}}^{\text{on}}·\left[Ca\right]·\left[B_{fix}\right]+k_{B_{fix}}^{\text{of}}·\left[Ca{B}_{fix}\right]-k_{B_{mob}}^{\text{on}}·\left[Ca\right]·\\ \left[B_{mob}\right]+k_{B_{mob}}^{\text{of}}·\left[Ca{B}_{mob}\right]-k_d^{\text{on}}·\left[Ca\right]·\left[B_d\right]\\ +k_d^{\text{of}}·\left[Ca{B}_d\right],\\ \frac{\partial [B_{fix}]}{\partial t}=-k_{B_{fix}}^{\text{on}}·\left[Ca\right]·\left[B_{fix}\right]+k_{B_{fix}}^{\text{of}}·\left[Ca{B}_{fix}\right],\\ \frac{\partial [Ca{B}_{fix}]}{\partial t}=k_{B_{fix}}^{\text{on}}·\left[Ca\right]·\left[B_{fix}\right]-k_{B_{fix}}^{\text{of}}·\left[Ca{B}_{fix}\right],\\ \frac{\partial [B_{mob}]}{\partial t}=D_{B_{mob}}·△\left[B_{mob}\right]-k_{B_{mob}}^{\text{on}}·\left[Ca\right]·\left[B_{mob}\right]\\ +k_{B_{mob}}^{\text{of}}·\left[Ca{B}_{mob}\right],\\ \frac{\partial [Ca{B}_{mob}]}{\partial t}=D_{B_{mob}}·△\left[Ca{B}_{mob}\right]+k_{B_{mob}}^{\text{on}}·\left[Ca\right]·\left[B_{mob}\right]\\ -k_{B_{mob}}^{\text{of}}·\left[Ca{B}_{mob}\right],\\ \frac{\partial [B_d]}{\partial t}=D_d·△\left[B_d\right]-k_d^{on}·\left[Ca\right]·\left[B_d\right]+k_d^{of}·\left[Ca{B}_d\right],\\ \frac{\partial [Ca{B}_d]}{\partial t}=D_d·△\left[Ca{B}_d\right]+k_d^{\text{on}}·\left[Ca\right]·\left[B_d\right]-k_d^{\text{of}}·\left[Ca{B}_d\right],\end{array}$$ (2)

where D_Ca, D_Bmob, and D_d are the diffusion constants for free Ca²⁺, the mobile buffer, and the fluorescent dye, respectively, δ (x − x₀, y − y₀, z − z₀) is the Dirac delta function denoting the calcium channel, where x₀, y₀, z₀ are coordinates of the center of cylinder base. Three-dimensional geometry with Cartesian coordinates was used in our modeling.

The action-potential-induced calcium influx i_Ca was modeled as a Gaussian-shaped calcium current, as measured in the presynaptic terminals (Llinás et al., 1976):

$$i_{Ca}=A·e^{-\frac{{(t-t_{peak})}^2}{\text{2}·{\sigma }^2}},$$ (3)

where A is current amplitude and t_peak is the time of the peak of the Gaussian calcium current. In this model, we have used the maximum of the presynaptic action potential as the starting point of the calcium current, since it is precisely the depolarization caused by the action potential that opens the presynaptic calcium channels. The parameter σ defines the width of the calcium current, for which we have also calculated the parameter t_1/2 (the width of the current at half-amplitude). The parameters t_1/2 and σ are connected by the equation:

$$t_{\frac{1}{2}}=2·\sqrt{\text{2\hspace{0.17em}}·\ln \left(\text{2}\right)}·\sigma$$ (4)

We have taken into account two additional calcium currents that pass through the cylinder base: the current representing the work of the membrane pumps and a leak current:

$$J=-V_{\text{max}}·\frac{\left[Ca\right]}{\left[Ca\right]\text{+}{K}_{pm}}\text{+}{K}_{\text{leak}}·\left(\left[C{a}_{\text{extra}}\right]\text{–}\left[Ca\right]\right),$$ (5)

where V_max is the maximum pump velocity, K_pm is the pump dissociation constant, K_leak is the membrane conductivity for calcium, and [Ca_extra] is the extracellular concentration of calcium.

For all species, the flux through all boundaries was null, i.e.,

$$\mathbf{n}·\left(-D\nabla \left[A\right]\right)=\text{0},$$

where n is normal to the surface cylinder, A is the designation of some species in the model. However, the current J through the cylinder base containing the calcium channel was present in the model throughout all the simulation. So for this base only:

$$-\mathbf{n}·\left(-D\nabla \left[Ca\right]\right)=J.$$

The initial conditions for all species were the equilibrium concentrations listed in Table 1.

The system of PDEs was solved using the finite element method, taking 0.1 μm as the size of elements in the volume of a cylinder and 0.1 nm near the point source, using Comsol Multiphysics 3.5 and Matlab.

The model parameters are specified in Table 1. To model the Ca²⁺ transients, we varied the concentrations of the mobile and fixed buffers, as well as the amplitude and duration of the inward Ca²⁺ current. We employed a human-based approach here, but the variations of all free parameters were made in the full physiological range in increments of 5% of the range. We then compared the resulting fluorescence signal of the model with the signal observed in experiments. The theoretical fluorescence signal was used to derive the total number of calcium–dye complexes in the model at each moment in time, as the fluorescence of these molecules gives rise to the fluorescence signal registered in the experiment. The concentration range of the mobile buffer was 50–500 μM, while the concentration range of the fixed buffer was 2000–12000 μ M. These parameters correspond to the values established for the nerve terminals in synapses of a crayfish (Vyshedskiy and Lin, 2000) and in synapses of the central nervous system (Wu and Saggau, 1994). The selection of parameters that provides the best agreement of the modeling and experimental curves with the calcium transient for the differing concentrations of fixed and mobile buffers are shown on Figure S2 in the Supplementary Materials.

Results

Action potential induced responses of Ca²⁺ dyes with differing affinities for Ca²⁺

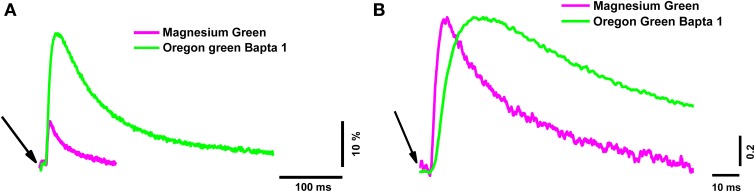
The peak of the fluorescence signal in nerve terminals loaded with the low-affinity dye MG was about 2.6 times smaller than in terminals loaded with the high-affinity dye OGB-1 (see Table 2 for details). The kinetics of the response of the low-affinity dye was significantly faster than the response of the high-affinity dye (Table 2 and Figure 1). Similar differences have been observed in synapses of the central nervous system (Regehr and Atluri, 1995) and in developing neuromuscular junctions of Xenopus (DiGregorio and Vergara, 1997). As described in the Materials and Methods section, the time parameters of fluorescence signals depend on the speed of the forward and reverse reactions of the formation of the calcium–dye complex. Thus, identical inward calcium currents evoked in nerve terminals loaded with dyes with different properties are accompanied by fluorescence signals with different amplitude and temporal properties. It is therefore impossible to accurately determine the behavior of the intracellular free calcium based on the response of only one fluorescent dye.

Table 2.

Summary of the characteristics of OGB-1 and MG fluorescence transients.

	Peak ΔF/F0 (%)	Rise time 20–80% (ms)	τ, (ms)
OGB-1	26 ± 6 (n = 9)	6.00 ± 0.36 (n = 9)	89.07 ± 7.34 (n = 9)
Magnesium Green	10 ± 3 (n = 6)	2.08 ± 0.23 (n = 6)	34.15 ± 4.06 (n = 6)

Data are presented as Mean ± SE, and n is the number of measured nerve–muscle junctions. Peak ΔF/F₀ is the averaged maximum ΔF/F₀ attained at a single spot location.

Figure 1.

The time course of calcium transients obtained in the nerve terminal from one electrical stimulus with two different dyes. Magnesium Green (magenta line) and Oregon Green BAPTA-1 (green line). (A) Averaged unnormalized calcium transients represented as ΔF/F₀. (B) Averaged calcium transients normalized to the maximum value to compare the time parameters. The averages were calculated from 60 responses. The beginning of the short (200 μs) electrical stimulus of the nerve terminal is indicated with arrows.

Simultaneous recording of presynaptic fluorescence signal and postsynaptic electrical response

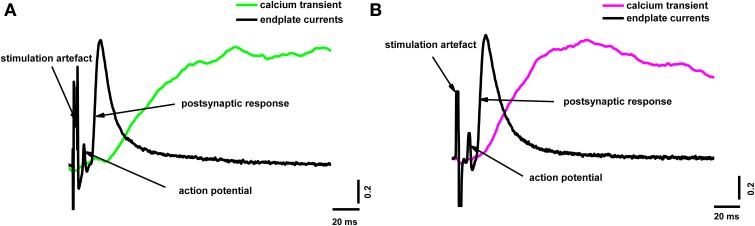
To reveal the correlation between the amplitude of the presynaptic calcium influx and neurotransmitter release, we simultaneously recorded the presynaptic fluorescence signal and the end-plate potential. Figure 2 shows the calcium signals and the extracellulary recorded action potentials of the nerve terminal and end-plate currents. It is clearly visible in Figure 2 that the postsynaptic current developed much faster than the fluorescence signal; in essence, the postsynaptic current ended before the fluorescence signal even reached its maximum. This means that, although the fluorescence signal occurs as a consequence of the interactions of calcium ions with the indicator in the nerve terminal of the frog neuromuscular junction, it does not directly reflect the change in Ca²⁺ concentration in the active release zones.

Figure 2.

Simultaneous recording of end-plate currents and fluorescence calcium transients caused by a single action potential in a terminal loaded with two different dyes. (A) Fluorescence calcium transient for Oregon Green BAPTA-1(green line), end-plate current (black line); (B) fluorescence calcium transient for Magnesium Green (magenta line), end-plate current (black line). The figure shows typical experimental recordings for each dye obtained from the average of 60 responses per experiment. Traces are normalized to the maximum values. End-plate currents were inverted to allow comparison with fluorescence signals.

Because electrophysiological techniques cannot be used to directly record calcium currents in the frog terminal, we used the mathematical model described in the Materials and Methods section to deduce the parameters of the inward calcium current that reproduces the observed fluorescence transient, and also in order to define a profile of calcium concentration changes at different points of the terminal, including the near-membrane space.

Model parameters and quantification of the endogenous calcium buffer concentration

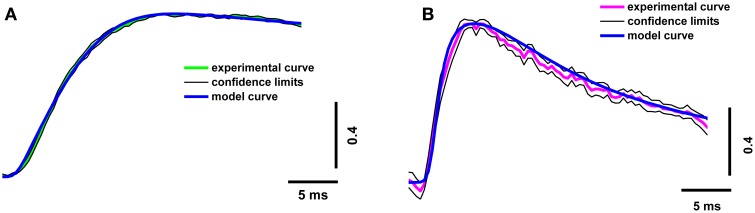
In order to increase the reliability of the model, we compared the theoretical and experimental fluorescence transients obtained with the different dyes and different regimes of nerve stimulation. As specified in Table 1, which shows the model parameters, the amplitude and duration of the calcium current and the concentrations of the fixed and mobile buffers were the variable parameters in the model. These were selected so that the model best reproduced the kinetics of the fluorescence transient for both dyes. We found that a presynaptic calcium current with amplitude 1.60 ± 0.08 pA and half-width 1.20 ± 0.06 ms resulted in the best agreement between the model and the experimental fluorescence transients. The presence in the axoplasm of a mobile calcium buffer at a concentration of 250 ± 13 μM and of fixed buffer at 8.0 ± 0.4 mM could explain the observed temporal differences in the measured fluorescence signal, compared with the postsynaptic response. We have checked additionally that, when all four model-derived parameters are within the intervals shown in Table 1, the shape of simulated fluorescence reproduces the shape of the experimental fluorescence (taking into account the dispersion of the experimental data; Figure 3). Figure S2 in the Supplementary Materials demonstrate the selection of parameters that provides the best agreement of the modeling and experimental curves with the calcium transient for the differing concentrations of fixed and mobile buffers.

Figure 3.

Superposition of experimental and model calcium transients in terminals loaded with two different dyes. (A) Experimental curve for Oregon Green BAPTA-1(green line), model calcium transient (blue line), confidence interval for experimental curve (thin black line); (B) experimental curve for Magnesium Green (magenta line), model calcium transient (blue line), and confidence interval for experimental curve (thin black line). Traces are normalized to the maximum value.

Fluorescence transients during rhythmic stimulation of the motor nerve

The neuromuscular junction in vivo operates in a mode of rhythmic activity, so it is important to estimate the intracellular calcium kinetics not only in response to individual stimuli, but also during repetitive stimulation. We estimated the properties of the calcium transients for the three signals occurring in response to a 50-Hz train of action potentials in the presence of dyes of both types.

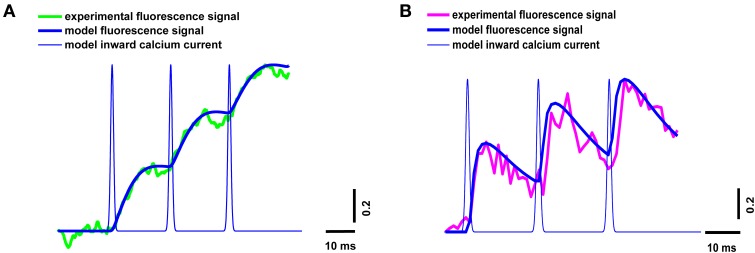
The parameters of the simulated fluorescence response were in a good agreement with those of the experimental response obtained using the high- and low-affinity dyes (Figure 4), thus confirming the validity of the model.

Figure 4.

Superposition of experimental and model calcium transients in the terminal loaded with two different dyes during a stimulus train consisting of three signals at 50 Hz. (A) Experimental curve for Oregon Green BAPTA-1(green line), model calcium transient (thick blue line), model inward calcium current (thin blue line); (B) experimental curve for Magnesium Green (magenta line), model calcium transient (thick blue line), model inward calcium current (thin blue line). Traces are normalized to the maximum value.

The estimation of calcium concentration in the near-membrane space

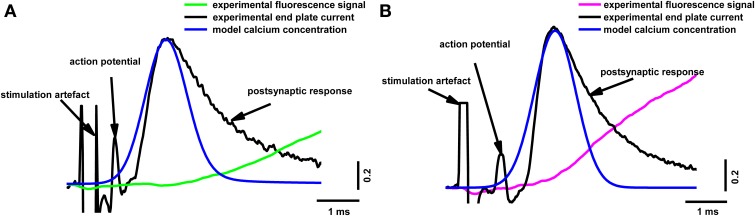
Our model allowed us to calculate the calcium distribution in different parts of the terminal. It is particularly important to estimate Ca²⁺ concentration in the near-membrane region, since this determines the number of released quanta and the kinetics of neurotransmitter release. Figure 5 shows the calculated dynamics of the calcium concentration at a distance of 15 nm from the calcium channel, in comparison with the experimental postsynaptic current and fluorescent signal. The beginning of the rise in the calcium concentration in the near-membrane space preceded the postsynaptic response, indicating that the real time between the beginning of the calcium response in the active zone and the beginning of the postsynaptic current (about 600 μs) was sufficient for the activation of the exocytosis machinery, the release of neurotransmitter, the activation of the postsynaptic receptors, and the opening of the postsynaptic ion channels.

Figure 5.

Superposition of the calculated calcium concentration dynamics at a distance of 15 nm from the calcium channel, with simultaneous recording of end-plate current and calcium transients induced by a single action potential in terminals loaded with two different dyes. (A) Fluorescence calcium transient for Oregon Green BAPTA-1(green line), experimental end-plate current (black line), model calcium concentration (blue line); (B) fluorescence calcium transient for Magnesium Green (magenta line), experimental end-plate current (black line), model calcium concentration (blue line). Traces are normalized to the maximum value. Experimental data are the same as in Figure 2.

Discussion

In a nerve terminal loaded with calcium-sensitive dye, calcium ions entering through Ca²⁺ channels bind to the dye, producing a change in its fluorescence intensity. Analysis of Ca²⁺-related fluorescent signals reveals the dynamics of calcium concentration in the nerve terminal which demonstrate, for example, that synaptic facilitation caused by the accumulation of intracellular calcium outlasts the increase in Ca²⁺ in the terminal (Regehr and Atluri, 1995). Analysis of Ca²⁺-dependent fluorescence changes has also been used to identify the types of voltage-gated calcium channels that participate in neurotransmitter release, and to clarify the degree of cooperativity of Ca²⁺ channels (Wu and Saggau, 1994; Mintz et al., 1995; Tsentsevitsky et al., 2014). While electrophysiological recording of Ca²⁺ currents provides a more direct measure (Vyshedskiy and Lin, 2000), the morphological features of some synapses—such as the neuromuscular junctions of mice, frogs, and other vertebrates—render the use of voltage clamp methods difficult. Therefore, the use of calcium-sensitive dyes is an alternative for estimating calcium influx into the nerve terminal.

The fluorescent signal had a very slow rise compared with the postsynaptic response, and presumably the calcium current. Similar observations have been made in the neuromuscular synapses of lizards and frogs (David et al., 1997; DiGregorio and Vergara, 1997; Bélair et al., 2005). However, this temporal difference between the beginning of the fluorescence signal and the postsynaptic potential has not always been observed, and it has generally been assumed that the fluorescence transient reflects the change in calcium concentration in the terminal, while its first derivative reflects the calcium current (Sabatini and Regehr, 1998). The lag observed in our study could be interpreted, for example, as a consequence of the presence of a high concentration of fixed buffer, resulting in slow diffusion of calcium into the terminal (Lin et al., 2005). In this case, calcium entering the terminal interacts directly with proteins of the exocytosis machinery to trigger neurotransmitter release, and only subsequently does the slow diffusion of calcium cause the formation of calcium–dye complexes and an appreciable fluorescence signal. Because we recorded the fluorescence from the entire volume of the terminal, the slow kinetics of the signal are likely to reflect a process of slow calcium distribution. Another reason why the postsynaptic current in Figure 2 develops earlier than the fluorescence signal is that the frog neuromuscular junction is a fast synapse (as opposed to slow NMDA, for example) with relatively short synaptic delays and quickly rising and falling postsynaptic currents. For the frog neuromuscular junction, the time between neurotransmitter release and the start of the postsynaptic current is very short (about 300–500 μs; Bukharaeva et al., 2002). In some other synapses, the slow activation of postsynaptic channels can mask the paradox shown in Figure 2. The current through these channels grows at a similar speed to the fluorescence signal (for example, Vyshedskiy and Lin, 2000) due to the slow activation.

Our mathematical model permits us to clarify the observation that the postsynaptic current develops much faster than the fluorescence signal. After the opening of the voltage-gated channels, Ca²⁺ enters the terminal and, in the process of diffusing away from the entry site, binds to the dye molecules that are distributed throughout the volume of the terminal. The rising phase of the fluorescent signal of the calcium–dye complex in the area recorded by the photodiode depends on the speed of calcium diffusion, which in turn depends on the concentration and properties of endogenous buffers. Endogenous calcium buffers play the leading role in the spatiotemporal distribution of Ca²⁺ (Sala and Hernandez-Cruz, 1990; Nowycky and Pinter, 1993). After the action-potential-triggered Ca²⁺ influx through the voltage-dependent channels, Ca²⁺ ions bind to the buffers within 10–50 nm of the entry site (Augustine and Neher, 1992; Neher, 1995). Further diffusion of Ca²⁺ depends mainly on the degree of mobility of Ca²⁺-binding sites. Immobile buffers, which are localized on cellular organelles or cytoskeleton elements, have a slower speed of diffusion than free calcium. Such fixed buffers delay diffusion, because they take up and bind calcium ions for some time, thus reducing the speed of calcium distribution within the space of the terminal (Zhou and Neher, 1993; Kits et al., 1999). This slowing of diffusion has important consequences for any intracellular calcium-dependent process.

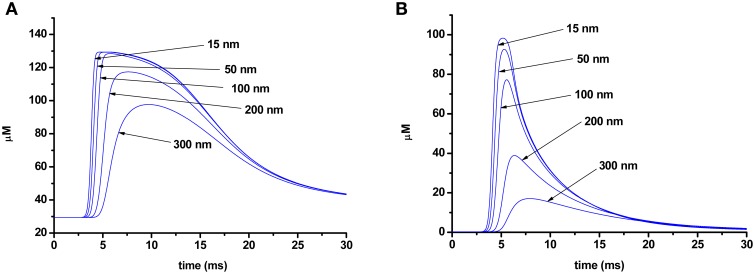
As Ca²⁺ slowly diffuses through the terminal, dissociation of the calcium–dye complexes begins, and the duration of the rising phase of the fluorescent signal also depends on the speed of this process. Figure 6 shows the changes in the concentration of a calcium–dye complex at various points of a terminal for the two different dyes. Dissociation of the calcium–dye complex is expected to occur faster in the case of a low-affinity dye, as the rate of the reverse reaction is greater than for the high-affinity dye. The phase of the signal rise ends when the rate of formation of calcium–dye complexes becomes slower than the rate of dissociation. For the low-affinity dye, dissociation occurs rapidly, and thus the rising phase of the signal is shorter. Conversely, the slower speed of dissociation of the high-affinity dye leads to a longer rising phase.

Figure 6.

Change in concentration of a calcium–dye complex at different distances from the point of calcium entry (15, 50, 100, 200, 300 nm) in the terminal loaded with Oregon Green BAPTA-1 (A) or Magnesium Green (B).

Our mathematical model shows that the kinetics of Ca²⁺ transients observed in the presence of dyes with different calcium affinity and different calcium–dye complex dissociation rates could be described using a fixed-buffer concentration of 8.0 ± 0.4 mM and a mobile-buffer concentration of 250 ± 13 μM. Similar results (7.5 mM for slow buffers) have been reported by Bennett et al. (2007), who compared experimental and model-derived presynaptic fluorescence signals during rhythmic stimulation of toad motor nerves, considering the mitochondria and endoplasmic reticulum as fixed buffers. Suzuki et al. (2000) have assumed the existence in the frog nerve terminal cytoplasm of a fixed low-affinity Ca²⁺ buffer at 10 mM concentration. Such fixed buffers can determine the early decay of Ca²⁺ transients after an action potential in crayfish neuromuscular terminals (Lin et al., 2005). Parameters determined from our modeling thus coincide with the values proposed by other authors (Aharon et al., 1994; Suzuki et al., 2000; Bennett et al., 2007).

The idea that the inclusion of fluorescent dyes itself increases the local Ca²⁺ buffering, thus altering the Ca²⁺ dynamics, is often encountered in the literature (e.g., Sabatini et al., 2002). But in our model the interaction of the dye with calcium and diffusion of the dye and the dye-calcium complex in the terminal are simulated separately (Equation 2). Thus, our estimates of buffers concentration are made already taking into account the dye influence on the calcium diffusion. In principle it was shown experimentally (Wu and Betz, 1996) that the calcium dye loading haven't any appreciable influence on the calcium dependent quantal release (parameters of the postsynaptic response or of the frequency of the miniature end-plate potentials do not change). It suggests that endogenous calcium buffers have the buffering capacity much stronger than fluorescent dyes. But our model allows even to check the changes in intracellular calcium distribution at fluorescent dye loading.

The presence of mobile and fixed buffers in the axoplasm explains the time discrepancy between the fluorescent signal and the postsynaptic response (Figures 2, 5). Estimation of the inward calcium current shows that the best agreement between model and experimental fluorescence transients was achieved at a current amplitude of 1.6 ± 0.08 pA and a half-width of 1.2 ± 0.06 ms (Figures 3, 4). Assuming that the conductance of presynaptic N-type calcium channels (which are dominant in frog nerve terminals) is 0.33 pA (Weber et al., 2010), we may conclude that about five channels are activated by a single action potential. These data correspond to the results of Shahrezaei et al. (2006), who showed that from two to six channels open per active zone per action potential; and that fusion of a single vesicle is triggered by the opening of one or two channels.

In summary, the analysis of fluorescence transients in the nerve terminal of the frog neuromuscular junction and the comparison of the kinetics of experimental and model responses allowed us to estimate the intracellular concentrations of fixed and mobile endogenous buffers, the properties of the calcium current, and the kinetics of the changes in calcium concentrations in the nerve terminal.

The high concentration of intracellular calcium buffers, which slow diffusion by binding calcium to cytoplasmic elements, has important consequences for any intracellular Ca²⁺ -dependent process. Diffusion cannot be ignored if the time course of the process studied is on the order of milliseconds, and may contribute to delayed asynchronous release of neurotransmitters (Rahamimoff and Yaari, 1973), calcium-induced calcium release from intracellular calcium stores (Akita and Kuba, 2008), facilitation and augmentation (Miller, 1991), and modulation of Ca²⁺-dependent deactivation of Ca²⁺ channels (Kreiner and Lee, 2006). High concentrations of endogenous buffers modify transmitter release at synapses (Caillard et al., 2000; Matveev et al., 2004).

In conclusion, the concentration of a calcium–dye complex is proportional to the concentration of Ca²⁺ at each point of the terminal volume. When studying small terminals with fast diffusion and a short time to equilibrium, the concentration of Ca²⁺ can be accurately estimated by the first derivative of the smoothed fluorescent signal (Sabatini and Regehr, 1998). Because of the slow “delayed” diffusion and the resulting longer time before equilibrium in the frog motor nerve terminal, the fluorescence signal does not correspond directly to Ca²⁺ concentration in the terminal, particularly near the active zone. However, mathematical modeling allows determination of Ca²⁺ concentration and mobile and fixed buffers concentrations near the membrane of the nerve terminal where the calcium-sensitive exocytosis proteins are placed.

Funding

This research has been performed under the Russian Government's Program for Competitive Growth of Kazan Federal University and was also supported by a grant of President of Russian Federation “Leading Scientific School” and a grants from the Russian Foundation for Basic Research (13-04-00886; 14-04-00790; 15-04-02983).

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary material

The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fnsyn.2014.00029/abstract