The impact of gradient strength on in vivo diffusion MRI estimates of axon diameter

Abstract

Diffusion magnetic resonance imaging (MRI) methods for axon diameter mapping benefit from higher maximum gradient strengths than are currently available on commercial human scanners. Using a dedicated high-gradient 3 T human MRI scanner with a maximum gradient strength of 300 mT/m, we systematically studied the effect of gradient strength on in vivo axon diameter and density estimates in the human corpus callosum. Pulsed gradient spin echo experiments were performed in a single scan session lasting approximately 2 h on each of three human subjects. The data were then divided into subsets with maximum gradient strengths of 77, 145, 212, and 293 mT/m and diffusion times encompassing short (16 and 25 ms) and long (60 and 94 ms) diffusion time regimes. A three-compartment model of intra-axonal diffusion, extra-axonal diffusion, and free diffusion in cerebrospinal fluid was fitted to the data using a Markov chain Monte Carlo approach. For the acquisition parameters, model, and fitting routine used in our study, it was found that higher maximum gradient strengths decreased the mean axon diameter estimates by two to three fold and decreased the uncertainty in axon diameter estimates by more than half across the corpus callosum. The exclusive use of longer diffusion times resulted in axon diameter estimates that were up to two times larger than those obtained with shorter diffusion times. Axon diameter and density maps appeared less noisy and showed improved contrast between different regions of the corpus callosum with higher maximum gradient strength. Known differences in axon diameter and density between the genu, body, and splenium of the corpus callosum were preserved and became more reproducible at higher maximum gradient strengths. Our results suggest that an optimal q-space sampling scheme for estimating in vivo axon diameters should incorporate the highest possible gradient strength. The improvement in axon diameter and density estimates that we demonstrate from increasing maximum gradient strength will inform protocol development and encourage the adoption of higher maximum gradient strengths for use in commercial human scanners.

1. Introduction

Axons are the structural and physiological conduit for signal transmission in the brain and therefore are one of the fundamental elements of brain function. The diameter of both myelinated and unmyelinated axons is related to the speed at which action potentials are conducted along the length of the axon (1, 2). In unmyelinated axons, a large diameter provides more ion channels per unit length and therefore a more rapid means of changing the inner to outer ion concentrations. This rate of change in the intra- versus extra-axonal ion concentration is what governs the conduction velocity of action potentials. Myelination increases conduction velocity through an entirely different mechanism known as saltatory conduction. For myelinated axons, ion channels and action potentials occur only at the gaps between the myelin, known as the nodes of Ranvier. Between these nodes of Ranvier, the current flows passively through the insulating myelinated portions, leading to an increased rate of conduction. In 1939, Hursh (2) showed the conduction velocity to be proportional to the square root of the diameter of unmyelinated axons and directly proportional to the inner membrane diameter of myelinated axons. In the peripheral nervous system, axon diameters range from 0.1 µm to about 20 µm, with unmyelinated axons being smaller than 2 µm and myelinated axons larger than 1 to 2 µm (3). In the central nervous system, myelinated axons as small as 0.2 µm have been observed (4), with axons below this size generally being unmyelinated. Variations in axon diameter are thought to be closely tied to function, with networks that demand fast response times (such as motor networks) demonstrating larger axon diameters. Therefore, a non-invasive method of mapping axon diameters would provide new insight into brain function and connectivity.

The ability to map axon diameters noninvasively in vivo has potential utility in tracking development, aging, and diseases of the central nervous system. Axon diameters have been shown to increase with age (5) and correlate with the stages of development (6). Prior studies indicate that smaller axons are more vulnerable to damage in multiple sclerosis (7, 8), whereas larger diameter axons are selectively affected in amyotrophic lateral sclerosis (9, 10). There is also a strong potential utility for axon diameter mapping in the study of psychiatric disorders, which are often hypothesized to be the result of abnormal signaling. Several studies have focused on the possibility of disconnections in psychiatric disorders (11, 12) and autism (13, 14); however, abnormal signaling rates due to differently sized axons could also contribute to symptoms in diseases such as schizophrenia (15).

Recognizing the potential impact of an MRI technique to map axon diameters, several groups have started to exploit the sensitivity of diffusion-weighted MRI (DW-MRI) to tissue microstructure for the purpose of estimating axon diameter distributions and fiber density in white matter bundles (16–28). DW-MRI is well-established clinically and plays a key role in the diagnosis of several neurological conditions including acute stroke (29–31) and the evaluation of brain tumors (32, 33) and traumatic brain injury (34, 35). DW-MRI is also used to map the orientation of white matter tracts, which can be achieved by measuring diffusion along multiple orientations and applying an analysis scheme such as diffusion tensor imaging (36), high-angular resolution diffusion imaging (HARDI) (37), q-ball (38) or diffusion spectrum imaging (39). It is only more recently, however, that there has been a heightened focus on using DW-MRI measurements to quantify the size of restrictive spaces in brain tissue.

One such genre of techniques focuses on the quantification of axon diameters and density in white matter (16–28). These methods generally acquire diffusion-weighted images with a range of q-values (diffusion-encoding gradient areas) and diffusion times (time between diffusion-encoding gradients). A model for intra- and extra-axonal diffusion signal decay is then fitted to the data. Large q-values are needed to resolve small differences in spin displacements, and short diffusion times are needed to capture restricted diffusion in small compartments. The simultaneous need for short diffusion times and large q-values places strong demands on MRI gradient hardware. The advent of higher maximum gradient strengths (G_max) on human MRI scanners (40–43) has enabled the translation of these methods from animal (21, 22, 44, 45) and ex vivo studies (19, 23, 24, 26, 28) to the in vivo human brain (23, 25, 27, 46). Recent simulation and ex vivo experimental results suggest the key role of G_max in detecting small diameter axons (~µm) and enhancing contrast between axon diameter estimates (45). Recognizing the differences in relaxation and diffusion properties of fixed and in vivo brain tissue (47–49), these results motivated us to perform a systematic study of the effect of gradient strength on in vivo axon diameter estimates. While the benefits of high gradient strengths have been evidenced in the animal literature (24, 45), the actual demonstration of axon diameter mapping methods using high gradient strengths in humans in vivo confirms that the performance of the hardware is sufficiently robust to line up with the predicted theoretical benefits. In this work, we study how the precision and mean estimates of axon diameter change with gradual increases in maximum gradient strength. This type of study is also critical for understanding how to interpret data acquired on standard clinical systems with 40–60 mT/m maximum gradient strengths, which may provide useful information but be biased or insensitive to restrictive spaces below a certain size.

Here we use a novel 3 T human MRI equipped with G_max of 300 mT/m (40) to acquire q-space data with a range of G_max values in the human corpus callosum in vivo. We find that, for the acquisition parameters, model and fitting routine used in our study, including higher G_max measurements decreases the uncertainty in axon diameter estimates (i.e., posterior probability density functions are narrower) and that the exclusive use of longer diffusion times results in larger axon diameter estimates. Axon diameter and density maps also appear less noisy and show improved contrast between different regions of the corpus callosum with higher maximum gradient amplitudes.

2. Methods

2.1. Data acquisition

With approval from the institutional review board, three healthy volunteers were scanned on a dedicated high-gradient (AS302) 3 T MRI scanner (MAGNETOM CONNECTOM, Siemens Healthcare) with a maximum gradient strength of 300 mT/m and maximum slew rate of 200 T/m/s. The slew rate was de-rated to a maximum of 62.5 T/m/s during diffusion encoding to prevent physiological stimulation. A custom-made 64-channel phased array head coil was used for signal reception (40). The experimental protocol consisted of sagittal 2-mm isotropic resolution diffusion-weighted spin-echo echo-planar imaging acquisitions with 17 contiguous slices centered on the midline corpus callosum. The following parameters were used: TE/TR = 120/3000 ms, parallel imaging using generalized auto calibrating partially parallel acquisitions (GRAPPA) with an acceleration factor of R = 2, diffusion gradient pulse duration δ = 8 ms, 39 diffusion gradient increments (10–293 mT/m) and 8 averages. The experiment was repeated for five different diffusion times Δ: 16, 25, 35, 60 and 94 ms. Diffusion gradients were applied in the z-direction orthogonal to the callosal fibers. Interspersed T₂-weighted (b = 0) images were acquired for each diffusion gradient increment and diffusion time combination. The maximum b-value at the longest diffusion time was 35,690 s/mm². The total acquisition time for each subject was 118 minutes.

The temporal signal-to-noise ratio (SNR) was estimated using 195 interleaved b = 0 data acquired between diffusion-weighted images through a voxel-wise calculation of the mean of the 195 b = 0 images divided by the standard deviation of the b = 0 images. The complex-valued data was combined across channels in the 64-channel coil, such that the magnitude bias could be estimated based on the correction for a single-channel coil (50). The mean temporal SNR within the genu ROI in the corpus callosum (shown in Fig. 2) was estimated to be about 10.

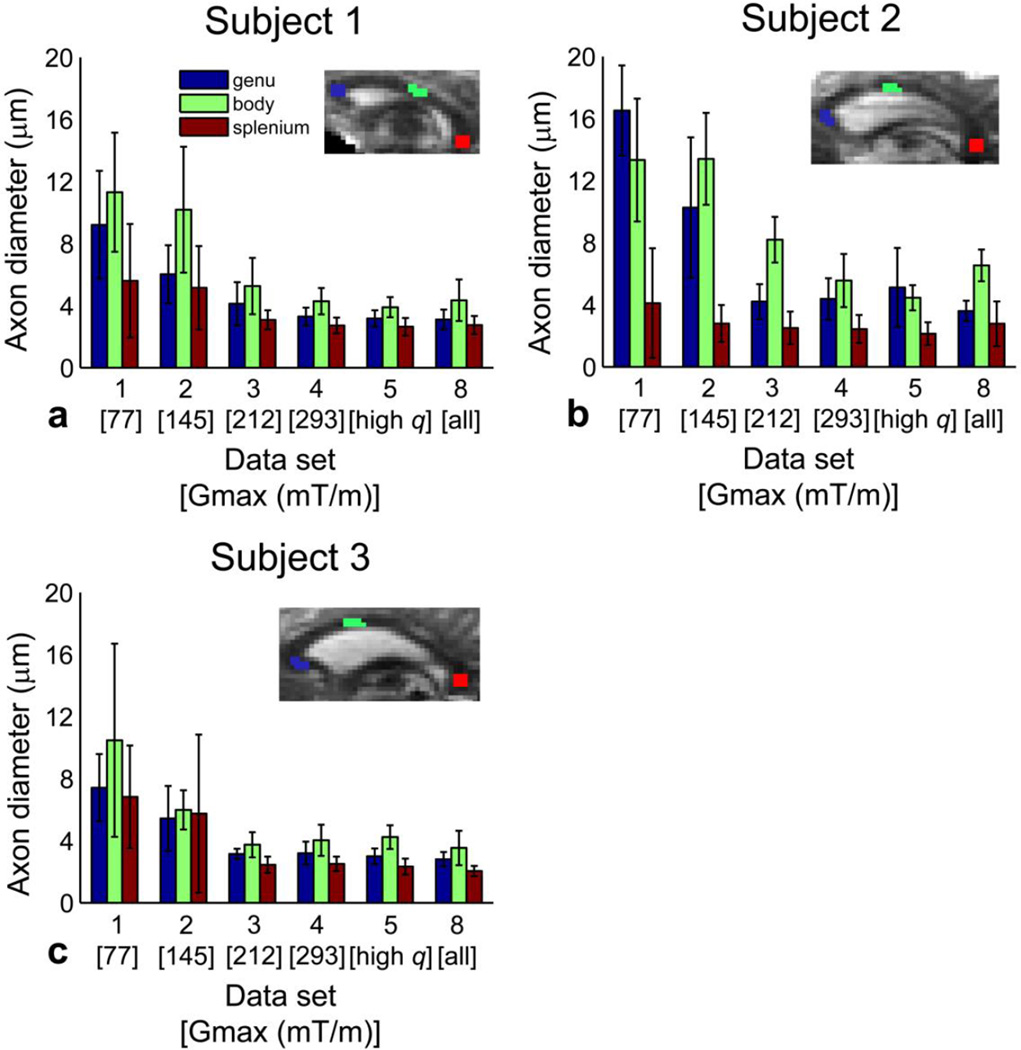
Figure 2.

Effect of G_max and q on mean axon diameter estimates in all three subjects. Mean and standard deviation of axon diameter estimates for data sets 1–5 and 8 within the genu, body, and splenium ROIs in the midline sagittal slice of the corpus callosum for (a) subject 1, (b) subject 2, and (c) subject 3. (Insets) Delineation of ROIs placed in the genu, body, and splenium of the midline sagittal slice of the corpus callosum overlaid on representative b = 0 images for each subject.

2.2. Data sets

The data were divided into the subsets listed in Table 1. These subsets represented data acquired with G_max of 77, 145, 212, and 293 mT/m (data sets 1–4) and high q values with G_max of 293 mT/m (data set 5), with q-space sampled using 16 linearly spaced q-values for each G_max (see Table 1 for list of q-values sampled). Data sets 1–5 each included 80 measurements. Additional subsets of the data represented different diffusion times, including short diffusion times Δ of 16 and 25 ms (data set 6), long diffusion times Δ of 60 and 94 ms (data set 7), and all diffusion times (data set 8) using all acquired q-value data for each diffusion time.

Table 1.

Diffusion-weighting parameters for data subsets.

Data set	Gmax (mT/m)	q-values in µm−1 (# of q-values)*	1/qmax (µm)	Diffusion times at each q-value (Δ, ms)	Total no. of measurements
1	77	0.0034 to 0.026 (16)	37.9	16,25,35,60,94	80
2	145	0.0034 to 0.049 (16)	20.3	16,25,35,60,94	80
3	212	0.0034 to 0.072 (16)	13.8	16,25,35,60,94	80
4	293	0.0034 to 0.1 (16)	10.0	16,25,35,60,94	80
5	293	0.045 to 0.1 (16)	10.0	16,25,35,60,94	80
6	293	0.0034 to 0.1 (39)	10.0	16,25	78
7	293	0.0034 to 0.1 (39)	10.0	60,94	78
8	293	0.0034 to 0.1 (39)	10.0	16,25,35,60,94	195

^*q values were linearly spaced for each data set.

2.3. Data preprocessing

Image warping caused by gradient nonlinearity was corrected by calculating the three-dimensional displacements generated by nonlinear terms in the magnetic field for each gradient coil (51). Correction of eddy current-induced distortions was achieved using opposite polarity DWI pairs (52), which were registered one to the other, constraining for the expected translations and dilations in the phase-encoding direction and shears in the slice plane. The halfway transform was then calculated and applied. To correct for inter-scan bulk motion, the T₂-weighted images (b = 0) acquired with each diffusion gradient/time combination were used to co-register all images using FLIRT (www.fmrib.ox.ac.uk/fsl). Eddy current correction and motion correction transformations were applied in a single step to prevent further blurring.

2.4. Signal model

We modeled diffusion in the corpus callosum as occurring in three compartments: restricted diffusion within an intra-axonal compartment, hindered diffusion in an extra-axonal compartment, and free diffusion in cerebrospinal fluid (CSF). The overall diffusion-weighted signal S was taken to be the sum of the restricted intra-axonal (S_r), hindered extra-axonal (S_h), and CSF compartment (S_csf) signal models weighted by their respective volume fractions: S = f_rS_r + f_hS_h + f_csfS_csf, where f_r is the fraction of water in the intra-axonal compartment, f_csf is the fraction of water in the CSF compartment, and f_h = 1 − f_r − f_csf is the fraction of water in the extraaxonal compartment.

Intra-axonal diffusion (S_r) was modeled by restricted diffusion in impermeable parallel cylinders of diameter a (53) as follows:

$$S_r=S_0\text{exp}\{-2{\mathrm{\gamma }}^2{G}^2\sum _{m=1}^{\infty }\frac{[2D_r{\alpha }_m^2\delta -2+2e^{-D_r{\alpha }_m^2\delta }+2e^{-D_r{\alpha }_m^2\mathrm{\Delta }}-e^{-D_r{\alpha }_m^2(\mathrm{\Delta }-\delta )}-e^{-D_r{\alpha }_m^2(\mathrm{\Delta }+\delta )}]}{D_r^2{\alpha }_m^6[{(a/2)}^2{\alpha }_m^2-1]}\}$$ (1)

where S₀ is the signal obtained at b = 0 without diffusion weighting, γ is the gyromagnetic ratio, G is the gradient strength of the diffusion-encoding gradients, D_r is the diffusion coefficient of water in the restricted compartment, δ is the diffusion gradient pulse duration, Δ is the diffusion time, a is the axon diameter, and α_m are the roots of the equation J'₁ (α_m(a/2)) = 0. J₁´ is the derivative of the Bessel function of the first kind, order one. The summation in Equation 1 was taken up to m = 10, with the contribution of terms m > 10 considered negligible. The signal model for intra-axonal diffusion accounts for diffusion during the gradient pulse (δ) using the Gaussian phase distribution approximation (53–56) as was done previously in Alexander et al. (23). Instead of assuming a gamma distribution of axon diameters (19), we fit the data to a single axon diameter as in (23).

Extra-axonal hindered diffusion was modeled by the one-dimensional Stejskal-Tanner equation (57): S_h = S₀exp[−(γδG)²(Δ−δ/3)D_h], where D_h is the hindered diffusion coefficient. To model the effect of CSF, which may have been introduced through partial volume averaging and CSF pulsation, we included a CSF compartment, following the approach of (22, 23). Free diffusion in CSF was modeled as isotropic Gaussian diffusion occurring with diffusion coefficient D_csf (22): S_csf = S₀exp[−(γδG)²(Δ−δ/3)D_csf].

2.5. Model fitting

Model fitting was performed on a voxel-wise basis in the midline sagittal slice of the corpus callosum using Markov chain Monte Carlo (MCMC) sampling, which generated posterior distributions of the model parameters given the data, similar to the approach of (20). A Rician noise model was adopted for parameter estimation as in (20, 23). The standard deviation of the noise σ = 0.1 was estimated from fitting the noise level in the data and corresponded to an SNR of 10. The total number of MCMC samples calculated for each voxel was 1,800. MCMC samples were saved at intervals of 100 iterations after an initial burn-in period of 20,000 iterations.

The parameters that were estimated from the model fitting were: axon diameter a, volume fraction of the restricted compartment f_r, volume fraction of the CSF compartment f_csf, and hindered diffusion coefficient D_h. Uniform priors with ranges given in parentheses were used for axon diameter a (0.2–40 µm), restricted fraction f_r (0–1), CSF fraction f_csf (0–1), and hindered diffusion coefficient D_h (0.1–2 µm²/ms). The restricted diffusion coefficient D_r was set to 1.7 µm²/ms. The diffusion coefficient of CSF (D_csf) was assumed to be that of free water at 37°C (3 µm²/ms). The mean and standard deviation of the estimates for axon diameter a, restricted fraction f_r, CSF fraction f_csf, and hindered diffusion coefficient D_h were then calculated for each voxel by taking the mean and standard deviation over the MCMC samples.

Regions of interest (ROIs) of 9 voxels each were manually drawn by a radiologist in the genu, body, and splenium of the midline sagittal slice of the corpus callosum as determined from the contrast on b = 0 and diffusion-weighted images (see insets in Figure 2 for ROI delineation). The mean of the posterior distribution for each fitted parameter was calculated on a voxel-wise basis using a Rician noise model, as described above. The mean estimates of the fitted parameters obtained from the posterior distributions were then combined for the voxels within each ROI to derive summary statistics (i.e., mean and standard deviation across the ROI) of the fitted parameters (see Figs. 2 and 3).

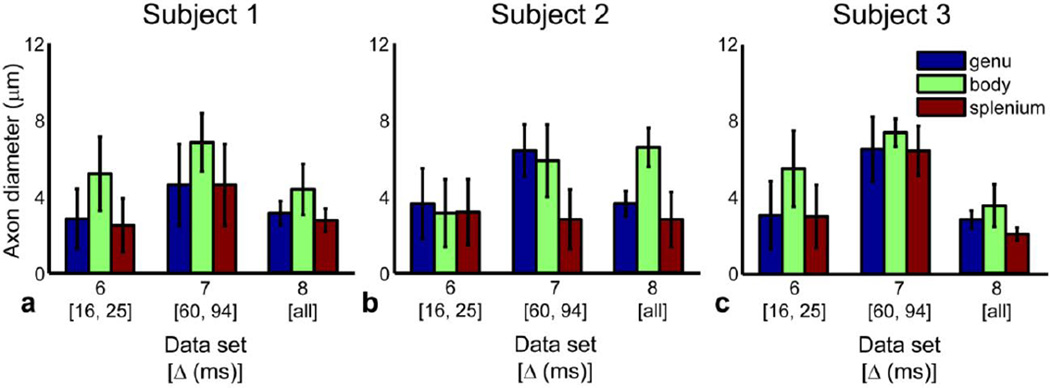
Figure 3.

Effect of diffusion time Δ on mean axon diameter estimates in all three subjects. Mean and standard deviation of axon diameter estimates for data sets 6–8 within the genu, body, and splenium ROIs in the midline sagittal slice of the corpus callosum for (a) subject 1, (b) subject 2, and (c) subject 3.

3. Results

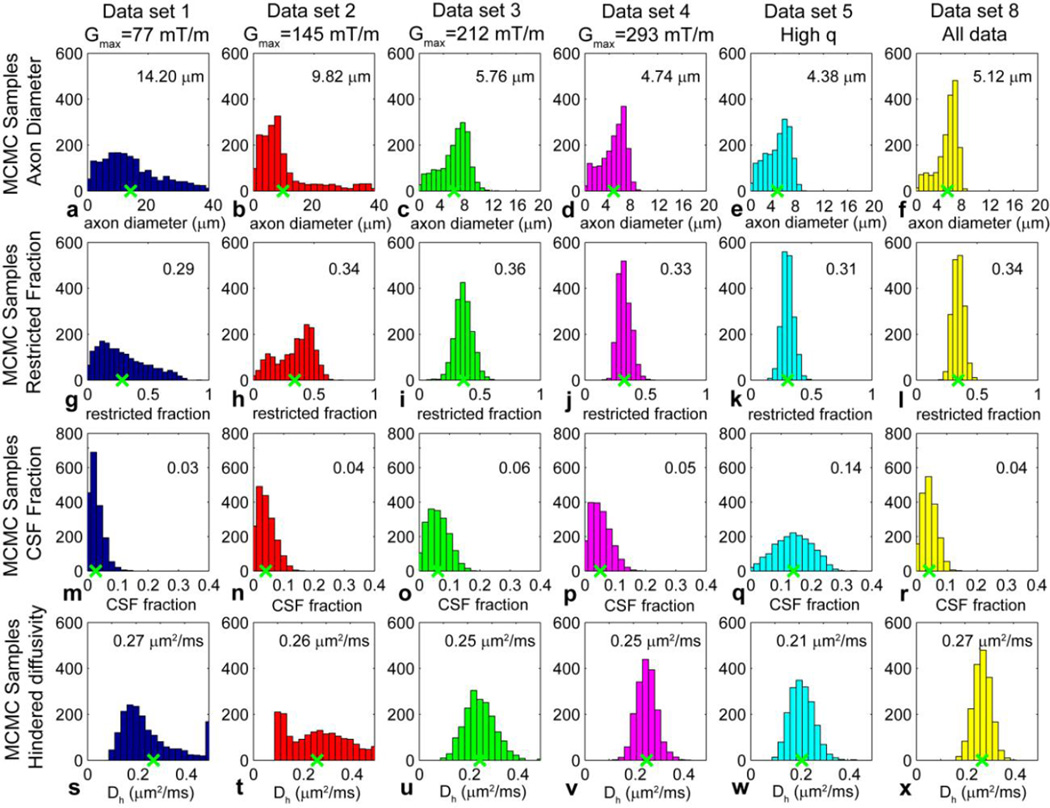
Figure 1 shows posterior distributions on axon diameter a, volume fraction of the intra-axonal compartment f_r, volume fraction of CSF f_csf, and hindered diffusion coefficient D_h for data sets 1–5 and 8 in Table 1 obtained with different G_max and q values. The posterior distributions shown were obtained from a representative voxel in the body of the corpus callosum of subject 1. The posterior distributions on axon diameter, restricted fraction, CSF fraction, and hindered diffusion coefficient became narrower with increasing G_max. The axon diameter estimate was larger (9.82 µm and 14.20 µm) for G_max ≤ 145 mT/m (data sets 1 and 2) and decreased (~4–5 µm) with increasing G_max. The axon diameter estimates from G_max of 293 mT/m (data set 4) matched most closely to the axon diameter estimate obtained when all of the acquired data was included in the fit (data set 8) (4.74 µm and 5.12 µm respectively). The histograms for axon diameter also showed relative invariance for axon diameters less than 3–4 µm, i.e., the low ends of the histograms tended to be flat (see Figs. 1c–f), suggesting a lower bound below which axon diameters could be recognized as small but not necessarily distinguishable in size from one another. The estimates for restricted fraction, CSF fraction, and hindered diffusion coefficient were similar across all G_max. These trends were representative of what was observed across subjects and in different regions of interest.

Figure 1.

Posterior distributions on (a–f) axon diameter a, (g–l) restricted fraction f_r, (m–r) CSF fraction f_csf, and (s–x) hindered diffusion coefficient D_h from a representative voxel in the body of the corpus callosum for data from subject 1 acquired at different G_max and q: (a, g, m, s) data set 1 (G_max = 77 mT/m); (b, h, n, t) data set 2 (G_max = 145 mT/m); (c, i, o, u) data set 3 (G_max = 212 mT/m); (d, j, p, v) data set 4 (G_max = 293 mT/m); (e, k, q, w) data set 5 (high q values); and (f, l, r, x) data set 8 (all data). The mean axon diameter, restricted fraction, CSF fraction, and hindered diffusion coefficient for each histogram is indicated by the green x along the x-axis and numerical value at the top right of each histogram. The bin size was set to 2 µm for the axon diameter estimates in (a) and (b) and 0.8 µm for the axon diameter estimates in (c), (d), and (e); 0.05 for the restricted fraction estimates in (g–l); 0.02 for the CSF fraction estimates in (m–r); and 0.025 µm²/ms for the hindered diffusion coefficient estimates in (s–x).

Figure 2 plots the mean and standard deviation of the axon diameter estimates for the genu, body, and splenium ROIs in the midline sagittal slice of the corpus callosum for data sets 1–5 and 8 in all three subjects. Again, it can be seen that the mean of the axon diameter estimates over each ROI decreased by two to three fold with increasing G_max. The standard deviation of the axon diameter estimates across the voxels in each ROI decreased by more than half with increasing G_max, suggesting improved spatial coherence in the parameter estimates for each ROI with increasing G_max. A trend toward smaller mean axon diameters in the genu and splenium compared to the body was more clearly seen at higher G_max, which is consistent with prior histological studies (58, 59).

Figure 3 shows the mean and standard deviation of the axon diameter estimates for short (Δ = 16 and 25 ms), long (Δ = 60 and 94 ms), and all diffusion times (Δ = 16, 25, 35, 60, 94 ms) using data acquired at all gradient strengths up to G_max of 293 mT/m for the genu, body, and splenium ROIs in the midline sagittal slice of the corpus callosum. The mean of the axon diameter estimates from data acquired with long diffusion times was up to two times larger than that obtained from data acquired with short diffusion times. The mean of the axon diameter estimates obtained using all the data (i.e., data set 8) was more similar in magnitude to the mean of the axon diameter estimates obtained from data acquired with short diffusion times. The axon diameter estimates at short and long diffusion times (data sets 6 and 7) also showed a larger standard deviation over each ROI by approximately two to three times on average compared to those obtained with all the data due to the smaller number of data points in data sets 6 and 7.

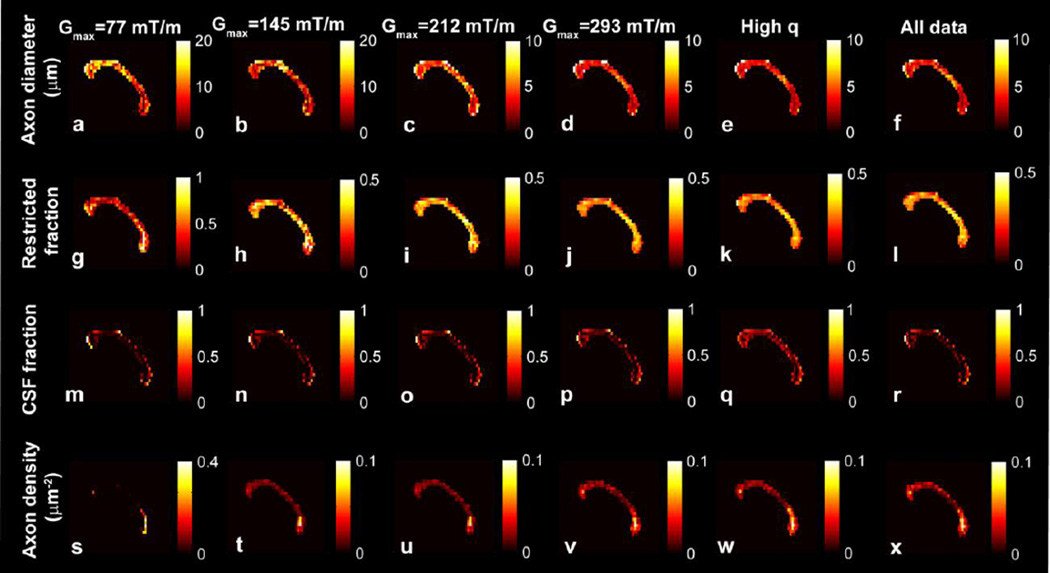
Figure 4 shows voxel-wise estimates of mean axon diameter, restricted fraction, CSF fraction and axon density for the midline sagittal slice of the corpus callosum of subject 1. The axon density was calculated by weighting the restricted fraction by the cross-sectional area of the axon, as described in (23). Regional variations in axon diameter and density became more pronounced at higher G_max, with evidence of smaller diameter and more tightly packed axons in the genu and splenium compared to the body. Increasing G_max also decreased the mean axon diameter estimate by half and the variation in axon diameter estimate between voxels by more than half. For G_max > 70 mT/m, the restricted fraction, CSF fraction, and axon density were similar to the values obtained at the highest G_max of 293 mT/m.

Figure 4.

Voxel-wise estimates in the midline sagittal slice of the corpus callosum of subject 1 for (a–f) axon diameter, (g–l) restricted fraction, (m–r) CSF fraction, and (s–x) axon density for different G_max, high q and all data (data sets 1–5 and 8). The voxel-wise axon diameter a, restricted fraction f_r, and CSF fraction f_csf values represent the means of the posterior distribution on a, f_r, and f_csf, respectively. The axon density represents the restricted fraction weighted by the cross-sectional area calculated from the mean axon diameter (23).

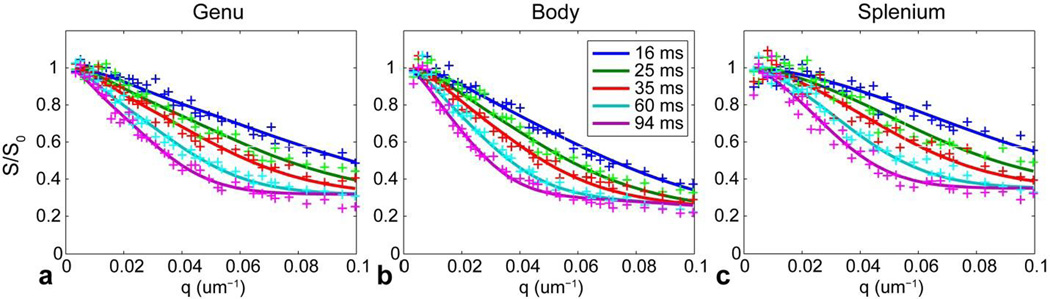
Figure 5 compares the measurements at different q-values with predictions from the model fitted to the ROI-averaged signal from the genu, body, and splenium of the corpus callosum in subject 1. The fitted parameters provided an accurate prediction of the expected signal decay for q-values below 0.08 µm⁻¹. However, the model underestimated the highest qvalue measurements by up to 10% for q-values above 0.08 µm⁻¹, especially for the longest diffusion time of Δ = 94 ms.

Figure 5.

Plots of the ROI-averaged signal in the genu, body, and splenium from the midline sagittal corpus callosum in subject 1 for different q and Δ listed in the legend. The solid lines represent the predicted signals from the fitted model. All measurements were normalized by the corresponding estimate of S₀ obtained at b = 0.

4. Discussion

We demonstrate the effect of gradient strength on in vivo axon diameter estimates in humans by performing a comprehensive set of measurements on a clinical MRI system equipped with 300 mT/m gradients. We find that the uncertainty in mean axon diameter estimates decreased with increasing G_max for the model and fitting method used here. Furthermore, increasing G_max appeared to decrease the axon diameter estimates throughout the corpus callosum. Known differences in axon diameter and density between the genu, body, and splenium of the corpus callosum became more reproducible at higher G_max.

This study represents the first empirical in vivo study of gradient strength on axon diameter estimates in humans and serves as a complement to the work of Dyrby et al. (45), which examined the effect of G_max on axon diameter index obtained from optimized multi-shell HARDI protocols for G_max of 60, 140, 200, and 300 mT/m in fixed monkey brain. Rather than applying an optimized protocol with orientationally invariant sampling of q-space, we focused on systematically incrementing through G_max and Δ. To minimize the number of required measurements such that all data could be acquired in a single scan session (118 minutes), we chose to keep the diffusion-encoding fixed along the craniocaudal direction (orthogonal to the fibers of the corpus callosum), as in the original AxCaliber implementation (19, 22). Prior studies from other groups have demonstrated bending and fanning of fibers at the genu and splenium of the corpus callosum (60, 61). Intra-voxel bending and fanning patterns can confound estimates of axon diameters that depend only on a single diffusion-encoding orientation assumed to be orthogonal to the white matter bundle at all locations. This is a potential confound in our measurements; however, in order to mitigate the influence of heterogeneous fiber orientations, we limited our measurements to the midline of the corpus callosum as closely as possible. We also fixed the gradient pulse width δ and echo time for all experiments to allow for direct comparison between axon diameter estimates obtained at different G_max and Δ.

The variance in axon diameter estimates for the lowest G_max of 77 mT/m was at least two times larger than for axon diameter estimates obtained at higher G_max, similar to results found by Dyrby et al. (45). In our experiments, since the diffusion gradient pulse duration (δ) and echo time were kept constant (leading to the same T₂ weighting for all measurements), the large variance in axon diameter estimates at lower G_max could be attributed to the lower diffusion weighting that was used to acquire the data. We hypothesize that the low q-values did not provide sufficient diffusion resolution to resolve restricted diffusion occurring in smaller diameter axons and therefore produced larger variance in the estimates of the mean axon diameter. Dyrby et al. (45) also observed less consistent measurements of axon diameter index at G_max of 60 mT/m using wider gradient pulses with longer diffusion gradient pulse duration (δ), diffusion time (Δ) and echo time compared to at higher G_max.

Regarding the effect of diffusion time on axon diameter estimates, the data obtained with longer diffusion times (Δ = 60 and 94 ms) yielded axon diameter estimates that were up to two times larger than axon diameter estimates obtained with shorter diffusion times (Δ = 16 and 25 ms) and all diffusion times (Δ) (Fig. 3). In order to choose an appropriate range of diffusion times, the diffusion time should be long enough such that the intra-axonal water will have sufficient time to probe the axonal boundaries, roughly on the order of a²/2D_r (62). The diffusion times Δ used here ranged from 16 to 94 ms and therefore correspond to mean diffusion displacements of 7–18 µm, respectively, assuming an intra-axonal diffusivity of 1.7 µm²/ms. Our results suggest that longer diffusion times (Δ > 60 ms) may lead to larger estimates of compartment size. Therefore, it is possible that other regions of the brain or spinal cord with different-sized axons may require sampling a different range of diffusion times.

4.1. Model assumptions and limitations

The estimates of axon diameter and density are dependent on the model used, and much work has been invested in testing and validating different biophysical models of axons in white matter (16–28). To model intra-axonal diffusion, we used the model of Neuman and others (53–56), which calculates the signal decay due to restricted diffusion in impermeable cylinders and includes a Gaussian phase approximation for diffusion during the gradient pulse. The availability of G_max up to 300 mT/m enabled us to achieve strong diffusion weighting with a relatively short gradient pulse duration (δ) of 8 ms; however, even the short δ used in our experiments may not have satisfied the short pulse approximation, particularly for the shortest diffusion time sampled here (Δ = 16 ms). The effects of exchange were not accounted for and could represent another potential confounding factor by blurring the compartment size estimate, particularly at longer diffusion times. Diffusion in the extra-axonal compartment was modeled as one-dimensional Gaussian diffusion, which was considered a reasonable first approximation. However, other groups have shown that this assumption is not strictly correct due to the time-dependence of the diffusion coefficient (63–65), which may cause the diffusivity to vary for different diffusion times and pose a potential confound to our quantitative accuracy. We also incorporated a CSF compartment in order to account for partial volume effects given the proximity of the corpus callosum to the ventricles, following the approach of (22). The CSF fraction was below 0.2 for the majority of the voxels in the corpus callosum, consistent with results obtained by others (22, 23).

This study uses a Rician noise model for parameter estimation in all measurements. We acknowledge that the noise may not be completely accounted for by a Rician distribution, given that the signal was averaged 8 times for each q-value and diffusion time combination prior to analysis and data were acquired with a phased-array coil and parallel imaging (66). Yet, the MCMC fitting was not very sensitive to the noise model with both Gaussian and Rician noise models showing similar results. The Rician noise model was chosen as it was considered a better approximation for the expected noise in the voxel-wise parameter estimates.

The axon diameters obtained from the measurements and model-fitting adopted here are on the same order as those reported from histology (58, 59) and are close to the values calculated from histology by Alexander et al. (23), accounting for shrinkage during histological preparation. It must be acknowledged that the measurements shown here may not be sensitive to small diameter axons below a threshold of approximately 3–4 µm, as shown in the histograms of Figure 1. This finding reflects constraints in the experimental parameters needed to distinguish very small diameter axons, including the need for very short diffusion times to probe the transition between free and restricted diffusion within small axons (in our experiments, Δ = 16 ms represented the lower bound on the diffusion time) as well as the need for even higher diffusion weighting to distinguish very small compartment sizes. Our results suggest a limit to the sensitivity of pulsed gradient spin echo experiments to very small diameter axons, in agreement with simulation and experimental results reported by others (19, 20, 23, 45). The lower bound is expected to decrease with higher G_max or possibly with the use of oscillating gradients that would enable shorter diffusion times to probe smaller displacements (67–69). Sequence optimization approaches have also been shown to improve compartment size estimation and increase sensitivity to small pore sizes compared to the standard pulsed gradient spin echo, particularly at lower maximum gradient strengths (70–72).

4.2. Future applications

Our results support the use of the highest available G_max to decrease variation in axon diameter estimates and improve contrast in axon diameter and density between different regions of the corpus callosum. Although measurements performed with lower G_max showed larger variation in the resulting axon diameter estimates and a bias toward larger mean axon diameters, the relative differences in axon diameter estimates within subregions of the corpus callosum may still provide useful information regarding the underlying white matter microstructure. The results suggest that quantitative measures of axon diameter are influenced by the selection of q and Δ, but relative differences between different regions of the corpus callosum appear to be preserved, especially at G_max above 145 mT/m. Furthermore, the estimates of the restricted and CSF fractions and axon density appeared to be less dependent on G_max and relatively invariant above G_max of 70 mT/m. These measures have been shown to be less sensitive to small axon diameters (23) and may represent relatively robust parameters for assessing white matter microstructure regardless of G_max. Axon density in particular could serve as a potential biomarker for axonal dropout in diseases such as multiple sclerosis and amyotrophic lateral sclerosis, in which axonal damage and loss are postulated to be the underlying substrate of clinical disability and neurodegeneration (8–10).

The importance of high G_max for accurate in vivo characterization of tissue microstructure motivates the development of stronger gradients for clinical MRI systems. A growing number of research scanners equipped with strong gradient systems have emerged in recent years (40, 41). Customized gradient coil inserts such as the Siemens SC72 gradient insert that is part of the Washington University-Minnesota consortium Human Connectome Project scanner are capable of generating maximum gradient strengths of 100 mT/m (41). The most recent generation of commercial scanners such as the Siemens Prisma and Philips Achieva 3T X-series (Quasar Dual gradient system) will feature integrated gradient systems with G_max of 80 mT/m and maximum slew rates of 200 and 100 mT/m/s, respectively. Still, the gradient strengths currently available on most clinical scanners remain in the range of 40–60 mT/m. Therefore, there is a great need for studies such as the one presented here that improve our understanding of how axon diameter estimates change at lower G_max and will help to facilitate translation of microstructural imaging methods to the clinical arena.

5. Conclusion

We present the first comprehensive empirical study from a clinical MRI system equipped with 300 mT/m gradients that demonstrates the effect of gradient strength on in vivo axon diameter estimates in humans. Our results suggest that an optimal q-space sampling scheme for estimating axon diameters should incorporate the highest possible gradient strengths. The smaller variance of axon diameter estimates at higher G_max agrees with findings from recent simulations and ex vivo experiments (45). The trends in axon diameter and density seen in different regions of the corpus callosum emerged at higher G_max > 145 mT/m and were consistent with those observed from histology (58, 59). The improvement in axon diameter and density estimates that we demonstrate from increasing G_max will inform protocol development and is one reason to encourage the adoption of higher gradient systems for use in human scanners.

Highlights.

• The effect of gradient strength on in vivo human axon diameter estimates was studied.

• Experiments were performed on a novel 3 T MRI with maximum gradients of 300 mT/m.

• Higher gradient strengths resulted in smaller, more robust axon diameter estimates.

• Shorter diffusion times resulted in smaller axon diameter estimates.