Abstract
Patients often respond differently to a treatment because of individual heterogeneity. Failures of clinical trials can be substantially reduced if, prior to an investigational treatment, patients are stratified into responders and nonresponders based on biological or demographic characteristics. These characteristics are captured by a predictive signature. In this paper, we propose a procedure to search for predictive signatures based on the approach of patient rule induction method. Specifically, we discuss selection of a proper objective function for the search, present its algorithm, and describe a resampling scheme that can enhance search performance. Through simulations, we characterize conditions under which the procedure works well. To demonstrate practical uses of the procedure, we apply it to two real-world data sets. We also compare the results with those obtained from a recent regression-based approach, Adaptive Index Models, and discuss their respective advantages. In this study, we focus on oncology applications with survival responses.
Keywords: biomarker, patient rule induction method (PRIM), patient stratification, predictive signature, subgroup analysis
1. Introduction
There is an increasing need of developing predictive signatures to identify right patient population for a treatment. By enriching responders in a target population, signature-based patient stratification reduces attrition rate of drug development projects in clinical phases and at the same time helps maximize patients' benefit offered by pharmaceutical intervention. In general, a signature captures some biological or demographical characteristics of patients. A signature-positivegroup is a population that satisfies certain criteria based on a signature. A population that does not meet the criteria is defined as a signature-negative group. In this paper, we consider a two-arm design situation where patients in the treatment arm are treated by an investigational treatment and patients in the control arm receive a standard of care (SOC). We say that a signature has predictive value if patients in a signature-positive group respond better in the treatment arm than in the control arm, and the treatment effect for patients in the signature-positive group is greater than the one for signature-negative patients. Therefore, a predictive signature identifies a subset of patients who should be treated by an investigational treatment rather than an SOC and attempts to maximize treatment effect in a signature-positive population. Figure 1 provides a motivating example where treatment and control cohorts have no difference in terms of patients' survival. After a predictive signature is learned and applied to patients' data at baseline, as shown in Figure 2, the signature-positive patients in the treatment arm have prolonged survival compared with those in the control arm, but we see a reverse pattern for the signature-negative patients. This example will make a case study discussed in details in this paper (Section 5).
Figure 1.
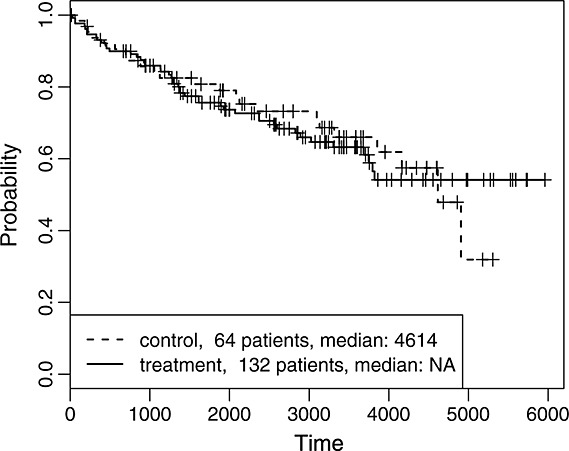
The Kaplan–Meier curves for two arms in the ER data set.
Figure 2.
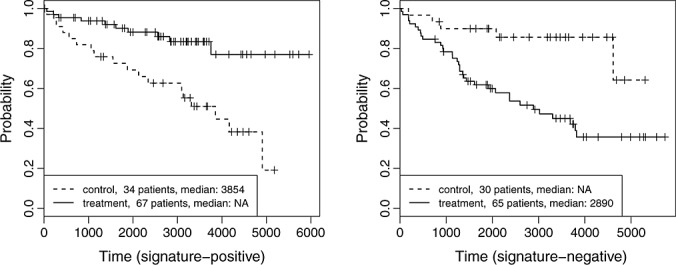
The Kaplan–Meier curves for the signature-positive group (left) and the signature-negative group (right) in the ER data set.
A promising method that can be applied to signature discovery is patient rule induction method or PRIM proposed by Friedman and Fisher 1. PRIM aims at finding bumps in a population ‘space’—a bump is defined by a subgroup of the population if the subgroup has a relatively high mean value of an objective function that describes a certain characteristic of the population. When efficacy is the characteristic of interest, bumps or subgroups in PRIM's formulation should correspond to signature-positive groups. The way PRIM naturally addresses the patient-stratification problem makes the method a good candidate approach for learning predictive signatures. Moreover, because PRIM describes a subgroup by a set of decision rules based on variables obtained for the population, these rules directly define a signature—this simplicity makes them easily applicable in clinics, which is another desirable property in signature development. An example of such rules would be as follows: A patient is signature-positive if his or her target gene's expression is greater than a threshold and his or her safety biomarker's protein level is less than a cutoff. Finally, we note that the word ‘patient’ in PRIM is an adjective, rather than a noun. It indicates that the rule induction method is not hasty or impulsive, in contrast to aggressive behaviors of other methods (for example, classification and regression trees (CART)), which had been discussed and compared with PRIM in 1. Rather than taking a large step that seems optimal for a current search iteration, PRIM adopts a smaller step that may be less optimal, but by doing so, it increases the likelihood for later steps to compensate previous mistakes or utilize structures discovered by earlier steps. Such patience helps the method induce superior rules than those produced by aggressive approaches.
Many efforts have been made to directly apply or adapt PRIM for finding prognostic rules in different biomedical areas. Because a dose-intensive treatment may only target patients with high risks due to its associated toxicity, LeBlanc et al. 2 tried to identify these patients by a PRIM-based method with survival data and six demographical or biomarker variables. They proposed two major operations beyond PRIM: Additional variable selection and making search follow a pre-determined direction of a variable. The direction indicates whether a variable is positively or negatively correlated with responses based on regression. In our study, we do not either assume that such direction is known a priori or determine it in advance, and we do not impose the constraint that search should follow only one direction of a variable. Later, LeBlanc et al. 3 simplified their algorithm and changed their objective function from previously employed hazard rates to hazard ratios based on Cox proportional hazards regression models. Liu et al. 4 applied PRIM to tissue microarray data on eight biomarkers of patients with renal cell carcinoma for identifying high-risk patients. They proposed to use deviance residuals (based on martingale residuals of an intercept-only Cox regression model) as their objective function for PRIM to optimize. Dyson et al. 5 employed PRIM to choose combinations of genetic and environmental risk factors that define groups of individuals having significantly different risk levels of ischemic heart disease. Using PRIM, Nannings et al. 6 discovered subgroups at a very high risk of dying in the population of very elderly intensive-care patients and revealed important prognostic factors from demographic, diagnostic, physiologic, laboratory, and discharge data. For a modified version of PRIM, Polonik and Wang 7 presented theoretical characterization of its outcomes and derived its convergence rates.
In drug development, the value of a signature substantially increases if it can predict drug response as opposed to just predicting disease risk. However, it has not been well studied how PRIM can be properly applied in predictive-signature development. Kehl and Ulm 8 made an attempt to apply PRIM for identifying such signatures. Nevertheless, their method relies on a strong assumption that a good prognostic model can be built for a control arm. Martingale residuals from fitting the prognostic model in a treatment arm are used to indicate efficacy, which is optimized by PRIM. Our approach employs a different objective function and thus avoids making that assumption. With respect to simulation design and case studies, the previous work was concerned with cardiology while our study will shed light on PRIM application in oncology trials. There are many tree-based methods for patient stratification. They can be better contrasted to our approach after readers have a good understanding of our objective function and search algorithm. Therefore, we defer related discussion to Section 6.
In this study, we make the following unique contributions to develop a PRIM-based procedure searching for predictive signatures with survival data as the measure of clinical outcome:
Choosing an appropriate objective function together with a constraint for the procedure and comparing them with the objective function employed by Adaptive Index Models or AIM 9 to highlight the key advantage of our choice;
Developing the procedure with an automatic parameter tuning step and coupling the procedure with a resampling scheme to help PRIM achieve more effective signatures;
Investigating the procedure's performance in some typical scenarios of oncology clinical trials by simulation and thus characterizing conditions that empower the procedure to function reasonably;
Demonstrating applicability of the procedure in two real-world data sets and comparing its stratification results with those produced by AIM to present their respective advantages.
This paper is organized as follows. Section 2 considers objective functions and a related constraint for PRIM in the context of discovering predictive signatures. We then describe our search procedure based on PRIM's framework in Section 3. We present results from a simulation study in Section 4 and from two case studies of real-world data sets in Section 5. We conclude this paper with a discussion in Section 6.
2. Objective function
We begin this section by introducing a model formulation to motivate an objective function and a related constraint we adopt for PRIM and then compare them with AIM's objective function to reveal their different implications for identifying predictive signatures. We refer to variables that define a signature as signature variables and other irrelevant variables as noise variables. Because we focus on applications with survival data, we describe the formulation with a proportional hazards regression model: h(t∣T,X) = h0(t)eL(T,X), where t is time, T is a treatment factor, and X denotes signature variables. For a patient indexed by i, a linear hazard score is modeled as follows:
| 1 |
where Ti=0 indicates that the patient is in the control arm and Ti=1 if the patient is in the treatment arm under a two-arm design, and the signature indicator Z(Xi) = 0 if the patient is stratified into a signature-negative group and Z(Xi) = 1 for the patient in a signature-positive group. Accordingly, β1 indicates the treatment effect for the signature-negative group, and β1+β2 suggests the treatment effect for the signature-positive group. In principle, any signature can define a signature-positive group (and thus a signature-negative group with complimentary rules) as long as it describes some characteristics of patients, but the signature may not be predictive. To define a predictive signature, we need to discuss the following two conditions on the treatment effects:
β1+β2<0—the treatment-effect condition;
β1+β2<β1, which can be reduced to β2<0—the interaction-effect condition.
The first condition is required to ensure signature-positive patients respond better to an investigational treatment compared with an SOC. The second condition means that the treatment effect in the signature-positive group should be greater than the signature-negative group; that is, the hazard ratio in the signature-positive group is smaller than the one in the signature-negative group. On the other hand, in practice, the estimates 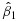 and
and 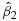 satisfying the inequality
satisfying the inequality 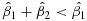 do not guarantee that the statistical significance of
do not guarantee that the statistical significance of 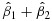 is greater than the significance of
is greater than the significance of 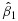 . If the sample size of the signature-positive group is small and thus it leads to a large standard error of
. If the sample size of the signature-positive group is small and thus it leads to a large standard error of 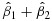 , the significance of
, the significance of 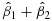 can be less than the one of
can be less than the one of 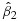 , suggesting an undesirable patient stratification. Therefore, to avoid this case, we need the following constraint: The signature-positive group's treatment effect should be more significant than the one of the signature-negative group. We call such a constraint the interaction-effect constraint. Similarly, the treatment-effect condition leads to the requirement that
, suggesting an undesirable patient stratification. Therefore, to avoid this case, we need the following constraint: The signature-positive group's treatment effect should be more significant than the one of the signature-negative group. We call such a constraint the interaction-effect constraint. Similarly, the treatment-effect condition leads to the requirement that 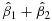 should be significantly smaller than zero. We refer to the requirement as the treatment-effect requirement. For a signature to be predictive in practice, it should satisfy both the treatment-effect requirement and the interaction-effect constraint.
should be significantly smaller than zero. We refer to the requirement as the treatment-effect requirement. For a signature to be predictive in practice, it should satisfy both the treatment-effect requirement and the interaction-effect constraint.
To avoid making assumptions of specific models, we adopted the approach of directly employing p-values of two-sample comparisons to indicate treatment effects. In applications of survival data, we use one-sided log-rank tests for comparisons. This approach was proposed by Lin et al. 10, but they were only concerned with the treatment-effect requirement and did not consider the interaction-effect constraint. We describe our objective function as follows. Let pv+ indicate significance of a one-sided test that examines whether signature-positive patients respond better to an investigational treatment compared with an SOC; denote by pv− significance of the same test for patients in a signature-negative group. pv+ and pv− can be used to capture the essence of the treatment-effect requirement and the interaction-effect constraint. Previously, we specified the two criteria in the setting of regression; now, we conceptually map the treatment-effect requirement to a small pv+ and map the interaction-effect constraint to the constraint pv+<pv−. To achieve a maximally beneficial treatment effect in the signature-positive group, we chose pv+ as the objective function of PRIM for its optimization. To drive the search toward satisfying the interaction-effect constraint, we enforce pv+<pv− in PRIM's search process. Such enforcement is not redundant. It is true that the constraint is automatically assured if a minimal pv+ achieved by PRIM is the global minimum; however, in cases where the minimal value is a local mode, pv+ could be greater than pv−, and thus, the interaction-effect constraint is violated. Although PRIM can result in a local optimum with respect to pv+, its stratification is still useful if the interaction-effect constraint holds. Therefore, the enforcement of the constraint in the search process is designed to help generate desired stratification. Moreover, when initial search steps start to explore a search space, it is possible that a minimal pv+ used for making local decisions is greater than pv−, and thus, it drives the search toward a potentially less meaningful direction. Readers may understand this statement better after reading through the search procedure in Section 3. Although the aforementioned patient property of PRIM can employ later steps to remedy mistakes made by previous search steps, these mistakes may still lead to less optimal solutions. We will demonstrate this point in our case study of a real-world data set.
Tian and Tibshirani 9 developed AIM for stratifying population into different risk groups and for detecting treatment-marker interactions. AIM searches for K covariates x1,…,xK and corresponding cutoffs c1,…,cK to build an index score 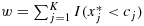 , where I() is a binary indicator function and
, where I() is a binary indicator function and 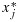 is either a covariate xj or its negative value −xj. To detect possible treatment-marker interaction, AIM maximizes a test statistic testing the treatment-score interaction term Tw in the following linear hazard score L = γ1T + γ2Tw, where T is a treatment factor with the same definition as in Eq. 1, and w is the aforementioned index-score variable. The authors suggested that patients can be stratified into a low-score group and a high-score group by comparing their index scores to median of all index scores. The high-score group defines a signature-positive group given a negative coefficient of the interaction term, with the remaining patients forming a signature-negative group; in case the coefficient sign is positive, the low-score group then defines a signature-positive group. In this way, the score-based patient stratification essentially defines Z in Eq. 1, with Z = 1 for patients in the signature-positive group and Z = 0 for the signature-negative patients. Given the definition, the AIM's formulation can be mapped or transformed into Eq. 1. Because such transformation will not affect any conclusion we draw, we will refer to the linear hazard score in Eq. 1 as the formulation for further discussion to maintain notational consistency. Also, for simplicity, unless there is a need for detailed specification, we will use the terms the treatment-effect condition and the interaction-effect condition to indicate two general requirements of a predictive signature instead of referring to various statistics employed by different approaches for these two conditions.
is either a covariate xj or its negative value −xj. To detect possible treatment-marker interaction, AIM maximizes a test statistic testing the treatment-score interaction term Tw in the following linear hazard score L = γ1T + γ2Tw, where T is a treatment factor with the same definition as in Eq. 1, and w is the aforementioned index-score variable. The authors suggested that patients can be stratified into a low-score group and a high-score group by comparing their index scores to median of all index scores. The high-score group defines a signature-positive group given a negative coefficient of the interaction term, with the remaining patients forming a signature-negative group; in case the coefficient sign is positive, the low-score group then defines a signature-positive group. In this way, the score-based patient stratification essentially defines Z in Eq. 1, with Z = 1 for patients in the signature-positive group and Z = 0 for the signature-negative patients. Given the definition, the AIM's formulation can be mapped or transformed into Eq. 1. Because such transformation will not affect any conclusion we draw, we will refer to the linear hazard score in Eq. 1 as the formulation for further discussion to maintain notational consistency. Also, for simplicity, unless there is a need for detailed specification, we will use the terms the treatment-effect condition and the interaction-effect condition to indicate two general requirements of a predictive signature instead of referring to various statistics employed by different approaches for these two conditions.
By focusing on the treatment-score interaction term, AIM directs the search to optimize the interaction-effect condition. However, a detected interaction effect may or may not lead to a predictive signature because the treatment-effect condition is ignored. Specifically, if 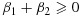 , as illustrated by the thicker line in Figure 3 (left), the investigational treatment is no better than the SOC in the signature-positive group. In this situation, the interaction effect can still be significant if the investigational treatment is significantly worse than the SOC in the signature-negative group, as shown in Figure 3 (right). Therefore, the resulting signature-positive group is not useful for identifying responders to the investigational treatment compared with the SOC; rather, the resulting signature-negative group reveals patients to whom the investigational treatment is even more harmful. If in this case a predictive signature exists but its interaction effect is less significant than the one just demonstrated, the signature will be missed by the search in AIM. Hence, AIM or, in general, a method only optimizing the interaction-effect condition has a limited utility on discovering predictive signatures. On the contrary, our choice of the objective function aims at enriching responders to an investigational treatment in a signature-positive group and thus does not have such limitation.
, as illustrated by the thicker line in Figure 3 (left), the investigational treatment is no better than the SOC in the signature-positive group. In this situation, the interaction effect can still be significant if the investigational treatment is significantly worse than the SOC in the signature-negative group, as shown in Figure 3 (right). Therefore, the resulting signature-positive group is not useful for identifying responders to the investigational treatment compared with the SOC; rather, the resulting signature-negative group reveals patients to whom the investigational treatment is even more harmful. If in this case a predictive signature exists but its interaction effect is less significant than the one just demonstrated, the signature will be missed by the search in AIM. Hence, AIM or, in general, a method only optimizing the interaction-effect condition has a limited utility on discovering predictive signatures. On the contrary, our choice of the objective function aims at enriching responders to an investigational treatment in a signature-positive group and thus does not have such limitation.
Figure 3.
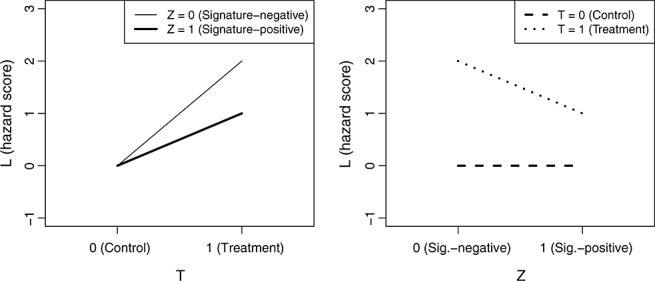
The interaction plots for treatment and signature from different perspectives to show a significant treatment–signature interaction effect with the lack of a desired treatment effect for signature-positive patients: Treatment factor as x-axis (left) and signature indicator as x-axis (right).
Moreover, even if we assume that AIM or a method can ensure the treatment-effect condition satisfied while optimizing the interaction-effect condition, its resulting signature can be less desirable than the one produced by a method optimizing the treatment-effect condition while making sure the interaction-effect condition satisfied. Let us consider the following example. Imagine that there exist two predictive signatures for a data set: Signature A has the maximum (treatment-score) interaction effect but a small beneficial effect of an investigational treatment over an SOC in its signature-positive group; in comparison to signature A, while signature B leads to a much larger or the largest beneficial treatment effect for signature-positive patients, it has a smaller interaction effect. Clearly, signature B is more helpful in identifying patients for maximizing efficacy of the investigational treatment than signature A. However, signature A would be reported by any method whose result is driven by the optimality of the interaction-effect condition. Therefore, in order to detect a predictive signature such as signature B, we recommend the approach that treats the treatment-effect condition as the primary objective function to be optimized and imposes the interaction-effect condition as a constraint that should not be violated, as opposed to an approach that treats the interaction-effect condition as the primary objective function and the treatment-effect condition as the constraint.
3. Search procedure
In this section, we present our procedure based on the PRIM's framework in the context of searching for predictive signatures. We also propose an automatic parameter-selection step and a resampling scheme to improve search performance. For the sake of simplicity, this study is concerned with continuous signature variables. But this is not a restriction in that with the same objective function, it is easy to extend the procedure to handle categorical variables in the way discussed by Friedman and Fisher 1.
3.1. The framework
Let us first introduce notation involved in the procedure description (Algorithm 1). Assume that there are p variables, and let xj denote a variable indexed by j, for j = 1,…,p. Let xjmin and xjmax be the minimum and maximum values of xj, respectively. xij is the value of xj for patient i. The set of indices of patients in a signature-positive group is denoted by G+. For patients indexed by G+, xj(α) denotes a quantile of their xj, corresponding to a probability α in the lower tail. Following this convention, xj(0) is the minimum value of xj and xj(1) the maximum value of xj. For a group of patients indexed by G, PG denotes the p-value of a one-sided test that examines whether patients receiving an investigational treatment respond better than patients treated by an SOC. Because the algorithm description employs set operations, we clarify relevant symbols here. Given two sets A and B, A ∩ B denotes the intersection between A and B; A ∪ B is the union of the two sets; A∖B denotes the set of elements that belong to A but not to B, and 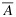 is complement of A. With aforementioned notation, we are ready to present the algorithm.
is complement of A. With aforementioned notation, we are ready to present the algorithm.
In line 1 of Algorithm 1, PRIM first splits the whole population in a study into two sets, D1 and D2. In D1, it learns a series of candidates for a signature-positive group, as detailed by lines 2-18. Then, one of the learned candidates is chosen to be reported if its corresponding grouping in D2 achieves the best stratification, as indicated by line 19. At this step, by treating decision rules associated with candidates as models, PRIM essentially utilizes data in D2 to select a final model. We will discuss more on this issue in Section 3.2. In our simulation study and case studies, we assign an equal number of samples to D1 and D2.

Learning candidates consists of three processes: peeling (lines 4-8), pasting (lines 9-13), and dropping (lines 14-18). While peeling aims at shrinking a candidate to generate a new one, the other two processes attempt to create new candidates via candidate expansion. Specifically, starting with a trivial candidate with all patients (line 3), PRIM tries to peel different subsets of patients who have extremely small or large values of a variable in lines 5-6. A parameter α (0 < α < 1) specifies the proportion of patients considered to be peeled in a current candidate group. A peeling occurs if its resulting candidate has the best stratification, as shown by lines 7-8. The peeling process is repeatedly applied to newly produced candidates until a pre-defined minimum support (or sample size) of a candidate is reached. Then, from the smallest or largest values of a variable in the current candidate, PRIM tentatively pastes patients who have immediate smaller or larger values back to the group, as indicated by lines 10-11. The amount to be pasted is up to α of the current group size. A pasting is actually made if it improves the stratification most, as suggested by lines 12-13, and pastings are repeated till no improvement can be gained. Furthermore, PRIM drops a rule that defines the current candidate and thus includes patients who are previously excluded according to the rule, as shown by lines 15-16. In lines 17-18, a rule is chosen to be dropped if its removal produces a candidate with the best stratification. Rules are sequentially dropped in this fashion to generate new candidates till no rule can be further dropped. The stop of the dropping process completes the candidate generation (lines 3-18) for a specific α value. Candidate generation continues for other α values as indicated in line 2.
In peeling process, the number of possible peelings (till all data are consumed by peeling) is around (logC0− logn)/(log(1 − α)), where C0 is a pre-defined minimum support or sample size of signature-positive groups and n is the sample size of a study. Because there are O(logn) peelings and p potential signature variables to be examined in one peeling, the number of computing operations is in the order of O(p logn). The same computational complexity holds for pasting. For the dropping process, the complexity is O(p) because at most 2p decision rules are sequentially dropped. After dropping, O(p logn) candidate rule sets need to be tested in D2. Therefore, the complexity of the algorithm is O(p logn). At the end of Section 4, we will present PRIM's running time in a simulation scenario given different number of variables and different sample sizes.
3.2. Parameter and candidate selection
A final candidate is selected among all candidates learned in the following process: (i) given a value of α—the parameter controlling the number of patients to be peeled and pasted—the process of peeling, pasting, and dropping learns a series of candidates (lines 3-18 of Algorithm 1); (ii) different α values induce different series of candidates by repeating the aforementioned learning (line 2). PRIM's inventors suggested that a pre-determined α value between 0.05 and 0.10 tends to work well because a small α value encourages the search procedure to be patient, the key feature making PRIM superior to other aggressive approaches. In this case, only the first learning component generates candidates.
Alternatively, they recommended that after applying PRIM with different α values, the user can choose a value that produces a candidate striking a trade-off between a p-value indicating treatment effect in a signature-positive group (pv+ for patients in the withheld data D2) and the corresponding group size or a trade-off between the p-value and the number of corresponding rules. The former trade-off intends to increase a signature's prevalence by sacrificing stratification performance—a larger p-value may allow more patients to be included in a signature-positive group; the latter balance prefers a simpler rule set over the one achieving the smallest p-value. With subjective judgment on these trade-offs, the user can select the candidate and a corresponding α value.
As just mentioned, these choices are suboptimal in terms of stratification performance. Our strategy is to generate multiple series of candidates corresponding to different α values (line 2 of Algorithm 1) and then select a value leading to a candidate that obtains the best stratification performance indicated by pv+ for patients in D2 (line 19). In this way, the parameter value and the candidate can be automatically decided. We prescribe the following values for α: 0.05, 0.06, 0.07, 0.08, 0.09, 0.10, 0.20, 0.30, 0.40, and 0.50. A finer resolution is used between 0.05 and 0.10 because small α values are more likely to encourage PRIM's patience and thus lead to a better solution. For an illustration, Figure 4 shows the minimal pv+ value (among pv+ values of a series of candidates) given each pre-specified value of α in a case-study data set. In this case, α = 0.09 and the corresponding candidate achieving the smallest pv+ were selected according to our strategy. It is of note that because pv+ for patients in D2 is employed for the aforementioned selection, it should not be used as a measure of PRIM's predictive performance; instead, we will describe a cross-validation (CV) measure in Section 5 to indicate generalizability of a learning method in future data.
Figure 4.
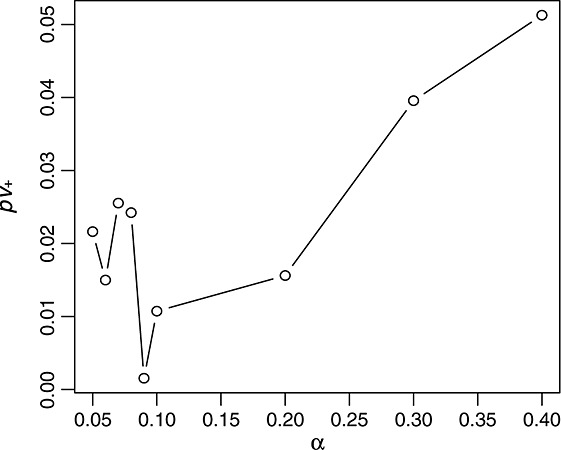
Minimal pv+'s given different α values based on results in the CHOP data set (see the case study in Section 5). Note that no stratification was generated given α = 0.50, and thus, no associated pv+ is visualized.
3.3. Multiple rule sets via covering
In the aforementioned subsections, we have explained how the procedure in Algorithm 1 finds a single set of conjunctive rules for defining a signature-positive group. As suggested by Friedman and Fisher 1, the same procedure can be applied repeatedly to discover multiple rule sets via a rule induction approach called covering 11. These rule sets can collectively define a signature-positive group. Specifically, we first exclude signature-positive patients who satisfy existing rules from data and then apply the search procedure to the remaining patients to learn another set of conjunctive rules. The disjunction of the newly discovered rules and the previously reported rules defines a new signature-positive group, which is the union of patients satisfying the new rules and patients satisfying the existing rules. Such repeated application stops till no rules can be further found or the treatment effect in a resulting signature-positive group is less significant than the treatment effect in the original population.
3.4. Resampling
As we will see in the simulation study (Section 4), PRIM's performance degrades as the number of noise variables increases. To help the algorithm focus on searching cutoffs for relevant variables, we propose the following resampling scheme to reduce search scope: PRIM is repeatedly applied to random samples of original data, and only top k variables that are most frequently returned by PRIM are selected as candidate variables for further consideration. PRIM then searches for signatures in original data with selected candidate variables as input variables.
Specifically, let 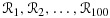 be 100 random samples of original data. Sampling is performed without replacement. In each sample, we draw 63.2% of original observations. That is the same number as the average number of distinct observations in a bootstrap sample 12. Bootstrapping is not directly utilized because replicated values cause peelings not to exclude the expected number of patients controlled by α. Given a random sample
be 100 random samples of original data. Sampling is performed without replacement. In each sample, we draw 63.2% of original observations. That is the same number as the average number of distinct observations in a bootstrap sample 12. Bootstrapping is not directly utilized because replicated values cause peelings not to exclude the expected number of patients controlled by α. Given a random sample  , PRIM proceeds as usual by first splitting
, PRIM proceeds as usual by first splitting  into D1 and D2 data sets and then searching for signatures. If PRIM reports xj as one of signature variables, an indicator function Ih(xj) = 1. Denote by H(xj) the selection frequency for xj:
into D1 and D2 data sets and then searching for signatures. If PRIM reports xj as one of signature variables, an indicator function Ih(xj) = 1. Denote by H(xj) the selection frequency for xj: 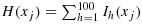 . After H(xj) for j = 1,…,p are calculated, they are sorted decreasingly into the list of H(x(1)),…,H(x(p)), where x(j) denotes the variable with its selection frequency at the j-th rank. Given the ranking, x(1),…,x(k) are chosen as the input variables for PRIM, and PRIM is applied to original data. The scheme was motivated by our observation that although PRIM cannot detect exactly a complete set of true signature variables in the presence of noise variables, it can frequently reveal some of them. The underlying assumption of the scheme is that variables repeatedly selected by PRIM in random samples of a population are likely to be true signature variables. For reference later, we call the search procedure coupled with the resampling scheme as Re-PRIM.
. After H(xj) for j = 1,…,p are calculated, they are sorted decreasingly into the list of H(x(1)),…,H(x(p)), where x(j) denotes the variable with its selection frequency at the j-th rank. Given the ranking, x(1),…,x(k) are chosen as the input variables for PRIM, and PRIM is applied to original data. The scheme was motivated by our observation that although PRIM cannot detect exactly a complete set of true signature variables in the presence of noise variables, it can frequently reveal some of them. The underlying assumption of the scheme is that variables repeatedly selected by PRIM in random samples of a population are likely to be true signature variables. For reference later, we call the search procedure coupled with the resampling scheme as Re-PRIM.
4. A simulation study
4.1. Simulation setup
To study the procedure's performance under different scenarios, we first describe a simulation setup as a baseline scenario and then compare it with other scenarios having different parameter settings. For signature-positive patients, their survival time S in a control arm follows an exponential model with a parameter 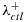 ,
, 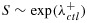 , and their survival time in a treatment arm
, and their survival time in a treatment arm 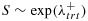 . For signature-negative patients, their survival time
. For signature-negative patients, their survival time 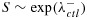 for the control arm and
for the control arm and 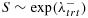 for the treatment arm. Survival time is randomly right-censored with probability 0.2. We assume
for the treatment arm. Survival time is randomly right-censored with probability 0.2. We assume 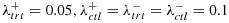 . The hazard ratio
. The hazard ratio 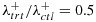 indicates a reasonable treatment effect for the signature-positive group while the ratio
indicates a reasonable treatment effect for the signature-positive group while the ratio 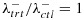 represents no treatment effect for the signature-negative group.
represents no treatment effect for the signature-negative group.
Two signature variables were simulated from a uniform distribution: X1,X2∼U(0,1). The conjunctive rules of 0.2≤x1≤0.9 and 0.2≤x2≤0.9 define a patient to be a signature-positive patient if his or her x1 and x2 values fall into the ranges. Later, we would also check the situation where the number of signature variables is increased to four. The percentage of signature-positive patients is known as prevalence. The prevalence given the aforementioned rules is around 50%. In addition to the signature variables, we also considered some noise variables as input variables of PRIM. A noise variable is generated from the same uniform distribution but is not involved in a signature definition. Denote by pn the number of noise variables. We examined settings where pn=0,2,4,6,8,32,128. With 32 or 128 noise variables, we tested the algorithm in the limit of its working conditions. It is less feasible to involve much more variables than the range we consider here for PRIM to properly identify predictive signatures in the settings of clinical trials. This is due to the challenges of limited sample size and realistic effect sizes in these applications. On the other hand, according to our experiences, it is not atypical that in an analysis task a signature is requested to learn from 8 or 10 variables. We will also evaluate PRIM's performance with eight variables for two real-world data sets later. In another study of rule-based subgroup identification 13, Lipkovich et al. conducted their simulation study in a similar scale in terms of the number of variables (given a sample size 900) with continuous responses, reflecting the same challenges as we face. We consider the total number of patients or the sample size n = 200,400,800,1600, and 3200. For every setting, an equal number of patients were assigned to each arm in each signature group. The range of sample sizes demonstrates situations of large clinical phase II or III studies. As we will see later in this section, less than 200 samples are not sufficient for PRIM to work for most of settings involving noise variables.
We refer to the aforementioned parameter settings as scenario 1. Later, we will report results on scenarios with a different number of signature variables, different prevalence, and a different effect size. Please see Table 1 for reference. The settings of these scenarios will be detailed when their results are presented. For each scenario, we simulated 1000 data sets and provided their performance summary. We compared the approach of collecting a single set of conjunctive rules (by applying the search procedure once) with the approach of collecting multiple rule sets by covering. They share similar performance in the simulation study. We will discuss results from the former approach because it allows us to directly compare estimated lower and upper bounds for signature variables with their true values. The minimum support of signature-positive groups was set at 20 for controlling stop of peelings. To give an idea about how fast the implemented procedure is, we recorded its running time for all the data sets in scenario 4 and will report timing summary when we discuss results in that scenario.
Table 1.
The parameter settings of different scenarios in simulation study.
| Scenario ID | 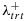 |
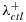 |
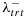 |
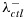 |
Signature variables | Lower bound | Upper bound |
|---|---|---|---|---|---|---|---|
| Scenario 1 | 0.05 | 0.10 | 0.10 | 0.10 | x1,x2 | 0.20 | 0.90 |
| Scenario 2 | 0.05 | 0.10 | 0.10 | 0.10 | x1,x2,x3,x4 | 0.00 | 0.85 |
| Scenario 3 | 0.05 | 0.10 | 0.10 | 0.10 | x1,x2 | 0.05 | 0.90 |
| Scenario 4 | 0.025 | 0.10 | 0.10 | 0.10 | x1,x2 | 0.20 | 0.90 |
4.2. Performance measures
After PRIM is applied to a simulated data set, one can imagine three possible scenarios of how well it detects true signature variables: (i) all true signature variables are captured, and no additional (noise) variables enter a signature; (ii) besides all true signature variables, some noise variables are returned; and (iii) the algorithm reports only some (or none) of true signature variables, possibly along with noise variables. The last two situations indicate partially correct results. To examine different degrees of correctness, we define different performance measures. The number of exact detection, nE, counts cases where the first situation happens in each simulation parameter setting. lEi and uEi are respective means of detected lower bounds and upper bounds of a signature variable xi in 1000 simulated data sets. The number of inclusive detection, nI, reports the number of cases where all signature variables are captured by a final rule set, which reflects the first and the second scenarios. Correspondingly, lIi and uIi are the respective means of detected lower and upper bounds of xi. The number of marginal detection, nMi, is the number of cases where a signature variable xi is ever detected in all three situations. lMi is the mean of detected lower bounds of xi, and uMi is the mean of detected upper bounds.
As an overall measure for patient stratification, classification measures such as sensitivity or recall rsens, specificity rspec, and precision rprec are reported. In the framework of a two-class problem, signature-positive patients are defined as observations in a positive class (or success class), and signature-negative patients are labelled as observations in a negative class (or failure class). Given these two classes, rsens denotes the proportion of true signature-positive patients detected among true signature-positive patients; rspec is defined as the proportion of true signature-negative patients detected among true signature-negative patients; rprec is the proportion of true signature-positive patients detected among signature-positive patients claimed by the procedure. Note that rsens, rspec, and rprec were computed in testing data rather than training: A signature was first learned from one data set and then applied to other data sets in the same simulation setting, and performance measurements in testing data sets were averaged to evaluate generalizability of a method. For example, given a scenario of 200 samples in a data set, a signature is learned from the data set and then is used to stratify samples in the other 999 data sets under the same simulation parameter setting (with 200 samples in each of the testing data sets). After stratification, the numbers of true/false positives and true/false negatives are collected for each testing data set. Based on the classification results, sensitivity, specificity, and precision are calculated—these three numbers are corresponding to the signature learned from one data set. Because there are 1000 data sets in each parameter setting, the aforementioned process is repeated for 1000 learned signatures. The results are then averaged for the 1000 signatures.
Because the goal of patient stratification is to identify a subpopulation having an improved treatment effect, a direct performance check is to examine whether the p-value indicating the treatment effect is improved or not in a signature-positive group. Specifically, let pv denote the p-value of a one-sided test that examines whether patients receiving an investigational treatment respond better than patients treated by an SOC; given pv+ and pv−, respectively, generated from the same test for patients in a signature-positive group and in a signature-negative group (as previously defined in Section 2), we check whether pv+ is smaller than pv, that is, whether we observe a better efficacy in the signature-positive group; we also calculate pv− to see whether the interaction-effect constraint pv+<pv− holds in a stratification. Consistent with the calculation of the classification measures, p-values were computed in each testing data set, resulting 999 p-values of each type (for example, pv+) for a learned signature and thus 1000 × 999p-values of each type for 1000 learned signatures in each parameter setting. Medians of p-values of each type were reported as performance measures because of skewness of p-value distributions.
4.3. A baseline scenario
When no noise variable is involved (settings with pn=0 in Table 2), even with a sample size n = 200, PRIM can well detect true signature variables and corresponding lower and upper bounds exactly. However, when noise variables are also given as input, the number of exact detection nE substantially drops. For example, there are only 45 hits of 1000 runs in exact detection for n = 200 and pn=4. To achieve a reasonable exact-detection rate and accurate bound estimation in the presence of noise variables, sample sizes need to be no less than 3200 for pn≤8, as highlighted by bold fronts in Table 2. On the other hand, requiring a smaller sample size for inclusive detection, the procedure can return true signature variables and their bounds in a considerable number of runs, for example, nI=714 for the setting with n = 400 and pn=2; nI=702 for n = 800 and pn=4. There are also a good number of hits (nI=786) with the sample size 3200 for 32 noise variables. This partially correct detection can also be observed for marginal detection. Because of the partial detection, the procedure achieves reasonably high rsens, rspec, and rprec (see bold fonts in Table 3). As a reference for comparison, stratification results from a random procedure are listed in braces in the table. The procedure randomly selects variables and their bounds to create signatures under the constraint of the same minimum support of signature-positive groups as the one specified for PRIM. In this comparison, PRIM is much more sensitive and more precise than the random procedure while being reasonably specific. Comparing to sample sizes needed for good classification results, a larger sample size is required to observe an improved efficacy in a signature-positive group as indicated by pv+<pv (Table 3). For example, in the case of no noise variable, n = 800 rather than n = 200 is necessary for pv+ to be less than pv. For pn=8, n = 1600 is required. When pn goes up to 32 and 128, n = 3200 becomes the only sample size, which makes it possible to observe improved treatment effects for signature-positive patients. We observed pv+<pv− for all sample sizes, which indicates the interaction-effect constraint generally holds in the results.
Table 2.
The results of exact and inclusive detections in scenario 1 for PRIM.
| n | pn | nE | lE1 | lE2 | uE1 | uE2 | nI | lI1 | lI2 | uI1 | uI2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 200 | 0 | 790 | 0.20 | 0.19 | 0.86 | 0.86 | 790 | 0.20 | 0.19 | 0.86 | 0.86 |
| 400 | 0 | 860 | 0.21 | 0.21 | 0.86 | 0.86 | 860 | 0.21 | 0.21 | 0.86 | 0.86 |
| 800 | 0 | 883 | 0.20 | 0.20 | 0.89 | 0.87 | 883 | 0.20 | 0.20 | 0.89 | 0.87 |
| 1600 | 0 | 937 | 0.19 | 0.19 | 0.90 | 0.90 | 937 | 0.19 | 0.19 | 0.90 | 0.90 |
| 3200 | 0 | 988 | 0.19 | 0.19 | 0.91 | 0.90 | 988 | 0.19 | 0.19 | 0.91 | 0.90 |
| 200 | 2 | 101 | 0.17 | 0.16 | 0.89 | 0.89 | 653 | 0.15 | 0.16 | 0.89 | 0.89 |
| 400 | 2 | 150 | 0.17 | 0.17 | 0.90 | 0.91 | 714 | 0.18 | 0.18 | 0.89 | 0.89 |
| 800 | 2 | 245 | 0.17 | 0.18 | 0.92 | 0.91 | 785 | 0.18 | 0.18 | 0.90 | 0.90 |
| 1600 | 2 | 430 | 0.17 | 0.16 | 0.92 | 0.92 | 877 | 0.17 | 0.17 | 0.91 | 0.91 |
| 3200 | 2 | 661 | 0.18 | 0.18 | 0.92 | 0.92 | 974 | 0.18 | 0.18 | 0.91 | 0.91 |
| 200 | 4 | 45 | 0.18 | 0.15 | 0.93 | 0.90 | 548 | 0.13 | 0.13 | 0.91 | 0.91 |
| 400 | 4 | 79 | 0.18 | 0.18 | 0.91 | 0.92 | 628 | 0.16 | 0.17 | 0.90 | 0.90 |
| 800 | 4 | 173 | 0.17 | 0.17 | 0.93 | 0.93 | 702 | 0.16 | 0.16 | 0.91 | 0.91 |
| 1600 | 4 | 308 | 0.17 | 0.16 | 0.93 | 0.93 | 797 | 0.16 | 0.16 | 0.92 | 0.92 |
| 3200 | 4 | 604 | 0.17 | 0.17 | 0.92 | 0.92 | 954 | 0.17 | 0.18 | 0.92 | 0.92 |
| 200 | 6 | 24 | 0.19 | 0.16 | 0.92 | 0.89 | 462 | 0.12 | 0.12 | 0.92 | 0.91 |
| 400 | 6 | 47 | 0.17 | 0.18 | 0.91 | 0.93 | 538 | 0.15 | 0.14 | 0.91 | 0.91 |
| 800 | 6 | 133 | 0.17 | 0.17 | 0.92 | 0.92 | 638 | 0.16 | 0.15 | 0.91 | 0.91 |
| 1600 | 6 | 286 | 0.16 | 0.15 | 0.93 | 0.94 | 738 | 0.16 | 0.16 | 0.92 | 0.92 |
| 3200 | 6 | 599 | 0.17 | 0.18 | 0.92 | 0.93 | 952 | 0.17 | 0.18 | 0.92 | 0.92 |
| 200 | 8 | 23 | 0.14 | 0.17 | 0.91 | 0.92 | 393 | 0.11 | 0.11 | 0.92 | 0.92 |
| 400 | 8 | 40 | 0.17 | 0.17 | 0.94 | 0.94 | 489 | 0.14 | 0.13 | 0.92 | 0.91 |
| 800 | 8 | 115 | 0.17 | 0.16 | 0.93 | 0.93 | 575 | 0.15 | 0.14 | 0.92 | 0.92 |
| 1600 | 8 | 256 | 0.17 | 0.17 | 0.94 | 0.95 | 710 | 0.16 | 0.16 | 0.93 | 0.93 |
| 3200 | 8 | 594 | 0.17 | 0.18 | 0.93 | 0.93 | 935 | 0.17 | 0.17 | 0.93 | 0.93 |
| 200 | 32 | 1 | 0.01 | 0.21 | 0.91 | 1.00 | 136 | 0.08 | 0.07 | 0.94 | 0.94 |
| 400 | 32 | 8 | 0.18 | 0.20 | 0.96 | 0.95 | 221 | 0.08 | 0.08 | 0.94 | 0.94 |
| 800 | 32 | 36 | 0.16 | 0.16 | 0.96 | 0.95 | 289 | 0.11 | 0.10 | 0.94 | 0.94 |
| 1600 | 32 | 141 | 0.16 | 0.15 | 0.95 | 0.95 | 424 | 0.13 | 0.13 | 0.95 | 0.94 |
| 3200 | 32 | 493 | 0.17 | 0.17 | 0.94 | 0.95 | 786 | 0.16 | 0.16 | 0.94 | 0.94 |
| 200 | 128 | 0 | — | — | — | — | 20 | 0.05 | 0.04 | 0.95 | 0.94 |
| 400 | 128 | 0 | — | — | — | — | 35 | 0.06 | 0.06 | 0.96 | 0.97 |
| 800 | 128 | 4 | 0.12 | 0.10 | 0.94 | 0.94 | 87 | 0.07 | 0.07 | 0.96 | 0.95 |
| 1600 | 128 | 37 | 0.14 | 0.15 | 0.98 | 0.98 | 141 | 0.11 | 0.11 | 0.96 | 0.96 |
| 3200 | 128 | 352 | 0.17 | 0.17 | 0.97 | 0.97 | 517 | 0.16 | 0.16 | 0.96 | 0.96 |
Table 3.
The results of marginal detection and stratification in scenario 1 for PRIM.
| n | pn | nM1 | nM2 | lM1 | lM2 | uM1 | uM2 | rsens | rspec | rprec | pv | pv+ | pv− |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 200 | 0 | 894 | 895 | 0.21 | 0.20 | 0.86 | 0.85 | 0.70 (0.47) | 0.76 (0.71) | 0.76 (0.60) | 8.4E-03 | 1.2E-02 | 1.7E-01 |
| 400 | 0 | 929 | 931 | 0.21 | 0.21 | 0.86 | 0.86 | 0.72 (0.44) | 0.78 (0.73) | 0.81 (0.60) | 2.7E-04 | 3.3E-04 | 1.2E-01 |
| 800 | 0 | 938 | 945 | 0.20 | 0.20 | 0.89 | 0.88 | 0.80 (0.42) | 0.79 (0.74) | 0.82 (0.59) | 8.7E-07 | 1.6E-07 | 1.3E-01 |
| 1600 | 0 | 971 | 966 | 0.19 | 0.18 | 0.90 | 0.90 | 0.90 (0.43) | 0.83 (0.74) | 0.86 (0.60) | 4.7E-12 | 4.3E-15 | 1.7E-01 |
| 3200 | 0 | 994 | 994 | 0.19 | 0.19 | 0.91 | 0.90 | 0.94 (0.41) | 0.89 (0.74) | 0.90 (0.58) | 3.7E-22 | 7.5E-31 | 2.1E-01 |
| 200 | 2 | 804 | 794 | 0.16 | 0.17 | 0.89 | 0.88 | 0.61 (0.33) | 0.71 (0.84) | 0.70 (0.68) | 8.4E-03 | 2.0E-02 | 1.0E-01 |
| 400 | 2 | 839 | 850 | 0.18 | 0.18 | 0.88 | 0.89 | 0.63 (0.25) | 0.73 (0.90) | 0.74 (0.70) | 2.7E-04 | 1.1E-03 | 4.9E-02 |
| 800 | 2 | 889 | 880 | 0.18 | 0.18 | 0.90 | 0.90 | 0.73 (0.21) | 0.73 (0.93) | 0.77 (0.71) | 8.7E-07 | 1.0E-06 | 4.9E-02 |
| 1600 | 2 | 940 | 933 | 0.17 | 0.17 | 0.91 | 0.91 | 0.85 (0.19) | 0.76 (0.93) | 0.80 (0.70) | 4.7E-12 | 6.9E-14 | 7.9E-02 |
| 3200 | 2 | 985 | 989 | 0.18 | 0.18 | 0.91 | 0.91 | 0.92 (0.18) | 0.85 (0.94) | 0.88 (0.72) | 3.7E-22 | 1.1E-29 | 1.5E-01 |
| 200 | 4 | 729 | 709 | 0.15 | 0.15 | 0.91 | 0.91 | 0.57 (0.28) | 0.68 (0.83) | 0.65 (0.61) | 8.4E-03 | 2.7E-02 | 8.5E-02 |
| 400 | 4 | 769 | 789 | 0.16 | 0.17 | 0.90 | 0.91 | 0.58 (0.22) | 0.70 (0.90) | 0.69 (0.67) | 2.7E-04 | 2.1E-03 | 3.2E-02 |
| 800 | 4 | 834 | 842 | 0.17 | 0.16 | 0.91 | 0.91 | 0.71 (0.17) | 0.68 (0.93) | 0.72 (0.68) | 8.7E-07 | 2.3E-06 | 3.4E-02 |
| 1600 | 4 | 900 | 886 | 0.17 | 0.16 | 0.92 | 0.92 | 0.83 (0.14) | 0.71 (0.95) | 0.77 (0.71) | 4.7E-12 | 3.0E-13 | 5.3E-02 |
| 3200 | 4 | 973 | 981 | 0.17 | 0.18 | 0.92 | 0.92 | 0.92 (0.09) | 0.82 (0.97) | 0.85 (0.70) | 3.7E-22 | 5.5E-29 | 1.3E-01 |
| 200 | 6 | 659 | 651 | 0.13 | 0.13 | 0.91 | 0.91 | 0.54 (0.26) | 0.66 (0.77) | 0.62 (0.55) | 8.4E-03 | 3.2E-02 | 7.3E-02 |
| 400 | 6 | 698 | 723 | 0.15 | 0.15 | 0.91 | 0.91 | 0.57 (0.17) | 0.67 (0.86) | 0.66 (0.57) | 2.7E-04 | 2.8E-03 | 2.6E-02 |
| 800 | 6 | 801 | 786 | 0.16 | 0.15 | 0.91 | 0.92 | 0.68 (0.13) | 0.66 (0.89) | 0.70 (0.59) | 8.7E-07 | 4.7E-06 | 2.1E-02 |
| 1600 | 6 | 869 | 857 | 0.16 | 0.16 | 0.93 | 0.92 | 0.82 (0.11) | 0.68 (0.91) | 0.74 (0.60) | 4.7E-12 | 7.0E-13 | 4.9E-02 |
| 3200 | 6 | 969 | 982 | 0.17 | 0.18 | 0.92 | 0.92 | 0.91 (0.08) | 0.81 (0.94) | 0.84 (0.64) | 3.7E-22 | 1.8E-28 | 1.1E-01 |
| 200 | 8 | 608 | 598 | 0.11 | 0.12 | 0.92 | 0.92 | 0.53 (0.32) | 0.64 (0.71) | 0.60 (0.54) | 8.4E-03 | 3.4E-02 | 7.0E-02 |
| 400 | 8 | 663 | 671 | 0.14 | 0.14 | 0.92 | 0.92 | 0.56 (0.20) | 0.65 (0.83) | 0.64 (0.58) | 2.7E-04 | 3.2E-03 | 2.4E-02 |
| 800 | 8 | 753 | 752 | 0.15 | 0.15 | 0.93 | 0.92 | 0.69 (0.13) | 0.63 (0.91) | 0.67 (0.63) | 8.7E-07 | 5.6E-06 | 2.2E-02 |
| 1600 | 8 | 849 | 839 | 0.16 | 0.16 | 0.93 | 0.93 | 0.81 (0.08) | 0.66 (0.95) | 0.73 (0.66) | 4.7E-12 | 1.5E-12 | 3.7E-02 |
| 3200 | 8 | 962 | 972 | 0.17 | 0.17 | 0.93 | 0.93 | 0.91 (0.05) | 0.78 (0.98) | 0.82 (0.68) | 3.7E-22 | 3.8E-28 | 1.2E-01 |
| 200 | 32 | 321 | 330 | 0.09 | 0.09 | 0.94 | 0.94 | 0.48 (0.29) | 0.59 (0.71) | 0.53 (0.49) | 8.4E-03 | 5.0E-02 | 5.1E-02 |
| 400 | 32 | 426 | 430 | 0.09 | 0.09 | 0.94 | 0.94 | 0.51 (0.21) | 0.59 (0.79) | 0.56 (0.49) | 2.7E-04 | 7.2E-03 | 1.2E-02 |
| 800 | 32 | 506 | 503 | 0.12 | 0.11 | 0.95 | 0.95 | 0.63 (0.14) | 0.54 (0.86) | 0.58 (0.49) | 8.7E-07 | 3.3E-05 | 5.9E-03 |
| 1600 | 32 | 654 | 648 | 0.13 | 0.13 | 0.95 | 0.95 | 0.81 (0.10) | 0.51 (0.90) | 0.63 (0.49) | 4.7E-12 | 1.1E-11 | 2.4E-02 |
| 3200 | 32 | 879 | 895 | 0.16 | 0.16 | 0.94 | 0.94 | 0.91 (0.07) | 0.68 (0.93) | 0.75 (0.49) | 3.7E-22 | 1.1E-26 | 1.2E-01 |
| 200 | 128 | 131 | 117 | 0.07 | 0.06 | 0.95 | 0.95 | 0.44 (0.36) | 0.58 (0.64) | 0.50 (0.49) | 8.4E-03 | 6.0E-02 | 4.2E-02 |
| 400 | 128 | 151 | 185 | 0.06 | 0.07 | 0.95 | 0.95 | 0.47 (0.33) | 0.56 (0.67) | 0.51 (0.49) | 2.7E-04 | 1.2E-02 | 8.1E-03 |
| 800 | 128 | 268 | 279 | 0.09 | 0.09 | 0.96 | 0.96 | 0.60 (0.33) | 0.47 (0.67) | 0.53 (0.49) | 8.7E-07 | 7.8E-05 | 3.1E-03 |
| 1600 | 128 | 394 | 371 | 0.11 | 0.11 | 0.96 | 0.96 | 0.78 (0.33) | 0.39 (0.67) | 0.56 (0.49) | 4.7E-12 | 1.6E-10 | 5.6E-03 |
| 3200 | 128 | 712 | 725 | 0.15 | 0.15 | 0.96 | 0.96 | 0.92 (0.32) | 0.52 (0.68) | 0.67 (0.49) | 3.7E-22 | 4.8E-25 | 1.4E-01 |
4.4. Resampling in the baseline scenario given 32 noise variables
As shown in Table 4, when Re-PRIM with k = 2 is applied to the cases of pn=32, it substantially improves the performance of PRIM under every sample-size condition listed in Table 2. In another way of understanding the results, we note that Re-PRIM needs less samples to make accurate detection: For exact detection, with n = 1600 instead of n = 3200, the method can detect the signature for 600 out of 1000 runs. With respect to stratification accuracy and p-values, the performance with n = 1600 in Table 5 is also much superior to the one (with n = 1600 and pn=32) in Table 3, where resampling was not employed. These results represent an ideal situation where the number of true signature variables is assigned to k, the parameter of Re-PRIM for determining the number of selected variables as final input of PRIM. If a larger k value is pre-specified, results are expected not to be better than those given an equivalent number of input noise variables. When the number of true signature variables is greater than a prescribed value of k, the resampling scheme induces bias by enforcing rule simplification while it reduces instability. Therefore, their trade-off decides whether the scheme can enhance PRIM's performance. In practice, cross-validation can be employed to choose an optimal parameter value in terms of predictive performance.
Table 4.
The results of exact detection in scenario 1 for Re-PRIM given pn=32.
| n | pn | nE | lE1 | lE2 | uE1 | uE2 |
|---|---|---|---|---|---|---|
| 200 | 32 | 30 | 0.16 | 0.20 | 0.87 | 0.88 |
| 400 | 32 | 77 | 0.21 | 0.19 | 0.87 | 0.86 |
| 800 | 32 | 261 | 0.21 | 0.20 | 0.89 | 0.88 |
| 1600 | 32 | 600 | 0.19 | 0.19 | 0.90 | 0.90 |
| 3200 | 32 | 936 | 0.19 | 0.19 | 0.90 | 0.90 |
Note: The results of inclusive detection are not shown because they are the same as those of exact detection when the number of input variables for the final learning is constrained to the number of true signature variables.
Table 5.
The results of marginal detection and stratification in scenario 1 for Re-PRIM given pn=32.
| n | pn | nM1nM2 | lM1 lM2 | uM1uM2 | rsens rspec rprec | pv pv+ pv− |
|---|---|---|---|---|---|---|
| 200 | 32 | 200 218 | 0.20 0.20 | 0.86 0.86 | 0.54 0.57 0.55 | 8.4E-03 3.9E-02 6.6E-02 |
| 400 | 32 | 312 310 | 0.21 0.21 | 0.86 0.86 | 0.59 0.58 0.59 | 2.7E-04 3.1E-03 2.6E-02 |
| 800 | 32 | 537 533 | 0.20 0.19 | 0.89 0.88 | 0.72 0.61 0.67 | 8.7E-07 3.3E-06 2.8E-02 |
| 1600 | 32 | 793 765 | 0.19 0.18 | 0.90 0.90 | 0.86 0.72 0.78 | 4.7E-12 7.6E-14 8.0E-02 |
| 3200 | 32 | 971 965 | 0.19 0.19 | 0.90 0.91 | 0.93 0.87 0.89 | 3.7E-22 1.4E-30 2.0E-01 |
4.5. A scenario with more signature variables
We next investigate a scenario where the number of signature variables increases from two to four (scenario 2 in Table 1). x3 and x4 are the additional signature variables. To maintain prevalence around 50%, the rules are tuned to be 0≤xi≤0.85, for i = 1,2,3,4. In this situation, a much larger sample size is required for PRIM to return proper results for both exact detection and inclusive detection (Table 6) in comparison with the baseline scenario (Table 2). For example, n = 3200 (instead of n = 200) is needed for the detection given no noise variable. Such a large sample size does not empower either the exact detection or inclusive detection after four or more noise variables are added. A minimal sample size 1600 is also required by marginal detection given pn≤8, and n = 3200 is needed given pn=32 (Table 7). To achieve satisfactory classification performance, n = 800 is necessary for the cases of pn≤8, and again, n = 3200 is demanded when pn is increased to 32. To achieve improved p-values in signature-positive groups, the method needs at least 1600 samples given pn≤8 and 3200 samples for pn=32. As previously seen in the baseline scenario, Re-PRIM with k = 4 considerably boosts exact detection (Table 8) in comparison to the results without involving resampling-based variable selection (Table 6). The method also substantially enhances marginal detection and stratification performance (Table 9).
Table 6.
The results of exact and inclusive detections in scenario 2 for PRIM.
| n | pn | nE | lE1lE2 lE3 lE4 | uE1 uE2 uE3 uE4 | nI | lI1 lI2 lI3 lI4 | uI1 uI2 uI3 uI4 |
|---|---|---|---|---|---|---|---|
| 200 | 0 | 382 | 0.08 0.08 0.09 0.09 | 0.86 0.86 0.86 0.85 | 382 | 0.08 0.08 0.09 0.09 | 0.86 0.86 0.86 0.85 |
| 400 | 0 | 411 | 0.07 0.08 0.08 0.07 | 0.84 0.83 0.83 0.83 | 411 | 0.07 0.08 0.08 0.07 | 0.84 0.83 0.83 0.83 |
| 800 | 0 | 437 | 0.05 0.05 0.05 0.05 | 0.84 0.83 0.83 0.84 | 437 | 0.05 0.05 0.05 0.05 | 0.84 0.83 0.83 0.84 |
| 1600 | 0 | 545 | 0.02 0.02 0.02 0.02 | 0.85 0.85 0.85 0.85 | 545 | 0.02 0.02 0.02 0.02 | 0.85 0.85 0.85 0.85 |
| 3200 | 0 | 728 | 0.01 0.01 0.01 0.01 | 0.85 0.85 0.86 0.85 | 728 | 0.01 0.01 0.01 0.01 | 0.85 0.85 0.86 0.85 |
| 200 | 2 | 25 | 0.06 0.05 0.07 0.04 | 0.87 0.89 0.86 0.89 | 255 | 0.06 0.07 0.07 0.07 | 0.88 0.87 0.87 0.87 |
| 400 | 2 | 26 | 0.04 0.03 0.03 0.07 | 0.87 0.85 0.84 0.85 | 310 | 0.07 0.07 0.07 0.07 | 0.85 0.85 0.85 0.84 |
| 800 | 2 | 81 | 0.03 0.03 0.02 0.02 | 0.85 0.83 0.84 0.84 | 338 | 0.05 0.05 0.04 0.04 | 0.84 0.83 0.84 0.85 |
| 1600 | 2 | 210 | 0.01 0.01 0.01 0.01 | 0.86 0.86 0.86 0.86 | 411 | 0.02 0.02 0.01 0.02 | 0.86 0.85 0.85 0.85 |
| 3200 | 2 | 462 | 0.00 0.00 0.00 0.00 | 0.86 0.85 0.85 0.86 | 644 | 0.00 0.00 0.01 0.01 | 0.86 0.85 0.85 0.86 |
| 200 | 4 | 10 | 0.05 0.08 0.07 0.06 | 0.83 0.94 0.89 0.91 | 194 | 0.06 0.06 0.06 0.06 | 0.88 0.90 0.89 0.89 |
| 400 | 4 | 8 | 0.03 0.08 0.04 0.04 | 0.88 0.86 0.83 0.89 | 220 | 0.06 0.06 0.06 0.06 | 0.87 0.86 0.85 0.87 |
| 800 | 4 | 28 | 0.02 0.02 0.01 0.03 | 0.86 0.85 0.85 0.87 | 241 | 0.05 0.04 0.05 0.04 | 0.85 0.85 0.85 0.85 |
| 1600 | 4 | 106 | 0.01 0.01 0.00 0.00 | 0.86 0.87 0.86 0.87 | 310 | 0.01 0.02 0.01 0.01 | 0.86 0.87 0.86 0.86 |
| 3200 | 4 | 361 | 0.00 0.00 0.00 0.00 | 0.86 0.85 0.86 0.86 | 565 | 0.00 0.00 0.00 0.00 | 0.86 0.86 0.85 0.86 |
| 200 | 6 | 2 | 0.01 0.18 0.01 0.02 | 0.78 1.00 0.85 0.90 | 128 | 0.05 0.06 0.05 0.06 | 0.89 0.90 0.90 0.90 |
| 400 | 6 | 4 | 0.01 0.03 0.05 0.06 | 0.83 0.87 0.79 0.89 | 177 | 0.06 0.06 0.05 0.06 | 0.87 0.87 0.87 0.88 |
| 800 | 6 | 22 | 0.01 0.03 0.02 0.02 | 0.86 0.87 0.85 0.86 | 213 | 0.03 0.04 0.04 0.04 | 0.85 0.85 0.86 0.86 |
| 1600 | 6 | 87 | 0.01 0.01 0.01 0.00 | 0.85 0.86 0.86 0.86 | 264 | 0.01 0.01 0.01 0.01 | 0.86 0.86 0.86 0.86 |
| 3200 | 6 | 290 | 0.00 0.00 0.00 0.00 | 0.86 0.85 0.86 0.86 | 494 | 0.00 0.00 0.00 0.00 | 0.86 0.86 0.86 0.86 |
| 200 | 8 | 0 | — — — — | — — — — | 109 | 0.06 0.05 0.05 0.05 | 0.90 0.91 0.90 0.89 |
| 400 | 8 | 2 | 0.01 0.04 0.09 0.05 | 0.93 0.84 0.81 0.81 | 144 | 0.06 0.05 0.05 0.05 | 0.88 0.87 0.88 0.89 |
| 800 | 8 | 19 | 0.00 0.02 0.01 0.01 | 0.85 0.83 0.85 0.85 | 171 | 0.04 0.05 0.04 0.03 | 0.86 0.87 0.86 0.86 |
| 1600 | 8 | 54 | 0.01 0.01 0.01 0.00 | 0.87 0.87 0.87 0.86 | 230 | 0.02 0.01 0.01 0.01 | 0.87 0.86 0.87 0.86 |
| 3200 | 8 | 234 | 0.00 0.00 0.00 0.00 | 0.86 0.85 0.86 0.86 | 445 | 0.00 0.00 0.00 0.00 | 0.86 0.86 0.86 0.86 |
| 200 | 32 | 0 | — — — — | — — — — | 9 | 0.05 0.02 0.02 0.03 | 0.93 0.95 0.94 0.94 |
| 400 | 32 | 0 | — — — — | — — — — | 33 | 0.03 0.04 0.02 0.03 | 0.93 0.93 0.93 0.93 |
| 800 | 32 | 0 | — — — — | — — — — | 41 | 0.02 0.02 0.03 0.02 | 0.90 0.90 0.90 0.90 |
| 1600 | 32 | 9 | 0.00 0.00 0.00 0.00 | 0.81 0.83 0.85 0.83 | 40 | 0.01 0.01 0.01 0.00 | 0.87 0.87 0.86 0.87 |
| 3200 | 32 | 105 | 0.00 0.00 0.00 0.00 | 0.86 0.85 0.86 0.86 | 209 | 0.00 0.00 0.00 0.00 | 0.86 0.86 0.86 0.87 |
| 200 | 128 | 0 | — — — — | — — — — | 0 | — — — — | — — — — |
| 400 | 128 | 0 | — — — — | — — — — | 1 | 0.00 0.00 0.00 0.01 | 0.94 0.92 0.93 0.76 |
| 800 | 128 | 0 | — — — — | — — — — | 5 | 0.02 0.02 0.01 0.02 | 0.95 0.98 0.91 0.94 |
| 1600 | 128 | 0 | — — — — | — — — — | 2 | 0.03 0.00 0.00 0.03 | 0.96 0.86 0.89 0.93 |
| 3200 | 128 | 27 | 0.00 0.00 0.00 0.00 | 0.86 0.85 0.86 0.86 | 47 | 0.00 0.00 0.00 0.00 | 0.86 0.86 0.86 0.87 |
Table 7.
The results of marginal detection and stratification in scenario 2 for PRIM.
| n | pn | nM1nM2nM3nM4 | lM1 lM2 lM3 lM4 | uM1uM2 uM3uM4 | rsensrspecrprec | pv pv+ pv− |
|---|---|---|---|---|---|---|
| 200 | 0 | 719 726 724 721 | 0.08 0.08 0.08 0.09 | 0.84 0.84 0.84 0.84 | 0.61 (0.30) 0.71 (0.82) 0.72 (0.65) | 5.5E-03 1.5E-02 9.0E-02 |
| 400 | 0 | 729 738 734 718 | 0.07 0.07 0.06 0.07 | 0.83 0.83 0.82 0.83 | 0.66 (0.21) 0.72 (0.87) 0.76 (0.65) | 1.6E-04 6.5E-04 4.7E-02 |
| 800 | 0 | 750 762 767 743 | 0.04 0.04 0.04 0.04 | 0.83 0.83 0.83 0.83 | 0.75 (0.18) 0.73 (0.89) 0.79 (0.64) | 2.2E-07 3.0E-07 4.3E-02 |
| 1600 | 0 | 827 825 804 835 | 0.02 0.02 0.02 0.02 | 0.85 0.85 0.85 0.85 | 0.86 (0.16) 0.77 (0.90) 0.83 (0.64) | 4.1E-13 3.1E-15 8.8E-02 |
| 3200 | 0 | 917 903 913 900 | 0.01 0.01 0.01 0.01 | 0.85 0.85 0.86 0.85 | 0.92 (0.14) 0.85 (0.91) 0.88 (0.62) | 1.1E-24 3.3E-32 1.3E-01 |
| 200 | 2 | 621 620 628 631 | 0.07 0.07 0.07 0.08 | 0.85 0.86 0.85 0.86 | 0.57 (0.27) 0.68 (0.83) 0.68 (0.63) | 5.5E-03 2.0E-02 7.0E-02 |
| 400 | 2 | 648 648 679 650 | 0.06 0.06 0.06 0.06 | 0.83 0.85 0.84 0.84 | 0.61 (0.20) 0.69 (0.88) 0.72 (0.64) | 1.6E-04 1.2E-03 2.9E-02 |
| 800 | 2 | 672 681 697 685 | 0.04 0.04 0.04 0.03 | 0.84 0.83 0.83 0.84 | 0.71 (0.14) 0.69 (0.91) 0.75 (0.65) | 2.2E-07 8.5E-07 2.4E-02 |
| 1600 | 2 | 737 726 739 771 | 0.01 0.01 0.01 0.01 | 0.85 0.85 0.85 0.85 | 0.85 (0.11) 0.71 (0.93) 0.79 (0.66) | 4.1E-13 1.8E-14 5.7E-02 |
| 3200 | 2 | 882 860 875 883 | 0.00 0.00 0.01 0.00 | 0.86 0.85 0.85 0.86 | 0.91 (0.08) 0.82 (0.96) 0.87 (0.66) | 1.1E-24 2.1E-31 9.5E-02 |
| 200 | 4 | 555 584 560 555 | 0.07 0.06 0.06 0.07 | 0.86 0.87 0.86 0.87 | 0.54 (0.25) 0.67 (0.77) 0.66 (0.56) | 5.5E-03 2.3E-02 6.0E-02 |
| 400 | 4 | 575 592 627 583 | 0.05 0.05 0.05 0.06 | 0.86 0.85 0.85 0.86 | 0.59 (0.17) 0.66 (0.85) 0.69 (0.57) | 1.6E-04 1.7E-03 2.3E-02 |
| 800 | 4 | 594 626 611 607 | 0.03 0.03 0.03 0.03 | 0.84 0.84 0.84 0.85 | 0.71 (0.12) 0.64 (0.89) 0.72 (0.57) | 2.2E-07 1.3E-06 2.0E-02 |
| 1600 | 4 | 692 674 684 701 | 0.01 0.01 0.01 0.01 | 0.86 0.86 0.86 0.85 | 0.84 (0.10) 0.66 (0.91) 0.76 (0.58) | 4.1E-13 4.9E-14 4.8E-02 |
| 3200 | 4 | 859 840 864 840 | 0.00 0.00 0.00 0.00 | 0.86 0.86 0.85 0.86 | 0.91 (0.07) 0.80 (0.93) 0.85 (0.60) | 1.1E-24 8.0E-31 7.9E-02 |
| 200 | 6 | 497 518 513 494 | 0.06 0.05 0.05 0.06 | 0.88 0.88 0.87 0.88 | 0.54 (0.34) 0.64 (0.74) 0.64 (0.59) | 5.5E-03 2.5E-02 5.7E-02 |
| 400 | 6 | 550 531 558 548 | 0.05 0.05 0.04 0.05 | 0.86 0.86 0.85 0.86 | 0.57 (0.22) 0.65 (0.83) 0.67 (0.60) | 1.6E-04 2.2E-03 1.9E-02 |
| 800 | 6 | 569 585 584 588 | 0.03 0.03 0.03 0.03 | 0.86 0.84 0.85 0.85 | 0.68 (0.13) 0.63 (0.91) 0.70 (0.63) | 2.2E-07 2.2E-06 1.4E-02 |
| 1600 | 6 | 652 638 633 672 | 0.01 0.01 0.01 0.01 | 0.85 0.85 0.85 0.85 | 0.83 (0.07) 0.65 (0.95) 0.75 (0.65) | 4.1E-13 9.6E-14 3.5E-02 |
| 3200 | 6 | 836 795 831 823 | 0.00 0.00 0.00 0.00 | 0.86 0.86 0.86 0.86 | 0.90 (0.04) 0.77 (0.97) 0.83 (0.66) | 1.1E-24 3.2E-30 6.6E-02 |
| 200 | 8 | 489 462 491 456 | 0.06 0.05 0.06 0.06 | 0.88 0.88 0.88 0.89 | 0.52 (0.27) 0.63 (0.77) 0.62 (0.57) | 5.5E-03 2.8E-02 5.3E-02 |
| 400 | 8 | 525 499 516 475 | 0.05 0.04 0.04 0.04 | 0.87 0.86 0.87 0.87 | 0.57 (0.17) 0.63 (0.86) 0.65 (0.59) | 1.6E-04 2.2E-03 1.9E-02 |
| 800 | 8 | 528 532 554 545 | 0.03 0.03 0.03 0.03 | 0.86 0.86 0.85 0.85 | 0.67 (0.12) 0.62 (0.91) 0.69 (0.59) | 2.2E-07 3.3E-06 1.0E-02 |
| 1600 | 8 | 616 628 610 628 | 0.01 0.01 0.01 0.01 | 0.86 0.85 0.86 0.86 | 0.82 (0.08) 0.62 (0.94) 0.73 (0.60) | 4.1E-13 1.7E-13 3.0E-02 |
| 3200 | 8 | 801 774 812 800 | 0.00 0.00 0.00 0.00 | 0.86 0.86 0.86 0.86 | 0.90 (0.05) 0.76 (0.96) 0.82 (0.61) | 1.1E-24 1.1E-29 5.3E-02 |
| 200 | 32 | 255 233 237 236 | 0.04 0.04 0.04 0.05 | 0.91 0.91 0.91 0.91 | 0.48 (0.27) 0.58 (0.73) 0.56 (0.52) | 5.5E-03 3.9E-02 3.9E-02 |
| 400 | 32 | 308 319 299 288 | 0.03 0.03 0.03 0.03 | 0.89 0.90 0.90 0.90 | 0.51 (0.17) 0.58 (0.83) 0.58 (0.52) | 1.6E-04 4.9E-03 9.4E-03 |
| 800 | 32 | 358 342 327 326 | 0.02 0.02 0.02 0.02 | 0.88 0.88 0.88 0.88 | 0.64 (0.10) 0.52 (0.90) 0.61 (0.52) | 2.2E-07 1.1E-05 4.7E-03 |
| 1600 | 32 | 393 414 413 433 | 0.01 0.01 0.01 0.00 | 0.86 0.86 0.86 0.86 | 0.82 (0.06) 0.49 (0.94) 0.65 (0.52) | 4.1E-13 1.3E-12 1.8E-02 |
| 3200 | 32 | 691 609 643 640 | 0.00 0.00 0.00 0.00 | 0.86 0.86 0.86 0.86 | 0.90 (0.04) 0.64 (0.96) 0.76 (0.52) | 1.1E-24 2.3E-28 5.9E-02 |
| 200 | 128 | 96 94 92 96 | 0.04 0.03 0.04 0.03 | 0.93 0.92 0.92 0.91 | 0.45 (0.40) 0.57 (0.60) 0.54 (0.52) | 5.5E-03 4.6E-02 3.4E-02 |
| 400 | 128 | 126 123 128 125 | 0.02 0.03 0.02 0.03 | 0.90 0.93 0.90 0.91 | 0.49 (0.35) 0.54 (0.65) 0.54 (0.52) | 1.6E-04 7.3E-03 6.8E-03 |
| 800 | 128 | 169 150 154 157 | 0.01 0.02 0.01 0.01 | 0.89 0.90 0.89 0.90 | 0.61 (0.33) 0.46 (0.67) 0.56 (0.52) | 2.2E-07 3.0E-05 2.0E-03 |
| 1600 | 128 | 229 224 196 216 | 0.00 0.00 0.00 0.00 | 0.88 0.87 0.87 0.87 | 0.79 (0.30) 0.37 (0.70) 0.58 (0.52) | 4.1E-13 1.6E-11 4.8E-03 |
| 3200 | 128 | 451 415 428 410 | 0.00 0.00 0.00 0.00 | 0.86 0.87 0.86 0.86 | 0.91 (0.26) 0.46 (0.74) 0.66 (0.52) | 1.1E-24 3.1E-26 4.4E-02 |
Table 8.
The results of exact detection in scenario 2 for Re-PRIM given pn=32.
| n | pn | nE | lE1 | lE2 | lE3 | lE4 | uE1 | uE2 | uE3 | uE4 |
|---|---|---|---|---|---|---|---|---|---|---|
| 200 | 32 | 0 | — | — | — | — | — | — | — | — |
| 400 | 32 | 0 | — | — | — | — | — | — | — | — |
| 800 | 32 | 12 | 0.02 | 0.04 | 0.01 | 0.05 | 0.84 | 0.85 | 0.86 | 0.85 |
| 1600 | 32 | 78 | 0.01 | 0.03 | 0.03 | 0.02 | 0.84 | 0.85 | 0.85 | 0.85 |
| 3200 | 32 | 463 | 0.01 | 0.01 | 0.01 | 0.01 | 0.85 | 0.85 | 0.85 | 0.85 |
Table 9.
The results of marginal detection and stratification in scenario 2 for Re-PRIM given pn=32.
| n | pn | nM1nM2nM3nM4 | lM1 lM2 lM3 lM4 | uM1 uM2 uM3 uM4 | rsens rspec rprec | pv pv+ pv− |
|---|---|---|---|---|---|---|
| 200 | 32 | 178 206 194 192 | 0.09 0.07 0.08 0.08 | 0.84 0.85 0.85 0.86 | 0.47 0.61 0.57 | 5.5E-03 3.9E-02 3.8E-02 |
| 400 | 32 | 259 251 267 240 | 0.06 0.07 0.06 0.07 | 0.84 0.83 0.84 0.84 | 0.50 0.62 0.60 | 1.6E-04 5.0E-03 8.4E-03 |
| 800 | 32 | 380 347 370 385 | 0.04 0.03 0.03 0.03 | 0.84 0.83 0.84 0.83 | 0.62 0.60 0.64 | 2.2E-07 1.1E-05 3.2E-03 |
| 1600 | 32 | 560 560 536 603 | 0.02 0.02 0.02 0.02 | 0.85 0.85 0.85 0.86 | 0.77 0.64 0.72 | 4.1E-13 1.2E-12 5.4E-03 |
| 3200 | 32 | 840 804 833 820 | 0.01 0.01 0.01 0.01 | 0.85 0.86 0.86 0.86 | 0.90 0.80 0.84 | 1.1E-24 1.6E-30 5.4E-02 |
4.6. A scenario with increased prevalence
To cover the scenario with a larger signature-positive population, we increased prevalence from 50% to 72% by decreasing the lower bound of a signature variable from 0.20 to 0.05 while keeping other parameter values the same (see scenario 3 in Table 1). The increased positive signals in the data lead to the following changes in stratification results: On average, rsens and rprec are increased by 9% and 20%, respectively, while rspec is decreased by 9%. Other results are similar to previous ones (Tables 2 and 3).
4.7. A scenario with a relatively large effect size
We change 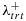 from 0.05 to 0.025, making a scenario where the effect size is increased twice as much as in the baseline scenario. This change decreases the hazard ratio in the signature-positive group from 0.5 to 0.25 (scenario 4 in Table 1). As highlighted in Table 10, PRIM only needs n = 800 to achieve similar results in Table 2 for pn=2 or 4 in exact detection. That is, only one quarter of the previously required sample size is needed. Similarly, it asks for n = 1600, one-half of the previous sample size to make better detection given pn=6 or 8. With 1600 samples, the method can achieve good results for pn=32 or 128, which is not obtainable even with 3200 samples in the baseline scenario. Sample sizes are also reduced by at least one-half for inclusive detection. The similar situation holds for marginal detection and stratification (Table 11). For example, given pn=8, n = 400 is sufficient for satisfactory results. That is, PRIM works well with one-fourth of the corresponding required sample size in Table 3. With many noise variables as in the case of pn=128, the method also performs reasonably given n = 1600.
from 0.05 to 0.025, making a scenario where the effect size is increased twice as much as in the baseline scenario. This change decreases the hazard ratio in the signature-positive group from 0.5 to 0.25 (scenario 4 in Table 1). As highlighted in Table 10, PRIM only needs n = 800 to achieve similar results in Table 2 for pn=2 or 4 in exact detection. That is, only one quarter of the previously required sample size is needed. Similarly, it asks for n = 1600, one-half of the previous sample size to make better detection given pn=6 or 8. With 1600 samples, the method can achieve good results for pn=32 or 128, which is not obtainable even with 3200 samples in the baseline scenario. Sample sizes are also reduced by at least one-half for inclusive detection. The similar situation holds for marginal detection and stratification (Table 11). For example, given pn=8, n = 400 is sufficient for satisfactory results. That is, PRIM works well with one-fourth of the corresponding required sample size in Table 3. With many noise variables as in the case of pn=128, the method also performs reasonably given n = 1600.
Table 10.
The results of exact and inclusive detections in scenario 4 for PRIM.
| n | pn | nE | lE1 | lE2 | uE1 | uE2 | nI | lI1 | lI2 | uI1 | uI2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 200 | 0 | 884 | 0.18 | 0.18 | 0.89 | 0.89 | 884 | 0.18 | 0.18 | 0.89 | 0.89 |
| 400 | 0 | 929 | 0.19 | 0.19 | 0.90 | 0.90 | 929 | 0.19 | 0.19 | 0.90 | 0.90 |
| 800 | 0 | 969 | 0.19 | 0.19 | 0.91 | 0.90 | 969 | 0.19 | 0.19 | 0.91 | 0.90 |
| 1600 | 0 | 997 | 0.19 | 0.19 | 0.91 | 0.90 | 997 | 0.19 | 0.19 | 0.91 | 0.90 |
| 3200 | 0 | 1000 | 0.20 | 0.20 | 0.90 | 0.90 | 1000 | 0.20 | 0.20 | 0.90 | 0.90 |
| 200 | 2 | 266 | 0.17 | 0.17 | 0.93 | 0.91 | 762 | 0.16 | 0.16 | 0.91 | 0.90 |
| 400 | 2 | 430 | 0.17 | 0.17 | 0.92 | 0.92 | 850 | 0.17 | 0.17 | 0.91 | 0.91 |
| 800 | 2 | 630 | 0.18 | 0.18 | 0.92 | 0.92 | 941 | 0.18 | 0.18 | 0.91 | 0.91 |
| 1600 | 2 | 784 | 0.19 | 0.19 | 0.91 | 0.91 | 997 | 0.19 | 0.19 | 0.91 | 0.91 |
| 3200 | 2 | 775 | 0.19 | 0.20 | 0.90 | 0.90 | 1000 | 0.20 | 0.20 | 0.90 | 0.90 |
| 200 | 4 | 176 | 0.16 | 0.16 | 0.93 | 0.93 | 687 | 0.14 | 0.14 | 0.91 | 0.92 |
| 400 | 4 | 334 | 0.17 | 0.16 | 0.93 | 0.93 | 789 | 0.17 | 0.16 | 0.92 | 0.92 |
| 800 | 4 | 580 | 0.17 | 0.17 | 0.92 | 0.93 | 925 | 0.17 | 0.17 | 0.92 | 0.92 |
| 1600 | 4 | 741 | 0.19 | 0.19 | 0.91 | 0.91 | 996 | 0.19 | 0.19 | 0.91 | 0.91 |
| 3200 | 4 | 772 | 0.19 | 0.19 | 0.90 | 0.90 | 1000 | 0.19 | 0.20 | 0.90 | 0.90 |
| 200 | 6 | 130 | 0.15 | 0.15 | 0.93 | 0.94 | 624 | 0.13 | 0.14 | 0.92 | 0.92 |
| 400 | 6 | 300 | 0.17 | 0.16 | 0.93 | 0.93 | 733 | 0.16 | 0.15 | 0.93 | 0.93 |
| 800 | 6 | 542 | 0.18 | 0.18 | 0.92 | 0.93 | 886 | 0.17 | 0.17 | 0.92 | 0.92 |
| 1600 | 6 | 771 | 0.19 | 0.19 | 0.92 | 0.91 | 994 | 0.19 | 0.19 | 0.91 | 0.91 |
| 3200 | 6 | 796 | 0.19 | 0.19 | 0.90 | 0.90 | 1000 | 0.19 | 0.19 | 0.90 | 0.90 |
| 200 | 8 | 82 | 0.15 | 0.17 | 0.92 | 0.94 | 526 | 0.13 | 0.13 | 0.93 | 0.93 |
| 400 | 8 | 259 | 0.17 | 0.16 | 0.94 | 0.93 | 677 | 0.15 | 0.15 | 0.93 | 0.93 |
| 800 | 8 | 531 | 0.18 | 0.18 | 0.92 | 0.93 | 862 | 0.17 | 0.17 | 0.92 | 0.93 |
| 1600 | 8 | 748 | 0.19 | 0.19 | 0.92 | 0.92 | 992 | 0.19 | 0.19 | 0.91 | 0.91 |
| 3200 | 8 | 795 | 0.19 | 0.19 | 0.91 | 0.91 | 1000 | 0.19 | 0.19 | 0.90 | 0.90 |
| 200 | 32 | 15 | 0.15 | 0.17 | 0.95 | 0.95 | 202 | 0.10 | 0.10 | 0.95 | 0.95 |
| 400 | 32 | 112 | 0.15 | 0.15 | 0.95 | 0.95 | 374 | 0.12 | 0.12 | 0.95 | 0.94 |
| 800 | 32 | 406 | 0.16 | 0.17 | 0.95 | 0.95 | 693 | 0.16 | 0.16 | 0.94 | 0.94 |
| 1600 | 32 | 747 | 0.18 | 0.18 | 0.93 | 0.92 | 960 | 0.18 | 0.18 | 0.92 | 0.92 |
| 3200 | 32 | 820 | 0.19 | 0.19 | 0.91 | 0.91 | 999 | 0.19 | 0.19 | 0.91 | 0.91 |
| 200 | 128 | 3 | 0.23 | 0.17 | 0.94 | 1.00 | 36 | 0.09 | 0.07 | 0.96 | 0.97 |
| 400 | 128 | 24 | 0.15 | 0.13 | 0.96 | 0.95 | 103 | 0.11 | 0.11 | 0.95 | 0.96 |
| 800 | 128 | 218 | 0.17 | 0.17 | 0.97 | 0.97 | 346 | 0.15 | 0.15 | 0.96 | 0.96 |
| 1600 | 128 | 721 | 0.18 | 0.17 | 0.94 | 0.94 | 884 | 0.17 | 0.17 | 0.94 | 0.94 |
| 3200 | 128 | 890 | 0.19 | 0.19 | 0.91 | 0.91 | 998 | 0.19 | 0.19 | 0.91 | 0.91 |
Table 11.
The results of marginal detection and stratification in scenario 4 for PRIM.
| n | pn | nM1nM2 | lM1 lM2 | uM1uM2 | rsens rspecrprec | pv pv+ pv− |
|---|---|---|---|---|---|---|
| 200 | 0 | 943 941 | 0.19 0.18 | 0.89 0.89 | 0.83 (0.47) 0.77 (0.71) 0.81 (0.60) | 4.6E-006 1.4E-006 1.4E-001 |
| 400 | 0 | 962 967 | 0.19 0.19 | 0.90 0.90 | 0.88 (0.44) 0.82 (0.73) 0.85 (0.60) | 1.4E-010 6.7E-013 1.5E-001 |
| 800 | 0 | 985 984 | 0.19 0.19 | 0.91 0.90 | 0.93 (0.42) 0.87 (0.74) 0.89 (0.59) | 3.2E-019 9.7E-026 1.7E-001 |
| 1600 | 0 | 999 998 | 0.19 0.19 | 0.91 0.90 | 0.96 (0.43) 0.93 (0.74) 0.94 (0.60) | 5.4E-037 4.4E-053 1.7E-001 |
| 3200 | 0 | 1000 1000 | 0.20 0.20 | 0.90 0.90 | 0.97 (0.41) 0.96 (0.74) 0.96 (0.58) | 7.5E-072 1.3E-107 1.8E-001 |
| 200 | 2 | 880 863 | 0.16 0.17 | 0.91 0.90 | 0.76 (0.33) 0.71 (0.84) 0.74 (0.68) | 4.6E-006 6.4E-006 5.8E-002 |
| 400 | 2 | 920 927 | 0.17 0.17 | 0.92 0.91 | 0.85 (0.25) 0.75 (0.90) 0.79 (0.70) | 1.4E-010 5.5E-012 9.4E-002 |
| 800 | 2 | 970 971 | 0.18 0.18 | 0.91 0.91 | 0.92 (0.21) 0.83 (0.93) 0.86 (0.71) | 3.2E-019 1.1E-024 1.2E-001 |
| 1600 | 2 | 999 998 | 0.19 0.19 | 0.91 0.91 | 0.96 (0.19) 0.91 (0.93) 0.92 (0.70) | 5.4E-037 3.7E-052 1.6E-001 |
| 3200 | 2 | 1000 1000 | 0.20 0.20 | 0.90 0.90 | 0.97 (0.18) 0.96 (0.94) 0.96 (0.72) | 7.5E-072 2.0E-107 1.8E-001 |
| 200 | 4 | 829 813 | 0.15 0.15 | 0.91 0.92 | 0.72 (0.28) 0.67 (0.83) 0.70 (0.61) | 4.6E-006 1.5E-005 3.5E-002 |
| 400 | 4 | 890 894 | 0.17 0.16 | 0.92 0.92 | 0.84 (0.22) 0.71 (0.90) 0.76 (0.67) | 1.4E-010 1.7E-011 6.3E-002 |
| 800 | 4 | 967 958 | 0.17 0.17 | 0.92 0.92 | 0.91 (0.17) 0.80 (0.93) 0.83 (0.68) | 3.2E-019 4.5E-024 9.8E-002 |
| 1600 | 4 | 998 998 | 0.19 0.19 | 0.91 0.91 | 0.95 (0.14) 0.91 (0.95) 0.91 (0.71) | 5.4E-037 1.0E-051 1.4E-001 |
| 3200 | 4 | 1000 1000 | 0.19 0.20 | 0.90 0.90 | 0.97 (0.09) 0.95 (0.97) 0.95 (0.70) | 7.5E-072 3.1E-107 1.9E-001 |
| 200 | 6 | 785 779 | 0.14 0.14 | 0.92 0.92 | 0.70 (0.26) 0.65 (0.77) 0.68 (0.55) | 4.6E-006 2.4E-005 2.5E-002 |
| 400 | 6 | 845 873 | 0.16 0.15 | 0.93 0.93 | 0.83 (0.17) 0.68 (0.86) 0.74 (0.57) | 1.4E-010 3.4E-011 5.6E-002 |
| 800 | 6 | 937 947 | 0.17 0.17 | 0.92 0.92 | 0.90 (0.13) 0.77 (0.89) 0.82 (0.59) | 3.2E-019 1.2E-023 8.6E-002 |
| 1600 | 6 | 998 996 | 0.19 0.19 | 0.91 0.91 | 0.95 (0.11) 0.90 (0.91) 0.91 (0.60) | 5.4E-037 2.1E-051 1.4E-001 |
| 3200 | 6 | 1000 1000 | 0.19 0.19 | 0.90 0.90 | 0.98 (0.08) 0.95 (0.94) 0.95 (0.64) | 7.5E-072 3.3E-107 2.0E-001 |
| 200 | 8 | 712 728 | 0.14 0.13 | 0.93 0.93 | 0.69 (0.32) 0.62 (0.71) 0.65 (0.54) | 4.6E-006 3.3E-005 2.1E-002 |
| 400 | 8 | 818 836 | 0.16 0.15 | 0.93 0.93 | 0.82 (0.20) 0.65 (0.83) 0.72 (0.58) | 1.4E-010 6.5E-011 4.3E-002 |
| 800 | 8 | 930 930 | 0.17 0.17 | 0.92 0.93 | 0.90 (0.13) 0.76 (0.91) 0.81 (0.63) | 3.2E-019 1.9E-023 8.7E-002 |
| 1600 | 8 | 998 994 | 0.19 0.19 | 0.91 0.91 | 0.95 (0.08) 0.89 (0.95) 0.90 (0.66) | 5.4E-037 4.9E-051 1.3E-001 |
| 3200 | 8 | 1000 1000 | 0.19 0.19 | 0.90 0.90 | 0.97 (0.05) 0.95 (0.98) 0.95 (0.68) | 7.5E-072 4.8E-107 2.0E-001 |
| 200 | 32 | 452 415 | 0.11 0.11 | 0.95 0.95 | 0.62 (0.29) 0.53 (0.71) 0.57 (0.49) | 4.6E-006 1.6E-004 6.4E-003 |
| 400 | 32 | 584 632 | 0.12 0.12 | 0.95 0.95 | 0.79 (0.21) 0.49 (0.79) 0.62 (0.49) | 1.4E-010 9.3E-010 1.6E-002 |
| 800 | 32 | 833 844 | 0.16 0.15 | 0.94 0.94 | 0.91 (0.14) 0.62 (0.86) 0.72 (0.49) | 3.2E-019 3.9E-022 1.1E-001 |
| 1600 | 32 | 982 978 | 0.18 0.18 | 0.92 0.92 | 0.95 (0.10) 0.83 (0.90) 0.86 (0.49) | 5.4E-037 2.1E-049 1.4E-001 |
| 3200 | 32 | 1000 999 | 0.19 0.19 | 0.91 0.91 | 0.97 (0.07) 0.94 (0.93) 0.94 (0.49) | 7.5E-072 3.7E-106 1.9E-001 |
| 200 | 128 | 181 182 | 0.10 0.09 | 0.96 0.96 | 0.58 (0.36) 0.47 (0.64) 0.51 (0.49) | 4.6E-006 3.8E-004 3.0E-003 |
| 400 | 128 | 336 336 | 0.11 0.11 | 0.96 0.96 | 0.75 (0.33) 0.39 (0.67) 0.55 (0.49) | 1.4E-010 6.8E-009 4.4E-003 |
| 800 | 128 | 595 603 | 0.14 0.14 | 0.96 0.96 | 0.90 (0.33) 0.44 (0.67) 0.62 (0.49) | 3.2E-019 4.2E-020 5.7E-002 |
| 1600 | 128 | 932 949 | 0.17 0.17 | 0.94 0.94 | 0.95 (0.33) 0.73 (0.67) 0.79 (0.49) | 5.4E-037 3.7E-047 1.7E-001 |
| 3200 | 128 | 1000 998 | 0.19 0.19 | 0.91 0.91 | 0.98 (0.32) 0.92 (0.68) 0.92 (0.49) | 7.5E-072 6.9E-105 2.4E-001 |
Figure 5 shows the running time of the method, the averages for 1000 data sets in each parameter setting of scenario 4. We conducted the simulations with R version 3.0.2 in computing servers that have dual Intel E5-2650L processors and at least 64 GB memory. Our program can finish within a few minutes given pn=8 and n = 3200 and return results in a couple of hours when pn increases to 128. As suggested by the algorithmic complexity O(p logn) (see discussion at the end of Section 3.1), the running time approximately shows logarithmic growth as sample size increases and linear growth given the increasing number of variables.
Figure 5.
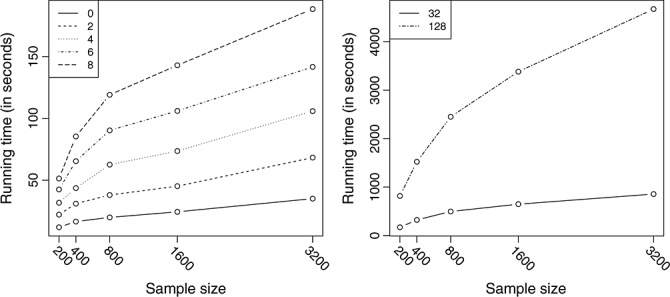
Running time of PRIM for scenario 4 (given different noise variables).
We summarize PRIM's performance in the simulation study as follows. PRIM can perform well in exact detection with hundreds of samples given no presence of noise variables, but this becomes less impressive as the number of true signature variables increases. However, given a few thousand samples that might be available in large phase III or even phase II trials, PRIM is capable of detecting at least some of true signature variables and thus stratifying a good number of patients into right groups in the presence of a moderate number of noise variables (up to 32 noise variables in our simulation study). Coupling with the proposed resampling scheme, PRIM can achieve satisfactory results with a substantially less number of samples. In scenarios having a relatively large but still realistic effect size, PRIM asks for no more than 1000 samples to accurately detect cutoffs and a few hundred samples to reasonably stratify patients given a small number of noise variables; moreover, it needs less than 2000 samples to perform well given 100 noise variables or so. Overall, the simulation study provides a general idea on conditions that enable PRIM to propose a relevant stratification of patients for therapy, such as manageable number of input variables and required sample sizes given different effect sizes.
5. Two case studies of real-world data sets
5.1. The data
We apply PRIM, Re-PRIM, and AIM to two real-world data sets collected by Loi et al. 14 and Lenz et al. 15, respectively. As part of the first study, gene expression was measured on an Affymetrix whole genome microarray platform for 414 patients with estrogen receptor (ER)-positive breast carcinomas. Among them, 137 patients received no systemic adjuvant treatment, and 277 patients received adjuvant tamoxifen only. To phrase the case in our terms, we refer to the untreated population as the control arm and the tamoxifen-treated population as the treatment arm even though the cohorts involved are not part of a single randomized trial. Relapse-free survival with right censoring was used as the clinical endpoint. We excluded 21 patients from analysis because their event indicators were missing. All the data are available at the Gene Expression Omnibus or GEO database with ID GSE6532. The other retrospective study 15 profiled gene expression (by Affymetrix chips) of 414 patients with diffuse large-B-cell lymphoma—181 patients received a combination chemotherapy with cyclophosphamide, doxorubicin, vincristine, and prednisone (CHOP), and 233 patients received rituximab in addition to CHOP (R-CHOP). To standardize terms, we refer to the group treated with CHOP as the control arm and the group treated with R-CHOP as the treatment arm. Clinical responses are given by overall survival with right censoring. These data can also be downloaded from the GEO database with ID GSE10846.
5.2. Procedure setup
We first present results of PRIM and Re-PRIM by only employing a single set of (conjunctive) rules and then discuss the utility of covering (multiple rule sets). The number of selected variables for Re-PRIM, k, is set at two given limited sample sizes in these two data sets. We applied the AIM implementation in the published R package AIM: To allow AIM to have an option analogous to pasting in PRIM, we specified AIM's parameter backfit = TRUE; to permit two splits for each variable as in PRIM, the parameter maxnumcut was set at two; we assigned 0.05 to mincut to make AIM's minimum cutting proportion comparable with the minimum value of α in PRIM; other parameters kept their default values. The aforementioned parameter settings make the AIM procedure more flexible than its default version and thus lead to a fair comparison with PRIM. To stratify patients by AIM, we followed the approach suggested by its inventors (see details in Section 2): Given index scores computed by AIM, patients are stratified into a low-score group and a high-score group depending on whether a patient's score is greater than the median score or not. These two groups can be defined to be signature-positive and signature-negative groups according to coefficient sign of the treatment-score interaction term in AIM's regression model.
5.3. Candidate gene selection
As mentioned before, it is a typical scenario that a few biomarker candidates are pre-determined based on prior knowledge for predictive-signature development. To mimic this scenario, we randomly drew a subset of observations from a data set and selected eight candidate genes by genome-wide analysis of association between gene expression and clinical responses in the subset. This subset of data would not be utilized any more after the selection of the candidates. Predictive signatures were developed with the selected candidates in remaining data. We refer to the remaining data as the ER data set and the CHOP data set for the two cases, respectively. The following selection procedure was employed to choose eight candidate genes based on the data of 196 patients randomly sampled from the first study 14: (i) a Cox proportional hazards model was fitted with expression profiles of a gene as a single predictor for the patients in the treatment arm and in the control arm separately; (ii) a gene was included for further consideration if its hazard ratio ≤ 0.5 or 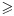 2 for the treatment arm, but for the control arm, its hazard ratio is in between 0.5 and 2 and the p-value for the regression coefficient
2 for the treatment arm, but for the control arm, its hazard ratio is in between 0.5 and 2 and the p-value for the regression coefficient 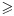 0.5 with a two-sided test; (iii) the genes retained were then ranked according to their p-values in the treatment arm, and top eight genes were selected. The conditions in the second step intend to select genes whose expression profiles are substantially associated with the patients' survival in the treatment arm but not associated with the response in the control arm. These genes have the potential to be interacted with treatments and thus meet the interaction-effect condition. For the other study, eight candidate genes were similarly chosen based on the data of 207 patients randomly drew. They served as basis of predictive-signature development in the remaining data.
0.5 with a two-sided test; (iii) the genes retained were then ranked according to their p-values in the treatment arm, and top eight genes were selected. The conditions in the second step intend to select genes whose expression profiles are substantially associated with the patients' survival in the treatment arm but not associated with the response in the control arm. These genes have the potential to be interacted with treatments and thus meet the interaction-effect condition. For the other study, eight candidate genes were similarly chosen based on the data of 207 patients randomly drew. They served as basis of predictive-signature development in the remaining data.
5.4. Performance measures
Figure 1 shows that two arms have no differentiation in responses in the ER data set (logrank p-value = 0.54). Based on a predictive signature learned by PRIM, patients were stratified into signature-positive and signature-negative groups. The signature-positive patients tend to respond better to the investigational treatment than the SOC, while the signature-negative patients reverse the pattern (Figure 2). It is of note that p-values from two-sample tests on these signature-positive or signature-negative patients are not valid measures to quantify predictive performance of PRIM because the data had already been explored for signature-learning—the separation between the curves simply illustrates training results. We adopt p-values based on 5-fold CV to quantify a method's predictive performance. In the CV process, a data set is randomly splitting into five subsets. In each fold, a method learns a signature from four subsets, and then based on the signature, patients in the remaining subset are labelled to be either signature-positive or signature-negative. Specifically, PRIM splits the four subsets into D1 and D2 to learn a signature from them, and similarly, the data in the four subsets serve as the input of Re-PRIM for signature-learning; after a signature is obtained, it is used to stratify patients in the remaining subset. To stratify all patients in the five subsets, the learning is repeated five times.
After all patients are stratified into signature-positive or signature-negative groups, a p-value is calculated for each group based on a one-sided two-sample test that examines whether an investigational treatment is better than an SOC. We refer to such p-values as CV p-values. CV p-values are similar to p-values presented in a pre-validation scheme by Tibshirani and Efron 16, which attempted to quantify significance of learned predictors and facilitate a fair comparison between a learned predictor and pre-defined covariates. Because of variability in random splittings, 5-fold CV is repeated for 100 random splits. In addition to p-values, we calculated hazard ratios for signature-positive or signature-negative groups in the CV process because they are helpful references for comparing an investigational treatment with an SOC. We refer to such hazard ratios as CV hazard ratios.
As presented earlier, the data explored for candidate genes selection were not used later. Therefore, the aforementioned CV was only applied to data that were never used for pre-selection of candidate genes—if it were applied to data including the samples from which candidate genes were selected, CV p-values would be a biased measure of predictive performance of a method. In addition, for CV p-values to be a proper measure of predictive performance of Re-PRIM, all steps in Re-PRIM including the resampling procedure for selecting candidate signature variables and PRIM for learning a final signature should only be applied to training data (four subsets of data in the case of a 5-fold CV) rather than all data in every fold of CV.
P-values and hazard ratios calculated in aforementioned CV process help reduce overoptimistic estimation because of using the same data twice (for both training and testing) and thus provide realistic estimation of predictive performance of a method. However, because these CV quantities are essentially based on retrospective analysis, they cannot replace the role of p-values or hazard ratios calculated based on randomized controlled trials (RCTs). To obtain a valid p-value or hazard ratio to confirm efficacy in a population with signature-positive status, investigators should conduct an RCT for that population. To validate the predictive value of a signature, an RCT is also needed to examine the lack of efficacy in a population with signature-negative status.
5.5. The results
Figure 6 shows the distributions of 100 CV p-values for signature-positive groups and 100 CV p-values for signature-negative groups from PRIM's results in the ER data set. Compared with the original p-value 0.54, the CV p-values for pv+ substantially shift to smaller values (with 93% of the CV p-values less than 0.54). This indicates that the stratification can potentially improve efficacy. In addition, the majority of CV p-values for pv+ are less than 0.2 while the majority of CV p-values for pv− are greater than 0.8. This demonstrates that the procedure is able to enrich the responders to the investigational treatment in signature-positive groups while it includes most of responders to the SOC in signature-negative groups. Because of skewness of the distributions, which is typical according to our empirical observations, we recommend to report median of CV p-values to represent their center and median absolute deviation to indicate variation. Similarly, we also report median and median absolute deviation of CV hazard ratios. Denote by pmcv+ the median of the CV p-values for signature-positive groups and pmcv− for signature-negative groups. Let HRmcv+ be the median of the CV hazard ratios for signature-positive groups and HRmcv− be the one for signature-negative groups. They are listed in Table 12 for reference.
Figure 6.
The distributions of CV p-values for PRIM in the ER data set: The left histogram is for pv+ and the right one for pv−.
Table 12.
Summary of the cross-validation results in the ER data set and the CHOP data set.
| ER | CHOP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| nm+ | pvmcv+ | pvmcv− | HRmcv+ | HRmcv− | nm+ | pvmcv+ | pvmcv− | HRmcv+ | HRmcv− | |
| PRIM | 80 (11) | 0.10 (0.09) | 0.86 (0.10) | 0.59 (0.14) | 1.50 (0.26) | 82 (13) | 0.012 (0.017) | 0.10 (0.09) | 0.44 (0.12) | 0.66 (0.13) |
| Re-PRIM | 86 (13) | 0.30 (0.19) | 0.71 (0.15) | 0.81 (0.20) | 1.22 (0.21) | 87 (15) | 0.009 (0.013) | 0.14 (0.15) | 0.44 (0.10) | 0.70 (0.13) |
| AIM | 148 (9) | 0.23 (0.09) | 0.93 (0.06) | 0.77 (0.08) | 2.35 (0.73) | 136 (15) | 0.043 (0.039) | 0.21 (0.15) | 0.60 (0.09) | 0.71 (0.17) |
| PRIM (M) | 102 (14) | 0.12 (0.10) | 0.88 (0.09) | 0.67 (0.14) | 1.63 (0.41) | 108 (16) | 0.010 (0.013) | 0.17 (0.14) | 0.49 (0.11) | 0.71 (0.17) |
| Re-PRIM (M) | 109 (11) | 0.28 (0.16) | 0.79 (0.16) | 0.82 (0.13) | 1.38 (0.34) | 102 (13) | 0.003 (0.004) | 0.26 (0.17) | 0.42 (0.09) | 0.80 (0.16) |
Note: Median absolute deviations are shown in braces. The letter M in braces indicates the approach of discovering disjunction of multiple conjunctive rule sets via covering.
Figure 7 illustrates the performance of Re-PRIM: It is not as good as PRIM, with more large CV p-values for signature-positive groups and more small CV p-values for signature-negative groups. Re-PRIM's pmcv+ is also substantially larger than PRIM's pmcv+ while its pmcv− is smaller—neither makes the method more favorable in this case.
Figure 7.
The distributions of CV p-values for Re-PRIM in the ER data set: The left histogram is for pv+ and the right one for pv−.
Figure 8 shows the results from AIM. The distributions share similar skewness with those in Figure 6. Compared with the distribution of CV p-values for signature-positive groups resulted from PRIM in Figure 6, the distribution from AIM significantly shifts to larger values (p-value = 7.05 × 10−6 by Wilcoxon rank sum test). This indicates that the treatment effect is much less obvious in AIM's signature-positive groups than in PRIM's signature-positive groups. Consistently, we also observed that AIM resulted in larger pmcv+ and HRmcv+ than PRIM (Table 12). Therefore, PRIM is more desirable in maximizing efficacy for signature-positive patients. On the other hand, with respect to CV p-values for signature-negative groups, AIM produces significantly larger values than those obtained by PRIM (p-value = 3.34 × 10−7). This suggests that although the signature-negative patients defined by both AIM and PRIM tend to respond better to the SOC than the investigational treatment, yet this response difference is considerably larger in AIM's stratification than in PRIM's. Along the same line of such observations, HRmcv− is substantially higher from AIM than from PRIM (Table 12). These reflect the discussion in Section 2 that AIM only focuses on the treatment-score interaction without considering which signature group leads to that interaction. We also report, nm+, the median of sample sizes of signature-positive groups in Table 12. AIM often generates a larger signature-positive group (nm+ = 148) in contrast to PRIM (nm+ = 80). This is useful when larger prevalence is required by real-world applications.
Figure 8.
The distributions of CV p-values for AIM in the ER data set: The left histogram is for pv+ and the right one for pv−. Note that because the method only returned valid results from 47 out of the 100 random splits but exited for other splits due to internal errors in the package AIM, illustrations and discussion were only based on the valid results.
In the CHOP data set, Re-PRIM is able to reduce the number of signature variables from six in PRIM's rules to two with similar performance, as indicated by pmcv+, pmcv−, HRmcv+, and HRmcv− (Table 12). Suggesting a stratification that can enhance efficacy, 73% of Re-PRIM's CV p-values for pv+ are less than 0.025, the p-value indicating the significance of the original treatment effect. The CV p-values for pv+ are also significantly smaller than those from AIM (p-value = 7.99 × 10−11), demonstrating better enrichment of responders to the treatment in signature-positive groups than that in AIM's results. Similar to the situation in the ER data, AIM generated larger CV p-values for pv− than those in Re-PRIM and PRIM, and it produced considerably larger signature-positive groups in this case (see nm+ in Table 12). Note that we only discussed valid results returned by AIM from 85 out of the 100 random splits because the procedure in the AIM package exited with errors for the other random splits of the data set in CV.
Employing the covering strategy, PRIM included more patients in signature-positive groups for the two data sets while maintaining similar treatment effects to those obtained by a single set of rules (see PRIM (M) in Table 12). In contrast to Re-PRIM using a single set of rules, Re-PRIM with multiple sets of rules achieved similar results (except higher prevalence) in the ER data set (see Re-PRIM and Re-PRIM (M) in Table 12), but in the CHOP data set, the method attained significantly better results as indicated by higher prevalence (p-value = 3.24 × 10−11) and smaller CV p-values for signature-positive groups (p-value = 2.48 × 10−4), along with larger CV p-values (p-value = 4.43 × 10−6) and hazard ratios (p-value = 1.97 × 10−4) for signature-negative groups. Although the increased prevalence by Re-PRIM (M) is still lower than the one from AIM, its enlarged CV p-values for signature-negative groups are significantly greater than those obtained by AIM (p-value = 2.48 × 10−2), along with significantly larger CV hazard ratios (p-value = 4.45 × 10−3). Overall, we observed some case-dependent advantages to employ multiple rule sets generated by the covering strategy.
As mentioned in Section 2, the interaction-effect constraint is not redundant partially because, without enforcing the constraint, the search procedure can initially be misled by a local decision that was based on a minimal pv+ with pv+>pv− and ends up with a less optimal solution. In search for a signature in the CHOP data set, such situation indeed occurred (with α = 0.2): While the original signature or rule set (selected according to PG, the stratification significance in D2 in line 19 of Algorithm 1) has pv+=0.016 and pv−=0.62, pv+ increases to 0.036 with pv− decreasing to 0.52 for the signature obtained by the search procedure without enforcing the interaction-effect constraint. This is because, without the enforcement, the procedure chose a signature-positive group that violated the constraint at the first search step. Therefore, it is necessary to ensure the constraint satisfied in the search process.
6. Discussion
In the simulation study, we presented a unimodal situation where signature-positive patients are centralized in one location of the population space. A much more challenging situation would be multimodal, with signature-positive patients located in more than one location. Besides the factors we considered to affect the performance of PRIM, number of modes and their relative positions and magnitudes may also impact final results. Although a single set of conjunctive rules are more feasible to implement and thus may be preferred by users in clinics, it is clear that such rules are not expressive enough to describe a multimodal situation well. It is interesting for a future study to examine whether the covering strategy with multiple rule sets can capture multiple modes accurately.
Another type of p-values examines whether signature-positive patients in a treatment arm respond better than signature-negative patients in a control arm. Such a p-value is relevant because in an ideal situation, a patient should receive a treatment based on positiveness of a predictive-signature-based diagnostic test—he or she should be treated by an investigational treatment only if his or her signature test is positive, and he or she may need to receive an SOC given a negative test result. Denote a p-value of this type by pve. Given a predictive signature, we cannot always expect pve to be small and its corresponding test to be significant. It is true that pve will be small if signature-negative patients treated by the SOC share the same survival profiles as signature-positive patients receiving the SOC; however, pve can be large if the former tends to live longer than the latter (for example, the case illustrated in Figure 2), that is, signature-positiveness actually indicates poor-prognosis. In our simulation study, signature-positive patients have the same survival profiles as signature-negative patients in the control arm, indicating that pve should be similar to pv+ and thus should be less than pv.
Many tree-based methods have been developed to identify subgroups that have maximal differential treatment effects by recursively partitioning population. Several examples are Negassa et al. 17, Su et al. 18, and Lipkovich et al. 13. They essentially aimed at maximizing significance of the interaction-effect condition (either through test statistics or p-values), which does not always lead to a predictive signature as discussed in Section 2. Besides this category of objective functions, in the subgroup identification based on differential effect search (SIDES) method, Lipkovich et al. 13 proposed a different one as the optimization criterion for splits inside a tree—significance of the treatment-effect condition in any one of two child nodes generated by a split. This is similar to our objective function. However, this objective function ignores the interaction-effect condition. Although they suggested a hybrid approach that attempts to incorporate this condition into an objective function by maximizing either the aforementioned significance or significance of the interaction-effect condition, the goal of this approach is a mixture and is less clear than the one of our constrained-optimization approach. Unlike the interaction-trees approach 18, which is concerned with treatment effect on the entire covariate space, SIDES focuses on treatment effect in specific areas of interest (and ignores complete estimation in the rest of the space)—such focal search is in essence similar to PRIM's bump hunting. To restrict search space, SIDES only allows a variable to define a subgroup in one direction with its cutoff (by either greater than or no less than the cutoff). PRIM permits both directions and thus is more expressive. Working with binary responses, Foster et al. 19 proposed a method called ‘Virtual Twins’ (VT) to identify a subgroup that has an improved treatment effect. Under the same two-arm design as in our study, VT first estimates a responding probability of an individual given the treatment he or she received and a responding probability of the same individual in a hypothetical scenario where he or she were treated by the other treatment that he or she did not actually receive. Such estimation is performed for all patients through a random-forest model with treatment factor and other covariates as input. Given the estimation, the difference between two probabilities of an individual can be calculated as a new response indicating an estimated treatment effect for the individual. Finally, a CART model is built with covariates to predict these new responses and thus specifies decision rules for identifying a subgroup with an enhanced treatment effect. The idea of the VT approach is very interesting, but it faces a great challenge that the random-forest model needs to accurately estimate responding probabilities given a real treatment or a counterfactual one.
Drug development is paying more and more attention to predictive signatures that stratify patients into groups, with the hope that signature-positive patients respond better to investigational treatments than SOC regimens. PRIM is a natural approach to this problem because its bump-hunting formulation fits exactly into the scenario of patient stratification—bumps are corresponding to signature-positive patients, and associated rules define a signature. It is also attractive because of its returning simple rules and its patient-search property: The former makes rules discovered by PRIM easily and directly applicable to patients by clinicians or other medical practitioners; the latter induces better decision rules than aggressive approaches. In this study, we proposed a search procedure based on PRIM's framework for predictive-signature development and suggested a parameter-selection step and a resampling scheme to improve the search. We investigated the procedure's performance by simulating typical situations where the procedure is expected to be applied and provided guidance on conditions under which the procedure can find relevant rules and reasonably stratify patients into different signature groups. By searching for signatures in two real-world data sets, we demonstrated that PRIM has a good potential for patient stratification in practice. In addition, we discussed the advantage of the objective function we adopted for PRIM by contrasting it to AIM's objective function, compared results of these two methods in the real-world data, and illustrated their respective superiorities in these scenarios. In summary, this paper provides a general and practical recipe for applying PRIM to predictive-signature development in oncology studies with survival responses.
Acknowledgments
We thank Robert J. Tibshirani for his helpful discussion on CV performance measures. We thank the editor, the associated editor, and two referees for their helpful comments and suggestions. This research was partially funded by National Institutes of Health grant 1R21 GM110450-01 (H.Z.).
References
- Friedman JH, Fisher NI. Bump hunting in high-dimentional data. Statistics and Computing. 1999;9:123–143. [Google Scholar]
- LeBlanc M, Jacobson J, Crowley J. Partitioning and peeling for constructing prognostic groups. Statistical Methods in Medical Research. 2002;11:247–274. doi: 10.1191/0962280202sm286ra. [DOI] [PubMed] [Google Scholar]
- LeBlanc M, Moon J, Crowley J. Adaptive risk group refinement. Biometrics. 2005;61:370–378. doi: 10.1111/j.1541-0420.2005.020738.x. [DOI] [PubMed] [Google Scholar]
- Liu X, Minin V, Huang Y, Seligson DB, Horvath S. Statistical methods for analyzing tissue microarray data. Journal of Biopharmaceutical Statistics. 2004;14(3):671–685. doi: 10.1081/BIP-200025657. [DOI] [PubMed] [Google Scholar]
- Dyson G, Frikke-Schmidt R, Nordestgaard BG, Tybjærg-Hansen A, Sing CF. An application of the patient rule-induction method for evaluating the contribution of the Apolipoprotein E and Lipoprotein Lipase genes to predicting ischemic heart disease. Genetic Epidemiology. 2007;31:515–527. doi: 10.1002/gepi.20225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nannings B, Abu-Hanna A, de Jonge E. Applying PRIM (patient rule induction method) and logistic regression for selecting high-risk subgroups in very elderly ICU patients. International Journal of Medical Informatics. 2008;77:272–279. doi: 10.1016/j.ijmedinf.2007.06.007. [DOI] [PubMed] [Google Scholar]
- Polonik W, Wang Z. PRIM analysis. Journal of Multivariate Analysis. 2010;101:525–540. [Google Scholar]
- Kehl V, Ulm K. Responder identification in clinical trials with censored data. Computational Satistics and Data Analysis. 2006;50:1338–1355. [Google Scholar]
- Tian L, Tibshirani R. Adaptive index models for marker-based risk stratification. Biostatistics. 2011;12(1):68–86. doi: 10.1093/biostatistics/kxq047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin X, Parks D, Cheng J, Lee K. Eastern North American Region (ENAR) Spring Meeting. Miami, Florida: 2011. Searching for clinically interesting subgroups using patient rule induction method; p. 24c. [Google Scholar]
- Mitchell TM. Machine Learning. New York: McGraw-Hill; 1997. [Google Scholar]
- Hastie T, Tibshirani RJ, Friedman J. The Elements of Statistical Learning: Data Mining, Inference and Prediction. New York: Springer; 2008. Second. [Google Scholar]
- Lipkovich I, Dmitrienko A, Denne J, Enas G. Subgroup identification based on differential effect search—a recursive partitioning method for establishing response to treatment in patient subpopulations. Statistics in Medicine. 2011;30:2601–2621. doi: 10.1002/sim.4289. [DOI] [PubMed] [Google Scholar]
- Loi S, Haibe-Kains B, Desmedt C, Lallemand F, Tutt AM, Gillet C, Ellis P, Harris A, Bergh J, Foekens JA. et al Definition of clinically distinct molecular subtypes in estrogen receptor-positive breast carcinomas through genomic grade. Journal of Clinical Oncology. 2007;25(10):1239–1246. doi: 10.1200/JCO.2006.07.1522. [DOI] [PubMed] [Google Scholar]
- Lenz G, Wright G, Dave SS, Xiao W, Powell J, Zhao H, Xu W, Tan B, Goldschmidt N, Iqbal J. et al Stromal gene signatures in large-B-cell lymphomas. The New England Journal of Medicine. 2008;359(1):2313–2323. doi: 10.1056/NEJMoa0802885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani RJ, Efron B. Pre-validation and inference in microarrays. Statistical Applications in Genetics and Molecular Biology. 2002;1(1):1–18. doi: 10.2202/1544-6115.1000. [DOI] [PubMed] [Google Scholar]
- Negassa A, Ciampi A, Abrahamowicz M, Shapiro S, Boivin J. Tree-structured subgroup analysis for censored survival data: validation of computationally inexpensive model selection criteria. Statistics and Computing. 2005;15:231–239. [Google Scholar]
- Su X, Tsai C, Wang H, Nickerson DM, Li B. Subgroup analysis via recursive partitioning. Journal of Machine Learning Research. 2009;10:141–158. [Google Scholar]
- Foster JC, Taylor JMG, Ruberg SJ. Subgroup identification from randomized clinical trial data. Statistics in Medicine. 2011;30:2867–2880. doi: 10.1002/sim.4322. [DOI] [PMC free article] [PubMed] [Google Scholar]


