Temperature dependence of predation depends on the relative performance of predators and prey

Abstract

The temperature dependence of predation rates is a key issue for understanding and predicting the responses of ecosystems to climate change. Using a simple mechanistic model, we demonstrate that differences in the relative performances of predator and prey can cause strong threshold effects in the temperature dependence of attack rates. Empirical data on the attack rate of northern pike (Esox lucius) feeding on brown trout (Salmo trutta) confirm this result. Attack rates fell sharply below a threshold temperature of +11°C, which corresponded to a shift in relative performance of pike and brown trout with respect to maximum attack and escape swimming speeds. The average attack speed of pike was an order of magnitude lower than the escape speed of brown trout at 5°C, but approximately equal at temperatures above 11°C. Thresholds in the temperature dependence of ecological rates can create tipping points in the responses of ecosystems to increasing temperatures. Thus, identifying thresholds is crucial when predicting future effects of climate warming.

1. Introduction

In light of the predicted climate warming, it is of paramount importance that we understand how increasing temperatures will affect ecosystems. While the direct effects of temperature on the performance of organisms are reasonably well known [1,2], predicting changes in the strength and direction of species interactions remains a challenging task. Over the last decade, the metabolic theory of ecology (MTE) has emerged as a general framework for studying the role of temperature in ecological systems [3]. Proponents of the MTE have suggested that the well-known Arrhenius equation, which was originally derived to describe chemical reaction rates, can serve as a mechanistic model for the temperature dependence of basal metabolism [4]. As the metabolism of all aerobic organisms share the same biochemistry, the theory states that this temperature dependence applies to the metabolism of all ectothermic animals as well as to a range of other biological rates that are linked to metabolism, including growth, development and maximal consumption rate [3–5]. While use of the Arrhenius equation as a mechanistic representation for the temperature dependence of physiological rates has been criticized [6–9], it has nevertheless become the standard method for modelling the temperature dependence of predation and consumption rates in population and community ecology [10–16]. It is therefore important to evaluate under which conditions this model is a useful representation of the temperature dependence of predator–prey interactions.

Predation differs from many other biological processes in that it depends on the relative performances of two actors—the predator and the prey. How consumption rate changes with temperature will consequently depend on how the relative performances of predators and prey change with temperature [17]. Physiological rates generally have unimodal temperature response curves, but there is considerable variation in both the optimal temperature and the slopes of the increasing and decreasing limbs of the curve [1,18–20]. Such variation is found between different species, different life stages and between different processes [1,9,18,21]. For example, Dell et al. [18] reported that organisms have a steeper thermal response for voluntary movements, such as searching for food, than when escaping predators. Thus, it can be hypothesized that the performance curves of predators and prey often intersect, and consequently that the attack success of predators may shift from being high at temperatures where they outperform their prey, to very low at temperatures where prey perform better than their predators. Identifying such thresholds in the strength of predator–prey interactions is critical for our ability to accurately predict the effects of climate warming on communities and ecosystems.

Dell et al. [17] outlined a framework for studying how the temperature dependence of the different components of the predation process combines to shape the temperature response of consumption. Here, we build on this work and derive a simple model to demonstrate that intersecting performance curves can lead to threshold effects, where attack rates drop dramatically at some threshold temperature. Moreover, we present corroborating data showing that the attack rate of northern pike (Esox lucius) feeding on brown trout (Salmo trutta) falls dramatically at temperatures below 11°C. We conclude that the temperature dependence for consumption rate may deviate considerably from the Arrhenius model when prey have temperature-dependent escape or defence capabilities.

(a). A model of the temperature dependence of attack rate

Here, we derive a conceptual model that describes how the relative performances of predator and prey influence the temperature dependence of attack rates. We define attack rate (A, unit: volume/time) as the product of contact rate (C, unit: volume/time) and attack success (S, dimensionless). The relationship between contact rate and movement speeds of predators and prey is often well described by the model 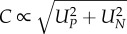, where U_P and U_N are the cruising speeds of predators and prey, respectively, e.g. when they search for food or some other resource [17,22–24]. If prey have significant escape or defence capabilities, the outcome of an encounter will depend on the relative performances of predators and prey. As a heuristic example, we assume that a predator–prey encounter leads to a running or swimming contest. The predator chases the fleeing prey and the difference between predator attack speed (V_P) and prey escape speed (V_N) controls the outcome. Specifically, we assume that the predator is successful (S = 1) if V_P > V_N and unsuccessful (S = 0) if V_P < V_N. As attack rate is the product of contact rate and attack success (A = CS) we obtain

1.1

and

1.2

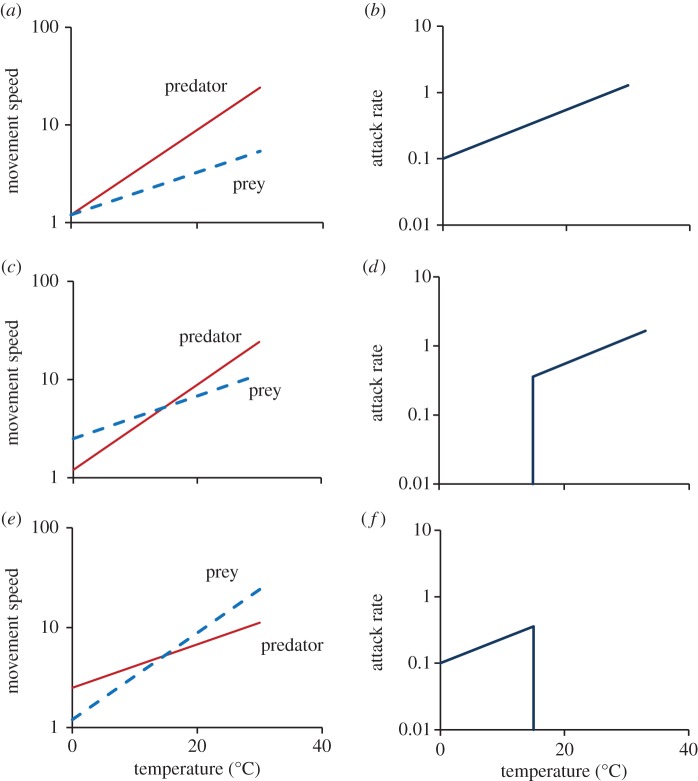
Both cruising speeds (U_P and U_N) and maximum movement speeds (V_P and V_N) can have hump-shaped temperature responses when plotted over large temperature ranges [25,26]. When this is the case the performance curves of predators and prey can intersect at several temperatures (see the electronic supplementary material, appendix S1). However, for the sake of simplicity, we assume that they increase exponentially with increasing temperature. Three interesting possibilities can be identified: (i) if predators outperform prey at all temperatures (S = 1), the attack rate is given by equation (1.2). The slope of the resulting temperature response for attack rate is then intermediate between the slopes for predator and prey cruising speeds (figure 1a,b); (ii) if predator attack speed has a stronger temperature response than prey escape speed and the two curves intersect (figure 1c), there will be no successful attacks at low temperatures (figure 1d); and (iii) if the two response curves intersect and prey escape speed has the strongest temperature response (figure 1e), the attack rate falls to zero at high temperatures (figure 1f).

Figure 1.

Temperature scaling of attack rate as it relates to the movement speeds of predators relative to prey. If predator attack speed is higher than prey escape speed, the temperature response of attack rate is controlled by the temperature response of the cruising speeds of predators and prey (a,b), (equation (1.2)). If predator attack speed has a steeper temperature response than prey escape speed and the two responses intersect, then the predicted attack rate falls to zero at temperatures below the intersection point (c,d). If prey escape speed has a steeper temperature response than predator attack speed, then the attack rate falls to zero at temperatures higher than the intersection point (e,f). (Online version in colour.)

Attack success is a binomial variable and generates a step function for the temperature dependence of attack rate. However, scaling up to the population level will yield a sigmoid function owing to individual variation in predator and prey performance. Traits other than movement speed can be crucial for the outcome of an encounter (acceleration, stamina, use of defence weaponry, perceptual capacity, etc.). However, the same principle should apply—the outcome is controlled by the difference between the predator's attack capacity and the prey's defence or escape capability.

2. Material and methods

(a). Attack rate for pike feeding on brown trout

Attack rates of northern pike feeding on brown trout were measured in circular outdoor pools (area 22.6 m², water depth 0.97 m). To provide cover for the fishes, an artificial macrophyte structure made from buoyant thin green polyester straps was placed in the centre of each pool (height ≈ 80 cm, diameter ≈ 90 cm). The water was heated in an external electrical heater and the temperature range studied was 3.5–22°C. The experiments were carried out between 23 July and 2 December. To reduce potential effects of seasonal variation in light intensity, the experiments were started 1 h after sunrise. The exact temperature during each experiment was measured with a temperature logger. As the water could be heated but not cooled, it was not possible to keep temperature and date orthogonal over the whole period. However, late in the season, when air temperatures typically ranged from 0 to 5°C, it was possible to keep them approximately orthogonal (time period: 15 October–2 December, temperature range 3.6–15.0°C).

We used 19 pike from two size classes (49–56 cm, n = 9 and 64–71 cm, n = 10) that were caught in Lake Ansjön in central Sweden (62.97° N, 16.09° E). The fish were kept in captivity for a minimum of three months before the experiment started, allowing them time to adjust to living in tanks and feeding under observation. During this time, they had a natural light regime and were given brown trout as food. Each experiment involved a single pike as a predator, and before the start of each experiment, the pike was starved for 10 days and allowed to acclimate to the experimental pool for 3 days. Temperatures in the holding tanks were kept within 5° of the temperature in the experimental pool. Each fish was tested at five to seven temperatures covering the whole temperature range. However, as a consequence of injuries during handling and accidental mortality, there were four individuals that were only tested at one to three temperatures.

One brown trout (14.9–15.1 cm) was used as prey in each experiment. These fish were offspring (F₃) of fish caught in the nearby River Oxsjöån (62.78° N, 16.76° E) and were reared in a hatchery that used water from Lake Ansjön. Twelve hours before the start of the experiment, the trout were placed in a net cage (height 0.8 m, diameter 0.8 m) within the pool. Experiments were started by lifting the net cage and the ensuing interaction was recorded with a video camera positioned on a 6 m high wooden frame. Experiments were terminated after 72 h if the brown trout was not caught. From the video footage, we measured the time (t) from when the cage was lifted until the brown trout was caught. The attack rate a (m³ h⁻¹) was estimated with the equation

2.1

where t is the time to capture and P is predator density.

Gut evacuation rate decreases with decreasing temperature. Thus, it can be hypothesized that attack rates were low at low temperatures because 10 days starving time was not long enough to make the pike hungry and fully motivated. To test if starvation time was long enough, we ran 13 additional experiments with three to four weeks starvation time at low temperatures (3.5–7.5°C) using individuals that were not included in the experiment described above. The capture success of these fish was then compared with fish that were starved for 10 days and tested at temperatures in the same range.

(b). Maximum swimming speed

The feeding experiment showed that attack rate fell to nearly zero below 11°C. We hypothesized that this threshold reflected a shift in relative swimming performance of trout and pike, such that the maximum escape speed of trout exceeded the maximum attack speed of pike at low temperatures. To test this hypothesis, we estimated the maximum swimming speed of pike when attacking brown trout from video sequences using Tracker v. 3.10 (http://www.cabrillo.edu/~dbrown/tracker/). For 12 of the experiments, the image quality was too low to allow reliable measurements of swimming speed.

Likewise, the quality of the video did not allow an accurate analysis of escape speed for the much smaller brown trout. Thus, we measured the escape speed of brown trout in a separate experiment where water depth was reduced to 0.4 m to improve visibility. We tested several types of threats, but found that having a person chasing the fish in the pool was a practical and efficient method. These experiments were performed with 10 brown trout (14.9–15.1 cm). The experiments were carried out between 30 September and 1 March. After each fish was placed in its experimental pool, it was allowed to acclimate for a minimum of 8 h. The fish was then chased repeatedly until it was obvious that it had reached a level of fatigue that made further top values of speed unlikely. For each individual, we measured maximum swimming speed at approximately 1.5, 5, 10, 15 and 20°C using the same method as for the attack rate experiments.

In order to enable a comparison of the maximum swimming speed of pike when attacking prey and when escaping a predator, we also carried out this experiment with seven pike individuals (size 63–65 cm) over the same time period.

(c). Statistical analyses

Relationships between explanatory variables and attack rates were examined with mixed effect survival models using the coxme and the coxph procedures in the coxme package in R [27]. We used survival models that could handle censored observations because the trout survived nearly 30% of the experiments. Hence, we used the time to capture, which is inversely proportional to attack rate (equation (2.1)), as the response variable. The explanatory variables included individual as a random factor, pike body size as a fixed factor, and temperature, temperature², day and day² as covariates.

Relationships between swimming speed and explanatory variables were examined with linear mixed effect models using the lme and gls procedures in the nlme package in R [28]. As explanatory variables, we included individual as the random factor, and temperature, temperature², date and date² as covariates. For pike feeding on trout, we also included pike size class as a fixed factor.

Model selection followed the strategy proposed in Zuur et al. [29]. We first included all fixed factors and covariates and examined the significance of the random factor with a likelihood-ratio test. We then examined whether the Akaike information criteria (AIC) values could be further reduced by excluding fixed factors and covariates.

In a second step, we examined whether the best models for the data from the attack rate experiment, which included temperature and temperature² as predictors, could be improved if the relationship with temperature was described using two regression lines and a breakpoint instead of the second order polynomial.

As an additional test of the relative importance of temperature and other seasonal effects, we ran corresponding analyses on a subset of the data, collected between 15 October and 2 December, where date and temperature were approximately orthogonal. To increase the power of the statistical tests, we also included the data from the 13 experiments with three to four weeks starvation time, which were collected over the same period. We did this as there were no significant effects of starvation time on the outcome of the experiments (see Results section). The correlation between date and temperature in the combined dataset was r = 0.048.

The strength of temperature responses is usually estimated by fitting the Arrhenius model to data. Thus, to facilitate comparison with other studies, we regressed the natural logarithm of attack rate on −1/kT, where k is Boltzmann's constant (8.167 × 10⁻⁵ eV K⁻¹) and T is temperature in Kelvin. The zero values that were recorded for attack rate were replaced with 0.013 prey h⁻¹ (1 prey in 72 h) when fitting the Arrhenius model and when plotting attack rate versus temperature. We used this method rather than adding a constant to all observations, as the latter procedure would alter the slope of the Arrhenius relationship. The data used in the analyses are provided in the electronic supplementary material, S2.

3. Results

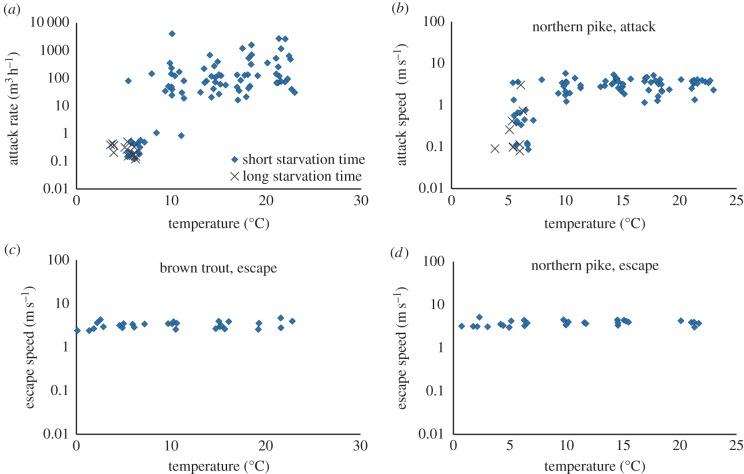
The attack rate of pike feeding on brown trout was best described by a model including temperature and temperature squared (table 1). The significant quadratic term reflects that attack rate decreased sharply at low temperatures (figure 2a). Inspection of the data in figure 2a suggests that the slope of the response curve shifts at approximately 11°C. Indeed, we found that the data were even better described by a piecewise regression model with a break point at 11.0°C (table 1). The corresponding activation energies were E_a ± s.e. = 8.89 ± 1.1 eV for low temperatures and 1.29 ± 0.38 eV for high temperatures. The sharp drop in attack rates shows that pike were unable to catch brown trout at low temperatures. Out of 29 trials run at temperatures below 7.5°C, pike only caught brown trout twice. This type of response is expected when predators and prey have intersecting performance curves and prey outperform predators at low temperatures (figure 1c,d).

Table 1.

Mixed effects survival models used to investigate relationships between attack rates and temperature, body size and date. (Body size class was included as a fixed factor, temperature and date as covariates and individual (ind) as a random factor. A separate model was developed with temperature described by two linear regression lines and a break point. Late season experiments were carried out between 15 October and 2 December.)

full model	best model	estimate ± s.e.	z-value	p-value	N	AICc for full model	AICc for best model
all experiments
ind, temp, temp2, date, date2, size class	temp	0.64 ± 0.16	4.1	<0.0001	83	464.5	458.1
	temp2	−0.017 ± 0.005	3.2	<0.005
	temp < breakpoint	0.99 ± 0.23	3.8	<0.0005	83		448.1
	temp > breakpoint	0.10 ± 0.038	2.7	<0.01
	breakpoint	11.0°C
late season experiments
ind, temp, temp2, date, date2, size class	temp	1.91 ± 0.62	3.1	<0.005	45	81.3	77.3
	temp2	−0.068 ± 0.026	2.5	<0.05
	date	−0.050 ± 0.021	2.4	<0.05

Figure 2.

Effect of temperature on attack rate and attack swimming speed of northern pike when feeding on brown trout (a,b), and escape speeds brown trout (c), and northern pike (d) when attacked by a human. A small random error was added to the data in (a) and (b) to visualize overlapping points. The pike were starved 10 days or three to four weeks prior to the foraging experiment. (Online version in colour.)

An alternative hypothesis for the low attack rate at low temperatures is that the starvation time was not long enough to make the pike hungry and fully motivated. However, increasing starvation time did not influence the proportion of successful attacks (two of 16 trials for 10 day starvation and zero of 13 trials for three- to four-week starvation, χ₁² = 1.54, p = 0.21) or the maximum attack speed by predators (mean ± s.e. = 2.31 ± 0.27 for 10 day starvation and 1.73 ± 0.32 for three- to four-week starvation, respectively, t = 1.31, p = 0.21).

Another hypothesis is that the low attack rate at low temperatures reflected an overall decrease in activity late in the season. When restricting the analysis to the period 15 October to 2 December, when date and temperature could be kept orthogonal, we found that the best model included strong effects of temperature and a weak but significant effect of date (table 1).

To test the hypothesis that the threshold in the attack rate curve was caused by intersecting performance curves, we compared the maximum swimming speeds for attacking pike and escaping brown trout (figure 2b,c). As shown in figure 3, the two performance curves do intersect at high temperatures, although it may be more accurate to describe them as divergent at low temperatures and overlapping at high temperatures. For pike attack speed, the best model included temperature and temperature² as predictors (table 2). The model was further improved by using a piecewise regression with a breakpoint at 10.8°C (figure 2b and table 2). The activation energy was 2.6 ± 0.7 eV below the breakpoint and 0.034 ± 0.11 eV above the breakpoint. The best model describing late seasonal data included only temperature (table 2).

Figure 3.

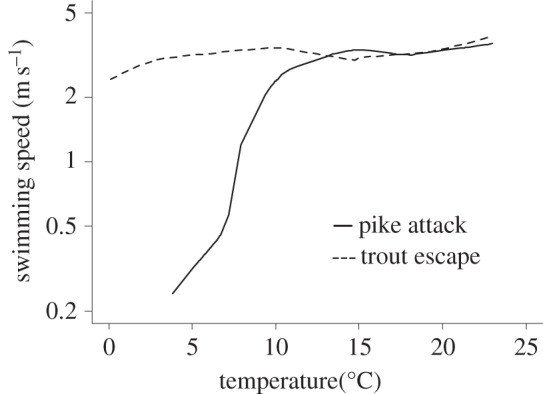
Temperature dependence for pike attack speed and brown trout escape speed. The curves were estimated with a non-parametric smoother (lowess [27]) using the data in figure 2b,c.

Table 2.

Mixed effects linear models used to investigate relationships between swimming speeds and temperature, date and body size. (Body size class was included as a fixed factor, temperature and date as covariates, and individual (ind) as a random factor. A separate model was developed for pike attack speed where temperature was described by two linear regression lines and a break point.)

full model	best model	estimate ± s.e.	t-value	p-value	N	AICc for full model	AICc for best model
pike feeding on trout, all experiments
ind, temp, temp2, date, date2, size class	temp	0.50 ± 0.09	5.6	<0.0001	75	212.5	188.5
	temp2	−0.014 ± 0.003	4.5	<0.0001
	temp < breakpoint	0.38 ± 0.05	7.2	<0.0001	75		161.3
	temp > breakpoint	−0.004 ± 0.02	0.17	n.s.
	breakpoint	10.8°C
pike feeding on trout, late seasonal experiments
ind, temp, temp2, date, date2, size class	temp	0.25 ± 0.06	4.3	<0.0001	37	149.6	122.0
pike escaping human attack
ind, temp, temp2 date, date2	intercept				29	34.7	−22.9
trout escaping human attack
ind, temp, temp2 date, date2	ind				28	42.2	−15.0

The maximum swimming speed for escaping brown trout showed a weak and non-significant temperature response (slope ± s.e. = 0.0066 ± 0.0033, p = 0.06, figures 2c and 3, E_a ± s.e. = 0.046 ± 0.034 eV). The best model included only the random factor, individual (table 1).

Pike escape speed did not show a threshold response and the relationship with temperature was weak and non-significant (figure 2d; slope ± s.e. = 0.0051 ± 0.0040, p = 0.21, E_a ± s.e. = 0.04 ± 0.03 eV).

4. Discussion

Our model predicts that the temperature curves for attack rate will exhibit marked thresholds when predators and prey have intersecting performance curves. Our empirical data for the interaction between northern pike and its prey, the brown trout, provide support for this idea. We found a threshold in attack rate which corresponded well with data on the relative performance of pike and brown trout with respect to maximum attack and escape swimming speeds. At temperatures below 11°C, most attacks were unsuccessful and the observed maximum attack speed of pike was much lower than the escape speed of brown trout. At higher temperatures, the maximum swimming speeds of pike and trout were approximately equal, suggesting that other factors controlled the outcome.

While the threshold in attack rate can be understood as a consequence of relative swimming performance, it is not clear why we see a threshold in the temperature curve for pike attack speed. The data for maximum escape speed show that pike can swim quickly at low temperatures, indicating that the low attack speed is not due to limited physiological capacity. Our observations of pike hunting behaviour support this interpretation. The pike typically started following the trout rather than using a strict ambush strategy. However, in contrast to their behaviour in warm water, they rarely made fully determined attacks at low temperatures. We speculate that this behaviour indicates temperature affects neurological processes, and that this put the pike at a disadvantage when the temperature is low. Catching prey is, in general, a more complicated task than escaping a predator. Intercepting fast-moving prey requires synchronisation of motoric, perceptual and cognitive processes, whereas escape often only requires rapid movements in a random direction. If the ability to perform complex tasks is more severely affected at extreme temperatures, this would lead to stronger temperature dependence for attack than for escape performance. An example of a perception trait with strong temperature dependence is the temporal resolution of eyesight, which determines the ability to detect rapid prey movements. E_a values reported by Fritsches et al. [30] for this trait in three large pelagic piscivores had a range of approximately 0.60–1.2 (recalculated from Q₁₀ values), which is considerably higher than the values observed for escape speed in this study (E_a ≈ 0.04–0.05). The fact that several species of large pelagic predators, including swordfish and some tunas and sharks, have evolved the ability to heat their eyes to as much as 10–14°C above ambient temperatures [31], indicates that low temporal resolution is indeed a problem for visual predators feeding on agile prey in low temperatures. An alternative explanation for low attack speed at low temperatures may be reduced motivation. A number of factors may influence the motivation to make a fully determined attack, including predation risk, hunger, prey availability and the probability that an attack is successful (which may relate to neurological processes). However, as the temperature dependencies of these processes are poorly known, it is not possible to predict the net effect of low temperatures on the motivation to perform an attack.

Besides the effects from attack success, the temperature dependence of attack rate in our conceptual model was controlled by the temperature dependence of contact rate. However, such effects cannot explain our experimental results. Even though activity levels of pike dropped considerably at low temperatures, agile trout and a relatively small spatial scale ensured that pike typically located trout quickly, throughout the temperature range of our experiments. Hence, also pike that failed to catch the trout in 72 h had often reacted by approaching or attacking the trout at the beginning of the experiment (electronic supplementary material, figure S3).

The existence of thresholds in crucial ecological rates has potentially far-reaching implications for the effects of warming on predator–prey dynamics and ecosystem stability. Most importantly, they may create tipping points by altering the outcome of competitive and predatory interactions. We may, therefore, expect warming to induce dramatic shifts in community composition and ecosystem function, as dominant species are gained or lost, especially in species-poor systems. The interaction between pike and brown trout provides an illustrative example. The threshold in the temperature dependence of attack rate that we observed in this study has an intriguing correspondence with observed patterns of coexistence between pike and brown trout in northern Scandinavia. The two species coexist in small cold lakes, but not in small warm lakes, where northern pike cause the extinction of brown trout [32]. The critical annual mean air temperature, that appears to form a tipping point, varies from +1°C for small lakes (1 ha) up to +3°C for larger lakes (100 ha). Thus, the predicted warming is expected to cause dramatic shifts in the composition of the species-poor communities of lakes in northern Scandinavia, with hitherto unstudied consequences for ecosystem function [32–34].

Given the potential importance of thresholds in the temperature response of consumption rates, it becomes important to ask under what conditions we should expect to see them and how common they are. The mechanism that we describe here, i.e. intersecting performance curves for predators and prey, requires that prey have significant escape or defence capabilities that are temperature dependent. Thus, this mechanism may produce thresholds for predators feeding on mobile prey but not for herbivores and predators feeding on sessile prey. Thresholds may also be a consequence of trade-offs that cause consumers to cease feeding above or below a certain temperature. For example, it is conceivable that the expected fitness gain from active foraging is outweighed by high energetic costs or a high risk of being preyed upon when foraging.

At present, little is known about how common these thresholds are. Published reviews of empirical data have been focused on the hypothesized generality of linear or quadratic relationships [5,9,19], typically ignoring deviations caused by strongly nonlinear responses. A re-examination of the data used in a meta-analysis of functional response parameters [19] showed that threshold effects are not uncommon [35–39]. Moreover, one may suspect that such effects are underreported, because experiments are generally set up in a temperature range where ‘something happens’ and predators actually catch prey.

The temperature dependence of attack rate for the pike–trout interaction is stronger than found in other published studies; the mean E_a-value for six studies reviewed ([19], excluding data from this study) was 0.62 (CI 95% = ± 0.36) to be compared with E_a = 1.29 at high temperatures and E_a = 8.89 at low temperatures for pike feeding on brown trout. As our study concerned piscivory and the other studies concern invertivory, we speculate that the response is stronger for piscivory than for invertivory. More studies of the temperature dependence of piscivory would allow this idea to be tested.

Our results illustrate that the outcome of predator–prey encounters can depend on a complex interaction of physiological capacities and behaviours of both predator and prey, resulting in threshold effects. Identifying such thresholds is crucial when predicting the effects of climate warming as they have the potential to create tipping points in the responses of ecosystems to increasing temperatures. Thus, we reiterate the point made by Vucic-Pestic et al. [40] that we need to distinguish between different organisms and systems to find general rules for determining whether the Arrhenius equation may be used, or if rigorously parametrized response curves are needed.

Ethics statement

The experiments were carried out under ethical approval A184-12.

Data accessibility

The data reported in this paper are provided in the electronic supplementary material as appendix S2.

Funding statement

This research was funded by grants from the Swedish Research Council FORMAS to G.E. (no. 2007-1149) and from Göran Gustavsson's Foundation for Nature and Environment in Lappland to G.Ö.