Abstract
Purpose
Quantification of small animal PET images necessitates knowledge of the plasma input function (PIF). We propose and validate a simplified hybrid single-input-dual-output (HSIDO) algorithm to estimate the PIF.
Procedures
The HSIDO algorithm integrates the peak of the input function from two ROI TACs with a tail segment expressed by a sum of two exponentials. Partial volume parameters are optimized simultaneously. The algorithm is validated using both simulated and real small animal PET images. In addition, the algorithm is compared to existing techniques in terms of area under curve (AUC) error, bias and precision of compartmental model micro-parameters.
Results
In general, the HSIDO method generated PIF with significantly (P<0.05) less AUC error, lower bias, and improved precision of kinetic estimates in comparison to the reference method.
Conclusions
HISDO is an improved modeling based PIF estimation method. This method can be applied for quantitative analysis of small animal dynamic PET studies.
Keywords: input function, PET, small animal imaging, compartment model
INTRODUCTION
PET imaging is an invaluable tool for diagnosis, staging, treatment monitoring, as well as in basic and clinical research. The combination of dynamic PET imaging with compartment models enables the quantitative evaluation of radiopharmaceutical kinetics in vivo. This task often requires the knowledge of the plasma time-activity curve (pTAC) of the radiopharmaceutical [1,2], which is commonly known as the plasma input function (PIF). The gold standard for the determination of PIF is an invasive blood-sampling procedure [3,4], in which activity concentrations of arterial blood samples are measured directly at timed intervals. This procedure is challenging for small animal studies because of the small size of animal blood vessels and the potential perturbation to the physiology due to the loss of blood [4]. Therefore, less invasive, image based PIF estimation techniques are desirable.
The simplest image based approach uses the time-activity curve (TAC) for region-of-interest (ROI) defined at major blood pool, such as left ventricle, left atrium or aorta [5–7], to approximate the PIF. While this approach can be used in human studies, it is impractical in small animals due to the much smaller size of the blood pool and severe partial volume and spill-over effects [4]. Alternatively, factor analysis either by an apex-seeking technique [8,9] or least square type of techniques [10,11] have been proposed. Recently, our group [12] and others [13,14] have proposed parametric-based approaches to estimate the PIF from multiple ROIs. In these approaches, the PIF is represented by a sum of exponentials and the PIF model parameters are estimated simultaneously with tissue kinetic parameters. The PIF in the abovementioned approaches is based on Feng’s PIF model, which assumes a bolus injection, i.e. instantaneous injection, and a simplified physiological model for the kinetics of the tracer [15]. The model-based PIF estimation approach has been applied to small animal PET studies with some degree of success [3,16]. In practice, however, the administration of the tracer is not instantaneous; rather, the tracer is injected over a period of a few seconds as an infusion. In addition, the duration of the “bolus” injection varies on a case by case basis. Thus, parametric methods of input function estimation, which assume a bolus injection, may not capture the true kinetics at the peak of the input function, which could have a negative impact on the quantitative analysis of the PET data, as suggested by others [17,18].
We have recently introduced a Hybrid Image and Blood Sampling (HIBS) algorithm whereby the peak of the image is derived from recovery-corrected image LV ROIs and the tail is derived from 5–7 blood samples, both of which are linked by a Bezier interpolation algorithm [19]. The HIBS algorithm is ideal for kinetic analysis of tracers using short-lived radionuclides such as 11C in 11C-palmitate or 11C-glucose where blood samples are readily available from metabolite (11C-CO2) correction analysis. For tracers where metabolites are not an issue, such as 2-deoxy-2-[18F]fluoro-D-glucose (FDG), it would be ideal to minimize the number of blood samples for the reconstruction of the input function. To that end, we propose a hybrid method that extracts the peak of the input function from the image while the tail of the input function is derived by fitting a parametric model. In addition, recovery and spillover values are fitted simultaneously. The method uses two ROIs drawn on the heart, thus eliminating the need to fit delay and dispersion parameters [16]. Such an approach captures the true peak of the image while minimizing the number of blood samples. We coined the method Hybrid Single-Input-Dual-Output (HSIDO) for PIF estimation. We validate the HSIDO algorithm with both simulated and real small animal FDG PET data. Finally, we compare performance of the HSIDO algorithm against a recently reported algorithm [3]. We show that the proposed algorithm performs better than available method both in terms of bias and precision of kinetic estimates.
MATERIALS & METHODS
FDG Compartment Model
The set of differential equations of the well established three-compartment model describing FDG uptake [20] is summarized here:
| (1) |
| (2) |
where, Cp is the plasma activity concentration, C1 is the activity concentration of free FDG in myocardium tissue, and C2 is the activity concentration of phosphorylated FDG in myocardium tissue. Both C1 and C2 contribute to the activity concentration of FDG (Ct) in myocardium tissue. The ordinary differential equations can be solved analytically [20] and the solution for Ct is:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where, ⊗ denotes for convolution.
| (8) |
Hybrid PIF and Dual Output Model
In lieu of Feng’s PIF model (Eq. 8) [15], a hybrid PIF model is proposed in this study. It is assumed that the two ROI TACs obtained at the cardiac region can be modeled as linear mixtures of the myocardial tissue activity concentration Ct, and the plasma activity concentration Cp essentially accounting for spillover and partial volume effects:
| (9) |
where, Cc is the ROI TAC for left ventricle (LV) cavity; Cm is the myocardium ROI TAC. The formula for Cc combines both the partial volume effect and the spill-over effect from neighboring myocardial tissue. The formula for Cm incorporates vasculature component in the tissue as well as partial volume and spill-over effects. The parameter fcc is the pure blood contribution to the LV ROI TAC, fmc is the pure tissue contribution to the LV ROI TAC, fcm is the pure blood contribution to the myocardial ROI TAC, and fmm is the pure tissue contribution to the myocardial ROI TAC. These factors include the impact of a number of factors, such as partial volume effects, spill-over effects, vasculature fraction, and blurring due to cardiac and respiratory motion. It should be noted that they have essentially the same meaning as in Ref. 3. The hybrid PIF model we propose to use is defined by the following equations:
| (10) |
This hybrid PIF model is motivated by the fact that the PIF is usually composed of a fast changing peak (0< t <τ), and a slow changing tail (t >τ). The peak portion of the PIF is difficult to be analytically expressed, while a two exponential formula can approximate the slow changing tail very well. On the other hand, the peak portion of the IF can be represented using the ROI TACs by solving Eq. 9 analytically as shown in Eq. 10. It should be noted that we are inherently assuming that at early times there is no prominent contribution to the ROI TACs other than the myocardial tissue and the PIF. This assumption is generally true for FDG studies if both the LV ROI and myocardial ROI are carefully defined. In this work, τ is set to 30 seconds based on the observation that the peak portion of the PIF generally ends before 30 seconds.
PIF Estimation Method
For a given set of parameters p (A1, A2, l1, l2, fcc, fmc, fcm, fmm, K1, k2, k3, and k4), the model ROI TACs can be calculated based on Eqs. 3–7 and 9–10. Therefore PIF can be estimated by finding the optimal set of parameters that fit the model to the measured ROI TACs. This can be achieved by minimizing the following weighted least square (WLS) objective function:
| (11) |
where, w1i, w2i, w3 are the weighting factors depending on the choice of weighting scheme; N is the number of frames for the dynamic PET study; M is the number of blood samples used as constraints; BSj is the jth blood sample activity concentration at the corresponding time tj. Ideally, the weighting factors should be inversely proportional to the variance of the corresponding measurements, which is often difficult to estimate. In this study, the ROI data are frame duration weighted [12], which means the variance in ROI measurements is assumed to be inversely proportional to the frame duration. The weighting factors for the blood sample measurements are set to the same value as the weighting factors for the frame with the longest frame durations. This entails that blood sample measurements are considered to be at least as reliable as the ROI measurement with the longest frame duration. This choice is empirical based on our experience with blood sample measurements and the PET data. More sophisticated weighting scheme can be used, for example, the ROI size and activity concentration can be taken into consideration, or the extended least square approach in Fang and Muzic [3] can be used. Once the optimal set of parameters is found after the minimization, the PIF can be generated using Eq. 10.
Simulation Data
Monte Carlo simulations were performed to generate 300 sets of simulated small animal FDG PET images. Dynamic MOBY phantom [21] incorporating both cardiac and respiratory motion was used to define the anatomy. Feng’s model with randomly generated parameters was used to simulate true bolus injection based PIF. Convolution of Feng’s model with a short step function of various lengths simulated the PIF for infusion. Combining the randomly generated kinetic parameters and the simulated PIFs, myocardial activity concentration curve Ct was calculated using Eqs.3–7. Assuming a vasculature fraction of 15%, digital dynamic FDG uptake phantom was generated by combining the model PIF, Ct, and the dynamic anatomical phantom. Simulated PET image was then generated based on the digital dynamic FDG uptake phantom by applying noise in the sinogram space as we have previously described [11]. The choice of vasculature fraction value was within the range of published studies [10,22,23]. It should be noted that the randomly generated IF parameters and kinetic parameters were all within the range of parameter values observed in our preliminary studies on real small animal FDG datasets. In the simulation study, 50 sets of simulated PET datasets were generated using bolus injection based PIFs. In addition, 50 simulated PET datasets each were generated for infusion of 0.6, 1, 2, 3 and 5 seconds. The simulated small animal PET datasets had a voxel size of 0.4 mm (in-plane) by 0.8 mm (slice thickness) and a spatial resolution of 1.7 mm (full-width-half-max) similar to typical small animal scanners. The frame durations were 3s × 1, 2s × 6, 5s × 9, 10s × 6, 30s × 4, 60s × 2, 120s × 2, and 300s × 10, for a one hour scan.
Mouse FDG Data
In addition to the simulation data, our method was also tested using mouse data obtained from the Crump Institute of Molecular Imaging, UCLA, [24,25]. Since these dataset is being used to compare multiple methods, we will briefly describe the experimental methods as reported in [24,25]: twelve C57BL/6 male mice weighing 22–36 g were anesthetized with 1.5–2% isoflurane. Five of the twelve mice were pretreated with insulin. The injection dose was 11–27 MBq, and 9–22 blood samples for each mouse were taken from femoral artery for activity concentration measurement. The mice were scanned with either microPET Focus-220 or microPET P4 scanner (both from Siemens Medical Solutions USA, Inc.) for either 60 min or 90 min. The images were reconstructed using filtered backprojection algorithm with a voxel size of 0.4 mm (in plane) by 0.8 mm (slice thickness). The PET image data and the blood sample measurements were both in PET units, a conversion factor of 534 MBq·mL−1/PET unit [16] was used for the conversion into MBq·mL−1.
ROI Definition
In order to apply the PIF estimation methods, two ROIs need to be defined on the dynamic PET images, one for the LV cavity and the other for the myocardial tissue. For both simulated and real small animal FDG PET datasets, the ROIs were defined in a semi-automated fashion using ANALYZE ™ [26] based on the summed image. Three dimensional region growing tool was used to semi-automatically define the ROIs based on the manually chosen seeds and a user defined intensity range. Manually drawn limit was necessary in some cases to prevent the region growing process going out to unintended areas. An example of defined ROIs is shown in Fig. 1, a typical LV cavity ROI has 36 voxels or 4.6 mm3, and a typical myocardium ROI has 501 voxels or 63.9 mm3. The user defined intensity range for region growing was selected so that the resulting ROI has a diameter of approximately 1.6 mm for the LV cavity; for the myocardium ROI the inner diameter was approximately 3.0 mm and the outer diameter was approximately 5.0 mm.
FIGURE 1.
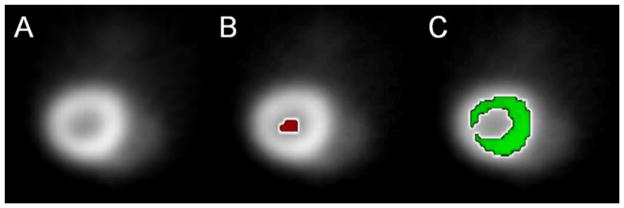
Illustration of typical ROI definition. (A) Cropped transverse slice of mouse FDG PET image. (B) Left ventricle cavity ROI. (C) Myocardial ROI.
Input Function Validation
The 300 simulated small animal datasets were used to validate the HSIDO PIF estimation method. For each dataset, LV TAC and myocardial TAC were obtained from the dynamic PET data and the defined ROIs. The PIF was then estimated using the HSIDO method with 0, 1, and 2 blood samples as constraints. Blood sample measurements were simulated based on the model PIF used for creating simulation data at 2600 and 2900 seconds. For comparison, the PIF estimation method reported by Fang and Muzic [3], which will be referred to as ‘CWRU’, was also applied using their code in the COMKAT package. Slight modification was made to handle cases with 2 blood samples as constraints. The initial values and bounds used for the PIF estimation were listed in Table 1. The same set of values was used for both the simulation data and the real mice FDG datasets. The initial values were chosen to match the mean parameter values observed in our preliminary study. It can be shown that the parameters, A1, A2, l1 and l2 has similar values for both Feng’s model (Eq. 8) and the hybrid PIF model (Eq. 10). This is most likely due to the fact that A3 and l3 in Feng’s model (Eq. 8) primarily contributes to the peak portion of the PIF and has minimum impact on the tail portion of the PIF due to the large l3. In addition the delay (t0) in Feng’s model also has very small impact on the tail portion of the PIF. As a direct measurement of the quality of the estimated PIF, area under curve (AUC) error, defined as the difference in AUC of the estimated PIF and the true PIF in percentage, was calculated. The AUC measurement is calculated based on the entire duration of the PET scan. Since it is important to know the impact of PIF estimation error on kinetic parameter estimation, the kinetic parameters were also estimated by fitting the compartmental model (Eqs. 3–7) to the myocardial TAC based on the estimated PIF. The kinetic parameter estimation error compared to the ground truth was also evaluated. In this work, we define bias (Eq. 12) as the mean error for any given kinetic parameter or AUC measurement; and we define precision (Eq. 13) as the standard deviation of a given measurement.
TABLE 1.
Initial Values and Bounds for Input Function Estimation.
| Parameter | Initial Value | Upper Bound | Lower Bound |
|---|---|---|---|
| K1 (min−1) | 0.89 | 2.0 | 0 |
| k2 (min−1) | 0.37 | 2.0 | 0 |
| k3 (min−1) | 0.17 | 0.5 | 0 |
| k4 (min−1) | 0.005 | 0.01 | 0 |
| fcc | 0.8 | 1.0 | 0.4 |
| fmc | 0.2 | 0.6 | 0 |
| fcm | 0.4 | 0.5 | 0 |
| fmm | 0.4 | 1.0 | 0.3 |
| A1 (MBq·mL−1) | 8.7 | 20.0 | 0 |
| A2 (MBq·mL−1) | 2.2 | 10.0 | 0 |
| A3a (MBq·min−1·mL−1) | 6,200.0 | 10,000.0 | 500.0 |
| l1 (min−1) | −5.2 | 0 | −15.0 |
| l2 (min−1) | −0.04 | 0 | −0.05 |
| l3 a (min−1) | −104.0 | 0 | −250.0 |
| t0 a (min) | 0 | 0.3 | 0 |
| w1 a | 1.0 | 3.0 | 0 |
| w2 a | 1.0 | 3.0 | 0 |
| w3 a | 0.1 | 0.1 | 0.05 |
Only for input function estimation using Fang and Muzic’s method (CWRU) [3].
| (12) |
| (13) |
In Eqs. 12 and 13, β̂i is the estimated parameter value and βi is the true parameter value, Mean and STD specify the functions to calculate the average and standard deviation of a variable respectively.
Application to Small Animal PET Data
The HSIDO PIF estimation method was further evaluated using the UCLA mice FDG datasets with 0, 1 or 2 blood sample measurements at late time points as constraints. The blood samples chosen to be used as constraints were selected from the last two blood samples available within the duration of imaging study, typically around 30 and 45 minutes. AUC error was evaluated by comparing the estimated PIF with the PIF obtained by linearly interpolating blood sample measurements. The HSIDO results were again compared to the CWRU results. Kinetic modeling was not performed since true parameter values were not known a priori for real datasets.
Statistical Analysis
One sided unpaired t test with a significance value of 0.05 was used to compare the measurement bias between two approaches, i.e. one blood sample vs. no blood sample, HSIDO PIF estimation vs. CWRU PIF estimation, etc. To compare the measurement precision between two approaches, one sided F-test was performed with a significance value of 0.05.
RESULTS
An example of estimated PIF for simulated data using HSIDO and CWRU method was illustrated in Figure 2A, the results were compared to the LV cavity ROI TAC as well as the true PIF. The PIF estimation and the kinetic parameter estimation results were summarized in Table 2 for bolus injection simulations. The estimated PIF using HSIDO method had an AUC error of 12.4 ± 16.8% (mean ± standarad deviation) without blood samples, the mean AUC error improved to 0.3 ± 6.8 % with one blood sample as constraint. The estimated PIF using CWRU method had an AUC error of 15.3 ± 22.1% without blood samples, and improved to 7.6 ± 12.2% with one blood sample as constraint (Table 2). The PIF AUC measurement improved significantly (P<0.05) in terms of both bias and precision with one blood sample constraint as compared to PIF estimated without blood sample constraints for both CWRU and HSIDO PIF estimation methods. However, the inclusion of a second blood sample did not significantly (P>0.05) improve the AUC measurements for either of the two PIF estimation methods (Table 2). The HSIDO method provided significantly better precision (P<0.05) in terms of AUC than the CWRU method regardless of the number of blood samples used. With 1 or 2 blood samples, the HSIDO method also provided significantly lower bias (P<0.05) in AUC measure than the CWRU method. In general, the kinetic parameter estimated using the HSIDO method had significantly better precision compared to the CWRU method (Table 2). The kinetic parameter estimation error was detailed in Table 2.
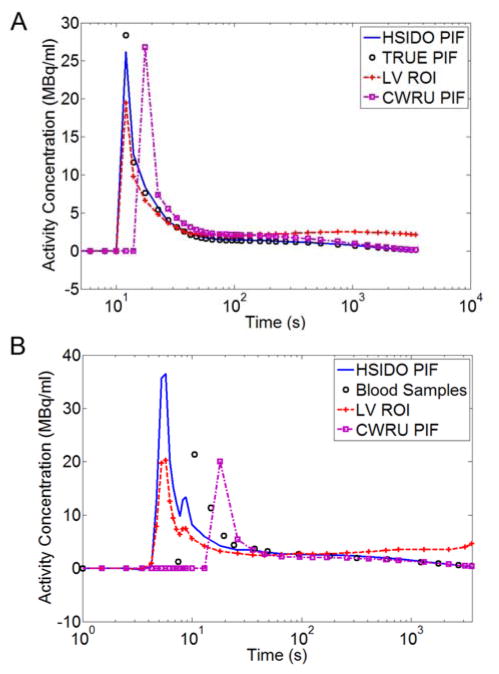
FIGURE 2.
(A) Example estimated PIFs using HSIDO and CWRU methods for a simulation study as compared to true PIF and the LV ROI TAC. (B) Example estimated PIFs using HSIDO and CWRU methods for a UCLA mouse dataset as compared to blood sample measurements and LV ROI TAC. The difference between HSIDO estimated PIF and blood measurement is mainly due to the delay and dispersion during the travel from heart to the blood sampling location, which resulted in a shorter and wider peak in the blood sample measurement in comparison to a taller and sharper peak at the heart region.
TABLE 2.
Input Function and Kinetic Parameter Estimation Error for Simulation Data with Bolus Injection. (mean ± standard deviation)(%).
| # Blood Samples | CWRU | HSIDO | |
|---|---|---|---|
| AUC | 0 | 15.3 ± 22.1 | 12.4 ± 16.8 § |
| 1 | 7.6 ± 12.2 *† | 0.3 ± 6.8 *†‡§ | |
| 2 | 3.9 ± 10.6 | 0.9 ± 5.7 ‡§ | |
| K1 | 0 | 8.4 ± 25.1 | −3.7 ± 15.8 § |
| 1 | 4.9 ± 25.2 | 3.1 ± 11.7 †§ | |
| 2 | 6.5 ± 25.4 | 2.3 ± 10.7 § | |
| k2 | 0 | 31.8 ± 52.1 | 9.3 ± 39.6 ‡§ |
| 1 | 18.3 ± 50.5 | 3.0 ± 32.6 ‡§ | |
| 2 | 10.5 ± 31.9 † | 3.9 ± 33.0 | |
| k3 | 0 | −1.9 ± 17.7 | −2.8 ± 12.9 § |
| 1 | −0.6 ± 16.4 † | −4.1 ± 7.3 § | |
| 2 | −1.6 ± 16.3 | −3.4 ± 6.5 § | |
| k4 | 0 | 34.2 ± 111.4 | 1.4 ± 30.8 ‡§ |
| 1 | 6.5 ± 36.7 † | −7.6 ± 29.6 †§ | |
| 2 | −1.1 ± 36.5 | −8.8 ± 29.9 | |
| Ki | 0 | −9.5 ± 14.8 | −9.1 ± 13.2 |
| 1 | −5.7 ± 9.5 † | −0.3 ± 6.7 *†‡§ | |
| 2 | −2.8 ± 10.6 | −1.0 ± 5.6 § |
CWRU: Input function estimation method in Ref. 3.
HSIDO: Input function estimation method developed in this study.
Measurement bias decreases significantly (P<0.05) over the same measurement obtained with one less blood sample.
Measurement precision improves significantly (P<0.05) over the same measurement obtained with one less blood sample.
HSIDO based measurement has significantly smaller bias (P<0.05) than CWRU based measurement.
HSIDO based measurement has significantly better precision (P<0.05) than CWRU based measurement.
The input function estimation results and the corresponding kinetic parameter estimation results were summarized in Table 3 for simulations with 2 and 5 seconds infusion. Similar results and trends were observed as for simulations with bolus injection and for simulations with other infusion time (result not shown). For 5 seconds infusions, the estimated PIF using HSIDO method had an AUC error of 6.9 ± 13.0% without blood samples, and the mean AUC error improved to −1.4 ± 7.0 % with one blood sample as constraint. The estimated PIF using CWRU method had an AUC error of 13.0 ± 20.7% without blood samples, and improved to 6.6 ± 9.6% with one blood sample as constraint (Table 3). With one blood sample as constraints the estimated PIF significantly improved in both precision and bias over PIF estimation without blood sample constraints. The kinetic parameters estimated using HSIDO were also significantly more precise than the CWRU method based kinetic parameters. The HSIDO method thus generated significantly more precise and less biased PIF in terms of AUC than CWRU method.
TABLE 3.
Input Function and Kinetic Parameter Estimation Error for Simulation Data with 2 and 5 Seconds Infusion. (mean ± standard deviation)(%).
| # Blood Samples | 2 seconds infusion | 5 seconds infusion | |||
|---|---|---|---|---|---|
|
| |||||
| CWRU | HSIDO | CWRU | HSIDO | ||
| AUC | 0 | 13.3 ± 21.1 | 9.3 ± 13.9 § | 13.0 ± 20.7 | 6.9 ± 13.0 ‡§ |
| 1 | 7.1 ± 10.6 *† | 0.1 ± 6.9 *†‡§ | 6.6 ± 9.6 *† | −1.4 ± 7.0 *†‡§ | |
| 2 | 4.6 ± 10.7 | 0.2 ± 6.3 ‡§ | 5.5 ± 10.9 | −0.9 ± 6.4 ‡§ | |
| K1 | 0 | 9.6 ± 26.4 | −4.8 ± 13.4 § | 13.5 ± 32.1 | −1.9 ± 13.5 ‡§ |
| 1 | 5.9 ± 25.9 | 1.7 ± 9.2 †§ | 11.8 ± 34.2 | 4.4 ± 10.3 †§ | |
| 2 | 9.2 ± 33.2 | 1.4 ± 8.5 § | 22.6 ± 58.1 | 3.2 ± 9.4 ‡§ | |
| k2 | 0 | 29.3 ± 52.4 | 2.3 ± 21.8 ‡§ | 39.9 ± 68.4 | 2.0 ± 21.7 ‡§ |
| 1 | 15.3 ± 41.4 | −0.9 ± 10.6 †‡§ | 24.0 ± 60.2 | −1.6 ± 9.6 †‡§ | |
| 2 | 18.6 ± 44.8 | −1.4 ± 10.4 ‡§ | 46.0 ± 112.2 | −2.4 ± 8.9 ‡§ | |
| k3 | 0 | −2.4 ± 20.3 | −2.5 ± 12.6 § | −1.1 ± 16.3 | −3.9 ± 12.2 § |
| 1 | −2.4 ± 17.2 | −3.6 ± 7.5 †§ | −3.1 ± 16.6 | −5.5 ± 6.5 †§ | |
| 2 | 0.1 ± 16.1 | −3.9 ± 7.2 § | −0.1 ± 17.9 | −5.5 ± 6.2 § | |
| k4 | 0 | 27.6 ± 101.6 | −6.5 ± 27.9 § | 15.4 ± 73.4 | −4.2 ± 28.6 § |
| 1 | −4.9 ± 36.0 † | −6.3 ± 25.9 †§ | −6.4 ± 41.1 † | −4.6 ± 28.9 †§ | |
| 2 | −8.3 ± 32.7 | −7.6 ± 28.7 § | −17.7 ± 36.4 | −5.1 ± 28.6 ‡§ | |
| Ki | 0 | −7.9 ± 15.0 | −7.5 ± 11.6 § | −7.9 ± 15.4 | −5.4 ± 11.4 § |
| 1 | −5.8 ± 9.0 † | −0.1 ± 6.8 *†‡§ | −5.5 ± 9.3 † | 1.5 ± 7.1 *†‡§ | |
| 2 | −3.8 ± 10.6 | −0.3 ± 6.1 ‡§ | −4.4 ± 11.4 | 1.0 ± 6.4 ‡§ | |
CWRU: Input function estimation method in Ref. 3.
HSIDO: Input function estimation method developed in this study.
Measurement bias decreases significantly (P<0.05) over the same measurement obtained with one less blood sample.
Measurement precision improves significantly (P<0.05) over the same measurement obtained with one less blood sample.
HSIDO based measurement has significantly smaller bias (P<0.05) than CWRU based measurement.
HSIDO based measurement has significantly better precision (P<0.05) than CWRU based measurement.
An example of the estimated PIF for the UCLA mice datasets was illustrated in Figure 2B. The results were compared with blood sample data as well as the LV cavity ROI TAC. There was a good agreement between the HSIDO estimated PIF and the blood sample measurements at late time points. The difference between HSIDO estimated PIF and the blood sample data at early time points was mainly due to delay and dispersion during the traveling of blood from the LV to the femoral artery where the blood samples were taken. The AUC errors for the PIF estimations were summarized in Table 4. The estimated PIF using Hybrid method had an AUC error of −2.9 ± 28.6% without blood samples, and the AUC error was 2.5 ± 11.5 % with one blood sample as constraint. The estimated PIF using CWRU method has an AUC error of 34.3 ± 52.4% without blood samples, and improved to 6.0 ± 21.2% with one blood sample as constraint (Table 4). Again, using one blood sample as constraint provided significantly more accurate PIF estimation than without blood sample constraint.
TABLE 4.
Input Function Estimation Error for UCLA Mice FDG Datasets. (mean ± standard deviation)(%).
| # Blood Samples | CWRU | HSIDO | |
|---|---|---|---|
| AUC | 0 | 34.3 ± 52.4 | −2.9 ± 28.6 †‡ |
| 1 | 6.0 ± 21.2 * | 2.5 ± 11.5 *‡ | |
| 2 | −5.3 ± 13.3 | −0.8 ± 12.3 |
CWRU: Input function estimation method in Ref. 3.
HSIDO: Input function estimation method developed in this study.
Measurement precision improves significantly (P<0.05) over the same measurement obtained with one less blood sample.
HSIDO based measurement has significantly smaller bias (P<0.05) than CWRU based measurement.
HSIDO based measurement has significantly better precision (P<0.05) than CWRU based measurement.
DISCUSSION
A HSIDO PIF estimation method was proposed and validated using both simulated and real mice FDG PET datasets. Unlike previous work where the PIF was represented by the Feng’s parametric model [3,12,13], we developed a hybrid PIF model that integrates the peak from ROI measurements with a two exponential tail model. The hybrid PIF model avoids the difficulty of analytically describing the peak portion of the PIF; instead, the ROI data was analyzed and the linear mixture model (Eq. 9) was solved for the peak portion of the PIF. We validated the reconstructed PIF by comparing AUC against simulated data as well as in comparison to published image-based PIF techniques. As the primary incentive in compartmental modeling of PET data is to extract kinetic estimates, we have further validated the HSIDO algorithm by evaluating bias and precision of micro-parameter kinetic estimates. In some aspect, the proposed algorithm is similar in spirit to the HIBS algorithm [19], which as we stated earlier is most applicable to tracers involving carbon-11 radionuclides where select blood samples are readily available. In contrast, the HSIDO algorithm is most applicable when metabolites are not an issue, such as FDG, as it minimizes the number of blood samples for the reconstruction of the input function. In addition, since arterial blood activity concentration usually converge with venous blood activity concentration at late time point, it is possible to use venous blood sampling instead of arterial blood sampling as constraints for the PIF estimation, which further simplifies the procedure.
The proposed HSIDO algorithm reduced the number of parameters to be estimated simultaneously during the modeling process from 15 to 12. This contributed to the more stable PIF estimation observed in this study. In addition, the image based PIF peak estimation without the need of a particular analytical form made it appropriate for different scenarios such as infusion or potentially other approaches for tracer introduction. Based on our observation, there was often a mismatch in peak time between the Feng’s model based input function estimation and imaging data. The mismatch, however, was not observed using the hybrid model. This is due to the over-simplified analytical form of Feng’s model which is insufficient in describing the early portion of the input function. On the other hand, the hybrid PIF model does not have this difficulty.
As we have mentioned earlier, the HSIDO method estimated the peak portion of the PIF by solving the mixture model (Eq. 9). An alternative approach was to assume tissue component to be negligible for the peak portion of the LV TAC, and therefore only partial volume correction was needed to obtain an estimation of the peak portion of the PIF. We also examined this approach; the results were less favorable. This might have been caused by the fact that the tissue component had a noticeable impact on the estimation of the peak portion of the PIF and cannot be neglected. Theoretically, the equation used to describe the peak portion of the PIF in Eq. 10 should also be able to describe the entire PIF. This appeared to be an attractive PIF model, since it further reduced the number of parameters to be simultaneously estimated to 8. However, in our experiences, this approach was less stable. Several factors might have contributed to this fact. Firstly, the noise in the ROI curve might propagate to the PIF, which could cause the optimization process to be difficult. Secondly, the two component mixture model was only an approximation of the ROI output. In fact, there were contributions to the ROI TACs from the background and other neighboring tissue due to partial volume and spill-over effects. While these contributions had a minimal impact on the peak portion of the PIF, the residue contribution from other tissue could become noticeable at the tail of the PIF.
As shown in Fig. 2B, there is a delay between the estimated PIF and the blood sample measurements using the HSIDO method as compared to the simulation study (Fig. 2A), this can be caused by the fact that the estimated PIF reflects the arterial blood activity concentration for the LV, while the blood sample measurements was taken from an artery some distance downstream of the LV, this delay and the dispersion effect could cause the difference between the estimated PIF and blood sample measurements. For the CWRU methods, since the variable, t0, in the Feng’s IF is estimated during the optimization process, however, based on our experience, the estimation for this variable is not stable and is sensitive to the values used to initialize the optimization. Therefore, we observed that the estimated peak for the PIF using the CWRU method can appear both before and after the true peak in the simulation studies. For the animal data experiment, this is compounded by the delay and dispersion effect due to the distance between LV and the arterial sampling location.
Ferl et al. also proposed a hybrid PIF model, in which the first 60 seconds of the PIF was estimated by partial volume, delay, and dispersion corrected LV ROI measurements, and the later part of the PIF was modeled using a four-exponential seven parameter formula [16]. The primary purpose for delay and dispersion correction was to account for the difference between the blood TAC at LV and the blood TAC at the tissue site due to the distance the blood had to travel from LV to tissue. In this work, since the ROI were chosen at the cardiac region in the vicinity of LV, the delay and dispersion effect could be neglected. Ferl et al. also accounted for the difference in activity concentration between whole blood and plasma using a one exponential model [16]. Instead, we adopted a similar approach as Fang and Muzic [3], where a constant ratio was assumed between whole blood and plasma activity concentration, hence the constant ratio can be lumped into K1 without the need to be modeled explicitly. In this work, a simplified model which assumes constant plasma-to-whole-blood ratio was used in order to compare the performance of the approach with existing work under the same circumstances. This simplification may leads to bias in modeling, especially for small animal studies. Appropriate plasma-to-whole-blood ratio model can be integrated into our HSIDO input function estimation framework for potentially further improvements of PIF estimation and kinetic modeling results. It should also be noted that since we are not explicitly modeling the plasma-to-whole-blood ratio and the hematocrit constant, the K1 parameter should be considered a lumped value of these constant and the true K1 values. For analysis of tissue away from the heart region, using the PIF estimated based on the cardiac ROIs may cause biases in the modeling process. It is potentially beneficial to include delay and dispersion modeling in a similar fashion as Ferl et al.’s work [16]. It should be noted that Ferl et al.’s PIF estimation method employed Bayesian constraints based on population data for the parameters to be estimated [16]. Therefore, prior knowledge of the population average kinetic behavior of the tracer is needed for the PIF estimation process. The PIF estimation method proposed herein does not require a priori information of the tracer kinetic property.
CONCLUSION
A hybrid input function model has been developed for compartment modeling based input function estimation using ROI TACs obtained from left ventricle and myocardial tissue. It was demonstrated that, with limited blood samples (1 or 2), improved input function estimation can be achieved as compared to the fully parametric estimation of the input function. The improved input function estimation also resulted in more accurate kinetic parameter estimates, both in terms of bias and precision. Therefore the HSIDO method can be applied to small animal imaging for kinetic analysis. The proposed method is implemented in MATLAB™ (The Mathworks, Inc) and available upon request.
Significance.
A novel input function model is proposed and validated for image based estimation of input function. The proposed method will enable accurate quantitative analysis of small animal PET images.
Acknowledgments
This project was supported by internal funding to KIS and partly by funding from the NIH/NHLBI grant 5-PO1-HL-13851 and the Washington University Small Animal Imaging Resource (WUSAIR) R24-CA83060.
References
- 1.Acton PD, Zhuang H, Alavi A. Quantification in PET. Radiol Clin North Am. 2004;42(6):1055–62. viii. doi: 10.1016/j.rcl.2004.08.010. [DOI] [PubMed] [Google Scholar]
- 2.Wienhard K. Measurement of glucose consumption using [18F]fluorodeoxyglucose. Methods. 2002;27(3):218–225. doi: 10.1016/s1046-2023(02)00077-4. [DOI] [PubMed] [Google Scholar]
- 3.Fang YH, Muzic RF., Jr Spillover and Partial-Volume Correction for Image-Derived Input Functions for Small-Animal 18F-FDG PET Studies. J Nucl Med. 2008;49(4):606–614. doi: 10.2967/jnumed.107.047613. [DOI] [PubMed] [Google Scholar]
- 4.Laforest R, Sharp TL, Engelbach JA, et al. Measurement of input functions in rodents: challenges and solutions. Nucl Med Biol. 2005;32(7):679–85. doi: 10.1016/j.nucmedbio.2005.06.012. [DOI] [PubMed] [Google Scholar]
- 5.Gambhir SS, Schwaiger M, Huang SC, et al. Simple noninvasive quantification method for measuring myocardial glucose utilization in humans employing positron emission tomography and fluorine-18 deoxyglucose. J Nucl Med. 1989;30(3):359–66. [PubMed] [Google Scholar]
- 6.Hoekstra CJ, Hoekstra OS, Lammertsma AA. On the use of image-derived input functions in oncological fluorine-18 fluorodeoxyglucose positron emission tomography studies. Eur J Nucl Med. 1999;26(11):1489–92. doi: 10.1007/s002590050484. [DOI] [PubMed] [Google Scholar]
- 7.Ohtake T, Kosaka N, Watanabe T, et al. Noninvasive method to obtain input function for measuring tissue glucose utilization of thoracic and abdominal organs. J Nucl Med. 1991;32(7):1432–8. [PubMed] [Google Scholar]
- 8.Buvat I, Benali H, Frouin F, Bazin JP, Di Paola R. Target apex-seeking in factor analysis of medical image sequences. Phys Med Biol. 1993;38(1):123–38. doi: 10.1088/0031-9155/38/1/009. [DOI] [PubMed] [Google Scholar]
- 9.Di Paola R, Bazin JP, Aubry F, et al. Handling of dynamic sequences in nuclear medicine. IEEE Transactions on Nuclear Science. 1982;NS-29:1310–1321. [Google Scholar]
- 10.Sitek A, Gullberg GT, Huesman RH. Correction for ambiguous solutions in factor analysis using a penalized least squares objective. IEEE Trans Med Imaging. 2002;21(3):216–25. doi: 10.1109/42.996340. [DOI] [PubMed] [Google Scholar]
- 11.Su Y, Welch MJ, Shoghi KI. The application of maximum likelihood factor analysis (MLFA) with uniqueness constraints on dynamic cardiac microPET data. Phys Med Biol. 2007;52(8):2313–34. doi: 10.1088/0031-9155/52/8/018. [DOI] [PubMed] [Google Scholar]
- 12.Su Y, Welch MJ, Shoghi KI. Single input multiple output (SIMO) optimization for input function estimation: a simulation study. Nuclear Science Symposium Conference Record, 2007 NSS ‘07 IEEE. 2007;6:4481–4484. [Google Scholar]
- 13.Feng D, Wong KP, Wu CM, Siu WC. A technique for extracting physiological parameters and the required input function simultaneously from PET image measurements: theory and simulation study. IEEE Trans Inf Technol Biomed. 1997;1(4):243–54. doi: 10.1109/4233.681168. [DOI] [PubMed] [Google Scholar]
- 14.Wong KP, Feng D, Meikle SR, Fulham MJ. Simultaneous estimation of physiological parameters and the input function--in vivo PET data. IEEE Trans Inf Technol Biomed. 2001;5(1):67–76. doi: 10.1109/4233.908397. [DOI] [PubMed] [Google Scholar]
- 15.Feng D, Huang SC, Wang X. Models for computer simulation studies of input functions for tracer kinetic modeling with positron emission tomography. Int J Biomed Comput. 1993;32(2):95–110. doi: 10.1016/0020-7101(93)90049-c. [DOI] [PubMed] [Google Scholar]
- 16.Ferl GZ, Zhang X, Wu HM, Huang SC. Estimation of the 18F-FDG Input Function in Mice by Use of Dynamic Small-Animal PET and Minimal Blood Sample Data. J Nucl Med. 2007 doi: 10.2967/jnumed.107.041061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Meyer C, Weibrecht M, Peligrad DN. Variation of Kinetic Model Parameters Due to Input Peak Distortions and Noise in Simulated 82Rb PET Perfusion Studies. Nuclear Science Symposium Conference Record, 2006 IEEE. 2006;5:2703–2707. [Google Scholar]
- 18.Wong K-P, Huang S-C, Fulham MJ. Evaluation of an Input Function Model that Incorporates the Injection Schedule in FDG-PET Studies. Nuclear Science Symposium Conference Record, 2006 IEEE. 2006;4:2086–2090. [Google Scholar]
- 19.Shoghi KI, Welch MJ. Hybrid image and blood sampling input function for quantification of small animal dynamic PET data. Nucl Med Biol. 2007;34(8):989–94. doi: 10.1016/j.nucmedbio.2007.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Phelps ME. PET : molecular imaging and its biological applications. New York: Springer; 2004. p. 621. [Google Scholar]
- 21.Segars WP, Tsui BM, Frey EC, Johnson GA, Berr SS. Development of a 4-D digital mouse phantom for molecular imaging research. Mol Imaging Biol. 2004;6(3):149–59. doi: 10.1016/j.mibio.2004.03.002. [DOI] [PubMed] [Google Scholar]
- 22.El Fakhri G, Sitek A, Zimmerman RE, Ouyang J. Generalized five-dimensional dynamic and spectral factor analysis. Med Phys. 2006;33(4):1016–24. doi: 10.1118/1.2179168. [DOI] [PubMed] [Google Scholar]
- 23.Su Y, Shoghi KI. Wavelet denoising in voxel based parametric estimation of small animal PET images: A systematic evaluation of spatial constraints and noise reduction algorithms. Phys Med Biol. 2008;53(21):5899–5915. doi: 10.1088/0031-9155/53/21/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. [Accessed March 2008];University of California Los Angeles Department of Molecular and Medical Phamacology UCLA Mouse Quantitation Project. ( http://dragon.nuc.ucla.edu)
- 25.Huang SC, Wu HM, Truong D, et al. A Public Domain Dynamic Mouse FDG MicroPET Image Data Set for Evaluation and Validation of Input Function Derivation Methods. Nuclear Science Symposium Conference Record, 2006 IEEE. 2006;5:2681–2683. [Google Scholar]
- 26.Robb RA, Hanson DP, Karwoski RA, et al. Analyze: a comprehensive, operator-interactive software package for multidimensional medical image display and analysis. Comput Med Imaging Graph. 1989;13(6):433–54. doi: 10.1016/0895-6111(89)90285-1. [DOI] [PubMed] [Google Scholar]