Time-Dependent Tree-Structured Survival Analysis with Unbiased Variable Selection through Permutation Tests

Abstract

Incorporating time-dependent covariates into tree-structured survival analysis (TSSA) may result in more accurate prognostic models than if only baseline values are used. Available time-dependent TSSA methods exhaustively test every binary split on every covariate; however, this approach may result in selection bias towards covariates with more observed values. We present a method that uses unbiased significance levels from newly proposed permutation tests to select the time-dependent or baseline covariate with the strongest relationship with the survival outcome. The specific splitting value is identified using only the selected covariate. Simulation results show that the proposed time-dependent TSSA method produces tree models of equal or greater accuracy as compared to baseline TSSA models, even with high censoring rates and large within-subject variability in the time-dependent covariate. To illustrate, the proposed method is applied to data from a cohort of bipolar youth to identify subgroups at risk for self-injurious behavior.

1. Introduction

Tree-structured survival analysis (TSSA) recursively identifies and executes binary splits on a sample to create covariate-based subsamples with more similar survival outcomes. One advantage of TSSA over other survival methods such as the Cox proportional hazards model is that TSSA provides clinically meaningful covariate cutoff values. However, one disadvantage of TSSA thus far is that there has been limited research on methods for including time-dependent covariates. Many covariate values change over the course of follow-up, and the incorporation of these updated measurements in a TSSA model may lead to more meaningful and accurate prognostic groups.

The use of updated measurements in TSSA is particularly relevant in biomedical applications. For example, when following a youth with bipolar disorder over time, it is important to repeatedly evaluate whether they are at risk for a suicide attempt so that medication and psychosocial treatments can be administered accordingly. Being in a depressed mood state is a known predictor for a suicide attempt [1]. However, because bipolar disorder is specifically characterized by changing mood states, a bipolar youth's mood state measured only at baseline is not likely to be a useful predictor during follow-up. Incorporating time-dependent mood information into TSSA could allow researchers to more accurately identify which youths with bipolar disorder are at risk for a suicide attempt.

1.1. Tree Modeling with Baseline Covariates

Traditional tree-structured methods perform an exhaustive search over all binary splits on all variables to identify the optimal split. The earliest work in this area was performed by Morgan and Sonquist [2]. Breiman et al. [3] popularized the model through their statistical program and unified framework, CART. Methods for survival outcomes within this framework were proposed by Gordon and Olshen [4], Segal [5], David and Anderson [6], LeBlanc and Crowley [7, 8], and Ahn and Loh [9], among others. Typically, these trees are first grown to their maximum size and then pruning algorithms based on cross-validation are used to find the “right-sized” tree.

One problem with exhaustively searching all possible splits is that it can be biased towards selecting variables with more observed values [10]. This means that a noisy covariate, which naturally has more values on which to split, could be selected over a less noisy covariate that is actually more informative [11]. To solve this problem with fixed-time covariates, several researchers, including LeBlanc and Crowley [8] and Jenson and Cohen [12], suggested the use of permutation or randomization tests. These types of tests produce an unbiased p-value that can be compared across covariates of different scales.

Hothorn et al. [10] embedded many permutation-based methods for unbiased baseline variable selection into a larger framework called Conditional Inference, which is rooted in the asymptotic theory of permutation tests developed by Strasser and Weber [13]. At each node, a global null hypothesis test of independence is used to determine whether there is an association between the outcome and the set of covariates. This global hypothesis test controls for overfitting and thus eliminates the need for complicated pruning algorithms. If the global null hypothesis of independence is rejected, the variable with the strongest association with the outcome (i.e., the smallest p-value) is selected and used to identify a binary cut-point to divide the node. Since these p-values are calculated based on permutation tests, they are not impacted by the original scale of the variable. Thus, they provide unbiased variable selection for the tree model.

1.2. Existing Time-Dependent TSSA Methods

Although methods for baseline TSSA are plentiful, only a handful of time-dependent TSSA methods have been proposed. Bacchetti and Segal [14] and Huang et al. [15] developed time-dependent TSSA methods that perform an exhaustive search over all possible binary splits on all covariates to identify the optimal split at each node. These methods are based on the two-sample rank statistic and piecewise exponential survival distribution, respectively. Bertolet and Brooks [16] proposed the use of a time-varying Cox model to select a binary covariate to split each node.

When time-dependent covariates are included in a TSSA model, there must be a method for handing subjects whose observations fall into different nodes throughout follow-up. Specifically, for a binary split C that divides a covariate into two disjoint subsets X_L and X_R, a single subject's repeatedly measured observations may fall into X_L at some time points and into X_R at other time points. Existing TSSA methods [14, 15, 16] handle this situation by dividing a subject's observations into two “pseudo-subjects”. The pseudo-subject with covariate values in X_L is sent to the left node, h_L, and the pseudo-subject with covariate values in X_R is sent to the right node, h_R. Additional details on the creation of pseudo-subjects are provided by Bacchetti and Segal [14].

If a time-dependent covariate changes monotonically over time, a subject's observations can switch nodes at most once. This results in each pseudo-subject being assigned data from a consecutive set of time points. However, if a time-dependent covariate changes non-monotonically over time, a subject's observations can switch between the left and right child node multiple times throughout follow-up. This results in each pseudo-subject being assigned a set of non-consecutive time points. There has been limited research on the impact of non-monotonically changing time-dependent covariates in TSSA, even though they are commonly observed in practice.

1.3. Proposed Time-Dependent TSSA Method

The existing time-dependent TSSA methods [14, 15, 16] provide an important methodological foundation. However, additional work is required to more confidently use time-dependent TSSA in practice. First, none of the available methods consider selection bias towards covariates with more possible split points. Since a time-dependent covariate will tend to naturally have more possible split points than its baseline counterpart (particularly if it is continuous), this is a critical next step for time-dependent TSSA. Second, to our knowledge, the accuracy of time-dependent TSSA methods with non-monotonically changing covariates has yet to be assessed through simulation studies. These types of covariates add complexity to the tree model and their impact needs to be investigated.

With this motivation, we present a novel TSSA method that incorporates both time-dependent and baseline covariates. Unlike previous time-dependent TSSA methods, the proposed method utilizes the general Conditional Inference algorithm presented by Hothorn et al. [10]. Thus, we use permutation tests to perform a global null hypothesis test of independence at each node and to select the variable with the strongest association with the outcome. However, our time-dependent TSSA approach diverges from the Conditional Inference framework because, unlike the other methods incorporated into this framework, our proposed permutation test is not yet embedded within Strasser and Weber's asymptotic theory of permutation tests [13].

Similar to existing time-dependent time-dependent TSSA methods, the proposed method uses pseudo-subjects to accommodate time-dependent covariates. However, unlike the existing research, which focused on binary and/or monotonically changing time-dependent covariates, we focus on continuous, non-monotonically changing time-dependent covariates in both our simulation and application. This is because continuous, non-monotonically changing time-dependent covariates are common in practice and present a challenge with respect to both variable selection bias and the impact of pseudo-subjects. However, the proposed methods can also be applied to non-continuous and/or monotonically changing time-dependent covariates.

The proposed time-dependent TSSA methodology is described in sections 2, 3, and 4. Section 2 provides an overview of the underlying model and the tree-growing procedure, section 3 presents the novel permutation test for time-dependent covariates, and section 4 describes how to use the proposed permutation test to fit a time-dependent TSSA model. In section 5 we present a simulation study that assesses the method's accuracy under a variety of data scenarios, including different levels of within-subject variability and censoring. In section 6 we apply the proposed method to data from a cohort of bipolar youth to identify subgroups at risk for self-injurious behavior. Finally, in section 7 we discuss conclusions, limitations, and future directions.

2. Overview of the Tree-Growing Procedure

2.1. Notation and Underlying Model

Each subject i = 1, . . . , N is observed at times T_i = {t_j : j = 1, . . . , J_i}, where T_i ⊆ T = {t_j : j = 1, . . . , J}. That is, T is the set of all J time points at which each individual i may be observed. Covariates X_ijk, k = 1, . . . , K, are observed for each subject i at each t_j in T_i. A vector of observations across all i, j, and/or k is denoted by replacing the respective subscript with a “.”, e.g., X_i.k = [X_i1k, . . . , X_iJik]·. Thus, the k^th covariate observed across all i and t_j is denoted by X_..k = [X^′_1.k, . . . , X^′_N.K]^′. If covariate k is measured at baseline only, then X_.jk = X_.1k for all j.

Each subject also has an event indicator δ_ij at each of their J_i time points. At times t₁, . . . , t_Ji−1, δ_ij = 0 because the survival outcome has not yet occurred. At time t_Ji, the subject either has a survival event, δ_iJi = 1, or is censored, δ_iJi = 0. We assume that the censoring time is independent of the covariate values. The survival outcome for subject i is denoted by Y_i = (T_i = t_Ji, δ_iJi). The survival outcome for all N subjects is denoted by Y = (T, δ).

The proposed model assumes that the set of observations {X_ij. : i = 1, . . . , N, j = 1, . . . , J}, can be partitioned into H disjoint subsamples, or “terminal nodes” through a series of binary questions of the general form “Is X_ijk ∈ X_L?”. Each terminal node h is associated with a hazard rate λ_h, where h = 1, . . . , H. However, because an individual's covariate values may change over time, the terminal node to which they are assigned (and by extension, their hazard rate) may also change over time. The L_i time points at which subject i switches terminal nodes are denoted by $t_{i1}^{\ast },t_{i2}^{\ast },\dots ,t_{i{L}_i}^{\ast }$. The cumulative hazard function for an individual i at time t_j given their time-dependent covariate values observed up to time t_j is defined as

$$H(t_j\mid X_{i..}^{\left(j\right)})=\{\begin{array}{cc}{\lambda }_i\left(0\right)t_j\hfill & \text{if}{t}_{i0}^{\ast }\le t_j<t_{i1}^{\ast }\hfill \\ {\lambda }_i\left(0\right)t_{i1}^{\ast }+{\lambda }_i\left(t_{i1}^{\ast }\right)(t_j-t_{i1}^{\ast })\hfill & \text{if}{t}_{i1}^{\ast }\le t_j<t_{i2}^{\ast }\hfill \\ ⋮\hfill & \hfill \\ \sum _{l=1}^{L_i}{\lambda }_i\left(t_{il-1}^{\ast }\right)(t_{il}^{\ast }-t_{il-1}^{\ast })+{\lambda }_i\left(t_{i{L}_i}^{\ast }\right)(t_j-t_{i{L}_i}^{\ast })\hfill & \text{if}{t}_{i{L}_i}^{\ast }\le t_j\le t_{J_i},\hfill \end{array}\phantom{\}}$$

where λ_i(t_j) is the hazard rate for subject i at time tj, $X_{i..}^{\left(j\right)}$ denotes the time-dependent covariates for subject i measured through time t_j, and $t_{i0}^{\ast }=0$.

When fitting a tree model, the aim is to identify the specific set of binary questions which lead to the H correct terminal nodes. This requires a method for identifying the correct covariate and cut-point on the full sample and then continuing this process recursively on each subsample until the best tree size has been obtained. After fitting the tree model, the terminal nodes can be summarized in order to characterize their survival distributions.

2.2. Algorithm

We adopt the general algorithm presented by Hothorn et al. [10] to identify the specific set of binary questions which lead to the H correct terminal nodes. Beginning at a node h, the steps in this algorithm are outlined below. Details of each step are provided in the subsequent sections.

1. Test the global null hypothesis of independence between the set of K covariates and the survival outcome Y using the methods proposed in section 3. If the null hypothesis is rejected, continue to step 2. Otherwise, do not split the node.

2. Select the covariate X_..k* associated with the smallest significance level. Then identify the best binary split C* on X_..k* . This split divides X_..k* into two disjoint subsets, ${\mathcal{X}}_R^{\ast }$ and ${\mathcal{X}}_L^{\ast }$. Execute the split C* to create a left child node $h_L=\{(X_{ij.},t_j,{\delta }_{ij}):X_{ij{k}^{\ast }}\in {\mathcal{X}}_L^{\ast }\}$ and a right child node h_R containing all other observations. Details of this step are presented in section 4.

3. Repeat steps 1 – 2 on nodes h_L and h_R.

3. Testing the Global Null Hypothesis of Independence at Each Node

At a node h, the global null hypothesis of independence assumes that the survival distribution does not depend on the covariate values. To test this global null hypothesis, we use permutation tests to obtain a significance level for each of the covariates and then combine these results to obtain an overall significance level. Therefore, in this section we first briefly review permutation tests for survival outcomes with continuous and non-continuous baseline covariates, as proposed by Sun and Sherman [17]. Next, we present novel permutation tests adapted for survival outcomes with continuous and non-continuous time-dependent covariates. Finally, we discuss how to combine the individual permutation test results to obtain a significance level for the global null hypothesis of independence. We note that the permutation tests described in this section are repeated at each node, and thus, the quantities that are used will differ for each node. However, for simplicity we suppress this notation.

3.1. Permutation Test for Baseline Covariates (Sun and Sherman [17])

For a baseline categorical variable X_.1k with M_k predefined strata, the permutation statistic is calculated as

$$U_k=\underset{m,j^{\prime }}{\max }\mid \sum _{j=1}^{j^{\prime }}{w}_{jm}\left(\frac{d_{jm}}{r_{jm}}-\frac{d_j}{r_j}\right)\mid$$ (1)

over m = 1, . . . , M_k and j^′ = 1, . . . , J, where d_jm denotes the number of events at t_j in stratum m, r_jm denotes the number in the risk set at t_j in stratum m, and w_jm is a weight function selected to emphasize early or late events. Similarly, d_j is the number of events over all strata at t_j and r_j is the size of the risk set over all strata at t_j.

For an ordered baseline variable X_.1k, first create M_k quantile-based strata. Ideally, each stratum should have at least 30 observations for sufficient power [17]. The permutation statistic is calculated as

$$S_k=\underset{m^{\prime },j^{\prime }}{\max }\mid \sum _{m=1}^{m^{\prime }}\sum _{j=1}^{j^{\prime }}{w}_{jm}\left(\frac{d_{jm}}{r_{jm}}-\frac{d_j}{r_j}\right)\mid$$ (2)

over m^′ = 1, . . . , M_k and j^′ = 1, . . . , J, where d_j, r_j, d_jm, r_jm, and w_jm are defined as in equation (1). The subscripts on S_k and U_k indicate only that their values are expected to differ depending on the covariate k.

If there is no association between X_.1k and Y , the permutation statistic is not expected to differ from the same statistic computed from a data set for which the N observations in X_.1k have been permuted. Thus, by developing a permutation distribution for the statistic, one has a standard by which to judge its extremeness and calculate a significance level. To develop this permutation distribution, first create P permutations of X _.1k, denoted $X_{.1k}^{\left(p\right)}$, p = 1, ..., P. Then calculate a permutation statistic $U_k^{\left(p\right)}$ or $S_k^{\left(p\right)}$ from each $X_{.1k}^{\left(p\right)}$ using equation (1) or (2).

After the permutation distribution has been developed, the significance level of the relationship between Y and a continuous baseline covariate X_.1k is calculated as

$${\varphi }_k=\sum _{p=1}^{P}I\{S_k\ge S_k^{\left(p\right)}\}∕P.$$ (3)

If X_.1k is a categorical covariate, the statistics S_k and $S_k^{\left(p\right)}$ in equation (3) are replaced with U_k and $U_k^{\left(p\right)}$, respectively.

3.2. Permutation Test for Continuous Time-Dependent Covariates

It is straightforward to extend the statistic S_k in equation (2) to accommodate a continuous time-dependent covariate X_..k by allowing the risk sets r_j and r_jm to change at each t_j. However, developing the permutation distribution for S_k with a time-dependent covariate is more challenging because: 1) the observations are clustered within each subject, 2) within each subject the observations may follow an individual trajectory, and 3) each subject may have a different number of observations.

Motivated by a method proposed by Field and Welsh [18] for bootstrapping clustered data, our strategy is to permute the random effects and residuals estimated from a mixed-effects model in order to predict permutations for each X_ijk. To accomplish this, we assume that each X_i.k, i = 1, . . . , N, follows an individual trajectory

$$X_{i,k}=Z_i^{\left(1\right)}\beta +Z_i^{\left(2\right)}{b}_i+{∊}_{i.},$$ (4)

where β is a q⁽¹⁾ × 1 vector of fixed effects, $Z_i^{\left(1\right)}$ is a J_i × q⁽¹⁾ design matrix linking β to X_i.k, b_i is a q⁽²⁾ × 1 vector of random effects distributed as N_q(2) (0, ∑), and $Z_i^{\left(2\right)}$ is a J_i × q⁽²⁾ design matrix linking b_i to X_i.k. Each ${∊}_{ij}\stackrel{i.i.d.}{\sim }N(0,{\sigma }_{∊}^2)$ is independent of the random effects b_i. The specific model structure in equation (4) can vary for each covariate k; however, this notation has been suppressed for simplicity.

At each node, the model in equation (4) is fit using standard ML or REML methods for all N subjects. We use the lme function from the nlme package in R [19, 20]. From the results, extract the vector of marginal parameter estimates $\widehat{\beta }$, the set of N vectors of empirical best linear unbiased predictions $\left\{{\widehat{b}}_i\right\}$, and the set of ${\sum }_{i=1}^N{J}_i$ conditional residuals $\left\{{\widehat{∊}}_{ij}\right\}$.

Create P permutations of the N vectors in the set $\left\{{\widehat{b}}_i\right\}$. The vector of random effects associated with the p^th permutation for subject i is denoted by ${\widehat{b}}_i^{\left(p\right)}$. Independently, create P permutations of the ${\sum }_{i=1}^N{J}_i$ residuals in the set $\left\{{\widehat{∊}}_{ij}\right\}$. The residual from the p^th permutation for subject i at t_j denoted by ${\widehat{∊}}_{ij}^{\left(p\right)}$. Then, construct p permutation replicates of each X_ijk as from the p^th permutation for subject i at t_j is denoted by ${\widehat{∊}}_{ij}^{\left(p\right)}$. Then, construct P paermutation replicates of each X_ijk as

$$X_{ijk}^{\left(p\right)}=Z_{ij}^{\left(1\right)}\widehat{\beta }+Z_{ij}^{\left(2\right)}{\widehat{b}}_i^{\left(p\right)}+{\widehat{∊}}_{ij}^{\left(p\right)},p=1,\dots ,P,$$ (5)

where $Z_{ij}^{\left(1\right)}$ and $Z_{ij}^{\left(2\right)}$ are the j^th rows of $Z_i^{\left(1\right)}$ and $Z_i^{\left(2\right)}$, respectively. This produces permutations $X_{..k}^{\left(p\right)}=[X_{1.k}^{{\left(p\right)}^{\prime }},\dots ,X_{N.k}^{{\left(p\right)}^{\prime }}]$, p = 1,...,P.

To develop the permutation distribution for S_k, a permutation statistic $S_k^{\left(p\right)}$ is calculated from each $X_{..k}^{\left(p\right)}$ using equation (2). The significance level of the relationship between Y and X_..k is then calculated using equation (3).

3.3. Permutation Test for Non-Continuous Time-Dependent Covariates

For an ordered, non-continuous time-dependent covariate X_..k, the statistic S_k in equation (2) is calculated using the M_k predefined ordered categories. If there are not enough observations in each predefined category, some categories could be combined to create fewer strata. For categorical time-dependent covariates, the statistic U_k in equation (1) is calculated.

We assume that that each non-continuous X_i.k follows a generalized linear mixed effects model,

$$g\left\{E(X_{i.k}\mid b_i)\right\}=Z_i^{\left(1\right)}\beta +Z_i^{\left(2\right)}{b}_i,$$ (6)

where g(·) links the conditional mean of X_i.k to the linear predictor. In this linear predictor, β is a q⁽¹⁾ × 1 vector of fixed effects, $Z_i^{\left(1\right)}$ is a J_i × q⁽¹⁾ design matrix linking β to g{E(X_i.k|b_i)}, b_i is a q⁽²⁾ × 1 vector of random effects distributed as N_q2 (0,Σ), and $Z_i^{\left(2\right)}$ is a J_i × q⁽²⁾ design matrix linking b_i to g{E(X_i.k|b_i)}. The conditional variance of X_i.k is given by v{E(X_i.k|b_i)}φ, where v(·) is a known variance function and φ is a dispersion parameter [21]. The specific model structure in equation (6) can vary for each covariate k; however, this notation has been suppressed for simplicity.

At each node, fit the model in (6) using all N subjects. Then extract the vector of marginal parameter estimates $\widehat{\beta }$ and the set of N vectors of estimated random effects $\left\{{\widehat{b}}_i\right\}$. Create P permutations of the N vectors in the set $\left\{{\widehat{b}}_i\right\}$, where the vector of random effects associated with the p^th permutation for subject i is denoted by ${\widehat{b}}_i^{\left(p\right)}$. Next, create permutations

$$E{\left(X_{ijk}{b}_i\right)}^{\left(p\right)}=g^{-1}\{Z_{ij}^{\left(1\right)}\widehat{\beta }+Z_{ij}^{\left(2\right)}{\widehat{b}}_i^{\left(p\right)}\},p=1,\dots ,P,$$

where $Z_{ij}^{\left(1\right)}$ and $Z_{ij}^{\left(2\right)}$ are defined as in equation (5). Finally, to get permutations of X_ijk, sample each $X_{ijk}^{\left(p\right)}$ from its distribution with mean $E{(X_{ijk}\mid b_i)}^{\left(p\right)}$, considering the dispersion parameter φ if necessary. For example, if X_ijk is binary (φ = 1), sample $X_{ijk}^{\left(p\right)}\sim Bernoulli\left(E{\left(X_{ijk}{b}_i\right)}^{\left(p\right)}\right)$. Because the conditional variance is defined as a function of the conditional mean, the residual does not need to be incorporated separately as was done for continuous $X_{ijk}^{\left(p\right)}$.

To develop the permutation distribution for S_k or U_k, a permutation statistic $S_k^{\left(p\right)}$ or $U_k^{\left(p\right)}$ is calculated from each $X_{..k}^{\left(p\right)}$ using equation (2) or (1), respectively. The significance level of the relationship between Y and X_..k is calculated as shown in equation (3).

3.4. Combining Individual Permutation Test Results for the Global Null Hypothesis Test

We use a method proposed by Efron and Tibshirani [22] to test the global null hypothesis of independence between Y and the set of K covariates while accounting for multiple comparisons. This method provides the correct level of significance for a set of K permutation tests by comparing φ_k* = min_k (φ_k) to its own permutation distribution.

To implement this method in TSSA, first apply a permutation test to each covariate under consideration for splitting the node. For each covariate k = 1, . . . , K, this produces a significance level φ_k, a test statistic S_k, and a permutation distribution $S_k^{\left(p\right)}$, p = 1, . . . , P . (For simplicity of notation in this section, we generically use S_k to denote statistics from either continuous or categorical covariates.) Then, compute the proportion of the permuted statistics at least as extreme as each $S_k^{\left(p\right)}$,

$$A_k^{\left(p\right)}=\sum _{p^{\prime }=1}^{P}I\left\{S_k^{\left(p^{\prime }\right)}\ge S_k^{\left(p\right)}\right\}∕P,p=1,\dots ,P,k=1,\dots ,K.$$

Next, compute the permutation replicates for φ_k*,

$${\varphi }_{k^{\ast }}^{\left(p\right)}=\underset{k}{\min }\left\{A_k^{\left(p\right)}\right\},p=1,\dots ,P.$$

Finally, compute the significance of the global null hypothesis test,

$$\varphi =\sum _{p=1}^{P}I\left\{{\varphi }_{k^{\ast }}^{\left(p\right)}\le {\varphi }_{k^{\ast }}\right\}∕P.$$

If φ is less than the selected type-1 error rate α, the global null hypothesis is rejected and the node is allowed to split.

Because the global null hypothesis at each node is adjusted for multiple comparisons, including too many unrelated covariates can mask the presence of a related covariate. For this reason, it is useful to carefully consider the set of covariates used in the proposed tree model. An exploratory approach for developing a pre-selected set of covariates is to first fit a tree model with a large α. Then, fit a second tree model using a more standard α and only include the covariates that entered into the first model. An alternative approach is to use clinical and research evidence to carefully specify an a priori hypothesis regarding a set of covariates that is expected to be related to the outcome and then grow the tree using only this set of covariates. We use the latter approach in the illustration in section 6.

4. Detecting and Executing the Optimal Binary Split

If the global null hypothesis is rejected at a node, the covariate associated with φ_k* = min_k (φ_k) is selected and denoted by X_..k*. It is possible for two or more covariates to have the same significance level, resulting in uncertainty regarding which variable to select. Most commonly, this will occur when the true significance levels for two or more covariates are less than 1/P , thus making it impossible to differentiate among them. Increasing P can provide more sensitivity for distinguishing among the tied covariates; however, the tradeoff is that it increases computation time in the tree algorithm. If two or more covariates remain tied even with a very large P , one could select multiple covariates as having equally strong associations with the outcome and then identify the best split out of all selected covariates.

After identifying the covariate X_..k* that has the strongest association with the outcome, the next step is to identify the best binary split on X_..k*. We recommend a two-sample rank statistic in the Tarone-Ware family, such as the Log Rank statistic, because it is relatively straightforward to implement for both baseline and time-dependent covariates. Bacchetti and Segal [14] originally proposed the use of this splitting statistic for a time-dependent TSSA method that exhaustively searches all binary split on all covariates. We briefly summarize this method here, and refer the reader to Bacchetti and Segal [14] for additional details.

For each possible binary split C that divides X_..k* into disjoint subsets X_L and X_R, calculate

$$TW=\frac{{\sum }_{j=1}^J{w}_j\{d_{jL}-E\left(d_{jL}\right)\}}{\sqrt{\left\{{\sum }_{j=1}^J{w}_j^{2}Var\left(d_{jL}\right)\right\}}},$$

where d_jL is the number of events among subjects with X_ijk* ∈ X_L at t_j and the w_j are weights. Setting w_j = 1 for all j results in the Log Rank statistic. Under the null hypothesis of a non-informative cutoff value C, TW follows a hypergeometric distribution with

$$E\left(d_{jL}\right)=\frac{r_{jL}{d}_j}{r_j}$$

and

$$Var\left(d_{jL}\right)=\frac{r_{jL}{d}_j(r_j-r_{jL})(r_j-d_j)}{(r_j-1)r_j^2},$$

where r_jL is the number of subjects at risk with X_ijk* ∈ X_L at t_j, d_j is the number of events at t_j, and r_j is the number of subjects at risk at t_j. To accommodate time-dependent covariates, the risk sets are allowed to change at each time point [14].

The split C that produces the maximum absolute value TW statistic is denoted by C*. This split divides X_..k* into disjoint subsets ${\mathcal{X}}_L^{\ast }$ and ${\mathcal{X}}_R^{\ast }$, thereby partitioning the sample into a left child node $h_L=\{(X_{ij.},t_j,{\delta }_{ij}):X_{ij{k}^{\ast }}\in {\mathcal{X}}_L^{\ast }\}$ and a right child node h_R containing all other observations. When X_..k* is a time-dependent covariate, the observations for a subject i will be divided between h_L and h_R if there are some time points for which $X_{ij{k}^{\ast }}\in {\mathcal{X}}_L^{\ast }$ and others for which $X_{ij{k}^{\ast }}\in {\mathcal{X}}_R^{\ast }$. Observations from subject i sent to h_L are indexed as pseudo-subject i_L; all other observations from subject i are sent to h_R and indexed as pseudo-subject i_R. At each t_j, a subject i may exist in may exist in either h_L or h_R, but not both. Thus, the survival event can only contribute to a single child node [14].

5. Simulation Study

This simulation study assessed the accuracy of trees grown using the proposed time-dependent TSSA method based on three levels of within-subject variability and three levels of censoring. After fitting each tree, we evaluated whether the correct covariate was selected to split each node and whether the cut-point was unbiased. We used an independent sample to determine whether the tree could accurately discriminate between two subjects with different survival outcomes. As a standard of comparison, we also fit trees that incorporated only baseline covariate values. All computing was performed in R.

5.1. Data Generation

For each of three levels of within-subject variability, ${\sigma }_{∊}^2=\{10,20,40\}$, a continuous time-dependent covariate was generated as $X_{ij1}\mid b_i\sim N(50+b_i,{\sigma }_e^2)$, with b_i ~ N(0, 20) and t_j = 0, . . . , 20. This resulted in intraclass correlations (ICCs) of .67, .50, and .33, corresponding to low, medium, and high within-subject variability, respectively. The ICC of .33 was selected to reflect the ICC of the “Percentage of Weeks in a Major Depressive Episode” time-dependent covariate from the Course and Outcome of Bipolar Youth (COBY) data presented in section 6. Although the maximum number of time points in the COBY study was 44, we used only 21 time points in the simulation study to shorten computational time. A fixed-time binary covariate X_..2 was also generated by first sampling X_i12 ~ Bernoulli(.5) and then setting X_ij2 = X_i12 for j = 2, . . . , 21. We included this binary covariate because the tree created with the COBY data split on a binary covariate and also because it emphasizes the utility of the proposed method with covariates measured on extremely different scales.

To generate the true event time T* (prior to any censoring), the simulated covariates X_..1 and X_..2 were first used to classify each subject's observations into a terminal node at each time point, as shown in Table 1. These hazard rates were selected so that the first split on X_ij1 had a slightly larger hazard ratio than the second split on X_ij2 and to ensure that data sets with 10%, 30%, and 50% censoring could be created given the constraint of a maximum observed event time of 20 (the last time point at which the time-dependent covariate can be observed).

Table 1.

Terminal nodes used in the simulation study.

Terminal Node	Cut Points	Hazard Rate
1.	Xij1≤ 50, Xij2 = 0	λi(tj) = .007
2.	Xij1 ≤ 50, Xij2 = 1	λi(tj) = .07
3.	Xij1 > 50	λi(tj) = .5

The time points at which subject i switches terminal nodes are denoted by $t_{i1}^{\ast },\dots ,t_{i{L}_i}^{\ast }$. These terminal node switches divide the observation period into a series of discrete time domains $D_{i1}=[0,t_{i1}^{\ast })$, $D_{i2}=[t_{i1}^{\ast },t_{i2}^{\ast })$, ... $D_{i\left(L_{i+1}\right)}=[t_{i{L}_i}^{\ast },20)$. The corresponding ranges of cumulative hazards over each domain are ${\mathcal{R}}_{i1}=[0,{\lambda }_i\left(0\right)t_{i1}^{\ast })$, ${\mathcal{R}}_{i2}=[{\lambda }_i\left(0\right)t_{i1}^{\ast },{\lambda }_i\left(0\right)t_{i1}^{\ast }+{\lambda }_i\left(t_{i1}^{\ast }\right)(t_{i2}^{\ast }-t_{i1}^{\ast })),\dots {\mathcal{R}}_{i(L_i+1)}=[{\sum }_{l=1}^{L_i}{\lambda }_i\left(t_{il-1}^{\ast }\right)(t_{il}^{\ast }-t_{il-1}^{\ast }),\infty )$, where λ_i(t_j) represents the hazard for subject i at t_j. The event time $T_i^{\ast }$ is then generated for each i = 1, . . . , N based hazard distribution

$$T_i^{\ast }=\{\begin{array}{cc}\frac{t_i}{{\lambda }_i\left(0\right)}\hfill & \text{if}{t}_i\in {\mathcal{R}}_{i1}\hfill \\ \frac{t_i-{\lambda }_i\left(0\right)t_{i1}^{\ast }+{\lambda }_i\left(t_{i1}^{\ast }\right)t_{i1}^{\ast }}{{\lambda }_i\left(t_{i1}^{\ast }\right)}\hfill & \text{if}{t}_i\in {\mathcal{R}}_{i2}\hfill \\ ⋮\hfill & ⋮\hfill \\ \frac{t_i-\sum _{j=1}^{L_i}{\lambda }_i\left(t_{ij-1}^{\ast }\right)(t_{ij}^{\ast }-t_{ij-1}^{\ast })+{\lambda }_i\left(t_{i{L}_i}^{\ast }\right)t_{L_i}^{\ast }}{{\lambda }_i\left(t_{i{L}_i}^{\ast }\right)}\hfill & \text{if}{t}_i\in {\mathcal{R}}_{i{L}_i}+1\hfill \end{array}\phantom{\}}$$

where t_i = − log(u_i), with u_i ~ Unif(0, 1) [23].

In the COBY data, some youth were censored at the end of the study observation period while others dropped out over the course of the study. To mimic this scenario, we generated the censoring distribution as C_i = P_i min(G_i, 20) + (1 − P_i)20, where P_i ~ Bernoulli(p) and G_i ~ Exp(.007). This resulted in approximately 10% censoring when p = 0, 30% censoring when p = .5, and 50% censoring when p = 1. The final observed survival time is denoted by $T_i=min(C_i,T_i^{\ast })$.

For each of the nine data scenarios (three levels of censoring and three levels of within-subject variability), 200 training and 200 testing data sets of N = 400 each were generated. This N was selected to reflect the COBY data. The relatively small number of simulations was a result of the computational intensity of the proposed methods.

5.2. Fitting and Evaluating the Tree Models

For each training data set, both a baseline tree and a time-dependent tree were fit. The baseline tree included only the baseline values of X_..1 and the baseline covariate X_..2. The time-dependent tree included the time-dependent covariate X_..1 and the baseline covariate X_..2. Although some tree simulations incorporate noise variables as competition, we included only the two relevant covariates because we have found that tree methods which require a global null hypothesis test at each node provide the most meaningful models when the set of covariates has been carefully selected a priori (see additional discussion in subsection 3.4). We wanted the simulation study to reflect this.

We used a linear mixed-effects model with only a fixed and random intercept to create each covariate's permutation distribution at each node. We set P = 1000 based on recommendations by Efron and Tibshirani [22], M = 5 based on simulations by Sun and Sherman [17], w_jm = 1 for all j and m, and α = .05. We used the Log Rank statistic to select the optimal split and required at least 30 observations in each child node.

To evaluate the structural accuracy of the models created using the training data, we calculated the proportion of trees that selected the correct covariate at the first split. Conditional on selecting the correct covariate at the first split, we calculated the bias of the cut-point at the first split and the proportion of trees that selected the correct covariate at the second split.

To evaluate the discriminative accuracy of the models, we used each baseline and time-dependent tree created with training data to classify time-dependent observations from an independent testing data set. We then calculated the time-dependent Harrell's C discrimination index using the Kaplan-Meier survival estimates at each node [24, 25]. This statistic can be interpreted as a time-dependent AUC measure, with higher values indicating the model can more accurately discriminate between two subjects with different survival outcomes. If a model did not identify any splits, the time-dependent AUC was set to .5 to indicate that it could not provide any information for distinguishing between two subjects’ survival outcomes.

5.3. Results

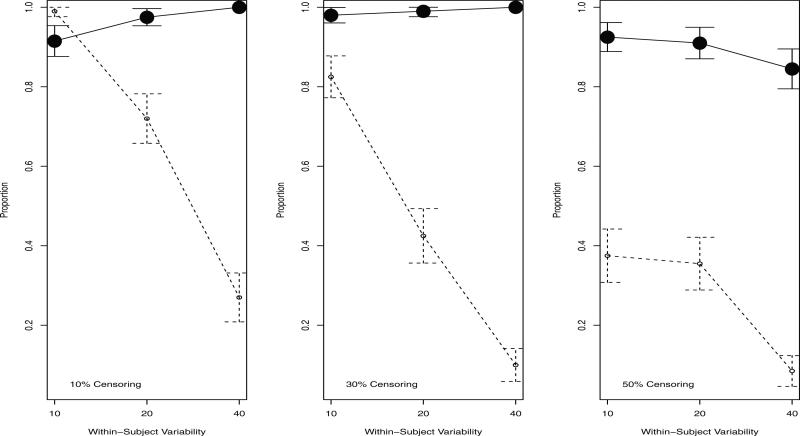
Figure 1 shows the proportion of trees that selected the correct covariate at the first split. Regardless of the amount of censoring or within-subject variability, the proportion of time-dependent trees that selected the correct covariate was estimated to be very high (between .85 and 1). The baseline tree model performed better than the time-dependent tree model under 10% censoring and low within-subject variability. Under these specifications, the baseline value is likely to be highly predictive of the value observed at the time of the event, but without the added complexity of the time-dependent covariate. However, the accuracy of the baseline tree model dropped very rapidly with larger levels of censoring and within-subject variability.

Figure 1.

Proportion (95% CI) of 200 trees that selected the correct covariate for split 1. This node split on a continuous, time-dependent covariate. Solid line: time-dependent tree. Dashed line: baseline tree.

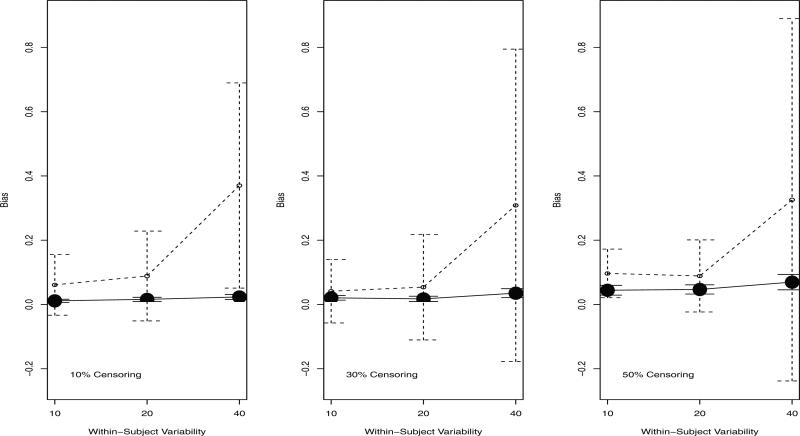
The bias of the selected cut-point at the first split is shown in Figure 2. The time-dependent trees had only a small estimated bias and had very tight confidence intervals, regardless of the level of censoring or within-subject variability. The baseline trees became more biased with larger confidence intervals as the within-subject variability increased. Because fewer baseline trees selected the correct covariate at the first split, there were fewer trees with which to estimate the bias of the cut-point. Thus, the wider confidence intervals for the baseline trees may reflect these smaller sample sizes.

Figure 2.

Mean bias (95% CI) of the selected cut-point at split 1 among trees with the correct variable selected at split 1. Solid line: time-dependent tree. Dashed line: baseline tree.

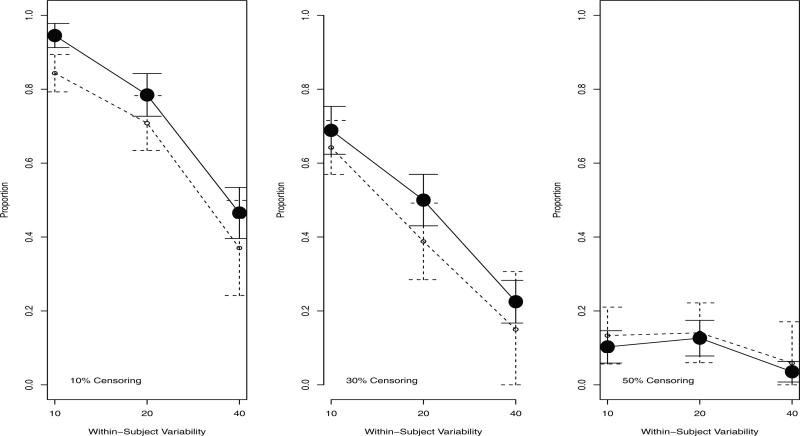
The proportion of trees that correctly selected the binary baseline covariate at split 2, conditional on having also selected the correct covariate split 1, is shown in Figure 3. Both the baseline and time-dependent trees were less likely to select the correct covariate at split 2 than at split 1. However, for the time-dependent trees, censoring and within-subject variability had a much greater impact at split 2 than at split 1. One explanation for this differential pattern is that the pseudo-subjects created at split 1 diminished the ability of the time-dependent tree model to select the correct covariate at subsequent splits. Another explanation is that the time-dependent covariate remained highly predictive even after the first split, and thus, the time-dependent trees continued to select it over the correct binary covariate.

Figure 3.

Proportion (95% CI) of trees that selected the correct variable for split 2, conditional on having selected the correct variable for split 1. Solid line: time-dependent tree. Dashed line: baseline tree.

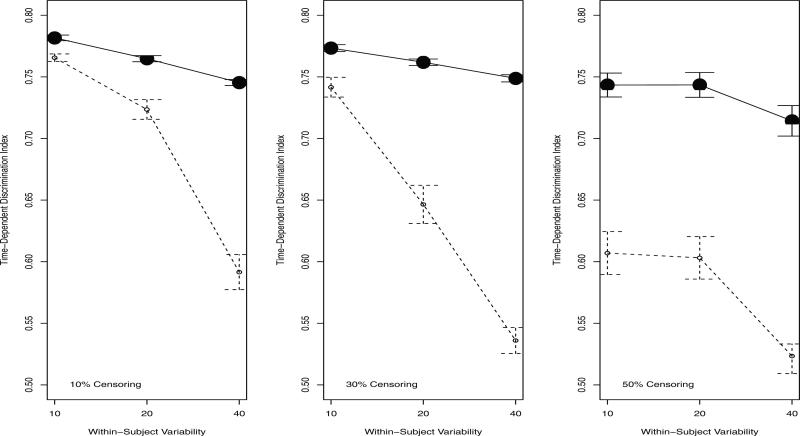
Figure 4 shows the time-dependent AUC. Note that the scale in this figure ranges only from .5 − 1. The time-dependent trees accurately discriminated between new subjects with different survival outcomes, with estimated AUCs ranging from .71 to .78. These values are all above the cutoff for a “large” effect size [26]. The relatively large AUC values at higher levels of censoring and within-subject variability (where the time-dependent trees were not likely to select the correct covariates at both splits) highlights an important feature of tree models. That is, even if the structure of the tree is not completely accurate, the model can still have good discriminatory abilities. The baseline trees were significantly worse at discriminating between subjects with different survival outcomes, with estimated AUCs ranging from .52 to .77. Overall, these findings indicate that incorporating time-dependent information can substantially increase the accuracy and clinical utility of TSSA models, especially with relatively large within-subject variability and high censoring rates.

Figure 4.

Time-dependent discrimination index (AUC) and 95% CI based on an independent sample of N = 200. A value of 1 represents perfect discrimination between individuals with different survival outcomes; a value of .5 is equivalent to discrimination based only on chance. Note that the scale ranges only from .5 to 1. Solid line: time-dependent tree. Dashed line: baseline tree.

6. Time to Self-Injury in Youth with Bipolar Disorder

The data used in this illustration are from a naturalistic, longitudinal study called “Course and Outcome of Bipolar Youth” (COBY) [27]. In our sample from this study, 386 youth with bipolar disorder were followed for up to 11 years. During this time, they had regular clinic assessments (approximately every 6 months) to retrospectively capture weekly data including their mood states (depressed, manic/hypomanic, or mixed), time spent in psychosocial inpatient or outpatient treatment, substance use, and any self-injury.

Previously, Goldstein et al. [1] used a time-dependent Cox model to explore factors associated with suicide attempts (self-injury with suicidal intent and/or lethality) using the COBY data. Because the weekly retrospective mood, treatment, and substance use data may be subject to recall bias and strong autocorrelation, they were summarized within 8-week intervals which were then used as time-dependent covariates in the Cox model. Results showed that having first-degree relatives with a mood disorder, spending more time in a depressed mood state, spending more time with mixed depression and mania/hypomania symptoms, spending more time with a substance use disorder, and spending less time in psychosocial treatment were all associated with increased risk of a suicide attempt. The use of 6- or 12-week summary intervals resulted in similar inferences.

To extend this work, our aim was to apply the proposed time-dependent TSSA method to the COBY data to identify subgroups with different levels of risk for self-injurious behavior. We focused on all incidents of self-injury instead of only those self-injurious behaviors with suicidal intent and/or lethality to increase the percentage of events (18% of youth had self-injuries that were rated as suicide attempts, while 33% of youths had any self-injury). Prior to fitting the tree model, we examined plots of the time-dependent covariates created based on 8- and 12-week intervals. The covariates based on 12-week intervals could be better approximated using a linear model and they also resulted in residuals that were more normally distributed. Since Goldstein et al.[1] obtained similar results when using 8- or 12-week intervals, we opted to use the covariates based on 12-week intervals for our analyses.

6.1. Model Fitting

We fit a time-dependent TSSA model that included a baseline indicator variable for whether the youth had any first-degree family members with a mood disorder and four time-dependent variables: 1) percentage of weeks spent in a depressed mood state, 2) percentage of weeks with mixed symptoms, 3) percentage of weeks with a substance use disorder, and 4) percentage of hours in psychosocial treatment. For comparison, we also fit a time-dependent Cox model and a baseline TSSA model. The time-dependent Cox model included the binary baseline covariate and continuous versions of the time-dependent covariates. The baseline TSSA model included the binary baseline covariate and only the baseline values of the time-dependent covariates (i.e., the observations from the first 12-week interval).

To develop a permutation distribution for each covariate at each node in the time-dependent TSSA model, we used linear mixed-effects models that incorporated only fixed and random intercept terms. This model was selected to provide a simpler illustration and also because COBY was a naturalistic study where youth were not necessarily expected to change systematically over time (this was also confirmed visually through plotting the data). Other TSSA model parameters were set equal to those used in the simulation study in section 5.

6.2. Results

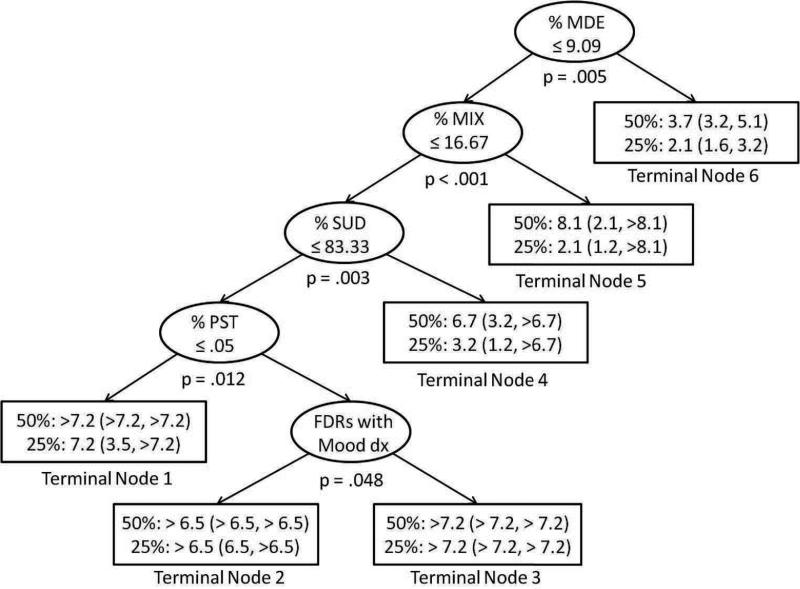
The time-dependent TSSA model is shown in Figure 5. All covariates previously found to be significant for predicting self-injury by Goldstein et al. [1] entered into the time-dependent TSSA model, confirming the relevance of these particular time-dependent and baseline covariates. Terminal nodes 1, 2, and 3 were associated with the lowest risk of self-injury. Youth would be classified into one of these three nodes if they spent ≤ 9.09% of the past 12 weeks in a major depressive episode, ≤ 16.15% of the past 12 weeks with mixed mood symptoms, and ≤ 83.33% of the past 12 weeks with a substance use disorder. Terminal nodes 4, 5, and 6 were associated with the highest risk of self-injury. Youth would be classified into one of these nodes if they spent > 9.09% of the past 12 weeks in a major depressive episode or > 16.67% of the past 12 weeks with mixed symptoms or > 83.33% of the past 12 weeks with a substance use disorder.

Figure 5.

Time-dependent tree-structured survival analysis model. Each terminal node of the tree shows estimated time to 50% events and 25% events, along with 95% confidence intervals. For continuous variables, observations ≤ the cut point are sent to the left child node. For the categorical variable, observations with no first degree relatives with a mood disorder are sent to the left child node. Abbreviations: % MDE = % Weeks in a major depressive episode, % MIX = % Weeks with mixed mood symptoms, % SUD = % Weeks with a substance use disorder, % PST = % Hours spent in inpatient or outpatient psychosocial treatment, FDRs with Mood dx = First degree relatives with a history of mood disorders.

When using only the baseline values of the time-dependent covariates, the global null hypothesis at the root node was not rejected (p = .082) so no splits occurred. Upon examining the individual permutation tests of the baseline covariates, the percentage of time spent in a mixed mood state during the first 12 weeks was significant (p = .032) and having a first degree relative with a mood disorder was also significant (p = .01). However, because the other three covariates had higher non-significant p-values, the global null hypothesis accounting for multiple comparisons was not rejected.

The results from the time-dependent Cox proportional hazards model are shown in Table 2. Spending more weeks in a major depressive mood state, spending more weeks with a substance use disorder, and having a first degree relative with a mood disorder were associated with a higher risk of self-injury. Neither the percent of weeks spent in a mixed mood state nor the percent of time in psychosocial treatment were significant predictors.

Table 2.

Results from the Cox proportional hazards model for time to self injury.

Covariate	β	Exp(β)	SE(β)	z	p-value
First Degree Relative with a Mood Disorder	0.550	1.733	0.251	2.19	.029
% Weeks in Major Depressive Mood State	0.019	1.019	0.003	6.40	< .001
% Weeks in Mixed Mood State	−0.001	0.999	0.004	−0.390	.700
% Weeks with Substance Use Disorder	0.006	1.006	0.002	2.22	.026
% Hours in Psychosocial Treatment	−0.007	0.993	0.006	−1.23	.220

The side-by-side comparison of the time-dependent Cox proportional hazards model and the time-dependent TSSA model emphasizes the benefits and the disadvantages of each. The time-dependent TSSA model is beneficial because it suggests specific cutoff values that indicate whether a youth is at higher or lower risk and also produces a simple, clinically meaningful algorithm for determining a new youth's risk group at any time across follow-up. Conversely, a benefit of the Cox model is that it quantifies the extent to which higher or lower values of each time-dependent covariate will change the risk of self-injury, which can also be meaningful. Thus, both models provide useful – but different – information on the impact that a particular covariate or set of covariates may have on a patient's survival.

Unlike the Cox model, the time-dependent TSSA model can easily accommodate more complex covariate relationships. Based on the Cox model results in Table 2 alone, it may appear that only three of the five covariates are meaningful for predicting time to self-injury. However, the time-dependent TSSA model reveals that the two variables which were not significant in the Cox model are actually predictive in some covariate-defined subsets of the data.

We compared the predictive abilities of the time-dependent Cox and TSSA models using the time-dependent AUC. The time-dependent TSSA model had an AUC of only .59, while the time-dependent Cox model had a much higher AUC of .71. These AUCs would likely be reduced if a second, independent sample (i.e., a sample not used to grow the tree) had been used for their estimation. The low AUC for the time-dependent TSSA model is not unexpected if one extrapolates the results of the simulation study, which was based on a much simplified version of the COBY data. Compared to the data used in the simulation, the actual COBY data used in this illustration had over double the number repeated measures, a larger proportion of censoring, and more time-dependent covariates. Thus, although the COBY data are ideal for highlighting the usefulness of the time-dependent TSSA model relative to the baseline TSSA model, the features of this data set provide a challenge with respect to the proposed model's predictive accuracy.

7. Discussion

This manuscript presents novel methodology for incorporating time-dependent covariates into tree-structured survival analysis (TSSA), including a new permutation test for time-dependent covariates. Unlike currently available methods, the proposed method reduces variable selection bias by selecting the covariate on which to split based on unbiased significance levels from permutation tests. In addition, pruning the tree is not required with the proposed method because a node only splits when the test of the global null hypothesis is rejected. This simplifies the tree growing procedure and also provides a level of significance for each split. Prior to our work, research in time-dependent TSSA focused primarily on the simpler yet somewhat impractical scenario of monotonically changing time-dependent covariates. However, the simulation studies and illustration presented herein show that the proposed time-dependent TSSA method performs well even with non-monotonically changing time-dependent covariates.

Although the proposed method has many benefits, there are also limitations to be considered. In particular, the proposed method is very computationally intensive because it requires a permutation test for each covariate at each node. The computational intensity is amplified when the data have a large number of subjects and/or a large number of observations per subject. There are also some restrictions on when the method would be appropriate. The censoring distribution should be independent of the covariates, and it must be reasonable to assume that the tree model would be constant over time. The illustration we presented was based on an observational study where the sample was not expected to change systematically, and thus, we believed that the assumption of a constant tree model over time was realistic. However, this may not be true for all studies.

The proposed method uses a mixed-effects model as a tool to create permutations for a time-dependent covariate X_..k. Therefore, the permutation test is limited by the accuracy of the model used to predict the time-dependent covariate. In the simulation and application sections, we modeled each X_..k with only fixed and random intercept terms in order to present straightforward examples. In practice, however, it is possible that additional fixed or random effects may be required to accurately model X_..k. In particular, time is commonly included as fixed and/or random effect when fitting a mixed-effects model. It is important to note that when additional fixed or random effects such as time are included in the model, the permutation test is actually assessing the strength of the relationship between Y and X_..k after adjusting for these other variables. Somewhat more complex is the scenario where clinical and/or demographic variables are required to accurately model the time-dependent covariates, because it is possible that these variables might also be considered to be predictors in the tree model. Further research must be performed in order to investigate the robustness of the proposed tree model when 1) the mixed-effects model requires additional covariates and/or is misspecified; and 2) assumptions of the mixed-effects model (e.g., normally distributed residuals) are not met.

There are a number of additional aspects of the model that need to be evaluated through further research. First, the number of strata required for the time-dependent permutation test should be investigated. More strata provide greater power to detect non-proportional hazards. However, if too many strata are used, there may not be enough unique observations in each strata at nodes further down the tree. Second, based on the low AUC observed in the COBY illustration, an important step will be to asses the proposed model with multiple time-dependent covariates and longer follow-up times. Third, the model should be assessed in the presence of informative censoring, which may be common in survival analysis. Finally, the proposed time-dependent TSSA method is based on permutation testing, which has previously been shown by Hothorn et al. [10] to produce unbiased baseline variable selection in tree models. Further research and simulation studies should be performed in order to prove the proposed permutation test is consistent and to quantify the extent to which the proposed time-dependent TSSA method reduces variable selection bias.