Abstract
We propose an echo planar imaging (EPI) distortion correction method (DR-BUDDI), specialized for diffusion MRI, which uses data acquired twice with reversed phase encoding directions, often referred to as blip-up blip-down acquisitions. DR-BUDDI can incorporate information from an undistorted structural MRI and also use diffusion-weighted images (DWI) to guide the registration, improving the quality of the registration in the presence of large deformations and in white matter regions. DR-BUDDI does not require the transformations for correcting blip-up and blip-down images to be the exact inverse of each other. Imposing the theoretical “blip-up blip-down distortion symmetry” may not be appropriate in the presence of common clinical scanning artifacts such as motion, ghosting, Gibbs ringing, vibrations, and low signal-to-noise. The performance of DR-BUDDI is evaluated with several data sets and compared to other existing blip-up blip-down correction approaches. The proposed method is robust and generally outperforms existing approaches. The inclusion of the DWIs in the correction process proves to be very important to obtain a reliable correction of distortions in the brain stem. Methods that do not use DWIs may produce a visually appealing correction of the non-diffusion weighted b = 0 s/mm2 images, but the directionally encoded color maps computed from the tensor reveal an abnormal anatomy of the white matter pathways.
Keywords: Echo planar imaging, Diffusion tensor imaging, Reversed phase encoding, Diffeomorphic image registration
1. Introduction
In the past couple of decades, Diffusion Tensor Imaging (DTI) (Basser et al., 1994; Pierpaoli et al., 1996) and high angular resolution diffusion imaging (HARDi) (Wedeen et al., 2000; Tuch, 2002, 2004; Tuch et al., 1999; Frank, 2002; Jansons and Alexander, 2003) have been extensively used to investigate the architecture of the human brain. Diffusion-weighted images (DWIs) required for these MRI techniques are generally acquired with echo planar imaging (EPI) (Turner and Le Bihan, 1990). EPI has the advantage of being a very efficient acquisition modality, with excellent signal-to-noise per time. However, a well-known problem in EPI is the presence of geometric distortions along the phase-encode direction caused by B0 field inhomogeneities (Jezzard and Balaban, 1995) and concomitant fields (Du et al., 2002). In addition, local compression due to these distortions cause “signal pile-ups” whereas expansions cause a decrease in signal intensities. These EPI distortions are different from eddy current distortions, which are caused by the rapid switching of the diffusion sensitizing gradients. While eddy current distortions affect the diffusion-weighted images significantly more than the images acquired without diffusion sensitization (so called b = 0 s/mm2 images), all images are affected by EPI distortions in the same manner. Negative effects of EPI distortions in diffusion MRI have been reported (Wu et al., 2008; Irfanoglu et al., 2012). Although most diffusion MRI processing pipelines include correction strategies for eddy current distortions, correction of EPI distortion is still rarely performed.
Correction of EPI distortions generally requires the acquisition of additional data. Jezzard and Balaban (1995) proposed to map the static magnetic field (or B0) and use this information to perform the EPI correction. Numerous other methods based on B0 mapping have been proposed (Reber et al., 1998; Lee et al., 2004; Pintjens et al., 2008; Techavipoo et al., 2009). Correction methods that do not require B0 field maps but other data types, such as dedicated T1 or T2 weighted structural targets, have also been proposed (Kybic et al., 2000; Wu et al., 2008; Tao et al., 2009; Irfanoglu et al., 2011). In their work, Wu et al. (2008) showed that their registration-based correction method performs similarly to B0 mapping methods.
Even though both B0 mapping and image registration based correction methods have been shown to improve geometric distortions (Wu et al., 2008; Irfanoglu et al., 2012), they are inadequate in the presence of extreme signal pile-up. Essentially, in regions of the distorted image with signal pile-ups, the resulting voxel signal is a superposition of signals from several voxels in the undistorted image, and the question of how to redistribute this signal back to its corresponding locations is an under-determined (one-to-many) problem and cannot be solved with typical EPI plus B0 maps or EPI plus structural information settings.
One solution to the signal pile-up problem involves the acquisition of the same image twice with reversed phase-encoding gradients, as initially proposed by Chang and Fitzpatrick (1992) for images suffering from field inhomogeneities due to imperfections in the magnet system or magnetization of the object being imaged. This method is referred to as “blip-up blip-down” in this work. The distortion field in the two images is reversed: the signal “pile-up” regions in one image correspond to regions of signal “dilution” and vice-versa. This provides the necessary information for the originally under-determined system to redistribute the signals to their correct locations. In their work adapting this method to EPI, Bowtell et al. (1994) and Morgan et al. (2004) proposed using the “cumulative line-integral” method, which states that the cumulative signal along a phase-encoding line between corresponding points in the up and down images should be equal and that these points should be equidistant to the true anatomical location. They also showed the improvements obtained with their method on diffusion data, specifically apparent diffusion coefficient maps obtained from three diffusion-weighted images (Morgan et al., 2000). Other groups have reported improvements with similar blip-up blip-down strategies for fMRI and DTI data (Voss et al., 2005a,b; Embleton et al., 2010). These methods suffer from numerical instabilities and because of their 1D nature (phase-encoding lines), the computed displacement fields were non-smooth. In their work, Andersson et al. (2003) proposed a different strategy, which aimed to estimate the B0 map from the two images acquired with reversed phase encoding, using an image restoration approach. This methodology, which was later released as part of the FSL package (Smith et al., 2004) under the name TOPUP, operates on 3D space instead of the initial method’s 1D and can redistribute the signal with a least-squares based method once the B0 map is estimated. TOPUP has since become a popular blip-up blip-down correction methodology and has been the tool of choice for the Connectome project (Sotiropoulos et al., 2013).
A few years ago, Holland et al. (2010) proposed a simple and efficient nonlinear, non-parametric image registration based EPI distortion correction scheme, EPIC, based on hierarchical smoothing of distorted images. This method has been experimentally implemented in a Siemens scanner (Benner et al., 2011) and its robustness tested under different conditions (Shin et al., 2011). In addition to diffusion MRI, it also has been applied to perfusion MRI (Vardal et al., 2013). Other forms of registration-based correction algorithms, such as Demons registration and variational optimization based methods have also been proposed in the blip-up blip-down context (Lyksborg et al., 2012; Olesch et al., 2010), and special deformation field regularizers to better physically model the displacement field have been employed (Ruthotto et al., 2012).
Blip-up blip-down protocols have also been used for purposes other than EPI distortion correction, such as eddy current correction for DWIs (Bodammer et al., 2004), vibration artifact correction (Mohammadi et al., 2012), correction of distortions due to metallic objects (Skare and Andersson, 2005) and N/2 ghosting (Xiang and Ye, 2007). There have also been significant developments on the acquisition front (Bhushan et al., 2013; Gallichan et al., 2010; Chang et al., 2013).
The aforementioned blip-up blip-down distortion correction methods significantly improve correction quality for EPI distortions, compared with field-mapping and registration techniques. However, there are instances in which they still perform sub-optimally. While experimenting with existing tools on highly distorted diffusion MRI data, we experienced less than satisfactory outcomes, possibly due to the limitations of the underlying physical model, i.e., the “blip-up blip-down distortion symmetry”, which assumes a constant B0 field regardless of subject motion, magnetic field drift from heating, and identical shimming between acquisitions. Furthermore, the presence of imaging artifacts, such as Gibbs ringing around signal pile-ups, N/2 ghosts, hitting the noise floor in expanded regions, and signal drop-outs, change the mass and the distribution of the cumulative signals. Finally, in the case of diffusion data, the deformation field to be used for correction is typically calculated using blip-up and blip-down b = 0 s/mm2 images. This deformation field may inadequately describe the distortion in regions with uniform T2 and proton density contrast. In this work, we propose a novel correction framework based on Diffeomorphic Registration for Blip-Up blip-Down Diffusion Imaging (DR-BUDDI). We will first build the mathematical framework of the proposed method and depict our entire processing pipeline, which is now part of the publicly available TORTOISE diffusion MRI processing package (Pierpaoli et al., 2010). We will then report DR-BUDDI’s performance relative to existing strategies and subsequently raise several questions that can potentially affect any blip-up blip-down correction approach and analyze their effects.
2. Materials and Methods
The distinct properties of the DR-BUDDI correction framework are as follows:
The deformation model (Section 2.1.1): In our experiments with existing registration-based blip-up blip-down correction methods, we observed that with very large distortions, the performance of the correction algorithm decreases significantly. Therefore, we aimed to use a deformation model capable of dealing with large deformations. A suitable deformation model for our framework is the symmetric, diffeomorphic, and time-varying velocity-based model proposed by Avants et al. (2008).
Two deformations (Section 2.1.1): One of the main assumptions of blip-up blip-down corrections is that the B0 field is constant between the acquisitions, hence the distortions are exactly the opposite of each other, disregarding possible inconsistencies introduced, for example, by subject motion or magnetic field drift. Therefore in our framework, instead of one deformation field (and its inverse), we use two codependent fields that are nearly the inverse of each other but allow flexibility to compensate for any changes in the B0 field.
Structural image information (Section 2.1.2): In the presence of very large distortions or other imaging artifacts, including additional a priori information from an undistorted target would be helpful. Therefore, we further constrain the deformation fields to pass through a distortion-free structural T2W image at the midtime point to improve registration accuracy.
Diffusion image information (Section 2.2.3): To achieve a robust registration in regions that appear homogeneous in the b = 0 s/mm2 images we hypothesized that adding information from the diffusion-weighted images would be beneficial. Therefore, the proposed method also employs pairs of blip-up blip-down diffusion-weighted images in addition to the b = 0 s/mm2 images.
Anisotropic deformation regularization (Section 2.2.4): Deformation regularization is a crucial component of each diffeomorphic registration algorithm. However, the scale of regularization kernels can also have an impact on registration quality. A new form of deformation regularization is employed to prevent bleeding of small structures into others. Instead of using traditional Gaussian or B-splines kernels, this method employs a partial differential equations (PDE) based regularization that results in locally anisotropic smoothing of the deformation fields.
2.1. Mathematical Framework for the Similarity Metrics
In this section, we will describe the mathematical foundations of DR-BUDDI.
2.1.1. Deformation Model – Metric 1 (ξ1)
Typically, a registration-based blip-up blip-down correction algorithm uses one deformation field and its inverse to maximize the similarity between the Jacobian manipulated transformed images. The similarity metric ξ is defined as:
| (1) |
where Iup and Idown are the blip-up and blip-down (b = 0 s/mm2) images, ϕ is the forward deformation field, is the Jacobian determinant of the deformation field, Ω is the image domain, and CC is the cross-correlation metric.
To achieve the goals described in Section 2, rather than a basic registration algorithm with one deformation, we propose using a large deformation diffeomorphic model with two deformations. Avants et al. (2008) proposed a non-linear, symmetric, time-varying velocity field based registration algorithm, namely SyN, which quickly became very popular in the image registration community thanks to the ANTS package (Avants et al., 2011). The fundamental idea behind SyN is that instead of registering the moving image to the fixed image, it registers both the fixed and the moving image to a middle image. It achieves this by first parameterizing the registration space with time [as initially proposed by Christensen et al. (1996)], with the fixed image representing the image at time point t = 0 and the moving image, the image at time t = 1. SyN then aims to maximize the similarity of the fixed image at time point t = 0.5 with the moving image at time point t = 0.5, with two deformation fields guiding each respective part. These deformation fields are guaranteed to be of approximately the same norm due to constant parameterization of time and gradient step length. The reader is referred to (Avants et al., 2008) for further details. The application of this strategy to the blip-up blip-down correction problem is particularly appealing because the undistorted EPI image we aim to compute can be considered as the middle image in the SyN formulation.
The first step is to define the blip up and down problem in the framework of the SyN formulation. If we consider the blip-up image as the image at t = 0 and the blip-down image as the image at t = 1, the middle image at t = 0.5 should ideally be the image free of distortions. Let ϕ1(x, t) be the time-varying displacement field that maps the fixed image to the moving image and ϕ2(x, t) be the field that maps the moving image to the fixed image. The middle images may be defined as: and . Then the original SyN formulation from Avants et al. (2008) can be defined without the regularization term as:
| (2) |
The derivations for the displacements computed using this metric can be found in Appendix A.1. This metric has desirable features; however, it needs to be adapted to the context of EPI distortion correction with blip-up blip-down images. First, there is an infinite number of middle images that are guaranteed to be of equal displacement from both original images, forming a hyper-plane where our desired undistorted image sis just a point. For our purposes, we need the registration to converge to that point. Additionally, this metric does not take into account signal compression and expansion that occur in EPI distortions. We address these issues as described in the following sections:
2.1.2. Constraining Registration with an Undistorted Structural Image – Metric 2 (ξ2)
The inability to guarantee that the middle images are distortion-free could be overcome if the time-dependent evolution of the registration were guided by the correct anatomy at the middle time point t = 0.5. Additionally, this guidance could also serve regularization purposes in the presence of undesired artifacts. For these reasons, we propose introducing an undistorted T2W structural image to the original SyN formulation of Equation 2. The metric ξ2 can be written as:
| (3) |
This metric encourages similarity between the structural and middle images. Note that this method is different from registering the blip-up and down images to the structural image because the displacement fields ϕ1 and ϕ2 are of the same norm and can be interrelated as further described in Section 2.2. Therefore, this formulation enforces the blip-up image to go through the structural image at t = 0.5 while being registered to the blip-down image (similarly for the down image), and thus the middle images are guaranteed to be distortion-free. However, this metric still does not include knowledge about signal pile-ups and expansions. The derivation of displacements originating from this metric can be found in Appendix A.2.
2.1.3. Incorporating Signal Expansion and Compression Information Using the Structural Image – Metric 3 (ξ3)
As described by Bowtell et al. (1994), once a perfect correspondence is established between the blip-up and down images, the final distortion-corrected and signal-redistributed image can be computed as the geometric average:
| (4) |
This image itself could be used within the optimization to maximize the similarity between the final reconstructed image and the structural image:
| (5) |
The displacement directions derived from Metric 3 can be found in Appendix A.3. Metric 3 relates the distortion corrected EPI image with properly redistributed signal, , to the structural image, hence overcoming the weaknesses of Metric 2. It should be noted that, with Metric 3, proper signal redistribution is obtained only for the combined image without the need to produce geometrically corrected individual images Iup and Idown. Desired results in terms of both geometrical correction of individual images and signal redistribution can be achieved when ξ2 and ξ3 are used together.
2.1.4. Incorporating Signal Compression in the Absence of a Structural Image – Metric 4 (ξ4)
The typical approach to include signal compression and expansion information in a registration framework is to modulate the transformed images’ signals with the Jacobian determinants of corresponding deformation fields (Tao et al., 2009; Holland et al., 2010). For completeness, we also include a metric incorporating this approach in the standard SyN formulation. Because our model does not assume absence of motion between the blip-up and down images, the phase-encode direction of the middle images does not have to coincide with an image axis, hence our deformation Jacobians are full 3 × 3 matrices instead of a single scalar. Thus, the middle images are defined as:
| (6) |
| (7) |
and our similarity metric employs these modulated images as:
| (8) |
This metric, although showing an improved handling of piled-up and expanded regions, also has drawbacks. Because this metric relies on the second order spatial derivatives of the deformation field, it is very sensitive to noise and artifacts, such as Gibbs ringing, and the deformation field has to be strongly regularized. Additionally, as stated in Andersson et al. (2003), computing the correct signal using blip-up and down images is almost always more robust than manipulating single images with Jacobians. Finally, some of the challenges involved with ξ1 still apply; the middle images are not guaranteed to be distortion-free images, and further guidance for the velocity fields is required, especially under non-ideal conditions.
In our software package TORTOISE, we give users the option to use any combination of the proposed metrics. ξ2 and ξ3 require an anatomical structural image, and ξ1 and ξ4 can be used if one is not available.
2.2. Constraints and Other Properties of the Registration
2.2.1. Phase-Encoding Direction
EPI distortions result in displacements along the phase-encoding direction . However, the gradient formulations in the Appendix produce free-form deformations, which need to be further constrained along to properly model the physical problem. Let and be the rotational components of the rigid (affine or quadratic) registration that map the blip-up and down images to the structural image, respectively. Assuming original phase encoding along the y-axis for simplicity of illustration, the new phase-encoding direction can be written as:
Therefore, for all metrics, the gradient vectors should be projected onto the new phase-encoding direction, so that for example for the up data:
2.2.2. Enforcing Deformation Equality
Theoretically, a deformation field ϕ and its inverse ϕ−1 would map the blip-up and blip-down image respectively onto the undistorted image. In Section 2.1, we intentionally modeled these two deformations separately as ϕ1 and ϕ2. Nevertheless, it is still desirable to have control over the degree of similarity imposed on the two deformations. For this reason, we introduce another term to our metrics to softly constrain the (inverse) similarity between the two fields:
| (9) |
where ‖.‖ is the L2 norm. Then the displacements can be rewritten as:
| (10) |
The formulation is similar for ϕ2 and the derivations can be found in Appendix A.4. The parameter β is a continuous user-defined parameter that forces ϕ1 and to be identical when set to one, and leave them independent when set to zero.
2.2.3. Incorporating Diffusion-Weighted Imaging Information
Traditionally, blip-up blip-down corrections have been performed on b = 0 s/mm2 images. b = 0 s/mm2 images are and proton density weighted. This weighting results in good discrimination between white matter, gray matter and cerebrospinal fluid (CSF), but does not allow the depiction of various pathways within white matter regions as they have homogeneous signal intensity. Therefore, the cost function of the registration within these regions is very flat in the b = 0 s/mm2 images. Using only b = 0 s/mm2 images to estimate the deformation field for correction may produce highly inaccurate results within white matter. Therefore, we investigated the advantage of adding DWIs to be used in a multi-channel registration framework. DWIs intrinsically contain diffusion anisotropy information; this information enables a better depiction of individual pathways in white matter regions. In such a multi-channel registration setting, each channel provides a displacement field; these fields are subsequently combined into a single field with different possible weightings. For example, Metric 2 becomes:
| (11) |
There are several choices for the DWI weight factors αi:
Manual weighting: Weights for each channel are entered manually as parameters to the correction. This approach provides the possibility of weighting artifactual images less than other channels.
Equal weighting: Weights are automatically computed to be equal for each channel.
Signal-based weighting: Weights are computed voxelwise relative to the signal level in the corresponding DWI, with less weighting for low signals to avoid having the registration driven by low signal-to-noise ratio features.
Median weighting: Instead of a weighted average of the deformation fields from each DWI channel, this approach chooses the median displacement for each voxel and provides robustness against artifactual results.
The number of diffusion-weighted images N to be used is a user-defined parameter. Our default setting employs six DWIs, the minimum number to cover all directional contrast, similar to the requirements in diffusion tensor computations. Registration time increases linearly with the number of DWIs.
Another issue is the use of acquired images versus synthesized images. In DR-BUDDI, users may use the real DWIs or perform a quick tensor fitting for both the blip-up and down DWI data sets, then estimate the b = 0 s/mm2 image and synthesize the DWIs from the initial diffusion tensors. If the use of acquired DWIs is selected, all the b = 0 s/mm2 images are first quadratically registered to the first one and averaged, then the first N DWIs are selected from the dataset. If the synthetic option is preferred, the b = 0 s/mm2 image is estimated from tensor fitting and N DWIs are synthesized based on a gradient scheme originating from the electro-static repulsion method (Jones et al., 1999).
2.2.4. Deformation Regularization
Traditionally, regularization of displacement fields has been achieved by convolution with Gaussian or B-splines kernels. In this work, we preferred to use an anisotropic filter to avoid blending neighboring regions such as the brain stem and the surrounding cerebrospinal fluid. For this purpose, the vector-valued image regularization framework proposed by Tschumperlé and Deriche (2005) is employed. For the details of the implementation of this filter within DR-BUDDI, refer to Appendix A.5.
2.2.5. Quadratic Registration-Based Initialization for Concomitant Fields
EPI distortions consist of susceptibility distortions and concomitant field distortions (Du et al., 2002). The latter is a global distortion that can be corrected with transformations similar to those used for eddy-current distortions that affect the diffusion-weighted images. Therefore, while performing the initial registration of the blip-up and down images to the structural image, we employ the quadratic transformation originally proposed by Rohde et al. (2004) to correct for eddy-current distortions. This approach provides a better initialization for the diffeomorphic registration and, therefore, a faster and more robust correction. The effect of this initialization is depicted in Figure 1.
Figure 1.
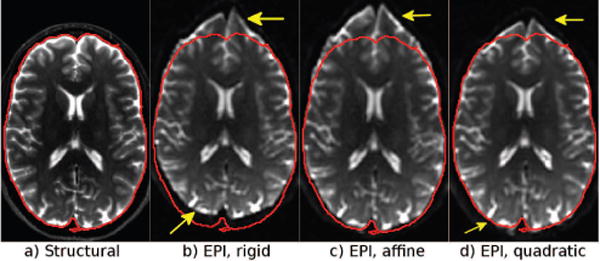
The effects of quadratic registration. A b = 0 image was registered to the corresponding (a) T2W structural image, (b) with rigid, (c) affine, and (d) quadratic registration. Neither rigid nor affine registration was able to provide a good initialization due to the global but nonlinear effects of the concomitant fields. Quadratic registration is able to correct for these distortions, and the remaining distortions can be solely attributed to local susceptibility effects.
2.3. Integration of DR-BUDDI in a Comprehensive DWI Preprocessing Framework
We integrated the proposed blip-up blip-down correction algorithm into the TORTOISE diffusion image processing software package (Pierpaoli et al., 2010). An illustration of the complete pipeline is depicted in Figure 2. Processing starts with independent motion and eddy current distortion corrections for both the blip-up and down data sets in the DIFFPREP tool of TORTOISE. After this step, all DWI volumes in both data sets are aligned to their corresponding b = 0 s/mm2 images and the B-matrices for all volumes are properly reoriented (Rohde et al., 2004). DIFFPREP also outputs two transformation files, one for each data set, describing the entire motion and eddy current distortions for all volumes. These transformation files are fed into the DR-BUDDI tool. The b = 0 s/mm2 images for both blip-up and down data are then quadratically registered to the structural image within DR-BUDDI to correct for concomitant field distortions and align both images to the structural image’s space, where blip-up blip-down correction is then performed using both the b = 0 and diffusion-weighted images. The resulting deformation fields are subsequently combined with each DWI’s motion and eddy current transformations to generate the overall displacement fields, which are used along with the original DWIs to generate the corrected blip-up and down diffusion data sets with one interpolation step. Lastly, these two data sets are combined using geometric averaging to generate the final corrected data set. Because of the B-matrix rotation process during motion correction in DIFFPREP, the two B-matrices of the corrected blip-up and down data sets will most likely not be identical. As a heuristic solution, the arithmetic average of these two B-matrices is output as the B-matrix of the final corrected data, which are ready for tensor operations in DIFFCALC. The TORTOISE package can be downloaded from: http://www.tortoisedti.org.
Figure 2.
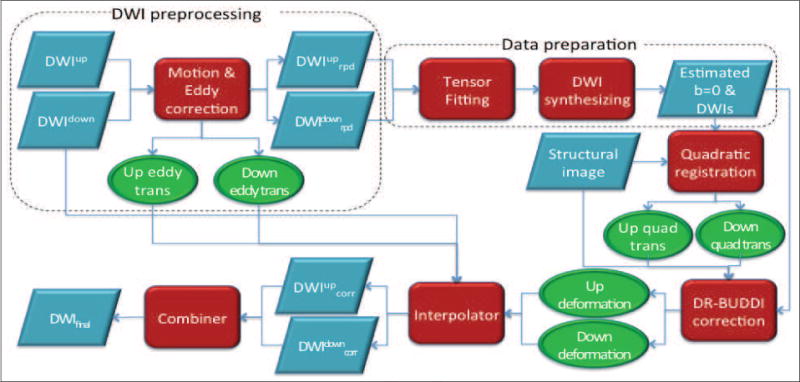
The pipeline employed in TORTOISE for blip-up blip-down correction.
2.4. Experimental Setup
2.4.1. MRI Data
Several types of data were used for the experiments of this work. The first two sets of data were collected with parameters representative of clinical scanning at 1.5T and 3T to test the performance of the algorithm under typical distortion levels. The first set of data (Test Set 1) was collected on a 1.5 Tesla scanner (GE Medical Systems) equipped with an 8-channel receive coil and consisted of five young subjects (2 males; mean age = 36, age range 24–48 years). DWIs were acquired with a single-shot spin-echo EPI sequence (FOV = 24 × 24 cm, slice thickness = 2.5 mm, matrix size = 96 × 96, 60 slices). No parallel imaging was used in this case. Each diffusion experiment consisted of two image volumes with b = 0 s/mm2 and 12 volumes with b = 1100 s/mm2. For each subject, the protocol was repeated, acquiring both phase-encoding directions, Anterior-Posterior (AP) and Right-Left (RL), with both blip-up and blip-down, yielding four data sets per subject: APup, APdw, RLup, RLdw. An undistorted T2W scan was also acquired with a fast spin-echo sequence (FOV = 24 cm, TR = 9000 ms, TE = 81.5 ms, matrix size = 256 × 256, slice thickness= 2.5 mm, 60 slices).
The second set of data (Test Set 2) was collected again on a population of five subjects (4 females, 1 male; age range 21–30 years) on a 3T Siemens Skyra scanner, to assess the correction performance on data acquired with parallel imaging at high field. DWIs were acquired with a 32 channel coil (FOV = 22 × 22 cm, slice thickness = 2 mm, matrix size = 110 × 110, 80 slices) and the GRAPPA factor was set to 2. Diffusion experiments consisted of five b = 0 s/mm2 and 30 volumes with b = 1100 s/mm2 (TE/TR = 91/12400 ms) with no repetition. Diffusion data for all four phase-encoding directions along with a T2W image were collected similarly to the previously described test set.
The third set of data (Test Set 3) was collected on a single subject with the aim of testing the algorithm on a high-quality, good spatial resolution and large number of gradients data set with large EPI distortions. Data from the same healthy female subject were collected on two 3 Tesla scanners, GE 750 and Siemens Skyra, with a 32-channel receive coil. DWIs were acquired with a single-shot spin-echo EPI sequence (FOV = 256 × 256 mm, slice thickness = 2 mm, matrix size= 128 × 128, 82 axial slices). No parallel imaging was used. Each diffusion experiment consisted of five image volumes with b = 0 s/mm2 and 30 volumes with b = 1100 s/mm2, yielding 10 b = 0 s/mm2 images and 60 DWIs. Similar to the procedure with previous data sets, the diffusion experiment was repeated to acquire APup, APdw, RLup, RLdw data sets, along with a high quality T2 weighted scan. The scans in the Skyra scanner were repeated, introducing mild subject motion.
The fourth set of data (Test Set 4) was selected because it had severe flow artifacts in b = 0 images, enabling us to test the robustness of the algorithm with respect to this type of artifact. One healthy subject was scanned with a Philips Achieva 3T scanner at 2 × 2 × 2 mm, FOV = 22 cm, matrix size= 128 × 128, 90 slices, TR = 11.5 s, TE = 92 ms. The diffusion experiment consisted of six b = 0 s/mm2 images, 6 b = 50 s/mm2 images, 6 b = 350 s/mm2 images, 6 b = 600 s/mm2 images, 6 b = 80 s/mm2 images and 36 b = 1100 s/mm2 images.
The last set of data (Test Set 5) was collected from an exvivo mouse on a Bruker 7T vertical scanner. The images were acquired with both a conventional (CPMG) spin-echo (SE) sequence and EPI. The DWIs acquired with the spin-echo sequence are not affected by EPI distortions and can be considered as undistorted ground truth images. Data from both sequences were acquired at 0.1 mm isotropic resolution, 160 × 120 matrix size and 100 slices. Similar to the previous datasets, EPI data were collected using all four phase encoding directions and consisted of 32 DWIs and 6 b = 0 s/mm2 volumes. Due to the longer acquisition time, the spin-echo sequence consisted of 10 DWIs with 2 b = 0 s/mm2 volumes.
2.4.2. Registration Quality Assessment
The proposed EPI distortion correction method was compared with two other blip-up blip-down methods: TOPUP from the FSL package (Andersson et al., 2003) and EPIC (Holland et al., 2010). For each method, the similarity of the corrected b = 0 s/mm2 images to the structural image was visually inspected and voxelwise local correlation maps of the signal intensities were also generated. Visual inspection was also performed on the DEC maps (Pajevic and Pierpaoli, 1999).
We tested quantitatively the performance of the various methods using the approach proposed by Wu et al. (2008). The APup–APdw data sets were used to generate the corrected data set APcorr, and similarly the RLup–RLdw data sets were used to generate RLcorr. Theoretically, a perfect correction should produce morphologically identical APcorr and RLcorr images, and maps of tensor quantities generated from these two data sets should be super-imposable. Therefore, correction performances were assessed by analyzing the voxelwise standard deviation (SD) maps of tensor-derived quantities such as fractional anisotropy (FA) and Trace (TR) computed from the two corrected datasets.
For a population analysis of SD maps, all diffusion tensors from both APcorr and RLcorr images for all subjects were first registered nonlinearly using DTITK (Zhang et al., 2006) to obtain the transformations that would morph each tensor to the average morphology of the population, and the resulting RLcorr deformations were applied to the SD maps to compute a population average SD map for the quantity of interest (TR or FA).
For the first two test sets, the Wilcoxon signed-rank test was used to determine whether one of the methods had statistically significantly (5% confidence level) lower SD values in a given voxel. For each method, the number of voxels where that method was statistically the best was counted, and this total was ranked against other methods’ totals. Additionally, whole brain median SD values were computed for each individual and for each method, for both FA and TR, and reported. A paired t-test was performed on the median values to determine significant differences. For Test Set 3, with only one subject, the difference image was displayed for visual inspection.
2.4.3. Additional Experiments
One of the goals of this work is to answer several previously uninvestigated questions pertaining to blip-up blip-down acquisitions and corrections. In this Section, we will describe these questions and our analysis methodologies to investigate them.
Blip-up blip-down symmetry: To test the potential advantages of using two deformation fields rather than one and its inverse in presence of motion, two data sets were selected from Test Set 3: one with minimal motion between the b = 0 images of the blip-up and down data sets and one with relatively large motion. This test was performed by setting β to 1 in Equation 10 both forcing inverse equality of deformations.
Effects of correction on directional information: To check the effects of using DWIs during correction, we used the GE data from Test Set 3 and compared the DEC maps produced after DR-BUDDI correction.
Flow artifacts in b = 0: Flow artifacts are more prominent in the b = 0 s/mm2 images than DWIs and using only b = 0 images might not produce the desired results. To assess the effects of flow artifacts, we used Test Set 4 and performed the correction twice with DR-BUDDI, once with only the b = 0 images and once with DWIs weighted significantly more and compared their performances.
Scanner manufacturer differences: EPI distortions may be a source of low reproducibility for data acquired on scanners from different manufacturers in multi-center studies. We tested the ability of DR-BUDDI processing with default parameters to increase reproducibility of DTI metrics on data acquired for Test Set 3. Single subject SD maps for FA and trace were computed with and without correction.
Gibbs ringing: Gibbs ringing is common on b = 0 s/mm2 images propagating from regions with extreme signal pile-up. To assess the effects of Gibbs ringing artifacts on DR-BUDDI correction, a data set from Test Set 3 with particularly evident signal pile-ups was selected. We tested two different DR-BUDDI settings: 1) the default, and 2) deformation regularization and DWI usage turned off.
2.4.4. Implementation and Settings
For the experiments in this paper, the default settings were used for the proposed and compared methods while testing the performance of DR-BUDDI with respect to the existing algorithms (Section 3.1). DR-BUDDI’s default settings can be found in Appendix A.6. For the additional experiments, DR-BUDDI parameters were altered or optimized but the outcomes were not compared to those of the other methods.
For each data set, the corresponding structural image was transformed into anterior commissure posterior commissure orientation and DR-BUDDI corrections were performed in this space. The DWIs were upsampled by a factor of 2. The experiments were run on a dual Intel Xeon system, utilizing DR-BUDDI’s fully parallelized architecture. A typical correction employing two metrics and seven pairs of images, on 1mm isotropic data after upsampling, took 45 minutes.
3. Results
3.1. Comparative Assesment of Correction Performance
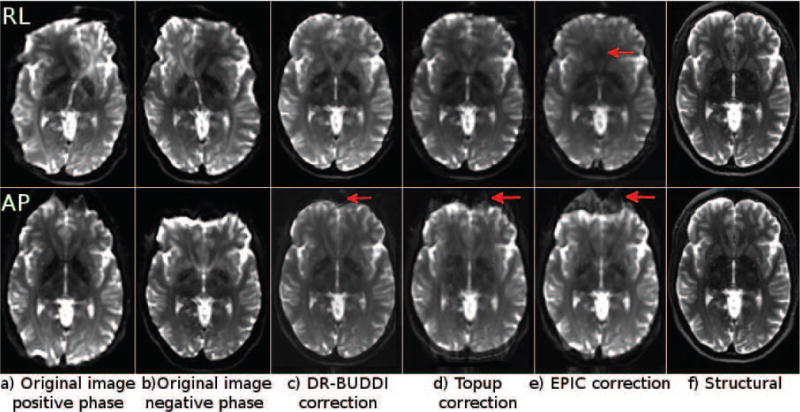
Figure 3 displays the original distorted and the corresponding corrected b = 0 s/mm2 images from the three algorithms tested using a single subject from Test Set 1. Data acquired with all four phase-encoding directions are presented along with the corresponding structural T2W image; images in the top row are encoded with RL and in the bottom row with AP.
Figure 3.
Original distorted images and their corrected versions created using three methods from a single subject of Test Set 1. The top row represents images with RL phase encoding and the bottom row with AP encoding. The structural image is the same for both rows.
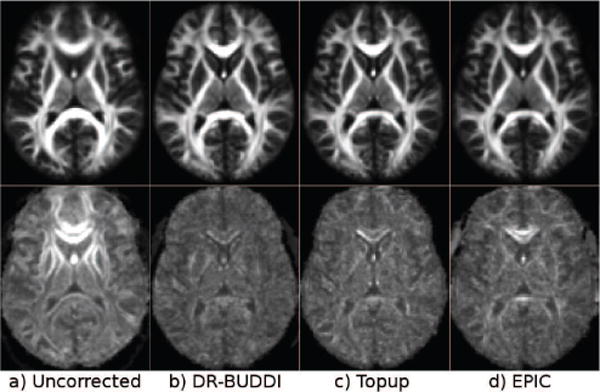
The corrected b = 0 images clearly show that all algorithms significantly decreased EPI distortions. DR-BUDDI correction produced sharp images with clearly visible tissue interfaces, where TOPUP produced images that were more blurred. At this slice level, signal pile-ups and expansions were very pronounced. DR-BUDDI was still able to correctly reconstruct the olfactory bulbs with anatomically plausible white matter bundles, even for the RL encoded data (arrow). TOPUP and EPIC could only partially achieve this for AP data, while for RL data, it appears that the corrected image was not consistent with the anatomy of this region. The inferior temporal lobes for both RL and AP corrected data were again anatomically more accurate with DR-BUDDI. Additionally, both TOPUP and EPIC introduced small artifactual bands in AP corrected data in the temporal lobe near the petrous sinus (arrows in AP panel).
Figure 4 displays spatially normalized population maps of both the mean and SD maps for FA computed from the APcorr and RLcorr data. The mean FA maps, including those computed from the uncorrected data, appear morphologically similar but with different degrees of blurring. The SD maps reveal clear differences. The uncorrected EPI distortions resulted in very high SD values in the genu and splenium of the corpus callosum (CC) and internal capsule. The SD map of DR-BUDDI shows almost no structures, except for a small band in the genu of the CC, while those of TOPUP and EPIC show high values at the periphery of the genu of the CC and cortical regions. The EPIC SD map also shows high values in the splenium of the CC.
Figure 4.
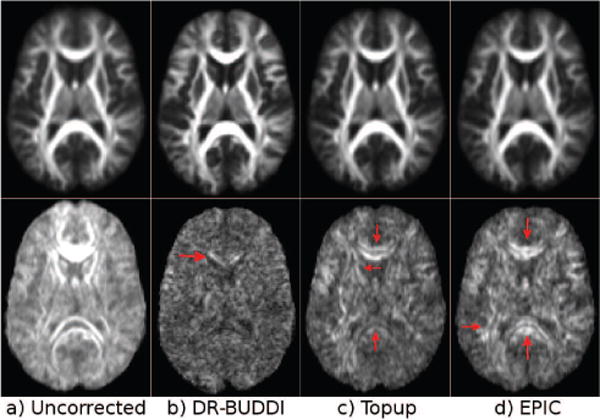
Population maps of the average (top row) and standard deviation (bottom row) of FA from AP and RL data from Test Set 1 (1.5T). Regions of high SD values indicate imperfect distortion corrections by the algorithms. (a) No EPI correction, corrected with (b) DR-BUDDI, (c) TOPUP, and (d) EPIC. All FA maps, and SD maps are displayed with identical brightness/contrast.
Figure 5 displays the same analysis as Figure 4 but for Test Set 2. SD maps computed from uncorrected data show large values indicating a significant amount of misalignment in several regions. Test Set 2 , however, has less amount of distortions than Test Set 1. Consequently, all three algorithms produced better quality corrections for this set. The regions showing high values in TOPUP’s and EPIC’s SD maps are the same as those found in Figure 4, but the magnitude of the effect is much lower. As for Test Set 1, DR-BUDDI showed good overall performance.
Figure 5.
Population maps of the average and standard deviation of FA between AP and RL corrected images from Test Set 2.
Figure 6 presents the same analysis as Figure 5 but at a different slice level. At this level, differences among methods can be observed in the orbitofrontal cortex on the average FA maps, where the white matter fiber bundles appear more accurately depicted after correction with DR-BUDDI (large arrows). The other methods also show larger SD values in this region. Additionally, differences among methods can also be observed in the cerebral peduncles (small arrows).
Figure 6.
Same data set of Figure 5 from Test Set 2 at a different slice level.
Table 1 and Table 2 present the results of the performance comparison across methods for Test Set 1 and 2, respectively. In this analysis, lower SD values indicate better performance, i.e., better agreement for tensor quantities computed from RLcorr and APcorr data. Results are reported for the whole brain median SD value analysis and the voxelwise Wilcoxon signed-rank test. In general DR-BUDDI outperformed the other two methods, except for three instances in which the median SD value of FA was not the lowest. The paired t-test analysis results were consistent with this scenario. For both test sets DR-BUDDI was significantly better than the other two methods for TR (all p-values less than 0.018), but for FA, statistical significance was only achieved with respect to EPIC with a p-value of 0.038 and a p-value of 0.0477 for the two test sets respectively. In the comparison with TOPUP, the p-values were 0.4 and 0.057.
Table 1.
Correction performance results across methods for Test Set 1. The whole brain median SD value for FA and TR for each individual (along with the corresponding ranks). The voxelwise Wilcoxon signed-rank test results are at the bottom of the panel as the number of voxels with the significantly lowest SD for each method. Trace SD values are in units of 10−6mm2/s.
| DR-BUDDI | TOPUP | EPIC | |
|---|---|---|---|
| Subject | FA SD/(method rank) | ||
| 1 | 0.136/(1) | 0.146/(3) | 0.139/(2) |
| 2 | 0.138/(1) | 0.140/(2) | 0.145/(3) |
| 3 | 0.138/(1) | 0.141/(3) | 0.140/(2) |
| 4 | 0.143/(2) | 0.143/(1) | 0.144/(3) |
| 5 | 0.140/(2) | 0.138/(1) | 0.147/(3) |
| # voxels with significantly lowest SD/(rank) | |||
| 64027/(1) | 45387/(2) | 32933/(3) | |
| Subject | TR SD/(method rank) | ||
| 1 | 8.311/(1) | 10.18/(3) | 9.701/(2) |
| 2 | 8.394/(1) | 9.904/(2) | 10.68/(3) |
| 3 | 7.261/(1) | 8.955/(3) | 8.905/(2) |
| 4 | 8.037/(1) | 9.223/(2) | 9.522/(3) |
| 5 | 7.463/(1) | 8.664/(2) | 9.418/(3) |
| # voxels with significantly lowest SD/(rank) | |||
| 73916/(1) | 53096/(2) | 24704/(3) | |
Table 2.
Correction performance results for Test Set 2 similar to Table 1.
| DR-BUDDI | TOPUP | EPIC | |
|---|---|---|---|
| Subject | FA SD/(method rank) | ||
| 1 | 0.119/(1) | 0.136/(3) | 0.134/(2) |
| 2 | 0.131/(2) | 0.129/(1) | 0.132/(3) |
| 3 | 0.120/(1) | 0.126/(3) | 0.123/(2) |
| 4 | 0.126/(1) | 0.134/(2) | 0.135/(3) |
| 5 | 0.124/(1) | 0.129/(3) | 0.128/(2) |
| # voxels with significantly lowest SD/(rank) | |||
| 63787/(1) | 25499/(3) | 60724/(2) | |
| Subject | TR SD/(method rank) | ||
| 1 | 7.860/(1) | 10.28/(3) | 10.25/(2) |
| 2 | 12.04/(1) | 12.05/(2) | 12.61/(3) |
| 3 | 8.344/(1) | 10.49/(2) | 10.52/(3) |
| 4 | 9.584/(1) | 12.42/(2) | 12.77/(3) |
| 5 | 8.621/(1) | 10.62/(2) | 10.76/(3) |
| # voxels with significantly lowest SD/(rank) | |||
| 59726/(1) | 23973/(3) | 54989/(2) | |
Figure 7 displays the original distorted images and outputs from the three correction algorithms from Test Set 3. As previously stated, parallel imaging was intentionally not used, hence the distortions in this test set are severe and more challenging than for typical data. Corrections were less accurate for all methods. Even though the results were acceptable for the RL data when the EPIC method was used, the algorithm failed to correct the distortions for the AP data due to the large motion between the blip-up and down acquisitions. DR-BUDDI again produced anatomically faithful images that appear sharper than those obtained with the other methods.
Figure 7.
Original distorted images and their corrected versions created using three methods with Test Set 3. The top row represents images with RL phase encoding and the bottom row with AP encoding. The structural image is repeated for convenience. Distortions in this set are very large.
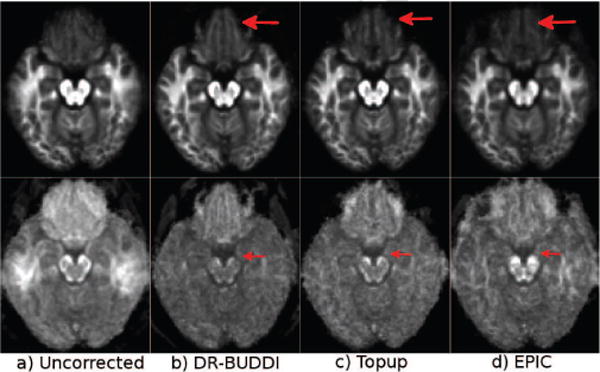
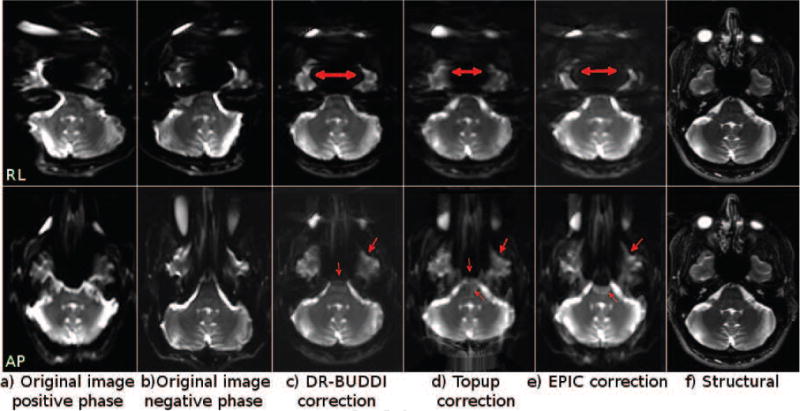
Figure 8 displays images again from Test Set 3 at the level of the brain stem. At this challenging level, DR-BUDDI was not able to correctly reconstruct the CSF surrounding the white matter within the brain stem with the AP data, whereas TOPUP could. However, with TOPUP, CSF also bled into the white matter and artifacts were introduced in background regions, though, the artifacts did not affect the brain tissue. EPIC failed again with the AP data. No algorithm was able to correctly reconstruct the temporal lobes with RL data, though the agreement of AP and RL corrected data was better with DR-BUDDI.
Figure 8.
Original distorted images and their corrected versions created using three methods with Test Set 3 at the brain stem level. The top row represents images with RL phase encoding and the bottom row with AP encoding.
The local cross-correlation maps created with a window size of 5, are displayed in Figure 9. They indicate the dissimilarities between the corrected AP images and the structural image. These maps provide an additional way of assessing correction quality. Overall DR-BUDDI showed a higher correlation with the undistorted T2WI than did TOPUP and EPIC. Differences are more pronounced in frontal and occipital areas, posterior portions of the cerebellum, and central white matter.
Figure 9.
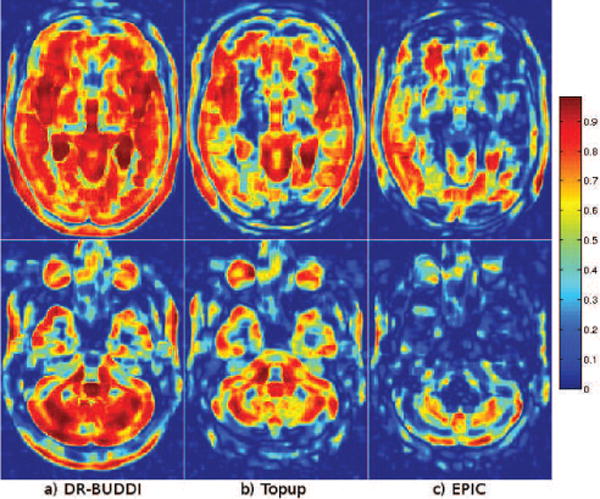
Local cross-correlation maps between different corrected images (AP) and the structural image. Warmer colors indicate higher local agreement between the corrected and the structural images.
Figure 10 displays the distorted b = 0 s/mm2 images from the RL encoded acqusition of Test Set 5, the DR-BUDDI corrected output and the distortion-free spin-echo CPMG data. This data set had distortions around the frontal and right-left regions (red arrows) and around an air bubble (yellow arrow). Figure 11, top row, displays the DEC maps for both the AP and RL EPI data corrected with DR-BUDDI and also the undistorted CPMG data. The DEC maps for the three sets are identical at visual inspection. The difference images of FA computed from the corrected EPI data and the undistorted spin-echo data (Figure 11 (d)–(f)) confirm that the corrected images are structurally very well-aligned to their undistorted counterpart. Only a few small structures around the corpus callosum and the cerebellar regions are present and the entire images, for both cases, are otherwise homogeneous. The air bubble affected the AP data slightly more but still only caused subtle deviations from the ground truth CPMG data.
Figure 10.
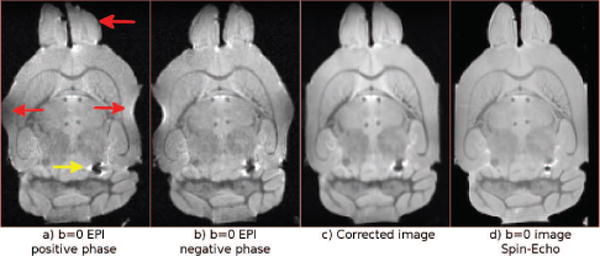
The b = 0 images from the mouse dataset (Test Set 5). The images in (a) and (b) are the raw images from the RL encoded EPI set, (b) is the output of DR-BUDDI correction and (d) is the distortion free spin-echo CPMG image.
Figure 11.
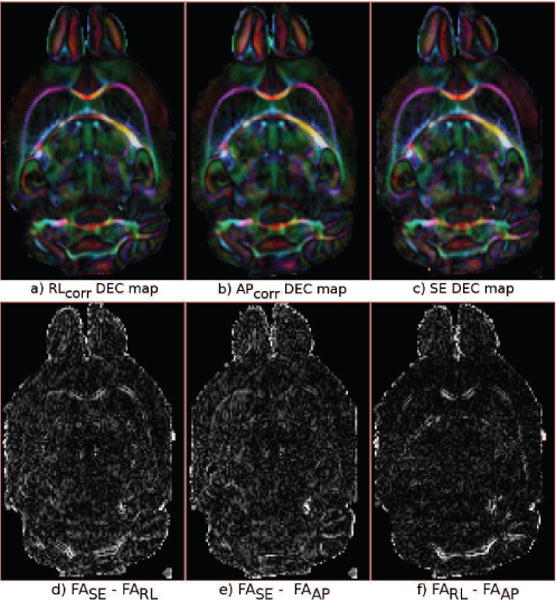
Top row: DEC maps computed from data corrected with DR-BUDDI with RL and AP encoding in (a) and (b) respectively. The DEC map in (c) is from the CPMG undistorted ground truth data. Bottom row: Differences in FA maps between data computed from d) CPMG and corrected RL encoded EPI, e) CPMG and corrected AP encoded EPI, f) the two corrected EPI data.
3.2. Results from Additional Experiments
3.2.1. Testing the Blip-up Blip-down Symmetry Principle
Figure 12 (a–b) displays the distorted images from two blip-up blip-down acquisitions (Test Set 3) with significant motion in one of the acquisitions. The same slice is visualized without any rigid registration. The AP data showed large misalignment between the blip-up and down images. The computed deformation fields are displayed in (c–d). The second and the fourth fields are the inverse fields; therefore should theoretically be identical to the first and third fields, respectively. These deformation fields were obtained after quadratically registering each image to the corresponding structural image and only represent the distortions due to susceptibility. The fields for the AP data are significantly different from each other, whereas the fields for the RL data, where motion was negligible, were very similar.
Figure 12.
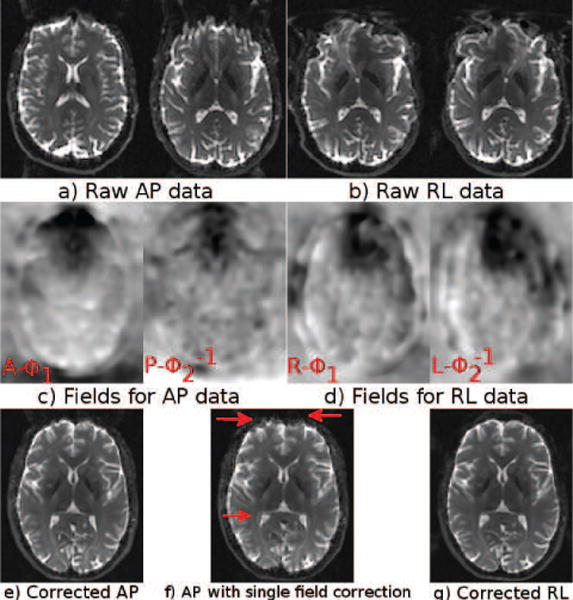
Two sets of data with varying amounts of motion.
We can hypothesize that the differences between R – ϕ1 and might be because of imperfect registration, gradient heating, or magnetic field drift. However, such issues can not explain the large difference between A – ϕ1 and . The images corrected with these deformation fields are in (e) and (g) respectively. The frontal region in these images was nicely corrected. A correction strategy that only used a single deformation field, P – ϕ2 and its inverse , produced the image displayed in (f) with artifacts indicated by the arrows.
Another test involved the analysis of one v.s. two deformation models. Figure 13 displays the computed deformation fields from Test Set 3, presented in Figure 7. The first two fields were generated using a two-deformation model, and the second pair used only a single deformation and its inverse. There was minimal motion between the blip-up and down images.
Figure 13.
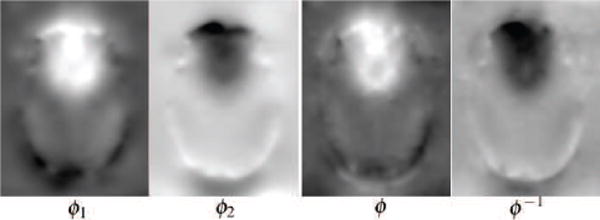
The outputs of the two-deformation v.s. one deformation model.
In this case, even with the two-deformation model, the displacement fields were almost inverses of each other. However, there were differences between ϕ1 and ϕ and ϕ2 and ϕ−1. The two deformation model is able to model a larger displacement with ϕ1 in the orbito-frontal region for the up image, whereas this was not needed for the down image as indicated by the similarity of ϕ2 and ϕ−1 in this region. Additionally, the two-deformation model was able to capture more local details due to the inherent smoothing with the single-deformation model.
3.2.2. b = 0 s/mm2 Artifacts
The b = 0 images from Test Set 4, for both the blip-up and down data sets, are presented in Figure 14. Inconsistent signal drops originating from flow voids ventral to the medulla could affect the quality of the correction. In this case, our proposed solution was to manually weight the DWIs more than the b = 0 s/mm2 images as signal originating from blood only affects the b = 0 s/mm2 images and is not present in the DWIs. Figure 15 presents the Trace images obtained with a correction that equally weighs all images and one that weighs DWIs significantly more. The brain stem better matched that of the structural image and was less affected by CSF partial voluming when the artifactual images were de-emphasized.
Figure 14.
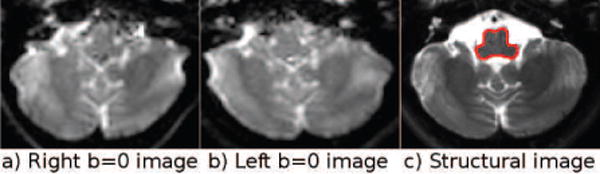
b = 0 s/mm2 images with artifacts.
Figure 15.
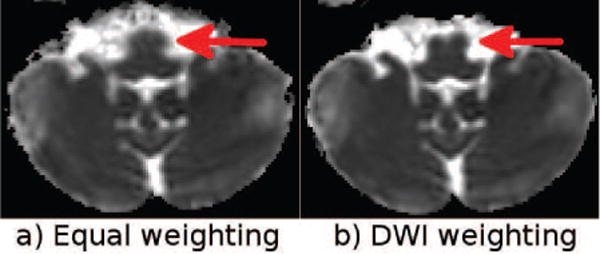
Trace maps computed with equal and DWI-emphasized weighting.
3.2.3. Effects of Using DWIs for Correction
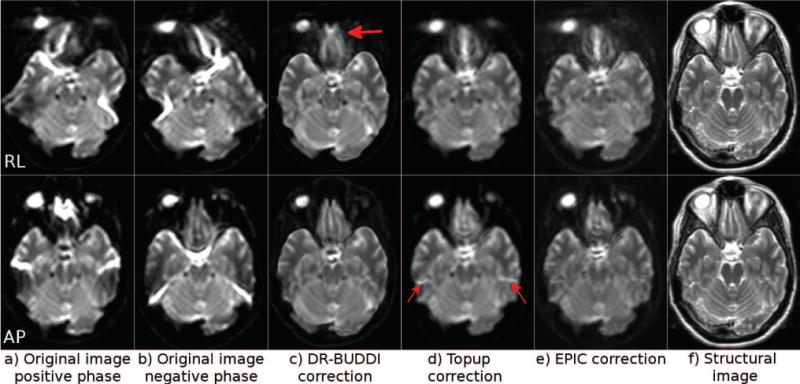
Figure 16 displays the effects of using DWIs together with the b = 0 image for correction. The pons is homogeneous in the T2W image and b = 0 images do not contain enough information for a correct registration of pathways. In fact, Figure 16.b shows that the transverse pontine fibers in the ventral aspect of the pons appeared broken, when only b = 0 images were used for correction (arrow). Including DWIs within DR-BUDDI’s vector-image registration framework solved this issue (Figure 16.c). Additionally, the shape of the cortical spinal tracts is also more accurate with correction using DWIs.
Figure 16.
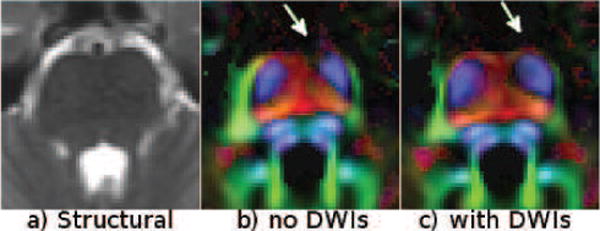
Effects of using DWIs for correction
Figure 17 displays the b = 0 s/mm2 and DEC images from the largely distorted RL data of Test Set 3, zoomed in to the brain stem region. Even though CSF bled into white matter regions to some degree, the corrections from all methods appear to be acceptable when only the b = 0 images are considered. However, one can observe significant differences between the methods in the DEC maps. With DR-BUDDI, which also used the DWIs to compute the deformation field, the CST (arrows) were clearly distinct and show high anisotropy, whereas with TOPUP, the two CST bundles were split into three (arrows) with an artifactual bundle created at the mid-sagittal line. This anatomically correct bundles also have reduced anisotropy. With EPIC, the two CST bundles were instead merged into a single one at the mid-sagittal line (arrow).
Figure 17.
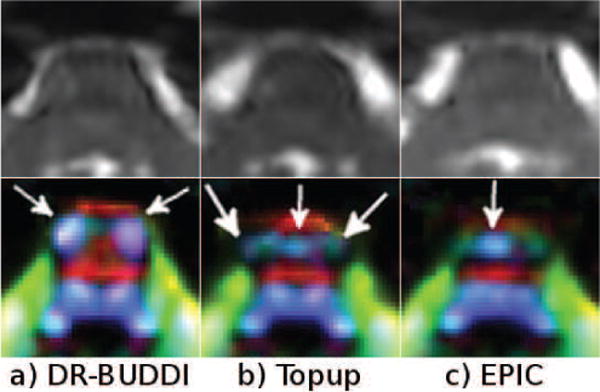
Pons from the RL Test Set 3 corrected with three methods.
3.2.4. Scanner Differences
With this analysis, our aim was to determine whether DR-BUDDI can be used to reduce the effect of the variability introduced by different levels of EPI distortions from different manufacturer magnets. Therefore, largely distorted data from Test Set 3 acquired with identical acquisition parameters on scanners from GE and Siemens were used. Distortion levels in the acquired data were significantly different across magnets. To determine this difference, the FA (and TR) maps computed from the uncorrected blip-up data acquired with the GE scanner were subtracted from the FA (and TR) maps computed from the uncorrected data from the Siemens scanner. This process was repeated for the uncorrected blip-down data sets and the data corrected with DR-BUDDI. Figure 18 displays these subtraction maps. Due to the difference in levels of distortions between these two magnets, both the FA and TR subtraction maps show large variations in several regions for both the uncorrected up and down data sets. However, DR-BUDDI was able to reduce this variability significantly (Figure 18.c).
Figure 18.
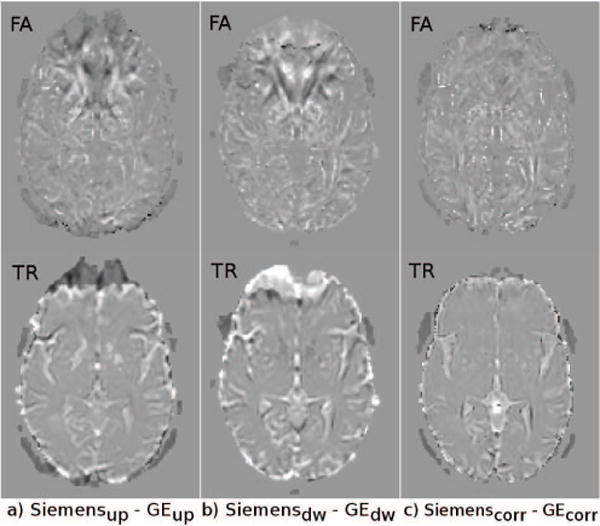
FA (top row) and TR (bottom row) difference maps between data acquired with scanners from different vendors.
3.2.5. Gibbs Ringing
Figure 19 displays a b = 0 image with Gibbs ringing artifacts due to extreme signal pile-ups around the eye regions (arrows). The deformation field in (b) is computed with DR-BUDDI using the image in (a) and its down version for correction, with no DWIs and no deformation regularization. As indicated by arrows in (b), the deformation field suffered greatly from the presence of such irregular image characteristics, and discontinuities or irregularities are visible even in the deformation fields. With the default settings (c), DR-BUDDI did not suffer from these issues because of the deformation regularizer, and, more importantly, because of its use of DWIs, which do not contain these types of artifacts.
Figure 19.
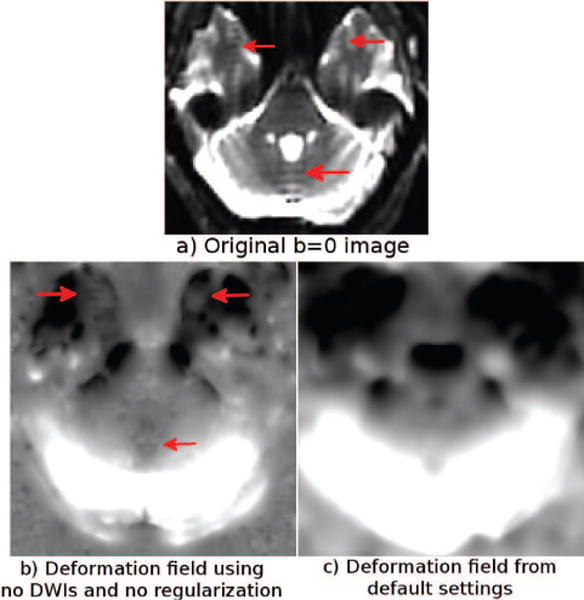
b = 0 s/mm2 image with Gibbs ringing artifacts due to signal pile-ups and the deformation field computed using this image, b) with no DWI or regularization, and c) with DWIs and regularization.
4. Discussion
We proposed a novel EPI distortion correction method, DR-BUDDI, for diffusion MRI datasets acquired with reversed phase-encoding directions. The proposed method is based on symmetric diffeomorphic registration principles and is capable of correcting for large deformations. It parameterizes the registration space with time and aims to find a middle image that is distortion-free by guiding the registration with additional information and constraints. The first piece of additional information is an anatomical, T2W, distortion-free structural image, which serves two purposes: 1) to guide the registration through a middle time point image that is distortion-free when displacements are large and 2) to regularize the registration and make it more robust in the presence of artifacts that may make the images inconsistent with the assumption that the transformations for correcting blip-up and blip-down images should be exactly the inverse of each other. The second piece of additional information comes from the use of diffusion-weighted images to help the correction in white matter regions that are homogeneous in b = 0 s/mm2 images and also to make the correction more robust to the presence of artifacts in the b = s/mm2 image from flow and Gibbs ringing.
DR-BUDDI outperforms the existing methods in most cases, particularly in the presence of motion or other imaging artifacts. It consistently produced sharper images with more distinct tissue interfaces and was very effective in preserving the anatomy of white matter pathways in regions of large distortions. Our primary criterion for judging the performance of the proposed algorithm was to assess the similarity of the corrected Right-Left (RL) phase encoded data to its Anterior-Posterior (AP) encoded counterpart with two subject populations on 1.5 and 3T scanners. In both cases, DR-BUDDI was generally superior to other methods in achieving anatomical similarity between tensor derived maps from corrected data acquired with RL and AP phase encoding.
Several common acquisition issues affect the quality of the blip-up blip-down correction methods. The first of these issues is motion between the blip-up and down scans. In general, the blip-up and down scans should image the same object in the same position, with identical orientation of phase encoding. Obviously, subject motion may violate these assumptions and may also produce a change in the local B0 field. From our initial observations we found that the effects of motion are not negligible with current blip-up blip-down acquisition schemes of acquiring a full dataset for blip-up, followed by blip-down (not interleaved). Simply rigidly aligning images and performing correction as if the phase-encoding directions of the images were aligned, and as if ∆B0 was identical, led to unsatisfactory results. DR-BUDDI accounts for the possibility that the phase-encode orientation of the blip-up and down images may be inconsistent, and uses a two-deformation field model with a structural target to increase robustness. These strategies helped to improve the correction quality in the presence of minor misalignment, but a robust solution is still needed in the case of large motion.
Another acquisition related issue is the use of parallel imaging. Due to the reduced degree of distortions, correcting the distortions in data acquired with parallel imaging was significantly less challenging than without parallel imaging. However, in our experience, images acquired with parallel imaging, regardless of the magnet manufacturer, suffer from some degree of ghosting. DR-BUDDI opens the possibility of obtaining usable images from 3T scans acquired without parallel imaging.
Numerous other issues affect correction quality as well. These include flow artifacts, Gibbs ringing, ghosting, hitting the noise floor in expanded regions, and gradient non-linearities. Even though we did not investigate all these issues, we have shown examples of how DR-BUDDI can handle Gibbs ringing and flow artifacts. Dealing with these challenges necessitates clever deformation regularization strategies or extra sets of images, which do not suffer from these issues. Using both structural and diffusion-weighted images within the DR-BUDDI framework provides fundamental improvements for the convergence of the algorithm to a more stable solution. However, in the presence of such artifacts, the parameters, specifically image and metric weights, need to be adjusted accordingly.
With our numerous experiments testing DR-BUDDI correction, we realized that no set of fixed parameters produced optimal results for all types of data. In general, we noticed that images with moderate to severe degree of distortions, including most 3T data acquired with parallel imaging on magnets by the three major manufacturers, can be very effectively corrected with the default settings. Tweaking of parameters was sometimes necessary for atypical data. For example, for data with extremely large EPI distortions, better correction performance was achieved by increasing the optimization step-length, the correlation window size or the time parameterization. Data with pronounced Gibbs’ ringing artifacts on the b = 0 s/mm2 images required further deformation field regularization by increasing the regularization operator’s kernel size and increasing the weighting of the DWIs, which do not suffer from these artifacts. We experienced few instances in which the initial quadratic or affine registration failed, in particular when we used a previously masked structural image. The solution in this case was to perform a rigid registration of the b = 0 images to the structural image, an option which is available to the user in DR-BUDDI. Additionally, we wanted to give users the ability to synthesize DWIs through the diffusion tensor model. In our experience, using the individual DWIs worked relatively well, however, it can be very time consuming for data sets with a large number of diffusion directions. Using synthetic images helps as a dimensionality reduction strategy and it can also be useful in situations where a few DWIs are artifactual.
Another important aspect we learned about in this work is how to assess the quality of corrections when dealing with diffusion MRI data. Traditionally, the similarity of the reconstructed b = 0 images to a distortion-free anatomical image has been the main assessment tool. However, we have often seen that even when the corrected b = 0 images seem perfectly aligned with the structural image, the directionality, size, and anisotropy of white matter bundles from the DWI data might be anatomically inaccurate. The most egregious examples were found in the pons, where the left and right motor pathways were sometimes fused into a single bundle or split into three bundles after correction. Therefore, we believe it is of fundamental importance to asses the quality of a blip-up blip-down correction method by checking the directionally encoded color maps and fiber tractography results as suggested in Irfanoglu et al. (2012). The Trace or Mean Diffusivity maps are also very important to assess the amount of CSF bleeding into parenchymal structures after registration.
As stated previously, motion has an effect on the B-matrices. After DR-BUDDI correction, we generate a corrected blip-up data set and a corrected blip-down data set, each with its own B-matrix, which are later combined with geometric averaging to generate the final signal-redistributed data. In the presence of motion, the B-matrices for the two corrected data sets can be significantly different, and the combination of these two B-matrices for the final data is mathematically not straightforward. In our software package, we simply linearly average these two matrices. This approximation is acceptable when motion is small but not when it is extreme. As a result of extreme motion, the distortions for the blip-up and down images will be significantly different and the corresponding diffusion-weighted volumes will have different diffusion contrasts. In this case, these volumes should either be excluded from the tensor computations or the two data sets should be concatenated rather than averaged geometrically.
The metrics proposed in this work assumed T2 contrast for the structural images because the cross-correlation measure used to derive the proposed metrics requires a similar contrast between the b = 0 s/mm2 and the structural images. In our experiments, the structural images were fat-suppressed T2W images. Another reason for using fat suppressed T2W images is that the strong signal from the soft tissue in the head in T1W images, as well as the non fat-suppressed T2W images, may cause the algorithm to stretch brain regions into the skull. To use T1W images as structural images, a mutual information version of the metrics proposed in this work should be implemented.
Another question related to the acquisition is about the choice of phase-encoding directions. In our previous work (Irfanoglu et al., 2012), we reported that data acquired with Right–Left (or Left–Right) phase encoding are more prone to spurious tract asymmetries between the right and left hemispheres and that this encoding option should be avoided if possible. However, the EPI distortion correction strategy used in that work was less effective than those achievable with blip-up blip down methods. Blip-up blip-down acquisitions and corrections show great potential in this area as we have shown in this work with the similarity of corrected images with AP and RL phase encoding. With RL phase encoding, the number of phase-encoding lines in RL acquisitions can be reduced when a rectangular FOV is used; this strategy will reduce echo time, and, consequently, increase SNR and possibly reduce total scan time. It may therefore be advantageous to consider using RL phase encoding for blip-up blip-down corrections.
In addition to DTI, we have been successfully using the proposed method with HARDI multi-shell acquisitions as well. Employing the b = 0 s/mm2 and the low q regime images to estimate the deformation fields and using these fields to correct the high q images has produced good results for diffusion models that are more complex than the diffusion tensor.
Finally, we would like to discuss the advantages of blip-up blip-down protocols. In general, because the modality and the quality of the acquisitions are limited by scan time, especially in clinical settings, one might question the marginal advantage of blip-up blip-down acquisitions. At this point, we can clearly state that the correction quality achieved with blip-up blip-down data for both the white matter and cortical gray matter regions is unmatched compared with previous correction approaches, such as field mapping or simple elastic registration. It is important to consider that even though the two datasets are merged into a single one, there is not a loss in terms of scan time because the merging operation also increases the SNR of the final images. Therefore, if scan time is an issue for DTI acquisitions, then it might be more advantageous to reduce the number of diffusion-weighted directions and acquire blip-up and down data. Therefore, considering the advantages, we expect the diffusion MRI field to move toward protocols with blip-up blip-down acquisitions for clinical scans in the near future.
Highlights.
The proposed EPI distortion correction method, DR-BUDDI, outperforms existing ones.
Blip-up blip-down symmetry principle does not always hold in practice.
Using a structural image and DWIs significantly improves correction quality.
Color and anisotropy maps should also be used to assess the quality of correction.
Artifacts from Gibbs ringing and flow voids may significantly affect correction.
Acknowledgments
This research was supported by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) and the National Institute of Neurological Disorders and Stroke (NINDS), National Institutes of Health (NIH). Support for this work included funding from Department of Defense in the Center for Neuroscience and Regenerative Medicine (CNRM)(HJF Award#: 30613610.0160855). The authors would also like to thank the Henry M. Jackson Foundation (HJF) for their administrative support and Dr. Holland for making his correction tool available to us. Finally, we would like to thank the NIH Diffusion-Weighted EPI Distortion Correction Working Group, consisting of Dr. Andrew Knutsen, Dr. Cibu Thomas, Dr. Stephano Marenco, Dr. Souheil Inati, Dr. Ziad Saad, Dr. John Butman, Dr. Dzung Pham, Dr. Govind Bhagavatheeshwaran, Dr. Vinai Roopchansingh, Dr. Sean Marrett, Dr. Lalith Talagala, and Dr. Alexandru Avram for providing a discussion environment that initiated this work. We also thank Liz Salak for editing this manuscript.
A. Appendix
A.1. Displacements from SyN Metric
For completeness, SyN displacement derivations will be repeated here. See Avants et al. (2008) for further details. Following the notations of Avants et al. (2008), let the local cross-correlation metric be:
| (12) |
| (13) |
| (14) |
with n the local correlation window size, μup the mean signal within this window from , and .
The displacements can be computed using Euler-Lagrange equations applied to Equation 12. From chain rule:
| (15) |
| (16) |
| (17) |
with
| (18) |
similarly:
| (19) |
A.2. Displacements When a Structural Image is Used
In Metric 3 of Equation 3, because the second term of the summation does not depend on ϕ1, its gradient reduces to zero. The gradient of the first term can be computed in the same manner as in Appendix A.1 to yield:
| (20) |
and for the down image:
| (21) |
A.3. Displacements from Signal Redistribution Metric
By chain rule, the displacements when a structural image and signal-redistributed image are used can be found as:
| (22) |
Similarly to the previous derivations:
| (23) |
and
| (24) |
| (25) |
A.4. Deformation Equality Soft Constraints
Assuming there is no motion between the up and down images and no changes in the B0 field, we would expect to be equal to . Then the weighted average for the new displacement, which assumes no motion but changes in the B0 field can be written as (with β ∈ [0, 1]):
| (26) |
In the presence of motion, one can not simply average the displacements from the two fields because the phase encoding directions are different. Therefore, one needs to rotate the displacement vector of the “other” field onto the current one. This can be done by using the rotation matrices that mapped both the up and down images onto the structural image. Hence, the rotated displacement vector can be written as:
| (27) |
producing the soft-constrained deformation field equation as:
| (28) |
A.5. Anisotropic Deformation Regularization
In this section, we will first recap the PDE regularization method for vector images proposed by Tschumperlé and Deriche (2005) and then describe how we use it in our framework. Let G(σ) be an isotropic Gaussian kernel with standard deviation σ, and let the displacement field originating from channel i of be Di. The traditional approach to regularize the deformation fields is with Gaussian convolution as:
where * is the convolution operator, which is identical to:
| (29) |
where Hi is the local Hessian matrix of the vector component Di, and time parameterization t defines the standard deviation σ in the convolution formulation. However, one is not restricted to isotropic Gaussian with this PDE-based formulation. If we introduce a 3 × 3 anisotropic structure diffusion tensor T (not to be confused with diffusion MRI tensor) to Equation 29, the new regularization equation becomes:
| (30) |
which is identical to:
One can choose any anisotropic diffusion tensor T to filter the image. However, to use a locally varying tensor T(x) that depends on local structures of image Di is a common and intelligent practice that prevents blurring and intermixing of image structures. Because Di is a displacement field and not a typical image in this work, we compute T(x) from the structure tensor field of the original images I′i. Let ∇ signify the spatial gradient operator. Then the structure tensor M(x) can be written as:
Note again that this structure tensor is based on the gradients of the original diffusion weighted and b = 0 images and not the displacement fields. Let u1(x), u2(x), u3(x) be the eigenvectors of M(x) and λ1,2,3(x) be the corresponding sorted eigenvalues. Then the anisotropic diffusion tensor is computed as [as in (Tschumperlé and Deriche, 2005)]:
| (31) |
where the functions fi(s) = (1 + s2)−1/i.
This formulation couples the different diffusion-weighted image channels through the structure tensor M and prevents the blurring of small structures in the transformed images by the deformation field regularizer.
A.6. DR-BUDDI Default Settings
Gradient descent step-length: 1.5
Correlation window size: 7
Initial registration type: Quadratic
b = 0 s/mm2 image type: From tensor estimation
DWI type: Synthesized
# of DWIS: 6
DWI and b = 0 image weighting: Equal
Metrics: ξ2 and ξ3
Metric weighting: Equal
Restriction: Along the phase-encode direction
Up and down deformation symmetry: Not enforced
Deformation regularization: Anistropic
# of anisotropic regularization steps: 5
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Andersson JL, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: Application to diffusion tensor imaging. NeuroImage. 2003;20(2):870–888. doi: 10.1016/S1053-8119(03)00336-7. [DOI] [PubMed] [Google Scholar]
- Avants B, Epstein C, Grossman M, Gee J. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis. 2008;12(1):26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants B, Tustison NJ, Song G, Cook PA, Klein A, Gee JC. A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage. 2011;54(3):2033–2044. doi: 10.1016/j.neuroimage.2010.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, Le Bihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. Journal of Magnetic Resonance. 1994;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Benner T, van der Kouwe AJ, Mainero C, Holland D, Dale AM. Automatic geometric distortion correction for single shot echo planar imaging. Proceedings of International Society of Magnetic Resonance in Medicine. 2011:4568. [Google Scholar]
- Bhushan C, Joshu A, Leahy RM, Haldar JP. Accelerating data acquisition for reversed-gradient distortion correction in diffusion MRI: A constrained reconstruction approach. Proceedings of International Society for Magnetic Resonance in Medicine. 2013:2387. doi: 10.1002/mrm.25026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodammer N, Kaufmann J, Kanowski M, Tempelmann C. Eddy current correction in diffusion weighted imaging using pairs of images acquired with opposite diffusion gradient polarity. Magnetic Resonance in Medicine. 2004;51:188–193. doi: 10.1002/mrm.10690. [DOI] [PubMed] [Google Scholar]
- Bowtell RW, McIntyre DJO, Commandre MJ, Glover PM, Mansfield P. Correction of geometric distortion in echo planar images. Proceedings of 2nd Annual Meeting of the SMR; San Francisco. 1994. p. 411. [Google Scholar]
- Chang H, Fitzpatrick JM. A technique for accurate magnetic resonance imaging in the presence of field inhomogeneities. IEEE TMI. 1992;11(3):319–329. doi: 10.1109/42.158935. [DOI] [PubMed] [Google Scholar]
- Chang HC, Chuang TC, Lin YR, Wang FN, Huang TY, Chung HW. Correction of geometric distortion in propeller echo planar imaging using a modified reversed gradient approach. Quantitative Imaging in Medicine and Surgery. 2013;3(2):73–81. doi: 10.3978/j.issn.2223-4292.2013.03.05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen G, Rabbitt R, Miller M. Deformable templates using large deformation kinematics. Image Processing, IEEE Transactions on. 1996;5(10):1435–1447. doi: 10.1109/83.536892. [DOI] [PubMed] [Google Scholar]
- Du YP, Zhou XJ, Bernstein MA. Correction of concomitant magnetic field-induced image artifacts in nonaxial echo-planar imaging. Magnetic Resonance in Medicine. 2002;48(3):509–515. doi: 10.1002/mrm.10249. [DOI] [PubMed] [Google Scholar]
- Embleton KV, Haroon HA, Morris DM, Ralph MAL, Parker GJ. Distortion correction for diffusion-weighted MRI tractography and fMRI in the temporal lobes. Human Brain Mapping. 2010;31(10):1570–1587. doi: 10.1002/hbm.20959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank LR. Characterization of anisotropy in high angular resolution diffusion-weighted MRI. Magnetic Resonance in Medicine. 2002;47:1083–1099. doi: 10.1002/mrm.10156. [DOI] [PubMed] [Google Scholar]
- Gallichan D, Andersson JLR, Jenkinson M, Robson MD, Miller KL. Reducing distortions in diffusion-weighted echo planar imaging with a dual-echo blip-reversed sequence. Magnetic Resonance in Medicine. 2010;64:382–390. doi: 10.1002/mrm.22318. [DOI] [PubMed] [Google Scholar]
- Holland D, Kuperman JM, Dale AM. Efficient correction of inhomogeneous static magnetic field-induced distortion in echo planar imaging. Neuroimage. 2010;50:175–183. doi: 10.1016/j.neuroimage.2009.11.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irfanoglu MO, Sammet S, Walker L, Pierpaoli C, Machiraju R. Susceptibility distortion correction for echo planar images with non-uniform b-splines grid sampling: A diffusion tensor image study. Proceedings of MICCAI. 2011:174–181. doi: 10.1007/978-3-642-23629-7_22. [DOI] [PubMed] [Google Scholar]
- Irfanoglu MO, Walker L, Sarlls J, Marenco S, Pierpaoli C. Effects of image distortions originating from susceptibility variations and concomitant fields on diffusion MRI tractography results. Neuroimage. 2012;15(61):275–288. doi: 10.1016/j.neuroimage.2012.02.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansons KM, Alexander DC. Persistent angular structure: new insights from diffusion MRI data. Inverse Problems. 2003;19:1031–1046. doi: 10.1007/978-3-540-45087-0_56. [DOI] [PubMed] [Google Scholar]
- Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magnetic Resonance in Medicine. 1995;34:65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magnetic Resonance in Medicine. 1999;42:515–525. [PubMed] [Google Scholar]
- Kybic J, Thevenaz P, Nirkko A, Unser M. Unwarping of unidi-rectionally distorted EPI images. IEEE Transactions on Medical Imaging. 2000;19(2):80–93. doi: 10.1109/42.836368. [DOI] [PubMed] [Google Scholar]
- Lee J, Laza M, Holden J, Griley E, Alexander AL. Correction of B0 EPI distortions in diffusion tensor imaging and white matter tractography. Proceedings of International Society of Magnetic Resonance in Medicine. 2004;11:2172. [Google Scholar]
- Lyksborg M, Lundell H, Reislve N, Siebner HR, Larsen R, Dyrby TB. Correcting geometric distortions of echo planar imaging using demons and reversed phase encoding. Proceedings of International Society for Magnetic Resonance in Medicine. 2012:2478. [Google Scholar]
- Mohammadi S, Nagy Z, Hutton C, Josephs O, Weiskopf N. Correction of vibration artifacts in DTI using phase-encoding reversal (COVIPER) Magnetic Resonance in Medicine. 2012;68:882–889. doi: 10.1002/mrm.23308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan PS, Bowtell RW, McIntyre DJO, Worthington BS. Correction of spatial distortion in EPI due to inhomogeneous static magnetic fields using reversed gradient method. Journal of Magnetic Resonance Imaging. 2004;19:499–507. doi: 10.1002/jmri.20032. [DOI] [PubMed] [Google Scholar]
- Morgan PS, Moody AR, Allder SJ, Bowtell RW. Correction of distortion in ADC maps using the reversed gradient method. Proceedings of International Society of Magnetic Resonance in Medicine. 2000:240. [Google Scholar]
- Olesch J, Ruthotto L, Kugel H, Skare S, Fischer B, Wolters CH. A variational approach for the correction of field-inhomogeneities in EPI sequences. Proceedings of SPIE. 2010;7623:76230K–76230K–8. [Google Scholar]
- Pajevic S, Pierpaoli C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: application to white matter fiber tract mapping in the human brain. Magnetic Resonance in Medicine. 1999;42:526–540. [PubMed] [Google Scholar]
- Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Chiro GD. Diffusion tensor MR imaging of the human brain. Radiology. 1996;201:637–648. doi: 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
- Pierpaoli C, Walker L, Irfanoglu MO, Barnett AS, Chang LC, Koay CG, Pajevic S, Rohde GK, Sarlls J, Wu M. Tortoise: an integrated software package for processing of diffusion MRI data. Proceedings of International Society of Magnetic Resonance in Medicine. 2010:1597. [Google Scholar]
- Pintjens W, Poot DHJ, Verhoye M, Linden AVD, Sijbers J. Susceptibility correction for improved tractography using high field DT-EPI. Proceedings of SPIE Medical Imaging. 2008 Feb;6914 [Google Scholar]
- Reber PJ, Wong E, Buxton R, Frank LR. Correction of off resonance related distortion in echo-planar imaging using epi-based field maps. Magnetic Resonance in Medicine. 1998;39:328–330. doi: 10.1002/mrm.1910390223. [DOI] [PubMed] [Google Scholar]
- Rohde GK, Barnett AS, Basser PJ, Marenco S, Pierpaoli C. Comprehensive approach for correction of motion and distortion in diffusion weighted MRI. Magnetic Resonance in Medicine. 2004;51(1):103–14. doi: 10.1002/mrm.10677. [DOI] [PubMed] [Google Scholar]
- Ruthotto L, Kugel H, Olesch J, Fischer B, Modersitzki J, Burger M, Wolters CH. Diffeomorphic susceptibility artifact correction of diffusion-weighted magnetic resonance images. Physics in Medicine and Biology. 2012;57(18):5715. doi: 10.1088/0031-9155/57/18/5715. [DOI] [PubMed] [Google Scholar]
- Shin W, Beall EB, Sakaie K, Li M, Holland D, Dale AM, Lowe M. Robustness of echo planar imaging (EPI) distortion correction in diffusion tensor imaging using forward/reverse phase encode directional b=0 scans. Proceedings of International Society of Magnetic Resonance in Medicine. 2011:3941. [Google Scholar]
- Skare S, Andersson JLR. Correction of MR image distortions induced by metallic objects using a 3D cubic B-spline basis set: Application to stereotactic surgical planning. Magnetic Resonance in Medicine. 2005;54:169–181. doi: 10.1002/mrm.20528. [DOI] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, Luca MD, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, Stefano ND, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23(1):208–219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Sotiropoulos SN, Jbabdi S, Xu J, Andersson JL, Moeller S, Auerbach EJ, Glasser MF, Hernandez M, Sapiro G, Jenkinson M, Feinberg DA, Yacoub E, Lenglet C, Essen DCV, Ugurbil K, Behrens TE. Advances in diffusion MRI acquisition and processing in the human connectome project. NeuroImage. 2013;80(0):125–143. doi: 10.1016/j.neuroimage.2013.05.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao R, Fletcher PT, Gerber S, Whitaker RT. A variational image-based approach to the correction of susceptibility artifacts in the alignment of diffusion weighted and structural MRI. Information Processing in Medical Imaging. 2009;21:651–663. doi: 10.1007/978-3-642-02498-6_55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Techavipoo U, Okai AF, Lackey J, Shi J, Dresner MA, Leist TP, Lai S. Toward a practical protocol for human optic nerve DTI with EPI geometric distortion correction. Journal of Magnetic Resonance Imaging. 2009;30:699–707. doi: 10.1002/jmri.21836. [DOI] [PubMed] [Google Scholar]
- Tschumperlé D, Deriche R. Vector-valued image regularization with PDEs: A common framework for different applications. IEEE Trans PAMI. 2005;27(4):506–517. doi: 10.1109/TPAMI.2005.87. [DOI] [PubMed] [Google Scholar]
- Tuch DS. Ph.D. thesis. Harvard university; Cambridge, MA: 2002. Diffusion MRI of complex tissue structure. [Google Scholar]
- Tuch DS. Q-ball imaging. Magnetic Resonance in Medicine. 2004 Dec;52(6):1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- Tuch DS, Weisskoff RM, Belliveau JW, Wedeen VJ. High angular resolution diffusion imaging of the human brain. Proceedings of International Society of Magnetic Resonance in Medicine. 1999:321. [Google Scholar]
- Turner R, Le Bihan D. Single-shot diffusion imaging at 2.0 tesla. Journal of Magnetic Resonance. 1990 Feb;86:445–452. [Google Scholar]
- Vardal J, Salo RA, Larsson C, Dale AM, Holland D, Groote IR, Bjrnerud A. Correction of B0-distortions in echo planar imaging based perfusion weighted MRI. Journal of Magnetic Resonance Imaging. 2013 doi: 10.1002/jmri.24213. [DOI] [PubMed] [Google Scholar]
- Voss HU, Watts R, Borja J, Ulug AM, Ballon D. Diffusion tensor imaging at 3T with strongly reduced geometric and intensity distortions. Proceedings of International Society of Magnetic Resonance in Medicine. 2005a:11. [Google Scholar]
- Voss HU, Watts R, Ulug AM, Kolbert KS, Borja J, Ballon D. Correction of spatial and intensity distortions in functional magnetic resonance imaging. Proceedings of International Society of Magnetic Resonance in Medicine. 2005b:1544. [Google Scholar]
- Wedeen VJ, Tuch D, Weigel M, Dou J, Weiskoff R, Chessler D. Mapping fiber orientation spectra in cerebral white matter with fourier-transform diffusion MR. Proceedings of International Society of Magnetic Resonance in Medicine. 2000;8:82. [Google Scholar]
- Wu M, Chang LC, Walker L, Lemaitre H, Barnett AS, Marenco S, Pierpaoli C. Comparison of EPI distortion correction methods in diffusion tensor MRI using a novel framework. Proceedings of MICCAI. 2008;11:321–329. doi: 10.1007/978-3-540-85990-1_39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang QS, Ye FQ. Correction for geometric distortion and N/2 ghosting in EPI by phase labeling for additional coordinate encoding (PLACE) Magnetic Resonance in Medicine. 2007;57(4):731–741. doi: 10.1002/mrm.21187. [DOI] [PubMed] [Google Scholar]
- Zhang H, Yushkevich PA, Alexander DC, Gee JC. Deformable registration of diffusion tensor MR images with explicit orientation optimization. Medical Image Analysis. 2006;10(5):764–785. doi: 10.1016/j.media.2006.06.004. [DOI] [PubMed] [Google Scholar]


