Abstract
The choice of a reference image typically influences the results of deformable image registration, thereby making it asymmetric. This is a consequence of a spatially non-uniform weighting in the cost function integral that leads to general registration inaccuracy. The inhomogeneous integral measure – which is the local volume change in the transformation, thus varying through the course of the registration – causes image regions to contribute differently to the objective function. More importantly, the optimization algorithm is allowed to minimize the cost function by manipulating the volume change, instead of aligning the images. The approaches that restore symmetry to deformable registration successfully achieve inverse-consistency, but do not eliminate the regional bias that is the source of the error. In this work, we address the root of the problem: the non-uniformity of the cost function integral. We introduce a new quasi-volume-preserving constraint that allows for volume change only in areas with well-matching image intensities, and show that such a constraint puts a bound on the error arising from spatial non-uniformity. We demonstrate the advantages of adding the proposed constraint to standard (asymmetric and symmetrized) demons and diffeomorphic demons algorithms through experiments on synthetic images, and real X-ray and 2D/3D brain MRI data. Specifically, the results show that our approach leads to image alignment with more accurate matching of manually defined neuroanatomical structures, better tradeoff between image intensity matching and registration-induced distortion, improved native symmetry, and lower susceptibility to local optima. In summary, the inclusion of this space- and time-varying constraint leads to better image registration along every dimension that we have measured it.
Keywords: Deformable image registration, volume-preserving constraints, symmetry, inverse-consistency, integral non-uniformity
1. Introduction
Image registration is a crucial step in numerous clinical and neuroscientific imaging studies involving the comparison of images, such as population investigations and longitudinal analyses. In the basic case with only two images involved, pairwise registration provides dense point-wise correspondences between voxels of the two input images. The set of such correspondences is often thought of as a transformation that takes each point in one image to the corresponding point in the other image. In that case, registration is said to align the two images; i.e., morph and overlay a moving image on a fixed image (or alternatively move both images) so that they appear similar or identical to each other. Interpreting registration as alignment requires the definition of a reference space, in which the images are aligned and compared. The choice of the reference influences the results, particularly when the transformation is assumed non-rigid (beyond merely translation and rotation) – as is necessary in most cross-subject registration applications. It is common to arbitrarily select the native space of one of the images (the space where the image is undistorted) as the reference space, hence the dependence of the results on the choice of the so-called reference image1. It must be noted that interpreting registration as alignment – and consequently selection of a reference image/space – is intrinsically unnecessary for many applications (e.g., comparison of local cortical thickness of two brain images, where correspondences established between the two images do not necessarily represent alignment). With no image designated as the reference, swapping the two images should not affect the resulting point-wise correspondences, making pairwise registration inherently symmetric with respect to the input images. Obtaining the same results after reversing the direction of registration – known as inverse-consistency2 – is therefore necessary for a pairwise registration method to be considered reliable and unbiased.3
Pairwise deformable registration is performed by maximizing some measure of similarity between the corresponding regions of the two images (for a survey, see (Sotiras et al., 2013)). Since a perfect match cannot generally be achieved due to noise and anatomical variability, typically a local image mismatch measure aggregated over the entire space is minimized. Such cost functions (CFs), with the most common example being the sum of squared difference (SSD) of image intensities, require the images to be aligned in a reference space in which the mismatch measure is integrated, thus raising the question of how to select a suitable reference space. Registration results depend on the choice of the reference as a consequence of the non-rigid (specifically, volume-changing) nature of the transformation, since, as we will see in Section 2.3, spatially uniform integration in the reference space is generally equivalent to nonuniform integration in (one or both) native spaces. In other words, for an arbitrary deformation, the integral of the mismatch measure has space-varying weightings in at least one of the native spaces of the images, with a weighting that varies depending on the deformation and the choice of the reference space. As we will see, the weighting in the CF integral is the Jacobian determinant of the transformation, which represents the local volume change in the deformation field. Assigning weighting to image regions introduces a regional bias. Furthermore, given that the weighting depends on the transformation, the optimization algorithm will drive the deformation also towards ‘lowering the weighting of the mismatched areas’, instead of only improving the alignment (e.g. by shrinking a region of one image so much as to make it almost vanish). Figure 1 presents an example of such a phenomenon, which results in a counterproductive increase in SSD in the native space of the interpolated image during registration. The dependence of the degree of expansion and shrinkage – representing the Jacobian determinant – on the choice of the reference image has also been observed by Cachier and Rey (2000), and has been reported to bias the quantification of the evolution of lesions in multiple sclerosis studies by hampering the equal retrieval of expanding and shrinking areas (Rey et al., 2002). These sources of error exist regardless of whether the reference space is chosen to be the native space of an input image or some sort of mid-space, as one or both of the native spaces of the images – which are the only physically meaningful spaces – will be integrated with regional bias.
Figure 1.
In this illustrative example, two one-dimensional images are registered by a given SSD-minimizing algorithm, with the blue image (the M-shaped intensity profile) chosen as the reference and the green one chosen as the interpolated (moving) image. The evolution of the registration is depicted from left to right, where the two rows visualize the process in the native spaces of the blue (top row) and the green (bottom row) images. Therefore, the deformations of the green (top row) and blue (bottom row) images are the inverse of each other. Given that the blue image matches better the background rather than the bright spot of the green image, the latter is shrunk in the reference space (top row). It can be seen that the SSD, while decreasing in the native space of the reference image (top row, where the CF integral is uniform), increases in the native space of the interpolated image (bottom row, where the CF integral is weighted by the volume change). The CF, being a non-uniform integral in the native space of the interpolated image, is here minimized by decreasing the weighting, even though resulting in an increase in the mismatch measure. (This toy example is provided to illustrate the disagreement on the decrease/increase in the SSD when the transformation is observed in the two native spaces, without commenting on whether the SSD-minimizing transformation here is the “expected” result. The two red curves in Figure 4 are another such example, yet using a symmetrization approach. For simplicity, we assume the regularization to be small relative to the data-attachment term.)
In standard implementation of deformable registration the reference space is commonly chosen as the native space of one of the images (say, the first image), and the results are consequently influenced by the ordering of the input images, thereby breaking the symmetry of registration. The spurious dependence of the point-wise correspondences on the choice of the reference image has been shown to be related to a bias introduced into the estimation of Alzheimer's disease effects (Fox et al., 2011; Hua et al., 2011; Thompson and Holland, 2011; Yushkevich et al., 2010). In longitudinal studies in particular, favoring one time point over another may result in errors dominating the subtle changes one seeks to measure (Reuter et al., 2012). In addition, in radiation therapy, the implication of registration asymmetry has been discussed for daily dose computation (Yang et al., 2008) and auto re-contouring (Ye and Chen, 2009). To address this issue, existing approaches primarily aim to restore inverse-consistency to registration by computing the integral in both image spaces and taking the average (Alvarez et al., 2007; Bondar et al., 2010; Cachier and Rey, 2000; Christensen and Johnson, 2001; Chui, 2001; Feng et al., 2009; Geng, 2007; Gholipour et al., 2010; Leow et al., 2007; Modat et al., 2012; Mohagheghian et al., 2010; Sabuncu et al., 2009; Tagare et al., 2009; Tao et al., 2009; Trouvé and Younes, 2000; Vercauteren et al., 2008b; Zeng and Chen, 2008; Zhang et al., 2006) or computing the integral in an abstract mid-space chosen to be “in between” the native spaces of the images (Beg and Khan, 2007; Chen and Ye, 2010; Joshi et al., 2004; Lorenzen et al., 2004; Lorenzi et al., 2013; Noblet et al., 2008; Škrinjar et al., 2008; Yang et al., 2008; Ye and Chen, 2009). Other approaches based on similar ideas have been proposed in the literature, including (Ashburner et al., 1999, 2000; Avants et al., 2008; Basri et al., 1998; Christensen and Johnson, 2003; Dedeoglu and Kanade, 2005; He and Christensen, 2003; Rogelj and Kovačič, 2006; Yanovsky et al., 2008b; Yeung et al., 2008). Although these methods are effective in making the registration invariant to the ordering of the input images, they do not alleviate the time-varying regional bias, which is the source of the problem. Indeed, inverse-inconsistency is merely a symptom of non-uniform integration of the mismatch measure on the images, and symmetrization of registration does not necessarily eliminate the underlying cause (non-uniformity of the integral) and the consequent inaccuracies introduced into the registration. Our underlying hypothesis is that the freedom for the algorithm to minimize the CF by altering the Jacobian determinant instead of improving image matching leads to suboptimal registration solutions in terms of 1) reduced image intensity matching, 2) increased (and unnecessary) distortion in the warp field, and 3) the creation of local minima that reduce the accuracy of the resulting correspondences.
In this work, instead of symmetrizing the CF, we address the root of the problem: non-uniform integrals of CFs defined on the native spaces of images. We propose to restrict the deformation such that the integrals in the native spaces of the images are (almost) unweighted, except in regions where weighting contributes (almost) no error to the CF. Our adaptive constraint – which, as we will see in Section 3.1, is quasi-volume-preserving (QVP) – keeps the deformation field away from zones that would lead to non-uniformity-induced error, by limiting the local volume changes except for regions where image intensities match well. As a result, the proposed method yields overall improvement in the alignment (Section 4) when incorporated in an SSD-like deformable registration algorithm.4 Furthermore, a natural consequence of the QVP constraint is that the values of the native CFs, i.e. those with uniform integral on the native space of an input image, remain arbitrarily close to each other throughout the registration. This property, which we shall name native symmetry, is a stronger form of symmetry and is improved by our method. Native symmetry implies that both native CFs agree on the progress of registration, as opposed to only one of them (as in asymmetric registration, e.g. Figure 1) or only the average of them (as in symmetrization). An additional advantage of restricting the deformation in dissimilar regions is helping to avoid entrapment of the iterative algorithm in local minima due to too much flexibility, thereby guiding it towards a good overall QVP fit before relaxing the constraints and achieving an optimum warp. This is particularly important in registration of medical images with possibly large anatomical variation. We will show improvement in registration in terms of better label alignment, better tradeoff between intensity matching and geometric distortion, native symmetry, and lower susceptibility to local optima, using two-dimensional (2D) non-diffeomorphic and three-dimensional (3D) diffeomorphic registration on several datasets.
This article extends our previous conference version (Aganj et al., 2013a). In particular, we provide a thorough theoretical justification (Section 2), more detailed description of the method (Section 3), more comprehensive experimental validation (Section 4), and further implementation details (appendices).
2. Spatial non-uniformity problem description
2.1. Definitions
The data attachment term of the standard asymmetric cost function (CF) that is minimized in deformable registration is defined as:
| (1) |
where Ω ⊆ ℝd is the d-dimensional image space, f, g, Ω ↦ ℝ are two input images, T: Ω ↦ Ω is the invertible transformation with respect to which the CF is minimized, and D:ℝ2 ↦ ℝ≥0 is the (often symmetric) nonnegative intensity distance (mismatch measure); e.g., defining D (u, v) := (u − v)2 results in the SSD CF.5 Some global regularization is also typically either added explicitly to this data-attachment CF, or performed at each iteration (see Appendix B). By searching for the transformation T that minimizes the CF, the optimization algorithm is expected to align corresponding regions of the two images.
Since image f is not deformed by T in the integral of Eq. (1), we say that the integral is represented in the native space of f. Image g, on the other hand, appears as g ∘ T in Eq. (1) and is generally deformed; however, by a simple change of variable y :=T(x), the same integral can be represented in the native space of g (see Eq. (3) below). We call If the f-native CF, since the integral of D is unweighted (taken uniformly) when represented in the native space of f.
2.2. Pitfalls of non-uniformity
We explain here the pitfalls of having a non-uniform (weighted) CF, which will help later to describe the key problem addressed in this paper. Let us assume that instead of Eq. (1), the following weighted version of it were minimized,
| (2) |
where WT: Ω ↦ ℝ≥0 is an arbitrary nonnegative weight function that generally depends on T. Allowing the image regions to contribute differently to the CF would introduce a multiplicative regional bias that would change throughout the registration process, depending on the input images and the registration parameters. More troublesome, however, would be the dependence of the bias on the transformation, thereby giving the optimization algorithm the ability to control the weighting in a counterproductive manner. More precisely, the algorithm would minimize such a weighted CF by:
searching for T that makes the transformed image better match the reference, f(x) ≈ g ∘ T(x), in a larger subset of Ω, and/or
manipulating T so as to lower the weighting WT(x), particularly in regions where the image intensities do not match well (i.e., with larger D).
The first point in this list is the raison d'être of CF optimization, and what the registration algorithm is supposed to do. The second, however, creates a mathematical loophole in the optimization, allowing the algorithm to not only evade its main task (i.e., decreasing D), but possibly lead the deformation towards even worse alignment (by changing T in a local fashion such that D increases, but both WT and the product D · WT decrease). It is important to avoid regionally biasing the CF integral (unless intentionally done for a particular benefit) to prevent such negative consequences and make the algorithm focus solely on improving the alignment. Next, we show that standard deformable registration algorithms have CFs that are non-uniform (weighted) in at least one of the two native spaces, thus suffering the disadvantages described here.
2.3. Intrinsic non-uniformity in standard deformable image registration
As discussed in Section 2.2, the mismatch measure D should be integrated uniformly in order to avoid registration inaccuracy. Yet, there are two native spaces – that of f and that of g – which are equally physically meaningful. The f -native CF (Eq. (1)) satisfies uniformity in the native space of f; however, rewriting it in the native space of g via the change of variable y :=T(x) leads to the following non-uniform integral:
| (3) |
where the function J: Ω ↦ ℝ>0 is the Jacobian determinant of the transformation, J (x): = det ∂T(x), which we assume to be positive (i.e., T preserves the topology). Given that J represents the relative volume change caused by the transformation and is in general inhomogeneous, we can see that the f -native CF is weighted by 1/J and does not satisfy uniformity in our second native space, i.e. that of g. The uniform CF in the native space of g, or the g-native CF, has the following form:
| (4) |
The change of variable y = T(x) again reveals that the g-native CF does not have a uniform representation in the native space of f:
| (5) |
It can be seen that, regardless of which native space is picked as the reference space, the undesirable weighting of the integral shows up in at least one of the native spaces (Figure 2a-c), except for the especially restrictive cases where J(x)=1 is imposed, such as in rigid registration, or more generally volume-preserving registration (Elen et al., 2008; Haber and Modersitzki, 2007; Hirota et al., 2000; Li et al., 2009; Loeckx et al., 2005; Mansi et al., 2011; Park et al., 2011; Rohlfing et al., 2003; Saddi et al., 2007; Tanner et al., 2002; Yin et al., 2009). Volume-preserving approaches, however, make the assumption that the deformation causes no local shrinkage or expansion, which may generally not be the case.
Figure 2.
a) Two images f (top) and g (bottom) are given as input to the registration algorithm. The deformed images in an intermediate registration iteration are illustrated in: b) native space of f, c) native space of g, and d) a mid-space. The grid distortion in (b,c,d) demonstrates that no matter what space is chosen to compute the CF integral, at least one of the images is integrated non-uniformly.
The lack of simultaneous uniformity of the CFs in both native spaces, as mathematically revealed above, is an inherent imperfection of standard deformable registration. Specifically, since the weighting J(x) is the local volume change, the algorithm may attempt to enforce artificial expansion or shrinkage – depending on which image is chosen as the reference – to decrease the weighted CF without accurate alignment (see Section 2.2). It is important to stress that this is not an esoteric argument that rarely occurs in practice; instead, it is inevitable in any nonlinear registration in any region in which there is an initial mismatch (see Figure 1 for an example). In these regions a biased CF integral will lead the algorithm to attempt to reduce J(x) (along with D) as much as possible within the limits of the imposed regularization. In fact, standard registration has been shown to privilege either expanding or shrinking regions depending on the choice of the reference (Cachier and Rey, 2000; Rey et al., 2002). The added global regularization restricts this artificial volume change, but only to some extent; therefore we need to further prevent this weight factor from interfering in the data-attachment term's driving of the registration towards the desired optimal alignment.
An implication of the non-uniform weighting in exactly one of the native spaces is that in general If ≠ Ig. Also, since:
| (6) |
one can see that the native CFs are inverse-inconsistent, i.e. If(f, g, T) ≠ If(g, f, T−1), and Ig(f, g, T) ≠ Ig(g, f, T−1). The primary approach in the literature to address this inverse-inconsistency is the minimization of the following average CF (Cachier and Rey, 2000; Christensen and Johnson, 2001; Tagare et al., 2009; Trouvé and Younes, 2000)6:
| (7) |
Substituting for Ig from Eq. (6), one can see that Iave is a symmetrized version of either of the native CFs and is therefore inverse-consistent, i.e. Iave(f, g, T) = Iave(g, f, T−1). However, by rewriting it in the native spaces of the two images, once using Eqs. (1,5) and again using Eqs. (3,4),
| (8) |
it turns out that Iave is a weighted integral in both native spaces (Figure 2d), and so the registration still incurs the regional bias errors (Section 2.2), in spite of its inverse-consistency.
In an alternative approach to restore symmetry, the mismatch error is integrated uniformly in an abstract mid-space, chosen to be equally close to both native spaces (Avants et al., 2008; Beg and Khan, 2007; Lorenzen et al., 2004; Noblet et al., 2008). Provided that the mid-space is chosen “in between” the two native spaces, changing the ordering of the input images will not affect the CF, hence the inverse-consistency. Nevertheless, it can be easily shown similarly as above that rewriting such a mid-space CF in the native spaces of the images, once again, results in the Jacobian determinant of the transformation (that takes the mid-space to the native space) to appear as a weighting in the native-space representations of the CF. Therefore, the integral of such a mid-space CF is non-uniform in both of the physically meaningful native spaces, and only uniform in the virtual mid-space, which is physically nonexistent and possibly changing during the registration process. As a consequence, the problems associated with the regional bias (Section 2.2) remain unresolved in these approaches. For instance, since the mid-space and the weighting often depend on T, the optimization algorithm has the ability to alter the mid-space so as to decrease the CF without necessarily making the two images more similar. An example of this behavior is when the algorithm changes T in such a way that regions with mismatching image intensities are shrunk in the mid-space. This results in a decrease in the (mid-space) CF but not necessarily in the native CFs, since the images will look more similar in the mid-space but not necessarily similar in the two native spaces. Constraints that are used to keep the mid-space “in between” the native spaces of the two images usually prevent such regions from totally shrinking, but depending on the strength of these constraints, partial shrinkage may still happen.
It should be noted that minimizing Iave or a mid-space CF results in transformations that are not necessarily minimizers of the native CFs, and for which, If and Ig are not necessarily equal. Here, we define the native symmetry property of an image registration algorithm, as the quality of producing transformations minimizing the native CFs, while keeping them equal (If= Ig). Rigid, and more generally any volume-preserving registration is natively symmetric (disregarding the asymmetry due to resampling artifacts (Aganj et al., 2013b; Reuter et al., 2010; Sabuncu et al., 2009)), since with J(x) = 1 everywhere, the two native CFs (Eqs. (1,5)) are always equal. Native symmetry is a stronger form of symmetry, indicating that both native CFs agree with the progress of registration. Neither asymmetric (minimizing either If or Ig) nor symmetrized (minimizing Iave or a mid-space CF) deformable registration is guaranteed to be natively symmetric.
3. Proposed methods
3.1. Quasi-volume-preserving constraint
In this work we introduce a constraint on the deformation field that keeps the non-uniformity error in the CF arbitrarily small. Examining Eqs. (3,5,8), we can see that the condition J(x) = 1, ∀x ∈ Ω would be sufficient for If, Ig, and Iave to be free of non-uniformity error. Nevertheless, such a restrictive volume-preserving constraint is not a necessary condition, as J can indeed be different from where the mismatch measure D is zero, and no error will yet arise from non-uniformity. Accordingly, by equating the integrand to its unweighted version, i.e. D(f(x),g ∘ T(x))J(x) = D(f(x),g ∘ T(x)), the following less restrictive constraint (here written in the native space of f) can also be seen to guarantee the elimination of the non-uniformity error:
| (9) |
Nonetheless, in practice, exact intensity matching, D(f(x),g ∘ T(x)) = 0, and absolute volume preservation, J(x) = 1, are seldom achieved. Thus, to allow for large deformations, particularly in the presence of noise and poor intensity match, here we propose the following relaxation of the above constraint, which we call the quasi-volume-preserving (QVP) constraint:
| (10) |
where the constant ε is a positive threshold on the local non-uniformity error. In fact, the prefix quasi- indicates the fact that volume preservation is imposed only in regions with disagreeing image intensities, as well as the relaxation of Eq. (9) to Ineq. (10). Roughly speaking, for a small ε, the QVP constraint ensures that there is almost no volume change (J(x) ≅ 1), except for regions where the image intensities almost match (D(f(x),g ∘ T(x)) ≅ 0).7 The performance of enforcing the QVP constraint with different values of ε has been evaluated in 3D brain image registration in Section 4.2. As we shall see, smaller values of ε, which further restrict the deformation, actually lead to improvements in the overall registration quality, indicating that the QVP constraint guides the registration away from problematic regions in the energy landscape, yielding better CF optima. A higher value for ε, however, might be needed to accommodate larger deformations and regions with poorer intensity match and higher noise (e.g., in longitudinal brain imaging when a tumor both grows and changes intensity).
By constraining the deviation of the volume change J(x) from as in the QVP inequality (10), the total non-uniformity error in the native CFs will be bounded by ε|Ω| (with |Ω| the size of the space), which can be made arbitrarily small by choosing a small enough ε.8 Remaining in this (almost) error-free QVP zone ensures that the optimization algorithm is not misled by a biased CF gradient that can potentially steer it away from the global minimum, for example, by encouraging complex warps in regions where no matching of image intensities is possible. In addition, by combining Eqs. (1,5,10), the error in native symmetry can similarly be seen to be bounded:
| (11) |
with Iave being close to both native CFs (using Eqs. (7,11)):
| (12) |
The local nature of the QVP constraint also ensures regional native symmetry; i.e., satisfying Ineq. (10) keeps native CFs defined in any local Ω′⊂Ω within ε|Ω′| of each other.9
By keeping the integrals of the CFs (almost) uniform in the native spaces of both images except for regions where non-uniformity barely perturbs the CF, the QVP constraint ensures that CF minimization is uniquely aimed at better alignment, and that no regional bias irrelevant to registration can be exploited to minimize the CF (Section 2.2).
3.2. Adaptive regularization interpretation
Enforcing the QVP constraint restricts J(x) to remain close to 1 in regions where the difference between the two images is large, but relaxes this restriction where the image intensities are similar. An additional practical advantage of the proposed method is its role as adaptive spatially-variant regularization (Cahill et al., 2009; Freiman et al., 2012; Glocker et al., 2009; Loeckx et al., 2004; Ou et al., 2011; Pace et al., 2013; Risholm et al., 2009; Staring et al., 2007; Stefanescu et al., 2004; Suárez et al., 2002; Tang et al., 2010). By restricting the deformation in regions where there is not a good match and letting the surrounding area to mostly drive the displacement, the QVP constraint allows the deformed image to “pass through” regions of poor match with restricted volume change, to potentially find regions where a good registration is possible, after which the constraint is naturally relaxed. Intuitively, the algorithm avoids fitting noise in regions where a good overall match cannot be found. Examples of such behavior are provided in sections 4.1.1 and 4.1.2.
The factor D in Ineq. (10) is the major contrast between our proposed approach and the volume-preserving methods in the literature (Section 2.3); our algorithm preserves volume only in regions where it finds no good match between the images. This means that the transformation may still contain compression and expansion in areas where the two images are locally similar, allowing good matching in regions where it is feasible. Although the QVP constraint is automatically relaxed in such similar-intensity regions, the inclusion of the global regularization still keeps the deformation field regular.10
3.3. Incorporation of the QVP constraint
The QVP constraint, which can be seen as a restriction on the feasible region of the optimization search space, can be applied to any deformable registration tool that optimizes an aggregate objective function, i.e. sum of a local similarity measure (such as SSD). To enforce the QVP inequality (10), at each iteration of the main registration algorithm we reduce the non-uniformity error:
| (13) |
until e(x) < ε for all x ε Ω. To that end, e(x) may be directly reduced by iteratively minimizing the integral ∫Ω R(e(x) − ε)dx to zero, with R(t) :=(t + |t|)/2 the ramp function, thereby satisfying e(x) < ε for all x. The dependence e(x) of on both T(x) and its derivative J(x), however, makes this direct minimization complicated.11 Thus, for simplicity and numerical stability, we choose a different approach to take T(x) to the QVP space.
To estimate the derivative e(x) of with respect T(x) to and moving T(x) in its descent direction, we first note that e(x) is the product of two factors: the mismatch measure D(f(x),g ∘ T(x)) and the Jacobian deviation |J(x)−1|. According to the product rule, d(uv) = vdu + udv, the derivative e(x) of has two terms, in each of which only one of the two factors is derived. The first term has the derivative of the mismatch measure D(f(x),g ∘ T(x)) and is a gradient term similar to that of the main optimization algorithm, simply leading to additional CF minimization. Since the mismatch measure is already minimized by the main optimization algorithm, we do not include this image-aligning term in the QVP constraining step,12 and rather focus on the second term of the derivative.
To reduce the Jacobian deviation factor |J(x)−1| of e(x), whose derivative appears in the second term of the derivative of e(x), we take advantage of the fact that the descent direction for the following measure of regularity (where K(x) is a weighting function),
| (14) |
is the well-known inhomogeneous diffusion, applied to the displacement field,
| (15) |
where t, γ, K(x), and are the diffusion iteration number, the step size, the space-variant diffusion coefficient, and the vector of all 1s, respectively. Therefore, the above diffusion process reduces the deviation of the Jacobian ∂T from the identity matrix (the higher K(x), the more strongly). We have shown in Appendix C that such small updates, while bringing the Jacobian ∂T closer to identity, also make the Jacobian determinant J asymptotically closer to 1. Since we want the diffusion to be much stronger in the areas with higher error, we make the diffusion coefficient grow quadratically with e(x) as follows:
| (16) |
It is important for K(x) to be a smooth function of e(x), as its derivative is computed in the diffusion process. We perform the inhomogeneous diffusion of Eq. (15) after both the main gradient-descent/Newton iteration and the standard demons regularization have been performed. To speed up the diffusion process, we apply a number of (10 in our experiments) iterations of diffusion, then update e(x) and K(x) with the new T(x), and if the QVP constraint e(x) < ε,∀x ∈Ω is not yet satisfied we repeat with further diffusion.13 The stopping criterion (satisfaction of QVP) makes this operation idempotent.
As we adopt the demons deformable registration (Thirion, 1998) in this work, the inhomogeneous blurring of the displacement field (primarily in areas with higher e(x)) at each registration iteration can be seen to be related to the Gaussian blurring (equivalent to homogeneous diffusion, see Appendix B) in the demons method, which blurs the displacement field at each iteration. However, a major contrast here is that the (space-variant) blurring depends on the mismatch measure D(f(x),g ∘ T(x)) that includes image data, since both (i) the spatial weighting of the diffusion K(x), and (ii) the important stopping criterion for the diffusion, i.e. the QVP inequality (10), depend on D(f(x),g ∘ T(x)).
We chose α = 70 in our experiments. Furthermore, to keep the diffusion stable, we choose the diffusion step size γ to be at most 2−(d+1) (Johnson et al., 2014), and threshold K(x) so it remains below a certain value (2 in our experiments). Also to make sure that local noise does not result in an over restrictive constraint, we denoise K(x) by a Gaussian low-pass filter with the standard deviation of 1 voxel, before using it in the diffusion step.
4. Results and discussion
To show that the proposed QVP constraint can be incorporated into and improve different implementations of deformable registration techniques, we validate it on both demons (in Matlab) and diffeomorphic demons (in Insight Toolkit (ITK)) registration. In all of the experiments, the image intensity values were initially scaled to be between 0 and 1.
4.1. Demons registration of 2D images
We first validate our method using 2D (non-diffeomorphic) demons registration by comparing the performance of the following three approaches: minimization of If, minimization of Iave, and minimization of Iave with the proposed QVP constraint (with the heuristically-determined optimum ε). Since with no explicit diffeomorphism constraints the topology is not necessarily preserved, for each method and experiment, we choose the optimum general demons regularization parameter λ (see Appendix B for definition) heuristically to achieve the best convergence with no observable topology break. For each experiment, we plot If and Ig with respect to the iteration number to assess the registration native symmetry by the extent to which these two native CFs agree with each other. We evaluate this throughout all the iterations, as opposed to only at the convergence, since this error is an aggregate measure of non-uniformity, which in turn can cause inaccurate gradient descent directions at every iteration and lead the optimization algorithm to undesirable solutions.14 In these non-diffeomorphic experiments, we also evaluate the overall results by the number of iterations that each algorithm takes to converge, and the best achievable ultimate CF value that preserves the topology, which is an indicator of the CF-distortion tradeoff. The experiments in this subsection are performed using our unidirectional Matlab implementation of CF minimization (Appendix A) and global regularization (Appendix B), meaning that only the forward CF needs to be explicitly evaluated.
4.1.1. Synthetic data
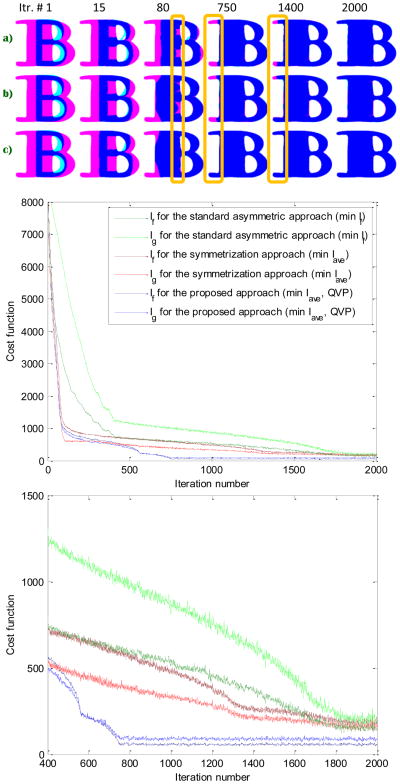
We first compare the three methods on synthetic data, by registering two letters ‘B’ with noticeably different shapes. As the plot in Figure 3 demonstrates, minimizing If (dark and light green) results in a relatively large difference Ig − If > 0, which is expected, since Ig is not in any form accounted for in the optimization. Minimizing Iave (dark and light red) reduces the gap between If and Ig, as equal weight is given to both of them in the optimization. Nevertheless, this approach – not being natively symmetric – does not guarantee the equality of the two native CFs. The proposed QVP approach with ε = .2 (dark and light blue), however, enforces a bound on |If − Ig| and therefore, as illustrated in the plot, produces transformations on the cost of which both native CFs agree (within the error margin ε). In addition, this method converges at an earlier gradient descent iteration (∼Itr. 750, see the orange rectangles in Figure 3 (top)) compared to the two others (∼Itr. 1800), while resulting in lower final native CF values than the standard asymmetric and the symmetrized approaches do.15
Figure 3.
Registration of synthetic data by a) minimizing If, b) minimizing Iave, and c) minimizing Iave with the proposed QVP constraint. Top: Cyan and magenta indicate respectively the reference and the interpolated images, with blue being their intersection. Middle/Bottom: The native CFs for each method, and a zoomed version.
The better convergence of the QVP method may be related to the fact that its optimum general regularization parameter λ = .2 is naturally lower compared to the other two techniques (λ = .3 and λ = .7 for the standard and the symmetrization methods), given that it also performs a separate inhomogeneous regularization (Eq. (15)). This method allows the transformation to freely absorb and compress one ‘B’ into the other, since the corresponding volume change happens in regions where the intensities match, for which the inhomogeneous regularization, and consequently the total regularization is weak. The inhomogeneous regularization, in contrast, prevents a topology break by regularizing more aggressively in areas where the difference between the two images (and therefore the SSD force) is large. Conversely, the other two methods need a higher λ to avoid topology break, and yet apply this strong general regularization to the entire image (including regions with matching intensities and no gradient force), hence a slower convergence and higher final CF (worse CF-distortion tradeoff).
4.1.2. X-ray images
Next, we compared the three methods on a pair of public jaw X-ray images acquired before (Figure 4a) and after (Figure 4b) an orthognathic surgery. Prior to deformable registration, high-resolution versions of the two images were superimposed, the upper jaws were rigidly aligned manually, and the images were low-pass-filtered and resampled to the lower resolution that is shown in Figure 4. As in the previous case, minimization of the standard asymmetric forward CF, If (Figure 4, the two green curves), soon creates a considerable gap between the native CFs. Minimizing Iave (Figure 4, the two red curves) results in a steady optimization of the average of the native CFs. However, since the native CFs are not individually considered, not only does the gap between them still mostly exist, but a jump that abruptly changes them – yet not their average – occurs around iteration 2000, which is possibly a sign of the potential susceptibility of the algorithm to local optima. In fact, an optimization algorithm might decide that it has converged and stop the procedure prematurely before iteration 2000, thus leaving the teeth region misaligned (as was actually the case here; the misalignment was observed in the deformed image for iterations before 2000). This is another example (similar to Figure 1) showing a transformation that decreases the SSD in one native space but increases it in the other native space, despite the fact that a symmetrized CF has been used. Conversely, the proposed QVP method with ε = .2 (Figure 4, the two blue curves) produces the smallest native CF gap for iterations before 2000, while obtaining the lowest final CF values (best CF-distortion tradeoff) compared to the standard asymmetric and the symmetrized approaches. The warped image obtained by the QVP approach is depicted in Figure 4c, along with the computed deformation field. Results from the two other methods were visually similar, except for the fact that the displacement in the upper jaw, which is supposed to be small because of the initial rigid alignment of the upper jaws, was lowest in the deformation obtained by the QVP approach (2.5 pixels, averaged in an upper jaw mask), and therefore least affected by the general regularization, compared to the standard (3.9 pixels) and the symmetrization (3.2 pixels) approaches. This is likely again due to the lower value of λ required by QVP, as explained in Section 4.1.1.
Figure 4.
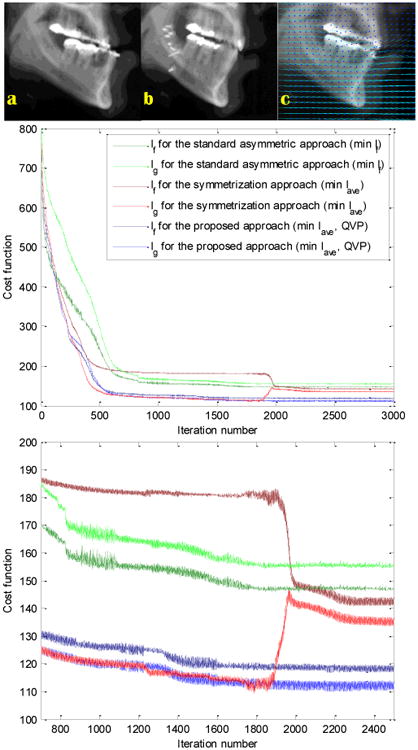
Top: X-ray images taken a) before and b) after surgery, with c) registration results using the proposed QVP approach. Middle/Bottom: Native CFs for the three methods, and a zoomed version.
4.1.3. Brain images
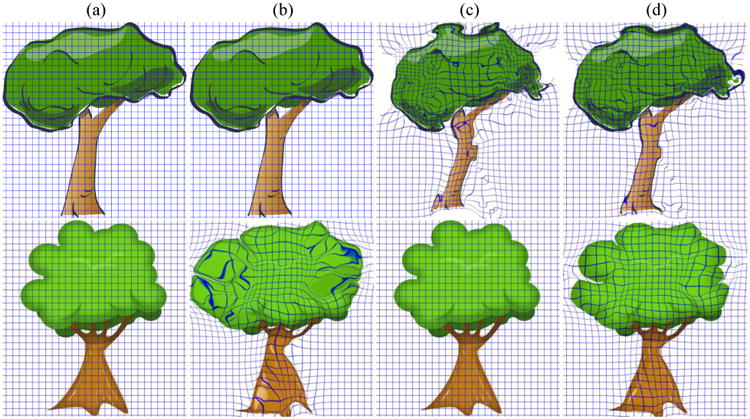
We also tested the three algorithms on the mid-sagittal planes of 20 brain images taken from the publicly available OASIS database (Marcus et al., 2007), which we pre-processed in FreeSurfer (Dale et al., 1999; Fischl, 2012; Fischl et al., 1999). The intensity-normalized and resampled volumes (1-mm3 isotropic voxel size) were made upright by robust rigid registration (Reuter et al., 2010) of each volume to its left-right mirrored version. The sagittal slice located four voxels to the right of the mid-sagittal plane was extracted from each volume, and to adjust for any nodding rotation, was rigidly registered to that slice of the first volume, and resampled to the size 128×128. Out of the 20 sagittal slices corresponding to the 20 subjects, the one closest (in L2 norm) to the rest was chosen as the reference, and non-rigidly registered to the other 19 subjects individually. For each subject and method, we ran the registration with 21 different values for general regularization parameter λ. We observed throughout our experiments that a lower value of λ that still preserved the topology consistently resulted in a lower final CF. Therefore, in order for each algorithm to present its best CF-distortion tradeoff, we inspected the results (19×3×21=1197 images), and for each subject and method we chose the one obtained with the lowest λ containing no visible topology break. The optimally chosen λ was the same for the symmetrization and the QVP (ε = .17) methods in 13 subjects; however, for the other 6 subjects, QVP passed the visual inspection test at a lower λ (see Figure 5 for examples). We computed the native asymmetry error as the mean absolute value of the difference of the two native CFs through all iterations. When averaged across subjects, this error was 161% and 16% higher for the asymmetric and the symmetrization techniques, respectively, compared to the proposed QVP approach. We also compared the final values of the native CFs, (If, Ig), among the methods, which were (30%, 56%) and (5%, 4%) higher for the asymmetric and the symmetrization approaches, respectively, compared to the QVP method. We hypothesized that the QVP approach results in a better CF-distortion tradeoff by producing ultimate native CF values (for the lowest λ preserving the topology) that are lower than those of the two other techniques. A left-tailed Student's t-test with a .05 significance level rejected the null hypothesis when comparing the QVP with both the asymmetric (p = 10−6) and the symmetrization (p = .02) approaches.
Figure 5.
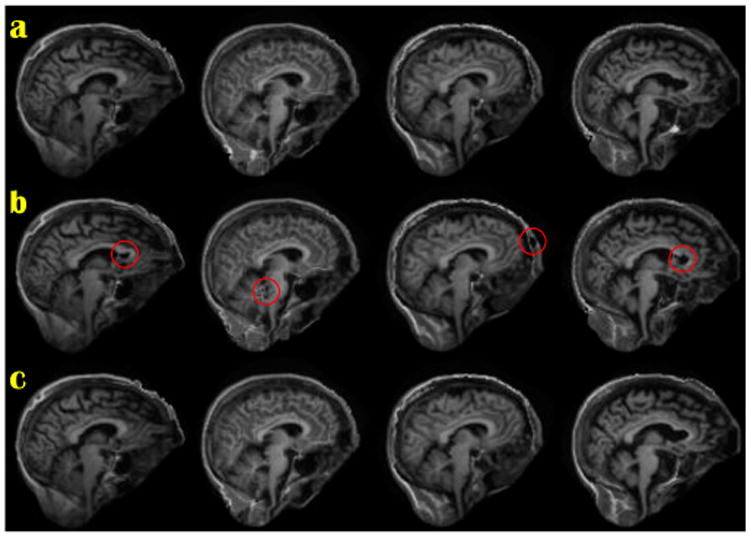
a) QVP registration results on four subjects with optimal values of λ. b) Results of Iave minimization using the same λ as in (a). Note the distortion due to under-regularization in the encircled areas. c) Results of Iave minimization using optimal (higher) values of λ, thus with higher CF values.
4.2. Diffeomorphic demons registration of 3D brain images
Next, we examined the effects of QVP constraining on the accuracy of registration using 3D labeled data, by incorporating the QVP constraint into the diffeomorphic demons registration module (Vercauteren et al., 2008a) of ITK. We randomly selected 50 pairs of images, with each image chosen from a set of 40 3D brain volumes that had 37 neuroanatomical structures manually labeled (Fischl et al., 2002). These pairs were registered with and without the QVP constraint for various values of λ (here the global regularization parameter of diffeomorphic demons) for 50 Newton iterations (enough for convergence). When QVP was used, four values of ε = .05, .1, .2, .3 were tried (with ε = .05 tried only for three values of λ because of its high computational cost).16
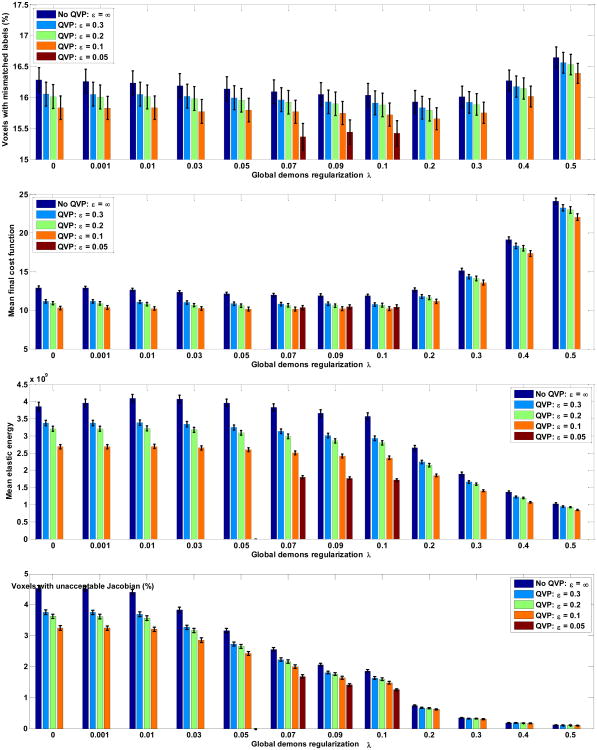
As illustrated in Figure 6, the inclusion of the QVP constraint consistently improved the results in every way that we quantified them. 1) QVP resulted in better alignment of manual labelings, i.e. lower number of differently-classified corresponding voxels (Figure 6, top). We then considered the CF-distortion tradeoff in the results. 2) QVP achieved a lower final CF value, despite the fact that it further regularizes the deformation field (Figure 6, 2nd row). This provides evidence that the QVP constraint leads the algorithm into a better optimum. 3) QVP resulted in transformations with lower distortion in terms of the elastic energy, computed following (Hagemann et al., 1999; Yanovsky et al., 2008a), and the number of voxels with Jacobian determinant values smaller than 10−3 or larger than 103 (Figure 6, two bottom rows). This improvement is expected, as QVP increases the regularization.
Figure 6.
Adding the QVP constraint to the diffeomorphic demons algorithm results in improved alignment of manual labelings (top), better intensity matching (2nd row), and less distortion (two bottom rows). Quantities are averaged across 50 experiments, and the error bars indicate the standard error of the mean. This is the optimum range for λ; we tried higher values of it, which degraded the performance of both methods, with QVP still outperforming.
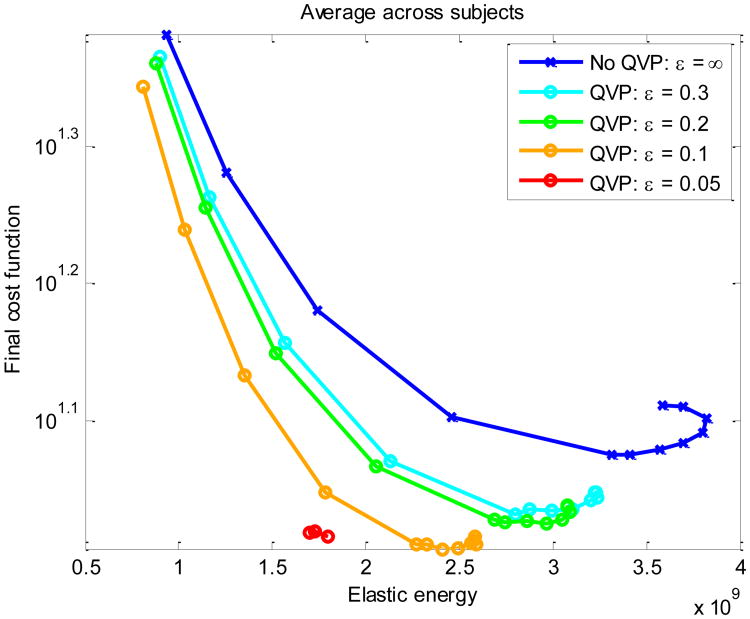
Figure 7 depicts the CF-distortion tradeoff for the experiments.17 Indeed, a tighter QVP constraint (smaller ε) always improved both the label matching and the CF-distortion tradeoff. (This is true for ε = .05 as well, even though it did not reduce the final CF as much as ε = .1.) Disabling the global regularization (λ = 0) did not produce the lowest CF, indicating that too much flexibility increases the chances of being trapped in a local optimum. We stress that while it is impossible to exactly match the amount of regularization in the QVP and non-QVP case, in all of the aforementioned registration experiments with a wide range of regularization levels the incorporation of the QVP constraint yielded better accuracy and image matching, and lower levels of distortion.
Figure 7.
CF-distortion tradeoff in diffeomorphic registration experiments. Each curve corresponds to a unique value of ε, and each point on the curve represents a different value of λ. For each point on the curve, the CF and distortion values have been averaged across subjects.
In practice, there may be a limit to the improvement that can be achieved by lowering ε. In particular, the number of necessary diffusion iterations (for each Newton iteration) goes to infinity as ε approaches zero, and for the extreme choice of ε = 0 the QVP constraint is never satisfied. In our experiments, an order of 1, 10, and 100 rounds of diffusion were needed for ε = .3, .2, ε = .1,and ε = .05, respectively, to satisfy QVP for all the voxels in the image.
Since the non-uniformity error is the culprit in breaking the symmetry of registration, it is expected that limiting this error by QVP constraining would make the registration more inverse-consistent. For the representative regularization value of λ = .1, we repeated the experiments above by swapping the order of input images and registering them again once without QVP, and a second time with QVP (ε = .3). We then computed the inverse-consistency error as , where T1 and T2 are the two transformations achieved by forward and backward registrations. As demonstrated by the histogram in Figure 8, in all of the experiments, enforcing the QVP constraint reduced the inverse-consistency error (mean ± SD: 5.2% ± 3.3%). A paired left-sided Wilcoxon signed rank test revealed the significance value of p = 3 × 10−8.
Figure 8.
The histogram of the decrease in inverse-consistency error by including the QVP constraint (ε = .3) confirms that reducing the non-uniformity error results in improvement in inverse-consistency.
5. Conclusions
We have proposed a quasi-volume-preserving (QVP) constraint on the deformation field in deformable registration that keeps the optimization algorithm away from the regions violating the uniformity of the cost function integral and consequently the symmetry. The main focus of this work is addressing the inaccuracies arising from the nonuniformity of the cost functions, which is the major distinction between our method and the symmetrization and mid-space techniques. In that regard, we have shown theoretically and through experiments that the QVP constraint improves, not only native symmetry, but the overall registration results. Enforcing the QVP constraint led to cross-subject registration with increased accuracy in the alignment of manually defined neuroanatomical structures, better tradeoff between the intensity error and distortion in the warp field, improved native symmetry, and reduced susceptibility to local optima. Subjects of the future research include: intrinsic enforcement of QVP via specific parameterization of the deformation field (without the need for blurring the displacement field), optimal ε determination based on image properties, proving the convergence and further stabilizing the diffusion step, and assessing the incorporation of QVP in the mid-space approaches.
Highlights.
We propose a quasi-volume-preserving (QVP) constraint in non-rigid registration.
QVP bounds the cost function nonuniformity error, thereby improving the alignment.
We show results using 2D demons and 3D diffeomorphic demons registration.
More accurate matching of manually defined labels is one of the improvements.
Acknowledgments
Support for this research was provided in part by the National Center for Research Resources (U24 RR021382), the National Institute for Biomedical Imaging and Bioengineering (NIBIB, P41-EB015896, R01EB006758), the National Institute on Aging (AG022381, 5R01AG008122-22, R01 AG016495-11), the National Center for Alternative Medicine (RC1 AT005728-01), the National Institute for Neurological Disorders and Stroke (R01 NS052585-01, 1R21NS072652-01, 1R01NS070963, R01NS083534), and was made possible by the resources provided by Shared Instrumentation Grants 1S10RR023401, 1S10RR019307, and 1S10RR023043. Additional support was provided by The Autism & Dyslexia Project funded by the Ellison Medical Foundation, and by the NIH Blueprint for Neuroscience Research (5U01-MH093765), part of the multi-institutional Human Connectome Project. IA was additionally supported by a grant from the Massachusetts Alzheimer's Disease Research Center (5 P50 AG005134), the MGH Neurology Clinical Trials Unit, and the Harvard NeuroDiscovery Center. MS received support from an NIBIB K25 grant (1K25EB013649-01) and a BrightFocus Alzheimer's disease pilot grant (A2012333).
Appendix A. Unidirectional minimization of the average cost function
We minimize the average CF (Eq. (7)) in the experiments of Section 4.1 via gradient descent in the same unidirectional manner as in (Leow et al., 2007), with differences that are outlined here. Basically, we calculate the variation of the average CF with respect to the transformation, δIave/δT(x), and update T(x) towards its opposite (descent) direction.
Iave is the sum of two terms, with the first term, If/2, being written in terms of T(x) as in Eq. (1). The variation of If with respect to T(x) is straightforward to compute:
| (17) |
where Dk is the partial derivative of D with respect to the kth argument, and ∇ is the image gradient operator. The second term of Iave is Ig/2, which is written in terms of T−1(y) as in Eq. (4) and, yet, is not an explicit function of T(x) 18 Here, instead of direct inversion of T, we compute the variation of Ig with respect to T(x) indirectly. First we note that the variation of Ig with respect to T−1(y) can be computed similarly to Eq. (17), as:
| (18) |
Let us assume that a small variation ΔT (x) changes the transformation as T*(x) = T(x) + ΔT(x). This change results in a small variation in T−1(y), as T−1*(y) = T−1(y) + ΔT−1(y). Keeping the first-order terms, the relationship T−1* ∘ T* (x) = x leads to:
| (19) |
where ∂T(x) is the Jacobian matrix of T(x) (Leow et al., 2007). Furthermore, by definition, Ig will vary as follows:
| (20) |
Making the change of variable y = T(x) and substituting for ΔT−1(T(x)) from Eq. (19) gives:
| (21) |
with J(x) := det ∂T(x). The variation of Ig with respect to T(x) is therefore derived as:
| (22) |
where C(x) = J(x)∂T(x)−1T is the cofactor matrix of ∂T(x), defined as Cij = (−1)i+jMij with M the minor of ∂T (i.e., Mij is the determinant of the matrix that results from deleting row i and column j of ∂T). Substituting from Eq. (18),
| (23) |
and combining Eqs. (7,17,23), the variation Iave of with respect to T(x) is derived as follows:
| (24) |
For instance, in case of the SSD CF, i.e. D(u, v) := (u − v)2, Eq. (24) reduces to:
| (25) |
Note that the descent direction for Iave was here computed by deriving both its terms –If and Ig – consistently with respect to T(x). On the contrary, in (Leow et al., 2007), the descent directions are computed separately for If and Ig with respect to T(x) and T−1(y), respectively, with the latter direction being subsequently translated in terms of change in T(x).19
Next, we explain how to incorporate the demons regularization symmetrically.
Appendix B. Unidirectional symmetric demons regularization
In addition to QVP, we used a global regularization in the experiments, which is an essential part of the demons registration (Thirion, 1998). In our 2D implementation in Section 4.1, we included a general Tikhonov term
(weighted by λ, with
 the identity matrix) inside the integral of the f-native CF (Eq. (1)), whereas in Section 4.2 we used ITK's built-in regularization. The variation of
with respect to T(x) can be derived as:
the identity matrix) inside the integral of the f-native CF (Eq. (1)), whereas in Section 4.2 we used ITK's built-in regularization. The variation of
with respect to T(x) can be derived as:
| (26) |
where is the Laplacian with respect to x performed on each element of T. Updating the deformation field in the opposite direction of this variation is equivalent to solving the diffusion equation, which in turn results in a Gaussian blurring in the displacement field, i.e. what is done directly in the original demons algorithm.20 The average CF in Eq. (7), however, includes the g-native CF (Eq. (4)), which also needs such a term as for the symmetry to be preserved. To minimize this term unidirectionally, we need to compute its variation with respect to T(x). As in Appendix A, we first compute its variation with respect to T−1(y),
| (27) |
and then derive its variation with respect to T(x) using the change of variable y = T(x) and Eq. (22), as:
| (28) |
So the problem boils down to the computation of , represented in x. The gradient of x with respect to y is simply the inverse Jacobian matrix:
| (29) |
which we shall denote by Q :=∂T−1.21 We now compute the divergence of the above:
| (30) |
where the subscript (:, k)means the kth column of the matrix. The chain rule implies:
| (31) |
and combining Eqs. (30,31) leads to:
| (32) |
We now compute
by taking the derivative of the relationship Q∂T =
 as follows:
as follows:
| (33) |
| (34) |
| (35) |
Equation (32) thus becomes:
| (36) |
with the vector h defined as:
| (37) |
The nth element of h can be calculated as follows:
| (38) |
where Tn is the nth element of T, and Hn is the Hessian matrix of Tn. By combining Eqs. (28,36), the variation of Rg with respect to T(x) is obtained as:
| (39) |
Therefore, we first compute the elements of the vector h(x), followed by the variation of Rg with respect to T(x), which allows for T−1(y) to be regularized without being explicitly calculated.
An issue that we faced in the computation of Eq. (39) is the calculation of the inverse Jacobian matrix Q where diffeomorphism is not preserved. As a remedy, we only performed the regularization of T−1 in regions where the Jacobian matrix had a positive determinant and singular values greater than a threshold (.25 in our experiments).
Appendix C. Deviation of the Jacobian determinant
Using the following Theorem, we can see that for a diffeomorphic d-dimensional transformation, J(x) − 1 is bounded from above and below by two functions of ‖∂T(x) −
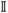 ‖F, as follows:
‖F, as follows:
| (40) |
Both of these bounds approach 0 monotonically as ‖∂T(x) −
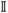 ‖F→0, thereby taking J(x) − 1 to 0 following the squeeze theorem.22
‖F→0, thereby taking J(x) − 1 to 0 following the squeeze theorem.22
Theorem. For a d × d matrix M with det M ≥ 0, we have the following bounds for det M:
| (41) |
where
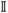 is the d × d identity matrix.
is the d × d identity matrix.
Proof. We have , where σk is the kth singular value of M. According to the triangular inequality for the Frobenius norm,
| (42) |
Combining this with the root mean square-geometric mean inequality, , yields:
| (43) |
which proves the right-hand side of Ineq. (41). Note that this upper bound is a supremum, since for a given ‖M−
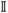 ‖F, equality can be achieved, e.g., for
. We did not need det M ≥ 0 to prove this upper bound.
‖F, equality can be achieved, e.g., for
. We did not need det M ≥ 0 to prove this upper bound.
Regarding the lower bound, one can see that for ‖M−
 ‖F≥1 the lower limit det M = 0 can be reached, for instance for a diagonal M whose first diagonal entry is 0, and all the rest of its d − 1 diagonal entries are equal to
. Concerning the case with ‖M −
‖F≥1 the lower limit det M = 0 can be reached, for instance for a diagonal M whose first diagonal entry is 0, and all the rest of its d − 1 diagonal entries are equal to
. Concerning the case with ‖M −
 ‖F < 1, we use the inequality σmin(A − B) ≤ σmin(A) + σmax(B) (Horn and Johnson, 1994), with σmin(A) and σmax(A) the minimum and maximum singular value of A, respectively. Letting A = M and B = M −
‖F < 1, we use the inequality σmin(A − B) ≤ σmin(A) + σmax(B) (Horn and Johnson, 1994), with σmin(A) and σmax(A) the minimum and maximum singular value of A, respectively. Letting A = M and B = M −
 gives:
gives:
| (44) |
Since σmax(M −
 ) ≤ ‖M −
) ≤ ‖M −
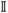 ‖F, we have:
‖F, we have:
| (45) |
Considering that
and the assumption 1 − ‖M −
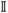 ‖F > 0, we raise Eq. (45) to the power of d, resulting in:
‖F > 0, we raise Eq. (45) to the power of d, resulting in:
| (46) |
Finally, we rewrite the two cases of ‖M −
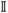 ‖F ≥ 1 and ‖M −
‖F ≥ 1 and ‖M −
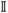 ‖F < 1 in the following compact form, which proves the left-hand side of Ineq. (41):
‖F < 1 in the following compact form, which proves the left-hand side of Ineq. (41):
| (47) |
Footnotes
Since the reference image is not interpolated during registration, we call the other image the interpolated image.
The terms “symmetry” and “inverse-consistency” have been used interchangeably in most of the literature.
We do not denote the images as “source” and “target”, and therefore register Image A and Image B, rather than Image A to Image B. However, we do not consider atlas-to-subject mapping as “pairwise registration” here, since such a registration is intrinsically asymmetric (Sabuncu et al, 2009). By pairwise registration, we mean that the input images are real and in physically existent spaces, such as registering brain images of two subjects, or of one subject at different time points.
Information theoretical objective functions also suffer from the problems described here. However, addressing them is beyond the scope of this paper.
This is the particular form of the CFs aggregating a local mismatch measure, the most common of which being the SSD. Several other CFs, such as normalized mutual information, correlation coefficient, local correlation, etc., cannot be expressed with Eq. (1).
More references are provided in Section 1.
Although the strict Eq. (9) is symmetric, its relaxation leading to Ineq. (10) introduces a level of asymmetry in the optimization space, which grows with ε. Symmetrization of (10) would require the additional constraint D(f(x), g ∘ T(x))|J−1(x) − 1| < ε, ∀x ∈ Ω, which, however, is over restrictive, especially that even in diffeomorphic registration diffeomorphism is sometimes violated leading to J(x) ≤ 0 for some voxels. Therefore, we only enforce Ineq. (10) in our experiments, as it fulfills the task of decreasing the non-uniformity error.
Using the change of variable y =T(x), this bound can be seen to exist on the non-uniformity error of both f- and g-native CFs.
Note that the closeness of the native CFs (native symmetry) is a nice byproduct, but not the goal of QVP constraining. Otherwise, simpler approaches could be used to keep If and Ig close to each other without necessarily achieving the goal of QVP, which is limiting the local non-uniformity error. In fact, since the QVP constraint is enforced everywhere in the image, it leads to one constraint per voxel after discretization, which may be several orders of magnitude more constraints than merely one bound on the native symmetry error.
Note that the primary motivation for the proposed work, however, is limiting the non-uniformity error and achieving more accurate registration. Therefore the QVP constraint is not a deformation model and the adaptive regularization is only a secondary motivation.
For instance for the SSD CF, where D(u, v) := (u − v)2, one can verify the following complex gradient direction for T(x), which is the variation of ∫Ω R(e(x) − ε)dx with respect to T(x):
where u(·) and δ(·) are the Heaviside step and the Dirac delta functions, respectively, and the cofactor matrix C(x) and the Hessian tensor H(x) are defined in Appendix A and Appendix B, respectively.
As we can see in the results (Section 4), although we have no such additional CF minimization, we obtain a lower CF value after the same number of gradient descent or Newton iterations (as well as better label matching and lower distortion). Devising a more direct strategy to enforce the QVP constraint is a subject of the ongoing research.
A drawback of this implementation is that we do not know beforehand how many blurring iterations are required, thus we cannot precisely predict the runtime of the algorithm. The runtime increases as ε decreases; however, it also depends on the input images and other parameters, such as the optimization and diffusion step sizes. A specific parameterization of the deformation field intrinsically satisfying the QVP constraint is a subject for future work. The operator introduced here is also not symmetric, as we intend to minimize the non-uniformity error, rather than to explicitly enforce symmetry. Note that the QVP constraint can be incorporated in non-rigid registration algorithms in various ways, the implementation of which is not the primary focus of this paper.
Since the QVP is incorporated in an already inverse-consistent method (minimization of Iave), we do not expect to see any further improvement in the inverse-consistency (contrary to native symmetry) here. Note that the QVP constraint is not employed for the purpose of inverse-consistency, but to improve the registration through minimization of the non-uniformity errors.
It should be noted that the number of iterations is not indicative of the computational cost in our implementation, since each iteration is more expensive in the QVP method than in the other two methods, given the extra step of diffusion. As mentioned before, the final CF values are the lowest achieved that preserve the topology, thereby indicating the CF-distortion tradeoff. The fact that the optimum λ was different for each method makes direct comparison of these convergence rates difficult. However, one can see that the best achievable convergence over a range of λ values was improved by enforcing the QVP constraint.
The standard symmetric-gradient implementation of ITK is not equivalent to minimizing Iave. Given that this subsection focuses on registration accuracy rather than symmetry, to keep the results fair and reproducible, we only included the QVP constraint and did not modify the ITK implementation any further. Contrary to our experiments in Section 4.1, where we showed improvement by QVP compared to symmetrized registration, in Section 4.2 we assess the inclusion of QVP in the ITK implementation that is not symmetric. Therefore, the improvements observed in this subsection may be as a result of the symmetry as well.
We also attempted to incorporate the QVP constraint into the more recent symmetric log-domain diffeomorphic demons registration (Vercauteren et al, 2008b). However, since this method parameterizes the transformation implicitly as a velocity field, and its public implementation does not allow for explicit modification of the deformation field, we could not apply the inhomogeneous diffusion of Section 3.3 directly to the deformation field. We tried applying the diffusion to the velocity field instead, but it performed poorly, since the QVP constraint is naturally very local, and any local modification of the velocity field propagates into a larger area in the deformation field. A specifically log-domain enforcement of the QVP constraint is a subject of the future research.
Please note that a fair and accurate assessment of QVP constraining using any other registration methods would require explicit implementation of QVP in their source codes with their specific deformation parameterization; otherwise, directly comparing our diffeomorphic demons implementation of QVP with other (non-demons, non-QVP) methods would cause the difference between the registration methods to dominate the QVP effect.
Although individual comparison of the final CF value or the distortion among methods might not be meaningful, here we compare the CF-distortion tradeoff among methods, which can be used as a criterion to assess registration algorithms.
Although Ig can be written with respect to T(x) as in Eq. (5), the inclusion of J(x) in the integral makes the computation of the variation complicated.
Replacing C(x) with ∂T(x) in Eqs. (24, 25) leads to the results in (Leow et al., 2007). In the case of 1D images, for instance, C1D(x) = 1 making Eq. (25) similar to the demons registration with symmetric gradients, whereas ∂T1D(x)= T1D′(x).
Using the displacement T(x) − x instead of the deformation T(x) field will not alter the regularization; the term x, being linear, is eliminated by the Laplacian, and being anti-symmetric, is cancelled out by the symmetric Gaussian blurring.
For brevity, we omit (x) in most of the rest of this appendix.
This approach may reduce also the divergence of the displacement field.
In addition, BF has a financial interest in CorticoMetrics, a company whose medical pursuits focus on brain imaging and measurement technologies. BF's interests were reviewed and are managed by Massachusetts General Hospital and Partners HealthCare in accordance with their conflict of interest policies.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Martin Reuter, Email: mreuter@nmr.mgh.harvard.edu.
Mert R. Sabuncu, Email: msabuncu@nmr.mgh.harvard.edu.
Bruce Fischl, Email: fischl@nmr.mgh.harvard.edu.
References
- Aganj I, Reuter M, Sabuncu MR, Fischl B. Proceedings of the IEEE International Symposium on Biomedical Imaging. San Francisco, CA, USA: 2013a. Symmetric non-rigid image registration via an adaptive quasi-volume-preserving constraint; pp. 234–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aganj I, Yeo BTT, Sabuncu MR, Fischl B. On Removing Interpolation and Resampling Artifacts in Rigid Image Registration. Image Processing, IEEE Transactions on. 2013b;22:816–827. doi: 10.1109/TIP.2012.2224356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarez L, Deriche R, Papadopoulo T, Sánchez J. Symmetrical Dense Optical Flow Estimation with Occlusions Detection. International Journal of Computer Vision. 2007;75:371–385. [Google Scholar]
- Ashburner J, Andersson JLR, Friston KJ. High-Dimensional Image Registration Using Symmetric Priors. NeuroImage. 1999;9:619–628. doi: 10.1006/nimg.1999.0437. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Andersson JLR, Friston KJ. Image registration using a symmetric prior—in three dimensions. Human brain mapping. 2000;9:212–225. doi: 10.1002/(SICI)1097-0193(200004)9:4<212::AID-HBM3>3.0.CO;2-#. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical image analysis. 2008;12:26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basri R, Costa L, Geiger D, Jacobs D. Determining the similarity of deformable shapes. Vision Research. 1998;38:2365–2385. doi: 10.1016/s0042-6989(98)00043-1. [DOI] [PubMed] [Google Scholar]
- Beg MF, Khan A. Symmetric data attachment terms for large deformation image registration. Medical Imaging, IEEE Transactions on. 2007;26:1179–1189. doi: 10.1109/TMI.2007.898813. [DOI] [PubMed] [Google Scholar]
- Bondar L, Hoogeman MS, Osorio EMV, Heijmen BJM. A symmetric nonrigid registration method to handle large organ deformations in cervical cancer patients. Medical Physics. 2010;37:3760–3772. doi: 10.1118/1.3443436. [DOI] [PubMed] [Google Scholar]
- Cachier P, Rey D. Symmetrization of the non-rigid registration problem using inversion-invariant energies: Application to multiple sclerosis. In: Delp S, DiGoia A, Jaramaz B, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2000. Springer; Berlin/Heidelberg: 2000. pp. 697–708. [Google Scholar]
- Cahill N, Noble JA, Hawkes D. A Demons Algorithm for Image Registration with Locally Adaptive Regularization. In: Yang GZ, Hawkes D, Rueckert D, Noble A, Taylor C, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2009. Springer; Berlin Heidelberg: 2009. pp. 574–581. [DOI] [PubMed] [Google Scholar]
- Chen Y, Ye X. Inverse Consistent Deformable Image Registration. In: Alladi K, Klauder JR, Rao CR, editors. The Legacy of Alladi Ramakrishnan in the Mathematical Sciences. Springer; New York: 2010. pp. 419–440. [Google Scholar]
- Christensen G, Johnson H. Invertibility and transitivity analysis for nonrigid image registration. Journal of Electronic Imaging. 2003;12:106–117. [Google Scholar]
- Christensen GE, Johnson HJ. Consistent image registration. Medical Imaging, IEEE Transactions on. 2001;20:568–582. doi: 10.1109/42.932742. [DOI] [PubMed] [Google Scholar]
- Chui H. Non-rigid point matching: Algorithms, extensions and applications. Yale University; 2001. [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical Surface-Based Analysis: I. Segmentation and Surface Reconstruction. NeuroImage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Dedeoglu G, Kanade T. On the Source of Asymmetry in Image Registration Problems. Carnegie Mellon University; 2005. [Google Scholar]
- Elen A, Hon Fai C, Loeckx D, Hang G, Claus P, Suetens P, Maes F, D'Hooge J. Three-Dimensional Cardiac Strain Estimation Using Spatio-Temporal Elastic Registration of Ultrasound Images: A Feasibility Study. Medical Imaging, IEEE Transactions on. 2008;27:1580–1591. doi: 10.1109/TMI.2008.2004420. [DOI] [PubMed] [Google Scholar]
- Feng W, Reeves SJ, Denney TS, Lloyd S, Dell'Italia L, Gupta H. A new consistent image registration formulation with a B-spline deformation model. Biomedical Imaging: From Nano to Macro, 2009 ISBI '09 IEEE International Symposium on. 2009:979–982. [Google Scholar]
- Fischl B. FreeSurfer. NeuroImage. 2012;62:774–781. doi: 10.1016/j.neuroimage.2012.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der KA, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis II: Inflation, flattening, and a surface-based coordinate system. NeuroImage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- Fox NC, Ridgway GR, Schott JM. Algorithms, atrophy and Alzheimer's disease: Cautionary tales for clinical trials. NeuroImage. 2011;57:15–18. doi: 10.1016/j.neuroimage.2011.01.077. [DOI] [PubMed] [Google Scholar]
- Freiman M, Voss S, Warfield S. Abdominal Images Non-rigid Registration Using Local-Affine Diffeomorphic Demons. In: Yoshida H, Sakas G, Linguraru M, editors. Abdominal Imaging Computational and Clinical Applications. Springer Berlin; Heidelberg: 2012. pp. 116–124. [Google Scholar]
- Geng X. Transitive inverse-consistent image registration and evaluation. University of Iowa; 2007. [Google Scholar]
- Gholipour A, Kehtarnavaz N, Yousefi S, Gopinath K, Briggs R. Symmetric deformable image registration via optimization of information theoretic measures. Image and Vision Computing. 2010;28:965–975. [Google Scholar]
- Glocker B, Komodakis N, Navab N, Tziritas G, Paragios N. Dense Registration with Deformation Priors. In: Prince J, Pham D, Myers K, editors. Information Processing in Medical Imaging. Springer; Berlin Heidelberg: 2009. pp. 540–551. [DOI] [PubMed] [Google Scholar]
- Haber E, Modersitzki J. Image registration with guaranteed displacement regularity. International Journal of Computer Vision. 2007;71:361–372. [Google Scholar]
- Hagemann A, Rohr K, Stiehl HS, Spetzger U, Gilsbach JM. Biomechanical modeling of the human head for physically based, nonrigid image registration. Medical Imaging, IEEE Transactions on. 1999;18:875–884. doi: 10.1109/42.811267. [DOI] [PubMed] [Google Scholar]
- He J, Christensen G. Large Deformation Inverse Consistent Elastic Image Registration. In: Taylor C, Noble J, editors. Information Processing in Medical Imaging. Springer; Berlin/Heidelberg: 2003. pp. 438–449. [DOI] [PubMed] [Google Scholar]
- Hirota G, Maheshwari R, Lin MC. Fast volume-preserving free-form deformation using multi-level optimization. Computer-Aided Design. 2000;32:499–512. [Google Scholar]
- Horn RA, Johnson CR. Topics in Matrix Analysis. Cambridge University Press; 1994. [Google Scholar]
- Hua X, Gutman B, Boyle CP, Rajagopalan P, Leow AD, Yanovsky I, Kumar AR, Toga AW, Jack CR, Jr, Schuff N, Alexander GE, Chen K, Reiman EM, Weiner MW, Thompson PM. Accurate measurement of brain changes in longitudinal MRI scans using tensor-based morphometry. NeuroImage. 2011;57:5–14. doi: 10.1016/j.neuroimage.2011.01.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson HJ, McCormick MM, Ibanez L, Consortium IS. The ITK Software Guide, Book 1: Introduction and Development Guidelines. 4 2014. [Google Scholar]
- Joshi S, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic atlas construction for computational anatomy. NeuroImage. 2004;23(Supplement 1):S151–S160. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]
- Leow AD, Yanovsky I, Ming-Chang C, Lee AD, Klunder AD, Lu A, Becker JT, Davis SW, Toga AW, Thompson PM. Statistical Properties of Jacobian Maps and the Realization of Unbiased Large-Deformation Nonlinear Image Registration. Medical Imaging, IEEE Transactions on. 2007;26:822–832. doi: 10.1109/TMI.2007.892646. [DOI] [PubMed] [Google Scholar]
- Li X, Dawant BM, Welch EB, Chakravarthy AB, Freehardt D, Mayer I, Kelley M, Meszoely I, Gore JC, Yankeelov TE. A nonrigid registration algorithm for longitudinal breast MR images and the analysis of breast tumor response. Magnetic Resonance Imaging. 2009;27:1258–1270. doi: 10.1016/j.mri.2009.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loeckx D, Drisis S, Maes F, Vandermeulen D, Marchal G, Suetens P. Plaque and Stent Artifact Reduction in Subtraction CT Angiography Using Nonrigid Registration and a Volume Penalty. In: Duncan J, Gerig G, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2005. Springer; Berlin Heidelberg: 2005. pp. 361–368. [DOI] [PubMed] [Google Scholar]
- Loeckx D, Maes F, Vandermeulen D, Suetens P. Nonrigid Image Registration Using Free-Form Deformations with a Local Rigidity Constraint. In: Barillot C, Haynor D, Hellier P, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2004. Springer Berlin; Heidelberg: 2004. pp. 639–646. [Google Scholar]
- Lorenzen P, Davis B, Joshi S. Model based symmetric information theoretic large deformation multi-modal image registration. Biomedical Imaging: Nano to Macro, 2004 IEEE International Symposium on. 2004;721:720–723. [Google Scholar]
- Lorenzi M, Ayache N, Frisoni GB, Pennec X. LCC-Demons: A robust and accurate symmetric diffeomorphic registration algorithm. NeuroImage. 2013;81:470–483. doi: 10.1016/j.neuroimage.2013.04.114. [DOI] [PubMed] [Google Scholar]
- Mansi T, Pennec X, Sermesant M, Delingette H, Ayache N. iLogDemons: A Demons-Based Registration Algorithm for Tracking Incompressible Elastic Biological Tissues. International Journal of Computer Vision. 2011;92:92–111. [Google Scholar]
- Marcus DS, Wang TH, Parker J, Csernansky JG, Morris JC, Buckner RL. Open Access Series of Imaging Studies (OASIS): Cross-sectional MRI data in young, middle aged, nondemented, and demented older adults. Journal of Cognitive Neuroscience. 2007;19:1498–1507. doi: 10.1162/jocn.2007.19.9.1498. [DOI] [PubMed] [Google Scholar]
- Modat M, Cardoso M, Daga P, Cash D, Fox N, Ourselin S. Inverse-Consistent Symmetric Free Form Deformation. In: Dawant B, Christensen G, Fitzpatrick J, Rueckert D, editors. Biomedical Image Registration. Springer; Berlin/Heidelberg: 2012. pp. 79–88. [Google Scholar]
- Mohagheghian F, Ahmadian A, Saberi H, Alirezaie J. Symmetric multi-scale image registration. Engineering in Medicine and Biology Society (EMBC), 2010 Annual International Conference of the IEEE. 2010:5931–5934. doi: 10.1109/IEMBS.2010.5627551. [DOI] [PubMed] [Google Scholar]
- Noblet V, Heinrich C, Heitz F, Armspach JP. Symmetric nonrigid image registration: Application to average brain templates construction. In: Metaxas D, Axel L, Fichtinger G, Székely G, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2008. Springer; Berlin/Heidelberg: 2008. pp. 897–904. [DOI] [PubMed] [Google Scholar]
- Ou Y, Sotiras A, Paragios N, Davatzikos C. DRAMMS: Deformable registration via attribute matching and mutual-saliency weighting. Medical image analysis. 2011;15:622–639. doi: 10.1016/j.media.2010.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pace DF, Aylward SR, Niethammer M. A Locally Adaptive Regularization Based on Anisotropic Diffusion for Deformable Image Registration of Sliding Organs. Medical Imaging, IEEE Transactions on. 2013;32:2114–2126. doi: 10.1109/TMI.2013.2274777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S, Kim B, Lee J, Goo JM, Shin YG. GGO Nodule Volume-Preserving Nonrigid Lung Registration Using GLCM Texture Analysis. Biomedical Engineering, IEEE Transactions on. 2011;58:2885–2894. doi: 10.1109/TBME.2011.2162330. [DOI] [PubMed] [Google Scholar]
- Reuter M, Rosas HD, Fischl B. Highly accurate inverse consistent registration: A robust approach. NeuroImage. 2010;53:1181–1196. doi: 10.1016/j.neuroimage.2010.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuter M, Schmansky NJ, Rosas HD, Fischl B. Within-subject template estimation for unbiased longitudinal image analysis. NeuroImage. 2012;61:1402–1418. doi: 10.1016/j.neuroimage.2012.02.084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rey D, Subsol G, Delingette H, Ayache N. Automatic detection and segmentation of evolving processes in 3D medical images: Application to multiple sclerosis. Medical image analysis. 2002;6:163–179. doi: 10.1016/s1361-8415(02)00056-7. [DOI] [PubMed] [Google Scholar]
- Risholm P, Samset E, Talos IF, Wells W. A Non-rigid Registration Framework That Accommodates Resection and Retraction. In: Prince J, Pham D, Myers K, editors. Information Processing in Medical Imaging. Springer; Berlin Heidelberg: 2009. pp. 447–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogelj P, Kovaˇiˇ S. Symmetric image registration. Medical image analysis. 2006;10:484–493. doi: 10.1016/j.media.2005.03.003. [DOI] [PubMed] [Google Scholar]
- Rohlfing T, Maurer CR, Jr, Bluemke DA, Jacobs MA. Volume-preserving nonrigid registration of MR breast images using free-form deformation with an incompressibility constraint. Medical Imaging, IEEE Transactions on. 2003;22:730–741. doi: 10.1109/TMI.2003.814791. [DOI] [PubMed] [Google Scholar]
- Sabuncu M, Yeo B, Van Leemput K, Vercauteren T, Golland P. Asymmetric image-template registration. In: Yang GZ, Hawkes D, Rueckert D, Noble A, Taylor C, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2009. Springer; Berlin/Heidelberg: 2009. pp. 565–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saddi KA, Chefd'hotel C, Cheriet F. Large deformation registration of contrast-enhanced images with volume-preserving constraint. 2007:651203–651203. [Google Scholar]
- Škrinjar O, Bistoquet A, Tagare H. Symmetric and Transitive Registration of Image Sequences. International Journal of Biomedical Imaging. 2008 doi: 10.1155/2008/686875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sotiras A, Davatzikos C, Paragios N. Deformable Medical Image Registration: A Survey. Medical Imaging, IEEE Transactions on. 2013;32:1153–1190. doi: 10.1109/TMI.2013.2265603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staring M, Klein S, Pluim JPW. Nonrigid registration with tissue-dependent filtering of the deformation field. Physics in medicine and biology. 2007;52:6879. doi: 10.1088/0031-9155/52/23/007. [DOI] [PubMed] [Google Scholar]
- Stefanescu R, Pennec X, Ayache N. Grid powered nonlinear image registration with locally adaptive regularization. Medical image analysis. 2004;8:325–342. doi: 10.1016/j.media.2004.06.010. [DOI] [PubMed] [Google Scholar]
- Suárez E, Westin CF, Rovaris E, Ruiz-Alzola J. Nonrigid Registration Using Regularized Matching Weighted by Local Structure. In: Dohi T, Kikinis R, editors. Medical Image Computing and Computer-Assisted Intervention — MICCAI 2002. Springer; Berlin Heidelberg: 2002. pp. 581–589. [Google Scholar]
- Tagare H, Groisser D, Skrinjar O. Symmetric non-rigid registration: A geometric theory and some numerical techniques. Journal of Mathematical Imaging and Vision. 2009;34:61–88. [Google Scholar]
- Tang L, Hamarneh G, Abugharbieh R. Reliability-Driven, Spatially-Adaptive Regularization for Deformable Registration. In: Fischer B, Dawant B, Lorenz C, editors. Biomedical Image Registration. Springer; Berlin Heidelberg: 2010. pp. 173–185. [Google Scholar]
- Tanner C, Schnabel JA, Degenhard A, Castellano-Smith AD, Hayes C, Leach MO, Hose DR, Hill DLG, Hawkes DJ. Validation of Volume-Preserving Non-rigid Registration: Application to Contrast-Enhanced MR-Mammography. In: Dohi T, Kikinis R, editors. Medical Image Computing and Computer-Assisted Intervention — MICCAI 2002. Springer; Berlin Heidelberg: 2002. pp. 307–314. [Google Scholar]
- Tao G, He R, Datta S, Narayana PA. Symmetric inverse consistent nonlinear registration driven by mutual information. Computer Methods and Programs in Biomedicine. 2009;95:105–115. doi: 10.1016/j.cmpb.2009.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thirion JP. Image matching as a diffusion process: An analogy with Maxwell's demons. Medical image analysis. 1998;2:243–260. doi: 10.1016/s1361-8415(98)80022-4. [DOI] [PubMed] [Google Scholar]
- Thompson WK, Holland D. Bias in tensor based morphometry Stat-ROI measures may result in unrealistic power estimates. NeuroImage. 2011;57:1–4. doi: 10.1016/j.neuroimage.2010.11.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trouvé A, Younes L. Diffeomorphic matching problems in one dimension: Designing and minimizing matching functionals Computer Vision - ECCV 2000. Springer; Berlin/Heidelberg: 2000. pp. 573–587. [Google Scholar]
- Vercauteren T, Pennec X, Perchant A, Ayache N. The Insight Journal. 2008a. Diffeomorphic Demons Using ITK's Finite Difference Solver Hierarchy. [Google Scholar]
- Vercauteren T, Pennec X, Perchant A, Ayache N. Symmetric Log-Domain Diffeomorphic Registration: A Demons-Based Approach. In: Metaxas D, Axel L, Fichtinger G, Székely G, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2008. Springer; Berlin Heidelberg: 2008b. pp. 754–761. [DOI] [PubMed] [Google Scholar]
- Yang D, Li H, Low DA, Deasy JO, Naqa IE. A fast inverse consistent deformable image registration method based on symmetric optical flow computation. Physics in medicine and biology. 2008;53:6143. doi: 10.1088/0031-9155/53/21/017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yanovsky I, Le Guyader C, Leow AD, Thompson PM, Vese L. Nonlinear Elastic Registration with Unbiased Regularization in Three Dimensions. MICCAI Workshop on Computational Biomechanics for Medicine 2008a [Google Scholar]
- Yanovsky I, Thompson PM, Osher S, Leow AD. Asymmetric and symmetric unbiased image registration: Statistical assessment of performance. Computer Vision and Pattern Recognition Workshops, 2008 CVPRW '08 IEEE Computer Society Conference on. 2008b:1–8. doi: 10.1109/CVPRW.2008.4562988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye X, Chen Y. A New Algorithm for Inverse Consistent Image Registration. In: Bebis G, Boyle R, Parvin B, Koracin D, Kuno Y, Wang J, Wang JX, Pajarola R, Lindstrom P, Hinkenjann A, Encarnação M, Silva C, Coming D, editors. Advances in Visual Computing. Springer; Berlin/Heidelberg: 2009. pp. 855–864. [Google Scholar]
- Yeung SK, Tang CK, Shi P, Pluim JPW, Viergever MA, Chung ACS, Shen HC. Enforcing stochastic inverse consistency in non-rigid image registration and matching. Computer Vision and Pattern Recognition, 2008 CVPR 2008 IEEE Conference on. 2008:1–8. [Google Scholar]
- Yin Y, Hoffman EA, Lin CL. Mass preserving nonrigid registration of CT lung images using cubic B-spline. Medical Physics. 2009;36:4213–4222. doi: 10.1118/1.3193526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yushkevich PA, Avants BB, Das SR, Pluta J, Altinay M, Craige C. Bias in estimation of hippocampal atrophy using deformation-based morphometry arises from asymmetric global normalization: An illustration in ADNI 3 T MRI data. NeuroImage. 2010;50:434–445. doi: 10.1016/j.neuroimage.2009.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng Q, Chen Y. Accurate Inverse Consistent Non-rigid Image Registration and Its Application on Automatic Re-contouring. In: Mandoiu I, Sunderraman R, Zelikovsky A, editors. Bioinformatics Research and Applications. Springer; Berlin/Heidelberg: 2008. pp. 293–304. [Google Scholar]
- Zhang Z, Jiang Y, Tsui H. Consistent multi-modal non-rigid registration based on a variational approach. Pattern Recognition Letters. 2006;27:715–725. [Google Scholar]