A supercritical density of fast Na⁺ channels ensures rapid propagation of action potentials in GABAergic interneuron axons

Abstract

Fast-spiking, parvalbumin-expressing GABAergic interneurons/basket cells (BCs) play a key role in feedforward and feedback inhibition, gamma oscillations, and complex information processing. For these functions, fast propagation of action potentials (APs) from the soma to the presynaptic terminals is important. However, the functional properties of interneuron axons remain elusive. Here, we examined interneuron axons by confocally targeted subcellular patch-clamp recording in rat hippocampal slices. APs were initiated in the proximal axon ~20 μm from the soma, and propagated to the distal axon with high reliability and speed. Subcellular mapping revealed a stepwise increase of Na⁺ conductance density from the soma to the proximal axon, followed by a further gradual increase in the distal axon. Active cable modeling and experiments with partial channel block indicated that low axonal Na⁺ conductance density was sufficient for reliability, but high Na⁺ density was necessary for both speed of propagation and fast-spiking AP phenotype. Our results suggest that a supercritical density of Na⁺ channels compensates for the morphological properties of interneuron axons (small segmental diameter, extensive branching, and high bouton density), ensuring fast AP propagation and high-frequency repetitive firing.

Fast-spiking, parvalbumin-expressing GABAergic interneurons/BCs play a key role in the function of neuronal networks. These interneurons mediate fast feedforward and feedback inhibition^1–3, generate network oscillations in the gamma frequency range^4–6, and contribute to complex information processing in neuronal networks, such as pattern separation⁷. For all of these functions, speed and reliability of signaling of GABAergic interneurons is critically important. In essence, BCs need to convert an excitatory input signal into an inhibitory output signal within a millisecond or less⁸. Furthermore, BCs need to reliably distribute this output signal onto a large number of target cells⁹. However, the subcellular mechanisms underlying speed and reliability in this important type of GABAergic interneuron are largely unclear.

The axon is a critical site for input–output conversion, because it mediates AP initiation, AP propagation, and finally transmitter release^10,11. Two major mechanisms are generally thought to promote rapid signal propagation in axons in the mammalian nervous system: large axon diameter and myelination¹⁰. However, BC axons have small diameter, branch extensively, and give rise to numerous en-passant boutons⁹. Thus, while enlargement of axon diameter may not be possible because of spatial constraints, myelination is precluded by the spatially overlapping functions of AP propagation and transmitter release. In a schematic ball-and-stick model, both axon collaterals and en-passant presynaptic terminals markedly decrease the speed and reliability of AP propagation (Supplementary Fig. 1). Thus, the cable structure of interneuron axons appears to be highly unfavorable for rapid and reliable AP propagation.

How is fast and reliable signaling in BC axons achieved in the presence of these morphological challenges? To address this question, we developed confocally targeted subcellular patch-clamp techniques that allow us to directly record from interneuron axons. Our results suggest that the Na⁺ conductance in BC axons is above the critical minimum required to ensure reliability, and that this supercritical density is important to ensure both the speed of AP propagation and the fast-spiking AP phenotype. Part of the results was previously published in abstract form (Hu and Jonas, 2012, Society for Neuroscience abstracts 238.06/C55).

RESULTS

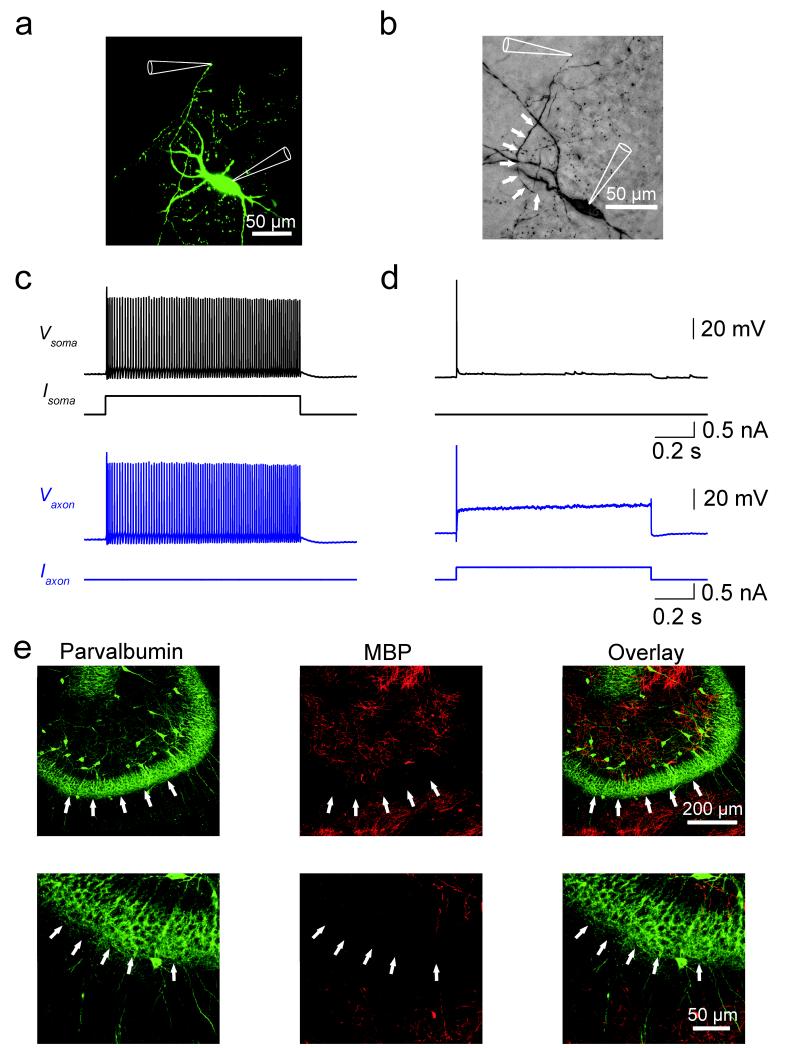
To directly examine the functional properties of interneuron axons, we performed confocally targeted subcellular patch-clamp recordings from fast-spiking, parvalbumin-expressing GABAergic interneurons in acute hippocampal slices¹² (Fig. 1). Axonal recordings were established in three steps. First, a somatic recording was obtained with a patch pipette containing Alexa Fluor 488. Second, the axon was visualized using fast confocal imaging after ~30 min filling time. Finally, recordings were made from either axon shafts (27 simultaneous axon–soma recordings) or small spherical axon expansions (87 simultaneous axon–soma recordings), which probably represent axon “blebs”¹³. Axonal recordings were readily obtained, consistent with the absence of myelination in BC axons. Lack of myelin was confirmed by the absence of double immunolabeling for myelin basic protein (MBP) and parvalbumin in the dentate gyrus granule cell layer (Fig. 1e; Supplementary Fig. 2; see Ref 14). Confocally targeted subcellular patch-clamp recording from BCs allowed us to measure absolute voltage changes in the axon with microsecond temporal resolution at defined locations up to 418 μm from the soma, covering a major part of the axonal arborization of these GABAergic interneurons⁹.

Figure 1.

Confocally targeted subcellular patch-clamp recording from axons of hippocampal fast-spiking, parvalbumin-expressing GABAergic interneurons.

(a) Confocal image of a BC in the dentate gyrus filled with Alexa Fluor 488 during the experiment. Confocal stack maximum projection.

(b) Same cell filled with biocytin during recording and labeled with 3,3′-diaminobenzidine as chromogen. White arrows indicate the axon trajectory. In a, b, recording pipettes are illustrated schematically.

(c, d) Train of APs evoked by a 1-s depolarizing current pulse applied at the soma (c) and the axon (at 177 μm; d). Black traces, somatic voltage and corresponding current. Blue traces, axonal voltage and corresponding current. Data in a–d are from the same cell.

(e) Double immunolabeling for parvalbumin (a selective marker of fast-spiking GABAergic interneurons) and myelin basic protein (MBP, a specific marker of myelination). Left, parvalbumin; center, MBP; right, overlay. Note the absence of colocalization between the two markers in the granule cell layer, suggesting that BC axons are largely unmyelinated. Experiments were repeated on 5 animals, giving consistent results. White arrows indicate the outer border of the granule cell layer. Lower micrographs are expanded versions of upper images.

Initiation and propagation of APs in BC axons

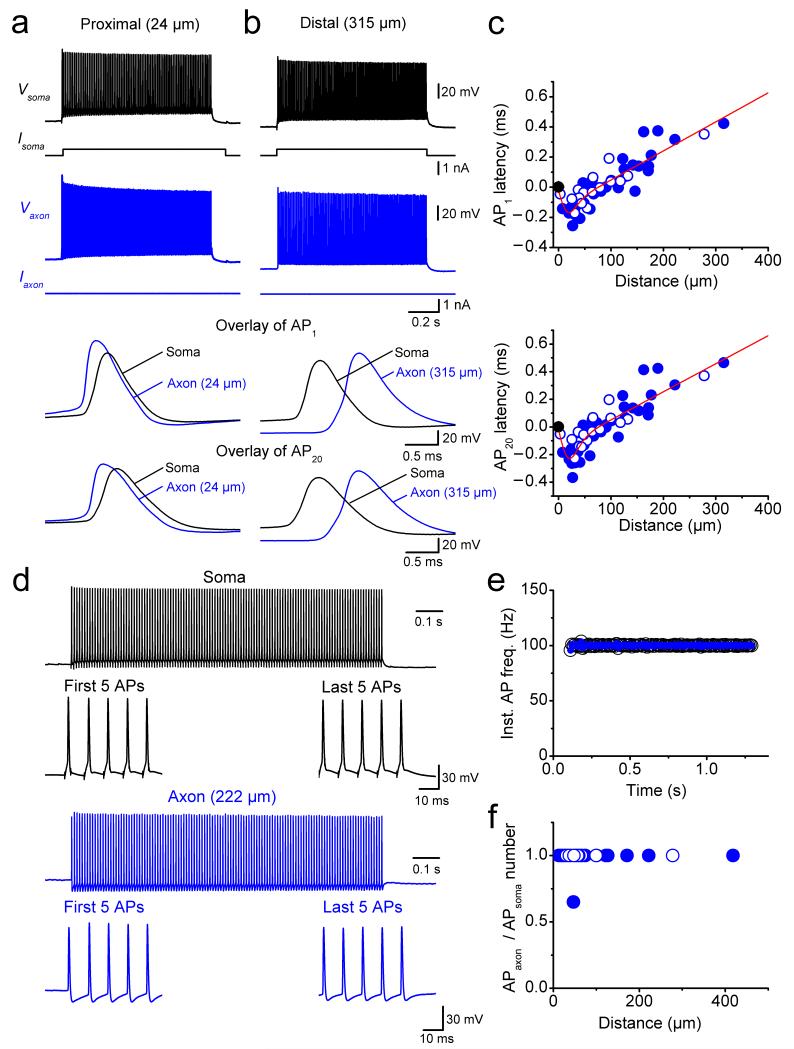
To determine the site of AP initiation and the characteristics of propagation, we made simultaneous recordings from the soma and the axon at various distances (Fig. 2). APs were evoked by somatic current injection and the latency between somatic and axonal APs was measured using the time points corresponding to half-maximal amplitude in the AP rising phase. For proximal axonal recording sites, the axonal AP preceded the somatic waveform, suggesting that the recording electrode was close to the site of AP initiation (Fig. 2a). For distal axonal recording sites, the somatic AP preceded the axonal signal, suggesting that the recording site was distal to the AP initiation site (Fig. 2b). To quantitatively localize the exact site of AP initiation during somatic current injection, we plotted the latency between axonal and somatic APs against the distance between the recording sites (Fig. 2c). Intriguingly, the latency–distance relation showed a sharp minimum at ~20 μm from the soma, indicating a proximal site of AP initiation in these GABAergic interneurons (Fig. 2c; 62 simultaneous axon–soma recordings). The latency–distance relation for the 20^th AP in a high-frequency train showed a very similar minimum (Fig. 2c), demonstrating that the location of the AP initiation site was constant during high-frequency firing. Thus, APs were robustly initiated in the axon at a proximal site. This situation is different from that in glutamatergic pyramidal neurons, where the AP initiation site is more remote^15–19.

Figure 2.

Proximal initiation and fast, reliable propagation of APs in interneuron axons.

(a) Simultaneous recording from the soma and the axon of a fast-spiking, parvalbumin-expressing BC during a long somatic current pulse. Black traces, somatic voltage and corresponding current; blue traces, axonal voltage and corresponding current. The axonal recording site was located 24 μm from the soma. Bottom traces show expanded views of the first and the 20^th AP in the high-frequency train.

(b) Another simultaneous recording from the soma and the axon, in which the axonal recording site was located 315 μm from the soma.

(c) Plot of latency between somatic and axonal AP against distance of the axonal recording site from the soma for the first AP (upper graph) and the 20^th AP (lower graph). Data from 62 axon–soma recordings. Data were fit with a bilinear function (continuous red line), giving a minimal latency at 20 and 22 μm and a propagation velocity of 0.52 m s⁻¹ and 0.49 m s⁻¹ for the first and the 20^th AP, respectively. Filled circles, recordings from axon varicosities; open circles, recordings from axon shafts.

(d) Simultaneous recording from the soma and the axon of a BC during a high-frequency train of short somatic current pulses (120 stimuli at 100 Hz; 3 ms, 1 nA). Black, somatic voltage; blue, axonal voltage. The axonal recording site was located 222 μm from the soma.

(e) Plot of instantaneous somatic and axonal AP frequency during the stimulation train (same cell as shown in d).

(f) Plot of ratio of number of APs in the axon over number of APs in the soma, plotted against distance of the axonal recording site. Data from 28 simultaneous axon–soma recordings.

To probe the reliability of AP propagation, we applied high-frequency trains of brief current pulses at the soma (120 APs at 100 Hz; Fig. 2d–f). Reliability was quantified as either the instantaneous AP frequency in the axon versus time during the train in a given cell (Fig. 2e) or as the ratio of axonal and somatic AP number versus distance in the cell population (Fig. 2f). The instantaneous AP frequency in the BC axon was identical to the corresponding somatic AP frequency, and the ratio of axonal to somatic APs was close to 1 (28 simultaneous axon–soma recordings). Identical results were obtained for high-frequency trains of APs evoked by 1-s depolarizing current pulses at the soma (86.4 ± 1.9 Hz; 92 simultaneous axon–soma recordings at the distances up to 418 μm from the soma). Thus, APs propagate from the initiation site into the distal BC axon with high reliability.

Finally, we quantified the velocity of AP propagation, fitting the latency–distance relation with a bilinear function with sigmoidal transition (Fig. 2c). On average, the velocity of orthodromic propagation was 0.52 m s⁻¹ for the first AP and 0.49 m s⁻¹ for the 20^th AP in a high-frequency train. Similar results were obtained at near-physiological temperature; under these conditions the orthodromic propagation velocity was 1.45 m s⁻¹ for the first AP and 1.42 m s⁻¹ for the 20^th AP in a high-frequency train (19 simultaneous axon–soma recordings; Supplementary Fig. 3). Thus, the conduction velocity is higher than that of unmyelinated axons of glutamatergic principal neurons under similar conditions^20,21.

Mechanisms of AP initiation and propagation

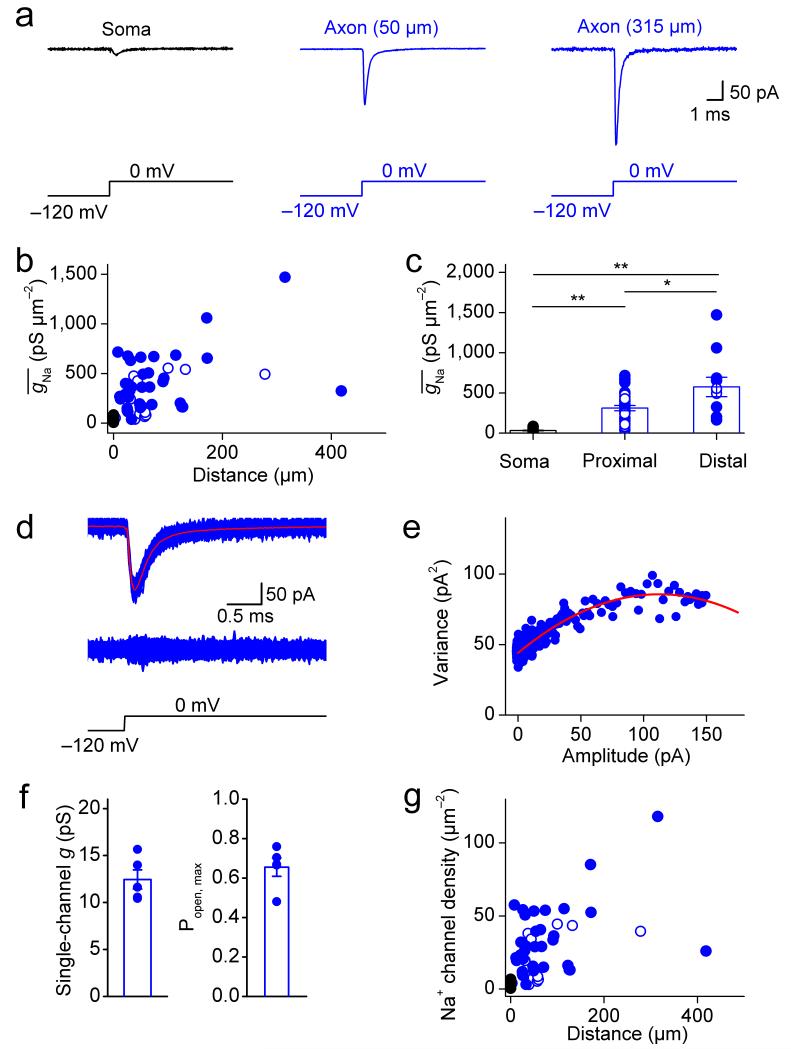
What are the mechanisms underlying the robust AP initiation in the proximal part and the reliable and fast propagation into distal parts of the interneuron axon? In pyramidal neurons, a high density of Na⁺ channels in the axon initial segment is thought to convey AP initiation at a proximal site^22,23. To test whether the Na⁺ channel distribution was similar in fast-spiking GABAergic interneurons, we measured Na⁺ channel density in axons using outside-out patches isolated at various distances from the soma (Fig. 3). Surprisingly, depolarizing voltage pulses evoked a large transient Na⁺ current in membrane patches isolated from both proximal and distal axonal sites, in marked contrast to the small current observed in somatic patches (Fig. 3a). To convert Na⁺ current amplitude into Na⁺ conductance density, we further determined the patch area by capacitance measurements (Supplementary Fig. 4). Plotting the maximal Na⁺ conductance density $\overline{g_{Na}}$ against distance revealed a stepwise increase from the soma to the proximal axon, followed by a further gradual increase in the distal axon (Fig. 3b). On average, $\overline{g_{Na}}$ was 31.9 ± 3.7 pS μm⁻² at the soma, 310.7 ± 32.7 pS μm⁻² in the proximal axon, and 574.3 ± 120.8 pS μm⁻² in the distal axon (P < 0.05; Fig. 3c; Supplementary Table 1). Thus, the Na⁺ conductance in BC axons was comparable to that of highly excitable invertebrate axons^24,25.

Figure 3.

A high Na⁺ channel density in interneuron axons.

(a) Na⁺ current in an outside-out patch in the soma, proximal axon (50 μm), and distal axon (315 μm from the soma). Na⁺ currents were evoked by a sequence of a prepulse to −120 mV followed by a test pulse to 0 mV (bottom). Black trace, somatic patch; blue traces, axonal patches.

(b) Summary plot of Na⁺ conductance density ($\overline{g_{Na}}$) against distance from the soma. Data from 48 axonal recordings and 24 somatic recordings.

(c) Summary bar graph showing $\overline{g_{Na}}$ in the soma (24 patches), proximal axon (< 100 μm, 37 patches) and distal axon (≥ 100 μm, 11 patches). Bars indicate mean ± SEM, circles represent data from individual experiments. * indicates 0.01 ≤ P < 0.05; ** indicates P < 0.01.

(d) Top, overlay of 300 axonal Na⁺ current traces, superimposed with the average (red). Center, superimposition of the difference of individual current traces from the mean. Bottom, voltage-clamp protocol for evoking Na⁺ current.

(e) Plot of variance versus mean from the experiment shown in (d). Red curve represents a parabolic function fit to the data points.

(f) Summary bar graph of single-channel conductance and maximal open probability of Na⁺ channels (both at 0 mV). Bars indicate mean ± SEM, circles represent data from individual experiments.

(g) Summary plot of Na⁺ channel density against distance from the soma. Symbol code in b, c, and g: Black symbols, somatic patches; blue symbols, axonal patches; filled circles, recordings from axon varicosities; open circles, recordings from axon shafts.

To convert conductance density into channel density, we performed nonstationary fluctuation analysis of Na⁺ currents in outside-out patches isolated from BC axons²⁶ (Fig. 3d–f). Fluctuation analysis revealed a single-channel conductance of 12.5 ± 1.0 pS and a maximal channel open probability of 0.66 ± 0.05 (5 axon patches; test pulse amplitude 0 mV). Based on these values, we estimate that the Na⁺ channel density was 2.6 channels μm⁻² in the soma, 25.0 channels μm⁻² in the proximal axon, and 46.1 channels μm⁻² in the distal axon (Fig. 3g). To quantitatively assess the Na⁺ peak conductance distribution, we compared a linear model, a step function, and a combined step–linear function. The combined step–linear function fit the data significantly better than the other models (P < 0.002), and all three functions fit the data significantly better than Gaussian functions with maximal density in the first 100 μm (P < 0.01). Thus, the Na⁺ channel distribution in BC axons markedly differs from that in principal neuron axons, where Na⁺ channels are concentrated in the axon initial segment^22,27–31.

Further analysis of gating kinetics and voltage-dependence of activation and inactivation revealed that Na⁺ channels in BC axons differed from somatic channels in their functional properties. First, the gating kinetics was faster for axonal than for somatic Na⁺ channels (Supplementary Fig. 5). While the activation time constant was 64 ± 6 μs in the axon versus 122 ± 34 μs in the soma (P > 0.2; 4 axonal and 9 somatic patches), the inactivation time constant was 303 ± 21 μs in the axon and 728 ± 98 μs in the soma (P < 0.01; 11 axonal and 9 somatic patches, respectively; test pulse amplitude 0 mV). Thus, the inactivation time constant was 2.4-fold faster for axonal than somatic Na⁺ channels. Furthermore, the midpoint potential of the activation curve of axonal channels was 10.9 mV more negative than that of somatic channels, whereas differences in the midpoint potential of the inactivation curves were less prominent (P < 0.01; Supplementary Fig. 6; Supplementary Table 1). In conclusion, our results suggest that the functional properties of Na⁺ channels in BC axons are specialized, in particular with respect to rapid inactivation kinetics. Rapid inactivation of axonal Na⁺ channels may increase the energetic efficiency of the AP in GABAergic interneuron axons^32,33.

Na⁺ channel density determines AP propagation speed

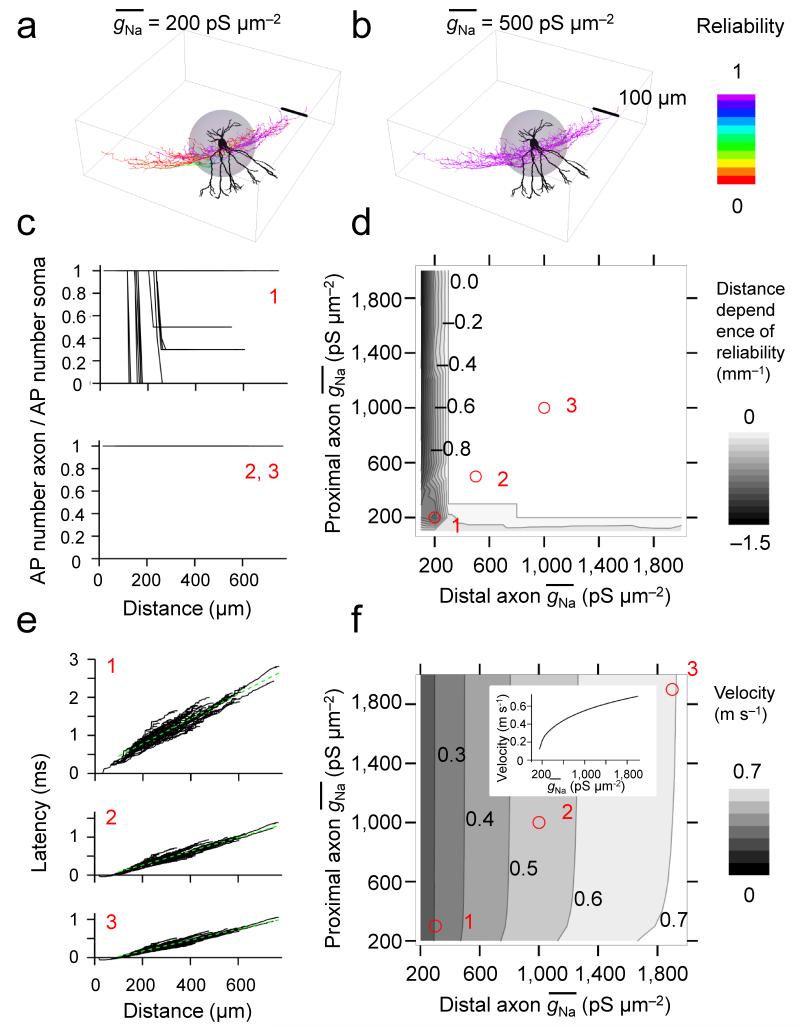
To quantitatively examine the relation between Na⁺ conductance density and AP propagation, we developed an active, morphologically realistic cable model of a fast-spiking GABAergic interneuron (Fig. 4). Voltage-gated Na⁺ and K⁺ channels represented by a Hodgkin-Huxley-type model^34,35 were incorporated into a detailed cable conductor model of a hippocampal BC (including soma, dendrites, and the entire axonal arborization⁹). The Na⁺ conductance in the proximal and distal axon was varied over a 20-fold range. We first examined how Na⁺ conductance affected the reliability of AP propagation^10,11 (Fig. 4a–d). A 100-Hz train of 10 APs was evoked by somatic current injection, reliability was computed for each axonal distance as the ratio of axonal over somatic AP number (Fig. 4c), and the global propagation characteristics were quantified as the slope of the reliability–distance curve (Fig. 4d). In the model, AP propagation was absolutely reliable above a critical value of $\overline{g_{Na}}$ > 200 pS μm⁻² in the proximal and distal axon. The experimentally determined $\overline{g_{Na}}$ was ~1.5 times higher than the critical value (defined based on reliability of AP propagation) in the proximal axon and ~2.8-times higher in the distal axon, indicating that Na⁺ channels in BC axons were expressed at “supercritical” density above the minimum required to ensure reliable AP propagation. Next, we tested how Na⁺ conductance affected the velocity of AP propagation (Fig. 4e, f). Increasing the Na⁺ conductance density above the critical value markedly increased the velocity of AP propagation. When $\overline{g_{Na}}$ in both the proximal and distal axon increased from 200 to 2000 pS μm⁻², the AP conduction velocity increased 3.27-fold (Fig. 4f). Similar results were obtained in five other fully reconstructed cells (Supplementary Fig. 7)⁹. Furthermore, similar results were obtained after increasing or decreasing the axon diameter by a factor of 1.5. Although increasing the axon diameter increased propagation velocity, while decreasing axon diameter decreased it, the dependence of velocity on $\overline{g_{Na}}$ qualitatively remained the same (Supplementary Fig. 8a, b). Thus, our conclusions were independent of the details of morphological properties of the BC axon. Finally, changing the gating kinetics of Na⁺ channel inactivation and K⁺ channel activation by a factor corresponding to a 5°C temperature change had only minimal effects on reliability and speed of AP propagation (Supplementary Fig. 8c, d). Taken together, these results suggest that a low Na⁺ channel density in the BC axon is sufficient for reliability, whereas a high density is necessary for fast AP propagation.

Figure 4.

Dependence of reliability and velocity of AP propagation on axonal Na⁺ conductance density in an active BC model.

(a, b) Plot of reliability of AP propagation, shown as color coding of the surface of the reconstructed neuron for $\overline{g_{Na}}$ = 200 pS μm⁻² (a) and 500 pS μm⁻² (b); proximal and distal $\overline{g_{Na}}$ were changed in parallel. Color scale bar indicates the reliability of propagation in the axon (inset, right); dendrites are depicted in black to indicate the lack of active AP propagation. Gray sphere represents the proximal region of the axon.

(c, d) AP propagation reliability–distance plots (c) and contour plot of the average slope of the reliability–distance relation as a function of proximal and distal $\overline{g_{Na}}$ (d). Red circles and numbers in d indicate the correspondence with the graphs shown in c. Numbers right-adjacent to contour lines in d indicate distance dependence of AP propagation reliability (in mm⁻¹; values in the range ± 0.02 were represented as 0; see gray scale bar on the right). In a–d, 100-Hz trains of 10 brief stimuli were applied to the soma and the number of successfully propagated APs in the axon was plotted against distance.

(e, f) Latency–distance plots (e) and contour plot of AP propagation velocity as a function of proximal and distal $\overline{g_{Na}}$. Dashed green lines in e indicate the results of linear regression for distances > 100 μm. Numbers right-adjacent to contour lines in f indicate AP propagation velocity (in m s⁻¹; see gray scale bar on the right). Red circles and numbers in f indicate the correspondence with the graphs shown in e. Inset in f shows one-dimensional representation for simultaneous changes in proximal and distal $\overline{g_{Na}}$. In e, f, single brief stimuli were used to evoke APs. All simulations were performed on cell 2 of Nörenberg et al.⁹.

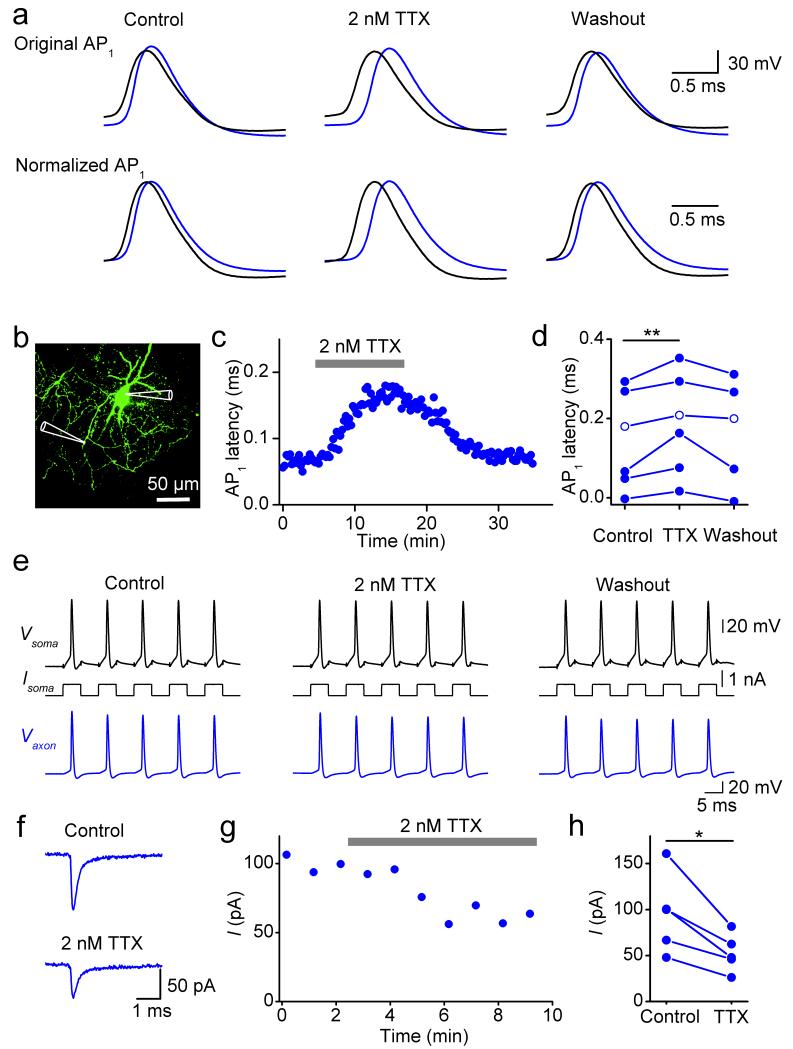
To experimentally test this hypothesis, we measured AP latencies between somatic and axonal sites in the presence of a low concentration of the Na⁺ channel blocker tetrodotoxin (TTX; Fig. 5). Bath application of 2 nM TTX in simultaneous axon–soma recordings significantly affected latency. On average, the latency of AP₁ increased to 131% of the control value (6 simultaneous axon–soma recordings at distances between 91 to 222 μm, Fig. 5a–d; P < 0.01). In contrast, reliability of AP propagation during high-frequency trains in the same recordings was maintained (Fig. 5e). In agreement with these results, bath application of 2 nM TTX also increased the latency of unitary inhibitory postsynaptic currents (IPSCs) in synaptically connected BC–granule cell (GC) pairs (Supplementary Fig. 9). Under comparable conditions, bath application of 2 nM TTX blocked 43.1 ± 3.9% of Na⁺ current in axonal outside-out patches (5 axon patches; P < 0.05; Fig. 5f–h). These results are consistent with the predictions of the active interneuron models (Supplementary Fig. 10), providing further evidence that a supercritical Na⁺ channel density in the BC axon is necessary for fast AP propagation.

Figure 5.

A supercritical Na⁺ channel density in the axon ensures fast AP propagation.

(a) Simultaneous axon–soma recordings in control conditions, in the presence of 2 nM TTX, and after washout. Upper traces are displayed at absolute voltage scale, lower traces are shown normalized to the same peak amplitude to facilitate comparison of the rising phase.

(b) Confocal stack maximum projection of a recorded BC. Recording pipettes are illustrated schematically.

(c) Plot of latency between axonal and somatic AP against experimental time during application of 2 nM TTX (horizontal bar).

(d) Summary graph of the effects of 2 nM TTX on latency between somatic and axonal AP. Data from 6 simultaneous axon–soma recordings at distances of 91 to 222 μm. Data from the same experiment were connected by lines. Open circles, data from the cell shown in Supplementary Fig. 10.

(e) Effects of 2 nM TTX on reliability of AP propagation during a high-frequency train (5 stimuli at 100 Hz; 5 ms, 0.7 nA). Data in (a–c, e) were obtained from the same experiment (axonal recording site 100 μm from the soma).

(f) Na⁺ current recorded from an outside-out patch isolated from the axon 66 μm from the soma before and after bath application of 2 nM TTX. Na⁺ currents were evoked by a sequence of a prepulse to −120 mV followed by a test pulse to 0 mV.

(g) Plot of Na⁺ current peak amplitude against experimental time during application of 2 nM TTX (horizontal bar) from the same experiment as shown in (f). Each data point represents the average of 6 consecutive peak current values.

(h) Summary graph of the effects of 2 nM TTX on Na⁺ peak current. Data from 5 axonal outside-out patches. Data from the same experiment were connected by lines.

In d and h, * indicates 0.01 ≤ P < 0.05 and ** indicates P < 0.01.

Na⁺ channel density contributes to AP phenotype

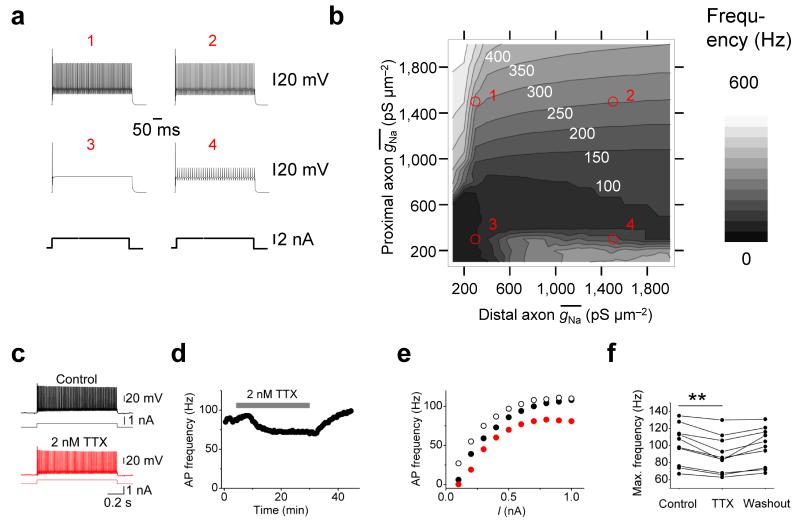
Our results indicate that axonal Na⁺ channel density affects reliability and velocity of AP propagation. Does it also affect the AP phenotype itself, such as the ability of BCs to generate high-frequency trains of APs?^36,37 To test whether the Na⁺ channel conductance density affects the fast-spiking AP generation, we again used a combined computational–experimental approach (Fig. 6). We first computed the dependence of maximal AP frequency during long current pulses on $\overline{g_{Na}}$ in the proximal and distal axon (Fig. 6a,b). Axonal Na⁺ conductance density markedly affected the maximal AP frequency during long current pulses. Interestingly, whereas the speed and reliability of AP propagation were primarily determined by $\overline{g_{Na}}$ in the distal axon (Fig. 4d,f), maximal firing frequency was largely controlled by $\overline{g_{Na}}$ in the proximal axon (Fig. 6b). To experimentally test the hypothesis that a high axonal Na⁺ channel density contributes to the fast-spiking AP phenotype, we measured AP frequency during long current pulses before and after bath application of a low concentration of TTX. In these experiments, 2 nM TTX significantly and reversibly reduced the maximal AP frequency (10 BC somatic recordings; P < 0.01; Fig. 6c–f). These results suggest that a supercritical Na⁺ channel density in the BC axon is necessary for the fast-spiking AP phenotype.

Figure 6.

A supercritical Na⁺ channel density contributes to the fast-spiking AP phenotype.

(a, b) Effects of Na⁺ conductance density on fast-spiking AP phenotype in a BC model. Example traces (a) and contour plot (b) of maximal AP frequency as a function of proximal and distal $\overline{g_{Na}}$. Red circles and numbers in b indicate the correspondence with the graphs shown in a. White numbers right-adjacent to contour lines in b indicate maximal AP frequency (in Hz; see gray scale bar on the right). APs were evoked by 500-ms current pulses (0.5 – 5 nA, 0.5 nA steps; 2.5 nA in a).

(c–f) Effects of 2 nM TTX on fast-spiking AP phenotype in experimental conditions. (c) Train of APs evoked by long current pulses under control conditions (top, black trace) and in the presence of 2 nM TTX (bottom, red trace).

(d) Plot of AP frequency in spike trains evoked by a 1-s depolarizing current pulse against experimental time during application of 2 nM TTX (horizontal bar). 500-pA current pulses were applied throughout. Data in c–e are from the same cell.

(e) Frequency–current relation in control conditions (black filled circles), in the presence of 2 nM TTX (red circles), and after washout (black open circles). Note that 2 nM TTX slightly, but reversibly, reduced the maximal AP frequency.

(f) Summary graph of the effects of 2 nM TTX on maximal AP frequency. Data from 10 BCs. Data from the same experiment were connected by lines. ** indicates P < 0.01.

DISCUSSION

The present study reveals several unexpected functional properties of axons of fast-spiking, parvalbumin-expressing GABAergic interneurons. First, APs are initiated in the proximal axon very close to the soma, and propagate to the distal axon with high reliability and speed. Second, BCs show a unique Na⁺ channel distribution profile, with a stepwise increase of Na⁺ conductance density from the soma to the proximal axon, followed by a further gradual increase in the distal axon. Third, our results suggest that the Na⁺ conductance in BC axons is above the critical minimum required to ensure reliability, and that this high density is necessary to ensure both the speed of AP propagation and the fast-spiking AP phenotype. Thus, a supercritical density of Na⁺ channels compensates for the morphological properties of interneuron axons (small segmental diameter, extensive branching, and high bouton density), ensuring rapid signaling in BCs.

Specific properties of AP initiation and propagation

The rules of AP initiation and propagation in BCs differ from those in pyramidal neurons in multiple ways. First, APs in BCs are robustly initiated at a proximal site, only ~20 μm from the soma. In contrast, in cortical pyramidal neurons the initiation site is more remote^16,17, sometimes even beyond the axon initial segment¹⁵. Second, APs in BCs propagate with almost absolute reliability, even during high-frequency trains. In contrast, in pyramidal neurons propagation appears to be less reliable^38–40. Finally, our results reveal that APs propagate in the BC axon with high speed. We estimate that the propagation velocity is ~0.5 m s⁻¹ at ~22°C and ~1.5 m s⁻¹ at near-physiological temperature. In contrast, AP propagation in nonmyelinated collaterals of principal neurons is slower (0.36 m s⁻¹ in CA3 pyramidal neurons²⁰; 0.24 m s⁻¹ in dentate gyrus granule cells²¹; all values at ~22°C).

Unique Na⁺ channel distribution profile

Our results reveal a unique spatial profile of Na⁺ channel distribution in BCs. Na⁺ channel density exhibits a ~10-fold stepwise increase from the soma to the proximal axon, followed by a further gradual increase in the distal axon. In contrast, Na⁺ channel density is very low in the dendrites¹². This channel distribution is different from that in cortical principal neurons, where Na⁺ channel density shows a peak in the axon initial segment, but is also significant in the dendrites^22,27–30. Thus, unlike many other cell types, BCs show a high degree of polarity, with a nonexcitable input region connected to a highly excitable output region.

The steep gradient in Na⁺ channel density between the soma and the axon initial segment appears to be sufficient to define the proximal initiation site; an absolute maximum of Na⁺ channel density in the initial segment is not required^18,29,41. In addition, the left-shifted activation curve of axonal Na⁺ channels may contribute to proximal initiation⁴², amplifying the gradient of available channels into a larger gradient of open channels. Furthermore, the high Na⁺ channel density in the distal axon plays a key role to ensure both reliability and speed of AP propagation. However, the two factors are differentially sensitive to Na⁺ conductance density. A low (critical) axonal Na⁺ conductance density is sufficient for reliability, whereas a high (supercritical) density is necessary to guarantee speed.

Effects of structural factors

Two structural factors are generally thought to accelerate AP propagation in axons¹⁰. One mechanism, used in invertebrates, is the increase of axon diameter, resulting in propagation velocities of up to ~20 m s^{−1 34}. Another mechanism is the formation of a myelin sheath, generating saltatory conduction⁴³. However, BC axons do not exploit these strategies. Average axon diameter is the submicrometer range⁹, and myelination is largely absent, as indicated by the lack of myelin basic protein immunoreactivity (see Methods). Furthermore, BC axons show several structural properties expected to slow down AP propagation, particularly a large number of axon collaterals and a high density of en-passant boutons⁹. The negative influence of both axon collaterals and boutons is demonstrated in our schematic ball-and-stick model (Supplementary Fig. 1), and the impact of en-passant boutons is further exemplified in hippocampal mossy fiber axons, in which the pearl-chain arrangement of large presynaptic terminals slows propagation⁴⁴. Our results suggest that the supercritical Na⁺ channel density in the BC axon compensates for these factors. Additionally, structural details may be important for AP propagation. First, branching of BC axons is often asymmetric, leading to geometric ratios close to 1 (Supplementary Fig. 7)⁹. Second, the majority of BC en-passant boutons have a diameter of < 2 μm, much smaller than that of mossy fiber terminals. Consequently, the negative effects of structural determinants on propagation velocity will be minimized, and compensation by the high axonal Na⁺ channel density will be more efficient.

Consequences for the fast-spiking AP phenotype

BCs generate APs at high frequency both under in vitro and in vivo conditions^4,45. Previous studies demonstrated that the expression of voltage-gated K⁺ channels of the Kv3 subtype play a key role for the fast-spiking AP phenotype^36,46. However, our results show that the high axonal Na⁺ channel density also plays a critical role. High Na⁺ channel density may have direct consequences, increasing the number of available Na⁺ channels during an AP train³⁷. In parallel, high Na⁺ channel density may have several indirect effects. For example, it will increase the amplitude of the AP overshoot, resulting in more efficient activation of Kv3 channels. This, in turn, will promote recovery of Na⁺ channels from inactivation. Our simulations suggest that the Na⁺ conductance in the proximal axon is more relevant for the fast-spiking phenotype than that in the distal axon (Fig. 6b). In contrast, distal Na⁺ conductance is more important for AP propagation velocity (Fig. 4f). Thus, although a high Na⁺ conductance is required for both fast propagation and high-frequency firing pattern, the responsible channels are located in different axonal subdomains.

Implications for brain energetics

Because of their high AP frequency under in vitro and in vivo conditions^4,45, BCs are expected to make a major contribution to the energy budget of the brain. From the perspective of energetics, the expression of a high density of Na⁺ channels in the axon may be disadvantageous. Both the synthesis of Na⁺ channel proteins and the reestablishment of ion gradients after an AP via the Na⁺ / K⁺ ATPase require adenosine triphosphate (ATP), with metabolic costs roughly proportional to channel number. This suggests that the advantages of the supercritical Na⁺ channel density (e.g. fast signaling) may outweigh the disadvantages (high energy consumption). However, our results also demonstrate that Na⁺ channels in BC axons show specialized gating properties, in particular, rapid inactivation. These differences in gating kinetics may be generated by different abundance of Na⁺ channel alpha subunits (Nav1.1 versus 1.6) and / or beta subunits (β1, β2, or β4)⁴⁷. Thus, the specific subunit composition of Na⁺ channels in the BC axon will minimize Na⁺ inflow during APs and reduce associated metabolic costs^31,33.

Implications for microcircuit and network function

Our findings suggest a likely picture of how fast-spiking, parvalbumin-expressing interneurons operate in the neuronal network. In combination, the absence of Na⁺ channels and the presence of Kv3-type K⁺ channels in the dendrites conveys sublinear integration properties to these cells and makes them particularly sensitive to distributed input¹². In contrast, the high density of Na⁺ channels in the axon conveys robust analogue–digital conversion and rapid propagation of the digital signal. These cellular properties are expected to be critically important for the function of BCs, which mediate fast feedforward and feedback inhibition in hippocampal microcircuits^2,3. It is well established that the time required for disynaptic inhibition in microcircuits can be as short as 1 ms⁸. Our results identify fast axonal propagation of APs as a key factor underlying rapid disynaptic inhibition.

Finally, our findings may be relevant for the understanding of dynamic network activity. Fast-spiking, parvalbumin-expressing GABAergic interneurons play a key role in the generation of network oscillations in the gamma frequency range^4–6. Establishing coherent oscillations in principal neuron–interneuron networks over distance is difficult, because axonal delays will disrupt the synchrony between spatially distributed cells^48–50. Expression of Na⁺ channels at a supercritical density in interneuron axons could extend the synchronization process over long distances, contributing to the generation of fast and coherent oscillatory reference signals for coding of information in memory circuits. Finally, our results may imply that the specific organization of excitability in interneuron axons could be altered in network diseases. Future work will be needed to address this possibility.

ONLINE METHODS

Axonal patch-clamp recording

Recording from axons of fast-spiking BCs of the dentate gyrus was performed according to previously established experimental protocols¹² (see Kim et al., Bischofberger et al., and Nevian et al. ^17,51,52). Transverse hippocampal slices (thickness 350 μm) were prepared from the brains of 17- to 22-day-old Wistar rats of either sex. Rats were maintained under light (7 am–7 pm) and dark cycle (7 pm–7 am) conditions and were kept in a litter of 8 animals together with the mother in a single cage. Animals were killed by rapid decapitation, in accordance with national and institutional guidelines. Slices were cut in ice-cold, sucrose-containing physiological extracellular solution using a vibratome (VT1200, Leica Microsystems), incubated in a maintenance chamber filled with standard physiological extracellular solution at ~34°C for 30 min, and subsequently stored at room temperature. Slices were then individually transferred into a recording chamber superfused with standard physiological extracellular solution. Recordings were performed at room temperature (22–25°C) or, in a subset of experiments, at near-physiological temperature (30–33°C) as indicated. In each experiment, temperature was held constant within ± 0.5°C.

For recording from interneuron axons, the following experimental strategy was implemented. First, a somatic recording was obtained, using an internal solution containing Alexa Fluor 488 (100 or 200 μM, Invitrogen). Second, after ~30 min of somatic whole-cell recording, the fluorescently labeled axon was tangentially traced from the BC soma through the granule cell layer with a Nipkow spinning disk confocal microscope (Ultraview live cell imager, Perkin Elmer, equipped with an Orca camera, Hamamatsu and an argon/krypton laser, excitation wavelength 488 nm). Exposure time was minimized to avoid phototoxic damage. Finally, fluorescent and infrared differential interference contrast (IR-DIC) images were compared and axons were patched under IR-DIC. Recordings were made from either axon shafts or small spherical axon expansions, presumably representing “blebs” formed during the slicing procedure¹³, from up to 10^th order axon branches at distances up to 418 μm from the soma. This procedure resulted in a simultaneous axon–soma recording configuration. From this configuration, axonal outside-out patches were subsequently obtained by slowly withdrawing the axonal pipette. In all cases, axons could be unequivocally distinguished from dendrites on the basis of smaller diameter, location within or adjacent to the granule cell layer, and abundance of tangential collaterals. Under our conditions, the proportion of recordings from glial cells was < 10%, consistent with the absence of myelination of axons of dentate gyrus BCs¹⁴ (Fig. 1e; Supplementary Fig. 2). For illustration and documentation purposes, 20 cells were rescanned with a Leica TCS SP5 II confocal microscope (Leica Microsystems).

Patch pipettes were fabricated from thick-walled borosilicate glass tubing (outer diameter: 2 mm, inner diameter: 1 mm) with a horizontal pipette puller (P-97, Sutter Instruments). When filled with internal solution, they had a resistance of 2–10 MΩ for somatic recording and 10–32 MΩ for axonal recording. For outside-out patch experiments to measure Na⁺ channel density, pipettes with a resistance of 4.9–32 MΩ were used. Current- and voltage-clamp recordings were performed using a Multiclamp 700B amplifier (Molecular Devices). In BC recordings, series resistance was 15–90 MΩ. Cells with somatic resting potentials more positive than −50 mV were discarded. Pipette capacitance and series resistance compensation (bridge balance) were applied throughout current-clamp experiments. Bridge balance was monitored and readjusted as required. BCs were held at a membrane potential of ~−65 mV, injecting a holding current at the soma (range: −150 to +200 pA) or at the axon (range: −20 to −100 pA).

Signals were low-pass filtered at 10 kHz (voltage traces) and 4 or 10 kHz (current traces), and sampled at 20–100 kHz with a CED power interface (Cambridge Electronic Design). Pulse protocols were generated using custom-made data acquisition software (FPulse versions 3.19 and 3.33, Ulrich Fröbe, University of Freiburg) running under Igor 6.20 (WaveMetrics). In a subset of experiments, Na⁺ currents were pharmacologically isolated with 5–20 mM tetraethylammoniumchloride (TEA), 1–10 mM 4-aminopyrididine (4-AP), and 0.1 mM CdCl₂ added to the bath solution. To measure the peak amplitude of voltage-gated Na⁺ current in outside-out patches, a pulse sequence composed of a 50-ms prepulse to −120 mV followed by a 30- or 100-ms test pulse to 0 mV was generated. For activation and inactivation protocols, prepulse and test pulse durations were the same, whereas amplitudes were varied as indicated. The holding potential before and after the pulse sequence was −90 mV. Voltage protocols were applied to outside-out patches once every 3–15 s. Leak and capacitive currents were subtracted online using a “P over −4” or “P over −8” correction procedure.

BCs were identified based on the non-accommodating, fast-spiking AP phenotype (average AP frequency > 50 Hz at room temperature and > 150 Hz at near-physiological temperature in response to 1-s, 0.3- to 1-nA somatic current pulses), and the localization of the axonal arbor, which was largely restricted to the granule cell layer in the confocal image. Identification during the experiment was confirmed by post-hoc biocytin labeling (Fig. 1b). Detailed light-microscopic analysis of the axonal arbor revealed that the majority of cells were classical BCs with tangential collaterals, forming basket-like structures around granule cell somata¹².

Paired BC–GC recordings

To examine the effects on Na⁺ channel block on synaptic latency, paired recordings were made between synaptically connected BCs and GCs⁵³ (Supplementary Fig. 9). In this set of experiments, the distance between somata of pre- and postsynaptic neurons was 219 ± 14 μm, and the recording temperature was 22–25°C. Series resistance in the postsynaptic GC was 6–14 MΩ and remained stable within each experiment. GCs were voltage-clamped at −80 mV without series resistance compensation. Latency was measured from the time point of the half-maximal amplitude of the presynaptic AP to the onset of the IPSC.

Solutions and chemicals

The standard physiological extracellular solution contained 125 mM NaCl, 25 mM NaHCO₃, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 2 mM CaCl₂, 1 mM MgCl₂, and 25 mM D-glucose (equilibrated with 95% O₂ and 5% CO₂ gas mixture). For BC axon–soma whole-cell and outside-out patch recording, the intracellular solution contained 120 mM K-gluconate, 20 mM KCl, 10 mM EGTA, 2 mM MgCl₂, 2 mM Na₂ATP, 10 mM HEPES, and 0.2% biocytin, pH adjusted to 7.3 with KOH. In a subset of experiments, 0.1 mM spermine was added to the internal solution. 100–200 μM Alexa Fluor 488 (Invitrogen) was added to the internal solution for all somatic recording electrodes. For BC–GC paired recording, the internal solution for the presynaptic BC contained 135 mM K-gluconate, 20 mM KCl, 0.1 mM EGTA, 2 mM MgCl₂, 2 mM Na₂ATP, 10 mM HEPES, and 0.2% biocytin, whereas the solution for the postsynaptic GC contained 145 mM KCl, 0.1 mM EGTA, 2 mM MgCl₂, 2 mM Na₂ATP, 10 mM HEPES, pH adjusted to ~7.3 with KOH. TEA, 4-AP, and CdCl₂ were from Sigma-Aldrich, TTX was from Alomone Labs.

Immunohistochemistry

Immunolabeling of neurons in the dentate gyrus was performed according to previously established protocols⁵⁴. Rats (17- to 22-day-old, covering the range used in electrophysiology experiments, Fig. 1e; or 6-week-old, Supplementary Fig. 2) were intracardially perfused with phosphate-buffered saline (PBS, composed of 0.1 M phosphate buffer + 0.9% NaCl, pH 7.4) for 5 min and subsequently with 1% paraformaldehyde (PFA) and 1% sucrose in PBS. After a postfixation of 2 h in 1% PFA and 1% sucrose in PBS and a subsequent incubation in 30% sucrose in phosphate-buffered solution (PB; 0.1 M, pH 7.35) for 12 h, 50-μm-thick slices were cut with a vibratome at −18°C. Slices were washed (3 × 10 min) with PBS and subsequently incubated in 10% normal goat serum for 1 h. They were then incubated for 24 h at room temperature with a rabbit polyclonal antibody against parvalbumin (PV-25, 1:1000, Swant) and a mouse monoclonal antibody against myelin basic protein (MBP; SMI99P-100, 1:1000, Sternberger Monoclonals) in PBS containing 5% normal goat serum and 0.3% Triton X-100. The antibody against parvalbumin was previously confirmed in PV knockout mice⁵⁴ and the antibody against MBP had been previously validated in Long Evans Shaker rats⁵⁵. After washing, slices were incubated for 12 h at 4°C with goat anti-rabbit Alexa Fluor 488 and goat anti-mouse Alexa Fluor 647 (both 1:1000; Invitrogen) in PBS containing 3% normal goat serum and 0.3% Triton X-100. Finally, slices were embedded in Prolong Gold Antifade (Invitrogen) and examined using a Leica TCS SP5 II confocal microscope (Leica Microsystems). Experiments were repeated on 5 animals for each age group, giving consistent results. Although the dentate gyrus granule cell layer was devoid of MBP immunoreactivity, strong immunolabeling was detected in stratum oriens-alveus and fimbria in adjacent CA3 and CA1 subfields. Whereas PV and MBP colocalization was completely absent in the dentate gyrus granule cell layer, slight colocalization was detected in CA3 and CA1 pyramidal cell layer (see Ref. 56).

Data analysis

Analysis was performed using Stimfit 0.9.2–0.13.2 (C. Schmidt-Hieber, UCL and José Guzmán, IST Austria), Clampfit 9 (Molecular Devices), Origin (Microcal), and Excel (Microsoft). AP amplitude was measured from threshold (40 V s⁻¹). Latency differences between somatic and axonal APs were quantified using the time points corresponding to half-maximal amplitude in the AP rising phase. To determine the AP initiation site, latency–distance data were fit with a bilinear function with sigmoidal transition of the form L(x) = (1 − f(x)) * a x + f(x) * (b x + c), where L is latency, x is distance, a and b are slope factors, c is an offset, and f(x) is a sigmoidal (Boltzmann-like) function. AP propagation velocity was obtained as 1 / b. For the experiments at near-physiological temperature, c was set to 0 to reduce the number of free parameters. Experiments in which the axon originated from one of the dendrites were excluded from this analysis (30 recordings in Fig. 2c; 4 recordings in Supplementary Fig. 3c).

Na⁺ channel activation curves were determined by calculating chord conductance values (g) from peak currents, assuming ohmic behavior and a reversal potential of 70 mV⁵⁷. Na⁺ conductance density ($\overline{g_{Na}}$) was calculated based on the peak current at 0 mV and the open probability at this membrane potential determined by nonstationary fluctuation analysis. Activation and inactivation curves were fit by a Boltzmann function f =1/{1+exp[(V_1/2 − V)/k]}, where V is the membrane potential, V_1/2 is the midpoint potential, and k is the slope factor. Na⁺ current activation time constant was obtained by fitting rise and early decay of the Na⁺ current with a function of the form I(t) = (1 − exp[- (t − δ)/τ_m]) (a exp[-(t − δ)/ τ_h] + b) for t > δ and I(t) = 0 for t ≤ δ, where δ is a delay, τ_m is activation time constant, τ_h is inactivation time constant, and a, b are amplitude values. Na⁺ current inactivation time constant was obtained by fitting the decay phase of the Na⁺ current with a single exponential. Na⁺ current deactivation time constant was either fit with a single exponential (at test voltage < −50 mV) or a biexponential function (at test voltage > −50 mV); in the latter case the deactivation time constant was taken from the fast component⁵⁸. Na⁺ channel single-channel conductance and open probability at the peak were estimated by nonstationary fluctuation analysis^26,44. To minimize the effects of rundown, data were analyzed in blocks of 10 traces each. Variance–mean data were fit with a parabolic function ${\sigma }^2\left(\mathrm{I}\right)=\mathrm{i}\mathrm{I}-{\mathrm{I}}^2∕\mathrm{N}+{{\sigma }_0}^2$, where σ² is mean variance, I is the mean current, i is the single-channel current, N is the number of available channels in the patch, and ${{\sigma }_0}^2$ is the baseline variance^26,44.

Membrane potentials are specified without correction for liquid junction potentials. Values indicate mean ± standard error of the mean (SEM). Error bars in figures also indicate SEM. No statistical methods were used to pre-determine sample sizes. Traces of Na⁺ currents shown in figures represent averages of 5–100 individual traces (except Fig. 3d). To account for the effects of low-pass filtering, traces were shifted by 32.9 μs with respect to the voltage pulse protocol⁴⁴. Significance of differences of mean values was assessed by a two-sided nonparametric Wilcoxon signed rank test or Wilcoxon rank sum test. Significance of differences of activation and inactivation curves was assessed with a bootstrap method⁴⁴. The significance level of statistic tests was set to P < 0.05. Distances were measured from the point of origin of the axon to the axonal recording site along the axonal trajectory in the fluorescent image, after sections at different focal planes had been merged following each experiment. To assess the possibility of a systematic bias between axon shaft and axon bleb recordings, we compared residuals y_i − f(x_i) between the two data sets (where x_i, y_i are the coordinates of each data point and f(x) represents the function fit to the total data set); no statistical differences were observed (latency–distance data, Fig. 2c, top: P > 0.2; $\overline{g_{Na}}$–distance data, Fig. 3b: P > 0.05).

For estimation of current and channel density, membrane patch area was estimated from the pipette resistance using a linear relation between patch area and pipette conductance (Supplementary Fig. 4). In a subset of outside-out patches (7 axon and 9 soma recordings), capacitance was directly measured by recording capacitive transients from outside-out patches before and after pushing the pipette tip gently into an insulating ball of silicone elastomer^44,59 (Sylgard 184; Dow Corning). A contribution from the pipette was corrected, assuming a pipette capacitance of 1 pF mm⁻¹ and an insertion depth of 10 μm.

To compare different Na⁺ conductance distributions (e.g. the nested models f(x) and g(x)), the sum of squared errors (SSE) between experimental data and model was calculated, and [(SSE_f − SSE_g) / k_f] / [SSE_g / (n − k_g)] was compared with F(k_f; n − k_g), where F is the F distribution, n is the number of data points, and k_f and k_g are the degrees of freedom⁶⁰. Nonnested models were compared with a bootstrap method⁶⁰.

Computational model of AP initiation and propagation in BC axons

Simulation of AP initiation and propagation was performed using NEURON 7.1⁶¹ in combination with Mathematica 8.01 (Wolfram Research) running under Windows XP x64 on a Lian Li desktop computer (72 GByte RAM) or under Windows 7 on a PC. Simulations were performed on detailed passive cable models of BCs taken from the previously published sample of Nörenberg et al., 2010⁹ (cell 2; 1017 sections total, or other cells from the sample as indicated). Neurons had been filled with biocytin during recording, stained with 3,3′-diaminobenzidine, and fully reconstructed (including soma, dendrites, and entire axon) using a Neurolucida reconstruction system, as described in the previous publication⁹. In the morphometrically detailed model, the specific cable parameters were set according to approximate average values (R_m = 10 kΩ cm², C_m = 0.9 μF cm⁻², and R_i = 170 Ω cm). Nonlinear capacitive currents were not included, because their effect on AP propagation is expected to be minimal for physiologically relevant channel density values⁶². To simplify the stability properties of the model, a high value of I_h conductance in the BC axon⁶³ was lumped into a uniform axonal R_m value of 10 kΩ cm². The integration time step was set to 5 μs. Na⁺ and K⁺ channels were inserted using the previously published Wang and Buzsáki (WB) model³⁵. WB channels were chosen, because they robustly confer a fast-spiking AP phenotype in single-compartment models³⁵. $\overline{g_{Na}}$ was set to 100 pS μm⁻² at the dendrite, 200 pS μm⁻² at the soma, and between 200 and 2000 pS μm⁻² in the axon. The maximal K⁺ conductance $\overline{g_K}$ was uniformly set to 300 pS μm⁻² in dendrites, soma, and axon. The reversal potential of the leak conductance was chosen as −70 mV. The border between proximal and distal axonal compartments was set at 120 μm distance from the center of the soma. Reliability of AP propagation was quantified as the ratio of the number of spikes in the first axonal segment (immediately adjacent to the soma) and that at a given axonal location. Spikelets with absolute peak amplitude < −40 mV were discarded from the count. Latency differences between somatic and axonal APs were quantified using the time points corresponding to the maximal rate of rise of the AP. Path distance was measured from the center of the soma. In all simulations, APs were evoked by brief or long current pulses (1–4 nA, 1 ms or 500 ms). For simulations with a schematic ball-and-stick model (Supplementary Fig. 1), both specific cable parameters (R_m = 10 kΩ cm², C_m = 0.9 μF cm⁻², and R_i = 170 Ω cm) and active conductances (WB) were chosen to be the same as those in the detailed models.