Abstract
Background
Neural information processing involves a series of nonlinear dynamical input/output transformations between the spike trains of neurons/neuronal ensembles. Understanding and quantifying these transformations is critical both for understanding neural physiology such as short-term potentiation and for developing cognitive neural prosthetics.
New method
A novel method for estimating Volterra kernels for systems with point-process inputs and outputs is developed based on elementary probability theory. These Probability Based Volterra (PBV) kernels essentially describe the probability of an output spike given q input spikes at various lags t1, t2, …, tq.
Results
The PBV kernels are used to estimate both synthetic systems where ground truth is available and data from the CA3 and CA1 regions rodent hippocampus. The PBV kernels give excellent predictive results in both cases. Furthermore, they are shown to be quite robust to noise and to have good convergence and overfitting properties. Through a slight modification, the PBV kernels are shown to also deal well with correlated point-process inputs.
Comparison with existing methods
The PBV kernels were compared with kernels estimated through least squares estimation (LSE) and through the Laguerre expansion technique (LET). The LSE kernels were shown to fair very poorly with real data due to the large amount of input noise. Although the LET kernels gave the best predictive results in all cases, they require prior parameter estimation. It was shown how the PBV and LET methods can be combined synergistically to maximize performance.
Conclusions
The PBV kernels provide a novel and intuitive method of characterizing point-process input–output nonlinear systems.
Keywords: System identification, Nonlinear modeling, Volterra modeling, Rodent hippocampus, Schaffer collateral, Short-term potentiation
1. Introduction
Information in the nervous system is encoded in precisely timed sequences of neuronal action potentials. A central goal of computational neuroscience is to understand how these series of spike trains are processed in the brain. In particular, three fundamental problems can be identified: how the brain maps external stimuli onto neural spike trains (encoding), how neural spike trains map onto bodily response (decoding), and finally how the spike trains of one neuronal population are mapped onto another. These problems are not just important for increasing our understanding of the brain, but they also have immediate applications to neuroprosthetics and brain–machine interfaces which aim to replace damaged brain regions in order to restore lost cognitive function. In particular, the encoding problem is central to neuroprosthesis which aim to replace damaged sensory systems such as the visual (Weiland et al., 2011), auditory (Loeb, 1990), and vestibular systems (Di et al., 2010). The decoding problem is central to motor prosthesis which aim to compensate for lack of movement either by reactivating muscle movement (Loeb et al., 2001) or by controlling external artificial actuators such as a computer cursors (Hochberg et al., 2006; Wolpaw and McFarland, 2004). Finally, the third problem is directly relevant to prosthesis which aim to replace lost cognitive function within the central nervous system and which have made much headway in recent years (Hampson et al., 2012; Berger et al., 2012; Marmarelis et al., 2012). This problem is distinct from the previous two in that both the input and the output signals are binary spike trains. Thus, this problem necessitates a highly robust and versatile modeling approach which may adequately describe the nonlinear dynamical transformation between these spike trains.
Traditional physiological modeling has often revolved around parametric approaches which incorporate a priori knowledge/assumptions about the system into model structure. Such models can be extremely useful and have successfully shed light on synaptic transmission and somato-dendritic integration (Dittman et al., 2000; Dayan and Abbott, 2001; London and Häusser, 2005); however, their use is limited to environments where one may confidently assume the underlying structure of the model. In the context of neuroprosthesis, when recording from arbitrary neurons in the brain, one may not make such assumptions since even if the neuronal presynaptic and postsynaptic dynamics are known, the anatomical connections between the recorded neurons are unknown. These connections are critical to the input–output dynamics of the neurons and include the number and location of the synapses between them and whether they are connected directly, through intermediate neurons, or both. Thus, this problem necessitates a nonparametric approach which estimates the model directly from the input–output data records without making any a priori assumptions of the connections. An additional benefit of the non-parametric approach is that the model will not change with future discoveries (Song et al., 2009, 2009). The nonparametric approach has a long history in sensory neuroscience and has been successfully applied to diverse areas such as the retina (Marmarelis and Naka, 1973), visual cortex (Rapela et al., 2006; Touryan et al., 2005), and auditory cortex (Eggermont, 1993; Slee et al., 2005).
The problem of modeling transformations between spike trains necessitates a nonlinear approach not only because this transformation is intrinsically nonlinear due to the presence of a threshold (Marmarelis et al., 1986), but also because nonlinear interactions are known to occur in the nervous system between pairs and triplets of input spikes (Dittman et al., 2000; Song et al., 2009). A powerful technique for characterizing nonlinear systems is the Volterra/Wiener functional approach which has had a long history in biological physiomodeling (Marmarelis and Marmarelis, 1978; Marmarelis, 2004). Several adaptations of this technique have been developed to solve the encoding problem, where a continuous signal is mapped onto a spike train. In particular, much attention in recent years has been given to this approach to map the receptive fields of retinal cells in the form of spike-triggered covariance (STC) (Schwartz et al., 2006). Also, several adaptations have been developed for the decoding problem which maps a spike train input to a continuous output (Van Steveninck and Bialek, 1988; Krausz, 1975; Marmarelis and Berger, 2005). In the present paper, we propose a Volterra functional style technique which is exclusively designed for systems with spike-train inputs and outputs. Although previous methods have attempted to solve this problem (Zanos et al., 2008; Song et al., 2007; Marmarelis et al., 2013), they have been, with few exceptions (Marmarelis et al., 2009), methods designed for continuous data and later applied to spike train data.
In this paper, we propose a nonparametric nonlinear Volterra-style model to describe spike train transformations. Our approach uses elementary probability theory to estimate Volterra style functionals, termed the Probability Based Volterra (PBV) kernels, which describe the nonlinear dynamical transformation between input and output spike trains. In brief, the qth order PBV kernel describes the probability of an output spike given q input spikes at various lags t1, t2, …, tq. These PBV kernels are shown to be equivalent to the Poisson–Wiener Kernels, and thus are capable of describing arbitrary finite memory nonlinear spike train transformations. The PBV method is then compared with two other methods found in the literature of estimating Volterra kernels. These methods are evaluated in terms of predictive power, convergence, overfitting, robustness to noise, and response to correlated inputs. Finally, the methods are applied to real spike train data obtained from the rodent hippocampus.
2. Methods
Nonparametric modeling approaches for point process systems aim to characterize a ‘black box’ or unknown functional which transforms the input spike train into the output spike train. Characterizing a ‘black box’ can be broken down in to the problems of model configuration and parameter estimation. In physiological systems, the problem of model configuration is further constrained by the need for such models to be physiologically plausible and prone to interpretation. Several methods exist for characterizing systems with point process inputs and outputs (Zanos et al., 2008; Song et al., 2007; Marmarelis et al., 2009, 2013). Here we chose the well-known Volterra framework to characterize our model and we developed a novel technique to estimate our Volterra kernel parameters which is customized to systems with point process inputs and outputs and is based on elementary probability theory. The Volterra kernels estimated by this technique will be referred to as the Probability Based Volterra (PBV) kernels.
2.1. Model configuration
In the Volterra functional expansion of an arbitrary nonlinear system, the system output, y[t], is described as the sum of the outputs of a series of functionals with increasing orders of nonlinearity:
| (1) |
where Fq(x[t], kq[τ1, …, τq]) is the qth order Volterra functional, which is essentially the qth order convolution of the input x[t] with the qth order Volterra kernel. It should be noted that here the kernels and input have been discretized in order to handle real data, much like in traditional spike-triggered analysis. Each Volterra functional describes interactions between up to q input spikes. For example, the first order kernel can be seen as weighing the contribution to the output of a single pulse t lags prior to the output. Thus, the first order Volterra functional describes a linear system and the first order Volterra kernel is equivalent to the well-known impulse response function. The second order Volterra functional, and the first nonlinear functional, describes second order nonlinear interactions between two input pulses, such as paired pulse facilitation and depression. Although theoretically we could construct an infinite order (Q = inf) system, in practice this is computationally impossible and physiologically unrealistic. Here, we curtail our system to a second order nonlinear system (Q = 2) as higher order nonlinearities have been shown to provide only slight improvements in modeling the nervous system (Song et al., 2007; Lu et al., 2011). Thus:
| (2) |
where is the predicted continuous output, and M is the system memory which describes how many lags of the input past affect the output. k1[τ] and k2[τ1, τ2] are the 1st and 2nd order Volterra kernels, respectively which are equivalent to the PBV kernels if estimated by the method described herein. Because the above equation will generate a continuous output and we are dealing with a point process system, we must threshold the continuous output, such that:
| (3) |
In this study, the threshold is set so that the number of spikes in the predicted spike train, yc[t], equals the number of spikes in the true spike train, y[t].
2.2. Model estimation
Several methods of estimating Volterra kernels exist in the literature. Norbert Wiener was the first to propose a method of estimating the kernels by orthogonalizing the Volterra functionals with respect to Gaussian white noise (GWN) inputs, giving rise to the well-known Wiener series (Wiener, 1966). The Wiener series was first popularized when the computationally feasible cross-correlation technique was introduced as a method of estimating the Wiener kernels (Lee and Schetzen, 1965; Marmarelis and Marmarelis, 1978). Since then several techniques have been developed which allow efficient estimation of Volterra kernels using shorter data records and arbitrary inputs. Here we develop a novel and intuitive technique for estimating the Volterra kernels for systems with point-process inputs and outputs which we call the Probability Based Volterra kernels. We later show that these kernels are essentially equivalent to the Wiener kernels specialized for point-process inputs.
The PBV kernels are estimated in a two-step process. First the qth order conditional probability kernels (CPKs) are calculated. Then the PBV kernels are obtained by removing lower order effects from the CPKs. The qth order CPK is defined as the probability of an output spike given q input spikes at t1, t2, …, tq lags prior to the output. The zeroth order CPK is defined as the probability of an output spike without any information of the input. Thus it is just the mean firing rate (MFR) of the output:
| (4) |
The first order CPK is:
| (5) |
In this section we will assume that the point process input is an uncorrelated Poisson process with rate . Later, in Section 2.4 we will show how one may partially correct the kernels for correlated/colored inputs. With this in mind, Eq. (5) becomes:
| (6) |
It should be noted that the 1st order kernel is a scaled version of traditional spike triggered average (STA) (De Boer and Kuyper, 1968). Similarly, the second order CPK is:
| (7) |
Notice that CPK2 is only defined when t1 ≠ t2, since for t1 = t2 = t, the numerator, y[t] ∩ x[t − τ] ∩ x[t − τ] reduces to y[t] ∩ x[t − τ]. Thus, CPK2 is set to 0 when t1 = t2. The same constraint applies to all higher order CPKs when any pair of lags is identical. This can also be intuitively understood by noting that the diagonal of the second order Volterra kernel describes the contribution of the square of the input pulse. Since we are dealing with binary point process signals, the square of the input equals the input, and thus the diagonal of the 2nd order kernel actually describes 1st order (linear) effects. Once again, by assuming a Poisson process input, Eq. (7) becomes:
| (8) |
Now, in order to obtain the PBV kernels lower order effects must be removed from the CPK kernels. This step can intuitively be understood since the conditional probability of a an output spike given a set of n1, n2, …, nq input spikes includes the probability of an output spike given every subset of lower order. For example, the probability of an output spike given an input spike includes the probability of an output spike firing spontaneously on its own. So, to isolate the first order dynamics, we must remove the zeroth order dynamics. Thus:
| (9) |
| (10) |
Similarly, to isolate second order effects, we must remove 0th and 1st order dynamics:
| (11) |
2.3. Relationship to Poisson–Wiener kernels
Marmarelis et al. derived the Poisson–Wiener (PW) functional expansion for arbitrary nonlinear systems with point process inputs and continuous outputs (Marmarelis and Berger, 2005). The PW kernels are obtained by orthogonalizing the system nonlinearity with respect to Poisson inputs, akin to how the Wiener kernels are obtained by orthogonalizing the system nonlinearity with respect to Gaussian white noise. However, the mathematically sophisticated derivation of the P–W kernels has limited their utilization in the broader neuroscience community. In Appendix A, we show that the PBV kernels are essentially equivalent to the PW kernels, albeit with a difference of scale:
| (12) |
| (13) |
This equivalence serves two purposes. First it establishes a solid theoretical footing for the PBV kernels on the basis of Wiener’s orthogonalization approach. Second, it provides an optimal scaling of the PBV kernels to achieve maximal predictive power. However, it should be emphasized that the PBV kernels are distinct from the PW kernels since the PW kernels are exclusively designed for systems with uncorrelated Poisson inputs and continuous outputs, while the PBV kernels are designed for systems with point-process inputs and outputs.
2.4. PBV kernels for correlated point-process inputs
Although ideally, one would probe a system with uncorrelated inputs, much work has been done in recent years to develop system estimation methods for correlated inputs. This is useful because (1) sometimes there is no opportunity to stimulate the system, and all one can do is record the naturally occurring endogenous system activity (Berger et al., 2012), and (2) much work in sensory neuroscience has shown that one can estimate a sensory neuron’s receptive field using much shorter data records by simulating the statistics of its natural stimuli, which usually have higher order statistical moments (Touryan et al., 2005).
The PBV kernels are derived for uncorrelated point-processes (i.e. Poisson processes), and would have biases if they were estimated with correlated point-process inputs. Any attempt to analytically derive PBV kernels for correlated point-processes would be extremely difficult, if not impossible, due to the ill-defined analytical nature of such processes as they are used here. Korenberg and Hunter (1990) has previously derived corrections for Wiener kernels estimated using correlated Gaussian inputs (see Appendix B). The method relies on the decomposition property of higher order moments of Gaussian processes, which does not apply to correlated point-process inputs. The main result of correction method is shown below:
| (14a) |
| (14b) |
where and K′2 are the biased/naive Wiener 1st order kernel vector and 2nd order kernel matrix estimated using correlated inputs, and K2 are the corrected Wiener kernels, and is the inverse of the Toeplitz autocorrelation matrix of x[t]. It should be noted that the correction in Eq. (14a) is identical to that derived by Theunissen et al. (2001) for STA.
Although Eq. (14) was derived for correlated Gaussian processes, we have found empirically that it can be used, with slight modification, to partially correct PBV kernels estimated from correlated point-process inputs. Namely, the modified form of Eq. (14) is:
| (15a) |
| (15b) |
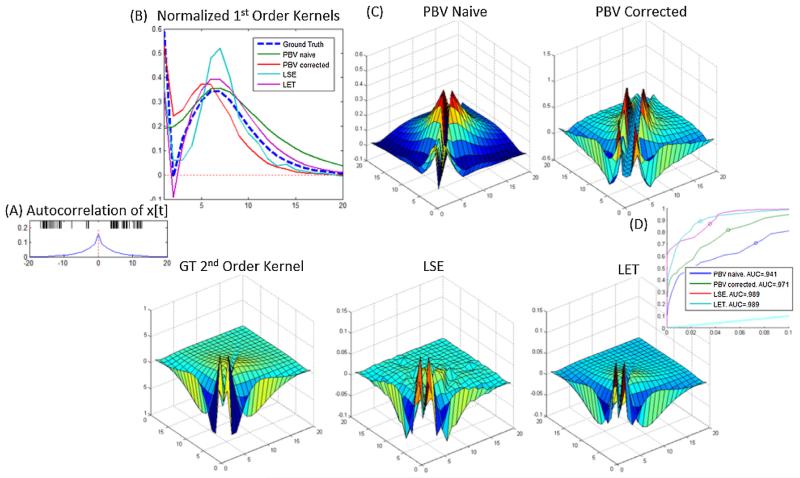
where once again the apostrophe indicates the biased PBV kernels. This correction implicitly imposes a smooth prior on the second order kernel by multiplying the true correction (Eq. (14)) with the input autocorrelation matrix. Imposing this smooth prior has been shown empirically to improve results (see Figs. 6 and 8).
Fig. 6.
Results for correlated point-process inputs. (A) Representative interval of correlated input x[t] (above) and autocorrelation of x[t] (below). (B) Ground truth and estimated 1st order kernels. Note that the naive PBV kernel fails to detect peak in the first bin. (C) Estimated ground truth and 2nd order kernels. (D) ROC plots of estimated models. Note that correction PBV kernels were able to achieve significant improvement over naive PBV kernels.
Fig. 8.
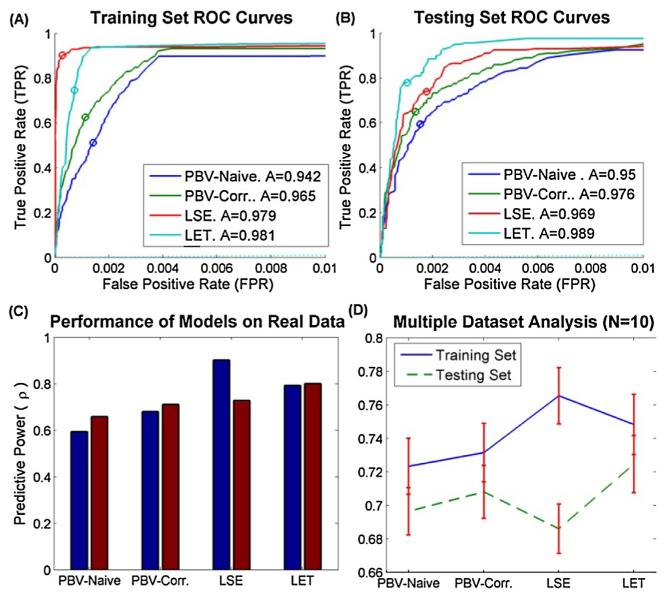
Predictive performance of models on real data. (A) Training set ROC curves (B) testing set ROC curves (C) Training and testing performance as measured by ρ. Note that LSE model has the most overfitting, while the remaining models are able to successfully avoid fitting noise. (D) Mean + SEM predictive power for N = 10 hippocampal datasets. Note that regularized LSE was used for all these cases.
2.5. Model validation
Two metric were used to evaluate the goodness-of-fit of the estimated PBV models. ROC curves, which evaluate the performance of a binary classifier, plot the true positive rate against the false positive rate over the putative range of threshold values for the continuous output, y (Zanos et al., 2008). The area under the curve (AUC) of ROC plots is used as a performance metric of the model, and has been shown to be equivalent to the Mann-Whitney two sample statistic (Hanley and McNeil, 1982). The AUC ranges from 0 to 1, with 0.5 indicating a random predictor and higher values indicating better model performance. The second metric used was the Pearson correlation coefficient, ρ, between the estimated prethreshold output, , and the true output, y[t]:
| (16) |
where is the mean of , and σy and are the variances of y[t] and respectively.
The ρ and AUC metrics were chosen as they measure the similarity between a continuous ‘prethreshold’ signal and a spike train. The continuous ‘prethreshold’ signal was chosen over adding a threshold trigger and comparing true output spike train with an output ‘postthreshold’ spike train for two reasons. First, this allows us to avoid specifying the threshold trigger value, which relies on the somewhat arbitrary tradeoff between true-positive and false-negative spikes (Marmarelis et al., 2012). Second, similarity metrics between two spike trains often require the specification of a ‘binning parameter’ to determine the temporal resolution of the metric (Victor and Purpura, 1997; van Rossum, 2001).
In order to compare the performance of the PBV model with other methods in the literature, we estimated the 2nd order Volterra model using two additional techniques. First, we estimated the kernels using the least squares estimation (LSE) technique (Korenberg et al., 1988; Marmarelis, 2004; Lu et al., 2011). This method finds the kernels which minimize by solving a matrix inversion problem. The standard LSE technique can be seen as projecting the input onto a ‘delta function basis’. An alternative, known as the ‘Laguerre expansion technique’ (LET), projects the input onto a set of L Laguerre basis functions and once again use least squares estimation to obtain the basis coefficients (Marmarelis and Orme, 1993). The Laguerre basis set, which was first suggested for use in physiological systems by Norbert Wiener Wiener (1966), is defined on [0, ∞], and is composed of increasing oscillations followed by an exponential decay, as is typical of many physiological systems. Indeed, this method, which has been successfully applied to several nonlinear physiological systems, has been shown to drastically reduce the amount of free parameters needed in the 2nd order Volterra model (Valenza et al., 2013; Kang et al., 2010; Marmarelis, 2004). In order to use the LET, one must specify the alpha parameter of the Laguerre basis functions. Here, the ground truth alpha was used for synthetic systems and no effort was made to search for alpha. In real rodent systems, alpha and L were determined by fitting the estimated 1st and 2nd order PBV kernels. This is a novel technique which has not been previously reported in the literature. An important advantage of both the LSE and LET techniques is that by solving the ‘inverse problem’ they are implicitly able to deal with correlated inputs without requiring any additional processing steps; however, this feature comes at the expense of additional computational power.
2.6. Data procurement
In this study the PBV method has been applied to both synthetic systems where ground truth is available and to real data recorded from the rodent hippocampus. In order to generate confidence bounds for the predictive power of the models when applied to synthetic data, a Monte Carlo approach was used with several trials (N = 30) of randomly generated systems. Each system was obtained by randomly generating coefficients for L = 3 Laguerre basis functions for the first and second order kernel. The output was generated by feeding a random point process input through the system and then thresholding the output so that the MFR of the output equaled the MFR of the input (i.e. ). To generate correlated point process inputs we fed GWN through a lowpass filter and then thresholded the output.
Rodent hippocampal data was collected in the labs of Dr. Deadwyler and Dr. Hampson at Wake-Forest University and has been described in detail in our previous publications (Hampson et al., 2012). Briefly, N = 10 male Long-Evans rats were trained to criterion on a two lever, spatial Delayed-NonMatch-to-Sample (DNMS) task. Spike trains were recorded in vivo with multi-electrode arrays implanted in the CA3 and CA1 regions of the hippocampus during performance of the task. Only neural activity from trials where the rat successfully completed the DNMS task was used. Spikes were sorted, time-stamped, and discretized using a 2 ms bin. Spike train data from 1 s before to 3 s after the sample presentation phase of the DNMS task was extracted and concatenated into one time series.
3. Results
3.1. Synthetic Poisson inputs
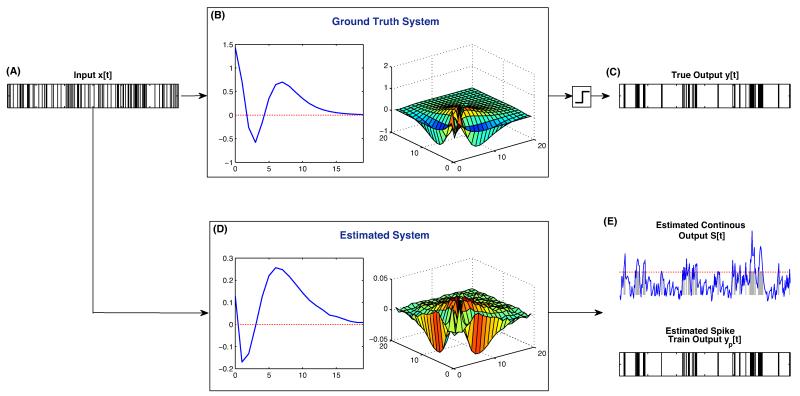
As an illustrative example consider the simulated 2nd order point process system shown in Fig. 1. Here, the input, x[t], shown in Fig. 1A is a 100,000 sample discretized Poisson process with probability of firing. This input is fed through the 2nd order Volterra system in Fig. 1B and then thresholded to generate the output y[t], shown in Fig. 1C. The input and output signals were then used to estimate the PBV kernels, shown in Fig. 1D. As can be seen, the estimated PBV kernels are able to reproduce the dominant features of the ground truth 1st and 2nd order kernels. For example, both 1st order kernels have two critical points, the first negative and the second positive, followed by an exponential decay. However, the kernels have slight differences. For example, the first critical point of the ground truth kernel occurs at bin 3, while that of the estimated kernel occurs at bin 2. These differences are not just the results of finite data records, but also due to the fact that the thresholding operator makes the system have an infinite order nonlinearity, while the PBV kernels are ‘truncated’ to the 2nd order. This truncation results in slightly biased 1st and 2nd order kernels due to their ‘absorbing’ the effects of higher order nonlinearities. As can be seen however, these biases are relatively minor. The input was fed through the estimated kernels to generate the predicted continuous output . As can be seen from Fig. 1E, the estimated prethreshold output compares quite favorably with the true spike train, y[t]. This can also be seen from the ROC plot in Fig. 2C, where the estimated PBV system had a near perfect AUC of.993. The output was then thresholded to produce the predicted spike train output, , shown in the bottom of Fig. 1E.
Fig. 1.
Representative ground truth and estimated system. Input spike train (A) is fed through the 2nd order nonlinear Volterra system, defined by the 1st and 2nd order kernels shown in (B), and then thresholded to generate the output in (C). The input and output point-process time series are then used to obtain the estimated PBV kernels shown in (D). The input is then fed through the estimated system to generate the estimated output in (E). The top plot in (E) shows the estimated continuous output () overlaid on the true output (in gray). The red vertical line shows the estimated threshold trigger value. The bottom plot in (E) shows the estimated spike-train output, . (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)
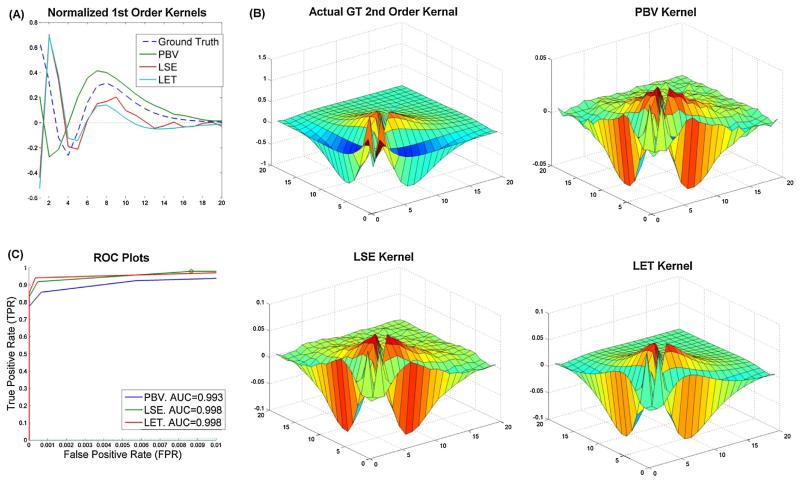
Fig. 2.
Comparison of results from 3 models for system in Fig. 1. (A) Ground truth and 3 estimated 1st order kernels. All 1st order kernels were normalized by their power to make comparison easier. Plot (B) shows the same for 2nd order kernels. Note that the diagonal of the 2nd order LET and LSE kernel was added to the 1st order kernel as these diagonals reflect 1st order dynamics (see text). (C) ROC plots for all three models. Note that the FPR (x-axis) extends only to.01 rather than 1 as in traditional ROC plots since the models were so accurate.
The 2nd order Volterra model was also estimated using the LSE and LET methods, as shown in Fig. 2. As can be seen, these methods were also able to successfully estimate the true kernels; however, like the PBV technique, they were also somewhat biased due to the absorption of higher order nonlinearities. For example, both the LSE and LET 1st order kernels had a peak in the 2nd bin which was absent from the true 1st order kernel. The LET kernels came closest to approximating the true kernels with as little noise as possible. However, this was partly because the ground truth dynamics were designed from Laguerre basis functions and the alpha parameter was known beforehand, which is rarely the case in reality. The standard LSE kernels were much more similar to the PBV kernels, albeit the LSE 1st order kernel was much noisier. Predictively, the LSE and LET techniques slightly outperformed the PBV technique (Fig. 2C), however at the expense of greater computational power (i.e. matrix inversion).
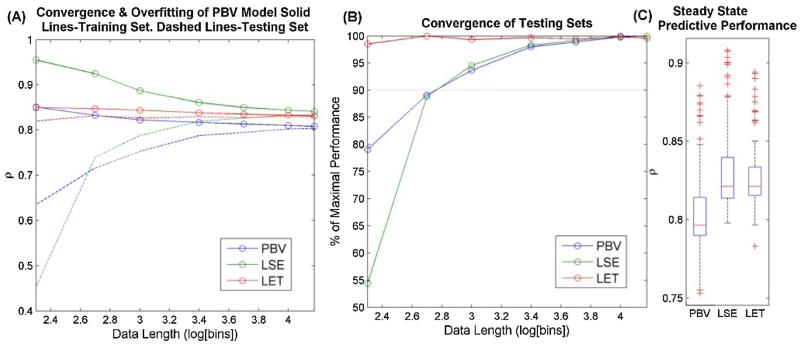
3.2. Convergence and overfitting
In experimental physiological system identification, the experimenter requires criteria to know how much data is needed to estimate a valid model. Usually, this choice is constrained by the inherent nonstationarities of physiological systems. Model convergence or ‘data hungriness’ describes the amount of data needed to successfully model the system. Overfitting describes how well the model estimated on the given dataset will generalize to other datasets acquired from the same system. Monte Carlo style simulations were performed to evaluate the convergence and overfitting properties of the three models. N = 30 trials were conducted with randomly generated synthetic systems as described in methods. For each synthetic system, the three estimation methods were applied to randomly generated training/in-sample data of various lengths from 200 to 15,000 bins. Then the predictive performance of the three estimated kernel sets was evaluated on testing/out-of-sample data of equal lengths.
The predictive power of the training and testing sets (solid and dashed lines respectively) is shown in Fig. 3 for the ρ metric. The convergence of the data is described by the shape of the testing set curve in Fig. 3A, and in particular how quickly this curve approaches a steady-state value. The LET model converges remarkably quickly, and achieves 98% of its maximal value with only 200 data points (Fig. 3B). As noted before however, this assumes that the ground truth dynamics can be expressed as a sum of L Laguerre basis functions and that the alpha parameter can be known with sufficient accuracy. The LSE and PBV kernels converge at approximately the same rate and they achieve over 90% of their maximal ρ value with 1000 data points. Overfitting is reflected by the difference in predictive power between training and testing sets. Once again the LET model has an extremely small amount of overfitting, even with extremely small data records (<4% overfitting with 200 bin data). The PBV and LSE models show more overfitting. They require 1000 data points in order to converge to >90% of their training value. The LSE model in particular is unreliable for shorter data records. In fact, for short records under 500 bins, the LSE method often failed due to ill conditioned matrices, which are common with binary data. At steady state the predictive power of the PBV, LSE, and LET models as measured by ρ was.797,.821, and.821, respectively (Fig. 3C). This confirms statistically what was seen in Fig. 2: that the PBV kernels are competitive with the LSE and LET kernels.
Fig. 3.
Convergence and overfitting analysis. Plot (A) shows the predictive power of both training (solid lines) and testing (dashed lines) sets for data of various lengths ranging from 200 to 15,000 data points. (B) The performance of the training set, normalized by its maximal (steady-state) performance. All points in A and B were averaged over N = 30 trials. (C) Boxplot of median and quartiles of steady state performance.
3.3. Model robustness
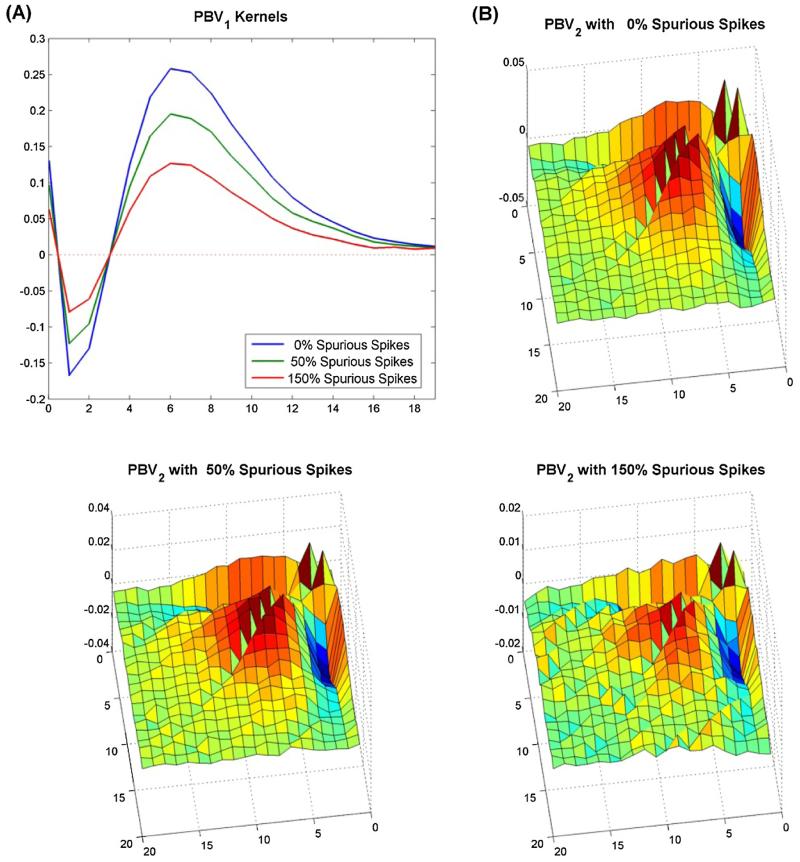
In experimental settings noise is an unavoidable reality which may arise in a variety of ways, including imperfect instrumentation and/or from unobserved inputs. Thus, any input–output model must be robust, i.e. be able to accurately estimate the underlying system even in the presence of noise. In many neuroprosthetic applications there is a large convergence of input neurons onto any given output neuron and only a small portion of these input neurons may be recorded. The unrecorded input neurons can be modeled as input noise. Thus, in order to examine the robustness of the PBV method, the PBV kernels were estimated with various amounts of spurious spikes added to the true/‘observed’ input spike train. Fig. 4 shows the estimated PBV kernels for the system in Fig. 1 with 0, 50%, and 150% spurious spikes added. As can be seen, the underlying form of the kernels remains remarkably consistent. The added noise manifests itself as high frequency ‘jitter’ in the estimated kernels rather than a change in form. This corresponds with theoretical findings that Wiener kernels are unbiased with uncorrelated Gaussian noise (Marmarelis and Marmarelis, 1978).
Fig. 4.
Degradation of PBV kernels with noise. PBV kernels were estimated for system in Fig. 1 with various amounts of spurious spikes added to the input. Degradation of 1st order kernels are shown in A, while degradation of 2nd order kernels are shown in (B).
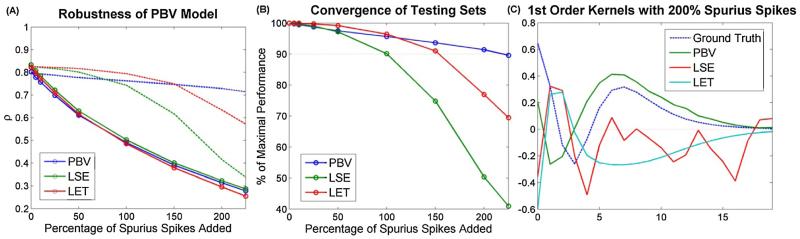
In low noise environments, the most robust model was the LET, since the kernels were confined to the Laguerre subspace and thus were immune to the high frequency jitters which permeated the PBV and LSE kernels. In high noise environments (<150% spurious input spikes), the PBV kernels proved to be the most robust since the least squares regression technique on which both the LET and LSE method rely is not well suited for input noise (Söderström, 1981). Although considering such high noise levels may seem superfluous, it is actually quite necessary in neuroprosthetic applications where the experimenter may have access to only a small handful of the hundreds of thousands of input neurons which may synapse onto the output neuron. It should be noted that although we only analyzed the robustness of the models to additive uncorrelated noise in the output, other types of noise exist including correlated noise, multiplicative noise, and output noise.
3.4. Correlated inputs
Correlated point-process inputs were generated by filtering Gaussian white noise through a lowpass filter and thresholding the filter output. The autocorrelation of x[t] is shown in Fig. 6A. The estimated naive and corrected PBV kernels are shown in Fig. 6B and C. As can be seen, the corrected PBV kernels come much closer to reproducing the ground truth kernels than the naive PBV kernels, establishing that the correction technique described in methods is indeed effective. However, the corrected PBV kernels are still far from the ground truth kernels. As mentioned previously, this is because the correction technique used is adapted from Gaussian inputs and used only heuristically with correlated point processes.
The obtained LSE and LET kernels obtained for the colored inputs are also shown in Fig. 6. No correction needs to be applied to these kernels since they solve the ‘inverse problem’ and can thus handle all types of inputs.
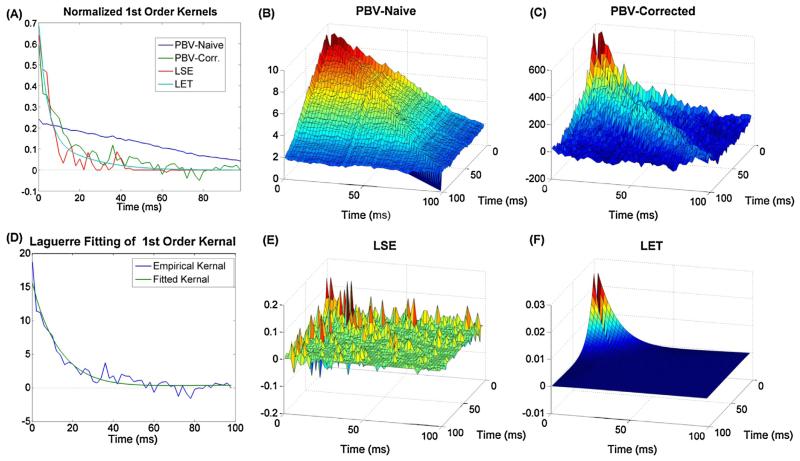
3.5. Real hippocampal data
The PBV method was applied to 10 datasets of CA3 and CA1 recordings from the rodent hippocampus (see methods). The input spike train had more power in the lower frequency ranges (<8 Hz) than higher frequency ranges and thus was not broadband/Poisson. The data was split in a training set and a testing set (33% of data). A representative example of the kernels estimated through the different estimation methods for one of the datasets is shown in Fig. 7, while the predictive power of these kernels is shown in Fig. 8A-C. The average predictive power over all datasets for training and testing sets, as measured by AUC is shown in Fig. 8D.
Fig. 7.
Estimated 1st order (A) and 2nd order (B) kernels for real rodent hippocampal data. Note ground truth is not available. (C) The results of fitting the estimated corrected 1st order PBV kernel with Laguerre basis functions. As can be seen, the parameters L = 2 and alpha = .8 gave excellent results.
As can be seen, the time-course of the decay of the 2nd order naive (non-whitened) PBV kernel is longer than that of the 2nd order whitened PBV kernel. This longer time course is the result of the correlated input biasing the estimated PBV kernel. By using the whitening technique described in section II.D, this bias is minimized. The success of the whitening method can be seen in Fig. 8, where the corrected PBV kernels clearly outperform the naive kernels. Interestingly, the PBV kernels actually performed slightly better in the testing set. This is an artifact of the inherent nonstationarities of physiological data, e.g. the selected testing interval had less noise than the training interval.
The obtained LSE kernels were found to be extremely noisy. Thus, LASSO regularization (Tibshirani, 1996) was used to limit the number of free parameters in the 2nd order kernel. Nonetheless, the obtained regularized LSE kernels, shown in Fig. 7A and D, were found to be quite noisy and difficult to interpret. This can also be seen in Fig. 8D, where the LSE kernels generalized to the testing set poorly. Notably, the LSE method had the greatest difference in predictive power between training and testing sets. This is presumably because, as shown in Fig. 5, the LSE kernels are very unreliable in environments with high levels of input noise. Rodent CA3 pyramidal cells, which are estimated to have on average 380,000 input synapses (West et al., 1991), can be presumed to have large amounts of unobserved inputs, which in the modeling context is equivalent to noise.
Fig. 5.
Robustness analysis. (A) Reduction of predictive power of models as increasing amounts of spurious spikes are added to the training set input. (B) Performance of training set normalized by their performance in noise-free environments. (C) Estimated 1st order kernels with 200% spurious spikes added to input. Notice the PBV kernel is the least affected. All points in (A) and (B) were averaged over N = 30 trials.
Although the LET also relies on least squares estimation, by confining the kernels to the Laguerre basis space, the LET avoids many of the issues of the LSE technique. In order to obtain good results with the LET technique, however, two conditions must be met: the underlying system dynamics must be expressible with Laguerre basis functions and the alpha and L parameters must be known with sufficient accuracy. Both of these conditions were satisfied by first fitting the obtained PBV kernels with Laguerre basis functions and selecting an ideal alpha and L. As can be seen in Fig. 7C, the PBV kernels can be excellently fit with alpha = 0.8 and L = 2. The LET was then used with these parameters to calculate the kernels shown in Fig. 7A and B. As can be seen in Fig. 8D, the obtained LET kernels gave the best results for both the training and testing set data.
The obtained corrected PBV and LET kernels were found to be very similar. Both 1st order kernels show an excitatory effect of the input onto the output with a time constant of roughly 30 ms. Furthermore, both showed strong 2nd order nonlinear facilitatory effects. This 2nd order facilitation corresponds to the well-studied short-term potentiation (STP) or paired-pulse facilitation commonly seen in neural systems. This phenomena has been studied previously in the context of nonlinear Volterra modeling (Song et al., 2009, 2009).
4. Discussion
In this paper, we have proposed and demonstrated the efficacy of the PBV methodology for modeling point-process single-input single-output systems such as those found in the nervous system. The PBV kernels are derived in a novel and intuitive way using elementary probability theory, which will hopefully make them more accessible to the broader neuroscience community, which is largely unfamiliar with nonlinear systems theory. The PBV kernels are obtained using a nonparametric/data-driven approach, which is ideal for situations where a priori information about the system cannot be assumed. Such situations commonly occur in neuroprosthetics which record/stimulate arbitrary neurons without knowing their anatomical connectivity. The only assumption of the PBV method is that the system under question be stationary and have finite memory.
The PBV method has shown itself to be remarkably robust to noise. Even with 150% spurious spikes in the input spike train (i.e. only 40% of true input spike train is observed), the estimated PBV kernels have shown only minor decreases in performance (see Fig. 4, 5). The PBV method has also been shown to have good convergence properties. Although the exact rate of convergence of any point-process model depends on the MFR rather than the recording length, we have shown that with synthetic systems of Poisson rate parameter of 0.2, the PBV kernels give excellent results with only 1000 data points, and with real hippocampal systems the PBV kernels achieved adequate performance with only 3 min of recording.
The PBV method was compared with two other previously used methods to model point process systems: the least squares estimation method and the Laguerre expansion technique. The PBV method is most naturally compared with the LSE method since both models have the same number of parameters and do not constrain the kernels to any fixed basis space as the LET method does. The LSE kernels had slightly better predictive power in noise-free synthetic systems (Fig. 3); however, they were shown to perform poorly in simulations featuring high input noise (Fig. 5). This failing was confirmed in real rodent hippocampal data where the 2nd order regularized LSE kernel had a high amount of jitter and was difficult to interpret (Figs. 7 and 8). Additionally, the PBV kernels can be estimated for Poisson inputs using much less computational power since they do not solve the inverse problem.
The LET kernels, like the LSE kernels minimize mean squared error (MSE); however, while the LSE kernels can be viewed as expanding the input on a basis of delayed delta functions, the LET method expands the input on a set of L Laguerre polynomials, whose rate of exponential decay depends on the alpha parameter. It should be noted that when alpha = 0 (i.e. immediate decay), the LET kernels become equivalent to the LSE kernels (Valenza et al., 2013). The LET kernels outperformed the other two models with regard to predictive power, convergence, and overfitting. However, the use of the LET technique assumes (1) that the underlying dynamics can be expressed by the sum of L Laguerre polynomials and (2) the alpha and L parameters can be known with sufficient accuracy. Examples of where the 1st assumption would fail include systems with high order nonlinearities such as a sigmoid (see discussion below) or systems with both fast and slow dynamics (Mitsis and Marmarelis, 2002; Mitsis et al., 2002). In these cases, the PBV method would be preferred over the basic LET method. In cases where the first assumption is met, such as rodent hippocampal CA3→CA1 dynamics (Song et al., 2007; Zanos et al., 2008), the PBV method can be used to estimate the alpha and L parameters which are required for proper use of the LET method. In previous work, these parameters were estimated using a global search (Lu et al., 2011). Here, we have shown that these parameters can be found more efficiently by first estimating the PBV kernels, which require no parameters, and then fitting the obtained PBV kernels with Laguerre polynomials to optimize for alpha and L (Fig. 7C). As another example, the LET kernels in Fig. 6 were reestimated using the alpha and L parameters obtained through this method. The predictive power of the kernels with estimated parameters differed from that of the kernels with ground truth parameters by less than 4%. Thus, the PBV and LET methods can be combined synergistically to maximize performance.
It should be noted that characterizing the nonlinear transformation between sets of neurons is conceptually very similar to the goal of identifying the receptive fields of sensory neurons such as V1 cells and auditory cells, which falls under the ‘encoding problem’ mentioned earlier. The main difference is that sensory neurons are assumed to transduce continuous stimuli from the outside world such as light and sound, whereas the neurons modeled here are assumed to only transduce the spiking history of their input neuron. Mathematically, the receptive field identification problem takes the form of identifying a function which maps a continuous stimulus onto a binary spike train, while the systems identification problem maps a binary spike onto another binary spike train. This difference is significant in our context as the probabilistic framework for estimating the Volterra kernels presented here is inapplicable with continuous inputs. Although they are not explicitly compared, the PBV method has many similarities to reverse correlation methods used in receptive field identification such as spike triggered averaging (STA) and spike triggered covariance (STC) (De Boer and Kuyper, 1968; Van Steveninck and Bialek, 1988; Schwartz et al., 2006). In fact, the first order PBV kernel is identical to the STA (albeit with a difference in scale). The second order kernel however is distinct from the STC covariance matrix, as the former is formed from the average value of the output with two input spikes at various lags, while the latter is the covariance of the STA matrix. Furthermore, in STC analysis, the covariance matrix is only an intermediate step in acquiring the set of linear filters of a system.
A 2nd order PBV model characterizes the response of a system to all pairs of input spikes at all temporal separations. This includes many well-known phenomena in nervous systems such as facilitation and depression, which are both under the umbrella category of short-term potentiation (STP). This motivated applying the PBV method to data recorded from the CA3 and CA1 regions of the rodent hippocampus, where STP is well known to occur and has been ascribed to accumulation of residual calcium and vesicle depletion in the presynaptic terminal (Liley and North, 1953; Katz and Miledi, 1968; Betz, 1970). As hypothesized, non-linear 2nd order effects were found in the form of facilitation. The observed facilitation justifies the utility of using nonlinear dynamical models when studying the nervous system, as opposed to linear dynamical models which are unable to describe such phenomena. It should be noted that Song et al. (2007) showed 3rd order nonlinear effects in the hippocampus which could in theory be modeled by the 3rd order PBV kernel. However, including the 3rd order kernel showed only minor improvements in predictive power and estimating the 3rd order kernel would require much longer data records. Finally, we should note that while in this paper the PBV method was applied to neuron action potential data, the method can be used to model arbitrary point process systems including highway traffic data (Alfa and Neuts, 1995; Krausz, 1975), heartbeat dynamics (Barbieri et al., 2005), and communications data (Frost and Melamed, 1994).
One fundamental limitation of the PBV approach is that it is designed for systems whose underlying dynamics can be characterized by a 2nd order Volterra series. This excludes a large number of systems such as neural networks which have a sigmoid non-linearity (Bishop et al., 2006). Furthermore, the 2nd order kernel, which is 2-dimensional can often be challenging to interpret, which is essential in biological physiomodeling. One solution is the Principal Dynamic Mode (PDM) approach which decomposes the 2nd order Volterra series into a Wiener cascade composed of a linear filterbank (the PDMs) followed by a static nonlinearity in a manner similar to what is done in STC analysis (Marmarelis, 2004). The PDMs are chosen as the most efficient linear basis set of the system. In SISO systems, the PDMs can be thought of as the eigenvectors of the combined 1st and 2nd order kernel matrix. For point-process systems, histogram based approaches have been successfully used to estimate the static nonlinearity. This allows the static nonlinearity to take on any arbitrary shape, including sigmoidal, and thus allow the estimated PDM model to cover a much broader set of nonlinear systems. Furthermore, the 1-dimensional nature of the PDMs makes them much more prone to interpretation than the kernel approach. In conclusion, with little additional computational power, the estimated PBV model can be converted into the more powerful and interpretable PDM model, as will be done in future work. Additionally, in future work the current model will be expanded to cover systems with multiple inputs, in a manner similar to how Wiener kernels were expanded for multiple inputs (Marmarelis and Naka, 1974).
HIGHLIGHTS.
PBV kernels are novel and intuitive way of modeling point-process systems.
PBV kernels gave excellent results for synthetic and real datasets from rodent hippocampus.
PBV kernels may be used synergistically with LET kernels to maximize performance.
Acknowledgements
This work was supported by NIH grant P41-EB001978 to the Biomedical Simulations Resource at the University of Southern California and DARPA contract N66601-09-C-2081.
Appendix A. Relation of PBV kernels with Poisson–Wiener kernels
Here we will show the equivalence between PBV kernels and the Poisson–Wiener kernels derived in Marmarelis and Berger (2005). The 0th PW kernel is exactly equivalent to the 0th PBV kernel, i.e.:
| (A.1) |
The 1st PW kernel is defined as:
| (A.2) |
where z[t] is the demeaned Poisson input, i.e. and μ2 is the variance of z[t], i.e.:
| (A.3) |
Thus, PW1 is:
| (A.4) |
This is exactly Eq. (11) in the text. Like the 2nd order PBV kernel, the 2nd order PW kernel is undefined for t1 = t2. For t1 ≠ t2, the second order PW kernel is:
| (A.5) |
Once again, the 2nd order PW kernel can be shown to be a scaled version of the 2nd order PBV kernel:
| (A.6) |
where in the above derivations, , , and were used respectively to represent y[t], x[t − τ1], and x[t − τ2] in order to promote clarity.
Appendix B. Derivation of Wiener kernels for correlated Gaussian inputs
In this section, we show how to correct the Wiener kernel estimated using the cross-correlation technique (Lee and Schetzen, 1965) from correlated Gaussian inputs. Namely, the biased Wiener kernel must be deconvolved with the autocorrelation matrix of the input. The proof will follow along the lines of that shown in Marmarelis and Marmarelis (1978) and Korenberg and Hunter (1990). Furthermore, it will be shown where exactly the proof breaks down for correlated point-process inputs.
To begin, we will assume that the arbitrary nonlinear functional which transforms the input time-series x[t] into the output time-series y[t] can be expressed in the form of a Volterra series:
| (B.1) |
where {kq} are the set of Volterra kernels, {Gq} are the set of Volterra functionals, and x[t] is an arbitrary zero-mean correlated random process. Later it will be shown what the implications are if x[t] is a correlated Gaussian process or a correlated point-process. For the purpose of this proof, we will assume a quadratic nonlinearity (Q = 2). This assumption has been shown to be quite reasonable in most cases, including point-process systems (Marmarelis et al., 1986; Marmarelis, 2004).
As a preliminary to the main proof, we will first derive the expected mean of the output y[t]:
| (B.2) |
Now, the middle term is 0 since x[t] is zero-mean, giving:
| (B.3) |
We begin the proof by defining the 2nd order cross-correlation, which is essentially equivalent to the 2nd order Wiener kernel (Lee and Schetzen, 1965)
| (B.4) |
where y0[t] is the demeaned output (i.e. ). Eq. (B.4) is then expanded as:
| (B.5) |
The definition of y[t] from Eq. (B.1) is now substituted into Eq. (B.5):
| (B.6) |
Eq. (B.6) can then be simplified by substituting Eq. (B.2) and noticing that the 1st terms cancel out, thus resulting in:
| (B.7) |
At this point we can see the difference between correlated Gaussian processes and correlated point-processes. The latter are mathematically ill-defined and thus their higher-order moments cannot be simplified any further analytically. Gaussian processes, however, are entirely defined by their 2nd order moments. Thus, very nice simplification properties exist for higher order moments of Gaussians (Marmarelis and Marmarelis, 1978). All odd order moments of Gaussians are zero so the first term of Eq. (B.7) vanishes. Furthermore, fourth order moments of Gaussians can be simplified via the Gaussian decomposition property (Marmarelis and Marmarelis, 1978). Thus, Eq. (B.7) becomes:
| (B.8) |
This is our final results and shows that the 2nd order cross correlation of a correlated Gaussian input and the output is the 2d convolution between the input autocorrelation matrix and the 2nd order Wiener kernel. Thus, the unbiased Wiener kernel can be attained by multiplying the biased Wiener kernel (which is defined by the second order cross-correlation of Eq. (B.4)), K2, with the inverse of the Toeplitz autocorrelation matrix, Φx (Korenberg and Hunter, 1990):
| (B.9) |
where is the corrected 2nd order Wiener kernel.
Empirically, for point-process systems it was found that a modified form of Eq. (B.9) gives better results (see Section 2.4):
| (B.10) |
References
- Alfa AS, Neuts MF. Modelling vehicular traffic using the discrete time Markovian arrival process. Transp Sci. 1995;29(2):109–17. [Google Scholar]
- Barbieri R, Matten EC, Alabi AA, Brown EN. A point-process model of human heart-beat intervals: new definitions of heart rate and heart rate variability. Am J Physiol Heart Circ Physiol. 2005;288(1):H424–35. doi: 10.1152/ajpheart.00482.2003. [DOI] [PubMed] [Google Scholar]
- Berger TW, Song D, Chan RH, Marmarelis VZ, LaCoss J, Wills J, et al. A hippocampal cognitive prosthesis: multi-input, multi-output nonlinear modeling and VLSI implementation. IEEE Trans Neural Syst Rehabil Eng. 2012;20(2):198–211. doi: 10.1109/TNSRE.2012.2189133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betz W. Depression of transmitter release at the neuromuscular junction of the frog. J Physiol. 1970;206(3):629. doi: 10.1113/jphysiol.1970.sp009034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop CM, et al. Pattern recognition and machine learning. Vol. 1. Springer; New York: 2006. [Google Scholar]
- Dayan P, Abbott LF. Theoretical neuroscience. The MIT Press; Cambridge, MA: 2001. [Google Scholar]
- De Boer E, Kuyper P. Triggered correlation. IEEE Trans Biomed Eng. 1968;3:169–79. doi: 10.1109/tbme.1968.4502561. [DOI] [PubMed] [Google Scholar]
- Di GJ, Gong W, Haburcakova C, Kögler V, Carpaneto J, Genovese V, et al. Development of a closed-loop neural prosthesis for vestibular disorders. J Autom Control. 2010;20(1):27–32. [Google Scholar]
- Dittman JS, Kreitzer AC, Regehr WG. Interplay between facilitation, depression, and residual calcium at three presynaptic terminals. J Neurosci. 2000;20(4):1374–85. doi: 10.1523/JNEUROSCI.20-04-01374.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eggermont JJ. Wiener and Volterra analyses applied to the auditory system. Hear Res. 1993;66(2):177–201. doi: 10.1016/0378-5955(93)90139-r. [DOI] [PubMed] [Google Scholar]
- Frost VS, Melamed B. Traffic modeling for telecommunications networks. IEEE Commun Mag. 1994;32(3):70–81. [Google Scholar]
- Hampson RE, Gerhardt GA, Marmarelis V, Song D, Opris I, Santos L, et al. Facilitation and restoration of cognitive function in primate prefrontal cortex by a neuroprosthesis that utilizes minicolumn-specific neural firing. J Neural Eng. 2012;9(5):056012. doi: 10.1088/1741-2560/9/5/056012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, et al. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006;442(7099):164–71. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- Kang EE, Zalay OC, Cotic M, Carlen PL, Bardakjian BL. Transformation of neuronal modes associated with low-Mg2+/high-K+ conditions in an in vitro model of epilepsy. J Biol Phys. 2010;36(1):95–107. doi: 10.1007/s10867-009-9144-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz B, Miledi R. The role of calcium in neuromuscular facilitation. J Physiol. 1968;195(2):481–92. doi: 10.1113/jphysiol.1968.sp008469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korenberg MJ, Hunter IW. The identification of nonlinear biological systems: Wiener kernel approaches. Ann Biomed Eng. 1990;18(6):629–54. doi: 10.1007/BF02368452. [DOI] [PubMed] [Google Scholar]
- Korenberg M, Bruder S, Mcllroy P. Exact orthogonal kernel estimation from finite data records: extending Weiner’s identification of nonlinear systems. Ann Biomed Eng. 1988;16(2):201–14. doi: 10.1007/BF02364581. [DOI] [PubMed] [Google Scholar]
- Krausz HI. Identification of nonlinear systems using random impulse train inputs. Biol Cybern. 1975;19(4):217–30. [Google Scholar]
- Lee Y, Schetzen M. Measurement of the Wiener kernels of a non-linear system by cross-correlation. Int J Control. 1965;2(3):237–54. [Google Scholar]
- Liley A, North K. An electrical investigation of effects of repetitive stimulation on mammalian neuromuscular junction. J Neurophysiol. 1953;16(5):509–27. doi: 10.1152/jn.1953.16.5.509. [DOI] [PubMed] [Google Scholar]
- Loeb GE, Peck RA, Moore WH, Hood K. BION system for distributed neural prosthetic interfaces. Med Eng Phys. 2001;23(1):9–18. doi: 10.1016/s1350-4533(01)00011-x. [DOI] [PubMed] [Google Scholar]
- Loeb GE. Cochlear prosthetics. Annu Rev Neurosci. 1990;13(1):357–71. doi: 10.1146/annurev.ne.13.030190.002041. [DOI] [PubMed] [Google Scholar]
- London M, Häusser M. Dendritic computation. Annu Rev Neurosci. 2005;28:503–32. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]
- Lu U, Song D, Berger TW. Nonlinear dynamic modeling of synaptically driven single hippocampal neuron intracellular activity. IEEE Trans Biomed Eng. 2011;58(5):1303–13. doi: 10.1109/TBME.2011.2105870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marmarelis V, Berger T. General methodology for nonlinear modeling of neural systems with Poisson point-process inputs. Math Biosci. 2005;196(1):1–13. doi: 10.1016/j.mbs.2005.04.002. [DOI] [PubMed] [Google Scholar]
- Marmarelis PZ, Marmarelis VZ. Analysis of physiological systems: the white-noise approach. 1978 [Google Scholar]
- Marmarelis PZ, Naka K. Nonlinear analysis and synthesis of receptive-field responses in the catfish retina. I. Horizontal cell leads to ganglion cell chain. J Neurophysiol. 1973;36(4):605–18. doi: 10.1152/jn.1973.36.4.605. [DOI] [PubMed] [Google Scholar]
- Marmarelis PZ, Naka K-I. Identification of multi-input biological systems. IEEE Trans Biomed Eng. 1974;(2):88–101. doi: 10.1109/TBME.1974.324293. [DOI] [PubMed] [Google Scholar]
- Marmarelis V, Orme M. Modeling of neural systems by use of neuronal modes. IEEE Trans Biomed Eng. 1993;40(11):1149–58. doi: 10.1109/10.245633. [DOI] [PubMed] [Google Scholar]
- Marmarelis V, Citron M, Vivo C. Minimum-order Wiener modelling of spike-output systems. Biol Cybern. 1986;54(2):115–23. doi: 10.1007/BF00320482. [DOI] [PubMed] [Google Scholar]
- Marmarelis VZ, Zanos TP, Berger TW. Boolean modeling of neural systems with point-process inputs and outputs. Part I: Theory and simulations. Ann Biomed Eng. 2009;37(8):1654–67. doi: 10.1007/s10439-009-9736-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marmarelis V, Shin D, Hampson R, Deadwyler S, Song D, Berger T. Design of optimal stimulation patterns for neuronal ensembles based on Volterra-type hierarchical modeling. J Neural Eng. 2012;9(6):066003. doi: 10.1088/1741-2560/9/6/066003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marmarelis VZ, Shin DC, Song D, Hampson RE, Deadwyler SA, Berger TW. Nonlinear modeling of dynamic interactions within neuronal ensembles using principal dynamic modes. J Comput Neurosci. 2013;34(1):73–87. doi: 10.1007/s10827-012-0407-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marmarelis VZ. Nonlinear dynamic modeling of physiological systems. Wiley-Interscience; 2004. [Google Scholar]
- Mitsis G, Marmarelis V. Modeling of nonlinear physiological systems with fast and slow dynamics. I. Methodology. Ann Biomed Eng. 2002;30(2):272–81. doi: 10.1114/1.1458591. [DOI] [PubMed] [Google Scholar]
- Mitsis G, Zhang R, Levine B, Marmarelis V. Modeling of nonlinear physiological systems with fast and slow dynamics. II. Application to cerebral autoregulation. Ann Biomed Eng. 2002;30(4):555–65. doi: 10.1114/1.1477448. [DOI] [PubMed] [Google Scholar]
- Rapela J, Mendel JM, Grzywacz NM. Estimating nonlinear receptive fields from natural images. J Vis. 2006;6(4):11. doi: 10.1167/6.4.11. [DOI] [PubMed] [Google Scholar]
- Söderström T. Identification of stochastic linear systems in presence of input noise. Automatica. 1981;17(5):713–25. [Google Scholar]
- Schwartz O, Pillow JW, Rust NC, Simoncelli EP. Spike-triggered neural characterization. J Vis. 2006;6(4):13. doi: 10.1167/6.4.13. [DOI] [PubMed] [Google Scholar]
- Slee SJ, Higgs MH, Fairhall AL, Spain WJ. Two-dimensional time coding in the auditory brainstem. J Neurosci. 2005;25(43):9978–88. doi: 10.1523/JNEUROSCI.2666-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song D, Chan RH, Marmarelis VZ, Hampson RE, Deadwyler SA, Berger TW. Nonlinear dynamic modeling of spike train transformations for hippocampal-cortical prostheses. IEEE Trans Biomed Eng. 2007;54(6):1053–66. doi: 10.1109/TBME.2007.891948. [DOI] [PubMed] [Google Scholar]
- Song D, Marmarelis VZ, Berger TW. Parametric and non-parametric modeling of short-term synaptic plasticity. Part I: Computational study. J Comput Neurosci. 2009;26(1):1–19. doi: 10.1007/s10827-008-0097-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song D, Wang Z, Marmarelis VZ, Berger TW. Parametric and non-parametric modeling of short-term synaptic plasticity. Part II: Experimental study. J Comput Neurosci. 2009;26(1):21–37. doi: 10.1007/s10827-008-0098-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theunissen FE, David SV, Singh NC, Hsu A, Vinje WE, Gallant JL. Estimating spatiotemporal receptive fields of auditory and visual neurons from their responses to natural stimuli. Netw Comput Neural Syst. 2001;12(3):289–316. [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc B Methodol. 1996:267–88. [Google Scholar]
- Touryan J, Felsen G, Dan Y. Spatial structure of complex cell receptive fields measured with natural images. Neuron. 2005;45(5):781–91. doi: 10.1016/j.neuron.2005.01.029. [DOI] [PubMed] [Google Scholar]
- Valenza G, Citi L, Scilingo E, Barbieri R. Point-process nonlinear models with Laguerre and Volterra expansions: instantaneous assessment of heartbeat dynamics. 2013 [Google Scholar]
- van Rossum MC. A novel spike distance. Neural Comput. 2001;13(4):751–63. doi: 10.1162/089976601300014321. [DOI] [PubMed] [Google Scholar]
- Van Steveninck RDR, Bialek W. Real-time performance of a movement-sensitive neuron in the blowfly visual system: coding and information transfer in short spike sequences. Proc R Soc Lond B Biol Sci. 1988;234(1277):379–414. [Google Scholar]
- Victor JD, Purpura KP. Metric-space analysis of spike trains: theory, algorithms and application. Netw Comput Neural Syst. 1997;8(2):127–64. [Google Scholar]
- Weiland JD, Cho AK, Humayun MS. Retinal prostheses: current clinical results and future needs. Ophthalmology. 2011;118(11):2227–37. doi: 10.1016/j.ophtha.2011.08.042. [DOI] [PubMed] [Google Scholar]
- West MJ, Slomianka L, Gundersen HJ. Unbiased stereological estimation of the total number of neurons in the subdivisions of the rat hippocampus using the optical fractionator. Anat Rec. 1991;231(4):482–97. doi: 10.1002/ar.1092310411. [DOI] [PubMed] [Google Scholar]
- Wiener N. Nonlinear problems in random theory. The MIT Press; Cambridge, MA: Aug, 1966. p. 142. ISBN 0-262-73012-X. [Google Scholar]
- Wolpaw JR, McFarland DJ. Control of a two-dimensional movement signal by a noninvasive brain–computer interface in humans. Proc Natl Acad Sci U S A. 2004;101(51):17849–54. doi: 10.1073/pnas.0403504101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanos TP, Courellis SH, Berger TW, Hampson RE, Deadwyler SA, Marmarelis VZ. Nonlinear modeling of causal interrelationships in neuronal ensembles. IEEE Trans Neural Syst Rehabil Eng. 2008;16(4):336–52. doi: 10.1109/TNSRE.2008.926716. [DOI] [PMC free article] [PubMed] [Google Scholar]