Hippocampal-neocortical functional reorganization underlies children's cognitive development

Abstract

The importance of the hippocampal system for rapid learning and memory is well recognized, but its contributions to a cardinal feature of children's cognitive development – the transition from procedure-based to memory-based problem solving strategies – are unknown. Here we show that the hippocampal system is pivotal to this strategic transition. Longitudinal fMRI in children, ages 7 to 9, revealed that the transition from use of counting to memory-based retrieval parallels increased hippocampal and decreased prefrontal-parietal engagement during arithmetic problem solving. Critically, longitudinal improvements in retrieval strategy use were predicted by increased hippocampal-neocortical functional connectivity. Beyond childhood, retrieval strategy use continued to improve through adolescence into adulthood, and was associated with decreased activation but more stable inter-problem representations in the hippocampus. Our findings provide novel insights into the dynamic role of the hippocampus in the maturation of memory-based problem solving, and establish a critical link between hippocampal-neocortical reorganization and children's cognitive development.

Children's cognitive development is analogous to “overlapping waves”¹, whereby advances are not characterized by broad and abrupt shifts from one stage of thinking to another, but rather by changes in the distributions of strategies children use for problem solving. At any given time, children have multiple approaches available to them: They may solve one addition problem by counting on their fingers and retrieve the answer to the next. The maturation of problem solving skills is characterized by a gradual decrease in the use of inefficient procedures such as counting and an increase in the use of memory-based strategies^1-4. It has been thought that this transition occurs because the use of embodied procedures can facilitate the development of more advanced and efficient memory-based approaches, a key feature of expertise especially at early phase of knowledge acquisition^{1, 3}. This pattern of strategy shifts has been found in children's arithmetic, spelling, reasoning, and social problem solving, among others^{5, 6}, but our understanding of the underlying neurodevelopmental processes is still in its infancy. At a behavioral level, the strategy shifts have been especially well characterized for numerical problem solving^{1, 5, 7}, making this domain an ideal model for studying the brain systems that underlie the general pattern of strategy shifts that characterizes children's cognitive development.

Early elementary school represents a critical period for the acquisition and mastery of arithmetic fact knowledge. Two decades of behavioral studies in children have demonstrated that a shift to memory-based problem solving is a hallmark of children's cognitive development in arithmetic as well as other domains^{1, 3, 4}. Use of memory-based approaches to solve addition problems predicts children's later achievement in mathematics and children with dyscalculia do not fully transition to use of memory-based strategies^8-10. Even children without dyscalculia show substantial variation in their transition to memory-based problem solving⁷, but nothing is known about the neural mechanisms that support more rapid gains in some children and slower gains in others. Importantly, arithmetic problem solving engages multiple neurocognitive systems, but the extent to which one region or another is engaged within these systems varies with children's degree of competence in the domain^{1, 9, 10}. Thus, longitudinal designs spanning the shift from procedure-based to memory-based strategies are critical for advancing our understanding of the brain systems pivotal to this transition^{9, 10}.

The brain systems that contribute to numerical competence include numerical and quantity representation systems anchored in core parietal circuits^{2, 11, 12}, and working memory systems in fronto-parietal cortices for active maintenance and manipulation of discrete quantities^{7, 13, 14}. Notably, recent studies in children have begun to emphasize neurodevelopmental models that go beyond parietal circuits foundational to numerical processing in adults. In particular, the hippocampal system appears to be critical for children's mathematics learning in ways that are not evident in adults who have mastered basic skills^{15, 16}. But there have been no investigations into the mechanisms by which the functional reorganization and refinement of neural activity patterns in the hippocampus, and its associated cortical circuits, contribute to the development of memory-based problem solving skills.

Although the hippocampus is known to play a central role in memory for individual stimuli such as words and pictures ¹⁷, its role in the early phase of knowledge acquisition in academic domains such as mathematics and language remains unknown. Influential models of memory formation posit that the hippocampal system fosters the gradual establishment of long-lasting knowledge represented in the neocortex, through its role in rapid learning and integration of new information into existing knowledge schema^18-20. In this view, the hippocampus plays a critical, but time-limited, role in the early phase of knowledge acquisition, and this hippocampal dependence is reduced following reconfiguration of neocortical connections and stabilization of newly acquired knowledge – a process referred to as consolidation^{18, 21}. Evidence for this model is primarily based on animal studies¹⁹, and how such mechanisms operate in humans, in particular during children's early learning, is unknown. Notably, no studies have investigated how the hippocampus supports the longitudinal shift from counting to memory-based problem solving in each child and whether its involvement is limited to the early phase of skill acquisition. Based on the “overlapping waves” model of cognitive development, we hypothesized that the emergence of memory-based problem solving would be associated with functional reorganization of the hippocampalneocortical system.

An important open question in developmental cognitive neuroscience is how newly acquired labile skills and knowledge are transformed into more stable representations^{5, 18}. Localization of brain activation has been the mainstay of approaches for examining functional reorganization with learning. This approach has provided useful information about the engagement of specific brain areas during problem solving, but it offers limited insights into the stability of the underlying neural representations. To mitigate this limitation we use novel trial-by-trial multivoxel pattern stability analyses^{22, 23} to investigate how neural representations of individual problems get refined with shifts to memory-based problem solving. We hypothesized that the hippocampal system would show more stable inter-problem representations with the continued development of memory-based problem solving during adolescence and adulthood.

Here we test these hypotheses by integrating longitudinal and cross-sectional fMRI and behavioral strategy assessment of arithmetical problem solving in 28 typically-developing children (ages 7–9) at two time points over a 1.2-year period, 20 adolescents (ages 14–17), and 20 adults (ages 19–22) (Fig. 1a-b; Table S1). We focused on arithmetic problem solving, because, as noted, strategy transitions in this domain are well understood and occur prominently within the age ranges we assessed in the longitudinal component. Participants’ problem solving was assessed using a well-validated trial-by-trial measure which classified strategies based on self-report and experimenter observation^{24, 25} (Online Methods). We conducted two fMRI experiments: one involving a block design to maximize efficiency and sensitivity²⁶ for examining overall task-related brain activation and connectivity associated with the transitions to memory-based strategies, and second, an event-related design to capture multivoxel activation patterns between arithmetic problems using innovative trial-by-trial stability analysis^{22, 27}. The two-fMRI tasks provided complementary information about the maturation of brain response, connectivity and stable inter-problem representations. Consistent with our hypotheses, children's use of memory-based strategies increased and use of counting strategies decreased over the 1.2-year interval, a pattern that continued into adolescence and adulthood. In parallel, we observed significant functional reorganization of the MTL-neocortical system, characterized by changes in hippocampal activation, functional connectivity and inter-problem representation stability. Our findings provide the first evidence for the emergence of fine-tuned hippocampal-neocortical circuits and stable brain representations leading to adult-like memory-based problem solving skills, and establish a novel link between hippocampal-neocortical systems and a cardinal feature of children's cognitive development.

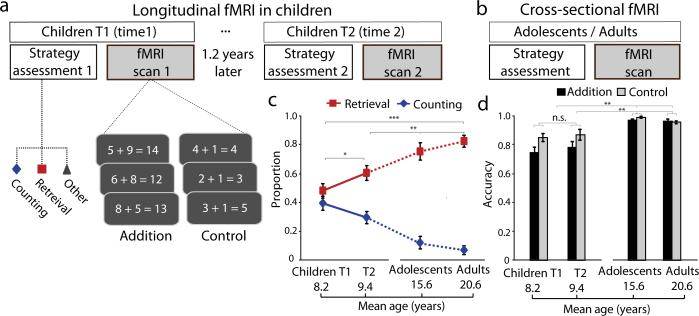
Fig. 1. Experimental design and behavioral results.

(a) For the longitudinal fMRI study, twenty-eight young children participated twice, first at Time-1 (T1) and then 1.2 years later at Time-2 (T2). Each child performed two arithmetic problem solving tasks involving single-digit addition. The first task involved verbal production of the answer, during which problem solving strategies were assessed, on a trial-by-trial basis (online Methods), outside the scanner. Based on the child's self-report and experimenter observations, the use of strategies for solving each problem was classified into counting or retrieval. The second task involved verification of whether an answer presented with an arithmetic problem was correct or not and was performed during fMRI scanning. The control task involved “n + 1” problems that are generally solved using a classic rule-based strategy with minimal changes in strategy shifts with development. (b) For the cross-sectional fMRI study, the same strategy assessment and fMRI tasks were performed by an additional group of 20 adolescents and 20 adults. (c) Developmental changes in the mix of strategies used for solving arithmetic problems, showing a gradual increase in memory-based retrieval and decrease in use of counting strategies. Solid lines represent data at T1 and T2 in children, and dotted lines represent data from adolescents and adults. (d) Developmental changes in task performance during fMRI from childhood through adolescence into adulthood. Notes: *P<0.05; ** P<0.01; ***P<0.001. Error bars represent standard error of mean throughout the whole manuscript.

Results

Longitudinal changes in strategy use during childhood, and further development through adolescence into adulthood

Longitudinal changes in children's problem solving between ages 7–9 involved increased use of memory-based strategies (t(27)=2.43, P=0.02) and decreased use of counting strategies (t(27)=– 2.16, P=0.04). Cross-sectional comparisons between children at Time 2, adolescents, and adults revealed that the transition to memory-based problem solving continued into adolescence and adulthood (F(2, 65)>3.78, Ps<0.028) (Fig. 1c). Post-hoc comparisons revealed greater memory-based strategy use in adolescents and adults than in children (Scheffe's Ps<0.03). These results indicate that children's arithmetic skill development is characterized by gradual changes in the distributions of strategies from childhood through adolescence into adulthood, with use of counting strategies decreasing in frequency and use of memory-based strategies (i.e. “retrieval fluency”) increasing in frequency.

Longitudinal changes in fMRI task performance during childhood

We then examined longitudinal changes in accuracy and reaction times (RTs) from the block and event-related fMRI experiments in children. Separate repeated analyses of variance (ANOVAs) for accuracy and RTs in the block fMRI task (Fig. 1d), with Task (Addition vs. Control) and Time (Time-1 vs. Time-2) as within-subject factors, revealed a main effect of Task for accuracy and RTs (F(1,27)>13.04, Ps<0.001), and a main effect of Time for RTs (F(1,27)=14.82, P<0.001). Follow-up tests revealed that children had lower accuracy and slower response in solving Addition than Control problems (t(27)<–4.64, Ps<0.001) and that children became faster (t(27)>2.65, Ps<0.013) over time (Fig. S1a-b).

Longitudinal changes in the event-related fMRI task showed the same pattern; Task effects for accuracy and RTs (F(1,19)=46.24, Ps<0.001), and a main effect of Time for RTs (F(1,19)=28.43, P<0.001), with significant gains in RTs from Time-1 to Time-2 (t(19)=6.87, Ps<0.001). Notably, we observed Task-by-Time interactions for both accuracy and RTs (F(1,19)>4.97, Ps<0.04) (Fig. S1c-d), with larger improvements in solving Addition (accuracy: t(19)=2.50, P=0.022; RTs: t(19)=5.63, P<0.001) than Control (accuracy: t(19)=0.68, P=0.50; RTs: t(19)=4.34, P<0.001) problems. Detailed results are provided in Supplemental Materials. In sum, convergent results from the behavioral, block and event-related fMRI tasks provide robust evidence that children's problem solving skills improved significantly over the 1.2-year interval.

Developmental changes in fMRI task performance from childhood through adolescence into adulthood

Analysis of cross-sectional behavioral data revealed main effects of Group for both accuracy and RTs in the block and event-related fMRI tasks (F(2,65)>12.28, Ps<0.001) (Fig. 1d, Fig. S1a-d), with higher accuracy and faster RTs in adolescents and adults compared to children (F(2, 65)>46.79, Ps<0.001). Critically, we observed significant Task-by-Group interactions for both accuracy and RTs (F(2, 65)>6.26, Ps<0.003), with larger developmental improvements for Addition (Ps<0.001) than Control (Ps<0.01) problems (Fig. S1a-b). The same pattern of results was found in the event-related fMRI task (Fig. S1b,d). Detailed results are provided in Supplemental Materials. These results provide robust evidence for improvements in problem solving skills from childhood through adolescence into adulthood.

Longitudinal changes in hippocampal and prefrontal-parietal engagement during childhood

Next, we examined longitudinal changes in children's brain response during addition problem solving from Time-1 to Time-2. Collapsing data across the two time points, we found a widely-distributed network of brain regions involved in solving addition problems, including the prefrontal cortex, parietal cortex, MTL, as well as the striatum and cerebellum (Table S2, Fig. S2). Compared to Time-1, children at Time-2 showed significantly higher activation in the bilateral hippocampus (peak at [28,–20,–18] and [–26,–22,–16], MNI coordinates thereafter) (Fig. 2a). In contrast, they showed reduced activation in the bilateral dorsolateral prefrontal cortex (DLPFC), left superior parietal lobule and right posterior parietal-occipital cortex (Fig. S3 and Table S3), brain areas implicated in working memory, executive control, and use of effortful counting strategies^{12, 13}.

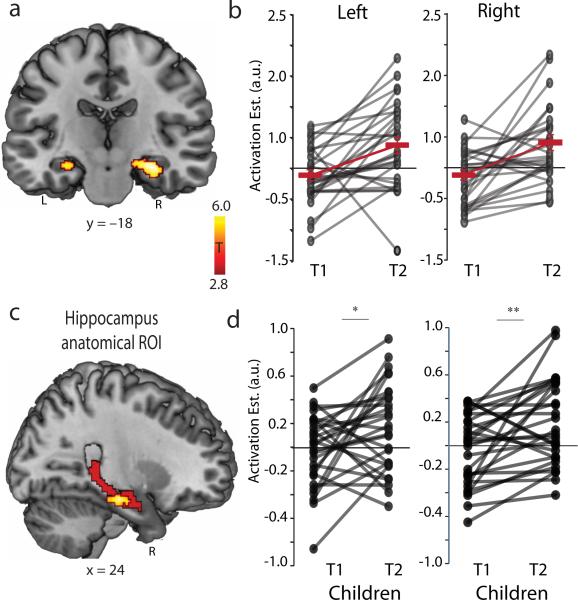
Fig. 2. Longitudinal changes in hippocampal engagement during childhood.

(a) Left and right hippocampus clusters which showed increased engagement during addition problem solving between Time-1 (T1) and Time-2 (T2). (b) Each line represents individual developmental trajectories of hippocampal engagement over time. Bold red lines represent group means at T1 and T2. (c) Sagittal view of anatomically defined region of interest (ROI) encompassing the entire right hippocampus (coded in red) and significant functional clusters from 2A (coded in hot orange). (d) Each line represents individual trajectories of hippocampal engagement over time within an anatomically defined ROIs. Bold red lines represent group means at T1 and T2. Notes: *P<0.05; ** P<0.01; L, left; R, right.

A follow-up region of interest (ROI) analysis of each child's longitudinal trajectory revealed that 23 of 28 children showed an increase in hippocampal activation over the 1.2-year period (Fig. 2b). Analysis of a priori anatomically-defined ROIs (Fig. 2c) spanning the entire long axis of the hippocampus also revealed a significant increase in hippocampal engagement (left: t(27)=2.39, P=0.02; right: (t(27)=3.26, P<0.01) (Fig. 2d). These results point to a robust longitudinal increase in hippocampal engagement and decrease in prefrontal-parietal engagement during problem solving, which parallel the shift from effortful counting to efficient memory-based strategies.

Longitudinal changes in hippocampal-neocortical connectivity predict improved memory-based problem solving

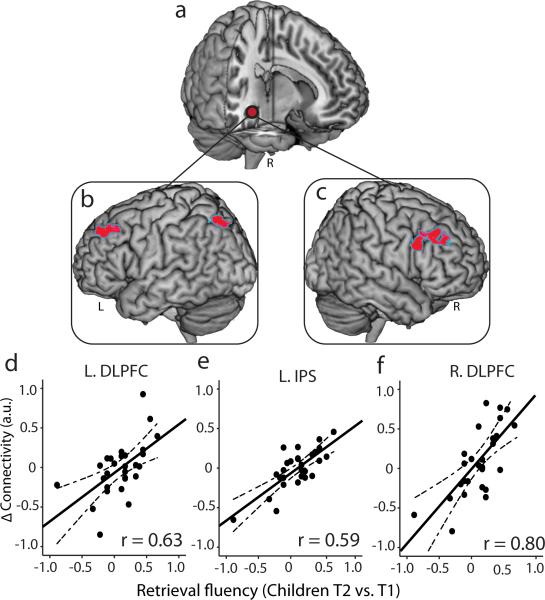
We then investigated how changes in hippocampal engagement and its connectivity with the neocortex contribute to children's transition to memory-based problem solving. Despite significant longitudinal increases in hippocampal engagement, changes in hippocampal activation were not predictive of individual improvements in children's retrieval fluency, accuracy, or RTs. Rather, increases in children's retrieval strategy use were predicted by the degree of hippocampal connectivity with other brain areas (Fig. 3a-c). Specifically, we examined longitudinal changes in hippocampal connectivity with every voxel in the brain²⁸ (Online Methods). We observed significant increases in hippocampal functional connectivity with dorsolateral, ventrolateral and ventromedial prefrontal cortex, and anterior temporal cortex over time (Fig. S4ac; Table S4). Critically, individual improvements in fact retrieval fluency were significantly correlated with the strength of hippocampal connectivity with multiple prefrontal and parietal cortex areas, including left and right DLPFC and left intra-parietal sulcus regions (Fig. 3d-f; Table S4) widely implicated in arithmetic problem solving^{4, 11, 12, 29, 30}. Using machine learning algorithms with cross-validation^{16, 31} (Online Methods), we confirmed that individual improvements in children's retrieval fluency from Time-1 to Time-2 could be reliably predicted by longitudinal changes in functional coupling of the hippocampus with the left DLPFC (r_{(predicted, observed)} = 0.53) and right DLPFC (r_{(predicted, observed)} = 0.71) and left intra-parietal sulcus (r_{(predicted, observed)} = 0.51) (Table S5). These results demonstrate that changes in hippocampal-neocortical functional circuits, rather than hippocampal activation levels, underlie individual gains in use of memory-based problem solving.

Fig. 3. Longitudinal changes in hippocampal-neocortical functional coupling in relation to individual improvements in children's retrieval fluency.

(a) Right hippocampus seed region used in task-related functional connectivity (i.e., psychophysiological interaction) analysis. (b, c) Left and right dorsolateral prefrontal cortex (DLPFC) and the left intraparietal sulcus (IPS) regions that showed increased functional connectivity with the hippocampus, as a function of longitudinal improvements in retrieval fluency from Time-1 (T1) to Time-2 (T2). (d-f) Scatter plots depict the relation between longitudinal changes in retrieval fluency (x-axes) and changes in functional connectivity strength from T1 to T2 (y-axes). The correlates are plotted for visualization purposes only. Notes: L, left; R, right.

Developmental changes in hippocampal engagement from childhood through adolescence into adulthood

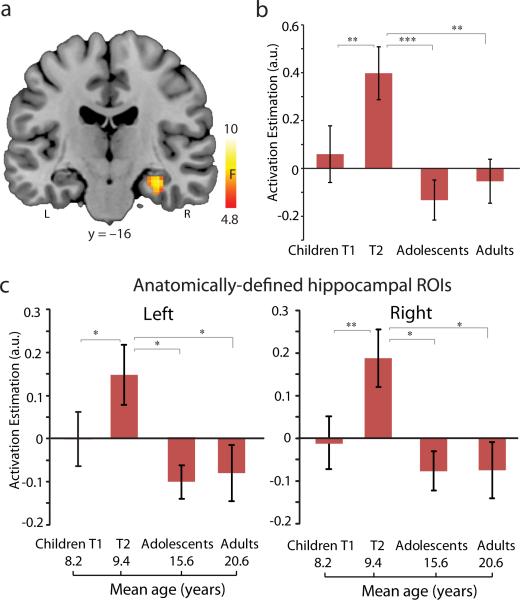
To characterize how hippocampal engagement during arithmetic problem solving unfolds with longer-term development, we examined cross-sectional fMRI data from children (Time-2), adolescents and adults at the whole brain level (Fig. S5; Table S6). This analysis identified a cluster in the right hippocampus (peak at [32,–16,–18]) that showed a significant omnibus Group effect (Fig. 4a-b; Table S7). A follow-up ROI analysis confirmed a main effect of group (F(2,65)=8.61, P<0.001), with larger hippocampal engagement for children at Time-2 compared to adolescents and adults (Scheffe's Ps<0.009). There were no differences between adolescents and adults (P=0.87), nor between them and children at Time-1 (t(46)<1).

Fig. 4. Longitudinal changes in hippocampal engagement during childhood, and further development through adolescence into adulthood.

(a) Right hippocampus showing main effect of Group across children, adolescents, and adults (omnibus F-contrast). (b) Bar graphs depict developmental changes in the functionally defined hippocampus cluster. (c) Bar graphs show developmental changes in the engagement of anatomically defined hippocampal regions of interest (ROI) (ROI mask is shown in Fig. 2C). Notes: * P<0.05; **, P<0.01; ***, P<0.001; L, left; R, right.

Additional analyses using anatomically-defined hippocampal ROIs again revealed a main effect of Group in the left (F(2,65)=3.35, P=0.04) and right (F(2,65)=3.91, P=0.025) hippocampus (Fig. 4c). The strongest engagement was observed in children at Time-2 (Scheffe's Ps<0.05), with no differences between adolescents and adults (P=0.68). These developmental changes were independent of general performance improvements (Fig. S6). Together with longitudinal fMRI data, these results demonstrate that hippocampal engagement during problem solving increases initially during middle childhood and subsequently decreases reaching adult-like levels by adolescence.

Maturation of neural representational stability from childhood through adolescence into adulthood

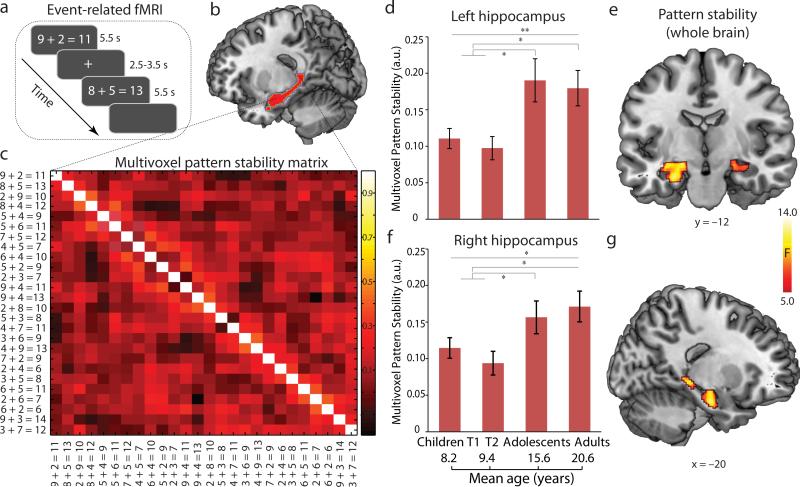
To further investigate the maturation and stabilization of neural representations underlying arithmetic problem solving, we analyzed event-related fMRI data acquired from a subgroup of 20 children, as well as the entire group of adolescents and adults (Fig. 5a). We implemented an innovative multivariate pattern analysis which provides a measure of the stability of neural representations, by examining trial-by-trial similarity of multivoxel activation patterns (Fig. 5c) associated with each correctly solved problem. This approach has superior sensitivity and reliability for capturing fine-grained spatially distributed activation patterns associated with learning and memory^{22, 23, 27}. We first performed a whole-brain analysis using a searchlight algorithm^{27, 32} to determine which brain areas exhibited developmental changes in inter-problem stability. This analysis revealed that the left and right hippocampus (peak at [–24,–12,–14], [–22,– 32,–4]; [22,–14,–14]) showed significant increases in inter-problem multivoxel pattern stability from childhood through adolescence into adulthood. Increased inter-problem stability was also observed in multiple prefrontal and temporal regions (Fig. S7 and Table S8).

Fig. 5. Inter-problem multivoxel pattern stability in the hippocampus in children at Time-1 (T1) and Time-2 (T2), adolescents, and adults.

(a) Event-related fMRI design of arithmetic problem solving task. (b) Sagittal slice of predefined region of interest (ROI) in the hippocampus used for the inter-problem pattern stability analysis. (c) 26 × 26 correlation matrix representing trial-by-trial brain activation pattern stability in the hippocampus during addition problem solving. (d-e) Inter-problem pattern stability in the left and right hippocampus for problems correctly solved by children at T1 and T2, adolescents, and adults. (f-g) Results of whole-brain analysis showing hippocampal regions that showed significant increases in inter-problem multivoxel pattern stability from childhood through adolescence into adulthood. Note that only correctly performed trials (problems) from each participant's event-related fMRI data were used in the analysis. Notes: a.u., arbitrary units; * P<0.05; **, P<0.01; L, left; R, right.

Additional analyses using anatomically-defined hippocampal ROIs again revealed significant developmental changes in inter-problem representation stability in the left and right hippocampus in children (Time-1 or Time-2), adolescents, and adults (F(2,57)>3.35, Ps<0.04) (Fig. 5b-e). Follow-up analyses revealed no differences between children at Time-1 and Time-2, but higher inter-problem stability in the left and right hippocampus in adolescents and adults compared to children (Scheffe's Ps<0.05). We observed similar results even after equating the number of correct problems across groups (Fig. S7a-d, Table S9). In sum, converging results from the whole-brain and ROI analyses indicate that inter-problem multivoxel patterns in the hippocampus become significantly more stable with development, reaching adult-like levels during adolescence.

Discussion

By integrating unique longitudinal and cross-sectional brain imaging data with behavioral strategy assessments, we examined the functional maturation of brain systems underlying the transition from counting to memory-based problem solving. Consistent with the “overlapping waves” model, children's use of memory-based strategies increased and use of counting strategies decreased over time. The MTL-neocortical system emerged as a key locus supporting this transition, characterized by increased hippocampal engagement, decreased prefrontal-parietal engagement, and increased functional connectivity between the hippocampus and multiple cortical regions. Crucially, increased hippocampal connectivity with prefrontal-parietal circuits predicted longitudinal gains in retrieval fluency. Beyond childhood, overall hippocampal engagement decreased through adolescence into adulthood. Remarkably, inter-problem multivoxel activation patterns in the hippocampus became more stable, reaching adult-like levels by adolescence. Our findings point to a pivotal role of the hippocampus and its functional circuits, in both the early emergence of children's memory-based problem solving and in the fine-tuning and stabilization of local-circuit representations in the development of adult-like problem solving by adolescence.

Longitudinal changes in hippocampal-neocortical engagement in the transition to memory-based problem solving

A shift from the use of counting to memory-based strategies was observed in children over a 1.2-year interval, and crucially, was associated with increased hippocampal engagement in problem solving. During this period, children showed decreased prefrontal-parietal engagement as observed in previous cross-sectional studies^{33, 34}. The greater prefrontal and posterior parietal recruitment at Time-1 likely reflects high levels of working memory and executive processing needed for implementing counting strategies^{7, 25}, at a stage when children are still learning to solve arithmetic problems^{5, 35, 36}. The increased hippocampal engagement is consistent with its known role in learning and memory for encoding and retrieval of facts and events^{17, 18, 21}, and matches our observation of greater reliance on memory-based retrieval of addition facts from Time-1 to Time-2. Thus, our longitudinal findings suggest that the recruitment of hippocampal-dependent memory processes plays an important role in the development of children's memory-based problem solving strategies.

Our findings point to a significant shift in the engagement of the hippocampal-dependent memory system, and concomitant decrease in the engagement of the prefrontal-parietal working memory system, consistent with our behavioral findings of a strategy shift to declarative memory-based retrieval during the early stages of arithmetic learning and skill acquisition^{1, 3}. Although no such longitudinal studies have yet been performed, a similar process may also apply to other academic domains and to language acquisition in young children^{37, 38}. Our findings are a significant advancement over previous cross-sectional studies^{17, 18}, and provide the first longitudinal evidence for the importance of the hippocampal-dependent memory system in children's cognitive development.

The developmental origins of the emergence of hippocampal activity and strategy shifts lie in children's educational experiences involving considerable practice with problems of the type used in our study³⁹. One possibility, consistent with the known functions of the hippocampus^{17, 18, 40}, is that children learn to associate individual problems with the correct answers. Repeated problem solving during the early stages of arithmetic skill development also contributes to memory re-encoding and consolidation, thus resulting in enhanced hippocampal activity and ability to recall basic arithmetic facts^{4, 16, 35}. It is also noteworthy that our findings are consistent with theoretical and computational models of early cognitive development which posit that children learn and acquire knowledge through experience-dependent plasticity in the MTL memory system^{38, 41}.

Longitudinal changes in hippocampal-neocortical connectivity predict children's gains in memory-based strategy use

Coordinated interactions between the hippocampus and neocortex are known to play an important role in memory formation and knowledge acquisition^{18, 19}. In conjunction with the longitudinal increase in hippocampal engagement, we observed that increased hippocampal functional coupling with prefrontal and parietal cortices was positively correlated with individual gains in use of memory-based strategies. Moving beyond standard regression approaches, prediction analyses based on machine learning algorithms further confirmed that changes in hippocampal functional coupling with prefrontal-parietal systems indeed predicted longitudinal gains in fact retrieval fluency. These results suggest that hippocampal-neocortical functional reorganization, rather than changes in regional activation by themselves, play an important role in children's shift from effortful counting to more efficient memory-based problem solving. Consistent with this view, a recent study found that increased intrinsic connectivity of the hippocampus with the neocortex predicted performance gains after 8 weeks of mathematics tutoring in children ages 7 to 9¹⁶. More broadly, hippocampal-neocortical interactions have been implicated in human episodic memory^{17, 21} and early stage of conceptual learning in adults^{18, 42}, but there has been limited evidence for its role in the development of children's memory-based problem solving skills. Findings from our longitudinal study in children thus establish a link between hippocampalneocortical functional reorganization and the emergence of memory-based problem solving during childhood.

Developmental changes in hippocampal engagement and inter-problem representational stability

Beyond childhood, use of memory-based strategies continued to improve, reaching an adult-like level during adolescence. Following the initial increase in hippocampal engagement during middle childhood, this hippocampal dependency decreased during adolescence and adulthood despite further improvements in memory-based problem solving. This pattern of initial increase and subsequent decrease in activation provides novel support for models of long-term memory consolidation which posit that the hippocampus plays a time-limited role in the early phase of knowledge acquisition^{18, 19}. Consistent with this pattern of developmental change, previous studies of adults have reported no reliable hippocampal engagement in basic arithmetic tasks. Together with the above longitudinal results, our findings suggest the hippocampal system is critical to children's early learning of arithmetic facts^{15, 35}, the retrieval of which is largely dependent on the neocortex in adults^{12, 33, 43}. Through further schooling and experience with mathematics, fact retrieval becomes increasingly independent of the hippocampal memory system during adolescence and adulthood.

Our observed changes in task-related mean activation and connectivity provide insights into hippocampal-neocortical functional reorganization underlying the shift to memory-based problem solving, but leave unclear the nature of neural processing and stability of representations associated with solving of individual problems. Although mean hippocampal activation decreased during adolescence, we observed that inter-problem pattern stability in the hippocampus, prefrontal and temporal cortices increased with the refinement of memory-based problem solving from childhood to adolescence and adulthood. Our findings complement univariate analysis of mean activation and connectivity and provide novel evidence that hippocampal multivoxel patterns become more stable with skill development.

Critically, our results show for the first time that with development, neural representations of basic arithmetic facts become more stable during adolescence and adulthood. At that point, although retrieval of arithmetic facts no longer requires the same level of engagement of the hippocampus-dependent memory system, the manner in which it is engaged becomes more stable across individual problems. This pattern of results is consistent with recent adult studies in memory encoding and retrieval tasks that found that greater pattern similarity across stimuli in the MTL predicts better behavioral performance, through strengthening of discrete information distributed over neocortical regions^{26, 27, 45}. These developmental changes likely reflect fine-tuned integration and reconfiguration of local functional circuits through experience-dependent plasticity^44-46. Our findings provide new insights into the mechanisms by which the hippocampus contributes to the maturation of memory-based problem solving skills from childhood through adolescence into adulthood and to knowledge acquisition in academically relevant domains such as mathematics.

Finally, it should be noted that while the multivariate approach we used has been demonstrated to have superior sensitivity to capture fine-grained activation patterns across spatially distributed voxels^{22, 27}, the precise neuronal mechanisms underlying formation of such stable multivoxel patterns remains unknown. Further studies with high-resolution imaging and dense neuronal recordings are needed to clarify the neural basis of the “representations” detected here.

Conclusion

By characterizing parallel changes in task-related brain activation, functional connectivity as well as stability of distributed neural representations with development, our study provides new insights into the mechanisms through which hippocampal-neocortical functional reorganization promotes the shift from use of effortful procedure-based to more efficient memory-based problem solving from childhood through adolescence into adulthood. More broadly, our study elucidates key neurobiological mechanisms underlying a cardinal feature of children's cognitive development.

Online Methods

Participants

A total of 68 children, adolescents and adults participated in this study. Twenty-eight typically developing children participated in a longitudinal fMRI study, and twenty healthy adolescents and twenty healthy young adults participated in a cross-sectional fMRI study. All participants were right handed, and no history of neurological or psychiatric diseases and no current use of any medication. Twenty-eight children (15 boys and 13 girls) were scanned twice (once at Time-1 and once at Time-2) separated by an interval of approximately 1.2 years. To minimize age-related variability within each group, children were selected from narrow age range of 7 to 9 (at the first time point; mean age, 8.26 ± 0.53), adolescents and adults were selected from narrow age ranges of 14 to 17 (mean age, 15.61 ± 1.40) and 19 to 22 (mean age, 20.50 ± 1.07), respectively. All participants had intelligence quotient (IQ) above 95 and below 135, as measured by the Wechsler Abbreviated Scales of Intelligence (WASI). Verbal, performance and full scale IQ scores were normalized according to each participant's age. Participants with dyscalculia or poor mathematics achievement, as assessed by the Wechsler Individual Achievement Test (WIAT-II) and attention deficit hyperactivity disorder (ADHD), as assessed by the Child Behavior Checklist (CBCL), were excluded. Participant demographics and statistics, including age, IQ and gender, are summarized in Table S1. The study protocol was approved by the Stanford University Institutional Review Board. Written informed consent was obtained from each participant as well as the child's legal guardian prior to their participation. Participants with root mean squared head motion, exceeding a voxel's width during MR scanning, were excluded from further analyses.

Children were recruited from elementary schools in the San Francisco Bay Area as part of a prospective longitudinal imaging study of cognitive development. Following behavioral and cognitive assessments and MRI scanning at Time-1, all potential participants were invited back for Time 2 assessments and MRI scanning approximately one year later. We included any child who had good quality behavioral and brain imaging data (see details below) at both time points. Adolescents and adults were recruited from high schools and community colleges around the Stanford University campus.

General experimental procedures

Each participant performed two single-digit addition problem solving tasks. The first involved verbal production of the answer to the problem (e.g. “3 + 8”), during which trial-by-trial strategy assessments were assessed outside the MRI scanner. The second was an arithmetic verification task which was performed during fMRI scanning (Fig. 1a-b). Details of the two arithmetic tasks are described below.

Strategy assessment

In the strategy assessment task, each participant's mix of strategies for solving standard single-digit addition problems was assessed using a standardized, well-validated trial-by-trial measurement that classified strategies based on experimenter observation and participant's self-report^{24, 25}. In this task, a set of 18 addition problems was carefully designed by selecting two addends from 2 to 9 (e.g., “2 + 9 = ?”), and sums ranging from 6 to 17. Problems with two identical addends (e.g., “5 + 5”) or with addends of 0 and 1 (e.g., “8 + 1” or “8 + 0”) were excluded, because they are known to evince less strategy variability^{7, 24, 35}. Half of the problems were randomly presented in larger addend plus smaller addend format (“9 + 2 = ?”), and the other half were presented in the opposite format (“3 + 8 = ?”).

During strategy assessment, 18 problems were centrally presented one by one on the computer screen, and there was no repetition within the set. Participants were asked to solve each problem without the use of paper and pencil as quickly as possible and to verbally state the answer out loud. Note that participants were explicitly instructed to use whatever strategy was easiest for them to get the answer. Participants were also asked to report how they solved each problem immediately after stating the answer. For each problem, the experimenter took detailed notes of overt signs of counting, such as finger usage, lip movement, or audible counting, and these were compared against each participant's self-report of how the problem was solved. Based on each participant's self-reported strategy and experimenter's observations, mixed strategies for solving addition problems were classified into two major categories of interest – “counting” (such as counting fingers, verbal counting, count by numbers, or counting in mind), and “direct retrieval” (such as just know, remember, or guess responses). Trials in which the experimenter noted overt signs of counting even when the child reported a retrieval strategy were classified as a “counting” trial. For each participant, we computed the proportion of trials in which memory-based direct retrieval or counting strategies were used, and remaining trials were endorsed into a category of no interest. This approach allows us to quantify the frequency of memory-based strategy use, i.e. “retrieval fluency”, which provides a reliable assessment of putative memory-based strategy use in arithmetic problem solving^{7, 24}.

Block design fMRI task

Participants solved an arithmetic verification task^{7, 35} during fMRI scanning. We used a block design fMRI paradigm to optimize signal detection and task-dependent functional connectivity analysis²⁶. The task consisted of sixteen blocks with four alternating conditions - solving standard single-digit addition problems (e.g., ‘5 + 9 = 14’), solving ‘plus 1’ (e.g., ‘5 + 1 = 6’) as a control addition condition, identifying the number “5” in a string of symbols and numbers, and passively viewing fixation. In the standard addition condition, equations with two different single-digit addends (e.g., ‘5 + 9 = 14’) were presented on the center of screen for 5 seconds, and participants were asked to judge whether the current equation was correct or not by a button press. Half of the equations were correct and the other half were incorrect. In each equation, one addend varied from 2 to 9 and the other varied from 2 to 5. Equations with two identical addends (i.e., tie problems) such as “5 + 5 = 10” were excluded. To avoid large variations in difficulty for addition equations, incorrect answers were restricted to a deviation by ±2 or ±1 from the correct answer, and the range of values of the smaller addend was restricted to ≤ 5 to allow children to execute the minimum counting strategy within the allotted 5-sec window provided for each problem in the scanner^{15, 35}. The control addition task was the same as the addition task except that one addend ranged from 2 to 9 whereas the other was always “1” (e.g., 5 + 1 = 7). We used the “n + 1” problem as a control task based on our previous studies^{15, 35}, as its format is very similar to the standard addition task and requires the same level of response selection. Importantly, it is already known that children show less variability in strategy use for solving “n + 1” problems, making it an ideal control task for our study^{4, 35}.

In each condition, equations were displayed on the center of the screen for 5 sec with an inter-trial interval of 500 msec. There were 18 trials of each task condition, broken up into four blocks of four or five trials; thus, each block lasted either 22 or 27.5 sec. The order of the blocks was pseudo-randomized across participants with the standard addition and control addition blocks always separated by either a number identification or a passive fixation block. Orders of addition and non-addition conditions were equally likely. The total length of the experimental run was 6 min and 36 sec.

Event-related fMRI task

After the block design fMRI experiment, participants underwent to an event-related fMRI while they were performing a similar arithmetic verification task. The event-related fMRI experiment was designed to examine changes in trial-by-trial multivoxel pattern stability^{22, 27} with development in terms of the “overlapping waves” model. The task consisted of 52 trials in total and half of them are standard single-digit addition problems and the other half are ‘plus 1’ problems as control condition. Each trial consists of a two-digit equation presented at the center of screen for 5.0 seconds and followed by a fixation period jittered from 2.5 to 3.5 seconds. Participants were asked to press a button indicating whether the answer was correct or not. Half of the equations were correct and the other half were incorrect. The order of 52 addition and control trials was pseudo-randomized across participants with the standard addition and control addition problems always interleaved by a low-level fixation period. The total length of the experimental run was 6 min and 30 sec. The other settings were identical with the block design fMRI task. For this event-related fMRI experiment, 8 children were excluded from further analyses because of either their incompleteness for the two time points or bad quality of fMRI data.

Behavioral data analysis

Participant demographic data and behavioral performance in strategy assessment and in block and event-related fMRI tasks were analyzed using Statistical Product and Service Solutions (SPSS, version 20.0, IBM, New York). We conducted 2-by-2 repeated measures analysis of variance (ANOVA) with Strategy (Retrieval vs. Counting) and Time (Children at Time-1 vs. at Time-2) as within-subject factors to examine longitudinal changes in the mix of strategies. We then conducted separate ANOVAs with Strategy as a within-subject factor and Group (Children Time-2 vs. Adolescents vs. Adults) as a between-subject factor to examine cross-sectional changes in the mix of strategies for addition problem solving from childhood, through adolescence into adulthood. Similarly, separate ANOVAs were conducted for accuracy and reaction times in the arithmetic verification task in both block design and event-related fMRI. Scheffe's procedure was used to correct for multiple comparisons in post-hoc tests.

fMRI data acquisition

Whole brain functional images were acquired from a 3T GE Signa scanner (General Electric, Milwaukee, WI) using a custom-built head coil with a T2*-sensitive gradient echo spiral in-out pulse sequence based on blood oxygenation level-dependent (BOLD) contrast (12). Twenty-nine axial slices (4.0 mm thickness, 0.5 mm skip) parallel to the AC–PC line and covering the whole brain were imaged with the following parameters: volume repetition time (TR) 2.0 sec, echo time (TE) 25 ms, 80° flip angle, matrix size 64 × 64, field of view 200 × 200 mm, and an in-plane spatial resolution of 3.125 mm. To reduce blurring and signal loss arising from field inhomogeneities, an automated high-order shimming method based on spiral acquisitions was used before acquiring functional images. A linear shim correction was applied separately for each slice during reconstruction using a magnetic field map acquired automatically by the pulse sequence at the beginning of the scan.

fMRI data analysis

Preprocessing

Images were preprocessed using Statistical Parametric Mapping (SPM8, http://wwwfil.ion.ucl.ac.uk/spm). The first eight volumes were discarded for stabilization of the MR signal. Remaining functional images were realigned to correct for rigid-body motion. Subsequently, images were slice-timing corrected, normalized into a standard stereotactic space, and resampled into 2 mm isotropic voxels. Finally, images were spatially smoothed by convolving an isotropic 3D-Gaussian kernel (6-mm full width at half maximum).

Univariate general linear model analysis

To assess task-related brain responses in the block design data, the addition and control conditions, along with the number identification condition were modeled as separate boxcar regressors and convolved with the canonical hemodynamic response function (HRF) implemented in SPM8. Additionally, motion parameters from the realignment procedure were included to regress out effects of head movement on brain response. We used a high-pass filtering using a cutoff of 1/128 Hz, global intensity normalization, and corrections for serial correlations in fMRI using a first-order autoregressive model (AR(1)) in the general linear model (GLM) framework.

Contrast images for addition vs. control conditions, generated at the individual level fixed-effects analyses, were submitted to a second-level group analysis treating participants as a random factor. A paired t-test was first conducted to examine longitudinal changes in brain activity associated with arithmetic problem solving over time (Time-1 vs. Time-2). One-way ANOVA were then conducted to examine cross-sectional changes in brain activity across children at Time-2, adolescents and adults. Significant clusters were determined using a height threshold of P < 0.01 and an extent threshold of P < 0.05 with family-wise-error corrections for multiple comparisons based on nonstationary suprathreshold cluster-size distributions computed using Monte Carlo simulations⁴⁷.

To characterize developmental changes in hippocampal engagement in addition problem solving, we performed a complementary ROI analysis using the entire hippocampus. Separate ROI masks for the hippocampus in left and right hemispheres were anatomically defined using the anatomical automatic labeling (AAL) template of the hippocampus. Parameter estimates (or β weights) associated with the two conditions of interest were extracted from these ROIs at the individual level using MarsBar (http://marsbar.sourceforge.net) and averaged across voxels within each region. Subsequently, extracted data were visualized using bar graphs, and submitted for statistical testing in SPSS 20.0. In order to create more precise masks of the hippocampus for children, we manually drew the left and right hippocampus (Figure S8) based on high-resolution T1-weighted brain templates from twelve 8.5-year-old children⁴⁸, and then transformed in the same stereotaxic standardized MNI space. We followed a widely-used protocol described by Pruessner and colleagues⁴⁹, integrated with landmarks included in Duvernoy⁵⁰ to demarcate the child hippocampus. We used the ITK-SNAP (www.itksnap.org) image viewer and segmentation tool to view and segment the MRI images. As shown in Figure S8, we found very similar pattern of results when using adult AAL masks and hand-drawn hippocampal masks based on pediatric brain images.

Task-dependent functional connectivity analysis

Task-dependent functional connectivity was examined using psychophysiological interaction (PPI) analysis²⁸. This analysis examined condition-specific modulation of connectivity of a specific ROI (the hippocampal seed here) with the rest of the brain, after removing potentially confounding influences of overall task activation and common driving inputs. The hippocampal seed was defined as a 6-mm sphere centered at the local peak of the cluster that showed significant longitudinal changes in brain activation between Time-1 and Time-2 in children. The mean time series from the seed ROI were then deconvolved so as to uncover neuronal activity (i.e., physiological variable) and multiplied with the task design vector contrasting the Addition and Control conditions (i.e., a binary psychological variable) to form a psychophysiological interaction vector. This interaction vector was convolved with a canonical HRF to form the PPI regressor of interest. The psychological variable representing the task conditions (Addition vs. Control) as well as the mean-corrected time series of the seed ROI were also included in the GLM to remove overall task-related activation as well as the effects of common driving inputs on brain connectivity. Brain regions showing significant PPI effects were determined by testing for a positive slope of the PPI regressor.

Contrast images corresponding to PPI effects at the individual-subject level were then entered into a group level statistical analysis. Developmental changes in retrieval fluency (i.e., the frequency of retrieval strategy use) from Time-1 to Time-2 were included as covariates of interest to determine brain areas in which longitudinal changes in retrieval fluency were associated with longitudinal changes in effective connectivity of the hippocampus. Note that we did not use changes in accuracy and reaction times (RTs) for the arithmetic tasks as a measure of strategic transitions, because these two measures are not specifically related to use of counting and memory-related strategies during problem solving. Similar to the GLM analysis above, significant clusters were determined using a height threshold of P < 0.01 and an extent threshold of P < 0.05 with family-wise-error corrections for multiple comparisons based on nonstationary suprathreshold cluster-size distributions computed using Monte Carlo simulations⁴⁷. To illustrate the brain-behavior relations we extracted data from significant clusters and plotted correlations for visualization purposes only.

Prediction analysis

To further confirm the robustness of the relation between longitudinal changes in hippocampal connectivity with fronto-parietal cortex and individual changes in retrieval fluency between Time-1 and Time-2, we used a machine learning approach with balanced 4-fold cross-validation^{16, 31}. The prediction analysis was conducted for confirmatory purposes because conventional regression models assess correlation coefficients which are sensitive to outliers and are correlational with no predictive value^{16, 31}. Longitudinal change in retrieval fluency was entered as a dependent variable and hippocampal connectivity was entered as an independent variable into a linear regression algorithm. r_{(predicted, observed)}, a measure of how well the independent variable predicts the dependent variable, was estimated using a balanced 4-fold cross-validation procedure. Data for these two variables from all children in the longitudinal experiment were divided into 4 folds so that the distributions of dependent and independent variables were balanced across folds. A linear regression model was built using 3 folds leaving out one fold, and this model was then used to predict the data in the left-out fold^{16, 31}. This procedure was repeated 4 times to compute a final r_{(predicted, observed)} representing the correlation between the data predicted by the regression model and the observed data. Finally, the statistical significance of the model was assessed using non-parametric testing approach. The empirical null distribution of r_{(predicted, observed)} was estimated by generating 1000 surrogate datasets under the null hypothesis that there was no association between changes in retrieval fluency and hippocampal activity (or hippocampal functional connectivity). Each surrogate dataset D_i of size equal to the observed dataset was generated by permuting the labels on the observed data points. The r_{(predicted, observed)i} was computed using the actual labels of D_i and predicted labels using the 4-fold balanced cross validation procedure described above. This procedure produced a null distribution of r_{(predicted, observed)} for the regression model. The statistical significance (p value) of the model was then determined by counting the number of r_{(predicted, observed)i} greater than r_{(predicted, observed)} and then dividing that count by the number of D_i datasets (1000 in our case).

Multivoxel pattern stability analysis of event-related fMRI data

Trial-wise estimation of brain responses

To assess task-related brain responses during solving each addition problem, each problem was modeled as a separate regressor with a duration of 5.5 seconds and convolved with a canonical hemodynamic response function (HRF) implemented in SPM8. This resulted in with 26 regressors for standard addition problems and 26 regressors for control problems. Contrast images for correct addition problems vs. rest fixation condition, generated at the individual level fixed-effects analyses, were submitted to subsequent multivariate pattern stability analyses for the hippocampal ROIs as well as for the whole brain.

ROI-based pattern stability analysis

Beta weights representing voxel-wise brain activation for each addition problems was extracted from voxels within the entire left and right anatomically-defined hippocampal ROI masks separately, and then reshaped into a single dimensional vector. Pairwise correlations among correct problems of interest were then computed among distributed voxels of each ROI. This ends up with N*(N-1)/2 pairwise correlation coefficients, where N represents the number of correctly solved problems. Pairwise correlation coefficients were then averaged as a measure of multivoxel pattern stability/similarity cross correctly solved problems. Averaged inter-problem pattern stability scores in the left and right hippocampus were separately computed for each participant. Note that any differences in overall mean signal of individual voxels within a given ROI would not impact the computation of multivoxel pattern stability. Separate one-way ANOVAs were conducted to compare differences in inter-problem pattern stability in the hippocampus from childhood (either Time-1 or Time-2) through adolescence into adulthood.

Whole-brain pattern stability analysis

A newly developed searchlight mapping method^{27, 32} was implemented to obtain a measure of inter-problem pattern stability in the neighborhood surrounding of each voxel within each participant's brain. Briefly, a 6-mm spherical region of interest (so-called the “searchlight”) centered on each voxel was first selected, and then inter-problem stability scores only for correctly solved problems within the sphere were computed using a pairwise correlation method. Pairwise correlation maps of two consecutive neighbor trials were excluded in order to mitigate potential collinearity because of close proximity in time. The averaged similarity scores were assigned to the central voxel and run through every voxel across the whole brain to create participant-specific searchlight maps. These searchlight maps were subsequently entered into a second-level random effects analysis to determine changes in pattern stability among children (at either Time-1 or Time-2), adolescent and adult groups. Significant clusters were determined using a height threshold of P < 0.01 and an extent threshold of P < 0.05 family-wise error correction for multiple comparisons based on Monte Carlo simulations⁴⁷.