Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Jan 7.
Published in final edited form as: Demogr Res. 2012 Mar 2;26:151–166. doi: 10.4054/DemRes.2012.26.6

Mapping the results of local statistics: Using geographically weighted regression

Stephen A Matthews 1, Tse-Chuan Yang 2
PMCID: PMC4286400  NIHMSID: NIHMS639342  PMID: 25578024

Abstract

The application of geographically weighted regression (GWR) – a local spatial statistical technique used to test for spatial nonstationarity – has grown rapidly in the social, health and demographic sciences. GWR is a useful exploratory analytical tool that generates a set of location-specific parameter estimates which can be mapped and analysed to provide information on spatial nonstationarity in relationships between predictors and the outcome variable. A major challenge to GWR users, however, is how best to map these parameter estimates. This paper introduces a simple mapping technique that combines local parameter estimates and local t-values on one map. The resultant map can facilitate the exploration and interpretation of nonstationarity.

Keywords: mapping, nonstationarity, local statistics, Geographically Weighted Regression (GWR)

1. Introduction1

Across the sciences there has been a recent emergence of techniques for examining local relationships in data based on analytical approaches that focus on subsets of data (e.g., locally weighted scatterplot smoothing (LOWESS) a technique developed by Cleveland, 1979). Techniques for the analysis of local spatial relationships also have recently emerged (for an overview see Lloyd, 2011).

The conventional approach in the empirical analyses of spatial data is to calibrate a global model. The term ‘global’ implies that all the spatial data are used to compute a single statistic or equation that is essentially an average of the conditions that exist throughout the study area in which the data have been measured. The underlying assumption in a global model is that relationships between the predictors and the outcome variable are homogeneous (or stationary) across space. More specifically, the global model assumes that the same stimulus provokes the same response in all parts of the study region. However, in practice, the relationships between variables might be nonstationary and vary geographically (Cressie, 1993; Jones and Hanham, 1995). Spatial nonstationarity exists when the same stimulus provokes a different response in different parts of the study region. If nonstationarity exists then there is a suggestion that different processes are at work within the study region.

Standard global modeling techniques, such as ordinary least squares (OLS) linear regression or spatial regression methods, cannot detect nonstationarity and thus their use may obscure regional variation in the relationships between predictors and the outcome variable. Public policy inference based on the results from global models, where nonstationarity is present but not detected, may be quite poor in specific local/regional settings (Ali, Patridge, and Olfert, 2007).

Geographically Weighted Regression (GWR) is a statistical technique that allows variations in relationships between predictors and outcome variable over space to be measured within a single modeling framework (Fotheringham, Brunsdon, and Charlton, 2002; National Centre for Geocomputation, 2009). As an exploratory technique GWR provides a great richness in the results obtained for any spatial data set and should be useful across all disciplines in which spatial data are utilized. Indeed, applications of GWR include studies in a wide variety of demographic fields including but not limited to the analysis of health and disease (Goovaerts, 2005; Nakaya et al, 2005; Yang et al, 2009; Chen et al, 2010), health care delivery (Shoff, Yang, and Matthews, forthcoming), environmental equity (Mennis and Jordan, 2005), housing markets (Fotheringham, Brunsdon, and Charlton, 2002; Yu, Wei, and Wu, 2007), population density and housing (Mennis, 2006), US poverty (Partridge and Rickman, 2005), poverty mapping in Malawi (Benson, Chamberlin, and Rhinehart, 2005), urban poverty (Longley and Tobon, 2004), demography and religion (Jordan, 2006), regional industrialization and development (Huang and Leung, 2002; Yu, 2006), traffic models (Zhao and Park, 2004), the Irish famine (Gregory and Ell, 2005), voting (Calvo and Escolar, 2003) as well as environmental conditions (Foody, 2003).

One of the challenges of GWR applications, however, is the presentation and synthesis of the large number of mappable results that are generated by local GWR models. In this short paper we describe an easy-to-use mapping approach that builds on a paper published by Mennis (2006). We continue in the next section with an overview of GWR modeling and introduce some of the mappable results. Section 3 of this paper includes a brief review of prior mapping approaches and a description of our mapping approach. We include several different GWR mapping strategies as illustration. The paper concludes with a short discussion section.

2: Geographically Weighted Regression (GWR)

Briefly, GWR extends OLS linear regression models by accounting for spatial structure and estimates a separate model and local parameter estimates for each geographic location in the data based on a ‘local’ subset of the data using a differential weighting scheme. The GWR model can be expressed as:

yi=β0(ui,vi)+∑j=1kβj(ui,vi)xij+εi

where yi is the value of the outcome variable at the coordinate location i where (ui,vi) denotes the coordinates of i, β0 and βj represents the local estimated intercept and effect of variable j for location i, respectively. To calibrate this formula, a bi-square weighting kernel function is frequently used (Brunsdon, Fotheringham, and Charlton, 1998a) to account for spatial structure. The locations near to i have a stronger influence in the estimation of βj(ui,vi) than locations farther from i. In the GWR model localized parameter estimates can be obtained for any location i which in turn allows for the creation of a map showing a continuous surface of parameter values and an examination of the spatial variability (nonstationarity) of these parameters.

Fotheringham et al. (2002) likened GWR to a ‘spatial microscope’ in reference to the ability to measure and visualize variations in relationships that are unobservable in aspatial, global models. This modeling approach places an emphasis on differences across space, and the search for the exception or local ‘hot spots.’

GWR is designed to answer the question, “Do relationships vary across space?” It is important to note that GWR approach does not assume that relationships vary across space but is a means to identify whether or not they do. If the relationships do not vary across space the global model is an appropriate specification for the data. GWR can be used as a model diagnostic or to identify interesting locations (areas of variation) for investigation. Researchers typically utilize the Akaike Information Criterion (AIC) (Akaike, 1974) to take model complexity into account and thus facilitating a comparison between the overall model results from a ‘global’ OLS linear regression model with those from the local GWR model. The AIC comparison will reveal whether an explicit spatial perspective significantly improves the model fit.2 A Monte Carlo approach is used to test for nonstationarity in individual parameters (Hope, 1968, Fotheringham, Brunsdon, and Charlton, 2002; Brunsdon, Fotheringham, and Charlton. 1998a). Both OLS linear regression and GWR models can be estimated in the GWR software (National Centre for Geocomputation, 2009)—current version is 4.0—as well as in ArcGIS 10 (ESRI, 2011), SAS® using Proc GENMOD (SAS, 2011) and a SAS macro developed by Chen and Yang (2011) and R using in spgwr (R Development Core Team, 2011). We refer readers to Fotheringham et al. (2002) for a more detailed presentation of the methodology and theory behind GWR (for a brief primer see National Centre for Geocomputation, 2009).

3. Mapping Local GWR results

As has been implied, local and global statistics differ in several important respects most notably that local statistics can take on different values at each location (see Table 1.1 in Fotheringham, Brunsdon, and Charlton, 2002; p. 6). In GWR, the regression is re-centered many times—on each observation—to produce locally specific GWR parameter results. These local GWR results combined generate a complete map of the spatial variation of the parameter estimates. That is, GWR results, unlike global model results, are mappable and ‘given that very large number of potential parameter estimates can be produced, it is almost essential to map them in order to make some sense of the patterns they display’ (Fotheringham, Brunsdon, and Charlton, 2002, p.7). Mapping GWR results facilitates interpretation based on spatial context and known characteristics of the study area (Goodchild and Janelle, 2004).

The statistical output of GWR software typically includes a baseline global model result (parameter estimates), GWR diagnostic information, a convenient parameter 5-number summary of parameter estimates that defines the extent of the variability in the parameter estimates (the 5-number summary is based on the minimum, lower quartile, median, upper quartile, and maximum local parameter estimates reported in the GWR model) and Monte Carlo test result for nonstationarity in each parameter. Even with the 5-number summary of parameter estimates and the formal Monte Carlo test if the researcher wants to better understand and interpret nonstationarity in individual parameters it is necessary to visualize the local parameter estimates and their associated diagnostics. GWR models estimate local standard errors, derive local t-statistics, calculate local goodness-of-fit measures (e.g., R2), and calculate local leverage measures. The output from GWR includes data that can be used to generate surfaces for each model parameter that can be mapped and measured, where each surface depicts the spatial variation of a relationship with the outcome variable.

One of the main challenges for users of GWR is the presentation and synthesis of the large number of results that are generated in local GWR models.3 Partly due to journal/publication limitations on the use of color a number of the early GWR papers used grey-scale maps. As parameter estimates and t-vales can take on both positive and negative numbers designing effective grey-scale maps showing local GWR was a major challenge. More recently the use of divergent color schemes (Brewer, 1994; 1996) represents a major improvement in visualizing GWR results (see Mennis, 2006). As Mennis (2006, p. 172) notes a main issue is that ‘the spatial distribution of the parameter estimates must be presented in concert with the distribution of significance, as indicated by the t-value, in order to yield meaningful interpretation of results.’ Mapping only the parameter estimate alone is misleading as the map reader has no way of knowing whether the local parameter estimates are significant anywhere on the map. Indeed, even with cross-reference to elements in the 5-number summary of parameter-estimates table (e.g., the lower and upper quartile range of parameter estimates) and the Monte Carlo test results does not arm the map reader with sufficient information to be able to discern the areas where local parameter estimates have significant local t-values.

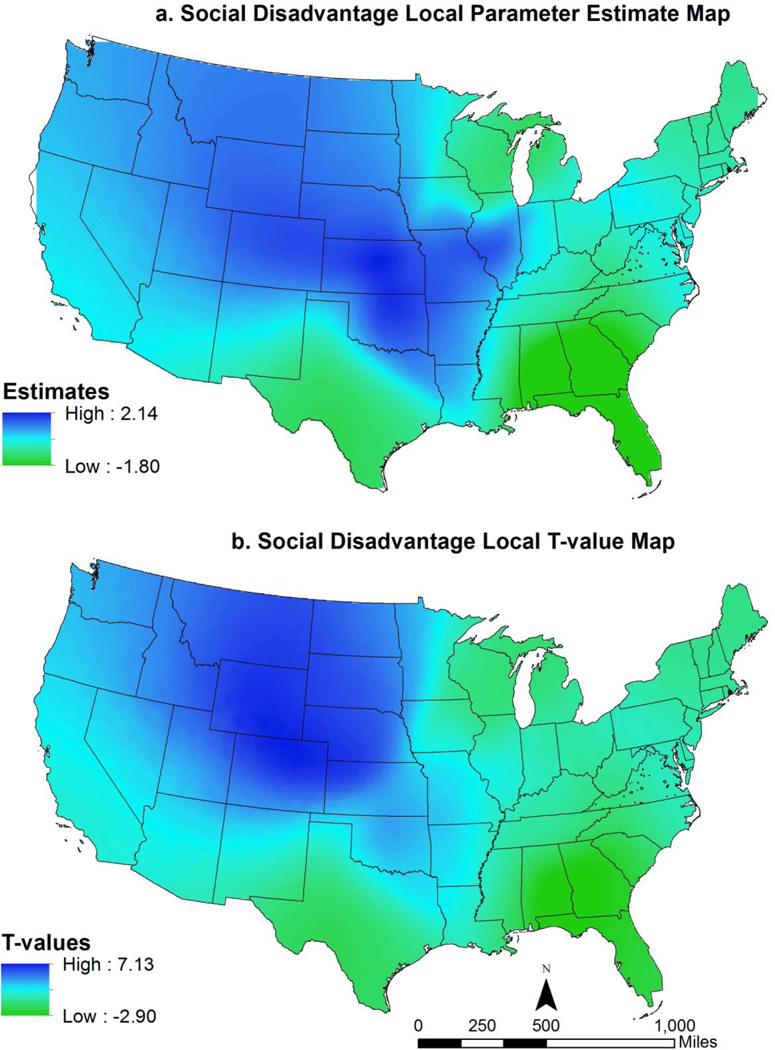
To better illustrate, we visualize the results of a GWR model where the county infant mortality rate is the outcome variable and social disadvantage (a composite variable) is the main predictor.4 Social disadvantage is a composite variable we have used in prior research (Yang, Teng, and Haran, 2009; Chen et al, 2012). The Monte Carlo test results indicated that the association between social disadvantage and infant mortality is nonstationary across place. A rudimentary, but an unsatisfactory strategy is to present two maps, one map showing the local parameter estimates for social disadvantage and the other map showing the local t-value for the same variable (see Figure 1a & 1b).

Figure 1.

Figure 1

Open in a new tab

a. Social Disadvantage Local Parameter Estimate Map

b. Social Disadvantage Local T-value Map

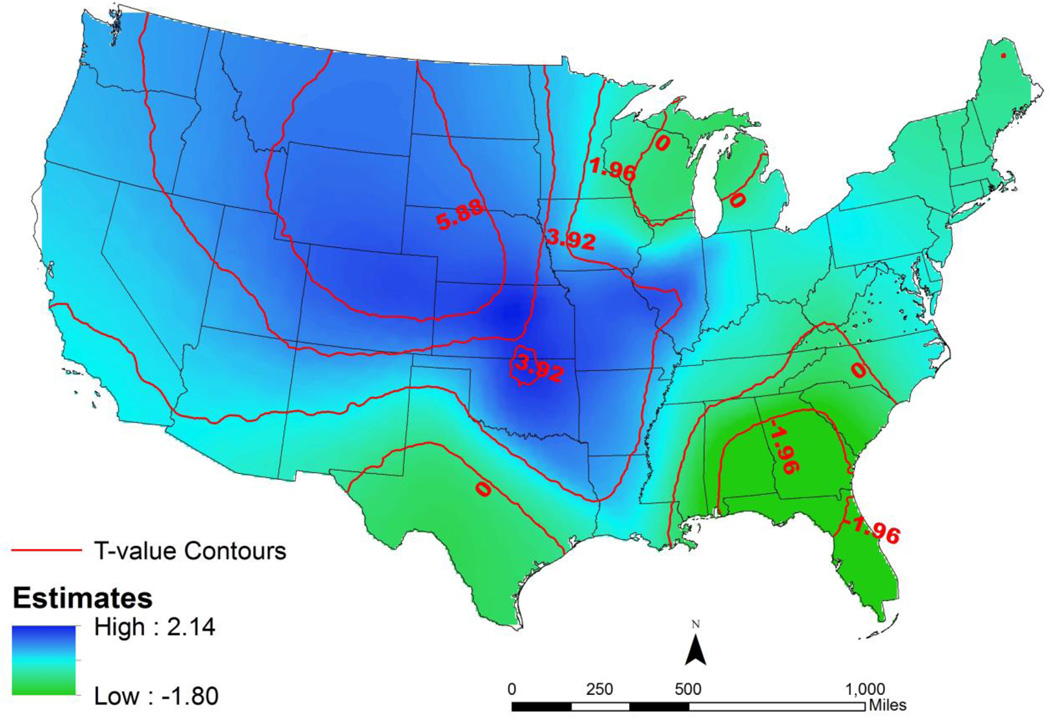
A more sophisticated approach is to overlay specific t-values (e.g., +/− 1.96) as isolines (or contour lines) on top of the parameter estimate surface (see Figure 2).5 The isolines can be defined for any set of data values (e.g., values that correspond to levels of statistical significance).6 The isoline method allows the map reader to read off both the approximate parameter estimate and the t-value for any location on the map. In our example the isolines are relatively easy to interpret but if the range of local t-values is wide it may be difficult to read off exact values, specifically when the isolines follow complex paths or are spaced relatively close together.

Figure 2.

Figure 2

Open in a new tab

Social Disadvantage Overlay of T-value as Isolines on Parameter Estimate Map

Another issue, common to all cartographic design, is the placement of text labels attached to the contour lines. In current GIS software these decisions can be automated based on optimum text-placement criteria but this does not guarantee the placement of text will not obscure salient areas of the map. The isoline approach places more burden on the map reader to recognize and then potentially eliminate from further consideration of those parts of the map where the local t-value is not significant. That is, this map form does not place visual emphasis on the parts of the surface where local parameter estimates are significant. In our own work we have experimented with the isoline overlay approach but in many of our applications we also wanted to show the basic outline of geographic areas (e.g., states or counties in US-based applications). When faced with such decisions regarding our own map design, the addition of isolines more often than not contributed to potential chartjunk (Tufte, 1983) and possibly more confusion for the map reader. We required a more elegant mapping design for our GWR applications.

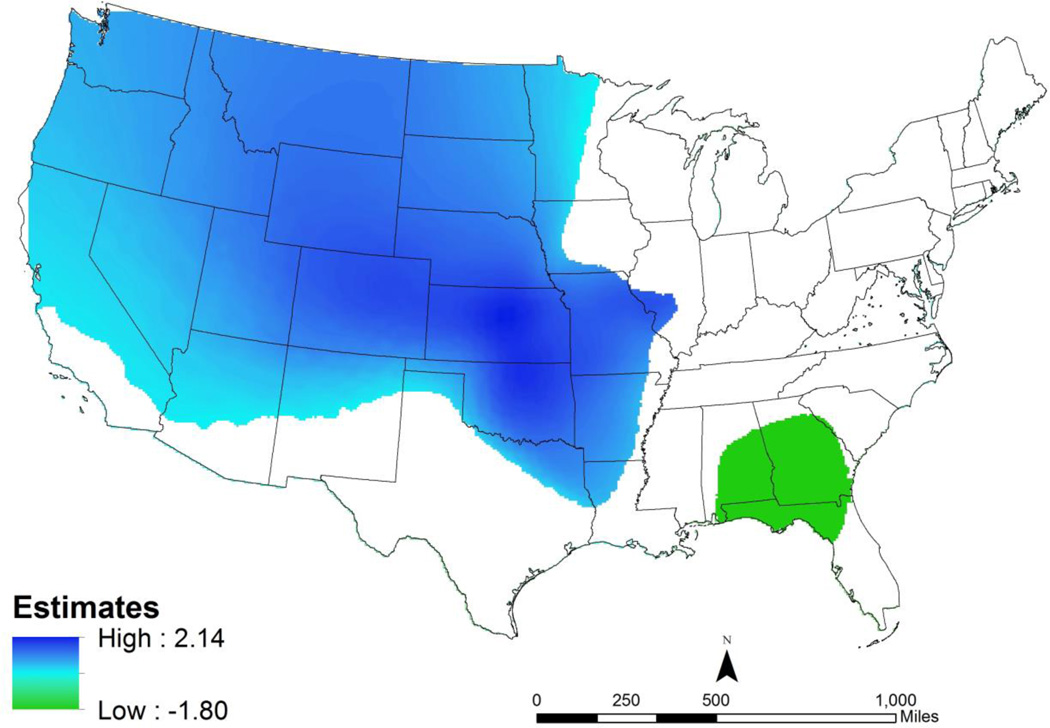
Mennis (2006) reminds GWR users that bivariate choropleth mapping is a viable approach for mapping the GWR parameter estimate and the local t values simultaneously. Bivariate choropleth mapping was first introduced by Olson (1975); see also Eyton (1984) and Dunn (1989). Further Mennis combines a bivariate choropleth mapping with masking approaches that effectively limit the presentation of results to only those areas of the study area (the map) where t-values are significant. We adapt the approach of Mennis (2006).7

Briefly, in ArcGIS 10 (ESRI, 2011) we create the surface of estimated coefficients and the local t-values for a selected parameter, social disadvantage. Within ArcGIS 10 it is trivial to set up a mask in one data layer (i.e., the local t-values) and to order this to be visually above or on top of another data layer (i.e., the local parameter estimate). The t-value data layer is set up so that data values lying between −1.96 and +1.96 are masked out (showing white on Figure 3) while data values smaller than −1.96 or greater than +1.96 are set to 100% transparency. Transparency means that the data stored in another data layer below will be seen unobstructed. Whereas Mennis uses a data classification scheme based on standard-deviation and N-class methods (based on optimal methods for maximizing within-class homogeneity) we use a continuous bivariate color scheme for the parameter estimate surface. In Figure 3 the significant positive parameters estimates are represented by shades of blue, while the significant negative parameter estimates are shades of green. We have used this map design in two prior papers (Chen et al, 2012; Shoff, Yang, and Matthews, forthcoming).

Figure 3.

Figure 3

Open in a new tab

Social Disadvantage With New Mapping Approach

4. Discussion

Fotheringham and colleagues developed GWR into a convenient, yet powerful, technique that explores spatial nonstationarity and provides mappable statistics to visualize the spatial patterns of the relationships between dependent and independent variables (Brunsden, Fotheringham, and Charlton, 1996; Brunsdon, Fotheringham, and Charlton, 1998a, 1998b; Fotheringham, Brunsdon, and Charlton, 1997; Fotheringham, Brunsdon, and Charlton, 2002). GWR has recently been identified as one of the geo statistical methods that should be promoted in health studies in light of the locality of health outcomes (Young and Gotaway, 2010). Moreover, it is argued that GWR can potentially make significant contributions to health research, such as allowing researchers to better understand the etiology and spatial processes, offering informative results beyond global models to facilitate place-specific health policy formation, and enabling scholars to explore questions that cannot be answered with traditional (global) analytical models. As we reported above, GWR is a useful exploratory technique in all demographic-related disciplines where spatial data are used and in applications where spatial nonstationarity is suspected (and should be checked for).

Like other analytic methods, GWR has limitations, including issues associated with multicollinearity, kernel bandwidth selection, and multiple hypothesis testing (Wheeler and Tiefelsdorf, 2005; Wheeler 2007, 2009; Cho et al, 2009; Jiang et al, 2010; Wheeler and Páez, 2010). Some of these issues have been addressed (Wheeler 2007, 2009). GWR is generally regarded as a useful tool for exploring spatial nonstationarity and interpolation (Páez, Long, and Farber, 2008; Wheeler and Páez, 2010) but further testing is required (Páez, Farber, and Wheeler, 2011).

In this brief paper we reviewed some standard but ultimately poor approaches to visualizing local parameter estimates. We offer a fairly simple map format based on the inherent strengths of a GIS and sound cartographic design that allows for two variables, specifically both local statistics – the parameter estimate and the t-value – to be mapped together, by laying one layer file above another layer. Using masking and transparency techniques on the local t-value layer we allow only the significant parameter estimate values to be visualized (see footnote 5). This mapping template allows the map reader to focus on the primary areas of interest in the map. This approach represents a significant improvement over mapping all local parameter estimates irrespective of whether they are significant.

Acknowledgements

This work was partially supported by internal funds from the Social Science Research Institute at Penn State. Additional support has been provided by the Geographic Information Analysis Core at Penn State's Population Research Institute, which receives core funding from the Eunice Kennedy Shriver National Institutes of Child Health and Human Development (R24-HD41025). We thank Nyesha Black, Aggie Noah, and Carla Shoff for their comments and suggestions regarding our manuscript. All errors remain our own.

Footnotes

1

The motivation for this paper stems from reading GWR papers and seeing many generic maps of local parameter estimates with no reference to significance levels and a general dissatisfaction with our own experience with maps of parameter estimate surfaces overlaid with t-value isolines. GWR is becoming more popular in spatial demography and it is important to design effective and useful maps of local GWR results. Several papers in this special collection on spatial demography use GWR.

2

It should be noted that the repeated use of data for local estimates calculation in GWR may lead to a problem that AIC fails to serve as a goodness-of-fit indicator. A permutation-based approach may provide a solution to this issue (see Salas et al., 2010). As a rule of thumb, a difference (or reduction) of > 3 in the AIC between the global model and the local GWR signifies better model fit (Forthingham, Brunsdon, and Charlton, 2002 p.70). Fotheringham, Brunsdon and Charlton, 2002, p. 95–102 discuss the use of AIC in model selection comparing global models and local GWR as well as two GWR models with different explanatory variables or with the same variables but different bandwidths.

3

Partly due to journal/publication limitations on the use of color a number of the early GWR papers use grey-scale maps. As parameter estimates and t-vales can take on both positive and negative numbers designing effective grey-scale maps showing local GWR was a major challenge. More recently the use of divergent color schemes (Brewer, 1994; 1996) represents a major improvement in visualizing GWR results (see Mennis, 2006).

4

This simple model includes other controls (e.g., race/ethnic composition).

5

We note that Byrne, Charlton, and Fotheringham (2009) use an adjustment to take advantage of the dependency between local GWR models based on a Bonferroni style adjustment for multiple hypotheses testing.

6

Mennis (2006) used data classes corresponding to significance levels (.10 and .01) in his bivariate maps – see Figure 6b, p. 176.

7

Our approach is based on the integrated use of GWR 3.0/4.0 and ArcGIS 10. Please contact the authors for a full description of the process and a tutorial document based on a sample data set. The tutorial document walks the user through different stages of the process from GWR output file results through to final map construction (the main stages in the process include the conversion of e00 files into coverage files, use of Spatial Analyst to create raster surfaces, and setting up the map design/template specifications).

Contributor Information

Stephen A. Matthews, Anthropology and Demography, Faculty Director of the Geographic Information Analysis Core, Population Research Institute, Social Science Research Institute, The Pennsylvania State University.

Tse-Chuan Yang, Geographic Information Analysis Core Population Research Institute, Social Science Research Institute, The Pennsylvania State University.

References

  1. Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19(6):716–723. [Google Scholar]
  2. Ali K, Partridge MD, Olfert MR. Can geographically weighted regressions improve regional analysis and policy making? International Regional Science Review. 2007;30:300–331. [Google Scholar]
  3. Benson T, Chamberlin J, Rhinehart I. An investigation of the spatial determinants of the local prevalence of poverty in rural Malawi. Washington DC: International Food Policy Research Institute; 2005. [Google Scholar]
  4. Brewer CA. Color use guidelines for mapping and visualization. In: MacEachren A, Taylor DRF, editors. Visualization in modern cartography. New York, NY: Elsevier; 1994. pp. 123–147. [Google Scholar]
  5. Brewer CA. Guidelines for selecting colors for diverging schemes on maps. The Cartographic Journal. 1996;33:79–86. [Google Scholar]
  6. Brunsdon C, Fotheringham AS, Charlton M. Spatial nonstationarity and autoregressive models. Environment and Planning A. 1998a;30(6):957–973. [Google Scholar]
  7. Brunsdon C, Fotheringham AS, Charlton M. Geographically weighted regression: modelling spatial non-stationarity. Journal of the Royal Statistical Society. Series D (The Statistician) 1998b;47(3):431–443. [Google Scholar]
  8. Byrne G, Charlton M, Fotheringham S. Multiple dependent hypothesis tests in geographically weighted regression. In: Lees BG, Laffan SW, editors. 10th International Conference on GeoComputation; UNSW, Sydney. 2009. Nov-Dec. [last accessed February 1, 2012]. Available online at http://www.biodiverse.unsw.edu.au/geocomputation/proceedings/PDF/Byrne_et_al.pdf. [Google Scholar]
  9. Calvo E, Escolar M. The local voter: a geographically weighted regression approach to ecological inference. American Journal of Political Science. 2003;47(1):189–204. [Google Scholar]
  10. Chen CY-J, Den W-S, Yang T-C, Matthews SA. Geographically weighted quantile regression (GWQR): An application to US mortality data. Geographical Analysis. 2012;44(2):xxx–xxx. doi: 10.1111/j.1538-4632.2012.00841.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chen VY-J, Wu P-C, Yang T-C, Su H-J. Examining non-stationary effects of social determinants on cardiovascular mortality after cold surges in Taiwan. Science of the Total Environment. 2010;408(9):2042–2049. doi: 10.1016/j.scitotenv.2009.11.044. [DOI] [PubMed] [Google Scholar]
  12. Chen VY-J, Yang T-C. SAS macro programs for geographically weighted generalized linear modeling with spatial point data: Applications to health research, Computer Methods and Programs in Biomedicine. 2011 doi: 10.1016/j.cmpb.2011.10.006. available online since 9 November 2011. [DOI] [PubMed] [Google Scholar]
  13. Cho S, Lambert DM, Kim SG, Jung S. Extreme coefficients in geographically weighted regression and their effects on mapping. GIScience and Remote Sensing. 2009;46(3):273–288. [Google Scholar]
  14. Cleveland WS. Robust locally weighted regression and smoothing scatterplots. Journal of the American Statistical Association. 1979;74(368):829–836. [Google Scholar]
  15. Cressie NAC. Statistics for spatial data. New York, NY: John Willey & Sons; 1993. [Google Scholar]
  16. Dunn R. A dynamic approach to two-variable color mapping. The American Statistician. 1989;43(4):245–252. [Google Scholar]
  17. ESRI. ArcGIS Desktop: Release 10. Redlands, CA: Environmental Systems Research Institute; 2011. [Google Scholar]
  18. Eyton DR. Map supplement: complementary-color, two-variable maps. Annals, Association of American Geographers. 1984;74(3):477–490. [Google Scholar]
  19. Foody GM. Geographical weighting as a further refinement to regression modelling: An example focused on the NDVI-rainfall relationship. Remote Sensing of the Environment. 2003;88(3):283–293. [Google Scholar]
  20. Fotheringham AS, Brunsdon C, Charlton ME. Two techniques for exploring non-stationarity in geographical data. Geographical Systems. 1997;4:59–82. [Google Scholar]
  21. Fotheringham AS, Charlton M, Brunsdon C. Geographically weighted regression: a natural evolution of the expansion method for spatial data analysis. Environment and Planning A. 1998;30:1905–1927. [Google Scholar]
  22. Fotheringham AS, Brunsdon C, Charlton ME. Geographically weighted regression: The analysis of spatially varying relationship. New York, NY: Wiley; 2002. [Google Scholar]
  23. Goodchild MF, Janelle DG. Spatially integrated social science. New York, NY: Oxford University Press; 2004. [Google Scholar]
  24. Goovaerts P. Proceedings of GIS Planet. Estoril, Portugal: 2005. May-Jun. Analysis and detection of health disparities using geostatistics and a space-time information system: the case of prostate cancer mortality in the United States, 1970–1994. 2005. [Google Scholar]
  25. Gregory IN, Ell PS. Analyzing spatiotemporal change by use of National Historical Geographical Information Systems: population change during and after the Great Irish Famine. Historical Methods. 2005;38(4):149–167. [Google Scholar]
  26. Hope ACA. A simplified Monte Carlo significance test procedure. Journal of the Royal Statistical Society: Series B (Methodological) 1968;30(3):582–598. [Google Scholar]
  27. Huang Y, Leung Y. Analyzing regional industrialization in Jiangsu province using geographically weighted regression. Journal of Geographical Systems. 2002;4:233–249. [Google Scholar]
  28. Jiang B, Yao X, Wheeler DC. Visualizing and diagnosing coefficients from geographically weighted regression models. In: Sui DZ, Tietze W, Claval P, Gradus Y, Park SO, Wusten H, editors. Geospatial analysis and modelling of urban structure and dynamics. Netherlands: Springer; 2010. pp. 415–436. [Google Scholar]
  29. Jones JP, III, Hanham RQ. Contingency, realism and the expansion method. Geographical Analysis. 1995;27:185–207. [Google Scholar]
  30. Jordan LM. Ph.D. Thesis. Boulder, Colorado: University of Colorado at Boulder, Department of Geography; 2006. Religion and demography in the United States: A geographical analysis. [Google Scholar]
  31. Lloyd C. Local models for spatial analysis. Second Edition. Boca Raton, FL: CRC Press; 2011. [Google Scholar]
  32. Longley PA, Tobon C. Spatial dependence and heterogeneity in patterns of hardship: an intra-urban analysis. Annals Association of American Geographers. 2004;94:503–519. [Google Scholar]
  33. Mennis JL. Mapping the results of geographically weighted regression. The Cartographic Journal. 2006;43(2):171–179. [Google Scholar]
  34. Mennis JL, Jordan LM. The distribution of environmental equity: exploring spatial nonstationarity in multivariate models of air toxic releases. Annals, Association of American Geographers. 2005;95(2):249–268. [Google Scholar]
  35. Nakaya T, Fotheringham AS, Brunsdon C, Charlton M. Geographically weighted Poisson regression for disease association mapping. Statistics in Medicine. 2005;24(17):2695–2717. doi: 10.1002/sim.2129. [DOI] [PubMed] [Google Scholar]
  36. National Center for Geocomputation. Maynooth, Ireland: National University of Ireland; 2009. [last accessed Feb 1, 2012]. http://ncg.nuim.ie/ncg/GWR/software.htm. [Google Scholar]
  37. Olson J. Spectrally encoded two-variable maps. Annals of the Association of American Geographers. 1981;71(2):259–276. [Google Scholar]
  38. Páez A, Farber S, Wheeler DC. A simulation-based study of geographically weighted regression as a method for investigating spatially varying relationships. Environment and Planning A. 2011;43:2992–3010. [Google Scholar]
  39. Páez A, Long F, Farber S. Moving window approaches for hedonic price estimation: an empirical comparison of modelling techniques. Urban Studies. 2008;45(8):1565–1581. [Google Scholar]
  40. Partridge MD, Rickman DS. Rural Poverty Research Center (RPRC) Working Paper-05--02. Columbia, MO: Rural Poverty Research Center; 2005. [Jaunary 2005]. Persistent pockets of extreme American poverty: people or place based? [Google Scholar]
  41. R Development Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2011. [last accessed February 1, 2012]. URL: http://www.R-project.org) [Google Scholar]
  42. Salas C, Ene L, Gregoire TGE, Sset N, Gobakken T. Modelling tree diameter from airborne laser scanning derived variables: a comparison of spatial statistical models. Remote Sensing of Environment. 2010;114:1277–1285. [Google Scholar]
  43. SAS. SAS Institute Inc.; Cary NC, USA: 2011. [Google Scholar]
  44. Shoff C, Yang T-C, Matthews SA. What has geography got to do with it? Using GWR to explore place-specific associations with prenatal care utilization. GeoJournal. doi: 10.1007/s10708-010-9405-3. (forthcoming). Online First January 21, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Tufte E. The visual display of quantitative information. Cheshire, CT: Graphics Press; 1983. [Google Scholar]
  46. Wheeler DC. Diagnostic tools and a remedial method for collinearity in geographically weighted regression. Environment and Planning A. 2007;39(10):2464–2481. [Google Scholar]
  47. Wheeler DC. Simultaneous coefficient penalization and model selection in geographically weighted regression: the geographically weighted lasso. Environment and Planning. 2009;41(3):722–742. [Google Scholar]
  48. Wheeler DC, Páez A. Geographically weighted regression. In: Fischer MM, Getis A, editors. Handbook of applied spatial analysis: Software tools, methods and applications. Berlin and Heidelberg: Springer; 2010. pp. 461–486. [Google Scholar]
  49. Wheeler DC, Tiefelsdorf M. Multicollinearity and correlation among local regression coefficients in geographically weighted regression. Journal of Geographical Systems. 2005;7:161–187. [Google Scholar]
  50. Yang T-C, Teng HW, Haran M. The impacts of social capital on infant mortality in the US: A spatial investigation. Applied Spatial Analysis and Policy. 2009;2(3):211–227. [Google Scholar]
  51. Yang T-C, Wu P-C, Chen VY-J, Su H-J. Cold surge: A sudden and spatially varying threat to health? Science of the Total Environment. 2009;407(10):3421–3424. doi: 10.1016/j.scitotenv.2008.12.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Young LJ, Gotway CA. Using geostatistical methods in the analysis of public health data: the final frontier? geoENV VII - Geostatistics for Environmental Applications. 2010;16:89–98. [Google Scholar]
  53. Yu D-L. Spatially varying development mechanisms in the Greater Beijing area: a geographically weighted regression investigation. Annals of Regional Science. 2006;40:173–190. [Google Scholar]
  54. Yu D-L, Wei YD, Wu C. Modeling spatial dimensions of housing prices in Milwaukee, WI. Environment and Planning B: Planning and Design. 2007;34(6):1085–1102. [Google Scholar]
  55. Zhao F, Park N. Transportation Research Record 1879. Wsashinton DC: Transportation Research Board, National Research Council; 2004. Using geographically weighted regression models to estimate annual average daily traffic; pp. 99–107. [Google Scholar]

RESOURCES