Abstract
The determination of a complete set of rate constants (free energy profiles; FEPs) for a complex kinetic mechanism is challenging. Enzymologists have devised a variety of informative steady-state kinetic experiments (e.g., Michaelis-Menten kinetics, viscosity dependence of kinetic parameters, KIEs, etc.) that each provide distinct information regarding a particular kinetic system. A simple method for combining steady-state experiments in a single analysis is presented here, which allows microscopic rate constants and intrinsic kinetic isotope effects to be determined. It is first shown that Michaelis-Menten kinetic parameters (kcat and KM values), kinetic isotope efffets, solvent viscosity effects, and intermediate partitioning measurements are sufficient to define the rate constants for a reversible uni-uni mechanism with an intermediate, EZ, between the ES and EP complexes. Global optimization provides the framework to combine the independent experimental measurements, and the search for rate constants is performed using algorithms implemented in the biochemical software COPASI. This method is applied to the determination of FEPs for both alanine racemase and triosephosphate isomerase. The FEPs obtained from global optimization agree with those in the literature, with important exceptions. The method opens the door to routine and large-scale determination of FEPs for enzymes.
Introduction
Enzymatic free energy profiles (FEPs; i.e., energies for all ground and transition states) provide profound insight into the nature of biological catalysis and its evolution. (1) The kinetic complexity of enzyme mechanisms has traditionally made the determination of FEPs a complex task requiring enzyme-specific experimental designs. Albery and Knowles presented a method for determining FEPs by using isotopic kinetic measurements for triosephosphate isomerase (TIM) (2), and later, proline racemase (3). Unfortunately, the mathematical framework they used is difficult for enzymological audiences, and is not fully general. Representative examples in the literature employ diverse kinetic information and no common framework. (4–18) A straightforward and general method for determining enzymatic FEPs would greatly aid efforts to understand the origins of biological catalysis.
Historically, attempts to define FEPs using steady-state experiments have had variable success (2, 16, 19, 20). For example, Knowles and coworkers were not able to define the energies of one transition state (DHAP binding) and two ground states (enediol and E-GAP intermediates) for TIM in a four step mechanism that includes a carbanionic intermediate (Scheme 1). Maurice and Bearne successfully employed kcat, KM, and viscosity effects to define a simplified three-step mechanism for mandelate racemase (21). To our knowledge, no work systematically examining the extent to which common steady-state kinetic experiments can define enzymatic FEPs has appeared.
Scheme 1.
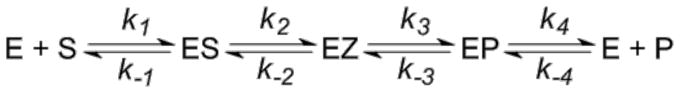
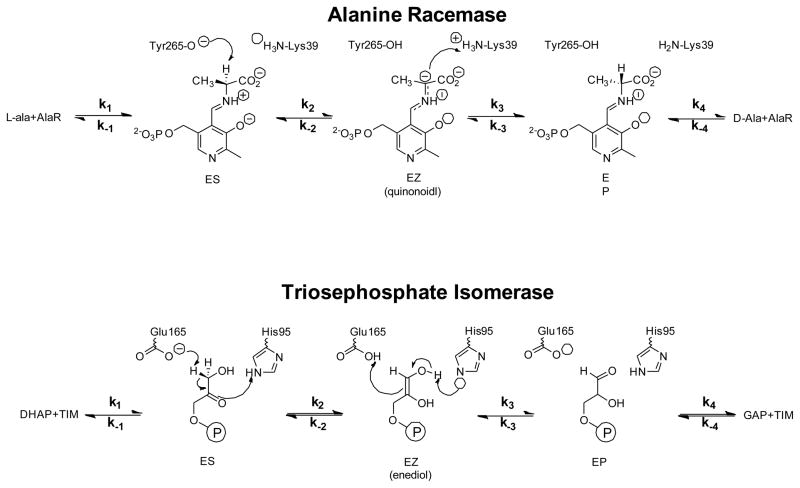
Kinetic mechanism for AR and TIM. ES and EP correspond to the enzyme/substrate (AR/L-Ala, TIM/DHAP) and enzyme/product (AR/D-Ala, TIM/GAP) complexes, respectively, while EZ corresponds to the intermediate (AR/quinonoid, TIM/enediol).
Alanine racemase (AR; EC 5.1.1.1) is a pyridoxal-5′-phosphate dependent amino acid racemase that catalyzes the reversible interconversion of alanine stereoisomers and provides bacteria with D-alanine for peptidoglycan biosynthesis. Trisoephosphate isomerase (TIM; EC 5.3.1.1) catalyzes the reversible interconversion of D-glyceraldehyde 3-phosphate (GAP) and dihydroxyacetone phosphate (DHAP) in glycolysis. Both enzymes employ a reversible uni-uni kinetic mechanism that is applicable to a wide variety of enzyme catalyzed reactions (Scheme 1). It encompasses five ground states coupled through four reversible steps, with two Michaelis complexes (ES and EP) and an intermediate (EZ) as enzyme-bound species.
Using this general mechanism as an example, we apply results from common steady-state kinetic experiments (e.g., kcat and Km, viscosity dependence of kcat/Km, KIEs, and intermediate partitioning) to determine FEPs. Global optimization is used to search for rate constant values that agree with experimental measurements. The procedure is illustrated here by application to AR and TIM, for which FEPs were determined previously (22, 23).
Experimental Section
Materials
AR from B. stearothermophilus was expressed and purified as previously described (24).
kcat and Km determination
kcat and Km values for AR were determined by global nonlinear regression fitting of a reversible Michaelis-Menten model to progress curves from previous work (22), using the parameter estimation task in COPASI (25, 26) with kcat and Km values as adjustable parameters (Figure 1A).
Figure 1.

Global fitting to AR progress curves, and UV-vis detection of the quinonoid intermediate. (A) Global nonlinear regression fitting of the reversible Michaelis-Menten mechanism to progress curves at pH 8.9 and 25 °C. Experimental data are in black and fitted curves are in red. The Michaelis-Menten parameters in Table 1 were derived from this fit. (B) Difference spectrum of AR at pH 8.9 and 25 °C: 3.5 mM AR in the presence of saturating D, L-alanine, minus AR without alanine. A positive peak near 500 nm is indicative of the quinonoid intermediate.
Quinonoid intermediate equilibrium constant
Absorbance spectra of 3.5 mM AR in 50 mM CHES pH 8.9 at 25 °C in the absence and presence of saturating D, L-alanine (250 mM) were recorded between 450 and 600 nm (Figure 1B). Quantification of the quinonoid intermediate concentration used a molar absorption coefficient of 40,000 (M·cm)−1 (27). KEZ was calculated based on the total enzyme concentration.
Equations
A. Michaelis-Menten parameters
Expressions for kcat and Km in terms of microscope rate constants for the mechanism presented in Scheme 1 were obtained using the net rate constant method of Cleland (28).
| (1) |
| (2) |
| (3) |
| (4) |
B. Viscosity dependence of kcat/Km
The dependence of enzyme reaction rate on solvent viscosity allows one to determine the extent to which transition states for bimolecular steps are rate-limiting. In typical viscosity experiments, kcat/Km and/or kcat is measured at different concentrations of a viscosogen (e.g., glycerol, sucrose). Brouwer and Kirsch (29) showed that the dependence of relative kcat/Km values [i.e., (kcat/Km)η0/(kcat/Km)η] on relative viscosity (η/η0) is linear, with k2/k−1 as the value of the slope for a minimal mechanism in which substrate binding is the only viscosity dependent step. This presentation is now common in the literature. The mechanism of Scheme 1 leads to Eq. (5) as an expression for the slope of a plot of relative kcat/Km vs. relative viscosity.
| (5) |
Here, superscript 0 indicates the value of a viscosity dependent rate constant in the absence of viscosogen (i.e., at a relative viscosity of 1). Identical equations are obtained for both directions of reaction, and this is borne out experimentally in the literature (21, 30, 31). Although the present work does not make use of viscosity effects on kcat, such measurements contain additional information that can be exploited (21). The absolute instead of relative values of kcat/KM provide additional information in the slope and intercept terms that can be used (21).
C. Intermediate partitioning
The EZ partition ratio (k−2/k3) is contained in, but not uniquely determined by, the ratio of the net rate constants for formation of either substrate or product from the intermediate. The ratio of these net rate constants can be obtained from experiments that quantify the relative rates of EZ reverting to substrate vs. proceeding to product. Traditionally, two types of experiments have been employed: 1) measuring the rate of isotope exchange from substrate to solvent relative to the rate of product formation, and 2) measuring the partitioning of an exogenously supplied, stable reaction intermediate to substrate vs. product. From Scheme 1, one can derive the partition ratio, θ, for EZ going to substrate vs. product.
| (6) |
D. KIEs
Both AR and TIM rapidly exchange a hydron from a substrate C-H bond for a solvent derived one at the EZ intermediate (32, 33). Isotope washout into the solvent pool leads to a single isotopically sensitive step (k2 or k−3, depending on the direction of the reaction) to be considered since the reverse of the isotopically sensitive step occurs with a solvent-derived hydron (protium) being transferred (2, 34). Following Northrop (35), expressions for the forward and reverse deuterium KIEs on kcat and kcat/Km are defined as follows.
| (7) |
| (8) |
| (9) |
| (10) |
These expressions can be combined in ratios to give Eqs. (11) and (12), where no value for the intrinsic KIE is required for application (36).
| (11) |
| (12) |
E. On-enzyme equilibria
For many enzymes, concentrations of reaction intermediates can be quantified with the system at equilibrium. Quantification can take the form of spectroscopic detection (such as the EZ intermediate in AR) or chemical analysis of quenched reactions. The equilibrium constant for the EZ intermediate with respect to the total enzyme concentration in the presence of saturating substrate and product is given in Eq. (13).
| (13) |
Numerical methods
Global optimization methods have broad application, including electrical circuit design, route planning for delivery services, protein structure prediction, pharmacokinetics, and chemical kinetics to name a few (37–43). Recently, advances in defining rate constants for complex chemical systems using a generalized Fisher equation and global optimization have been made. (44, 45)
The optimization process used here does not involve numerical integration of differential rate equations to obtain the time dependence of concentrations as is required for global nonlinear regression of progress curves. In global optimization, the adjustable parameters (rate constants) are altered by the algorithm of choice, and the new parameters are simply used to calculated a new value for the target function. This is less computationally demanding than fitting to primary kinetic data via numerical integration, allowing much greater exploration of parameter space for a given set of computational facilities. For example, the genetic algorithm (GA) in COPASI on a single core of a 2.8 GHz AMD PhenomII 830 achieves ~108 evaluations/hr in global optimization, yet only ~105 evaluations/hr when fitting to 8 progress curves (500 data points each) via numerical integration. This ~1000-fold difference is significant in the search for rate constants.
Global optimization algorithms fall into four main categories: random, deterministic, stochastic (e.g., simulated annealing), and heuristic (e.g., genetic algorithms, swarm algorithms) (46). The freely available biochemical simulation and analysis software COPASI (25) implements examples of all these categories, and was used here.
One key to defining enzymatic FEPs by global optimization is the definition of the target function (also known as the “merit” or “loss” function). A sum of squared absolute values of residuals between calculated and experimental values divided by the experimental value (“mean normalized” least squares target function) was chosen (Eq. 14).
| (14) |
Here, kL is kcat for the L→D direction, KL is KM for the L→D direction, “Visc” is the effect of viscosity on relative kcat/KM values, etc. Random initial values for all parameters were set automatically by COPASI at the beginning of each optimization run. The use of the mean normalized difference between calculated and observed values weights the different measurements equally. This is essentially a sum of chi squared statistics for each experimental measurement. (47) It is analogous to the commonly used relative weighting scheme in nonlinear regression. (48)
The usual chi squared used in nonlinear regression replaces the mean of the experimental measurement by the standard deviation of the experimental measurement in the denominator, weighting measurements based on their uncertainties. This “error normalized” target function was explored, as was a least absolute deviations target function that is less sensitive to outlier observations. (49)
Microscopic rate constants and intrinsic KIEs (where applicable) were adjustable parameters. For bimolecular constants, the lower bound was kcat/Km for the respective direction, and the upper bound was 109 M−1s−1 (diffusion limit). For unimolecular constants, the lower bound was kcat for the respective direction, and the upper bound was 1012 s−1 (vibrational limit). The values of intrinsic deuterium KIEs were limited to the semi-classical range of 1 – 6. The use of these limits is important for restricting the parameter space searched to a productive one.
The search of parameter space was performed in two phases. First, a broad search over the rate constant limits given above was performed using the “genetic algorithm” in COPASI. Second, a focused search was performed to define well the sum of squared residuals (SSR) surface: narrower limits on each parameter that corresponded to a 50-fold increase in SSR from the lowest values obtained in the first search were set. The latter employed the “particle swarm” algorithm in COPASI. The searches employed here were comprised of 105–106 independent calculations. Each calculation started with randomized initial values for the parameters, within the specified limits. This was automated using the “parameter scan” task in COPASI.
The errors on the fitted parameter values were estimated using a Monte Carlo procedure as described by Motulsky. (48) An alternative is to use an F statistic to determine confidence intervals, but this is considerably more complicated for the present application because of the large number of parameters and the need to account for covariation. (48)
Results
A. Reproduction of Synthetic FEPs
First, it is important to ask and answer the question of whether or not the experimental measurements available inherently contain enough information to define the rate constants for the mechanism in Scheme 1. To this end, a set of rate constants for the mechanism was assumed, hypothetical values of experimental measurements (see Tables 1 and 2 for the measurements at issue) were calculated based on the assumed rate constant values, and these calculated values were employed in global analysis to find rate constants that are concordant with them. This theoretical exercise determines whether or not the proposed experimental measurements (Tables 1 and 2) retain enough information to reproduce the rate constants that generated them, under the applied constraints.
Table 1.
Values of experimental measurements used in the FEP calculations for AR. EZ corresponds to the quinonoid intermediate. Errors are given in parentheses.
| L→D | D→L | |
|---|---|---|
| kcat (s-1) | 1740 (10) | 1280 (12) |
| Km (mM) | 5.4 (0.1) | 4.0 (0.1) |
| Dkcat | 1.5 (0.1) | 1.4 (0.03) |
| D(kcat/Km) | 1.6 (0.1) | 1.3 (0.1) |
| Rel visc slope | 0.015 (0.015) | |
| θ | 0.5 (0.1) | |
| KEZ | 1.6·10−4 (0.4·10−4) | |
Table 2.
Values of experimental measurements used in the FEP calculations for TIM. EZ corresponds to the enediol intermediate. Errors are given in parentheses.
| DHAP→GAP | GAP→DHAP | |
|---|---|---|
| kcat (s−1) | 750 (50) | 8350 (350) |
| Km (mM) | 1.35 (0.15) | 0.05 (0.01) |
| Dkcat | 3.4 (0.1) | 1.6 (0.1) |
| D(kcat/Km) | 3.4 (0.1) | 1.6 (0.1) |
| Rel visc slope | 0.8 (0.1) | |
| θ | 3 (1) | |
| KDHAP | 0.95 | |
| KGAP | ≤0.05 | |
| KEZ | ≤0.05 | |
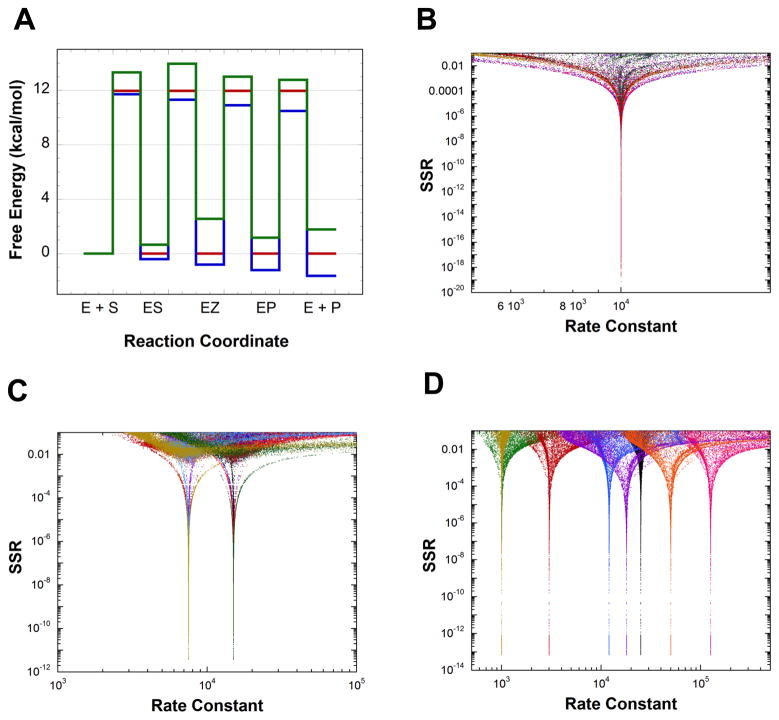
Figure 2A presents three dissimilar, hypothetical FEPs from which rate constants for the mechanism shown in Scheme 1 were calculated. These rate constants were used to calculate hypothetical values of kcat and KM for both directions, the slope of relative kcat/KM vs. relative viscosity, θ, KEZ, and KIEs on both kcat and kcat/KM for both directions (assuming intrinsic KIEs of 2). The hypothetical values were used in global optimization to find sets of rate constants that are consistent with them. Figures 2B–D show the results of global optimization. The only sets of rate constants that give low SSR values (the lower the SSR value, the better the fit) are the original rate constants derived from the hypothetical FEPs, and only intrinsic KIEs of 2 were returned (not shown). This computational exercise shows that the measurements employed here contain in principle (in practice, depending on the errors in the measurements) sufficient information to define the rate constants for the mechanism of Scheme 1 as well as the intrinsic KIEs on the steps leading to the EZ intermediate for three dissimilar FEPs.
Figure 2.
Definition of synthetic FEPs by global optimization using Michaelis-Menten constants, intermediate partitioning, solvent viscosity effects, intermediate equilibrium constant, and KIEs. Rate constants were calculated from the free energy profiles in part A. These rate constants were used to calculate theoretical values for the measurements, which were used in global optimization to find sets of rate constants compatible with them. Only the original rate constants used to calculate the theoretical measurements are returned as good solutions from global optimization. (A) Three synthetic FEPs used to calculate rate constants. Standard state is 1 mM. (B) Rate constants vs. SSR from global optimization for calculations based on the red FEP in part A. (C) Rate constants vs. SSR from global optimization for calculations based on the blue FEP in part A. (D) Rate constants vs. SSR from global optimization for calculations based on the green FEP in part A.
The contributions of different types of experiments to the definition of the red FEP in Figure 2A (all rate constants equal 10,000 s−1 at a standard state of 1 mM) was explored by removing them one at a time from the target function. Removing the KIEs prevents definition of the rate constants for this FEP (Figure S1A). On the other hand, removing KEZ does not affect the definition of either the rate constants or the intrinsic KIEs (Figure S1B). Removing either θ or viscosity prevents definition of the rate constants and intrinsic KIEs (Figure S1C–D). Removal of the Michaelis-Menten constants was not explored since they are the most straight-forward measurements to make and are generally available.
B. Alanine Racemase
The FEP for AR was determined using published data (22, 24, 34). COPASI was used to reanalyze pH 8.9 racemization progress curves by globally fitting them to the reversible Michaelis-Menten mechanism to get forward and reverse kcat and Km values (Figure 1A). The viscosity dependence of kcat/Km, and the KIEs were from Spies et al. (22) and Sun et al. (24), respectively. The value of θ was taken from Faraci & Walsh (34). The equilibrium constant for quinonoid intermediate formation (KEZ) was determined in the present work to have a value of (1.6 ± 0.4) × 10−4 (Figure 1B; Table 1). The experimental measurements used for AR are summarized in Table 1.
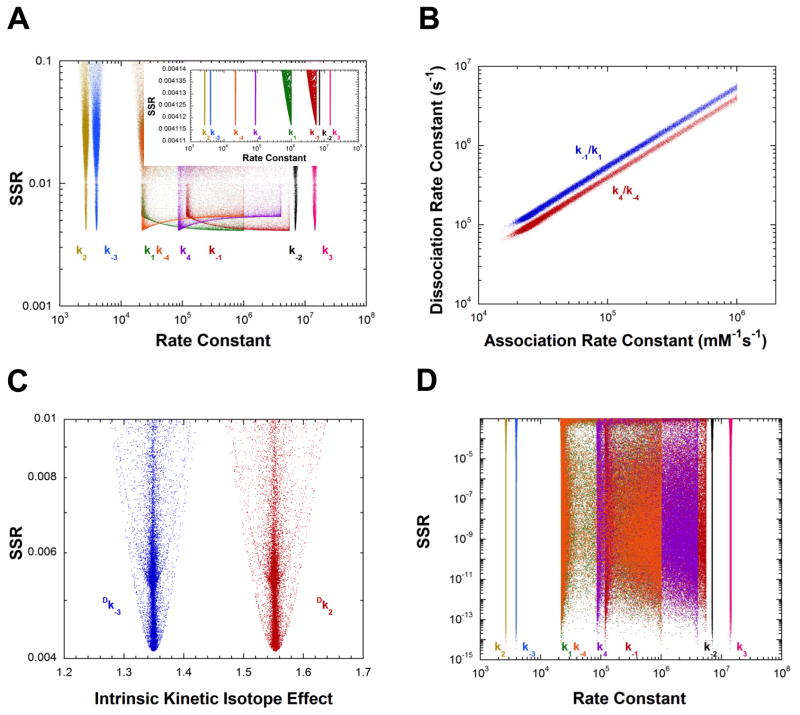
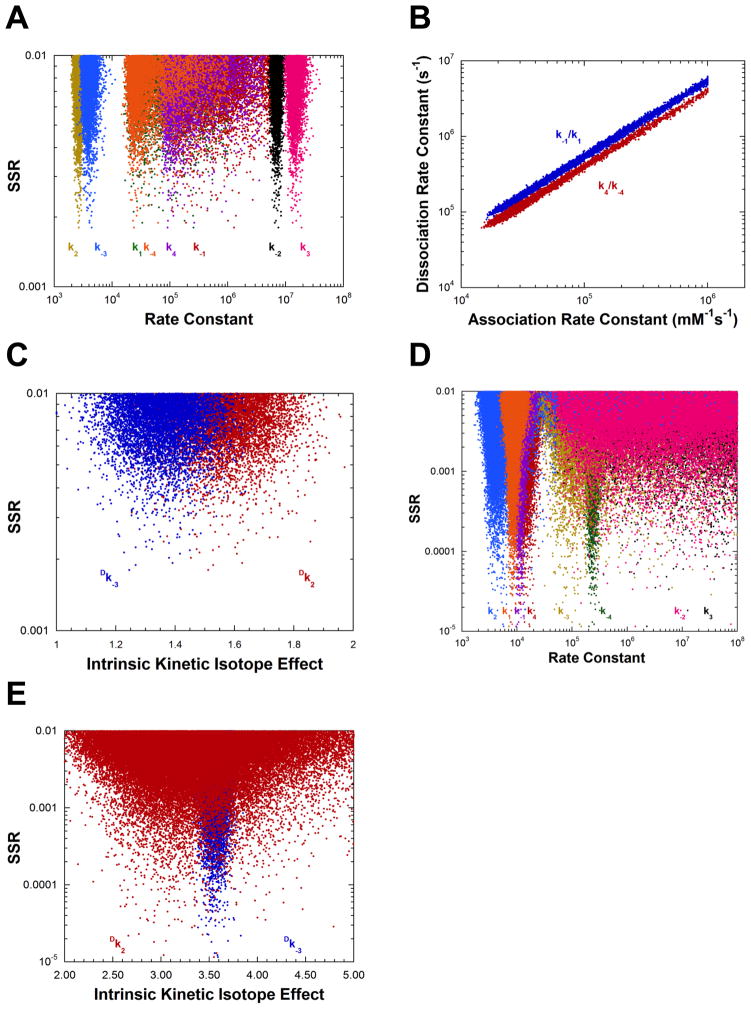
The results presented in Figure 3A show that the measurements presented in Table 1 are sufficient to define well four of the eight rate constants for AR using the “mean normalized” least squares target function (Eq. 14). The values of k1 and k−1 (L-alanine association and dissociation) show no minima in their distributions, while the minima for k4 and k−4 are shallow. Figure 3B presents the correlation between the association and dissociation rate constants for both L- and D-alanine over a wide range of values for the best 5% of solutions found. These linear correlations have slopes equal to the KM values for the corresponding substrate (Tables 1 and 3), illustrating that the binding of both L- and D-alanine is a rapid equilibrium process under the present experimental conditions. Importantly, Figure 3C shows that the values of the intrinsic KIEs (Table 4) are well determined by the experimental measurements presented in Table 1. Thus, for AR the values of eight parameters are determined from global optimization: four rate constants, two equilibrium constants, and two intrinsic KIEs.
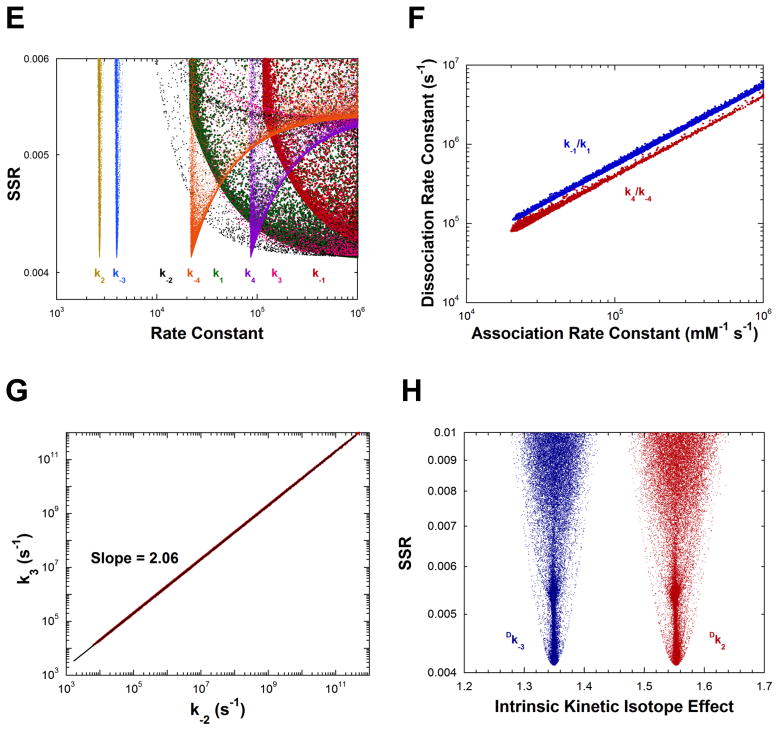
Figure 3.
Analysis of AR rate constants and intrinsic KIEs by global optimization. (A) Rate constants vs. SSR. The inset shows an expanded view of the best solutions obtained. (B) Plot of the substrate association vs. dissociation rate constants, showing the linear correlation between them for the best 5% of solutions found. The values of the dissociation rate constants are much greater than the competing deprotonation steps, indicating rapid equilibrium binding of both D- and L-alanine. The slope of the correlations are identical within error to the KM values of the corresponding substrates. (C) Intrinsic KIEs vs. SSR obtained in global analysis. (D) Rate constants vs. SSR from calculations in which the KIEs were not included in the target function. The correlation between association and dissociation rate constants is essentially identical to that presented in part B. (E) Rate constants vs. SSR from calculations in which Kez was not included in the target function. (F) Plot of the substrate association vs. dissociation rate constants, showing the linear correlation between them for the best 5% of solutions found, for calculations in part E. (G) Plot of k−2 vs. k3 (i.e., quinonoid decomposition rate constants) for calculations in part E for the best 5% of solutions found. (H) Intrinsic KIEs vs. SSR for calculations in part E.
Table 3.
Rate Constants for AR and TIM from Global Optimization.a
| k−1/k1 (mM) | k1 (mM−1s−1) | k−1 (s−1) | k2 (s−1) | k−2 (s−1) | k3 (s−1) | k−3 (s−1) | k4 (s−1) | k−4 (mM−1s−1) | k4/k−4 (mM) | |
|---|---|---|---|---|---|---|---|---|---|---|
| AR | 5.5 (0.3) | >105 | >106 | 2600 (200) | 6.8 106 (0.7 106) | 1.4 107 (0.3 107) | 4000 (700) | 9 104 (80 104) | 2 104 (20 104) | 4.0 (0.2) |
| TIM | 8400 (1500) | 1.1 104 (0.2 104) | 4000 (1600) | >108 | >109 | 5 105 (20 105) | 1.2 104 (0.3 104) | 2.3 105 (0.3 105) |
Table 4.
Intrinsic KIEs for AR and TIM from Global Optimization.a
| Dk2 | Dk−3 | |
|---|---|---|
| AR | 1.55 (0.11) | 1.35 (0.09) |
| TIM | 3.56 (0.08) | 3.3 (0.5) |
When the observed KIEs are removed from the target function, the results in Figure 3D are obtained. The values of k2 − k−3 are well determined and identical to those obtained when KIEs are included. The ratios of the association and dissociation rate constants are also well determined and have slopes equal to the KM values for the respective substrates (not shown).
Figures 3E–H present the results of calculations in which KEZ (the equilibrium constant for formation of the carbanionic quinonoid intermediate on substrate-saturated enzyme) was not included in the target function. The values of k2 and k−3 are well determined but those of k−2 and k3 (the rate constants for decomposition of the quinonoid). That is, the energy of the quinonoid intermediate is not defined. The ratios of the association and dissociation rate constants are well determined and have slopes equal to the KM values for the respective substrates (Figure 3F). The ratio of the barriers facing the quinonoid intermediate is also well defined as shown by the linear relationship between k−2 and k3 in Figure 3G. The slope of the linear correlation (2.06) is the same as the ratio of k−2 and k3 presented in Table 1 for calculations that include KEZ. Lastly, the intrinsic KIEs are well defined without KEZ in the target function (Figure 3H) and have values identical to those obtained when KEZ is included (Figure 3C). Calculations without θ or without viscosity in the target function were not successful at defining either the rate constants (Figures S2A and B) or the intrinsic KIEs (not shown).
C. TIM
The FEP for TIM from baker’s yeast was calculated for pH 7.5 and 30 °C. The experimental measurements for TIM were taken from the literature. (23, 30, 50) This included values for kcat, KM, KIEs, θ, and the slope of the viscosity dependence of relative kcat/Km values. The fractional on-enzyme equilibrium values are from C-13 NMR experiments with saturated enzyme. (51) These values are in agreement with those from FTIR, P-31 NMR, and high resolution crystallographic studies. (52–57)
It was not possible, despite an intensive effort, to find good solutions using the reported values and estimated errors. It was concluded that one or more of the experimental values is either inaccurate or its error underestimated. Viscosity dependence measurements are notoriously difficult to perform with high precision. The viscosity dependence of relative kcat/Km values was reanalyzed based on the tabular data presented. (30) Point-by-point correction of the wild type values using those of the mutant enzyme (the authors corrected by subtracting slopes of fitted lines) led to a weighted average relative viscosity dependence of 0.8 with an estimated error of 0.1, which were used here. It seemed reasonable that the NMR experiments, in which a limit of detection of ~1% for either E-GAP or E-enediol was reported, could be quantitatively imprecise. Therefore, the limits of detection for E-GAP or E-enediol were increased to 5%. The reported values of θ for yeast TIM were variable, leading to a value of 3 ± 1 for this observation. (23) A summary of the measurements used for calculating the TIM FEP is presented in Table 2.
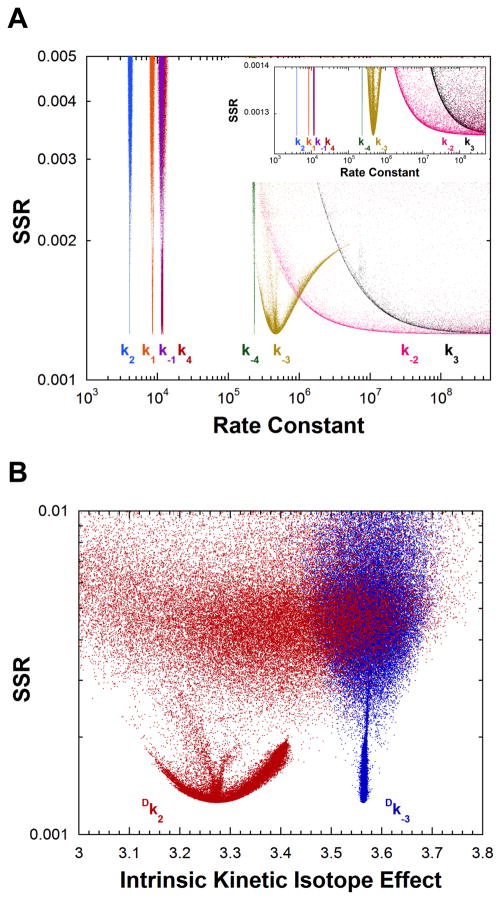
The corrected experimental measurements define all rate constants except those for enediol decomposition (i.e., the energy of the enediol intermediate in not defined) as shown in Figure 4A, although the distribution for k−3 has a shallow minimum. The values of the rate constants for TIM taken from Figure 4A are given in Table 3. QM/MM calculations on TIM show that ~6 kcal/mol is a reasonable estimate for the energy of the enediol intermediate. (58, 59) The present results suggesting k−2 has a value >108 s−1 and k3 has a value >109 s−1 are in accord with this estimate. The intrinsic KIEs are also defined as shown in Figure 4B, and are reported in Table 4.
Figure 4.
Analysis of yeast TIM rate constants and intrinsic KIEs by global optimization. (A) Rate constants vs. SSR. Six rate constants are defined. The inset shows an expanded view of the best solutions obtained. (B) Intrinsic KIEs vs. SSR.
D. Estimation of Errors in the Fitted Parameters
The experimental measurements employed in the target function each have an error associated with them. These experimental errors should be propagated into the fitted parameters obtained from global optimization. The propagation of experimental errors was achieved numerically by a Monte Carlo approach in which many independent calculations were run with values for the experimental measurements in the target function being randomly sampled from Gaussian distributions. (48)
With the “parameter scan” task, COPASI has the capability of sampling a “global quantity” from a normal distribution with an associated standard deviation. This facility was used to propagate errors from the experimental measurements into the parameters obtained from global optimization. The experimental observations used in the target function were each assigned to a global quantity. The corresponding global quantities replaced the values of the observations in the target function. Large-scale global optimizations were then performed to assess the effect of normally distributed experimental errors on the calculated parameter distributions.
The results of the error propagation calculations for AR are shown in Figures 5A–C, while those for TIM are presented in Figures 5D and E. As expected, the distributions are significantly broader than those presented in Figures 3A–C and 4A and B. The errors on the rate constants and intrinsic KIEs reported in Tables 3 and 4 are derived from these results. Since the experimental values in the target function are sampled from a Gaussian distribution, the resulting fitted parameter distributions follow a Gaussian distribution. The standard deviation of the distribution of each fitted parameter is a valid estimate of the true uncertainty in that parameter, and was used here. (48)
Figure 5.
Propagation of experimental errors in the observations into the calculated rate constants and KIEs. Values of observations used in the target function were sampled from a normal distribution based on the reported values and errors in Tables 1 and 2. Points in the figures represent separate calculations in which each observation value in the target function was randomly sampled from its distribution. (A) AR rate constant vs. SSR. (B) Plot of the substrate association vs. dissociation rate constants for AR, showing the linear correlation between them for the best 5% of solutions found. (C) Intrinsic KIEs vs. SSR for AR. (D) Rate constants vs. SSR for TIM. (E) Intrinsic KIEs vs. SSR for TIM.
E. Alternative Target Functions
The least absolute deviation target function (i.e. Eq. 14 with absolute values raised to the first power, not the second) was applied to both AR and TIM. The results for AR are shown in Figure S3 while those for TIM are in Figure S5. The least absolute deviation results give essentially identical best values for all rate constants and intrinsic KIEs. The major difference is in the shapes of the distributions.
The “error normalized” chi squared target function also gives results similar to those with Eq. 14 for both AR and TIM (Figures S4 and S6). The largest differences are found in the results with TIM where the distributions for k2 and k−3 are significantly broader. Overall, it appears that all three common types of target functions yield valid estimates of the rate constants and intrinsic KIEs for both enzymes. The broader distributions for TIM using the “error normalized” chi squared target function point to significant experimental errors in the TIM values used (Table 2). This is not surprising given the difficulties encountered with the TIM values taken directly from the literature, as described above.
Discussion
Attempts to define FEPs for enzyme catalyzed reactions from mainly steady-state kinetic measurements have had variable success. A well known example is that of Knowles et al. where the FEP for TIM was partially defined using various isotopic measurements (1, 2, 33, 60–62). Other notable examples include work by Knowles et al. on proline racemase, Pollack et al. on ketosteroid isomerase, Laidler et al. on lactate dehydrogenase, and Bearne et al. on mandelate racemase, although this is by no means an exhaustive list (14, 20, 21, 63–70). This work extends these previous efforts, leading to a general method for FEP determination based mainly on steady-state measurements.
AR FEP
The kinetic model for AR includes a carbanionic quinonoid intermediate that was demonstrated to exist using multiple KIEs. (32) In that work, the decrease in the primary substrate KIE when H2O was changed to D2O showed that the two isotopes are transferred in separate transition states (i.e., stepwise interconversion of L and D external aldimines with a carbanionic intermediate between them). The asymmetry in the reductions of the primary KIEs by D2O indicated that the barrier for the quinonoid intermediate going to the L external aldimine is higher than that for going to the D external aldimine. This conclusion is supported by the observation that equilibrium overshoots in racemization progress curves for protiated substrates conducted in D2O only occur in the L→D direction. (22)
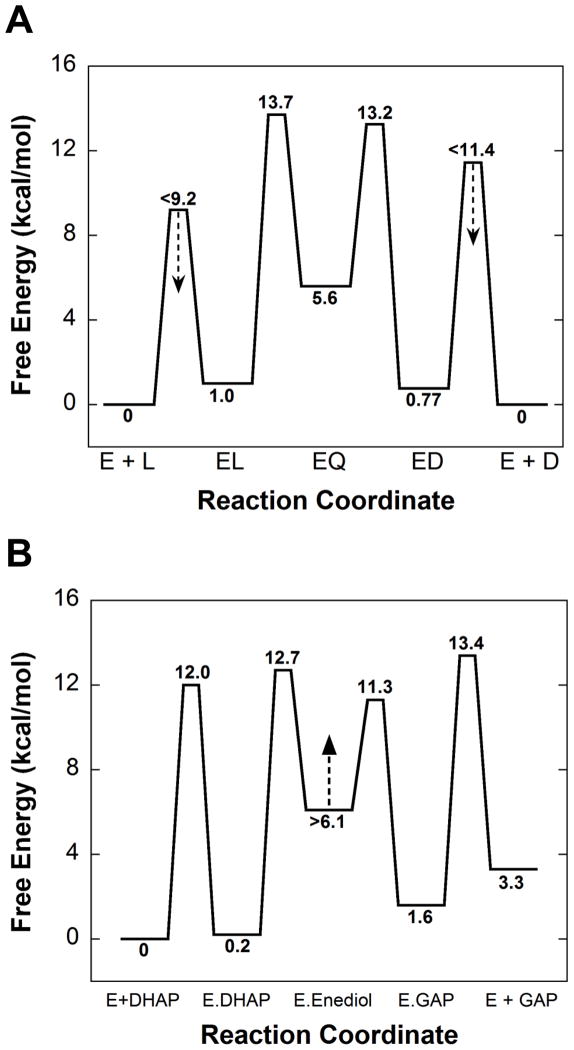
The FEP for AR (Figure 6A) is very similar to that obtained previously using different methods, and reproduces the asymmetry in the rate constants for quinonoid decomposition described above. (22, 71) A major difference is that the energy of the quinonoid intermediate is well defined here. Earlier, only a lower limit on the energy of this intermediate (≥4 kcal/mol higher than the aldimine intermediates) was defined. The calculations in which KEZ was not included in the target function (Figure 3E) similarly allow one to define a limit on the energy of the quinonoid intermediate of >4.5 kcal/mol higher than the aldimine intermediates. Incorporation of the spectroscopic results presented in Figure 1B into the target function allow its energy to be defined as 4.6 kcal/mole higher than the L-alanine external aldimine intermediate. This is in reasonable agreement with the value of 6.6 kcal/mole from QM/MM calculations by Major and Gao. (72, 73)
Figure 6.
Free energy profiles determined from global optimization. (A) Alanine Racemase. (B) Triosephosphate isomerase. Values are for unhydrated glyceraldehyde. The standard state for both enzymes was taken as 1 mM.
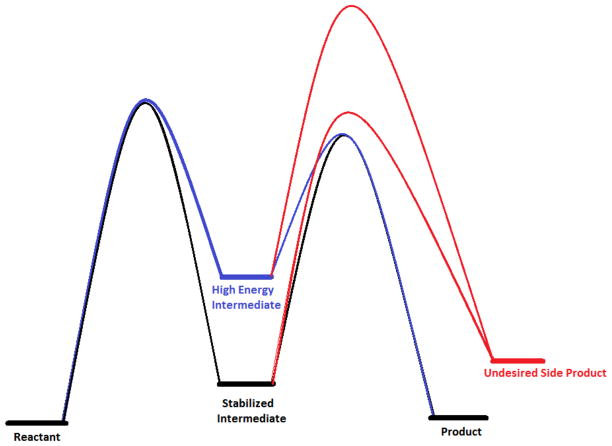
The high energy of the quinonoid intermediate was previously interpreted in terms of enhancing reaction specificity, since it is from this intermediate that competing pathways such as transamination branch. (22) This is illustrated in Figure 6. If the activation energy for the undesired reaction (transamination via protonation of the quinonoid at C4′) is invariant, raising the energy of the intermediate while maintaining the transition state energy for racemization increases the flux through the desired reaction. For AR, the rate-limiting process for transamination from the quinonoid intermediate is likely the movement of Lys39 or Tyr265 away from Cα toward C4′, which is not expected to be influenced by the quinonoid energy.
An important finding from the large-scale sampling employed here is that the rate constants for external aldimine formation are not precisely defined as was previously reported, (22, 71) but their ratio is. That is, external aldimine formation is a rapid equilibrium process. This agrees with the lack of solvent viscosity dependence at this pH, and pH profiles with alanine and the slow substrate serine in which intrinsic substrate pKas are observed. (22, 32) The ratios of dissociation and association constants reproduce well the KM values determined experimentally and used in the target function (Figure 3B, Tables 1 and 3).
TIM FEP
Using information that was available to Knowles et al., the method described here defines all of the energies they were able to define, as well as two additional ones: the transition state energy for DHAP binding, and the ground state energy for the E-GAP intermediate. (2, 23) Knowles et al. stated that they could not define well the energy of the enediol intermediate for either the chicken or yeast isozymes. In the present work, it was also not possible to precisely define the energy of this intermediate but the results in Figure 4A allow one to set a limit of >6 kcal/mol higher than that of the E-DHAP complex. This value is in general agreement with QM/MM calculations from several laboratories. (58, 59, 74–76) It runs contrary to the proposal of Albery and Knowles that this intermediate is well stabilized as a result of evolutionary perfection. (1)
Work by Richard et al. has characterized the TIM catalyzed phosphate elimination reaction that leads from the enediol intermediate to the undesired methylglyoxal side-product. (77, 78) We propose that the high energy of the enediol intermediate in TIM serves the purpose of increasing reaction specificity, as proposed above for AR. This is again illustrated in Figure 6. For TIM, we assume that the barrier to phosphate elimination is independent of the energy of the enediol intermediate, being determined, for example, by the rate of opening the loop that covers the active site. (79) Therefore, if the energy of the enediol intermediate is increased, the separation between the transition states for the productive and nonproductive pathways increases, thereby increasing isomerization reaction specificity. Thus, there may be additional evolutionary pressure to increase the energy of the enediol intermediate while maintaining diffusion controlled kinetics for isomerization since high reaction specificity is presumably also selected for in the process of evolutionary perfection of enzymes.
Additional comments
The inability to define well the energy of the quinonoid intermediate in AR and the enediol intermediate in TIM entirely from kinetic data is a practical not a theoretical one. This is illustrated by calculations (Figure S7) in which the rate constants and intrinsic KIEs reported in Tables 3 an 4 were used to calculate values for the experimental observations. The latter were then used in the target function for global optimization (as was done for the calculations presented in Figure 2). For AR, the value of KEZ was not included in the target function.
The results presented in Figure S7 show that for both AR and TIM, the energies of the quinonoid and enediol intermediates can indeed be defined by the steady-state kinetic measurements employed, even though they are high with respect to the other intermediates. The calculations presented in Figures 2 and S7 used six significant figures throughout, and this level of precision is not generally achievable experimentally. The degree of precision required in the experimental measurements is determined by the extent to which the fastest rate constants contribute to rate limitation in the measurements employed in the target function (if no precise equilibrium measurements on the intermediate are used). In AR and TIM, the rate constants for quinonoid and enediol decomposition are so high that they contribute very little to rate limitation, thus requiring unattainably high precision kinetic measurements to define them.
An important finding presented here is that one can directly and precisely define the values of KIEs on individual isotopically sensitive steps (i.e., the intrinsic KIEs) in enzymatic reactions using global optimization. Measurements of KIEs on kcat and kcat/KM do not generally give intrinsic KIEs since they are commonly masked by kinetic complexity. (35) Enzymologists often go to pH extremes, or use slow substrates to extract intrinsic KIEs, which are the only values that can be interpreted in terms of transition state structure. The accuracy of intrinsic KIEs determined by global optimization will obviously depend on the overall accuracy and precision of the experimental measurements employed. Thus, a carefully conducted, uniform set of measurements that includes KIEs should allow precise definition of intrinsic KIEs along with the values of all microscopic rate constants.
Neither AR nor TIM are amenable to common rapid kinetic experiments (i.e., stopped-flow or chemical-quench flow). Either the individual steps are too fast (i.e. >2000 s−1), or the intermediates have no spectroscopic signal, or they are unstable to chemical-quench, or they are not appreciably populated. Temperature-jump methods, which are less common and more difficult, are the only rapid kinetic alternative. The present method is the most straight-forward choice for defining the FEPs of these and similar enzymes.
The broad, large-scale searches at the heart of the present method are enabled by powerful heuristic search algorithms (e.g., genetic algorithm, particle swarm algorithm). These are very effective at broadly searching parameter space. Importantly, they do not follow gradients like commonly used descent methods such as the Levenberg-Marquardt algorithm, which lead only to the nearest minimum. (80, 81) Large-scale searches over all of parameter space also free the experimentalist from the hazard of providing subjective initial estimates for parameters as required by gradient methods. Instead, all of the reasonable parameter space can be successfully searched using large-scale global optimization based on randomized parameter estimates. This is facilitated by virtue of global optimization being ~1000-fold faster than fitting time dependent data by numerical integration-based global nonlinear regression.
The use of COPASI for global optimization has the advantages of familiarity and simplicity for chemists and biochemists since this is the target audience of the software, and it is free. (25, 26) It is straightforward to set up complex reaction schemes and the equations corresponding to the measurements employed, and running global optimization (or nonlinear regression on time-course data) is uncomplicated. Nevertheless, this type of problem is suited to commercial software (MATLAB, Mathematica, LIONsolver, Excel Solver addin) that perform global optimization, as well as many noncommercial ones.
The experimental observations used here are by no means exhaustive. Others that could be employed include additional isotopic experiments (e.g., heavy atom KIEs, solvent KIEs, equilibrium perturbations, etc.), viscosity dependence of kcat, viscosity dependence of absolute rather than relative values of kcat/KM, and pre-steady-state kinetics in which the observed signal can be unambiguously described in terms of the microscopic rate constants of a substantiated mechanism. The creativity of the experimentalist and the availability of a measurable signal are the only limits.
It will be important to explore in future studies the applicability of this method to other common enzymatic mechanisms. For example, is it possible to determine rate constants for mechanisms in which a chemical step is irreversible? Extension to other kinetic mechanisms such as ping-pong or sequential multi-substrate ones is also important.
The general, straight-forward nature of the method outlined here and the common experiments required open the door to routine determination of enzymatic free energy profiles without need for resorting to traditional time- and material-intensive methods (at least for the general mechanism of Scheme 1). One can also envision application to large-scale enzyme characterization efforts, which could provide an important foundation for understanding the detailed basis of catalytic strategies used by different enzyme families. (82)
Supplementary Material
Figure 7.
Illustration of how increasing the energy of an intermediate susceptible to side reactions can reduce the flux through the side reaction. If the barrier to the undesired side reaction is unaltered, raising the energy of the intermediate decreases the flux through it by increasing the separation between the desired (blue) and undesired (red) transition states.
Scheme 2.
Chemical mechanisms for AR and TIM.
Acknowledgments
Supported by grant GM54779 from the U.S. National Institutes of Health
Footnotes
Additional supplemental material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Albery WJ, Knowles JR. Evolution of enzyme function and the development of catalytic efficiency. Biochemistry. 1976;15:5631–5640. doi: 10.1021/bi00670a032. [DOI] [PubMed] [Google Scholar]
- 2.Albery WJ, Knowles JR. Free-energy profile of the reaction catalyzed by triosephosphate isomerase. Biochemistry. 1976;15:5627–5631. doi: 10.1021/bi00670a031. [DOI] [PubMed] [Google Scholar]
- 3.Albery WJ, Knowles JR. Energetics and mechanism of proline racemase. Biochemistry. 1986;25:2572–2577. doi: 10.1021/bi00357a043. [DOI] [PubMed] [Google Scholar]
- 4.Hayashi H, Kagamiyama H. Reaction of aspartate aminotransferase with L-erythro-3-hydroxyaspartate: involvement of Tyr70 in stabilization of the catalytic intermediates. Biochemistry. 1995;34:9413–9423. doi: 10.1021/bi00029a017. [DOI] [PubMed] [Google Scholar]
- 5.Fierke CA, Johnson KA, Benkovic SJ. Construction and evaluation of the kinetic scheme associated with dihydrofolate reductase from Escherichia coli. Biochemistry. 1987;26:4085–4092. doi: 10.1021/bi00387a052. [DOI] [PubMed] [Google Scholar]
- 6.Mehl A, Xu Y, Dunaway-Mariano D. Energetics of pyruvate phosphate dikinase catalysis. Biochemistry. 1994;33:1093–1102. doi: 10.1021/bi00171a007. [DOI] [PubMed] [Google Scholar]
- 7.Al-Shawi MK, Senior AE. Complete kinetic and thermodynamic characterization of the unisite catalytic pathway of Escherichia coli F1-ATPase. Comparison with mitochondrial F1-ATPase and application to the study of mutant enzymes. The Journal of biological chemistry. 1988;263:19640–19648. [PubMed] [Google Scholar]
- 8.McQueney MS, Anderson KS, Markham GD. Energetics of S-adenosylmethionine synthetase catalysis. Biochemistry. 2000;39:4443–4454. doi: 10.1021/bi992876s. [DOI] [PubMed] [Google Scholar]
- 9.Keshwani MM, Harris TK. Kinetic mechanism of fully activated S6K1 protein kinase. The Journal of biological chemistry. 2008;283:11972–11980. doi: 10.1074/jbc.M800114200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Behravan G, Jonsson BH, Lindskog S. Fine tuning of the catalytic properties of carbonic anhydrase. Studies of a Thr200→His variant of human isoenzyme II. European journal of biochemistry / FEBS. 1990;190:351–357. doi: 10.1111/j.1432-1033.1990.tb15582.x. [DOI] [PubMed] [Google Scholar]
- 11.Kurz LC, Constantine CZ, Jiang H, Kappock TJ. The partial substrate dethiaacetyl-coenzyme A mimics all critical carbon acid reactions in the condensation half-reaction catalyzed by Thermoplasma acidophilum citrate synthase. Biochemistry. 2009;48:7878–7891. doi: 10.1021/bi9006447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.O’Brien PJ, Lassila JK, Fenn TD, Zalatan JG, Herschlag D. Arginine coordination in enzymatic phosphoryl transfer: evaluation of the effect of Arg166 mutations in Escherichia coli alkaline phosphatase. Biochemistry. 2008;47:7663–7672. doi: 10.1021/bi800545n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wells TN, Fersht AR. Use of binding energy in catalysis analyzed by mutagenesis of the tyrosyl-tRNA synthetase. Biochemistry. 1986;25:1881–1886. doi: 10.1021/bi00356a007. [DOI] [PubMed] [Google Scholar]
- 14.Borgmann U, Moon TW, Laidler KJ. Molecular kinetics of beef heart lactate dehydrogenase. Biochemistry. 1974;13:5152–5158. doi: 10.1021/bi00722a016. [DOI] [PubMed] [Google Scholar]
- 15.Zhadin N, Gulotta M, Callender R. Probing the role of dynamics in hydride transfer catalyzed by lactate dehydrogenase. Biophysical journal. 2008;95:1974–1984. doi: 10.1529/biophysj.108.132464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Miller SM, Klinman JP. Deduction of kinetic mechanisms from primary hydrogen isotope effects: dopamine beta-monooxygenase-A case history. Methods in enzymology. 1982;87:711–732. doi: 10.1016/s0076-6879(82)87036-5. [DOI] [PubMed] [Google Scholar]
- 17.Banerjee SK, Holler E, Hess GP, Rupley JA. Reaction of N-acetylglucosamine oligosaccharides with lysozyme. Temperature, pH, and solvent deuterium isotope effects; equilbrium, steady state, and pre-steady state measurements. The Journal of biological chemistry. 1975;250:4355–4367. [PubMed] [Google Scholar]
- 18.Anderson KS, Sikorski JA, Johnson KA. A tetrahedral intermediate in the EPSP synthase reaction observed by rapid quench kinetics. Biochemistry. 1988;27:7395–7406. doi: 10.1021/bi00419a034. [DOI] [PubMed] [Google Scholar]
- 19.Goldberg JM, Kirsch JF. The reaction catalyzed by Escherichia coli aspartate aminotransferase has multiple partially rate-determining steps, while that catalyzed by the Y225F mutant is dominated by ketimine hydrolysis. Biochemistry. 1996;35:5280–5291. doi: 10.1021/bi952138d. [DOI] [PubMed] [Google Scholar]
- 20.Hawkinson DC, Eames TC, Pollack RM. Energetics of 3-oxo-delta 5-steroid isomerase: source of the catalytic power of the enzyme. Biochemistry. 1991;30:10849–10858. doi: 10.1021/bi00109a007. [DOI] [PubMed] [Google Scholar]
- 21.St Maurice M, Bearne SL. Kinetics and thermodynamics of mandelate racemase catalysis. Biochemistry. 2002;41:4048–4058. doi: 10.1021/bi016044h. [DOI] [PubMed] [Google Scholar]
- 22.Spies MA, Woodward JJ, Watnik MR, Toney MD. Alanine racemase free energy profiles from global analyses of progress curves. Journal of the American Chemical Society. 2004;126:7464–7475. doi: 10.1021/ja049579h. [DOI] [PubMed] [Google Scholar]
- 23.Nickbarg EB, Knowles JR. Triosephosphate isomerase: energetics of the reaction catalyzed by the yeast enzyme expressed in Escherichia coli. Biochemistry. 1988;27:5939–5947. doi: 10.1021/bi00416a018. [DOI] [PubMed] [Google Scholar]
- 24.Sun S, Toney MD. Evidence for a two-base mechanism involving tyrosine-265 from arginine-219 mutants of alanine racemase. Biochemistry. 1999;38:4058–4065. doi: 10.1021/bi982924t. [DOI] [PubMed] [Google Scholar]
- 25.Mendes P, Hoops S, Sahle S, Gauges R, Dada J, Kummer U. Computational modeling of biochemical networks using COPASI. Methods Mol Biol. 2009;500:17–59. doi: 10.1007/978-1-59745-525-1_2. [DOI] [PubMed] [Google Scholar]
- 26.Hoops S, Sahle S, Gauges R, Lee C, Pahle J, Simus N, Singhal M, Xu L, Mendes P, Kummer U. COPASI--a COmplex PAthway SImulator. Bioinformatics. 2006;22:3067–3074. doi: 10.1093/bioinformatics/btl485. [DOI] [PubMed] [Google Scholar]
- 27.Christen P, Metzler DE. Transaminases. Vol. 24. Wiley; New York: 1985. [Google Scholar]
- 28.Cleland WW. Partition analysis and the concept of net rate constants as tools in enzyme kinetics. Biochemistry. 1975;14:3220–3224. doi: 10.1021/bi00685a029. [DOI] [PubMed] [Google Scholar]
- 29.Brouwer AC, Kirsch JF. Investigation of diffusion-limited rates of chymotrypsin reactions by viscosity variation. Biochemistry. 1982;21:1302–1307. doi: 10.1021/bi00535a030. [DOI] [PubMed] [Google Scholar]
- 30.Sampson NS, Knowles JR. Segmental motion in catalysis: investigation of a hydrogen bond critical for loop closure in the reaction of triosephosphate isomerase. Biochemistry. 1992;31:8488–8494. doi: 10.1021/bi00151a015. [DOI] [PubMed] [Google Scholar]
- 31.Blacklow SC, Raines RT, Lim WA, Zamore PD, Knowles JR. Triosephosphate isomerase catalysis is diffusion controlled. Appendix: Analysis of triose phosphate equilibria in aqueous solution by 31P NMR. Biochemistry. 1988;27:1158–1167. doi: 10.1021/bi00404a013. [DOI] [PubMed] [Google Scholar]
- 32.Spies MA, Toney MD. Multiple hydrogen kinetic isotope effects for enzymes catalyzing exchange with solvent: Application to alanine racemase. Biochemistry. 2003;42:5099–5107. doi: 10.1021/bi0274064. [DOI] [PubMed] [Google Scholar]
- 33.Herlihy JM, Maister SG, Albery WJ, Knowles JR. Energetics of triosephosphate isomerase: the fate of the 1(R)-3H label of tritiated dihydroxyacetone phsophate in the isomerase reaction. Biochemistry. 1976;15:5601–5607. doi: 10.1021/bi00670a026. [DOI] [PubMed] [Google Scholar]
- 34.Faraci WS, Walsh CT. Racemization of alanine by the alanine racemases from Salmonella typhimurium and Bacillus stearothermophilus: energetic reaction profiles. Biochemistry. 1988;27:3267–3276. doi: 10.1021/bi00409a022. [DOI] [PubMed] [Google Scholar]
- 35.Northrop DB. The expression of isotope effects on enzyme-catalyzed reactions. Annu Rev Biochem. 1981;50:103–131. doi: 10.1146/annurev.bi.50.070181.000535. [DOI] [PubMed] [Google Scholar]
- 36.Klinman JP, Matthews RG. Calculation of substrate dissociation-constants from steady-state isotope effects in enzyme-catalyzed reactions. Journal of the American Chemical Society. 1985;107:1058–1060. [Google Scholar]
- 37.Villaverde AF, Ross J, Moran F, Balsa-Canto E, Banga JR. Use of a Generalized Fisher Equation for Global Optimization in Chemical Kinetics. J Phys Chem A. 2011;115:8426–8436. doi: 10.1021/jp203158r. [DOI] [PubMed] [Google Scholar]
- 38.Joo K, Lee J. Methods for accurate homology modeling by global optimization. Methods Mol Biol. 2012;857:175–188. doi: 10.1007/978-1-61779-588-6_7. [DOI] [PubMed] [Google Scholar]
- 39.Williams GA, Dugan JM, Altman RB. Constrained global optimization for estimating molecular structure from atomic distances. J Comput Biol. 2001;8:523–547. doi: 10.1089/106652701753216521. [DOI] [PubMed] [Google Scholar]
- 40.Kim S, Li L. A novel global search algorithm for nonlinear mixed-effects models using particle swarm optimization. J Pharmacokinet Phar. 2011;38:471–495. doi: 10.1007/s10928-011-9204-6. [DOI] [PubMed] [Google Scholar]
- 41.Altschuler EL, Williams TJ, Ratner ER, Dowla F, Wooten F. Method of Constrained Global Optimization. Phys Rev Lett. 1994;72:2671–2674. doi: 10.1103/PhysRevLett.72.2671. [DOI] [PubMed] [Google Scholar]
- 42.Balsa-Canto E, Banga JR, Egea JA, Fernandez-Villaverde A, de Hijas-Liste GM. Global optimization in systems biology: stochastic methods and their applications. Adv Exp Med Biol. 2012;736:409–424. doi: 10.1007/978-1-4419-7210-1_24. [DOI] [PubMed] [Google Scholar]
- 43.Polisetty PK, Voit EO, Gatzke EP. Identification of metabolic system parameters using global optimization methods. Theor Biol Med Model. 2006;3 doi: 10.1186/1742-4682-3-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ross J, Fernandez Villaverde A, Banga JR, Vazquez S, Moran F. A generalized Fisher equation and its utility in chemical kinetics. Proc Natl Acad Sci U S A. 2010;107:12777–12781. doi: 10.1073/pnas.1008257107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Villaverde AF, Ross J, Moran F, Balsa-Canto E, Banga JR. Use of a generalized fisher equation for global optimization in chemical kinetics. J Phys Chem A. 2011;115:8426–8436. doi: 10.1021/jp203158r. [DOI] [PubMed] [Google Scholar]
- 46.Moles CG, Mendes P, Banga JR. Parameter estimation in biochemical pathways: a comparison of global optimization methods. Genome research. 2003;13:2467–2474. doi: 10.1101/gr.1262503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Greenwood PE, Nikulin MS. A guide to chi-squared testing. Wiley; New York: 1996. [Google Scholar]
- 48.Motulsky H, Christopoulos A. Fitting models to biological data using linear and nonlinear regression : a practical guide to curve fitting. Oxford University Press; Oxford ; New York: 2004. [Google Scholar]
- 49.Narula SC, Saldiva PH, Andre CD, Elian SN, Ferreira AF, Capelozzi V. The minimum sum of absolute errors regression: a robust alternative to the least squares regression. Stat Med. 1999;18:1401–1417. doi: 10.1002/(sici)1097-0258(19990615)18:11<1401::aid-sim136>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 50.Krietsch WK, Pentchev PG, Klingenburg H, Hofstatter T, Bucher T. The isolation and crystallization of yeast and rabbit liver triose phosphate isomerase and a comparative characterization with the rabbit muscle enzyme. European journal of biochemistry / FEBS. 1970;14:289–300. doi: 10.1111/j.1432-1033.1970.tb00289.x. [DOI] [PubMed] [Google Scholar]
- 51.Rozovsky S, McDermott AE. Substrate product equilibrium on a reversible enzyme, triosephosphate isomerase. Proc Natl Acad Sci U S A. 2007;104:2080–2085. doi: 10.1073/pnas.0608876104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Belasco JG, Knowles JR. Direct observation of substrate distortion by triosephosphate isomerase using Fourier transform infrared spectroscopy. Biochemistry. 1980;19:472–477. doi: 10.1021/bi00544a012. [DOI] [PubMed] [Google Scholar]
- 53.Komives EA, Chang LC, Lolis E, Tilton RF, Petsko GA, Knowles JR. Electrophilic catalysis in triosephosphate isomerase: the role of histidine-95. Biochemistry. 1991;30:3011–3019. doi: 10.1021/bi00226a005. [DOI] [PubMed] [Google Scholar]
- 54.Lodi PJ, Chang LC, Knowles JR, Komives EA. Triosephosphate isomerase requires a positively charged active site: the role of lysine-12. Biochemistry. 1994;33:2809–2814. doi: 10.1021/bi00176a009. [DOI] [PubMed] [Google Scholar]
- 55.Webb MR, Standring DN, Knowles JR. Phosphorus-31 nuclear magnetic resonance of dihydroxyacetone phosphate in the presence of triosephosphate isomerase. The question of nonproductive binding of the substrate hydrate. Biochemistry. 1977;16:2738–2741. doi: 10.1021/bi00631a023. [DOI] [PubMed] [Google Scholar]
- 56.Campbell ID, Jones RB, Kiener PA, Waley SG. Enzyme-substrate and enzyme-inhibitor complexes of triose phosphate isomerase studied by 31P nuclear magnetic resonance. Biochem J. 1979;179:607–621. doi: 10.1042/bj1790607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Jogl G, Rozovsky S, McDermott AE, Tong L. Optimal alignment for enzymatic proton transfer: structure of the Michaelis complex of triosephosphate isomerase at 1.2-A resolution. Proc Natl Acad Sci U S A. 2003;100:50–55. doi: 10.1073/pnas.0233793100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zhang X, Harrison DH, Cui Q. Functional specificities of methylglyoxal synthase and triosephosphate isomerase: a combined QM/MM analysis. Journal of the American Chemical Society. 2002;124:14871–14878. doi: 10.1021/ja027063x. [DOI] [PubMed] [Google Scholar]
- 59.Guallar V, Jacobson M, McDermott A, Friesner RA. Computational modeling of the catalytic reaction in triosephosphate isomerase. J Mol Biol. 2004;337:227–239. doi: 10.1016/j.jmb.2003.11.016. [DOI] [PubMed] [Google Scholar]
- 60.Fisher LM, Albery WJ, Knowles JR. Energetics of triosephosphate isomerase: the nature of the proton transfer between the catalytic base and solvent water. Biochemistry. 1976;15:5621–5626. doi: 10.1021/bi00670a030. [DOI] [PubMed] [Google Scholar]
- 61.Leadlay PF, Albery WJ, Knowles JR. Energetics of triosephosphate isomerase: deuterium isotope effects in the enzyme-catalyzed reaction. Biochemistry. 1976;15:5617–5620. doi: 10.1021/bi00670a029. [DOI] [PubMed] [Google Scholar]
- 62.Fletcher SJ, Herlihy JM, Albery WJ, Knowles JR. Energetics of triosephosphate isomerase: the appearance of solvent tritium in substrate glyceraldehyde 3-phosphate and in product. Biochemistry. 1976;15:5612–5617. doi: 10.1021/bi00670a028. [DOI] [PubMed] [Google Scholar]
- 63.Fisher LM, Belasco JG, Bruice TW, Albery WJ, Knowles JR. Energetics of proline racemase: transition-state fractionation factors for the two protons involved in the catalytic steps. Biochemistry. 1986;25:2543–2551. doi: 10.1021/bi00357a039. [DOI] [PubMed] [Google Scholar]
- 64.Belasco JG, Bruice TW, Fisher LM, Albery WJ, Knowles JR. Energetics of proline racemase: rates, fractionation factors, and buffer catalysis in the oversaturated region. Nature of the interconversion of the two forms of free enzyme. Biochemistry. 1986;25:2564–2571. doi: 10.1021/bi00357a042. [DOI] [PubMed] [Google Scholar]
- 65.Belasco JG, Bruice TW, Albery WJ, Knowles JR. Energetics of proline racemase: fractionation factors for the essential catalytic groups in the enzyme-substrate complexes. Biochemistry. 1986;25:2558–2564. doi: 10.1021/bi00357a041. [DOI] [PubMed] [Google Scholar]
- 66.Belasco JG, Albery WJ, Knowles JR. Energetics of proline racemase: double fractionation experiment, a test for concertedness and for transition-state dominance. Biochemistry. 1986;25:2552–2558. doi: 10.1021/bi00357a040. [DOI] [PubMed] [Google Scholar]
- 67.Fisher LM, Albery WJ, Knowles JR. Energetics of proline racemase: tracer perturbation experiments using [14C]proline that measure the interconversion rate of the two forms of free enzyme. Biochemistry. 1986;25:2538–2542. doi: 10.1021/bi00357a038. [DOI] [PubMed] [Google Scholar]
- 68.Fisher LM, Albery WJ, Knowles JR. Energetics of proline racemase: racemization of unlabeled proline in the unsaturated, saturated, and oversaturated regimes. Biochemistry. 1986;25:2529–2537. doi: 10.1021/bi00357a037. [DOI] [PubMed] [Google Scholar]
- 69.Pollack RM. Enzymatic mechanisms for catalysis of enolization: ketosteroid isomerase. Bioorg Chem. 2004;32:341–353. doi: 10.1016/j.bioorg.2004.06.005. [DOI] [PubMed] [Google Scholar]
- 70.Borgmann U, Laidler KJ, Moon TW. Four-and five-step kinetic models of lactate dehydrogenase. Can J Biochem. 1976;54:915–918. doi: 10.1139/o76-129. [DOI] [PubMed] [Google Scholar]
- 71.Spies MA, Toney MD. Intrinsic primary and secondary hydrogen kinetic isotope effects for alanine racemase from global analysis of progress curves. Journal of the American Chemical Society. 2007;129:10678–10685. doi: 10.1021/ja067643k. [DOI] [PubMed] [Google Scholar]
- 72.Major DT, Nam K, Gao J. Transition state stabilization and alpha-amino carbon acidity in alanine racemase. Journal of the American Chemical Society. 2006;128:8114–8115. doi: 10.1021/ja062272t. [DOI] [PubMed] [Google Scholar]
- 73.Major DT, Gao J. A combined quantum mechanical and molecular mechanical study of the reaction mechanism and alpha-amino acidity in alanine racemase. Journal of the American Chemical Society. 2006;128:16345–16357. doi: 10.1021/ja066334r. [DOI] [PubMed] [Google Scholar]
- 74.Wang M, Lu Z, Yang W. Nuclear quantum effects on an enzyme-catalyzed reaction with reaction path potential: proton transfer in triosephosphate isomerase. J Chem Phys. 2006;124:124516. doi: 10.1063/1.2181145. [DOI] [PubMed] [Google Scholar]
- 75.Alagona G, Ghio C, Kollman PA. The intramolecular mechanism for the second proton transfer in triosephosphate isomerase (TIM): a QM/FE approach. J Comput Chem. 2003;24:46–56. doi: 10.1002/jcc.10153. [DOI] [PubMed] [Google Scholar]
- 76.Cui Q, Karplus M. Triosephosphate isomerase: a theoretical comparison of alternative pathways. Journal of the American Chemical Society. 2001;123:2284–2290. doi: 10.1021/ja002886c. [DOI] [PubMed] [Google Scholar]
- 77.Go MK, Koudelka A, Amyes TL, Richard JP. Role of Lys-12 in catalysis by triosephosphate isomerase: a two-part substrate approach. Biochemistry. 2010;49:5377–5389. doi: 10.1021/bi100538b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Richard JP. Kinetic parameters for the elimination reaction catalyzed by triosephosphate isomerase and an estimation of the reaction’s physiological significance. Biochemistry. 1991;30:4581–4585. doi: 10.1021/bi00232a031. [DOI] [PubMed] [Google Scholar]
- 79.Pompliano DL, Peyman A, Knowles JR. Stabilization of a reaction intermediate as a catalytic device: definition of the functional role of the flexible loop in triosephosphate isomerase. Biochemistry. 1990;29:3186–3194. doi: 10.1021/bi00465a005. [DOI] [PubMed] [Google Scholar]
- 80.Johnson KA. Fitting enzyme kinetic data with KinTek Global Kinetic Explorer. Methods in enzymology. 2009;467:601–626. doi: 10.1016/S0076-6879(09)67023-3. [DOI] [PubMed] [Google Scholar]
- 81.Johnson KA, Simpson ZB, Blom T. FitSpace explorer: an algorithm to evaluate multidimensional parameter space in fitting kinetic data. Anal Biochem. 2009;387:30–41. doi: 10.1016/j.ab.2008.12.025. [DOI] [PubMed] [Google Scholar]
- 82.Gerlt JA, Allen KN, Almo SC, Armstrong RN, Babbitt PC, Cronan JE, Dunaway-Mariano D, Imker HJ, Jacobson MP, Minor W, Poulter CD, Raushel FM, Sali A, Shoichet BK, Sweedler JV. The Enzyme Function Initiative. Biochemistry. 2011;50:9950–9962. doi: 10.1021/bi201312u. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.