Task specificity of attention training: the case of probability cuing

Abstract

Statistical regularities in our environment enhance perception and modulate the allocation of spatial attention. Surprisingly little is known about how learning-induced changes in spatial attention transfer across tasks. In this study, we investigated whether a spatial attentional bias learned in one task transfers to another. Most of the experiments began with a training phase in which a search target was more likely to be located in one quadrant of the screen than in the other quadrants. An attentional bias toward the high-probability quadrant developed during training (probability cuing). In a subsequent, testing phase, the target's location distribution became random. In addition, the training and testing phases were based on different tasks. Probability cuing did not transfer between visual search and a foraging-like task. However, it did transfer between various types of visual search tasks that differed in stimuli and difficulty. These data suggest that different visual search tasks share a common and transferrable learned attentional bias. However, this bias is not shared by high-level, decision-making tasks such as foraging.

Humans possess powerful mechanisms for statistical learning, allowing us to extract visual or auditory regularities from the environment (Orbán, Fiser, Aslin, & Lengyel, 2008; Reber, 1993; Saffran, Aslin, & Newport, 1996). Even subtle statistical regularities, such as the transitional probability between sounds or novel shapes, are easily extracted, often after just minutes of exposure (Fiser & Aslin, 2001, 2005; Hay, Pelucchi, Graf Estes, & Saffran, 2011; Olson & Chun, 2001; Saffran et al., 1996; Swallow & Zacks, 2008; Turk-Browne, 2012). Statistical learning not only allows us to perceptually distinguish learned from unlearned information, but also changes how we act in the world. An important mechanism by which statistical learning changes behavior is attention (Brady & Chun, 2007; Chun & Jiang, 1998; Zhao, Al-Aidroos, & Turk-Browne, 2013). For example, past learning of important locations changes how we attend to the visual environment in the future. However, surprisingly little is known about whether these changes in spatial attention generalize across different visual tasks.

In the present study, we examined whether visual statistical regularities extracted in the context of one task produce a general spatial bias that is observable in other tasks, or whether the learned spatial bias is task-specific. Addressing this question has practical implications for understanding the generalizability of attention training from one task to another. In addition, it helps elucidate the nature of statistical learning and its impact on spatial attention. Previous research has not yielded definitive answers to this question. On the one hand, an active task is often unnecessary to produce visual statistical learning, which can take place after passive exposure to objects or sounds (Folstein, Gauthier, & Palmeri, 2010; Reber, 1993; Saffran et al., 1996). Learning occurs in an unsupervised fashion (Fiser & Aslin, 2001), and its outcome is detectable in a variety of testing tasks (Turk-Browne, Jungé, & Scholl, 2005). These findings may suggest that learning is task-independent. On the other hand, studies have shown that the training task sometimes modulates what is learned. For example, when performing a task that extracts the “summary statistics” of an array of lines (e.g., the average orientation), participants fail to learn the co-occurrence of lines on that array (Zhao, Ngo, McKendrick, & Turk-Browne, 2011). In addition, spatial context learning of a visual display shows limited or no transfer between visual search and change detection tasks (Jiang & Song, 2005). These findings raise the possibility that the effects of statistical learning on spatial attention could be task-specific.

We examined the task specificity of attention training via location probability learning. In this paradigm, participants search for a target among distractors. Across multiple trials, the target is more often found in some locations than in others. Although participants usually cannot identify the high-probability locations, they nevertheless find the target more quickly and with greater efficiency when it appears in those locations (Jiang, Swallow, & Rosenbaum, 2013). Because the probability that a target will appear in a particular location cues spatial attention, enhanced search at high-probability locations is known as probability cuing (Druker & Anderson, 2010; Geng & Behrmann, 2002, 2005; Jiang, Swallow, Rosenbaum, & Herzig, 2013; Miller, 1988).

Like explicitly cued attention, probability cuing reflects a spatial bias toward certain locations. However, unlike explicit cuing, probability cuing relies on incidental, long-term statistical learning of the target's likely locations (Geng & Behrmann, 2005; Jiang, Swallow, Rosenbaum, & Herzig, 2013). Once acquired, probability cuing exhibits striking long-term persistence. The spatial bias toward the previously trained high-probability locations is robust one week after training, and over several hundred trials of extinction retraining (Jiang, Swallow, Rosenbaum, & Herzig, 2013). It persists even after participants are told that the target's location will be random (Jiang, Swallow, & Sun, 2014). In addition, this bias is predominantly egocentric. The learned spatial bias persists in the same visual field locations following changes in the observer's viewpoint (Jiang & Swallow, 2013a, 2013b).

The persistence of probability cuing over time raises questions about whether it generalizes across tasks, or whether it is specific to the training task. Previous research has not systematically addressed this question. Most models of spatial attention depict it as a priority map that weighs some locations more heavily than others (Bisley & Goldberg, 2010; Fecteau & Munoz, 2006; Itti & Koch, 2001). The priority weights are determined by top-down factors, such as the observer's explicit goal, and bottom-up factors, such as perceptual saliency (Desimone & Duncan, 1995; Egeth & Yantis, 1997; Wolfe, 2007). In addition, one's past experience often guides spatial attention (Awh, Belopolsky, & Theeuwes, 2012; Chun, 2000; Hutchinson & Turk-Browne, 2012; Jiang, Swallow, Rosenbaum, & Herzig, 2013; Jiang, Won, & Swallow, 2014). Yet, unlike an explicit goal or perceptual saliency, previous experience includes a possibly infinite amount of information. It is unclear whether momentary attentional allocation draws upon all prior experience or only relies on experience from the same task.

Evidence for a generic spatial attention map has come from neurophysiological studies that link the posterior parietal cortex to the attentional priority map (for a review, see Bisley & Goldberg, 2010). Because the posterior parietal cortex is broadly involved in a variety of visual attention tasks (Duncan, 2010; Jiang & Kanwisher, 2003; Wojciulik & Kanwisher, 1999), it is possible that training in any task will result in a generic and persistent change in how visual space is priori-tized. This view predicts that the attentional bias acquired from one task (such as visual search) should persist when people perform a different task (such as foraging).

However, task specificity in probability cuing could occur if learning influences mechanisms that are used in one task but not in another. For example, the feature integration theory distinguishes feature search from conjunction search. Simple feature search (such as finding a red object among green ones) reflects simultaneous, parallel distribution of attention across all locations, whereas conjunction search (such as finding a red vertical among green verticals and red horizontals) relies on the serial allocation of attention from one location to another (Treisman, 1988). Unlike the feature integration theory, the guided search model treats feature search and conjunction search as different ends of a continuum (Wolfe, 2007): Some search tasks are highly efficient, whereas others require serial scrutiny of the search items (Wolfe, 1998). If different search tasks rely on different mechanisms, then probability cuing might not transfer across them.

The following experiments present our systematic attempt at characterizing the task specificity of probability cuing. These empirical data are the basis for placing changes in spatial attention on a continuum ranging from not at all specific to highly task-specific. In turn, they help us understand how the visual system uses previous experience to prioritize spatial attention.

Experiment 1

We started out by testing the most generic view: When performing a task, the visual system favors locations that were prioritized in previous tasks. A straightforward way to implement a task-general attentional bias is by modulating the weights on a generic attentional priority map. Locations that were important in the training task receive higher weights on the priority map. The same map may then be used when performing additional tasks. If this occurs, then an attentional bias developed in one task (such as visual search) should persist when the task changes (e.g., to foraging).

We used two tasks in Experiment 1: a standard visual search task, in which participants searched for a T target among L distractors, and a foraging-like task, in which participants guessed the location of hidden treasure under one of several items (Fig. 1). Both tasks involved finding a “target” among several nontargets. However, the search task was visually guided and required matching the search items to a target template (the “T”). It involves frequent stop-and-go until the target was found. In contrast, the treasure hunt task was primarily a high-level decision-making task. Participants had no way of knowing which item contained treasure; they only found out after they had selected an item and received feedback. The treasure hunt task was modeled after foraging-like tasks, in which human behaviors follow the “matching law” (Herrnstein, 1974). Specifically, the probability that people will choose a given location is correlated with the probability that the target is in that location (Baum, 1974; Pierce & Epling, 1983). Thus, both visual search and treasure hunt are likely to produce an attentional bias toward the high-probability locations. But does this bias transfer between tasks?

Fig. 1.

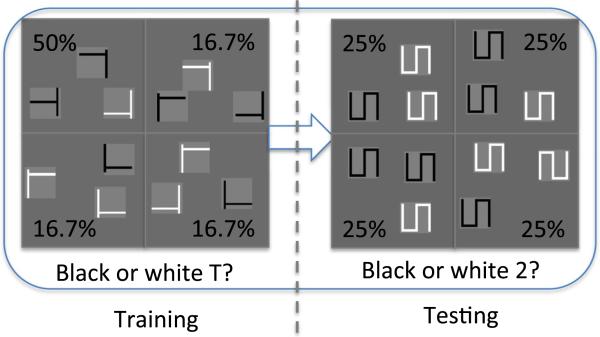
A schematic illustration of the tasks and stimuli used in Experiment 1. a In Experiment 1A, the visual search and treasure hunt tasks differed in set sizes and display appearances. b In Experiment 1B, the two tasks had similar set sizes and display appearances. Items are not drawn to scale, and the quadrant borders were not actually shown in the experiment

The participants in Experiment 1 were tested in two consecutive phases. In the training phase, they performed either the visual search task or the treasure hunt task. The target appeared in a selected “rich” visual quadrant on 50% of the trials, and in any one of the other three “sparse” quadrants on 16.7% of the trials. In the testing phase, they performed the other task. Because we were interested in the persistence of the trained attentional bias, we did not introduce a new attention bias in the testing phase. Instead, the target was equally likely to appear in any of the four quadrants (25%) during testing. If all tasks share a common and transferrable attentional priority map, then probability cuing acquired in one task should transfer to the other task.

Two versions of Experiment 1 were administered to different participants. In Experiment 1A (Fig. 1a), the search and treasure hunt tasks differed in their set sizes (12 items in the visual search task and eight items in the treasure hunt task) and stimuli (T/Ls vs. treasure chests). In Experiment 1B (Fig. 1b), the two tasks used similar displays (eight items in both tasks, and the treasure chests were represented by Ls). Testing both versions informed us about the specificity of probability cuing to tasks and display properties.

Method

Participants

A group of 48 students (18–35 years old) from the University of Minnesota completed Experiment 1 in exchange for extra course credit and a small prize. They were naive to the purpose of the study and had normal or corrected-to-normal visual acuity. Half of the participants completed Experiment 1A, and the other half, Experiment 1B.

Equipment

Participants were tested individually in a room with normal interior lighting. They sat in front of a 19-in. CRT monitor. The viewing distance was approximately 57 cm but was unconstrained. The experiment was programmed with Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) implemented in MATLAB (www.mathworks.com).

Visual search

To initiate each trial, participants clicked on a small square (0.34° × 0.34°) with a mouse. The square was presented at a random location within the central 2° × 2° region of the monitor. The mouse click required eye–hand coordination and enforced fixation prior to the next trial. After the click and a 200-ms blank period, the search display was presented. Participants were asked to find the T and to report whether it was rotated to the left or the right. Both accuracy and speed were emphasized. The display was presented until a response was made. Three rising tones lasting a total of 300 ms followed a correct response. A buzz (200 ms) and a blank interval (2 s) followed an incorrect response.

The search display contained one Tand several Ls (11 Ls in Exp. 1A, and 7 Ls in Exp. 1B). Each search item subtended 1.37° × 1.37°. The T was tilted 90° randomly to the left or to the right. The orientation of each L was randomly chosen from four possible orientations (0°, 90°, 180°, or 270°). The two segments of the L had a small offset (0.17°).

The search items were black presented against a gray background. The items were presented at randomly selected locations within an invisible 10 × 10 matrix (22.2° × 22.2°), with the constraint that an equal number of items appeared in each quadrant.

Treasure hunt

As in the visual search task, participants clicked on a small square to initiate each trial of the treasure hunt task. After a 200-ms blank period, they were shown eight identical treasure chests (1.37° × 1.37°, Exp. 1A) or eight randomly oriented Ls (Exp. 1B). Two items were in each quadrant, placed at random locations on the display (as in the visual search). Participants were told that one of the eight items contained gold coins, whereas the others contained old boots. They were given one chance to guess where the gold coins were by clicking on one of the items. The display was erased with the mouse click, revealing at the chosen location either gold coins (along with a high tone) or old boots (along with a low tone) for 300 ms. This was followed by a feedback display that lasted 1 s. The feedback display was similar to the treasure hunt display, except that the contents of all of the treasure chests or Ls were revealed (i.e., one of them had gold coins, the rest of them had old boots). Participants received 1 point for each trial on which gold coins were found. They accumulated points and traded them for pieces of candy or a cash prize of similar value (1 cent per point).

Design

The experiment was divided into two consecutive phases that differed in the task and the target's location probability. There were 384 trials in each phase, binned into 32 blocks of 12 trials each. We chose 12 trials as the size of an experimental block because this was the smallest number of trials necessary to produce a balanced experimental design across conditions. Half of the participants in each experiment performed visual search in the training phase and treasure hunt in the testing phase, whereas the other half had the reverse order.

During the training phase, the target's location probabilities were unequal across the four quadrants. The target appeared in a “rich” quadrant on 50% of the trials, and in any one of the three “sparse” quadrants on 16.7% of the trials. The specific quadrant that was “rich” was counterbalanced across participants, but it remained the same during training for a given participant. Participants were not informed of this manipulation. In the testing phase, the target appeared with equal probabilities in each visual quadrant (25%).

Participants completed ten practice trials in each task at the beginning of the experiment. Upon completion of the experiment, they were asked to identify the rich quadrant with a mouse click.

Results

In this experiment and subsequent ones, the overall accuracy in visual search was higher than 96%. Analyses of variance (ANOVAs) on accuracy revealed no speed–accuracy trade-off in any of the experiments. The mean RT for correct trials was calculated for each participant after outliers had been removed (RTs longer than 10 s were outliers—typically less than 0.3% of trials).

In the treasure hunt task, we measured the percentage of trials on which participants chose a location in the rich (or previously rich) quadrant, as opposed to the sparse quadrants.

Experiment 1A

We first examined the data from participants who were trained in visual search and tested in treasure hunt (Fig. 2).

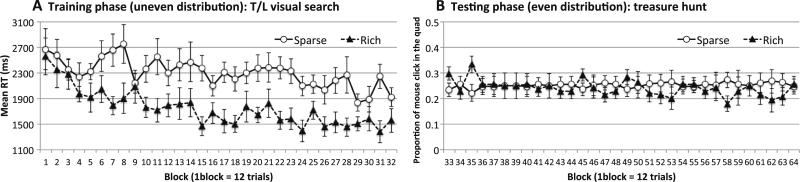
Fig. 2.

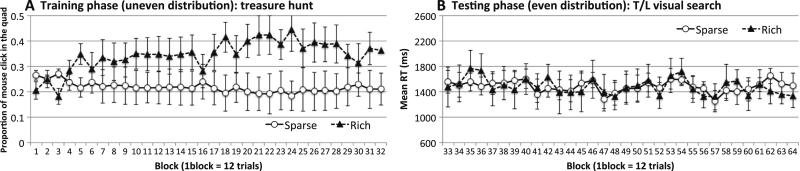
Experiment 1A's results, from participants trained in visual search and tested in a treasure hunt. a Visual search RTs during training. b Proportions of trials on which a treasure chest was chosen in the trained rich quadrant, as opposed to in one of the sparse quadrants. Chance was .25. Error bars in this and all subsequent figures show ±1 SE of the mean between participants

Training (visual search)

RTs were significantly faster when the target fell in the rich quadrant rather than the sparse quadrants, F(1, 11) = 44.56, p < .001, η_p² = .80. RTs also improved as the experiment progressed, F(31, 341) = 3.51, p < .001, η_p² = .24. The two factors showed a marginal interaction, F(31, 341) = 1.41, p < .08, η_p² = .11. Probability cuing was absent in Block 1 (p > .13) but developed after several dozen trials.

Testing (treasure hunt)

If probability cuing resulted in a general spatial bias toward the rich quadrant, then the proportion of trials on which people chose the rich quadrant in the treasure hunt task should exceed chance (.25). But on the contrary, participants were no more likely to select a location in the (visual search) rich quadrant than in the sparse quadrants, F < 1.

Next we examined the data from participants trained in treasure hunt and tested in visual search (Fig. 3).

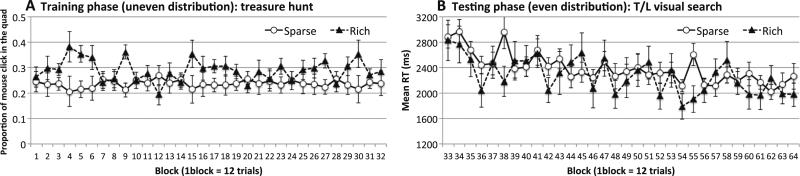
Fig. 3.

Experiment 1A results, from participants trained in a treasure hunt and tested in visual search. a Proportions of trials on which people chose a treasure chest in the rich quadrant as opposed to any of the sparse quadrants. b Visual search RTs as a function of whether the quadrant that the target appeared in had been rich or sparse during training. Error bars show ±1 SE of the mean

Training (treasure hunt)

Participants were more likely to choose a box in the rich quadrant than in any of the sparse quadrants in the training phase, F(1, 11) = 5.85, p < .034, η_p² = .35. This bias developed over time, resulting in a significant Quadrant × Block interaction, F(31, 341) = 1.52, p < .041, η_p² = .12. Thus, the treasure hunt task yielded a bias toward the rich quadrant.

Testing (visual search)

We found no evidence of transfer between tasks. Visual search RTs improved as testing progressed, F(31, 341) = 2.53, p < .001, η_p² = .19. However, they were unaffected by the quadrant condition, F(1, 11) = 1.81, p > .20, and no interaction emerged between quadrant and block, F < 1. The bias to choose a box in the rich quadrant during training did not transfer to a task that required participants to search through and identify items in the display.

Experiment 1B

Could the lack of transfer in Experiment 1A be attributed to a change in display characteristics between the two tasks? After all, the two tasks differed in their numbers of items and in the appearances of the items. To address this possibility, we examined the data from Experiment 1B, which equated the numbers of stimuli and their appearances across the two tasks.

Training (visual search)

As is shown in Fig. 4, people who conducted visual search in the training phase were significantly faster when the target was in the rich quadrant rather than the sparse quadrants, F(1, 11) = 51.78, p < .001, η_p² = .83. This effect did not interact with block, F < 1. The difference between the rich and sparse conditions in Block 1 could be attributed to noise, since each block contained only six trials per condition. Alternatively, it could reflect short-term trial sequence effects. Specifically, because the target was more likely to appear in the rich quadrant, immediate repetition of the target's quadrant happened more often in the rich than in the sparse condition (Walthew & Gilchrist, 2006). To ensure that participants had acquired long-term learning of the target's location probability, we examined data from the second half of training (Blocks 17–32) and separated trials with or without an immediate repetition of the target's quadrant. The RT advantage in the rich condition was substantial (440 ms, p < .001), even on trials without an immediate repetition of the target's quadrant. Thus, participants showed a spatial bias toward the rich quadrant in the visual search task.

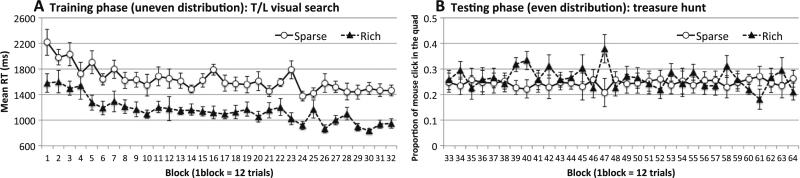
Fig. 4.

Experiment 1B's results, from participants trained in visual search and tested in a treasure hunt. a Visual search RTs during training. b Proportions of trials on which an item was chosen in the trained rich quadrant as opposed to the sparse quadrants. Chance was .25. Error bars show ±1 SE of the mean

Testing (treasure hunt)

The attentional bias did not persist in the treasure hunt task (Fig. 4b). Participants were no more likely to choose an item in the rich quadrant than in the sparse quadrants in the treasure hunt task, F < 1.

Training (treasure hunt)

As is shown in Fig. 5, participants trained in the treasure hunt task of Experiment 1B developed a preference for the rich quadrant. They were more likely to click on an item in the rich quadrant than in any of the sparse quadrants, F(1, 11) = 3.62, p = .084, η_p² = .25, and this preference increased as training progressed: F(31, 341) = 1.76, p < .009, η_p² = .14, for the interaction between condition and block.

Fig. 5.

Experiment 1B's results, from participants trained in treasure hunt and tested in visual search. a Proportions of trials on which people chose an item in the rich quadrant rather than one in a sparse quadrant. b Visual search RTs as a function of whether the quadrant that the target appeared in had been rich or sparse during training. Error bars show ±1 SE of the mean

Testing (visual search)

The preference for the rich quadrant, however, did not transfer to visual search. Search RTs were not faster when the target was in the rich quadrant rather than the sparse quadrants, nor did target quadrant interact with block, Fs < 1.

A further analysis that combined the data from Experiments 1A and 1B yielded the same pattern of statistical results as those reported for each individual experiment: Probability cuing was highly significant in the training task but did not persist in the testing task.

At the end of the experiment, participants were asked to identify the rich quadrant. Thirteen (five trained in treasure hunt and eight trained in visual search) of the 48 participants correctly identified the rich quadrant. This number did not differ from chance, p > .50. None of the effects reported in this experiment differed between participants who correctly identified the rich quadrant and the other participants, all ps > .10 for the interaction between participants (“aware” or “unaware”) and the other experimental factors. This was also the case in subsequent experiments. As in other studies (Geng & Behrmann, 2002; Jiang, Swallow, & Rosenbaum, 2013), probability cuing was incidental. Because explicit recognition contributed little to performance, and because the issue of explicit awareness has been addressed more fully elsewhere (e.g., Geng & Behrmann, 2002; Jiang, Swallow, Rosenbaum, & Herzig, 2013; Jiang, Swallow, & Sun, 2014), we will not discuss the recognition data further.

Discussion

Experiment 1 provided evidence against the idea that the attentional bias acquired from one task reflects a generic and transferrable change in spatial attention. On the contrary, probability cuing developed in a visual search task did not persist when participants performed treasure hunt, or vice versa. The lack of transfer was found even when the visual displays were similar between the two tasks (Exp. 1B). Thus, the data from Experiment 1 suggest that changes in the attentional priority map are task-specific.

When trained in treasure hunt, participants developed a preference for the rich quadrant. It may seem surprising that the preference for the rich quadrant (28% in Exp. 1A and 36% in Exp. 1B) was less than the probability that the gold coins would appear in the rich quadrant (50%). However, 50% was not the asymptote level of performance. In reinforcement learning, the asymptote level is jointly determined by the environmental statistics and reinforcement history. The probability that a specific choice will be made follows the Softmax function (Sutton & Barto, 1998), which in our study may be simplified to

$$e^{p-\mathrm{rich}}∕\left(e^{p-\mathrm{rich}}+e^{p-\mathrm{sparse}1}+e^{p-\mathrm{sparse}2}+e^{p-\mathrm{sparse}3}\right).$$

Plugging in the probabilities for the rich quadrant (.5) and the sparse quadrants (.167) yields an asymptote level of 31.7% for the rich quadrant.¹ The observed data in the treasure hunt task therefore match what is expected. Nonetheless, learning from the treasure-hunt task failed to influence attentional allocation in the subsequent visual search task, and vice versa.

Experiment 2

We next set out to test the opposite view about the task specificity of probability cuing: When prioritizing attention, the visual system only considers prior experience from the same task. Consequently, the priority weights for locations are reset in a new task to reflect only the current task's goals and perceptual saliency, but not previous experience. This view predicts a high degree of task specificity. Because potentially an infinite number of tasks exist, to keep the research tractable, we restricted our investigation to visually guided search tasks. The first study—Experiment 2—involved two visual search tasks of different targets and distractors, but with similar levels of search efficiency (slopes). In one task, participants searched for a T target among L distractors and reported the T's color. In the other task, they searched for a rotated 2 among rotated 5s and reported the 2's color (Fig. 6). Pilot data from nine participants showed equivalent search slopes on target-present trials: 98 ms/item in the T/L task and 97 ms/item in the 2/5 task. Despite this similarity, the T/L and 2/5 tasks constituted a noticeable change in task. As will be shown later, search RTs in one task improved with training, but suddenly slowed down when the other task began. If changes in spatial attention are task-specific, then probability cuing should not persist across the T/L and 2/5 tasks.

Fig. 6.

Schematic illustration of the tasks and design used in Experiment 2. Participants searched for a target and reported its color. The items are not drawn to scale, and the quadrant borders as well as the targets’ spatial probabilities were not actually shown in the experiment

Method

Participants

A group of 16 new participants from the University of Minnesota completed Experiment 2 for extra course credit or $10/h. Their characteristics were similar to those from Experiment 1.

Task

Participants conducted visual search throughout the experiment, but the search items were either a Tand several Ls or a rotated 2 and several rotated 5s. There were 12 items in each display, and the color of each item was randomly determined to be either black or white. Participants were asked to find the target (T in the T/L task and 2 in the 2/5 task) and to press a button to report its color.

Design

Half of the participants performed the T/L task during training and the 2/5 task during testing; the other half had the reverse order. For all participants, the target was more often found in a rich quadrant (50%) during training, but its location probability was random during testing (25% in each quadrant). As in Experiment 1, 384 trials were presented in each phase.

All other aspects of the experiment were the same as those of Experiment 1.

Results

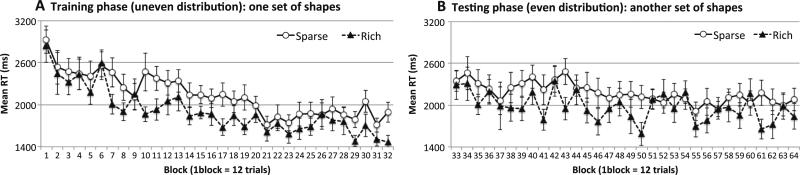
As is shown in Fig. 7, probability cuing emerged in the training phase and persisted in the testing phase.

Fig. 7.

Results from Experiment 2. Participants performed a T/L search task in the training phase and a 2/5 search task in the testing phase, or vice versa. Error bars show ±1 SE of the mean

Training

In the training phase, participants were significantly faster when the target fell in the rich quadrant rather than in the sparse quadrants, F(1, 15) = 9.98, p < .006, η_p² = .40, demonstrating probability cuing. RTs were also faster as the experiment progressed, F(31, 465) = 7.88, p < .001, η_p² = .34, but the two factors did not interact significantly, F(31, 465) = 1.04, p > .35. RTs did not differ between the rich and sparse conditions in the first block (p > .50), but were significantly faster in the rich than in the sparse condition by the end of training (Block 32, p < .02). The magnitude of probability cuing was smaller in this experiment than in Experiment 1. This reduction may be attributed to a strategy of searching only through one set of colored items and reporting whether the target was present in that set (e.g., the white items). Because probability cuing scales with set size (Geng & Behrmann, 2005; Jiang, Swallow, & Rosenbaum, 2013), a reduction in the effective set size would reduce its magnitude.

Testing

Although the search task changed, the learned attentional bias persisted. In the testing phase, we observed a significant main effect of target quadrant, F(1, 15) = 7.66, p < .014, η_p² = .34, with faster RTs when the target lay in the previously rich quadrant. RTs were unaffected by block, F(31, 465) = 1.46, p > .15, or a Block × Quadrant interaction, F(31, 465) = 1.06, p > .35. Probability cuing persisted even though the change in task yielded a substantial increase in search RTs: The RT in the first block of the testing phase (Block 33) was 660 ms slower than the RT in the last block of the training phase (Block 32), F(1, 15) = 19.25, p < .001, η_p² = .56.

Discussion

Experiment 2 showed that the attentional bias that was acquired during the T/L search task persisted when participants performed the 2/5 task, and vice versa. Although changes in item identity resulted in a substantial rise in search RTs, they did not reset the learned attentional bias. These data provide strong evidence for the presence of a common and transferrable spatial attentional bias for the T/L and 2/5 tasks. In contrast, Experiment 1 showed that this commonality did not extend to the treasure-hunt task. Together, the first two experiments rule out the two extreme views. Statistical learning of the target's location probability produces an attentional bias that is neither fully transferrable across tasks nor hyperspecific to the training task.

Experiment 3

The contrast between Experiments 1 and 2 raises questions about what other tasks might share a transferrable learned attentional bias. To address this question, in Experiments 3– 5 we tested some of the most commonly used visual search tasks in the laboratory. The feature integration theory divides visual search into feature search and conjunction search (Treisman, 1988), whereas the Guided Search model considers all tasks as falling on a continuum ranging from highly efficient to highly inefficient search (Wolfe, 2007). These models do not explicitly address whether training effects are transferrable across different search tasks. If an attentional bias developed in one task persisted when people perform another task, this finding would provide some of the strongest evidence for the use of a common and transferrable spatial attention map for these tasks.

Experiment 3 tested the hypothesis that tasks similar in search efficiency share a common attentional priority map, but tasks dissimilar in search efficiency rely on different spatial attention maps (the search efficiency hypothesis). This hypothesis was motivated by the larger literature on implicit learning. Limited transfer across tasks is a hallmark of implicit learning (Dienes & Berry, 1997). For example, artificial grammar learning and sequence learning are specific to the surface features of the tasks. Transfer is limited when the underlying statistical structure remains the same but the surface features change (e.g., from one set of letters to another, or from the visual to the auditory modality; Berry, Banbury, & Henry, 1997; Dienes & Berry, 1997). Similarly, motor skill learning is specific to the difficulty of the training task. In a rotary pursuit task, transfer of skills was reduced if people were trained on an easy task (e.g., with a slow speed) and tested on a difficult task (e.g., fast speed), or vice versa (Namikas & Archer, 1960). As a form of implicit learning, probability cuing may be similarly constrained.

To test the search efficiency hypothesis, we employed two T-among-L search tasks. The target T and distractor Ls were either highly similar (difficult search) or dissimilar (easy search), producing different search slopes. We examined whether probability cuing persisted across changes in search efficiency.

Method

Participants

A group of 64 participants completed Experiment 3.

Stimuli

Participants searched for a T target among a varying number of L distractors and reported the orientation of the T. The offset between the two segments of the Ls was 0° in the easy task and 0.27° in the difficult task (see Fig. 8).

Fig. 8.

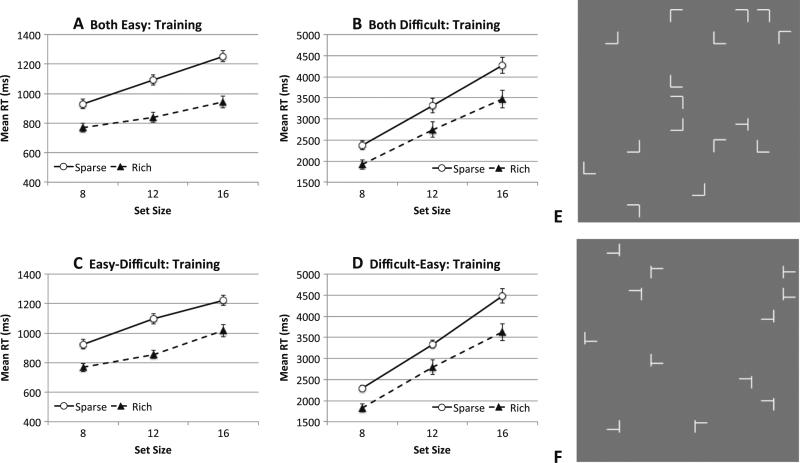
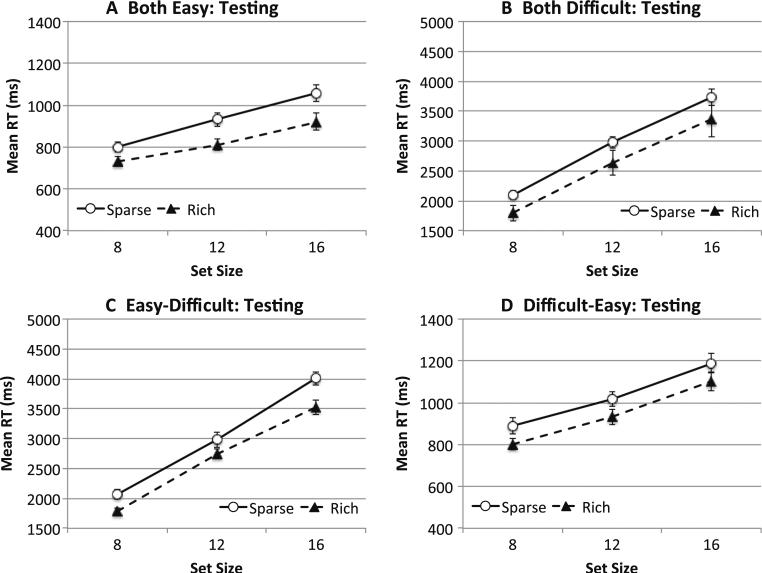
Results from the training phase of Experiment 3. During training, the participants in panels a and c performed an easy search task, whereas those in panels b and d performed a difficult search task. Note that the y- axes are optimized for each panel and differ for the easy and difficult tasks. Error bars show ±1 SE of the mean. Panels e and f show sample displays in the easy and difficult tasks, respectively

Design

Participants completed two consecutive phases. The target's location probability was biased toward a rich quadrant (50% of the trials) in the training phase, but was unbiased (25% in each quadrant) in the testing phase. In addition, to verify that the difficulty manipulation was effective, we manipulated the number of items in the display (8, 12, or 16). The trial number changed slightly from those in previous experiments to accommodate the set size manipulation: 360 trials were presented in a randomly intermixed order in each phase.

Participants were divided into four groups based on the tasks they performed in the two experimental phases. There were 16 participants in each group. Throughout the experiment, the both-easy group performed only the easy task, whereas the both-difficult group performed only the difficult task. The easy–difficult group performed the easy task during training but the difficult task during testing, and the difficult– easy group had the reverse order.

Results

This experiment produced a large amount of data, owing to the presence of four participant groups and the addition of a set size manipulation. For readability, we have simplified the data report by averaging across different blocks. Figure 8 shows data from the training phase separately for the four groups of participants.

Training phase

Because the training task was the same for the participants in the both-easy and easy–difficult groups and for those in the both-difficult and difficult–easy groups, our ANOVA included Training Task Difficulty (easy or difficult) as a between-groups factor, and Probability Cue Condition (sparse or rich) and Set Size (8, 12, or 16) as within-groups factors. All main effects were significant: RTs were faster in the rich than in the sparse condition, F(1, 62) = 72.15, p < .001, η_p² = .54; faster in the easy than in the difficult task, F(1, 62) = 554.71, p < .001, η_p² = .90; and faster when fewer items were on the display, F(2, 124) = 566.85, p < .001, η_p² = .90. Our manipulation of task difficulty was effective, as we verified with a significant interaction between difficulty and set size, F(2, 124) = 321.71, p < .001, η_p² = .84, in which search slopes differed substantially: 33 ms/item in the easy task and 232 ms/item in the difficult task. In addition, a significant interaction was observed between quadrant condition and set size, F(1, 62) = 16.01, p < .001, η_p² = .21: Search slopes were shallower in the rich than in the sparse condition. Finally, a significant three-way interaction showed that the effects of probability cuing on search slope were greater in the more difficult search task, F(2, 124) = 5.59, p = .005, η_p² = .083.

Testing phase

Having observed a significant probability-cuing effect in the training phase, we now turned to the question of whether the persistence of cuing depended on the match of search efficiency between the training and testing tasks. Figure 9 plots data from the four groups of participants during testing.

Fig. 9.

Results from the testing phase of Experiment 3. During testing, the participants in panels a and d performed an easy search task, whereas those in panels b and c performed a difficult search task. Note that the y-axes are optimized for each panel and differ for the easy and difficult tasks. Error bars show ±1 SE of the mean

In the testing phase, the four groups differed not only in the difficulty of visual search but also in whether the testing task matched the training task. We therefore conducted an ANOVA using Task Difficulty (easy or difficult) and Task Status (match or mismatch) as between-groups factors, and Quadrant Condition (sparse or rich) and Set Size as within-groups factors. This analysis produced a significant main effect of quadrant condition, F(1, 60) = 20.16, p < .001, η_p² = .25, suggesting that probability cuing persisted in the testing phase. In addition, RTs were faster when fewer items were on the display, F(2, 120) = 407.48, p < .001, η_p² = .87. RTs were slower and search slopes were steeper in the more difficult task, F(1, 60) = 596.71, p < .001, η_p² = .91, and F(2, 120) = 221.65, p < .001, η_p² = .79, respectively. Importantly, whether task difficulty matched between training and testing did not influence search RTs, F(1, 60) = 1.58, p > .20, nor did this factor interact with condition (rich or sparse), F < 1. None of the higher-order interactions involving task status (match or mismatch) and condition was significant, all Fs < 1. All other interaction effects did not reach significance, smallest p = .08. Thus, a tenfold change in search slope did not affect how probability cuing persisted in the testing phase.

Discussion

Experiment 3 showed that probability cuing persisted following a change in search difficulty. These data suggest that changes in search efficiency do not necessarily change how previous experience influences visual search. This finding is surprising, considering that probability cuing results from implicit learning, which previously has been shown to produce limited transfer (Dienes & Berry, 1997). One way to account for this discrepancy may be to consider the processes involved in serial search, which relies on the movement of spatial attention from one location to the next as well as on object recognition (Wolfe, 2007). Although recognition and categorization may take longer in the more difficult than in the easy task, the roles of attentional shifts across tasks may be similar, and this similarity may account for the transfer of cuing between the two tasks. This possibility is consistent with an earlier proposal that probability cuing reflects the reinforcement of attentional shifts that land on targets (Jiang, Swallow, & Capistrano, 2013).

Experiment 4

According to the Guided Search model (Wolfe, 2007), feature and conjunction search differ chiefly in how efficiently perceptual features and explicit goals guide attention. When a single feature distinguishes the target from distractors (e.g., red vs. green color), the featural difference can effectively guide attention to the target, producing shallow search slopes. However, much like conjunction search, feature search tasks differ widely in efficiency. Some feature search tasks, such as finding a vertical line (0°) among 20°-tilted lines, yield steep search slopes (Wolfe, Friedman-Hill, Stewart, & O'Connell, 1992). Importantly, differences between feature and conjunction search tasks could reflect recognition processes rather than qualitative differences in how spatial attention moves from one location to another. In Experiment 4, we tested whether probability cuing persisted when one of the two tasks was a feature search task, whereas the other was a conjunction search task.²

Method

Participants

A group of 32 new participants completed Experiment 4: 16 in each of Experiments 4A and 4B.

Design

The two tasks used in Experiment 4 were a T/L spatial configuration search task and a line orientation feature search task. On each trial, participants saw an array of items (T and Ls, or lines). In the T/L task, the target was a T and the distractors were Ls. In the line orientation task, the target was a vertical line (1.37° in length) and the distractors were slanted lines (also 1.37° in length) tilted ±20° away from the vertical (approximately half of the distractors tilted clockwise and the other half tilted counterclockwise). In both tasks, half of the items were black and the other half were white. Participants were asked to find the target and to report whether it was black or white. The number of items on the display could be 8, 12, or 16.

The participants in Experiment 4A performed the orientation search task in the training phase and the T/L task in the testing phase. Those in Experiment 4B had the reverse order. As in the previous experiments, the target was more often found in a rich quadrant in the training phase, but its location was random in the testing phase. There were 360 trials in each phase. Because the smallest number of trials to produce a balanced design was 36, the data were divided into ten blocks in each phase. Other aspects of the experiment were the same as in Experiment 3.

Results

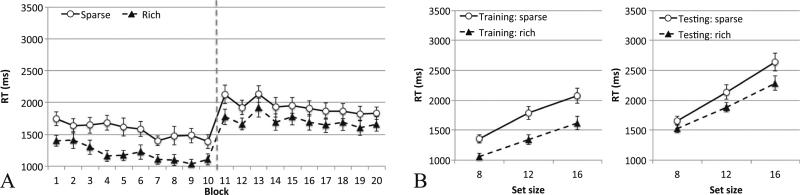
Experiment 4A

Training (difficult feature search)

As is shown in Fig. 10a, in the training phase, participants acquired probability cuing in the feature search task. An ANOVA on probability cue condition and block showed that RTs were significantly faster in the rich than in the sparse condition, F(1, 15) = 56.72, p < .002, η_p² = .79, and also improved as the experiment progressed, F(9, 135) = 7.30, p < .001, η_p² = .32. These two factors did not interact significantly, F(9, 135) = 1.80, p = .074.

Fig. 10.

Results from Experiment 4A: Participants performed the line orientation feature search task in the training phase and the T/L spatial configuration search task in the testing phase. a Data across the 20 blocks of trials (each block contained 36 trials). b Data across the entire training (left) and testing (right) phases. Error bars show ±1 SE of the mean

Testing (T/L search)

When the task changed to the T/L search task, overall RTs increased substantially (p < .001). However, probability cuing persisted: RTs were significantly faster in the rich than in the sparse condition, F(1, 15) = 17.70, p < .001, η_p² = .54. This effect did not interact with block, F < 1. As is shown in Fig. 10b, the search slope was shallower in the rich condition than in the sparse condition, producing a significant interaction between cue condition and set size: F(2, 30) = 4.01, p < .05, η_p² = .21, in the training phase; F(2, 30) = 3.34, p < .05, η_p² = .18, in the testing phase. Thus, training in a difficult feature search task produced an attentional bias that transferred to a spatial configuration search task.

Experiment 4B

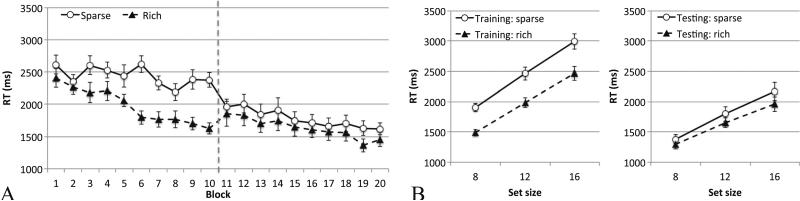
Training (T/L search)

In the training phase (Fig. 11a), the T/L search task produced a significant probability-cuing effect, F(1, 15) = 27.76, p < .001, η_p² = .65. This effect increased with training, yielding a significant interaction between cue condition and block, F(9, 135) = 4.36, p < .001, η_p² = .23.

Fig. 11.

Results from Experiment 4B: Participants performed the T/L search task in the training phase and the line orientation feature search task in the testing phase. a Data across the 20 blocks of trials (each block contained 36 trials). b Data across the entire training (left) and testing (right) phases. Error bars show ±1 SE of the mean

Testing (difficult feature search)

Probability cuing persisted in the difficult feature search task. The main effect of cue condition was marginally significant when the data were separated into ten blocks of trials (Fig. 11a), F(1, 15) = 4.45, p < .052, η_p² = .23, but reached significance when the data were averaged across blocks (Fig. 11b), F(1, 15) = 4.60, p < .05, η_p² = .24. Probability cue condition did not interact with set size in either the training phase, F < 1, or the testing phase, F(2, 30) = 1.25, p > .30.

Discussion

The data from Experiment 4 were consistent with the idea that location probability learning resulted in a transferrable attentional bias between a difficult feature search task and a conjunction search task (the T/L spatial configuration search task). In Experiment 4A, participants performed the T/L task in the testing phase, and their performance was clearly influenced by prior training in a difficult feature search task. The participants in Experiment 4B also demonstrated transfer of location probability learning: After acquiring probability cuing in the T/L search task, they continued to favor the previously rich quadrant in a difficult feature search task. Thus, probability cuing transferred from a difficult feature search task to a conjunction search task, and vice versa.

Although transfer was evident in both experiments, the magnitude of the probability-cuing effect decreased in the testing phase (from 394 to 249 ms in Exp. 4A and from 465 to 147 ms in Exp. 4B). Some of this decrease could reflect a change in statistics, since the degree of reduction was no greater in Experiment 4A than in Experiment 3. However, because the reduction was immediately observed in Experiment 4B when the task changed, it could also reflect the change in task. In Experiment 5, we further examined the transfer between conjunction and feature search tasks.

Experiment 5

Under which conditions would the visual system draw upon previous experience in prioritizing spatial attention? So far, our investigation has focused on one factor: consistency between the previous tasks and the current one. However, when the task changes, other attentional cues may change the utility of the probability cue. If the new task contains strong top-down goals or salient perceptual features, these cues may overshadow the use of the learned probability cue. In fact, several recent studies have shown that explicit cues interfere with implicitly guided attention (Jiang, Swallow, & Rosenbaum, 2013; Rosenbaum & Jiang, 2013). In addition, implicit attentional cuing is weakened when participants search for a simple feature target (Druker & Anderson, 2010; Geyer, Zehetleitner, & Müller, 2010; Kunar, Flusberg, Horowitz, & Wolfe, 2007). Thus, when examining the task specificity of probability cuing, it is important to consider the utility of previous experience relative to other attention cues.

Simple feature search tasks, such as finding a white letter among black letters, involve efficient guidance of spatial attention. Because perceptual saliency is a potent cue for spatial attention, probability cuing should have a limited impact on simple feature search. Consequently, after training in a conjunction search task, the resulting probability cue should have limited to no impact on a subsequent feature search task. The reduction in probability cuing in Experiment 4B was consistent with this idea. The more efficient the feature search task is, the less likely probability cuing would transfer from conjunction search to feature search. This prediction would be tested in Experiment 5A.

The reverse scenario—transfer from simple feature to conjunction search—is more difficult to predict. As had been shown in a previous study, probability cuing could be observed even when the display contained just a single item (Druker & Anderson, 2010). This raises the possibility that locations that frequently contain a target are prioritized, even when no search is necessary. When subsequently probed with a conjunction search task, probability cuing may exert a strong influence on spatial attention, paradoxically increasing the size of cuing from training to testing. Alternatively, it is possible that training in a simple feature search task might induce only a weak attentional bias, and the salient perceptual cue might overshadow the learning of the probability cue. Probability cuing would therefore not be revealed, even when probed with a conjunction search task. These contrasting predictions would be tested in Experiment 5B.

Method

Participants

A group of 24 participants completed this experiment, 12 in Experiment 5A and 12 in Experiment 5B.

Design and procedure

In these experiments, participants searched for a T target among L distractors and reported the direction of the T (left or right). In the training phase, the location of the T was biased toward a rich quadrant (50% of trials). In the testing phase, the T's location was random, appearing in each quadrant 25% of the time. There were 384 trials in each phase.

In the training phase of Experiment 5A, the target and distractors had the same color, necessitating the several shifts of attention that are characteristic of conjunction search. In the testing phase, the target was in one color (e.g., white), but the distractors were in another color (e.g., black). Thus, the task involved simple feature search. Although the detection of a color singleton may not demand spatial attention (Treisman, 1988), to identify the target's orientation participants would need to shift attention to the target's location. The feature task therefore likely involved one attentional shift from the default location (i.e., the fixation point) to the target's location.

Experiment 5B was similar, except for the order of tasks: Participants were trained in the simple feature search task and tested in the conjunction search task. We examined whether the spatial bias developed from simple feature search would persist in the conjunction search task.

Although we did not measure search slopes directly, on the basis of similar visual search experiments we estimated the search slope to be 0 ms/item in the feature search task and about 100 ms/item in the conjunction search task.

Results

Figures 12 and 13 show the results from Experiments 5A and 5B, respectively.

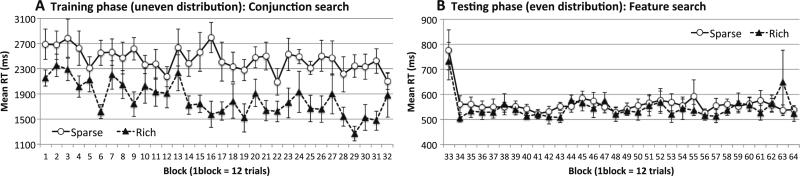
Fig. 12.

Results from Experiment 5A. a Training phase, involving conjunction search. b Testing phase, involving feature search. Error bars show ±1 SE of the mean

Fig. 13.

Results from Experiment 5B. a Training phase, involving feature search. b Testing phase, involving conjunction search. Error bars show ±1 SE of the mean

Experiment 5A: conjunction to feature search

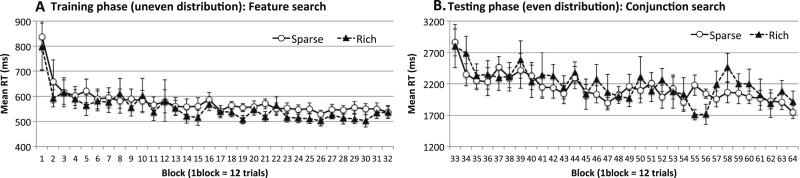
Training (conjunction search)

In the conjunction search task, RTs were significantly faster when the target appeared in the rich quadrant rather than the sparse quadrants, F(1, 11) = 70.26, p < .001, η_p² = .87, and RTs also improved as the experiment progressed, F(31, 341) = 2.33, p < .001, η_p² = .18. The two factors did not interact, F(31, 341) = 1.15, p > .25; learning emerged early and was maintained for most of the training phase. The size of the effect was large: By the end of training, the RT in the rich condition was 25% faster (about 800 ms) than that in the sparse condition.

Testing (feature search)

RTs improved, primarily from the first to the second testing blocks, F(31, 341) = 3.62, p < .001, η_p² = .25. However, they were unaffected by quadrant condition, F(1, 11) = 3.22, p > .10. The two factors did not interact, F < 1. Even the first block after transfer showed no effect of target quadrant, p > .50.

Experiment 5B: feature to conjunction search

Training (feature search)

RTs were significantly faster when the target lay in the rich quadrant rather than the sparse quadrants, F(1, 11) = 14.66, p < .003, η_p² = .57, and RTs also improved as the experiment progressed, F(31, 341) = 5.13, p < .001, η_p² = .32. We found no interaction between target quadrant and block, F < 1. A significant probability-cuing effect emerged in the training phase, although the magnitude of the effect was small.

Testing (conjunction search)

Probability cuing failed to transfer from feature to conjunction search. RTs improved as testing progressed, F(31, 341) = 2.52, p < .001, η_p² = .19, but they were unaffected by target quadrant, F(1, 11) = 1.05, p > .30, or a Quadrant × Block interaction, F < 1. Even the first testing block showed no advantage for the previously rich quadrant, p > .50. No evidence emerged that the simple feature search task had produced a robust and transferrable change of attention.

Discussion

Probability cuing did not transfer from conjunction search to feature search (Exp. 5A). Even though a strong attentional bias had developed in the training phase, it did not influence performance in the simple feature search task. These data are compatible with the idea that probability cuing is only one of several sources of spatial attention. Its utility in guiding attention is substantially reduced in the presence of other strong top-down or bottom-up cues.

Conversely, probability cuing also failed to transfer from feature search to conjunction search (Exp. 5B). Although the target was frequently located in a rich quadrant in the training phase, and an attentional shift was necessary to identify the target, this did not result in a strong and transferrable attentional bias to the subsequent conjunction search task. These data differed from those of Experiment 4A, in which a strong and transferrable probability-cuing effect was observed when participants were trained in a difficult feature search task. The highly salient perceptual cue used in Experiment 5B likely overshadowed location probability learning. Thus, frequently placing a target in one visual quadrant was insufficient to produce a strong attentional preference for those locations.

General discussion

Recently, several researchers have proposed that one's previous experience influences visual attention (Awh et al., 2012; Chun, Golomb, & Turk-Browne, 2011; Hutchinson & Turk-Browne, 2012; Jiang, Swallow, & Rosenbaum, 2013). However, unlike explicit behavioral goals and perceptual saliency, previous experience contains a vast amount of information. When performing a task, how does the visual system determine which, if any, of one's previous experience is relevant? The larger implicit-learning literature predicts limited transfer of implicitly acquired knowledge across tasks and context (Berry et al., 1997; Dienes & Berry, 1997), a prediction that fits the instance theory of attention and automaticity (Logan, 2002). But what constitutes a meaningful change in task and context? How does learning interact with other cues of attention? Several answers have emerged from the present study.

First, the visual system is more likely to rely on previous experience if no other strong cues already exist to guide attention. When a salient visual feature already guides attention, probability cuing from a previous task does not affect performance in the current task (Exp. 5A). In the absence of other cues, however, location probability learning has a substantial influence on behavior. This influence persists over several hundred trials and across many, though not all, types of task changes.

Second, among visually guided search tasks, location probability learning produces a highly transferrable change in attentional bias. Probability cuing transferred between the T/ L and 2/5 tasks, between easy and difficult conjunction search tasks, and between difficult feature search and conjunction search tasks. Conjunction and simple feature search tasks appear to present an exception (Exp. 5), though this lack of transfer is likely attributable to the presence of a perceptually salient cue.

Third, the effects of probability cuing appear to be confined to visually guided search tasks. Experiment 1 showed no transfer between visual search and a foraging-like treasure hunt task. When performing a treasure hunt task in which the treasure was more often located in one visual quadrant, participants showed an increasing tendency to choose an item in that quadrant. These highly rewarded locations, however, were not prioritized in the subsequent visual search task. Conversely, after developing a strong preference for the rich quadrant in the visual search task, participants were no more likely to select an item in that quadrant in the subsequent treasure hunt task. Probability cuing is therefore unlikely to be due to a generic change in spatial attention.

These findings suggest that the effects of learning statistical regularities on attention may be limited to the specific mechanisms used in the training and transfer tasks. Probability cuing transferred between tasks only when both involved serial shifts of attention from one item to the next and when no other salient cues were available. What is the mechanism that allows for this transfer? One possibility is that transfer reflects relatively stable changes to the attentional priority map (Bisley & Goldberg, 2010; Fecteau & Munoz, 2006; Itti & Koch, 2001; Wolfe, 2007). Most theories of spatial attention suggest that the attentional priority map combines perceptual input with goals and other cues to guide attention to behaviorally relevant spatial locations (Bisley & Goldberg, 2010; Wolfe, 2007). However, these discussions of the attentional priority map have been largely agnostic as to whether the same map is used in different search tasks. The high degree of transfer across search tasks in this study suggests that this is likely to be the case.

A second, though not exclusive, possibility is that probability cuing produces stable and transferrable changes in what we have called “procedural attention” (Jiang, Swallow, & Capistrano, 2013). Probability cuing in visual search tasks is coded in a head-centered reference frame, does not update with movements through space, and increases the number of first saccades to the rich region (Jiang & Swallow, 2013b; Jiang, Won, & Swallow, 2014). In addition, it appears to operate in a manner that is qualitatively different from goal-driven or explicit attentional biases (Jiang, Swallow, & Rosenbaum, 2013; Jiang, Swallow, & Sun, 2014; Jiang, Won, & Swallow, 2014). We have taken these findings to suggest that probability cuing influences how attention moves through space, by increasing the likelihood that it moves in a certain direction. This view could help account for the lack of transfer between visual search and a treasure hunt. Visual search involves a series of attentional shifts, each of which is made by jointly considering the current visual input, the current trial's search history, and previous history in similar tasks. In contrast, no visual cues aid performance in the treasure hunt task—all of the items are visually identical. The task also does not involve search. Rather, it relies on a high-level decision that is based entirely on the reinforcement history of previous choices. Thus, the need to move attention through space (rather than shared visual space) may be a critical factor in determining whether probability cuing transfers between tasks.

A consideration of how attention moves through space raises the possibility that not all visually guided search tasks would show transferrable attentional biases. Tasks that rely primarily on eye movements (such as the ones used here) may differ qualitatively from tasks that rely on body and head movements (such as real-world search tasks). In addition, tasks that are “data limited,” such as by visual crowding, may differ qualitatively from tasks that are “resource limited,” such as simple visual search (Norman & Bobrow, 1975). These predictions should be tested in future research.

Although we have emphasized the procedural component of attention training, we also recognize the contribution of other sources of attention, such as explicit goals. The mechanisms that govern task specificity likely differ between implicitly learned attention and explicit, goal-driven attention. Whereas implicitly learned attention shows transfer across tasks that involve similar shifts of attention, the task instructions may change the pattern of cross-task transfer. For example, if participants know that the treasure box is often located where the visual search target is, they may explicitly look for target-rich regions in the search task and prioritize these regions when performing the treasure hunt. Therefore, when predicting whether attentional training transfers across tasks, important factors to consider are whether training affects the procedural or explicit component of attention and what the participants’ explicit goals are.

Our study can be related to the broader literature on attention training. The rapid acquisition of probability cuing indicates a high degree of plasticity in spatial attention. This finding is consistent with other observations of attention training. For example, professional sports, action videogame playing, and laboratory training enhance performance on multiple-object tracking and other attention tasks (Anguera et al., 2013; Faubert, 2013; Green & Bavelier, 2003; Makovski, Vázquez, & Jiang, 2008; Thompson et al., 2013). In addition, training in an n-back task can substantially improve performance in that task (Jaeggi, Buschkuehl, Jonides, & Perrig, 2008; Jaeggi, Buschkuehl, Jonides, & Shah, 2011). However, several studies have shown that attention training shows limited transfer to other tasks, such as in tests of fluid intelligence (Jaeggi et al., 2011; Owen et al., 2010; Redick et al., 2013; Thompson et al., 2013). To the degree that broad transfer is observed (e.g., from action videogame playing), the findings may be attributed to a common component across many tasks (e.g., probabilistic inference; Green, Pouget, & Bavelier, 2010). We believe that the key to resolving the controversy regarding whether attention training generalizes will be to perform a detailed analysis of the processes and components involved in the training and testing tasks. Transfer is more likely to occur if the training and testing tasks share critical components. The present study relied on such an analysis in revealing the moderate task specificity of probability cuing. This approach may be useful in other studies of attention training.

Our study raises questions about the real-world implications of location probability learning. Does a 1-h training session in the lab produce a durable, transferrable change in participants’ spatial attention subsequently? Although such a change is possible, we believe that its impact on daily activities would likely be limited. First, although probability cuing shows long-term persistence, its persistence is adaptable to new visual statistics. The spatial bias is weakened over extinction retraining (e.g., probability cuing was weaker in the testing phase than the training phase of Exps. 3 and 4). In addition, a new spatial bias emerges if the rich quadrant changes to a new region (Jiang, Swallow, Rosenbaum, & Herzig, 2013). Second, serial shifts of attention are relatively uncommon in real-world tasks. For instance, real-world search tasks often rely on salient features and explicit goals. These cues may reduce the utility of probability cuing (Jiang, Swallow, Rosenbaum, & Herzig, 2013; Rosenbaum & Jiang, 2013). Nonetheless, to the degree that a real-world task matched the laboratory training task (e.g., serial scanning, without other attention-guiding cues), some transfer would be expected. With these constraints in mind, probability cuing may be exploited to facilitate performance in the real world.