Abstract
Rotating-frame separated-local-field solid-state NMR experiments measure highly resolved heteronuclear dipolar couplings which, in turn, provide valuable interatomic distances for structural and dynamic studies of molecules in the solid-state. Though many different rotating-frame SLF sequences have been put forth, recent gains in ultrafast MAS technology have considerably simplified pulse sequence requirements due to the suppression of proton-proton dipolar interactions. In this study we revisit a simple two-dimensional 1H-13C dipolar coupling/chemical shift correlation experiment using 13C detected Cross-Polarization with a Variable Contact time (CPVC) and systematically study the conditions for its optimal performance at 60 kHz MAS. In addition, we demonstrate the feasibility of a proton-detected version of the CPVC experiment. The theoretical analysis of the CPVC pulse sequence under different Hartmann-Hahn matching conditions confirms that it performs optimally under the ZQ (w1H-w1C=±wr) condition for polarization transfer. The limits of the cross polarization process are explored and precisely defined as a function of offset and Hartmann-Hahn mismatch via spin dynamics simulation and experiments on a powder sample of uniformly 13C-labeled L-isoleucine. Our results show that the performance of the CPVC sequence and subsequent determination of 1H-13C dipolar couplings are insensitive to 1H/13C frequency offset frequency when high RF fields are used on both RF channels. Conversely, the CPVC sequence is quite sensitive to the Hartmann-Hahn mismatch, particularly for systems with weak heteronuclear dipolar couplings. We demonstrate the use of the CPVC based SLF experiment as a tool to identify different carbon groups, and hope to motivate the exploration of more sophisticated 1H detected avenues for ultrafast MAS.
Keywords: Ultrafast MAS, Separated-Local-Field, Solid-State NMR, Cross Polarization
Introduction
Solid state NMR spectroscopy (ssNMR) has become a powerful tool for obtaining atomic-level structural and dynamic insight into a variety of challenging molecular systems including inorganic materials, membrane proteins, supramolecular assemblies, etc [1-4]. Separated-local-field (SLF) experiments serve as one example of the spectroscopy's powerfully informative potential as it measures heteronuclear dipolar couplings providing inter-nuclear distances along with dynamic order parameters [5-10]. SLF pulse sequences reported in the literature are generally classified as either laboratory or rotating-frame experiments. Rotating-frame techniques such as PISEMA (polarization inversion spin exchange at the magic angle) [8,11,12], HIMSELF/HERSELF (heteronuclear isotropic mixing leading to spin exchange via the local field, or heteronuclear rotating frame spin exchange via the local field) [13, 14] and their variants have been widely used in structural studies on membrane proteins and liquid crystalline materials as they provide highly resolved spectral lines in the heteronuclear dipolar coupled dimension.
In solids, the applicability of SLF techniques depends in part on the suppression of the 1H-1H dipolar interaction (the major perpetrator to spectral resolution), which is typically accomplished by employing any combination of MAS and multiple-pulse addendums, such as Lee-Goldberg, to the SLF sequence [3, 8,11-20]. However, with the recent developments in probe technology, which have provided commercially available MAS probes capable of ∼60 kHz spinning with the fastest achieved at an impressive 110 kHz [21-31], the dominant 1H-1H anisotropic spin interactions are largely averaged, thereby providing the desired spectral resolution and precluding the need for their RF driven suppression (beyond simple 1H decoupling during X nuclei detection, which may be achieved at significantly lower RF field strengths at ultrafast MAS[32-36]). This enables a realm of proton-detected experiments in solids, which additionally provide significant improvements in signal to noise as well as shortening experimental times [37,38]. For example, in combination with selective deuteration, ultrafast 1H NMR is already playing a significant role in the structural study of biomolecules [23,31, 38-52]. These advantages are of principal importance to proton based experiments where the requirement of small rotor volumes and sample quantity for ultrafast MAS is not a major limitation. This restriction does impose some difficulties for samples dilute in the nuclei of interest as is the case for experiments on less abundant nuclei. As a point of precautionary advise, we also mention that temperature gains can be as high as 30∼40 K for long experimental times due to spinning induced frictional heating under ultrafast spinning. This can insert some uncertainty in the accuracy of measured parameters such as dipolar coupling constants through temperature dependent dynamics along with being potentially hazardous to heat sensitive samples. Nevertheless, ultrafast MAS can be used for high throughput measurement of heteronuclear dipolar couplings using simple pulse sequences without the need for the homonuclear dipolar decoupling.
The use of ultrafast MAS was recently employed to accurately measure heteronuclear dipolar couplings with a simple 13C detected cross-polarization (CP) based rotating-frame SLF experiment [53]. This 2D ‘cross-polarization with a variable contact time’ (CPVC) SLF experiment simultaneously increments the duration of the spin-lock RF pulses in both 1H and 13C RF channels to encode 1H-13C dipolar couplings in the second (or indirect) dimension. The aforementioned advantages for these experiments under ultrafast MAS make this a simple and elegant approach which is easy to implement. In this study we revisit this strategy by first examining the efficiency of the 2D CPVC SLF technique against Hartman-Hahn mismatch and resonance offset. Additionally, we also demonstrate a new CPVC pulse sequence with proton-detection (abbreviated as CPVC-H) under ultrafast MAS and demonstrate its unique advantage as a spectral editing tool for poorly resolved 1H spectral lines. We hope this serves as an example to excite the community for the design of new proton-detected ultrafast techniques in light of the considerable advantages proton-detection can offer.
Experiment and Simulation
Materials
Uniformly 13C-labeled L-isoleucine and glycine powder samples were purchased from Cambridge Isotope Laboratory (Andover, MA), and a uniformly 13C,15N-L-alanine was purchased from Isotec (Champaign, IL). All samples were used as received without any further purification.
Solid-State NMR spectroscopy
All NMR experiments were performed on an Agilent VNMRS 600 MHz solid-state NMR spectrometer equipped with a 1.2 mm triple-resonance MAS probe operating at 599.8 MHz for 1H and 150.8 MHz for 13C. All reported results were obtained at 60 kHz MAS. The sequences used for the 2D CPVC experiments are shown in Figure 1. The proton 90° pulse length was 1.2 μs for 13C-detected CPVC experiment, and 1.9 μs for the CPVC-H experiment. Proton decoupling during 13C signal acquisition was achieved by employing the SPINAL-64 sequence [54] at an RF field strength of 45 kHz. The 13C chemical shift was externally referenced to adamantane by setting its low-field 13C resonance to 38.5 ppm, while the 1H chemical shift was referenced to glycine by setting the carbonyl/amino proton signal to 8.5 ppm.
Figure 1.
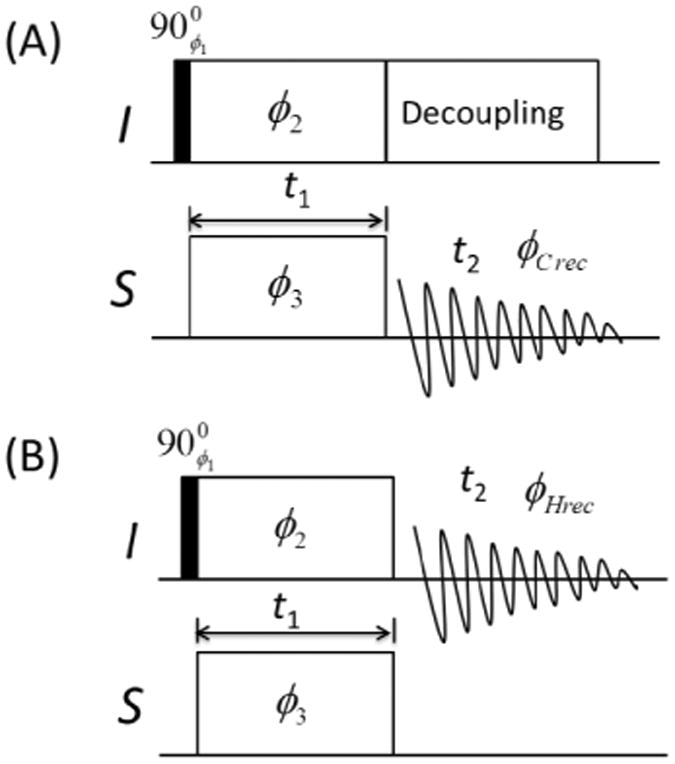
Schematics of radio-frequency pulse sequences used in this study for 13C-detected (A) and 1H-detected (B) cross-polarization with a variable contact time (CPVC) 2D SLF experiment. The t1 incrementation was achieved by simultaneously increasing the spin-lock durations in the cross-polarization sequence. SPINAL-64 was used to decouple protons during signal acquisition for the 13C-detected CPVC experiment. The following phase cyclings were used in the experiment: ϕ1=0,2,0,2; ϕ2=1,1,1,1; ϕ3=0,0,1,1; ϕCrec=0,2,1,3; ϕHrec=0,2,0,2.
Spin Dynamics Simulations
All numerical simulations were performed at 60 kHz MAS using the SIMPSON software [55,56]. For the 13C-detected CPVC sequence, an isolated 1H-13C spin pair with strong (22.3 kHz) and weak (5.0 kHz) heteronuclear dipolar couplings was used in the simulation. The 1H-13C dipolar splitting was obtained by directly measuring the frequency difference between the two singularities in the dipolar coupling lineshapes. For the CPVC-H sequence, we used the spin ½ nuclei in an isolated CH2 group with its geometry in glycine; the 1H-13C-1H angle was 109.5°. The 1H-1H and 1H-13C dipolar couplings were set at 21.0 and 22.5 kHz, respectively.
Theoretical analysis
For simplicity, we assume an isolated 13C-1H pair was for our theoretical treatment. Assuming complete averaging of the 1H-1H dipolar coupling by ultrafast MAS, the rotating-frame Hamiltonian describing the cross polarization process under MAS is given by [57]
| (1) |
where w1I and w1S are the radio-frequency fields used for spin-lock on the I and S spin channels, respectively, and ΔwI and ΔwS are the resonance offset frequencies for I and S nuclei, respectively. The heteronuclear IS dipolar coupling constant b(t) in equation (1) is defined as
| (2) |
where r is the internuclear distance, θ is the angle between the internuclear vector and the external magnetic field, and γI and γS are the gyromagnetic ratios of I and S nuclei respectively.
By defining the effective field angles as , , the Hamiltonian in the doubly tilted frame can be written as [57]
| (3) |
Assuming a small offset frequency, that is w1I ≫ |ΔwI|, w1S ≫ |ΔwS|, cosθI = cosθS ≈ 0; therefore, the effective Hamiltonian can be approximated as
| (4) |
with
| (5) |
and
| (6) |
According to the Hartmann-Hahn matching condition, polarization transfer occurs when weS + εweI ≈ nwR (ε = ±1, n=0,±1, ±2). This condition is referred to as zero-quantum (ZQ) CP when ε = −1 and double-quantum (DQ) CP whens ε = +1. The transferred CP signal at a contact time τ is given as [58]
| (7) |
with Δνn = w1S + w1I − nwR.
For different matching conditions (as defined by n = 0, ±1, ±2), the term bn can be written as follows:
| (8a) |
| (8b) |
| (8c) |
where β is the angle between the internuclear vector and the MAS rotor axis.
It is worth noting that the n=0 matching condition corresponds to the static case in the theoretical treatment presented above. Under fast MAS the n=0 Hartmann-Hahn matching condition, i.e. second-order CP (SOCP), can also lead to heteronuclear polarization by the second-order cross terms between homonuclear and heteronuclear dipolar couplings or the isotropic scalar (or J) couplings where the latter is often neglected in solids due to its relatively small magnitude [59, 60]. It should be mentioned that at least two I spins are necessary for this type of CP-based magnetization transfer. In an I2S spin system, the second-order cross-term between homonuclear and heteronuclear dipolar couplings can be described as:
| (9) |
where wS1 and wS2 are dependent on the homonuclear and heteronuclear dipolar couplings as well as the spinning rate of the sample and RF field strength [59, 60]. As such, the n=0 Hartmann-Hahn matching condition is not suitable for polarization transfer in this CPVC experiment, as the heteronuclear dipolar interaction during cross-polarization is also affected by the homonuclear dipolar interaction.
This theoretical approach applies to both the 13C-detected and 1H-detected CPVC experiments, as both I and S spins have identical roles during the spin-lock period. However, an important distinction arises between the two pulse sequences as we have neglected the homonuclear dipolar interaction in the beginning of the calculation [57]. Therefore, it is expected that the zero-frequency peak in the spectra obtained from the CPVC-H experiment will be much larger than that obtained using the 13C-detected CPVC experiment as 1H-1H dipolar couplings are much larger than 13C-13C dipolar couplings. To circumvent this problem, we have developed a procedure for eliminating the zero-frequency peak in the heteronuclear dipolar coupling dimension of a 2D CPVC spectrum as discussed below.
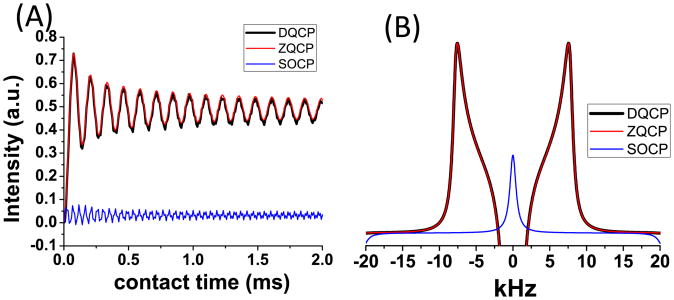
Numerically simulated heteronuclear dipolar coupling spectra obtained from the CPVC method for different Hartman-Hahn matching conditions on an isolated 13C-1H spin pair are shown in Figure 2. A well-defined lineshape for the C-H dipolar splitting can be obtained via DQ or ZQ CP, while the dipolar splitting is completely absent under SOCP as predicted earlier. It is important to note that the DQ-CP condition requires a relatively small RF field making the associated 13C-1H dipolar coupling lineshape quite sensitive to 13C resonance offset. As such, the higher RF field used in the ZQ-CP makes it a better choice for the measurement of heteronuclear dipolar couplings in the CPVC experiment.
Figure 2.
Simulated time dependence of I-S dipolar coupling (A) and dipolar splitting spectra (B) for ZQ CP with w1H=160 kHz and w1C=220kHz, DQ CP with w1H=20kHz and w1C=40 kHz, and SOCP with w1H= w1C=40 kHz. Results show superior performances of DQ and ZQ CP sequences and the inefficiency of SOCP sequence. ZQCP is recommended due to other advantages as mentioned in the main text.
Treatment for eliminating the zero-frequency peak
As seen in Figure 2, a large negative zero-frequency peak exists in the I-S dipolar coupling spectra of ZQ or DQ CP, which can hinder the interpretation of experimental data. In practice, a special algorithm or processing method has to be applied in order to suppress the zero-frequency peak (also known as the axial peak) to obtain interpretable 2D SLF spectra. For the CPVC experiments performed on the Agilent VNMRS 600 MHz solid-state NMR spectrometer, we applied the “solvent subtraction” utility to suppress the zero-frequency peak in the I-S dipolar coupling dimension of the 2D spectrum. In Figure 3 we illustrate the axial peak suppression strategy for numerical simulations. First we apply a DC offset to the time-domain dipolar coupling oscillations in Figure 3(A and B). This curve is subsequently apodized as shown in Figure 3C followed by Fourier transformation. The Fourier Transformation in Figure 3 demonstrates the use of this procedure in producing the final clear lineshape as shown in the bottom right of Figure 3.
Figure 3.
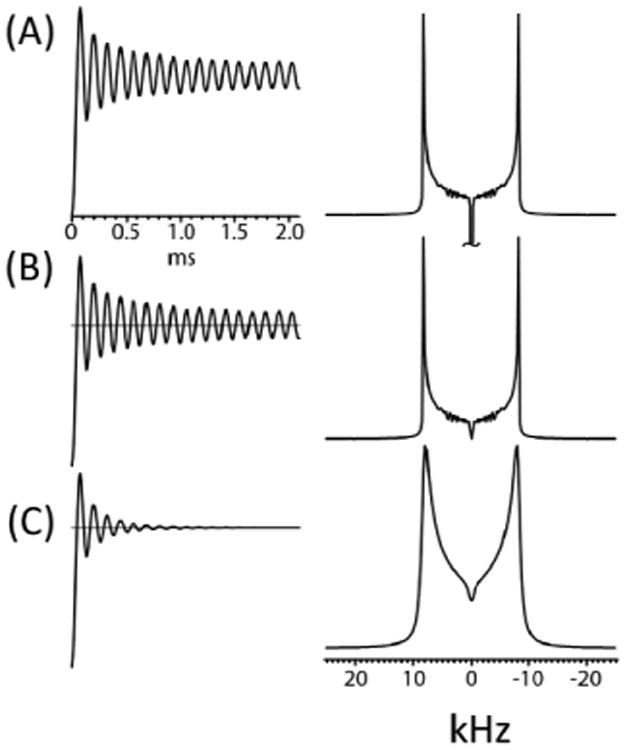
A simple data processing procedure to surpress axial peaks in 2D CPVC SLF spectra. Time-domain signals (left) and corresponding Fourier-transformed frequency spectra (right). (A) An oscillating buildup curve from CPVC before (A) and after compensation for the DC offset without (B) and with (C) apodization.
Results and Discussion
The great advantage of the CPVC experimental approach over previous SLF experiments is the suppression of 1H-1H dipolar interactions by ultrafast MAS—not RF driven schemes--which considerably simplifies experimental setup in comparison to such sequences that employ, for instance, Lee-Goldberg or other homonuclear decoupling multiple pulses. The parameters for the CPVC experiment that must be carefully optimized for accurate results are the RF offset and Hartmann-Hahn matching. Herein, we systematically discuss these two experimental factors and their corresponding influence on the dipolar splittings observed in the heteronuclear dipolar coupling dimension of the 2D CPVC SLF spectrum. As both the CPVC and CPVC-H pulse sequences are exactly the same outside of the acquisition period, we limit this discussion to results from the carbon detected version.
Resonance offset effects on CPVC performance
In rotating-frame SLF experiments like PISEMA [8, 9], dipolar splittings are quite sensitive to the 1H frequency offset which can potentially distort the accuracy of the extracted interatomic distances. This limitation is not an issue in the CPVC experiment due to the high proton RF field strength used during CP. Applied proton RF fields can be as high as 200 kHz for ultrafast MAS probes due to the utilization of micro RF coils, while the frequency offsets are generally less than 5 kHz from the center of the proton spectrum on a 600 MHz NMR spectrometer. With these numbers in mind Eq. 5, , shows that the frequency offset has a small influence on the effective RF field strength. Thus, the proton resonance offset is of little concern to the effective RF field on the proton channel. The wider chemical shift range for 13C nuclei (200 ppm corresponds to ∼30 kHz at 600 MHz) comprises a greater fraction of the applied RF field making it a legitimate concern, and necessitating the need for high 13C RF field amplitudes for uniform excitation over the entire 13C chemical shift range. Using high RF amplitudes can, however, result in RF induced heating which is undesirable for heat-sensitive samples. The balance of these restrictions for such samples makes it crucial to know the effect of 13C resonance offset on the efficiency of the CPVC SLF sequence.
As shown in Figure 4A and 4C under high RF irradiation (160 kHz and 220 kHz for 1H and 13C, respectively) the resonance offset has limited effect on the dipolar splitting;. the resonance offset only begins to have an influence when the offset frequency is greater than 15 kHz, which is generally the maximum resonance offset when the 13C carrier frequency is placed at the center of the spectrum. Therefore, as with the 1H channel, we can then safely neglect resonance offset effects at high RF fields. Outside of 15 kHz, we found that the dipolar splitting is more sensitive to the offset for a weakly 1H-13C dipolar coupled spin system (Figure 4C) than for a strongly dipolar coupled spin system (Figure 4A). For a resonance offset of 30 kHz, the 1H-13C dipolar splitting changes by <1 kHz for the strongly dipolar coupled spin system, while it deviates by nearly a factor of two for the weakly dipolar coupled spin system. Naturally, a high RF field strength is preferred to reduce any resonance offset effects for an accurate determination of heteronuclear dipolar couplings. To explore the effect of lower RF field strengths, we investigated the 1H-13C dipolar splitting as a function of 13C RF field strength in Figure 4B and 4D. This was done for the same weak and strongly dipolar coupled 1H-13C pin pair by assuming an offset of 15 kHz then simultaneously varying the 1H and 13C fields to maintain the match condition. The results clearly show that the dipolar splitting value begins to obviously deviate from the actual value when the 13C RF field amplitude is below 140 kHz. These simulated results are experimentally demonstrated in Figure 5 on a uniformly 13C-labeled isoleucine powder sample. For clarity, we only report the dipolar splitting spectral slice observed for the CHα group (Figure B-E). The RF carrier frequency was set at on-resonance and 10 kHz off-resonance (below) from the CHα resonance frequency. As shown in Figure 5B and 5D, when a relatively high RF field (210 kHz) was used for 13C, the resonance offset had no influence on the measured dipolar coupling value but did distort the observed lineshape. Even for an RF field as low in strength as ∼130 kHz, the observed offset (10 kHz) effect on the dipolar splitting is negligible but again results in a distorted lineshape. A 13C-1H dipolar splitting value of ∼16.5 kHz is measured corresponding to a dipolar coupling of 23.2 kHz after taking into account the scaling factor of 0.71. Our efforts to compensate the offset dependence by using a ramped spin-lock pulse severely distorted the observed dipolar coupling lineshape shown in Figure 5E.
Figure 4.
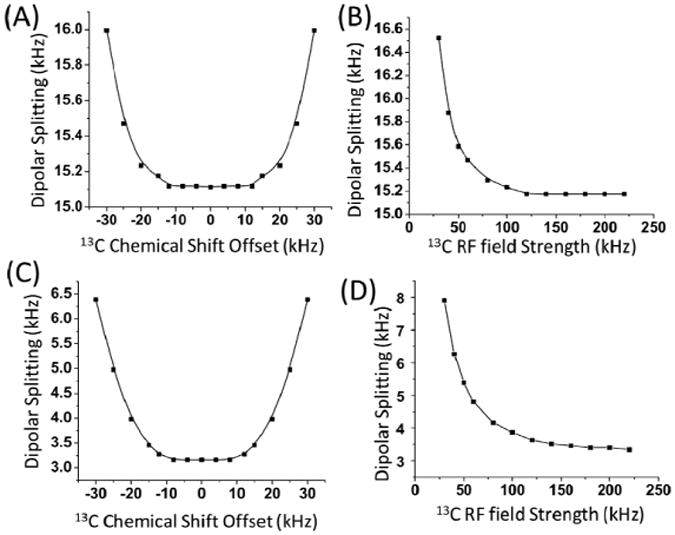
Simulated dipolar splitting as a function of (A and C) 13C resonance offset and (B and D) 13C RF field amplitude during the cross-polarization process for an isolated 13C-1H spin pair with a heteronuclear coupling of 22.3 kHz (A and B) or 5 kHz (C and D). For (A, C), the RF field amplitudes used were 160 kHz and 220 kHz on the proton and carbon channels, respectively. For (B,D), the 13C frequency offset was set at 15 kHz and the 1H field amplitude was varied with the 13C field amplitude so that w1H-w1C=60 kHz when w1C 160 kHz and w1C-w1H=60 kHz when w1C 160 kHz.
Figure 5.

(A) 13C-detected 2D CPVC SLF spectrum of a uniformly-13C-labelled isoleucine powder sample obtained at 60 kHz MAS. 1H-13C dipolar splitting spectra for the CHα group extracted from 2D CPVC SLF spectra obtained under various conditions: with the 13C carrier frequency set at the 13Cc resonance position (B) and 10 kHz offset below the 13Cαresonance frequency (C, D, E). For (B, C, D), constant amplitude spin-locks were used for Hartmann-Hahn CP, while for (E) a ramped-CP was used with a 15% ramp size on the 13C spin-lock. For the ramped-CP, the ramp ratio is defined as (whighest-wlowest)/(whighest+wlowest).
Hartmann-Hahn mismatch effects on CPVC performance
The Hartmann-Hahn matching condition has a strong influence on signal sensitivity as well as the dipolar coupling scaling factor making it an important parameter for the performance of the 2D CPVC SLF experiment. As shown in Eq.(8), the heteronuclear dipolar coupling scaling factor is approximately 0.71 for the ZQ(DQ)-1 CP (|w1H ± w1C|=60 kHz) and 0.5 for the ZQ(DQ)-2 (|w1H±w1C|=120 kHz) CP. As discussed above, the 13C RF amplitude during CP should be ∼140 kHz or larger to minimize any resonance offset effect. This requirement far exceeds the frequency condition for DQ-CP indicating that DQ-CP efficiency would be greatly affected by the offset frequency. As ZQ-2-CP (|w1H-w1C|=2wr kHz) has a smaller dipolar coupling scaling factor than the ZQ-1-CP (|w1H-w1C|=wr kHz), we prefer ZQ-1-CP and restrict our discussion to it. The simulated effect of the Hartmann-Hahn mismatch on the dipolar splitting is shown in Figure 6. It is clear, particularly for the weak 1H-13C dipolar coupled system, that the dipolar splitting is quite sensitive to the Hartmann-Hahn match conditions. We compared the constant amplitude versus ramped-CP, and found that due to the high sensitivity to Hartmann-Hahn mismatch the constant-amplitude CP irradiation is preferable over the ramped-CP. While ramped-CP is often used to enhance polarization transfer, as it can restore a flat Hartmann-Hahn matching profile and overcome the effects of RF inhomogeneity and resonance frequency offset [61] its use here under ultrafast MAS—as shown in Figure 5D-- proved less effective. If employed, only a very small ramp ratio is suitable, as otherwise it will result in inaccurate dipolar splittings. The distorted result in Figure 5D, for instance, was obtained using the modest ramp ratio (defined as (whighest-wlowest)/(whighest+wlowest)) of 15%.
Figure 6.
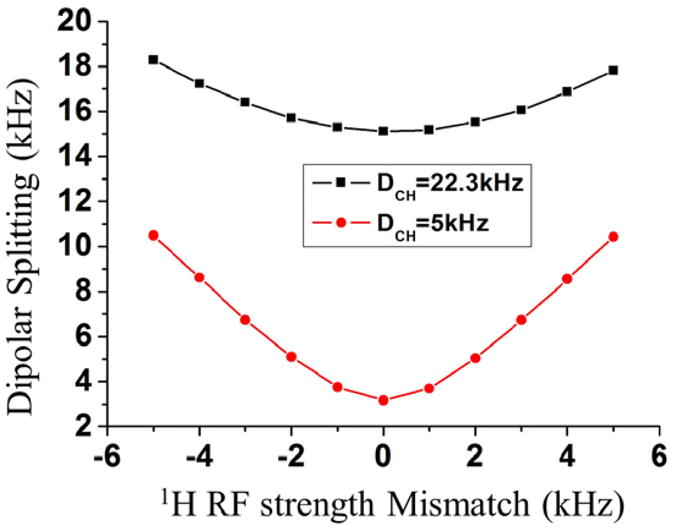
Simulated dipolar splitting as a function of Hartman-Hahn mismatch 1H RF amplitude during the CP process for an isolated 13C-1H spin pair with strong or weak heteronuclear dipolar couplings. During cross polarization, the 13C RF amplitude was set at 220 kHz, while it is 160 kHz on the 1H channel when the mismatch was zero.
We mention as a practical note that the instabilities of RF power amplifier and mechanical spinning-induced heating in the probe-head can alter the RF power for the spin-locks, and therefore the Hartman-Hahn match, in the CPVC experiments [62]. To avoid these problems, we re-calibrated and optimized the RF power levels right before the start of each experiment. Nevertheless it was found that the RF power levels can fluctuate on the experimental time (about 30 min). This raises a non-trivial point to the importance and challenge of temperature control under ultrafast MAS.
In summary, the weak heteronuclear dipolar coupled spin system is more sensitive to the 13C resonance offset as well as the Hartmann-Hahn matching conditions than the strongly dipolar coupled spin system. The sensitivity of the observed dipolar splitting values to the 13C resonance offset can be generally overcome by applying high RF fields. Care should be taken when calibrating the Hartmann-Hahn match as the performance of the CPVC sequence is quite sensitive to any mismatch. We recommend a constant amplitude CP as the best choice for an efficient polarization transfer in the CPVC experiment.
Proton-detected CPVC experiments
With the development of ultrafast MAS probe technology and the corresponding gains in spectral resolution, proton-detection is gaining more popularity within the solid-state NMR community, as it can improve the signal-to-noise of spectra as well as reduce the measurement time compared to low-γ nuclei detection [37]. Here, we propose a proton-detected CPVC pulse sequence (called CPVC-H) shown in Figure 1B, and present an experimental demonstration on U-13C-glycine in Figure 7. The 1D 1H spectrum under 60 kHz MAS is shown at the top of Figure 7A, where three peaks are partially resolved. Their corresponding dipolar splitting spectra are shown in Figure 7B. The peak around 8.5 ppm comprises of overlapping contributions from COOH and NH2 groups. Since the NH2 protons are not bonded to a carbon, in the second dimension of the CPVC-H experiment, we do not expect to see any contribution from the NH2 protons. As a result, in the heteronuclear dipolar coupling dimension of the 2D CPVC-H spectrum of glycine shown in Figure 7, we observe a small 1H-13C dipolar splitting of 2.4 kHz arising only from COOH protons, which corresponds to a 1H-13C dipolar coupling of around 3.4 kHz after taking the scaling factor (∼0.71) into consideration. The peaks at 4.4 and 2.4 ppm correspond to the protons of the CH2 group. We measured a dipolar splitting value of 16.2 kHz, corrected to 22.8 kHz after taking the scaling factor into account, which is in good agreement with previously published results [63,64]. The center peak in the dipolar splitting spectra of the CH2 group may result from the slight overlap of the proton signals from COOH and CH2 groups. The CPVC-H method is quite similar to the CPVC experiment proposed by Amoureux et al. [53]. Therefore, the dipolar coupling constants (and thus the bond length) measured by CPVC-H should have similar accuracies as obtained with CPVC, which, as reported by the Amoureux group, are in good agreement with X-ray diffraction analysis [53]. In Figure 7C, we demonstrate how the proton-detected CPVC experiment can be utilized to differentiate chemical groups with different 1H-13C dipolar couplings from 1D slices extracted from the dipolar dimension.
Figure 7.
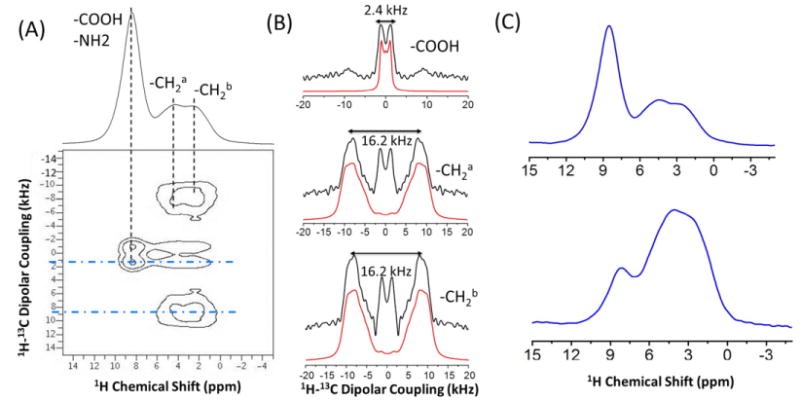
(A) The 1H-detected 2D CPVC SLF spectrum of U-13C-glycine powder sample with the 1H chemical spectrum shown at the top. (B) 1H-13C dipolar splitting spectral slices extracted along the F1 dimension at different 1H chemical shifts corresponding to the black dashed lines in (A). Simulated spectra are shown in red and experimental in black. The line broadening used for the simulation of the dipolar splitting spectra of COOH and CH2 groups are 500 and 1500 Hz, respectively. (C) 1H spectral slices extracted along points in the dipolar coupling dimension which correspond to the blue (dot-dash) lines of the 2D spectrum in (A).
Another experimental demonstration of the 2D CPVC-H method on a powder sample of U-13C,15N-L-alanine is shown in Figure 8, where obvious differences in the dipolar coupling spectra for the CH3, CH and COOH groups can be observed. The rapid rotation of the CH3 group averages the dipolar splitting to a relatively small value, 5.4 kHz, corresponding to a heteronuclear 1H-13C coupling of 7.6 kHz after the scaling factor. In contrast, the CH group is quite rigid and exhibits a dipolar splitting of 15.5 kHz, corresponding to a heteronuclear 1H-13C dipolar coupling of 21.8 kHz. This demonstrates nicely the use of the CPVC-H experiment for the dynamic studies of molecules. The measured 1H-13C dipolar coupling value is very small for the COOH group, as the proton is not directly bonded to 13C. The wiggle in the dipolar splitting lineshape of the COOH group is an experimental artifact, which could be suppressed by increasing the number of t1 experiments. Both sets of experimental results show how the proposed CPVC-H experiment is an efficient method for the measurement of heteronuclear dipolar couplings under ultrafast MAS conditions. Interestingly, a comparison of 1H detected and 13C detected experiments on U-13C,15N-alanine show a significant enhancement in sensitivity due to proton detection: 5.6, 4, and 6.2 for CH3, CH and COOH groups.
Figure 8.
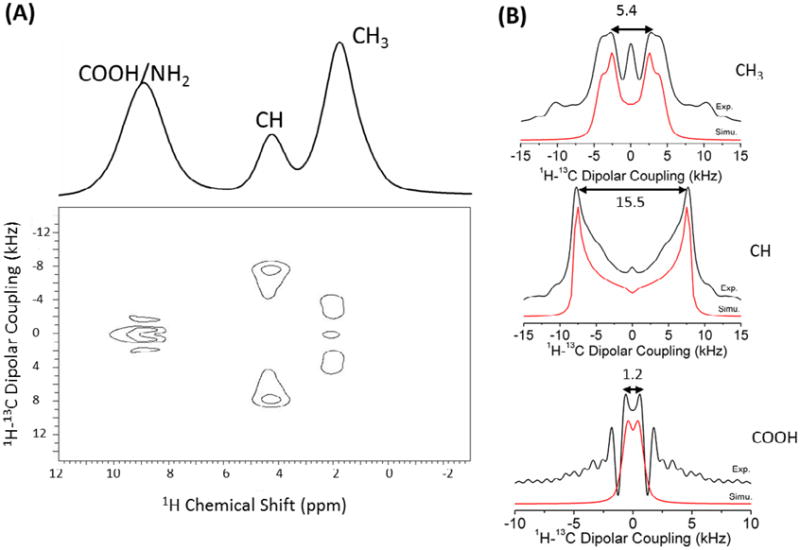
(A) The 1H-detected 2D CPVC SLF spectrum of a powder sample of U-13C-15N-L-alanine with the 1H spectrum shown at the top. (B) 1H-13C dipolar splitting spectral slices extracted along the dipolar coupling dimension at different 1H chemical shift values. Simulated (red) and experimental (black) spectra are compared. The line broadening factors used in the simulation of the dipolar splitting spectra of CH3, CH, and COOH groups are 900, 300 and 1000 Hz, respectively. 32 t1 increments were used for encoding heteronuclear dipolar couplings.
Conclusion
In this study, we have investigated and reported the limiting factors of a simple and robust 2D CPVC SLF pulse sequence under ultrafast MAS via numerical simulations and experiments on a uniformly-13C-labeled isoleucine powder sample. The effects of 13C resonance offset frequency and Hartmann-Hahn mismatch were systematically analyzed for strongly and weakly heteronuclear dipolar coupled systems. A high RF field (>∼140 kHz) on the 13C channel is essential in overcoming the offset effects of the large spectral width of the 13C chemical shift. Our results suggest that a constant-amplitude CP is far better than a ramp-CP for heteronuclear polarization transfer in the CPVC experiment. In addition, we have also demonstrated a proton-detected CPVC SLF experiment on U-13C-glycine and U-13C-15N-L-alanine, and shown its utility as a quick and simple method for the measurement of heteronuclear dipolar couplings. We hope the proton-detected SLF experiment serves as an example of the advantages of proton detected ultrafast experiments, and excites the community for the design of additional experiments of its kind.
Highlights.
A 1H-evolved, 1H-detected rotating-frame SLF is demonstrated under ultrafast MAS.
CP-based SLF sequence is quite sensitive to Hartmann-Hahn mismatch.
CP-based SLF sequence is insensitive to offset when high RF fields are used.
A constant-amplitude-CP SLF renders a better performance than a ramped-CP SLF.
1H-detection greatly enhances the sensitivity of CP-based rotating-frame SLF.
Acknowledgments
This research was supported by funds from National Institutes of Health (GM084018 and GM095640 to A.R.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Tycko R. NMR at Low and Ultralow Temperatures. Acc Chem Res. 2013;46:1923–1932. doi: 10.1021/ar300358z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Knight MJ, Felli IC, Pierattelli R, Emsley L, Pintacuda G. Magic Angle Spinning NMR of Paramagnetic Proteins. Acc Chem Res. 2013;46:2108–2116. doi: 10.1021/ar300349y. [DOI] [PubMed] [Google Scholar]
- 3.Schmidt-Rohr K, Spiess HW. Multidimensional solid-state NMR and polymers. Academic Press; 1994. [Google Scholar]
- 4.Ramamoorthy A, editor. NMR spectroscopy of biological solids. CRC Press; 2010. [Google Scholar]
- 5.Müller L, Kumar A, Baumann T, Ernst RR. Transient Oscillations in NMR Cross-Polarization Experiments in Solids. Phys Rev Lett. 1974;32:1402–1406. [Google Scholar]
- 6.Waugh JS. Uncoupling of local field spectra in nuclear magnetic resonance: determination of atomic positions in solids. Proc Natl Acad Sci USA. 1976;73:1394–1397. doi: 10.1073/pnas.73.5.1394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Schmidt-Rohr K, Nanz D, Emsley L, Pines A. NMR Measurement of Resolved Heteronuclear Dipole Couplings in Liquid Crystals and Lipids. J Phys Chem. 1994;98:6668–6670. [Google Scholar]
- 8.Ramamoorthy A, Wei YF, Lee Dong-Kuk. PISEMA Solid-State NMR Spectroscopy. Annu Rep NMR Spectrosc. 2004;52:1, 52. and references cited therein. [Google Scholar]
- 9.Nevzorov AA, Opella SJ. Selective Averaging for High-Resolution Solid-State NMR Spectroscopy of Aligned Samples. J Magn Reson. 2007;185:59–70. doi: 10.1016/j.jmr.2006.09.006. [DOI] [PubMed] [Google Scholar]
- 10.Bertelsen K, Paaske B, Thøgersen L, Tajkhorshid E, Schiøtt B, Skrydstrup T, Nielsen NC, Vosegaard T. Residue-Specific Information about the Dynamics of Antimicrobial Peptides from 1H-15N and 2H Solid-State NMR Spectroscopy. J Am Chem Soc. 2009;131:18335–18342. doi: 10.1021/ja908604u. [DOI] [PubMed] [Google Scholar]
- 11.Wu CH, Ramamoorthy A, Opella SJ. High-resolution heteronuclear dipolar solid-state NMR spectroscopy. J Magn Reson A. 1994;109:270–272. [Google Scholar]
- 12.Ramamoorthy A, Opella SJ. Two-dimensional chemical shift/heteronuclear dipolar coupling spectra obtained with polarization inversion spin exchange at the magic angle and magic-angle sample spinning (PISEMAMAS) Solid State Nucl Magn Reson. 1995;4:387–392. doi: 10.1016/0926-2040(95)00054-t. [DOI] [PubMed] [Google Scholar]
- 13.Yamamoto K, Dvinskikh SV, Ramamoorthy A. Measurement of heteronuclear dipolar couplings using a rotating frame solid-state NMR experiment. Chem Phy Lett. 2006;419:533–536. [Google Scholar]
- 14.Dvinskikh SV, Yamamoto K, Ramamoorthy A. Heteronuclear isotropic mixing separated local field NMR spectroscopy. J Chem Phys. 2006;125:034507–034513. doi: 10.1063/1.2212939. [DOI] [PubMed] [Google Scholar]
- 15.Munowitz MG, Griffin RG, Bodenhausen G, Huang TH. Two-dimensional rotational spin-echo nuclear magnetic resonance in solids: correlation of chemical shift and dipolar interactions. J Am Chem Soc. 1981;103:2529–2533. [Google Scholar]
- 16.van Rossum BJ, Ladizhansky V, Vega S, de Groot HJM. A Method for Measuring Heteronuclear (1H-13C) Distances in High Speed MAS NMR. J Am Chem Soc. 2000;122:3465–3472. [Google Scholar]
- 17.Nevzorov AA, Opella SJ. A “Magic Sandwich” pulse sequence with reduced offset dependence for high-resolution separated local field spectroscopy. J Magn Reson. 2003;164:182–186. doi: 10.1016/s1090-7807(03)00240-4. [DOI] [PubMed] [Google Scholar]
- 18.Grinshtein J, Frydman L. Solid State Separated-Local-Field NMR Spectroscopy on Half-Integer Quadrupolar Nuclei: Principles and Applications to Borane Analysis. J Am Chem Soc. 2003;125:7451–7460. doi: 10.1021/ja0214025. [DOI] [PubMed] [Google Scholar]
- 19.Yamamoto K, Durr UHN, Xu J, Lm SC, Waskell L, Ramamoorthy A. Dynamic interaction between membrane bound full length cytochrome p450 and b5 observed by solid-state NMR spectroscopy. Scientific Reports (Nature) 2013;3:2538. doi: 10.1038/srep02538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang R, Chen Y, Chen T, Sun PC, Li B, Ding D. Accessing Structure and Dynamics of Mobile Phase in Organic Solids by Real-Time T1C Filter PISEMA NMR Spectroscopy. J Phys Chem A. 2012;116:979–984. doi: 10.1021/jp2078902. [DOI] [PubMed] [Google Scholar]
- 21.Kobayashi T, Mao K, Paluch P, Nowak-Król A, Sniechowska J, Nishiyama Y, Gryko DT, Potrzebowski MJ, Pruski M. Study of Intermolecular Interactions in the Corrole Matrix by Solid-State NMR under 100 kHz MAS and Theoretical Calculations. Angew Chem. 2013;125:14358–14361. doi: 10.1002/anie.201305475. [DOI] [PubMed] [Google Scholar]
- 22.Parthasarathy S, Nishiyama Y, Ishii Y. Sensitivity and Resolution Enhanced Solid-State NMR for Paramagnetic Systems and Biomolecules under Very Fast Magic Angle Spinning. Acc Chem Res. 2013;46:2127–2135. doi: 10.1021/ar4000482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nishiyama Y, Malon M, Ishii Y, Ramamoorthy A. 3D 15N/15N/1H chemical shift correlation experiment utilizing an RFDR-based 1H/1H mixing period at 100 kHz MAS. J Magn Reson. 2014;244:1–5. doi: 10.1016/j.jmr.2014.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nishiyama Y, Zhang R, Ramamoorthy A. Finite-pulse radio frequency driven recoupling with phase cycling for 2D 1H/1H correlation at ultrafast MAS frequencies. J Magn Reson. 2014;243:25–32. doi: 10.1016/j.jmr.2014.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ye YQ, Malon M, Martineau C, Taulelle F, Nishiyama Y. Rapid measurement of multidimensional 1H solid-state NMR Spectra at ultra-fast MAS frequencies. J Magn Reson. 2014;239:75–80. doi: 10.1016/j.jmr.2013.12.010. [DOI] [PubMed] [Google Scholar]
- 26.Bertini I, Emsley L, Felli IC, Laage S, Lesage A, Lewandowski JR, Marchetti A, Pierattelli R, Pintacuda G. High-resolution and sensitivity through-bond correlations in ultra-fast magic angle spinning (MAS) solid-state NMR. Chem Sci. 2011;2:345–348. [Google Scholar]
- 27.Laage SGN, Marchetti A, Sein J, Pierattelli R, Sass HJ, Grzesiek S, Lesage A, Pintacuda G, Emsley L. Band-Selective 1H-13C Cross-Polarization in Fast Magic Angle Spinning Solid-State NMR Spectroscopy. J Am Chem Soc. 2008;130:17216–17217. doi: 10.1021/ja805926d. [DOI] [PubMed] [Google Scholar]
- 28.Zhang R, Ramamoorthy A. Performance of RINEPT is amplified by dipolar couplings under ultrafast MAS conditions. J Magn Reson. 2014;243:85–92. doi: 10.1016/j.jmr.2014.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Holland GP, Cherry BR, Jenkins JE, Yarger JL. Proton-detected heteronuclear single quantum correlation NMR spectroscopy in rigid solids with ultra-fast MAS. J Magn Reson. 2010;202:64–71. doi: 10.1016/j.jmr.2009.09.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Saalwächter K, Lange F, Matyjaszewski K, Huang CF, Graf R. BaBa-xy16: Robust and broadband homonuclear DQ recoupling for applications in rigid and soft solids up to the highest MAS frequencies. J Magn Reson. 2011;212:204–215. doi: 10.1016/j.jmr.2011.07.001. [DOI] [PubMed] [Google Scholar]
- 31.Agarwal V, Penzel S, Szekely K, Cadalbert R, Testori E, Oss A, Past J, Samoson A, Ernst M, Böckmann A, Meier BH. De Novo 3D Structure Determination from Sub-milligram Protein Samples by Solid-State 100 kHz MAS NMR Spectroscopy. Angew Chemie Int Ed. 2014;53:1–5. doi: 10.1002/anie.201405730. [DOI] [PubMed] [Google Scholar]
- 32.Ernst M, Samoson A, Meier BH. Low-power decoupling in fast magic-angle spinning NMR. Chem Phys Lett. 2001;348:293–302. [Google Scholar]
- 33.Ernst M, Samoson A, Meier BH. Low-power XiX decoupling in MAS NMR experiments. J Magn Reson. 2003;163:332–339. doi: 10.1016/s1090-7807(03)00155-1. [DOI] [PubMed] [Google Scholar]
- 34.Kotecha M, Wickramasinghe NP, Ishii Y. Efficient low-power heteronuclear decoupling in 13C high-resolution solid-state NMR under fast magic angle spinning. Magn Reson Chem. 2007;45:S221–S230. doi: 10.1002/mrc.2151. [DOI] [PubMed] [Google Scholar]
- 35.Weingarth M, Bodenhausen G, Tekely P. Low-power decoupling at high spinning frequencies in high static fields. J Magn Reson. 2009;199:238–241. doi: 10.1016/j.jmr.2009.04.015. [DOI] [PubMed] [Google Scholar]
- 36.Agarwal V, Tuherm T, Reinhold A, Past J, Samoson A, Ernst M, Meier BH. Amplitude-modulated low-power decoupling sequences for fast magic-angle spinning NMR. Chem Phys Lett. 2013;583:1–7. [Google Scholar]
- 37.Paulson EK, Morcombe CR, Gaponenko V, Dancheck B, Byrd RA, Zilm KW. Sensitive High Resolution Inverse Detection NMR Spectroscopy of Proteins in the Solid State. J Am Chem Soc. 2003;125:15831–15836. doi: 10.1021/ja037315+. [DOI] [PubMed] [Google Scholar]
- 38.Marchetti A, Jehle S, Felletti M, Knight MJ, Wang Y, Xu ZQ, Park AY, Otting G, Lesage A, Emsley L, Dixon NE, Pintacuda G. Backbone Assignment of Fully Protonated Solid Proteins by 1H Detection and Ultrafast Magic-Angle-Spinning NMR Spectroscopy. Angew Chemie. 2012;124:10914–10917. doi: 10.1002/anie.201203124. [DOI] [PubMed] [Google Scholar]
- 39.Zhou DH, Shah G, Cormos M, Mullen C, Sandoz D, Rienstra CM. Proton-Detected Solid-State NMR Spectroscopy of Fully Protonated Proteins at 40 kHz Magic-Angle Spinning. J Am Chem Soc. 2007;129:11791–11801. doi: 10.1021/ja073462m. [DOI] [PubMed] [Google Scholar]
- 40.Zhou DH, Shah G, Mullen C, Sandoz D, Rienstra CM. Proton-Detected Solid-State NMR Spectroscopy of Natural-Abundance Peptide and Protein Pharmaceuticals. Angew Chem. 2009;121:1279–1282. doi: 10.1002/anie.200801029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chevelkov V, van Rossum BJ, Castellani F, Rehbein K, Diehl A, Hohwy M, Steuernagel S, Engelke F, Oschkinat H, Reif B. 1H Detection in MAS Solid-State NMR Spectroscopy of Biomacromolecules Employing Pulsed Field Gradients for Residual Solvent Suppression. J Am Chem Soc. 2003;125:7788–7789. doi: 10.1021/ja029354b. [DOI] [PubMed] [Google Scholar]
- 42.Chevelkov V, Rehbein K, Diehl A, Reif B. Ultrahigh Resolution in Proton Solid-State NMR Spectroscopy at High Levels of Deuteration. Angew Chem Int Ed. 2006;45:3878–3881. doi: 10.1002/anie.200600328. [DOI] [PubMed] [Google Scholar]
- 43.Nishiyama Y, Endo Y, Nemoto T, Utsumi H, Yamauchi K, Hioka K, Asakura T. Very fast magic angle spinning 1H-14N 2D solid-state NMR: Sub-micro-liter sample data collection in a few minutes. J Magn Reson. 2011;208:44–48. doi: 10.1016/j.jmr.2010.10.001. [DOI] [PubMed] [Google Scholar]
- 44.Zhou DH, Rienstra CM. High-performance solvent suppression for proton detected solid-state NMR. J Magn Reson. 2008;192:167–172. doi: 10.1016/j.jmr.2008.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Huber M, Hiller S, Schanda P, Ernst M, Böckmann A, Verel R, Meier BH. A Proton-Detected 4D Solid-State NMR Experiment for Protein Structure Determination. ChemPhysChem. 2011;12:915–918. doi: 10.1002/cphc.201100062. [DOI] [PubMed] [Google Scholar]
- 46.Chevelkov V, Habenstein B, Loquet A, Giller K, Becker S, Lange A. Proton-detected MAS NMR experiments based on dipolar transfers for backbone assignment of highly deuterated proteins. J Magn Reson. 2014;242:180–188. doi: 10.1016/j.jmr.2014.02.020. [DOI] [PubMed] [Google Scholar]
- 47.Asami S, Reif B. Proton-Detected Solid-State NMR Spectroscopy at Aliphatic Sites: Application to Crystalline Systems. Acc Chem Res. 2013;46 doi: 10.1021/ar400063y. [DOI] [PubMed] [Google Scholar]
- 48.Park SH, Yang C, Opella SJ, Mueller LJ. Resolution and measurement of heteronuclear dipolar couplings of a noncrystalline protein immobilized in a biological supramolecular assembly by proton-detected MAS solid-state NMR spectroscopy. J Magn Reson. 2013;237:164–168. doi: 10.1016/j.jmr.2013.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zhou D, Nieuwkoop A, Berthold D, Comellas G, Sperling L, Tang M, Shah G, Brea E, Lemkau L, Rienstra C. Solid-state NMR analysis of membrane proteins and protein aggregates by proton detected spectroscopy. J Biomol NMR. 2012;54:291–305. doi: 10.1007/s10858-012-9672-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhou DH, Shea JJ, Nieuwkoop AJ, Franks WT, Wylie BJ, Mullen C, Sandoz D, Rienstra CM. Solid-State Protein-Structure Determination with Proton-Detected Triple-Resonance 3D Magic-Angle-Spinning NMR Spectroscopy. Angew Chem Int Ed. 2007;46:8380–8383. doi: 10.1002/anie.200702905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Bertini I, Emsley L, Lelli M, Luchinat C, Mao J, Pintacuda G. Ultrafast MAS Solid-State NMR Permits Extensive 13C and 1H Detection in Paramagnetic Metalloproteins. J Am Chem Soc. 2010;132:5558–5559. doi: 10.1021/ja100398q. [DOI] [PubMed] [Google Scholar]
- 52.Miah HK, Bennett DA, Iuga D, Titman JJ. Measuring proton shift tensors with ultrafast MAS NMR. J Magn Reson. 2013;235:1–5. doi: 10.1016/j.jmr.2013.07.005. [DOI] [PubMed] [Google Scholar]
- 53.Paluch P, Pawlak T, Amoureux JP, Potrzebowski MJ. Simple and accurate determination of X-H distances under ultra-fast MAS NMR. J Magn Reson. 2013;233:56–63. doi: 10.1016/j.jmr.2013.05.005. [DOI] [PubMed] [Google Scholar]
- 54.Fung BM, Khitrin AK, Ermolaev K. An Improved Broadband Decoupling Sequence for Liquid Crystals and Solids. J Magn Reson. 2000;142:97–101. doi: 10.1006/jmre.1999.1896. [DOI] [PubMed] [Google Scholar]
- 55.Bak M, Rasmussen JT, Nielsen NC. SIMPSON: A General Simulation Program for Solid-State NMR Spectroscopy. J Magn Reson. 2000;147:296–330. doi: 10.1006/jmre.2000.2179. [DOI] [PubMed] [Google Scholar]
- 56.Tošner Z, Andersen R, Stevensson B, Edén M, Nielsen NC, Vosegaard T. Computer-intensive simulation of solid-state NMR experiments using SIMPSON. J Magn Reson. 2014;246:79–93. doi: 10.1016/j.jmr.2014.07.002. [DOI] [PubMed] [Google Scholar]
- 57.Wu XL, Zilm KW. Cross Polarization with High-Speed Magic-Angle Spinning. J Magn Reson A. 1993;104:154–165. [Google Scholar]
- 58.Amoureux JP, Pruski M. Theoretical and experimental assessment of single- and multiple-quantum cross-polarization in solid state NMR. Mol Phys. 2002;100:1595–1613. [Google Scholar]
- 59.Lange A, Scholz I, Manolikas T, Ernst M, Meier BH. Low-power cross polarization in fast magic-angle spinning NMR experiments. Chem Phys Lett. 2009;468:100–105. [Google Scholar]
- 60.Scholz I, Meier BH, Ernst M. Operator-based triple-mode Floquet theory in solid-state NMR. J Chem Phys. 2007;127:204504. doi: 10.1063/1.2800319. [DOI] [PubMed] [Google Scholar]
- 61.Metz G, Wu XL, Smith SO. Ramped-Amplitude Cross Polarization in Magic-Angle-Spinning NMR. J Magn Reson A. 1994;110:219–227. [Google Scholar]
- 62.Langer B, Schnell I, Spiess HW, Grimmer AR. Temperature Calibration under Ultrafast MAS Conditions. J Magn Reson A. 1999;138:182–186. doi: 10.1006/jmre.1999.1717. [DOI] [PubMed] [Google Scholar]
- 63.Dvinskikh SV, Zimmermann H, Maliniak A, Sandstrom D. Heteronuclear dipolar recoupling in liquid crystals and solids by PISEMA-type pulse sequences. J Magn Reson. 2003;164:165–170. doi: 10.1016/s1090-7807(03)00180-0. [DOI] [PubMed] [Google Scholar]
- 64.Zhao X, Edén M, Levitt MH. Recoupling of heteronuclear dipolar interactions in solid-state NMR using symmetry-based pulse sequences. Chem Phys Lett. 2001;342:353–361. [Google Scholar]