Abstract
Pushing objects in the presence of body asymmetries could increase the risk of back injury. Furthermore, when the object is heavy, it could exacerbate the effects induced by asymmetrical posture. We investigated how the use of asymmetrical posture and/or upper extremity movement affect vertical torque (Tz) and center of pressure (COP) displacement during pushing. Ten healthy volunteers were instructed to push objects of three different weights using two hands (symmetrical hand use) or one hand (asymmetrical hand use) while standing in symmetrical or asymmetrical foot-positions. The peak values of Tz and COP displacement in the medial-lateral direction (COPML) were analyzed. In cases of isolated asymmetry, changes in the Tz were mainly linked with effects of hand-use whereas effects of foot-position dominated changes in the COPML displacement. In cases of a combined asymmetry, the magnitudes of both Tz and COPML were additive when asymmetrical hand-use and foot-position induced the rotation of the lower and upper body in the same direction or subtractive when asymmetries resulted in the rotation of the body segments in the opposite directions. Moreover, larger Tz and COP displacements were seen when pushing the heavy weight. The results point out the importance of using Tz and COPML to describe the isolated or combined effects of asymmetrical upper extremity movement and asymmetrical posture on body rotation during pushing. Furthermore, it suggests that a proper combination of unilateral arm movement and foot placements could help to reduce body rotation even when pushing heavy objects.
Keywords: body rotation, vertical torque, center of pressure, symmetrical and asymmetrical posture, pushing weight
Introduction
Pushing is commonly used when opening doors or moving grocery shopping carts, as well as while moving goods in warehouse and distribution settings (Baril-Gingras and Lortie, 1995; Chang and Drury, 2007; Marras et al., 2009). Pushing activities are associated with 9–20% work-related musculoskeletal disorders and low-back injuries (Hoozemans et al., 1998). The majority of studies are focused on investigating the magnitudes and directions of exerted pushing force (Al-Eisawi et al., 1999; Hoozemans et al., 2007; Lee, 2011). Many activities involving pushing an object with only one hand are associated with loading body segments asymmetrically. Furthermore, health care workers frequently adopt asymmetrical postures, including lateral bending and trunk turning, laterally positioned arms and sideward force exertion during patients handling activities (Theilmeier et al., 2010). Turning the patient in bed or repositioning in the seat of the wheelchair are performed while standing asymmetrically (Skotte et al., 2002), which may induce high load on the spine and lead to health-related absenteeism (Theilmeier et al., 2010; Videman et al., 2005). Rotational moment at the spine is influenced by the activation of muscles predominately on one side of the body. This in turn creates the rotation of the body and as a result, maintenance of vertical posture during asymmetrical pushing could be more challenging. The weight of the object has been considered as an important ergonomic factor that affects pushing posture and muscle activities (Hoozemans et al., 2002; Jung et al., 2005). Large trunk twisting moments and muscle activities were reported when pushing heavier loads (Lee et al., 2010).
Several measurement approaches are used to analyze activities performed in standing. Among them are recording the displacement of the center of pressure (COP) or the torque calculated around the vertical axis (Dalleau et al., 2007), which could be used to describe body rotation (Kumar and Narayan, 2006). While COP measures provide important information about changes in postural control (Lee and Aruin, 2013, 2014; Macpherson et al., 1989; McIlroy and Maki, 1996), which allow to describe the body movements in the both, anterior-posterior/medial-lateral directions, they have limitations. For example, measures of the COP displacement could not reveal the information about the body rotation, which is important for evaluation of certain tasks involving asymmetrical body posture. At the same time, measuring vertical torque (Tz) could provide information pertaining to rotation of the body. Thus, the positive/negative Tz values corresponding to counterclockwise/clockwise rotation have been documented during performance of unilateral arm-raising movements (Bleuse et al., 2005; Yamazaki et al., 2005).
Selection of a proper measure becomes especially important when studying tasks involving asymmetry of body posture or movement. Therefore, the aim of the current study was to investigate how the vertical torque and the COP displacement change in response to symmetrical or asymmetrical pushing movement and stance as well as the weight of the object to be pushed. We hypothesized that when pushing with two hands (symmetrical movement) and in symmetrical stance, the magnitudes of torque and COP displacement would be minimal compared to asymmetrical conditions. Second, we hypothesized that if asymmetry of the pushing movement or stance is present, the torque and COP displacement would be specific to the induced asymmetry. Moreover, depending on the combination of the asymmetry of the hand-use and foot-position, we expect to observe changes in each the torque and COP displacement either in the same or opposite directions.
Methods
Participants
Ten volunteers (five females and five males, age 29.4 ± 3.9 years, height 170.7 ± 8.3 cm and mass 69.9 ± 14.4 kg) without known neuromuscular disorders or history of musculoskeletal problems within the past 12 months participated in the experiment. The average weight and height of male and female fall into the 50th and 75th percentile of the population respectively (Halls and Hanson, 2008). The study was approved by the Institutional Review Board and all the subjects signed a consent form.
Experimental procedure
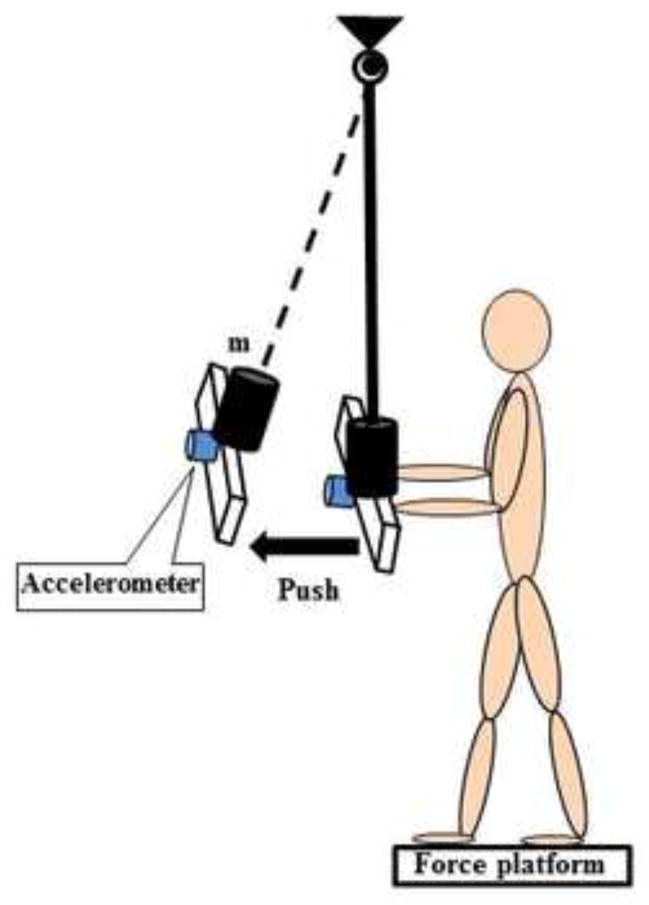
Subjects were instructed to push the handle (61 × 9 × 2 cm) attached to an aluminum pendulum (Fig 1) using two hands and using the right hand only and the left hand only. The height of the pendulum was adjusted to match the subject’s hand position. The weight of the pendulum with the handle was 6.66 N (NW: no weight). Extra light and heavy weights (111.13 and 222.26 N) were affixed to the handle (LW: light weight or HW: heavy weight). Pushing a two–wheeled hand cart with similar maximum weight is common in ergonomics studies (Nimbarte et al., 2013). The subjects stood in front of the pendulum on the top of the force platform (with feet shoulder width apart and the five degree toe-out foot progression angle) either in symmetrical stance (feet parallel to each other) or asymmetrical stance (right/left foot forward and left/right foot backward). In the asymmetrical stance, the subjects placed the front/back foot near the front/back edge of the force platform. The required foot positions were marked with chalk and the subjects were required to maintain the same foot position in all trials in a particular series. In all the experimental conditions, the subjects were instructed to stand upright with both their upper arms at the sides of their trunk, at 90 degrees of elbow flexion and wrist extension, with the palms slightly contacting the positions marked with chalk on the wooden handle. When pushing with one hand, the ipsilateral arm maintained the position as described above and the contralateral arm remained loosely by the side of the body. The subjects were instructed to push the handle using only trunk motion without wrist flexion and without taking a step or lifting the heels from the surface of the force platform. The task was performed in a self-paced manner after receiving the experimenter’s command “push”. Several practice trials were provided to familiarize subjects with the task. Each subject performed the experimental task of pushing the pendulum handle when the following three conditions were manipulated: 1) foot-position: parallel, right foot forward and left foot forward stances; 2) hand-use: both, right hand pushing and left hand pushing; 3) weight: 0, 111.13 and 222.26 N. Five trials (each 5 seconds in duration) were performed in each of 27 experimental conditions and the order of conditions was generated randomly for each subject by MATLAB (MathWorks, Natick, MA, USA) function. Subjects were provided with 30 seconds to 1 minute rest periods to avoid effects of fatigue. The study was conducted during one session and lasted approximately one hour.
Fig. 1.
The schematic representation of the experimental setup. As an example, the experimental condition with two hands pushing the pendulum while standing with right foot forward and left foot backward is shown. m- is the additional weight attached to the pendulum.
Data collection
Ground reaction forces and moments of forces were recorded from a force platform (Model OR-5, AMTI, USA). An accelerometer (Model 208C03, PCB Piezotronics Inc., USA) was attached to the pendulum (Fig 1); its signal was used to determine the moment when the pendulum started moving away.
The forces, moments of forces, and accelerometer signals were synchronized and digitized with a 16-bit resolution at 1,000 Hz by means of an analog-to-digital converter and customized LabVIEW 8.6.1 software (National Instruments, Austin TX, USA). All data was stored on a computer for further processing.
Data processing and analysis
All data was processed offline using MATLAB software. The accelerometer data was used to determine the moment the pendulum started moving away (T0) using an approximate generalized likelihood ratio algorithm (Staude and Wolf, 1999).
The vertical component of the ground reaction force (Fz), the horizontal components of ground reaction force in the anterior-posterior (AP) direction (Fy), and in the medial-lateral (ML) direction (Fx) and the moments of forces around the frontal axis (Mx) and the sagittal axis (My) were filtered with a 20Hz low-pass, 2nd order, zero-lag Butterworth filter. Time-varying COPAP and COPML traces were calculated using the following approximations (Winter et al., 1996):
where dz is the distance from the surface to the platform origin (0.038m). Furthermore, the time-varying vertical torque (Tz) was calculated using the following approximation (Bouisset and Zattara, 1987):
It was demonstrated that measuring the COPAP during forward pushing is not always informative as the COP shifts backward then forward regardless of the asymmetry of stance and movement (Lee and Aruin, 2013, 2014). Thus, in the current study, the peak values of the vertical torque (Tz) and the COP displacement in the ML direction (COPML) were calculated. Variables of Tz and COPML were calculated for each trial and averaged over five trials to represent each condition.
Three-way repeated measures ANOVAs were performed with factors: weight, hand-use and foot-position separately for the Tz and COPML. A factor of weight was considered as a category parameter. Post hoc comparisons were done using Tukey’s Honestly Significant Difference test for significant interactions and main effects. Statistical difference was set at p <0.05. Means and standard errors are presented.
Results
Vertical Torque
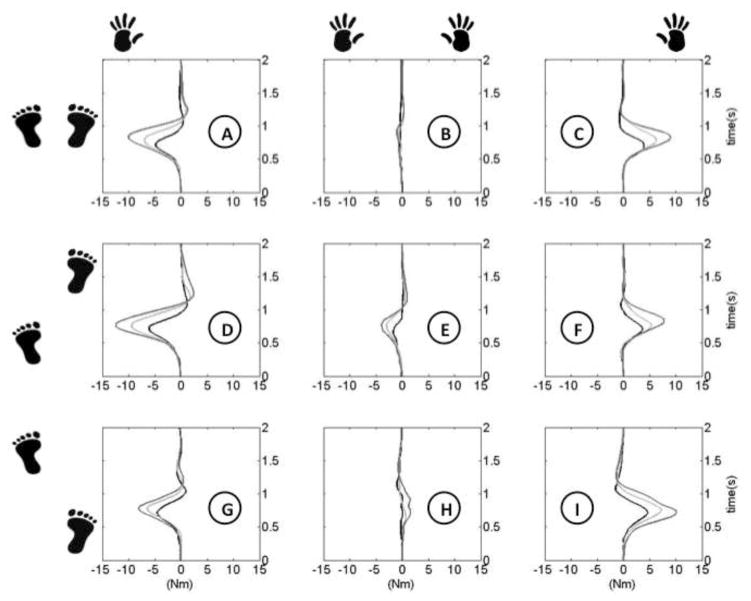
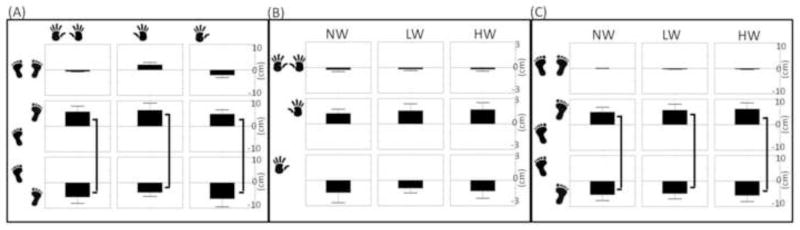
The averaged Tz, trajectories as a function of time are shown in Fig. 2. When pushing with two hands while standing symmetrically, the torque is close to zero Nm (Fig 2B). However, when the subjects were required to push with two hands while standing in asymmetrical stance, the Tz trajectories deviated towards the side of the back leg (Fig 2E, 2H). Moreover, when pushing was performed with one hand (asymmetry of pushing), the magnitude of the torque increased noticeably with the Tz trajectory moving towards the side of the pushing hand regardless of the feet position. In addition, the magnitudes of the torque were much larger in conditions with combined asymmetry of pushing movement and stance. This could be seen, for example, in conditions of pushing with the left-hand while standing with the right foot forward (Fig 2D), compared to asymmetrical push in symmetrical stance (Fig 2A). Similar effects of combined asymmetry could be seen when comparing Tz magnitudes during pushing with the right hand while standing with left foot forward (Fig 2I) and pushing with the right hand while standing symmetrically (Fig 2C). The increase in the Tz magnitude in conditions of using the hand on the side of the backward leg is a reflection of the added effects of the two asymmetries. On the contrary, the magnitudes of Tz in the trials with pushing with the right-hand while standing with right foot forward (Fig 2G) and pushing with the left-hand while standing with left foot forward (Fig 2F) were smaller compared to conditions when pushing with the hand on the side that is opposite to the foot placed forward. In this case, the smaller Tz magnitudes reflect the subtraction of the effects of asymmetries in conditions when pushing using the hand on the side of the forward leg.
Fig. 2.
Trajectories of the vertical torque during pushing an object are shown for the group. Experimental conditions: 1) Hand-use (shown with the hand prints on the top): Pushing with only the left hand, both hands and only the right hand; 2) Foot-position (shown with the foot prints on the left): Standing with the left foot forward, parallel stance and with the right foot forward. Changes in the amount of weight to be pushed (no additional weight, light weight and heavy weight) are shown with the light gray, dark gray and black lines respectively. Positive sign represents clockwise rotation and negative sign represents counter-clockwise rotation
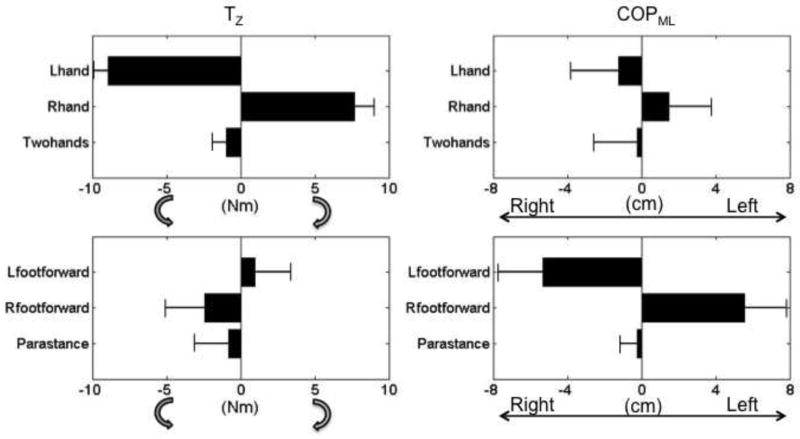
Torque (Tz) was significantly affected by the main effect of hand-use and foot-position (Table 1). The values of Tz were −0.96 ± 0.95 Nm, 7.70 ± 1.26 Nm and -8.96 ± 1.39 Nm when pushing the pendulum with two hands, right hand only and left hand only respectively (averaged through feet-positions and weight conditions). For effects of foot-position, the values of Tz were −0.79 ± 2.30 Nm in the symmetrical (parallel) stance condition, −2.42 ± 2.64 Nm in the right-foot forward condition and 0.98 ± 2.37 Nm in the left-forward condition, which were averaged through hand-use and weight conditions (Fig 3). The three-way repeated measures ANOVA also revealed that Tz was significantly affected by the interactions between each of the two factors (Table 1). The magnitudes remained about zero Nm when two hands were used to push the pendulum regardless of the foot-position (Fig 4A) or weight (Fig 4B). The torques were significantly different between pushing with bilateral hands and unilateral hands (p<0.001). In addition, when the pendulum was pushed with the right hand, the Tz were positive reflecting the clockwise body rotation and when the push was performed with the left hand, the Tz was negative reflecting the counterclockwise body rotation. The increase in weight of object to be pushed resulted in an increase of the Tz magnitudes. Thus when pushing the pendulum with one hand, Tz magnitudes were significantly larger in the heavy weight (HW) conditions than in the no weight (NW) conditions (Fig 4B). Increases in Tz magnitudes from no-weight to heavy weight were observed during the three foot-position conditions. A significant difference between foot-position was seen only in the HW condition (Fig 4C).
Table 1.
The results of three-way repeated measure ANOVAs for the Tz and COPML.
| TZ | COPML | |||
|---|---|---|---|---|
| Main Effect | F(2,18) | p | F(2,18) | p |
| Pushing movement (P) | 89.442 | <.001 | 22.898 | <.001 |
| Stance (S) | 17.428 | <.001 | 33.068 | <.001 |
| Weight (W) | 1.039 | .374 | 0.086 | .918 |
|
| ||||
| 2 Way Interaction | F(4,36) | p | F(4,36) | p |
| P×S | 10.285 | <.001 | 16.176 | <.001 |
| P×W | 53.739 | <.001 | 0.480 | .750 |
| S×W | 10.305 | <.001 | 3.633 | .014 |
|
| ||||
| 3 Way Interaction | F(8,72) | p | F(8,72) | p |
| P×S×W | 1.700 | .113 | 1.959 | .064 |
F and p values are presented and significant p-values are indicated in bold.
Fig. 3.
The effects of weight, pushing movement and stance on the Tz magnitude and COPML displacement.
Fig. 4.
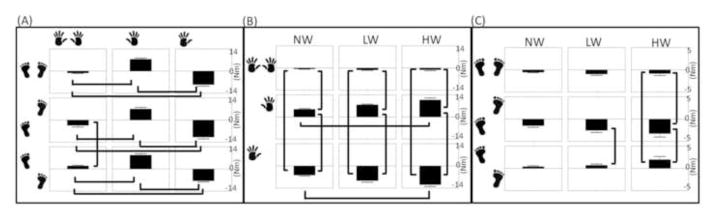
The interaction between pushing movement and stance (A), pushing movement and weight (B) and stance and weight (C) for Tz. Brackets show statistical significance (p<0.05).
The COPML displacement
The magnitudes of the COPML displacement were significantly affected by hand-use and foot-position. Moreover, the data shown in Table 1 revealed interactions between hand-use and foot-position as well as foot-position and weight. Specifically, the COPML displacements shown in Fig 3 were −0.22 ± 2.36 cm, 1.48 ± 2.27 cm and −1.23 ± 2.54 cm when pushing the pendulum with two hands, right hand only and left hand only respectively (data averaged through feet-position and weight conditions). For the main effect of foot-position, the displacements were −0.23 ± 0.93 cm in parallel stance, 5.58 ± 2.19 cm in right-foot forward condition and −5.31 ± 2.43 cm in the left-foot forward condition (averaged through hand-using and weight conditions). When the two factors of hand-use and foot-position (Fig 5A) or foot-position and weight (Fig 5B) are taken into consideration, the magnitudes were close to zero cm in the parallel stance condition. The observed positive COPML displacements suggest that the COPML moved to the left side when the right foot was placed forward. The negative COPML magnitudes while standing in the left-foot forward condition confirm that COPML was shifted to the right side. Significant difference in the COPML displacement was observed only between the right-foot and left-foot forward conditions with increased magnitudes in the extra weight of the pendulum (Fig 5C).
Fig. 5.
The interaction between pushing movement and stance (A), pushing movement and weight (B) and stance and weight (C) for the COPML displacement. Statistical significance (p<0.05) is shown with brackets.
Discussion
The present study was conducted to investigate how changes in the symmetry of stance, hand use and weight of the object to be pushed affect the magnitude of the vertical torque and the COP displacement. The Tz was most sensitive to the changes in symmetry of the task induced by the hand used for pushing. Thus, the clockwise body rotation reflected in the positive Tz magnitudes (Bleuse et al., 2008; Yamazaki et al., 2005) was observed when pushing with the right hand. The counterclockwise body rotation (corroborated by the negative Tz) was found in the left-hand pushing conditions. On the contrary, the displacement of COP in the ML direction was mainly associated with which foot was placed forward or backward with minor changes induced by the symmetrical and asymmetrical pushing movement. The COPML displacement principally shifted towards the foot placed backward. Finally, pushing the heaviest object only enlarged the magnitudes of Tz and COPML and did not affect the patterns induced by asymmetrical hand-use or foot-position.
Pushing in symmetrical conditions
When the pushing task was performed in symmetrical stance using two hands, the Tz and COPML values remained around zero, which suggests that there was no body rotation. This outcome is in line with the observation of symmetrical muscle activities of the left and right trunk and lower extremity muscles in conditions with the symmetrical stance and pushing movement (Lee and Aruin, 2013, 2014). Thus our first hypothesis, that when pushing with two hands and standing symmetrically the magnitudes of the torque and COPML displacement would be minimal, was supported.
The effect of isolated asymmetry
Main effects of hand-use and foot-position both significantly affected the magnitudes of Tz, however, the values were larger in the asymmetrical hand-use conditions (Fig 2A and 2C) rather than the asymmetrical foot-position conditions (Fig 2E and 2H). This implies that the torque was mainly affected by asymmetry of hand-use. Furthermore, the interactions between the two factors indicate that the effects of hand-use should be taken into consideration to explain the effects of asymmetrical posture in pushing. In the current study, clockwise body rotation (positive Tz value) was observed when using the right hand to push the pendulum. The counterclockwise rotation (negative Tz) was observed when pushing with the left hand. Similar asymmetry specific changes in the torque were described previously for the unilateral arm-raising movement (Bleuse et al., 2005; Bleuse et al., 2008; Bleuse et al., 2006; Yamazaki et al., 2005).
While hand-use asymmetries affected torque, changes in the COPML displacement were mainly associated with the foot-position. Thus, the COPML displacement deviated towards left side when right-foot was placed forward and vice versa in the right-foot forward condition. Similar stance-dependent changes in the COPML displacement were reported previously while studying the tasks of quiet standing involving different foot positions (Bonnet, 2012; Mochizuki et al., 2004; Wang and Newell, 2012).
The effect of combined asymmetry
Body rotation is mainly elicited by unilateral upper limb movement to push an object. Thus, body rotations were reported during rapid and asymmetrical arm movements (Yamazaki et al., 2005). Moreover, pushing while standing with the left foot forward and right foot backward resembles the heel-striking phase of gait, which confirms the trunk is rotating clockwise during asymmetrical stance (Li et al., 2001). The combined asymmetries of right hand-use and left foot placed forward created body rotation in a clockwise direction. This resulted in an increased Tz magnitude, which reflects the additive effect of the two asymmetries. Similar but opposite in sign increase in the Tz magnitude was seen in the condition of left hand-use with right foot forward. Conversely, the magnitude of Tz was smaller in the conditions of right/left foot forward with right/left hand pushing (reflecting the subtractive effect of the two asymmetries). This could be explained by the described rotation of body segments in the opposite directions during performance of the unilateral arm-raising movement. Thus pushing with the right hand induces rotation of the upper body in a clockwise direction. However, standing with the right foot forward creates rotation of the lower body in a counterclockwise direction. Additionally, in conditions of standing asymmetrically and pushing with one hand additive or subtractive effects of the combined asymmetry could be seen in the COPML magnitudes.
Pushing a heavy object requires exerting larger forces that could result in a large mechanical load on the low-back (Al-Eisawi et al., 1999; Hoozemans et al., 2007). In the current study, pushing the pendulum with the heavy weight attached resulted in larger magnitudes of torque and COP displacement (seen in Fig 4 and Fig 5); however, the difference between the conditions with three different weights was not statistically significant. Nevertheless, this finding suggests that the paths of Tz and COPML displacement were determined by asymmetries of hand-use and foot-position. On the other hand, it looks like an increase in weight of the object was associated with exerting larger force needed to perform the task which was resulted in the larger magnitude of Tz, reflecting greater body rotation.
Exerting asymmetrical pushing forces between left and right hands in turning a cart resulted in increased trunk rotation (Lee et al., 2012). Moreover, the patient handling activities are frequently performed while standing asymmetrically. Such a body position is common when turning the patient in bed or repositioning posteriorly in the seat of the wheelchair (Skotte et al., 2002). Although the advances of asymmetrical standing are associated with the ability of a person to generate much stronger push forces and maintain proper balance control (Brace, 2005), it is possible that generation of large moments around the vertical axis could increase the risk of back injury (Liu et al., 1985; Marras et al., 2009). The magnitudes of Tz and COPML displacement in each experimental condition with pushing different weights recorded in the current study were smaller in conditions with combined asymmetry of pushing movement and stance as compared to conditions of an isolated asymmetry of stance or hand-use. As such, the study outcome provides a base for optimization of the pushing task by, for example, pushing with the right hand while standing with the right foot forward. Thus, we can suggest that using a proper combination of asymmetrical pushing movement and stance may help to minimize the magnitude of vertical torque and COP displacement as well as stabilize balance even when pushing heavier objects.
Study Limitations
We explored pushing forward while standing in symmetrical or asymmetrical postures and applying force to the moving object with two hands or one hand. Thus, these results apply primarily to pushing tasks as would be experienced when manipulating a cart or carrying a patient without turning. The heaviest pushing weight was 222.26 N which is comparable with the weight of a 196 N two–wheeled hand cart used to study dynamic pushing. Since the pushing weight used in ergonomics studies can range from 196 N to 3136 N (Hoozemans et al., 1998; Nimbarte et al., 2013), additional studies are need to investigate vertical torque (Tz) and COP displacement during pushing of heavier objects. The observed reduction in the vertical torque while performing pushing task in the presence of the combined asymmetries might not be associated with the reduction in the internal musculoskeletal reactions. Finally, the linkage between vertical torque and the risk of back injury needs to be studied in the future by obtaining kinematic data, EMG data, and by using biomechanical simulation to provide comprehensive knowledge for the optimization of pushing posture and movement to reduce potential risks of injuries.
Conclusion
Effects of isolated hand-use asymmetry were reflected by changes in vertical torque, while alterations in isolated foot-position asymmetry were seen as changes in the COPML displacement. The effect of both asymmetries on vertical torque magnitude and COP displacement was either additive or subtractive depending on the combination of asymmetries. Body rotation could be reduced by performing the pushing task with the proper combination of asymmetrical foot-position and hand-use even when pushing the heavy weight. The findings provide additional information on the importance of taking the vertical torque and COP displacement into consideration when describing the effects of asymmetry during pushing.
Acknowledgments
This work was supported in part by the NIDRR grant # H133P110004 and NIH grant # HD064838.
Footnotes
Conflict of interest statement
The authors have no conflict of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Al-Eisawi KW, Kerk CJ, Congleton JJ, Amendola AA, Jenkins OC, Gaines WG. The effect of handle height and cart load on the initial hand forces in cart pushing and pulling. Ergonomics. 1999;42:1099–1113. [Google Scholar]
- Baril-Gingras G, Lortie M. The handling of objects other than boxes: Univariate analysis of handling techniques in a large transport company. Ergonomics. 1995;38:905–925. doi: 10.1080/00140139508925159. [DOI] [PubMed] [Google Scholar]
- Bleuse S, Cassim F, Blatt JL, Defebvre L, Derambure P, Guieu JD. Vertical torque allows recording of anticipatory postural adjustments associated with slow, arm-raising movements. Clinical biomechanics. 2005;20:693–699. doi: 10.1016/j.clinbiomech.2005.03.005. [DOI] [PubMed] [Google Scholar]
- Bleuse S, Cassim F, Blatt JL, Labyt E, Bourriez JL, Derambure P, Destee A, Defebvre L. Anticipatory postural adjustments associated with arm movement in Parkinson’s disease: a biomechanical analysis. Journal of neurology, neurosurgery, and psychiatry. 2008;79:881–887. doi: 10.1136/jnnp.2006.107318. [DOI] [PubMed] [Google Scholar]
- Bleuse S, Cassim F, Blatt JL, Labyt E, Derambure P, Guieu JD, Defebvre L. Effect of age on anticipatory postural adjustments in unilateral arm movement. Gait & posture. 2006;24:203–210. doi: 10.1016/j.gaitpost.2005.09.001. [DOI] [PubMed] [Google Scholar]
- Bonnet CT. Broad stance conditions change postural control and postural sway. Journal of motor behavior. 2012;44:125–131. doi: 10.1080/00222895.2012.654526. [DOI] [PubMed] [Google Scholar]
- Bouisset S, Zattara M. Biomechanical study of the programming of anticipatory postural adjustments associated with voluntary movement. J Biomech. 1987;20:735–742. doi: 10.1016/0021-9290(87)90052-2. [DOI] [PubMed] [Google Scholar]
- Brace T. The dynamics of pushing and pulling in the workplace: assessing and treating the problem. AAOHN J. 2005;53:224–229. quiz 230. [PubMed] [Google Scholar]
- Chang SK, Drury CG. Task demands and human capabilities in door use. Applied ergonomics. 2007;38:325–335. doi: 10.1016/j.apergo.2006.04.023. [DOI] [PubMed] [Google Scholar]
- Dalleau G, Allard MS, Beaulieu M, Rivard CH, Allard P. Free moment contribution to quiet standing in able-bodied and scoliotic girls. European spine journal: official publication of the European Spine Society, the European Spinal Deformity Society, and the European Section of the Cervical Spine Research Society. 2007;16:1593–1599. doi: 10.1007/s00586-007-0404-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halls SB, Hanson J. Average height and weight charts: Showing percentiles and variance for men and women. 2008 ( http://www.halls.md/chart/height-weight.htm)
- Hoozemans MJ, Slaghuis W, Faber GS, van Dieën JH. Cart pushing: The effects of magnitude and direction of the exerted push force, and of trunk inclination on low back loading. International Journal of Industrial Ergonomics. 2007;37:832–844. [Google Scholar]
- Hoozemans MJ, van der Beek AJ, Fring-Dresen MH, van der Woude LH, van Dijk FJ. Low-back and shoulder complaints among workers with pushing and pulling tasks. Scand J Work Environ Health. 2002;28:293–303. doi: 10.5271/sjweh.678. [DOI] [PubMed] [Google Scholar]
- Hoozemans MJ, van der Beek AJ, Frings-Dresen MH, van Dijk FJ, van der Woude LH. Pushing and pulling in relation to musculoskeletal disorders: a review of risk factors. Ergonomics. 1998;41:757–781. doi: 10.1080/001401398186621. [DOI] [PubMed] [Google Scholar]
- Jung MC, Haight JM, Freivalds A. Pushing and pulling carts and two-wheeled hand trucks. International Journal of Industrial Ergonomics. 2005;35:79–89. [Google Scholar]
- Kumar S, Narayan Y. Torque and EMG in rotation extension of the torso from pre-rotated and flexed postures. Clinical biomechanics. 2006;21:920–931. doi: 10.1016/j.clinbiomech.2006.04.017. [DOI] [PubMed] [Google Scholar]
- Lee YJ. Dissertation. VU University; Amsterdam: 2011. Control of trunk movement: Perturbations in cart pushing. [Google Scholar]
- Lee YJ, Aruin AS. Three components of postural control associated with pushing in symmetrical and asymmetrical stance. Experimental brain research. 2013;228:341–351. doi: 10.1007/s00221-013-3567-4. [DOI] [PubMed] [Google Scholar]
- Lee YJ, Aruin AS. Isolated and combined effects of asymmetric stance and pushing movement on the anticipatory and compensatory postural control. Clinical neurophysiology : official journal of the International Federation of Clinical Neurophysiology. 2014;125:768–776. doi: 10.1016/j.clinph.2013.09.036. [DOI] [PubMed] [Google Scholar]
- Lee YJ, Hoozemans MJ, van Dieen JH. Trunk muscle control in response to (un)expected turns in cart pushing. Gait & posture. 2012;36:133–138. doi: 10.1016/j.gaitpost.2012.02.005. [DOI] [PubMed] [Google Scholar]
- Lee YJ, Hoozemans MJ, van Dieën JH. Oblique abdominal muscle activity in response to external perturbations when pushing a cart. J Biomech. 2010;43:1364–1372. doi: 10.1016/j.jbiomech.2010.01.022. [DOI] [PubMed] [Google Scholar]
- Li Y, Wang W, Crompton RH, Gunther MM. Free vertical moments and transverse forces in human walking and their role in relation to arm-swing. The Journal of experimental biology. 2001;204:47–58. doi: 10.1242/jeb.204.1.47. [DOI] [PubMed] [Google Scholar]
- Liu YK, Goel VK, Dejong A, Njus G, Nishiyama K, Buckwalter J. Torsional fatigue of the lumbar intervertebral joints. Spine. 1985;10:894–900. doi: 10.1097/00007632-198512000-00006. [DOI] [PubMed] [Google Scholar]
- Macpherson JM, Horak FB, Dunbar DC, Dow RS. Stance dependence of automatic postural adjustments in humans. Experimental brain research. 1989;78:557–566. doi: 10.1007/BF00230243. [DOI] [PubMed] [Google Scholar]
- Marras WS, Knapik GG, Ferguson S. Loading along the lumbar spine as influence by speed, control, load magnitude, and handle height during pushing. Clinical biomechanics. 2009;24:155–163. doi: 10.1016/j.clinbiomech.2008.10.007. [DOI] [PubMed] [Google Scholar]
- Mcllroy WE, Maki BE. Age-related changes in compensatory stepping in response to unpredictable perturbations. J Gerontol A Biol Sci Med Sci. 1996;51:M289–296. doi: 10.1093/gerona/51a.6.m289. [DOI] [PubMed] [Google Scholar]
- Mochizuki G, Ivanova TD, Garland SJ. Postural muscle activity during bilateral and unilateral arm movements at different speeds. Experimental brain research. 2004;155:352–361. doi: 10.1007/s00221-003-1732-x. [DOI] [PubMed] [Google Scholar]
- Nimbarte AD, Sun Y, Jaridi M, Hsiao H. Biomechanical loading of the shoulder complex and lumbosacral joints during dynamic cart pushing task. Applied ergonomics. 2013;44:841–849. doi: 10.1016/j.apergo.2013.02.008. [DOI] [PubMed] [Google Scholar]
- Skotte JH, Essendrop M, Hansen AF, Schibye B. A dynamic 3D biomechanical evaluation of the load on the low back during different patient-handling tasks. J Biomech. 2002;35:1357–1366. doi: 10.1016/s0021-9290(02)00181-1. [DOI] [PubMed] [Google Scholar]
- Staude G, Wolf W. Objective motor response onset detection in surface myoelectric signals. Medical engineering & physics. 1999;21:449–467. doi: 10.1016/s1350-4533(99)00067-3. [DOI] [PubMed] [Google Scholar]
- Theilmeier A, Jordan C, Luttmann A, Jager M. Measurement of action forces and posture to determine the lumbar load of healthcare workers during care activities with patient transfers. Ann Occup Hyg. 2010;54:923–933. doi: 10.1093/annhyg/meq063. [DOI] [PubMed] [Google Scholar]
- Videman T, Ojajarvi A, Riihimaki H, Troup JD. Low back pain among nurses: a follow-up beginning at entry to the nursing school. Spine. 2005;30:2334–2341. doi: 10.1097/01.brs.0000182107.14355.ca. [DOI] [PubMed] [Google Scholar]
- Wang Z, Newell KM. Asymmetry of foot position and weight distribution channels the inter-leg coordination dynamics of standing. Experimental brain research. 2012;222:333–344. doi: 10.1007/s00221-012-3212-7. [DOI] [PubMed] [Google Scholar]
- Winter DA, Prince F, Frank JS, Powell C, Zabjek KF. Unified theory regarding A/P and M/L balance in quiet stance. Journal of neurophysiology. 1996;75:2334–2343. doi: 10.1152/jn.1996.75.6.2334. [DOI] [PubMed] [Google Scholar]
- Yamazaki Y, Suzuki M, Ohkuwa T, Itoh H. Maintenance of upright standing posture during trunk rotation elicited by rapid and asymmetrical movements of the arms. Brain research bulletin. 2005;67:30–39. doi: 10.1016/j.brainresbull.2005.05.015. [DOI] [PubMed] [Google Scholar]