Dynamic Simulation of Tibial Tuberosity Realignment: Model Evaluation

Abstract

The current study was performed to evaluate a dynamic multibody model developed to characterize the influence of tibial tuberosity realignment procedures on patellofemoral motion and loading. Computational models were created to represent four knees previously tested at 40°, 60° and 80° of flexion with the tibial tuberosity in a lateral, medial and anteromedial position. The experimentally loaded muscles, major ligaments of the knee, and patellar tendon were represented. A repeated measures ANOVA with post-hoc testing was performed at each flexion angle to compare data between the three positions of the tibial tuberosity. Significant experimental trends for decreased patella flexion due to tuberosity anteriorization and a decrease in the lateral contact force due to tuberosity medialization were reproduced computationally. The dynamic multibody modeling technique will allow simulation of function for symptomatic knees to identify optimal surgical treatment methods based on parameters related to knee pathology and pre-operative kinematics.

Introduction

Lateral patellar maltracking is a primary contributor to patellofemoral pain and instability (Fulkerson and Shea, 1990; Colvin and West, 2008). Several surgical options are available to treat patellofemoral disorders, with tibial tuberosity osteotomy and realignment a common approach. The tuberosity is typically medialized to reduce the lateral component of the force applied to the patella by the patellar tendon. Medialization is frequently combined with anteriorization to reduce patellofemoral compression (Fulkerson, 2004; Mihalko et al., 2007).

The authors have developed a model for dynamic multibody simulation of knee function (Kim et al., 2013) that can be used to evaluate tibial tuberosity realignment. Several computational models have been used to study the influence of tuberosity realignment on patellofemoral mechanics (Benvenuti et al., 1997; Cohen et al., 2003; Elias and Saranathan, 2013; Shirazi-Adl and Mesfar, 2007). The current model improves upon existing models by accounting for variations in tibiofemoral kinematics that are caused by tibial tuberosity realignment (Mani et al., 2011, Elias et al., 2014) within a relatively fast and efficient analysis. The current study focuses on evaluation of the computational model by comparison to in vitro experimental data.

Methods

Computational models were created to represent four knees (three female, one male, age range of 62 to 74 years) that were previously tested in vitro to evaluate the influence of tibial tuberosity realignment on knee kinematics and the pressure applied to patellofemoral cartilage (Mani et al., 2011; Saranathan et al., 2012). The knees were tested in isometric extension at 40°, 60° and 80° of flexion (Fig. 1A) with the tibial tuberosity in three positions: lateral (5 mm lateral to normal), medial (10 mm medial to lateral position) and anteromedial (10 mm anterior to medial position). Anatomically-oriented forces were applied to produce a total quadriceps force of 586 N, including representation of a weak vastus medialis obliquus (Elias et al., 2009), and a total hamstrings force of 200 N. Flexion angles lower than 40° were not tested due to concerns of inducing patellar instability (Saranathan et al. 2012). The patellofemoral pressure distribution was measured using thin film sensors (I-Scan 5051, Tekscan, Boston, MA). Magnetic tracking sensors (TrakSTAR, Ascension Technology, Burlington, VT) with static resolutions for measures of translation and rotation of 0.5 mm and 0.1°, respectively, were fixed to the femur, patella and tibia. Anatomical landmarks were digitized to create reference axes for quantifying tibiofemoral (Mani et al., 2011) and patellofemoral (Saranathan et al., 2012; Elias et al., 2011) kinematics.

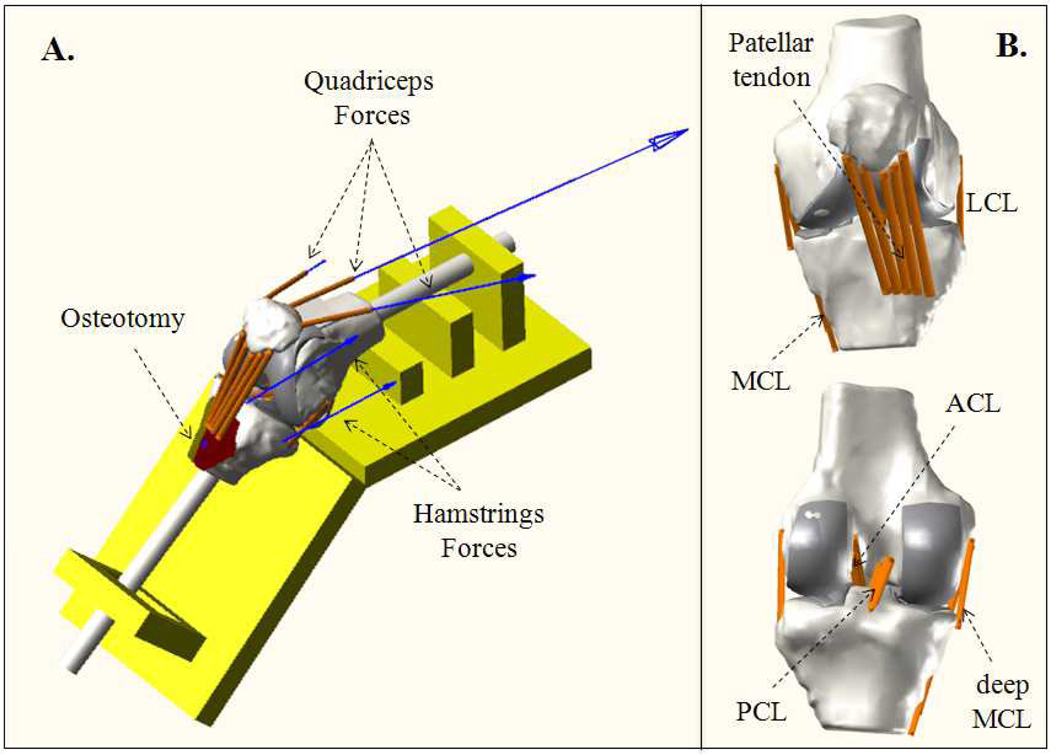
Figure 1.

(A) Computational representation of a knee on the testing frame, including representation of the ostetomized tibial tuberosity and simulated quadriceps and hamstrings forces. (B) Frontal and back views of the knee joint with ligamentous structures.

A previously described technique for multibody dynamics simulation of knee function (Kim et al., 2013; Kwon et al., 2014) was used to replicate the experimental tests. Computational models representing the bones and cartilage of the knee were created from MRI data at full extension and positioned within a graphical representation of the experimental test frame (Elias and Saranathan, 2013). Tendon and ligament attachments on the bones were based on measurements from the tested knees and anatomical landmarks. The anterior and posterior cruciate ligaments (ACL, PCL) and the medial and lateral collateral ligaments (MCL, LCL) were represented with multiple bundles (Blankevoort et al., 1991; Yoon et al., 2010, Li et al., 1999) and governed by a previously described nonlinear force-strain relationships (Blakevoort and Huiskes, 1996), including parallel dampers. The patellar tendon was represented with five elements assigned a total stiffness of 2000 N/mm (Elias and Saranathan, 2013). Contact between cartilage surfaces was governed by simplified Hertzian contact (Guess et al., 2013) according to:

$$F_c=k{\delta }^n+B(\delta )\delta \prime$$

where F_c is the contact force in the cartilage, k is the contact stiffness coefficient, δ is the penetration of surfaces, δ' is the penetration velocity, n is the compliance exponent and B(δ) is the damping coefficient. The contact parameters for the tibiofemoral joint were k = 500 N/mm, B(δ) = 5 Ns/mm, and n = 1.5 (Bloemker et al., 2012; Guess et al., 2010). The meniscus was not represented.. The patellar cartilage was divided into 103 discrete rigid elements (Guess, 2012; Guess et al., 2013), with an average (± standard deviation) surface area of 9 ± 1.5 mm². The contact parameters were k = 120 N/mm, B(δ) = 5 Ns/mm and n = 1.0 (Guess, 2012).

The experimentally applied quadriceps and hamstrings forces were applied to the fully extended knee using a multibody dynamics software package (Recurdyn, Function Bay, Korea). The knees were flexed until the designated flexion angle was reached, without constraining any additional degrees of freedom. Tibiofemoral and patellofemoral translations and rotations were quantified based on four link kinematics chains consisting of cylindrical joints, as described for the floating axis convention (Grood and Suntay, 1983), that connected the tibia and patella to the femur. Computational measures of patellar flexion, lateral shift and lateral tilt were compared to experimental values. As the primary tibiofemoral parameter influenced by tuberosity medialization (Mani et al., 2011), with a direct influence on the lateral orientation of the patellar tendon, tibial external rotation was also compared to the experimental data. The patellofemoral force distribution was characterized as the percentage of the total compressive force applied lateral to the patellar ridge. A two level (computational vs. experimental, tuberosity position) repeated measures ANOVA was performed at each flexion angle. Follow-up single level ANOVA’s with a post-hoc Student-Newman-Keuls test were used to identify significant (p < 0.05) differences between individual tuberosity positions.

Results

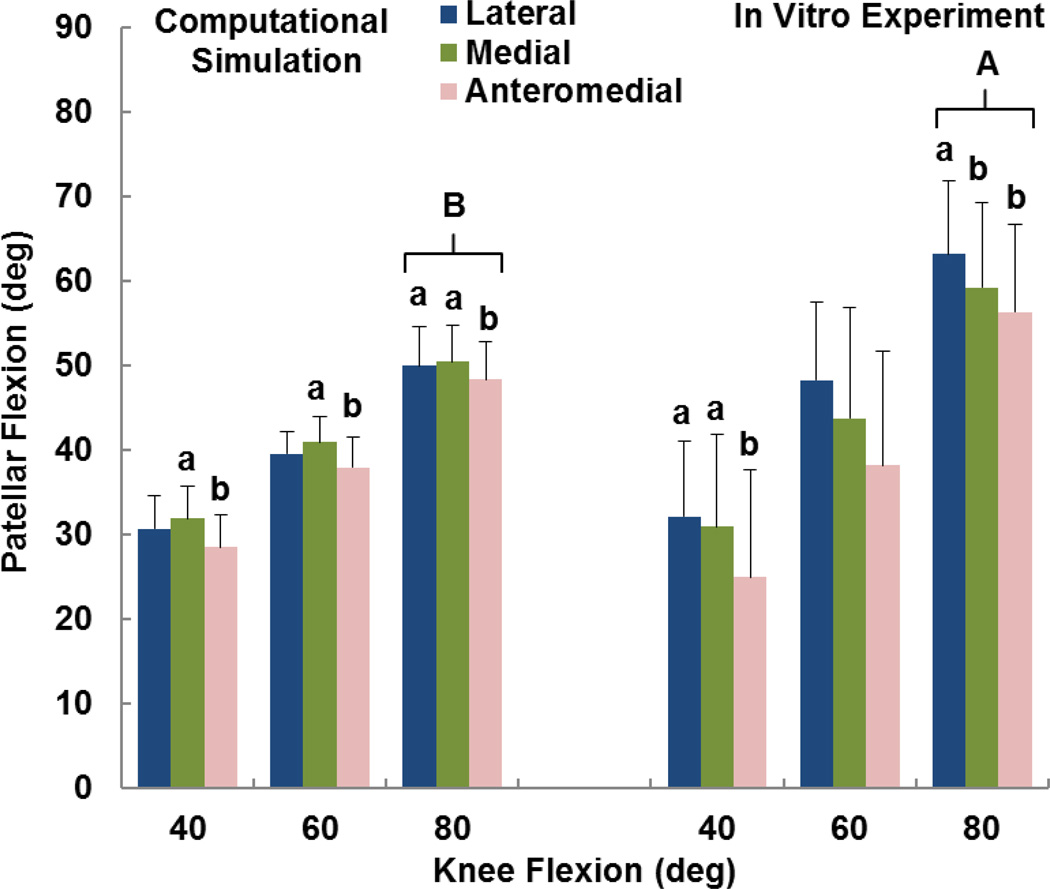
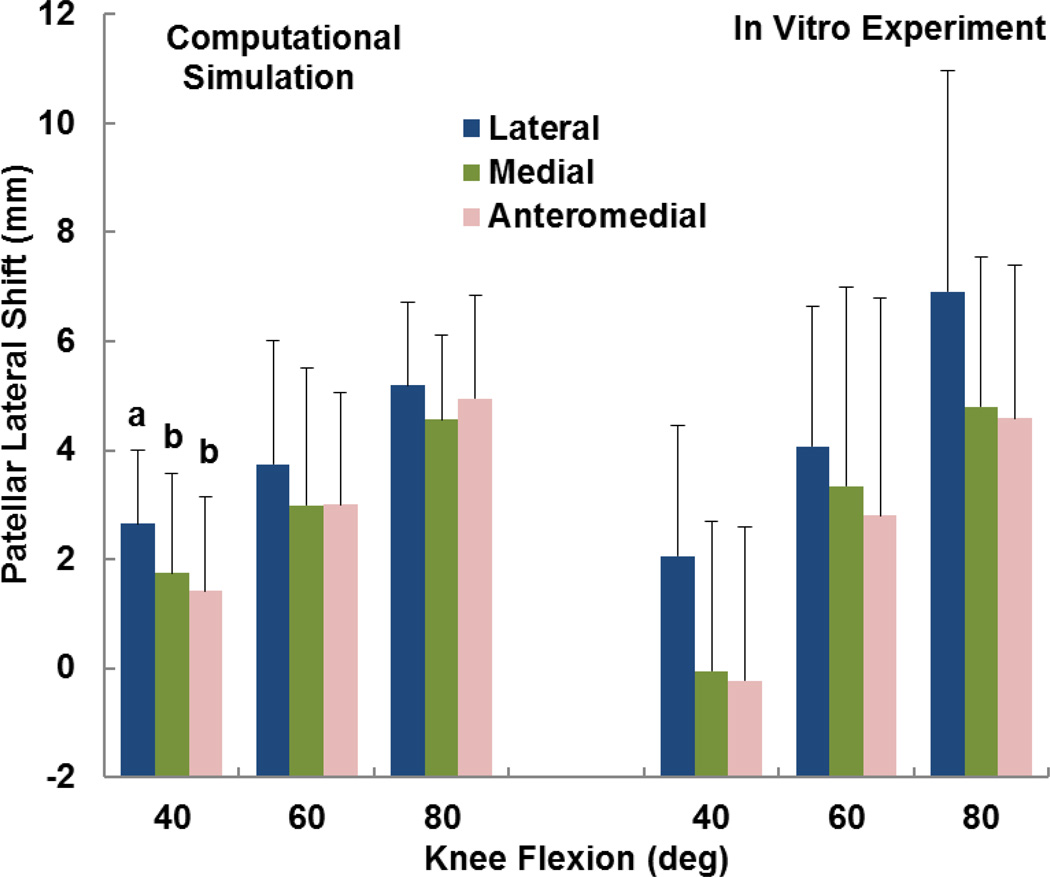
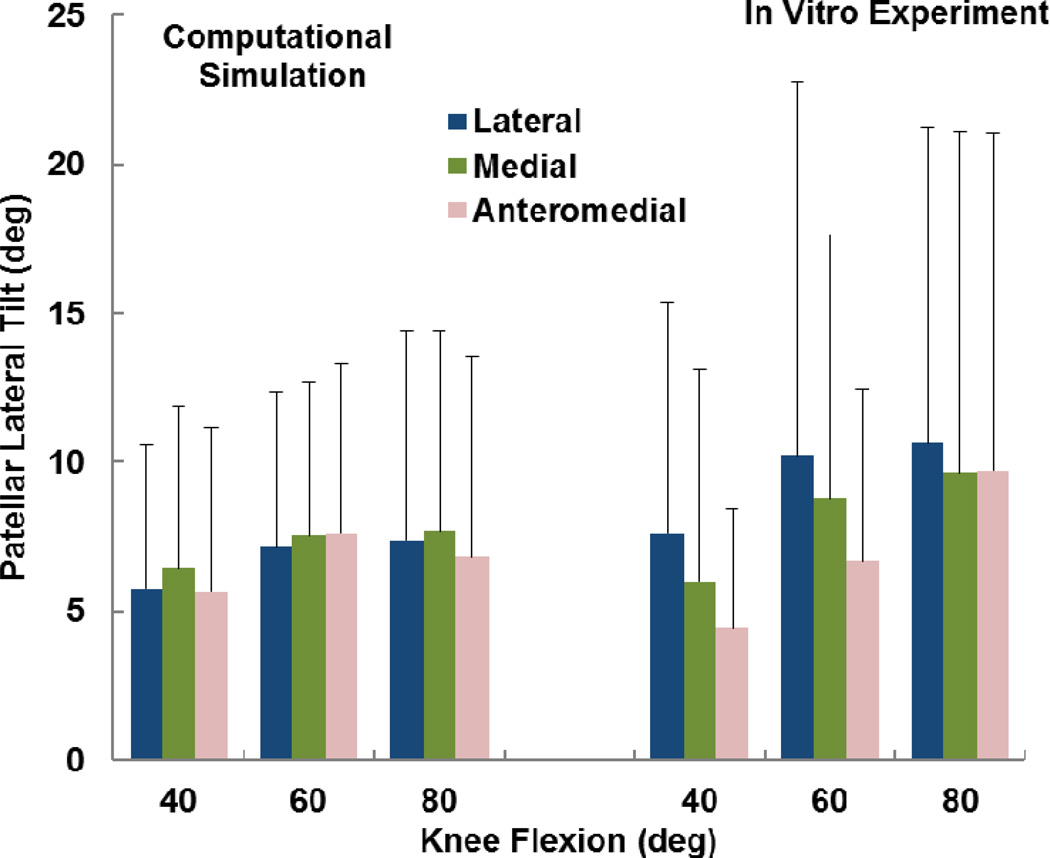
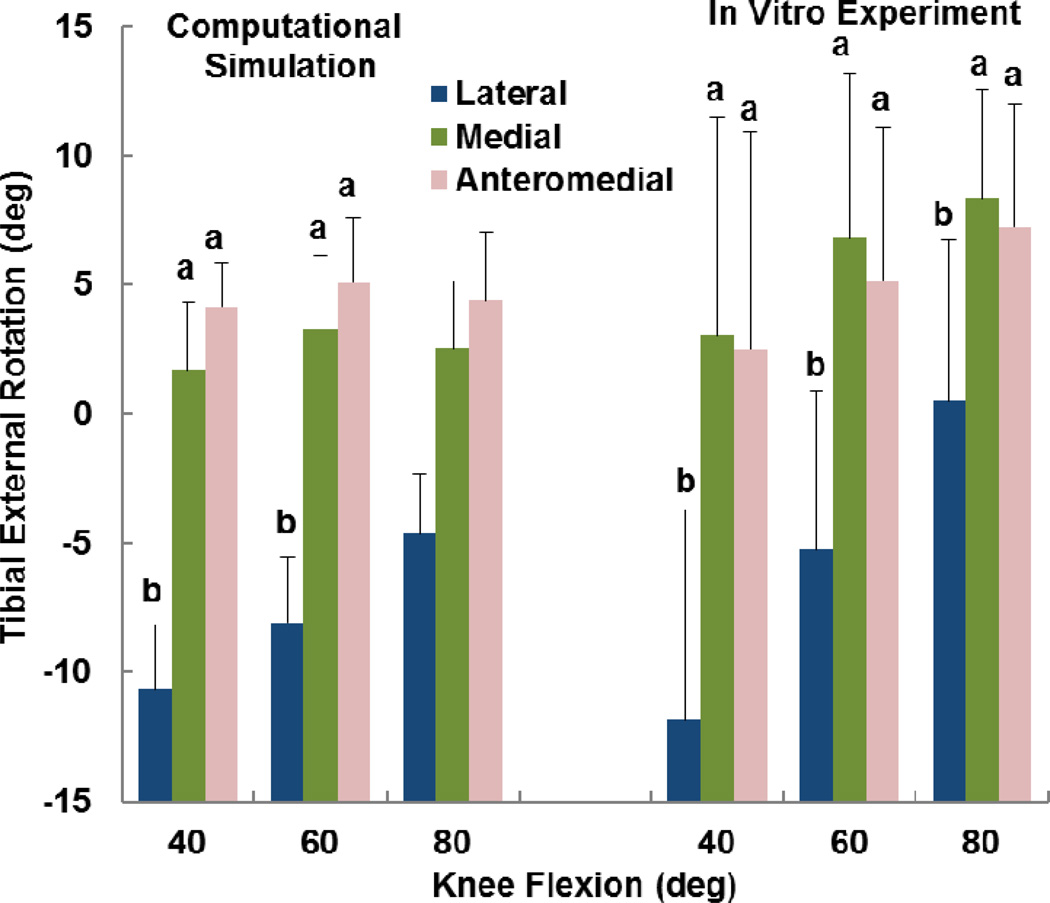
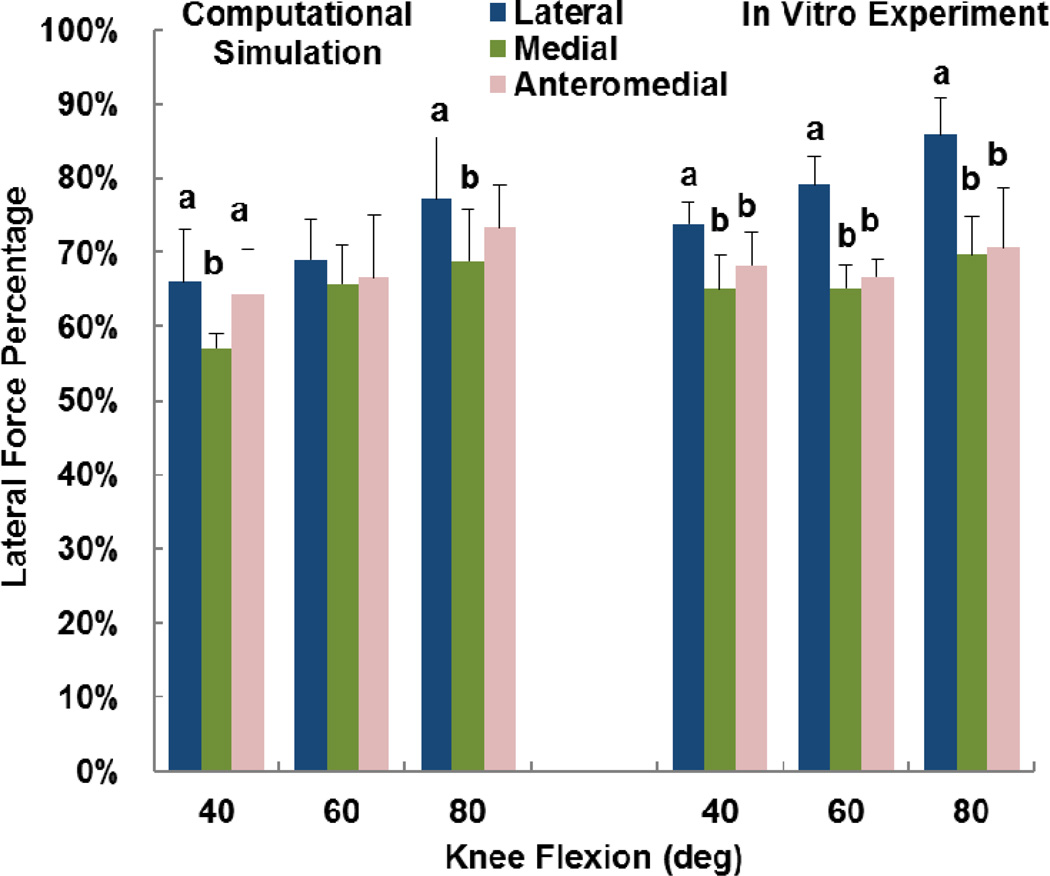
The computational and experimental data showed similar trends for the influence of tibial tuberosity position on kinematics and the force distribution. For the computational and experimental data, the anteromedial position of the tuberosity produced significantly lower patellar flexion than at least one of the other tuberosity positions for all conditions except the experimental data at 60° (p < 0.05) (Figure 2). For the computational and experimental data, the patellar lateral shift tended to be largest with the tuberosity in the lateral position (Figure 3), but the difference was only significant for the computational data at 40° (p < 0.05). The experimental trends for patellar shift nearly reached significance at 40° (p = 0.064) and 80° (p = 0.055). No significant trends relating patellar tilt to tibial tuberosity position were identified for the computational or experimental data (p > 0.1, Figure 4). Tibial external rotation was smallest with the tuberosity in the lateral position for every case except for the computational data at 80° (p < 0.01) (Figure 5). The lateral force percentage was significantly larger with the tuberosity in the lateral position than for the medial position for every case except for the computational data at 60° (p < 0.03, Figure 6). At 80° of flexion, the computational patellar flexion was significantly larger than the experimental flexion (p < 0.05), but no other significant differences were identified between the computational and experimental data (p > 0.25).

Figure 2.

Average (+ standard deviation) patellar flexion from computational simulation and the in vitro experimental study. Significant differences at a flexion angle due to altering the position of the tibial tuberosity are marked with different small letters (a > b). A significant difference between the experimental and computational data at 80° of flexion is also marked (A > B).

Figure 3.

Average (+ standard deviation) patellar lateral shift from computational simulation and the in vitro experimental study. Significant differences at a flexion angle due to altering the position of the tibial tuberosity are marked with different letters (a > b).

Figure 4.

Average (+ standard deviation) patellar lateral tilt from computational simulation and the in vitro experimental study. No significant differences were identified due to altering the position of the tibial tuberosity.

Figure 5.

Average (+ standard deviation) tibial external rotation from computational simulation and the in vitro experimental study. Significant differences at a flexion angle due to altering the position of the tibial tuberosity are marked with different letters (a > b).

Figure 6.

Average (+ standard deviation) lateral force percentage from computational simulation and the in vitro experimental study. Significant differences at a flexion angle due to altering the position of the tibial tuberosity are marked with different letters (a > b).

Discussion

Multibody dynamic modeling was evaluated as a tool to characterize the influence of tibial tuberosity realignment on patellar mechanics. Models were created to represent a subgroup of specimens from previous in vitro experimental studies (Mani et al., 2011; Saranathan et al., 2012), which showed the primary experimental trends noted for the entire study. Modeling reproduced experimentally measured trends of decreased patellar flexion caused by tuberosity anteriorization and increased tibial external rotation and decreased lateral contact caused by tuberosity medialization. A decrease in lateral patellar translation with tuberosity medialization was also shown computationally, which was shown experimentally with the full group of specimens (Saranathan et al., 2012). No relationship was identified between tibial tuberosity position and patellar tilt for either the computational or experimental data. The magnitudes of the computational output were generally similar to the experimental measures, with the only significant difference a larger experimental patellar flexion at 80° of knee flexion. While several other studies have included evaluation of patellofemoral computational models (Besier et al., 2008; Farrokhi et al., 2011; Kwak et al., 2000, Baldwin et al., 2009; Heegaard et al., 1995, Elias et al., 2004; Elias et al., 2010; Elias and Saranathan, 2013), the current study uniquely focuses on changes in patellofemoral mechanics related to tibial tuberosity realignment while incorporating tibiofemoral degrees of freedom. A primary advantage of computational modeling includes the ability to evaluate surgical options during dynamic function while representing the pathology and patellar maltracking that are common for patients with instability

Computationally efficient analysis requires simplification of the components of the knee. A limited number of soft tissues of the knee were represented, focusing on those deemed most critical based on prior work with the model (Kim et al., 2013; Kwon et al., 2014). The properties of the cartilage, ligaments, and patellar tendon were simplified, with material properties obtained from a variety of other experimental and modeling studies noted throughout the manuscript. Further development of the representations of soft tissues may improve the agreement between the computational and experimental data. The cartilage on the patella was represented with only 103 elements, which limited the ability to accurately characterize parameters such as the maximum pressure. Reducing the size of the elements would improve the resolution of the pressure measurements, but increase the computational demands for the analysis. Approximately 20 minutes of computational time on a desktop computer was required for each analysis. Some differences noted between the computational and experimental kinematics data could be related to computational representation of the experimental coordinate systems. The in vitro study relied on digitization of anatomical landmarks to create the coordinate systems, and these landmarks were open to interpretation on the computational models.

Conclusions

The dynamic multibody modeling technique represents a new step in the development of a computational model for evaluating surgical options performed to treat patellofemoral disorders. The multibody modeling technique allows characterization of how tibial tuberosity realignment influences patellofemoral kinematics and the pressure distribution. Models can be rapidly developed to represent symptomatic knees from imaging data and easily manipulated to vary the position and orientation of anatomical structures and the properties of soft tissues. Computational models with these capabilities are needed for studies identifying optimal surgical treatment methods based on parameters related to knee pathology and pre-operative kinematics.