SPECIMEN SIZE AND POROSITY CAN INTRODUCE ERROR INTO μCT-BASED TISSUE MINERAL DENSITY MEASUREMENTS

Abstract

The accurate measurement of tissue mineral density, ρ_m, in specimens of unequal size or quantities of bone mineral using polychromatic μCT systems is important, since studies often compare samples with a range of sizes and bone densities. We assessed the influence of object size on μCT measurements of ρ_m using (1) hydroxyapatite rods (HA), (2) precision-manufactured aluminum foams (AL) simulating trabecular bone structure, and (3) bovine cortical bone cubes (BCt). Two beam-hardening correction (BHC) algorithms, determined using a 200 and 1200 mg/cm³ HA wedge phantom, were used to calculate ρ_m of the HA and BCt. The 200 mg/cm³ and an aluminum BHC algorithm were used to calculate the linear attenuation coefficients of the AL foams. Equivalent ρ_m measurements of 500, 1000, and 1500 mg HA/cm³ rods decreased (r²> 0.96, p< 0.05 for all) as HA rod diameter increased in the 200 mg/cm³ BHC data. Errors averaged 8.2% across these samples and reached as high as 29.5%. Regression analyses suggested no size effects in the 1200 mg/cm³ BHC data but differences between successive sizes still reached as high as 13%. The linear attenuation coefficients of the AL foams increased up to approximately 6% with increasing volume fractions (r²> 0.81, p< 0.05 for all) but the strength of the size-related error was also BHC dependent. Equivalent ρ_m values were inversely correlated with BCt cube size (r²> 0.92, p< 0.05). Use of the 1200 mg/cm³ BHC ameliorated the size-related artifact compared to the 200 mg/cm³ BHC but errors with this BHC were still significant and ranged between 5% and 12%. These results demonstrate that object size, structure, and BHC algorithm can influence μCT measurements of ρ_m. Measurements of ρ_m of specimens of unequal size or quantities of bone mineral must be interpreted with caution unless appropriate steps are taken to minimize these potential artifacts.

Introduction

Measurement of equivalent bone tissue mineral density (ρ_m) using polychromatic planar radiography and computed tomography are established techniques whose precision, accuracy, and potential sources of error have been well studied [e.g., ^{1, 2–6}]. Polychromatic micro-computed (μCT) tomographic analyses of bone were originally focused only on structural assessments of trabecular and cortical bone tissue [7, 8] and not measurements of ρ_m. Recently, methods for the measurement of ρ_m have been developed for polychromatic μCT and several studies have incorporated these techniques [9–22]. However, only a few published studies of the precision and accuracy of μCT-based equivalent ρ_m have been performed to date [23–26], in contrast to the numerous studies completed for clinical CT [1–6, 27–38].

The accuracy and precision of μCT-based measurements of ρ_m can be affected by factors related to the scan settings, tissue samples, and scan artifacts. Recent studies have examined the influence of factors such as the x-ray tube voltage, current intensity, and sample dimensions [24, 25, 39, 40]. Beam-hardening related artifacts such as streaking [41], dark banding [low attenuation spots between two higher density objects; ^{42, 43, 44}], cupping [26, 45], as well as ring artifacts [41, 46] can introduce errors in measured attenuation values. One topic of specific interest is the effect of sample dimensions or bone mass differences on the accurate measurement of ρ_m since (1) object thickness (size) is known to impact linear x-ray attenuation independent of ρ_m [1, 42, 44] and (2) a wide range of orthopedic and bone biology studies incorporate specimens of varying size or quantities of bone including animal models of osteoporosis (disease), bone biomechanics, bone tissue engineering, aging, and interspecies studies of bone structure and function [21, 22, 47–57]. For polychromatic computed tomography x-ray systems, the measured attenuation coefficient value of rod-like objects made of hydroxyapatite, for example, will be lower in larger rods compared to smaller ones. This results from the cupping beam-hardening artifact [42] wherein the lower energy photons of a polychromatic source are absorbed more than higher energy photons as they pass through the center of the object (full thickness). This alters the energy spectrum of the x-ray beam, causing an increase in its mean energy. A polynomial correction determined using a calibration wedge phantom of known density and increasing thicknesses can be used to mitigate or correct size-related artifact in measurements of ρ_m. It should be noted that when a polynomial beam-hardening correction is chosen and applied to a scan, an assumption about the material density of the scanned region is made (e.g., the average mineral density of the specimen is assumed to be similar to the density of the specific phantom used, for example 200 mg HA/cm³ or 1200 mg HA/cm³).

Size-dependency of μCT-based measurements of ρ_m has previously been reported [24]. Mulder and colleagues used standards of dipotassium phosphate solution (K₂HPO₄) varying in concentration (up to 800 mg/cm³) and diameter (12 mm, 20 mm, and 36 mm) to assess the accuracy of ρ_m measurements. The authors noted that μCT-determined ρ_m of similar phantom concentrations varied as the phantom size increased; accuracy errors averaged over all results (all different scan settings) reached up to 10%. Further questions and concerns remain regarding the size-related artifact in equivalent ρ_m measurements. First, while Mulder et al [24] first reported an average of 10% error or less, some of their results showed errors as high as 15% and a later report indicated that errors as high as 25% were possible [58]. If size-dependent error in ρ_m is that high, it is important to further document this error because biologically- and mechanically-relevant differences in ρ_m are reported to be on the order of 5% or less [53, 59–61]. A situation where size-related error is this large might lead to results driven by bone mass differences between groups being misinterpreted as biologically significant. In addition, expansion on Mulder et al.’s [24, 58] work is necessary because they used K₂HPO₄ phantoms that ranged greatly in absolute dimensions (12 to 36 mm) and which were scanned at different voxel dimension settings. Size-dependency of μCT measurements of ρ_m were not assessed within a single scan/voxel setting and across smaller absolute dimensions, which better approximate the dimensions of small animal bones commonly assessed in μCT studies. Furthermore, it is important to document the size effect with real bone samples and models structurally similar to trabecular bone to understand how the interaction of size and structure may affect ρ_m measurements.

To address these limitations and extend earlier work assessing the size-dependency of μCT ρ_m measurements, we conducted a study to address two research questions. First, will specimen dimensions or mass differences introduce error into μCT-measured ρ_m when scan settings are held constant, and if so, are results dependent on the structure of the specimens? Second, will the choice of beam hardening correction algorithms affect the results in a size-dependency study? Systematic analysis of μCT-based measurements of ρ_m in three different bone or bone-like models and using three different density-targeted beam hardening corrections, including a 200 and 1200 mg HA/cm³ correction and an aluminum correction as well, were used address these research questions.

Materials and Methods

Three different models were used to assess the effect of specimen size on μCT-based ρ_m measurements: (1) hydroxyapatite rods, (2) aluminum porous foams, and (3) bovine cortical bone cubes.

Hydroxyapatite Rods

Solid hydroxyapatite (HA) rods (CIRS, Virginia, USA) of increasing diameter were initially used to assess the effect of size on bone tissue density measurements. Rod diameters included 3, 7, 12, and 14 mm (Fig. 1a). The effect of size was assessed at six different densities: 0, 50, 150, 500, 1000, and 1500 mg HA/cm³. These rods contained HA crystals embedded in resin (Fig. 1a). Rods were immersed in saline and scanned using a high-resolution desktop μCT system (μCT-40, Scanco Medical AG, Switzerland) equipped with an aluminum filter 0.5 mm thick. Scan settings included 70 kV, 114 mA, 30 mm field of view, 1024 x 1024 pixel matrix, and an isotropic voxel size of 0.030 mm. Rods were scanned individually and placed in the center of the field of view. Fifty slices were acquired beginning 3 mm below the top of all rods. Previous precision assessments indicated that coefficients of variation of repeat scans and intra-phantom variability were lower than 6%. Data were filtered through two second-order polynomial beam-hardening corrections (BHC) provided by the manufacturer (Scanco Medical AG), determined using a 200 and 1200 mg HA/cm³ wedge phantom, prior to the measurement of ρ_m. Briefly, the BHCs were created by scanning sections of increasing thickness in step-wedges comprised of HA in resin at a density of 200 mg/cm³ or 1200 mg/cm³. A polynomial algorithm was then derived to correct for the non-linearity in the plot of linear attenuation and wedge thickness that is due to beam-hardening. The lower density target was originally designed for analyses including cancellous bone and the higher density BHC for analyses of teeth and other dense objects.

Figure 1.

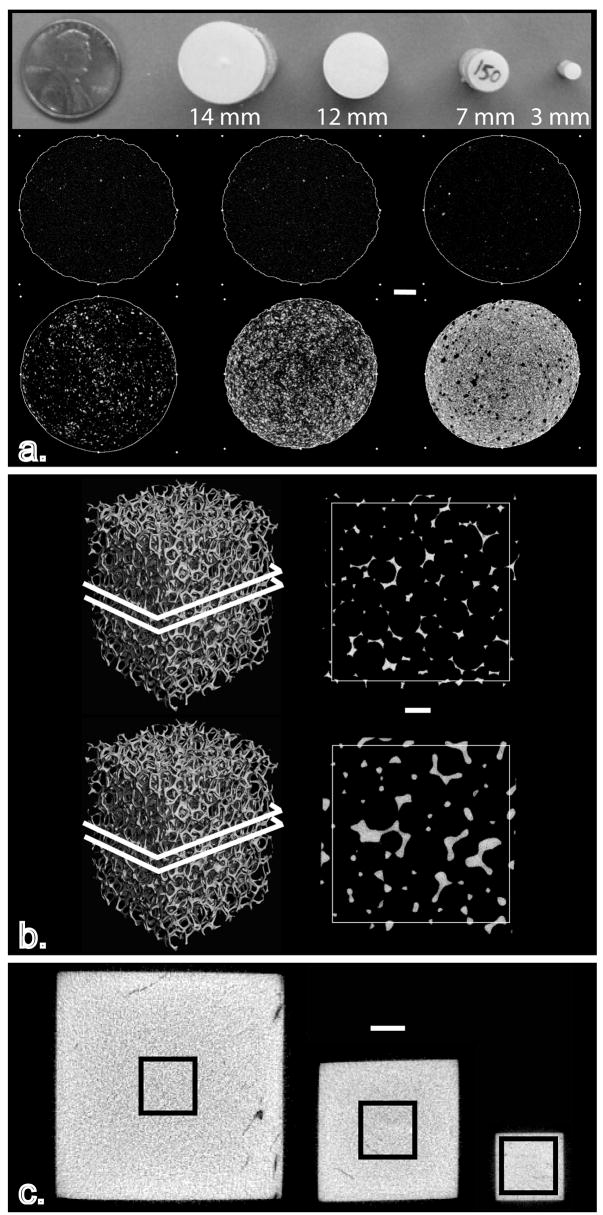
Image showing all the models used to assess the influence of size on the measurement of ρ_m using μCT: (a) hydroxyapatite rods ranging in size from 3–14 mm and varying in hydroxyapatite concentration, (b) precision-made porous aluminum foams ranging in aluminum volume fraction from approximately 5% to 12% and, (c) bovine cortical bone cubes were extracted and then alternately scanned and reduced in size twice. White scale bars = 2 mm

Circular regions of interest (ROI) were created on each of the 50 acquired image slices. ROI were placed centrally within the boundary of the rod, resulting in a ROI diameter smaller than that of the rod.

Aluminum Precision-Made Porous Foams

Nine precision-manufactured aluminum (AL) foams 6101-T6 (ERG Materials and Aerospace Corp. California, USA) were scanned immersed in saline. Three different volume fractions of aluminum (AV/TV) were included (n=3/group): 4–6%, 7–8% and 10–12%. The outer dimensions of all specimens were 15.01 mm X 15.01 mm X 20.95 mm (Fig. 1b). The density provided by the manufacturer for the AL foams was 2700 mg AL/cm³. Scan settings were 70 kV, 114 μA, 300 ms integration time, 30 mm field of view, and a 2048 x 2048 pixel matrix, resulting in approximately 0.015 mm isotropic voxels. Fifty-three slices were acquired one millimeter below the superior edge of the aluminum foam. Image data were processed with a 200 mg HA/cm³ BHC and a BHC determined using an aluminum wedge phantom (AL BHC).

Square ROI 890 x 890 pixels (13.35 x 13.35 mm) were positioned within the boundaries of the aluminum foam across all slices. After thresholding, the average linear attenuation coefficient of the solid phase was measured in the VOI after peeling away two pixels off every surface of the aluminum to avoid the influence of partial volume averaging at the boundary of the material. Since the range of average column thickness in the aluminum lattice was 0.157 – 0.391 mm, after the two pixel surface peel, at least 0.097 mm (6 pixels or 61% of the object at that site) remained of the object to measure linear attenuation coefficient of the solid phase. We recorded the linear attenuation coefficient instead of a ρ_m value since it was nonsensical to report the density of aluminum in milligrams of hydroxyapatite as would be the case with the 200 mg HA/cm³ BHC. Since this is a porous solid, the measurement of the linear attenuation coefficient required the implementation of a threshold to segment the aluminum foam from the background. The application of a threshold presents a different set of problems and assumptions that can impact measurements of structure and/or density. Two different threshold protocols were implemented on the same image data to assess the effect of object size/mass on μCT-based measurements of density. First, an adaptive, iterative algorithm (AIT) that selects a threshold based on the image grayscale histogram was used to determine the threshold for each specimen [48, 51, 54, 62–67]. Next, a single, fixed gray-scale intensity (FIXED) threshold value of 269 (or 8814 on a 16-bit signed image) was applied to all aluminum samples.

Bovine Cortical Bone Cubes

Young bovine cortical bone (BCt) cubes of decreasing dimensions were also used to assess the effect of size on μCT-based measurements of ρ_m. Cortical bone was extracted from the femoral shaft of six young bovines. A low-speed saw (Buehler Ltd., Lake Bluff, IL) was used to prepare 12 mm cubes, which were then scanned by μCT while immersed in saline. After scanning, the central 7 mm cube was extracted using the low speed saw and scanned again. In a final step, the central 3 mm cube was extracted and scanned (Fig. 1c). In all instances, the following scan parameters were used: 70 kV, 114 μA, 30 mm field of view, 1024 x 1024 pixel matrix, and an isotropic voxel size of 0.030 mm. Approximately 400, 234, and 100 slices were acquired for the 12 mm³, 7 mm³, and 3 mm³ BCt cubes, respectively.

Tissue density was measured in a centrally placed 2.75 mm cubic volume of interest (VOI) in all specimens, thus setting up a repeat measurement of the same volume across the specimens at different sizes (Fig. 1c). As with the HA rods analyses, ρ_m was measured for data processed with the 200 and 1200 mg HA/cm³ BHC.

Data Analysis

Absolute and relative differences in ρ_m between specimens of different size were calculated. All results were analyzed with linear regression to evaluate the strength of the size effect [68]. A regression with a slope significantly greater than zero indicated that ρ_m changed significantly as a function of object size or porosity. Only the HA results appeared non-linear in scatterplots of ρ_m against rod diameter and thus, results were analyzed in raw space as well as after natural log transformation [68]. In addition to regression, the following analyses were completed on the non-bone models. Paired t-tests assessed significant differences between HA results acquired with different BHC. Three-way ANOVA was used to test for significant differences in the AL porous foam samples with the AV/TV, threshold method, and BHC as independent variables. Lastly, in the bovine bone cortical cubes, two-way ANOVA, with Tukey-Kramer post-hoc comparisons was used to test for significant differences in the BCt cubes. The independent factors in this two-way ANOVA were cube size and the beam-hardening correction applied. All statistical tests were performed in SPSS v. 8.0 and the significance threshold was set to α=0.05.

Results

Hydroxyapatite Rods

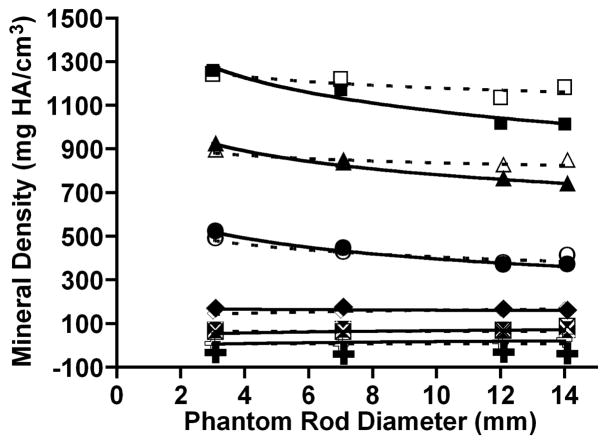
Results of the HA rod analyses are shown in Figure 2. Size had no effect on ρ_m measured with the 200 mg HA/cm³ BHC by μCT for the lowest density phantoms of 0, 50 and 150 mg HA/cm³ (Fig. 1a). But in the highest three rod densities, HA tissue density measured with the 200 mg HA/cm³ BHC decreased as HA rod diameter increased. The apparent non-linear pattern of ρ_m change was similar across the 500, 1000, and 1500 mg HA/cm³ phantoms. Measured ρ_m decreased sharply between 3 and 7 mm rods and plateaued between 12 and 14 mm rods (Fig. 2, Table 1). We found a very strong association between ρ_m and rod diameter for the 500, 1000, and 1500 mg HA/cm³ samples (all r²≥0.96, and all p< 0.05). Natural log regressions of ρ_m against rod diameter for the 500, 1000, and 1500 mg HA/cm³ samples had similar results as the linear regression analyses (all r²≥0.97, and all p< 0.05). Percent decreases in measured ρ_m between successive rod diameters for these HA samples reached as high as 17% (Table 1). The greatest effect of HA rod size on μCT measured ρ_m with the 200 mg HA/cm³ BHC was observed for the 500 mg HA/cm³ phantoms, where the measured ρ_m decreased by 15% between 3 and 7 mm diameters and 17% between 7 and 12 mm diameters.

Figure 2.

Bivariate plot of tissue mineral density (ρ_m) and HA rod phantom diameter. Solid lines represent data processed with the 200 mg HA/cm³ BHC and the dashed lines represent the data processed with the 1200 mg HA/cm³ BHC. Symbols indicate suite of HA rod densities: B, 1500 mg HA/cm³ (200-BHC), G, 1500 mg HA/cm³ (1200-BHC), H, 1000 mg HA/cm³ (200-BHC), C, 1000 mg HA/cm³ (1200-BHC), J, 500 mg HA/cm³ (200-BHC), E, 500 mg HA/cm³ (1200-BHC), F, 150 mg HA/cm³ (200-BHC), p, 150 mg HA/cm³ (1200-BHC), 1, 50 mg HA/cm³ (200-BHC), M, 50 mg HA/cm³ (1200-BHC), ♋, 0 mg HA/cm³ (200-BHC), ☺, 0 mg HA/cm³ (1200-BHC).

Table 1.

Percent changes (△) in ρ_m measurement in all models and beam hardening corrections.

Material	Sample/Procedure	Size Range	Interval △ ρm (%)		Maximum △ ρm (%)
			200-BHC	1200-BHC	200-BHC	1200-BHC
HA	500 mg HA/cm3	3–7 mm	−15.0	−13.1
		7–12 mm	−17.1	−11.5	29.5	23.1
		12–14 mm	0.3	8.9
	1000 mg HA/cm3	3–7 mm	−9.5	−5.4
		7–12 mm	−8.9	−2.5	19.9	7.7
		12–14 mm	−2.9	2.6
	1500 mg HA/cm3	3–7 mm	−7.1	−1.9
		7–12 mm	−13.0	−7.0	19.5	8.7
		12–14 mm	−0.4	4.1
			200-BHC	Al-BHC	200-BHC	Al-BHC
AL foams	Fixed Threshold	6%–8% AV/TV	1.6	2.5
		8%–12% AV/TV	1.0	1.9	2.6	4.4
	Adaptive Threshold	6%–8% AV/TV	2.5	3.4
		8%–12% AV/TV	1.3	2.2	3.8	5.6
			200-BHC	1200-BHC	200-BHC	1200-BHC
BCt cubes		3–7 mm	−14.0	−5.0
		7–12 mm	−10.0	−7.0	−22.7	−11.7

When the 1200 mg HA/cm³ BHC was used, regression analysis indicated that ρ_m was unaffected by rod diameter (Fig. 2). Paired t-tests indicated that in the 500, 1000, and 1500 mg HA/cm³ rods, ρ_m was significantly higher in the 12 mm and 14 mm diameters relative to the 200 mg HA/cm³ data (p<0.05). These increases flattened the regression relative to the 200 mg HA/cm³ BHC results. Although the 1200 mg HA/cm³ BHC regressions were not significant for all densities and this BHC mitigated the large size-related errors between successive rod diameters, large differences in ρ_m between samples were not eliminated. The average error between the 3 and 7 mm rods was 6.8% (±5.7) for the 500, 1000, and 1500 mg HA/cm³ densities. The average error between the 7 and 12 mm rods for these same densities was 7.0% (± 4.5). Lastly, the average error between the 12 to 14 mm rods for these densities for was 5.2% (± 3.3). The maximum error, observed between 3 mm and 14 mm 500 mg/cm³ rods, was approximately 23%.

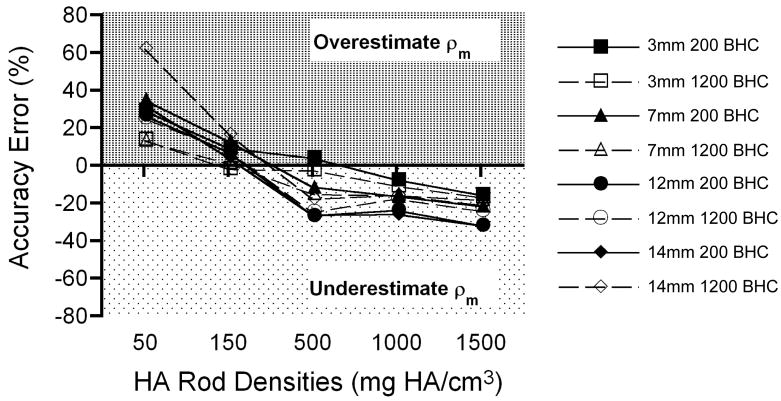
In addition to the size-related artifacts described above, analyses indicated accuracy error in ρ_m measurements of the HA rods. In all rods with HA (≥50 mg/cm³), the accuracy error exhibited two trends (Fig. 3). Bone tissue density measurements in low density (≤150 mg/cm³) phantoms were generally overestimated regardless of the BHC used. High density phantoms (≥ 500 mg/cm³) were underestimated regardless of the BHC used. Figure 3 shows these patterns of over- and underestimation as a function of phantom rod density. The largest accuracy errors were observed in the 50 mg HA/cm³ rods. The average error for this target density was 30.7% (± 3.6) with the 200 mg HA/cm³ BHC and 31.2% (± 23.1) with the 1200 mg HA/cm³ BHC. Accuracy errors were the smallest in 150 mg HA/cm³ rods, averaging 8.1% (± 3.7) with the 200 mg HA/cm³ BHC and 6.6% (± 7.1) with the 1200 mg HA/cm³ BHC. Accuracy errors progressively increased as the rod densities increased. Average errors for the 500, 1000, and 1500 mg/HA rods were 17.3% (± 11.5), 18.7% (± 8.3), and 25.6% (± 8.0), respectively, with the 200 mg HA/cm³ BHC. The errors observed with the 1200 mg HA/cm³ BHC for the same rod densities included 15.3% (± 9.4), 15.2% (± 2.9), and 20.3% (± 3.2), respectively.

Figure 3.

Graph depicting the trends in accuracy error (y-axis) as a function of the HA rod density (x-axis). Regardless of the BHC used, ρ_m was overestimated in low density HA rods and underestimated in high density HA rods.

Aluminum Precision-Made Porous Foams

For the data treated with the 200 mg HA/cm³ BHC, the increase in linear attenuation coefficient over the entire range of AV/TV values was 4% for images thresholded by the AIT algorithm versus 3% for images segmented with a fixed threshold (Fig. 4a and Table 1). Similarly, for the AL BHC data, the linear attenuation coefficient increased 5% and 4% in the AIT- and FIXED-treated data, respectively (Fig. 4b, Table 1). Three-way ANOVA indicated that there were significant differences in the linear attenuation coefficient between all groups and that the relative volume of aluminum (i.e., AV/TV), threshold protocol (AIT v. FIXED), and BHC (200 mg HA/cm³ v. AL) each had small but significant influences on the linear attenuation coefficient (AV/TV: p< 0.001, threshold: p= 0.001, BHC p< 0.001). In addition, the influence of both the threshold protocol and BHC on the linear attenuation coefficient depended on the AV/TV, as evidenced by a significant interaction term in the AVOVA (Threshold x AV/TV: p< 0.05, BHC x AV/TV: p< 0.01). The AV/TV-related increases for the 200 mg HA/cm³ BHC (Fig. 4a), as indicated by the regression slopes, did not differ between threshold methods (homogeneity of slopes: p= 0.17) but the regression lines were significantly different in elevation (elevation differences: p= 0.001). The same held true for the AL BHC results (Fig. 4b, homogeneity of slopes: p= 0.16, elevation differences: p= 0.006). However, the regression slopes were significantly different when results within a threshold method were compared. For both the FIXED and AIT threshold methods, the slopes of the regression lines were greater for images treated with the AL BHC compared to the 200 mg HA/cm³ BHC (FIXED homogeneity of slopes: p= 0.01, AIT homogeneity of slopes: p= 0.05).

Figure 4.

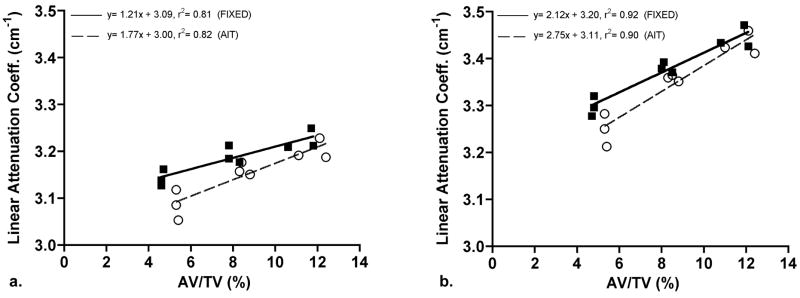
Bivariate regression of the linear attenuation coefficient and aluminum porous foam volume fraction (AV/TV) treated with (a) 200 mg HA/cm³ BHC and the (b) AL BHC. The solid line (with closed squares) represents data processed with the FIXED threshold method and the dashed line (with open circles) represents the data processed with the AIT threshold method.

Bovine Cortical Bone Cubes

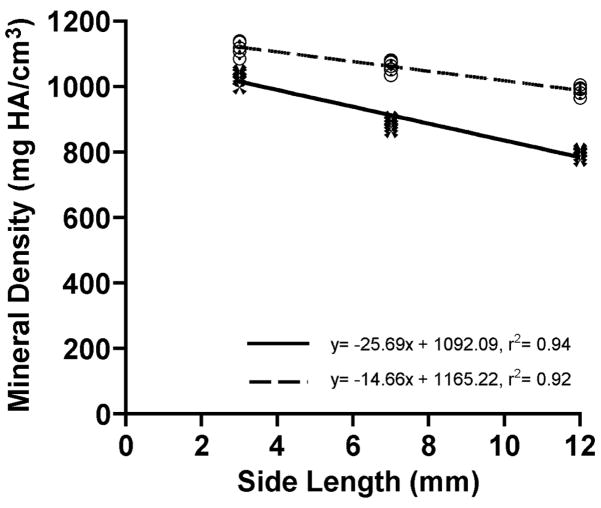
Results of the BCt analyses are summarized in Figure 5 and Table 1. Bone tissue density measured with the 200 mg HA/cm³ BHC decreased as BCt cube size increased (r²= 0.94, p< 0.05). Bone tissue mineral density decreased 14% between the 3 and 7 mm cubes and 10% between the 7 and 12 mm cubes. In contrast, ρ_m values acquired with the 1200 mg HA/cm³ BHC decreased by 5% and 7% in the same intervals, respectively. In spite of the smaller decreases in ρ_m between successive cube sizes, linear regression analysis indicated that ρ_m was still influenced by cube size after processing through the 1200 mg HA/cm³ BHC (r²= 0.92, p< 0.05). Two-way ANOVA results indicated that specimen size and BHC, as well as the interaction of these terms, had a significant influence on the ρ_m (p< 0.001 for all terms). Bovine cortical bone cube ρ_m values measured with the 1200 mg HA/cm³ BHC were significantly greater than ρ_m measurements with the 200 mg HA/cm³ BHC (p< 0.001). The percentage increases in the 1200 mg HA/cm³ BHC measurements relative to the 200 mg HA/cm³ BHC were 9%, 20%, and 24% for the 3, 7, and 12 mm cubes, respectively. Lastly, Tukey-Kramer post hoc comparisons revealed significant differences between all BCt cube sizes within a BHC. Even the 5% ρ_m decrease between the 3 and 7 mm cubes measured with the 1200 BHC, which was the smallest ρ_m decrease between the BCt groups, was significantly different (p< 0.05).

Figure 5.

Bivariate plot of tissue mineral density (ρ_m) and bovine cortical bone (BCt) cube side length. Solid line (with dark cross symbols) represents data processed with the 200 mg HA/cm³ BHC and the dashed line (with open circles) represents data processed with the 1200 mg HA/cm³ BHC.

Discussion

The primary goal of this study was to determine the influence of mass- or size-related differences on μCT-measurements of ρ_m. Tests were completed on three models that offered different attributes. The results culled from these three model systems clearly demonstrate that differences in specimen size can introduce error into μCT-based ρ_m measurements. This study also revealed that several factors, and their interactions, could influence the strength of the size-related artifact. These factors include the shape/structure of the specimen, the beam-hardening correction implemented, and the threshold method used (if cancellous bone is analyzed).

The data suggest that the directionality of the size-related artifact will depend on the shape and structure of the specimen as well as the relative amount of material in the specimen. In the solid samples (BCt or solid-like HA rods) error manifested as a decrease in ρ_m with increasing size versus an increase in the porous material. The inverse effect of specimen size on μCT-measured ρ_m is due to a cupping artifact, a well-known phenomenon that results from beam hardening [42, 44]. Figure 6 shows an example of the cupping artifact in a μCT image of a homogeneous liquid dipotassium phosphate phantom. As demonstrated by this set of images, the cupping artifact is characterized by a radial decrease in the grayscale intensity from the periphery of the object inwards. In the image (6b), there is a 17% drop in grayscale intensity between the edge of the phantom and its central region.

Figure 6.

Micro-computed tomography images (0.036 mm isotropic voxels) demonstrating the cupping artifact in a liquid dipostassium phosphate phantom. The grayscale intensity profile (a) of the original image (b) confirms the presence of the cupping artifact characterized by radial decreases in the grayscale intensity from the periphery towards the center. Although the grayscale changes appear subtle to the naked eye, the grayscale values in the center of the image are approximately 17% lower than the values along the outer limit of the phantom. Reduction of the image’s grayscale dynamic range (c) visually reinforces the pixel intensity decreases radially inward in the liquid phantom image, as characterized by the grayscale profile.

The aluminum foam models suggest, at the very least, that after some transition of relative tissue volume between a solid and a porous solid, the size-related error becomes positively correlated with material amount. Since only three models were tested and two (BCt cubes and porous foams) represent opposite ends of the porosity spectrum, it is impossible to determine where this transition might lie. It is interesting to note that the HA rods are actually quasi-solids in the sense that they are solid objects created of HA crystals and resin, where the resin not only serves to adhere the material but also represents a low density, soft-tissue analog in the phantoms. HA volume fractions were not measured in the rods but the images indicate that the 500 mg HA/cm³ rods are low in relative solid volume compared to the 1000 and 1500 mg HA/cm³ rods. The fact that the HA samples demonstrated an inverse size-effect as rod diameter increased hints at a similar size-related error direction in long bone metaphyseal regions, such as the distal femur, and recently reported preliminary data support this argument [69].

Methods used to correct beam hardening artifacts include three general approaches: (1) use of hardware filters of the photons such as aluminum, aluminum-copper, or brass, (2) pre or postprocessing using algorithmic corrections, or (3) dual-energy imaging [70]. Two of these three approaches were utilized in this study including a physical filter and algorithmic pre-processing of the data. The dual-energy approach has been used in clinical CT [e.g.,^{4, 71, 72}] but it has not been developed for μCT [though it is conceptually possible with two successive scans at high and low energies, see 73]. The system used in this study, like most clinical and research CT and μCT, uses a physical filter (aluminum) to initially reduce beam-hardening artifacts. The manufacturer-provided beam hardening corrections used were second-order polynomial corrections derived from step-wedge phantoms of the described materials; a long-established and well-described approach to beam hardening correction [74–76]. The beam-hardening corrections implemented were moderately successful in correcting the size effect on the ρ_m measurements but no single correction worked in all instances. The 200 mg HA/cm³ BHC corrected the size-related error of the HA rods up to 150 mg/cm³ but not above that and the 1200 mg HA/cm³ BHC regression results suggested that size-related artifacts were eliminated across the full range of rod diameters. However, large differences remained between successive rods (e.g., 13% between 3 and 7 mm 500 mg/cm³ rods and 7% between 7 and 12 mm 1500 mg/cm³ rods) even though the regression was not significant. In contrast to the HA analyses, neither BHC managed to eliminate the size-related artifact observed in the BCt cubes, the only actual bone samples in the study. Cube ρ_m pair-wise differences as small as 5% (between 3 and 7 mm cubes) were significant. Smaller average ρ_m differences between AL foam groups also led to a significant size-related measurement error and the strength of the error was BHC-dependent. The BHC dependence of the size-related measurement error highlights the critical importance of BHC choice prior to any analysis of ρ_m. Moreover, CT image reconstruction and algorithm-based beam hardening correction is an active area of research and a variety of studies have reported methodological variations [70, 77–89]. Given our results, it is recommended that performance of various mathematical beam-hardening corrections in the use of μCT be further investigated.

Many studies have demonstrated the threshold dependency of μCT-based structural analyses of bone [64, 90–94]. This study highlights the fact that the threshold method applied affects ρ_m measurements in cancellous bone as well. The AIT method, relative to the FIXED method, resulted in a higher calculated AV/TV (Fig. 4) and thicker columns of aluminum (trabeculae) in the porous foams (data not shown). Thicker columns (trabeculae) most likely included more boundary pixels of lower attenuation (due to partial volume averaging) that decreased the average attenuation of the AIT-treated volumes, especially low AV/TV specimens. The maximum error (Table 1) introduced by the AIT threshold method increased 27% (AL-BHC) and 46% (200-BHC) relative to the FIXED method.

Accuracy error in ρ_m measurement has previously been reported for several x-ray based modalities including μCT [4, 24, 25, 28, 39, 40, 46, 58, 69, 95]. The HA rod analyses in this study point to the presence of accuracy error in measurements of ρ_m and the influence of BHC on the sign of the accuracy error. As demonstrated in Figure 3, low density phantom ρ_m was generally overestimated and high density phantom ρ_m was overestimated. Overall, the mean accuracy error with the 200 mg HA/cm³ (20.1% ±10.4) was slightly more than that with the 1200 mg HA/cm³ (17.2% ±12.7). A similar accuracy error was recently reported with the 200 mg HA/cm³ BHC [25]. Moreover, other studies have reported accuracy error in μCT measurements of ρ_m [24, 40, 96], though it is important to note that not all μCT studies have documented accuracy error [23]. The patterns of over- and underestimation of ρ_m as a function of the specimen density were also recently noted in a preliminary study [40]. One factor contributing to this accuracy error may be the beam-hardening algorithms we implemented. Second order polynomial beam-hardening corrections are often satisfactory for soft tissue but eighth to tenth order polynomial corrections have been recommended for high density materials such as bone [75]. Another factor that may explain ρ_m accuracy error of high-density objects is extrapolation error introduced by the fact that the systems are calibrated with HA phantoms that only reach as high as 800 mg HA/cm³ [96, see 25 for a description of the calibration phantoms].

The results of this study confirm and extend published efforts by Nazarian et al. [25] and Mulder et al. [24] which show that scan settings and specimen parameters can influence μCT-based ρ_m measurements. Mulder et al. [24] first reported that specimen size could introduce artifact into μCT-based equivalent ρ_m measurements. The results presented here demonstrate that statistically significant size-related errors are still present in absolutely smaller (sized like mouse and rat long bones) and highly porous objects (e.g., aluminum foams). Data acquired in our study at other voxel dimensions (0.020 and 0.036 mm isotropic voxels) demonstrated the same specimen size-related artifacts.

This study has implications for studies of bone incorporating different designs or specimen types. First, the absolutely large maximum errors reported with the HA and BCt samples suggest that caution should be taken when interpreting ρ_m values in ontogenetic (or aging) studies and studies across adults of different species that range greatly in body mass [e.g.,^{47, 48, 54, 97, 98}]. In such studies, it will be challenging to discern biologically relevant changes in ρ_m from differences in bone mass. In addition, the use of a single BHC for all samples in ontogenetic studies may not be appropriate since the true ρ_m should differ between very young and more mature specimens. Based on the BCt cubes, ρ_m differences of 12% to 23% (maximum errors in BCt cubes) may still be the result of bone mass differences between specimens.

We also suggest that some caution be taken, at the present time, interpreting pre-clinical studies comparing metaphyseal-like bone from control and treatment groups. In such studies, while comparisons are typically relative to control groups, and thus absolute accuracy is not as important, these comparisons usually involve an experimental group with either more or less bone mass. The BCt and HA data point to the real possibility that bone mass driven differences in ρ_m will be mistaken for biologically significant changes in bone tissue mineral density. Given the average error between successive BCt cube dimensions (for 200 and 1200 mg HA/cm³ BHC), we suggest that μCT-based ρ_m differences between 6% and 12% still be approached with caution at this time.

As already noted, the direction of the size-related error was dependent on the specimen structure. This suggests that a separate set of considerations may apply to studies of trabecular bone cores. Trabecular bone volume fraction changes in experimental animal models and human osteoporosis range broadly [16, 17, 61, 99–102]. The AL foams used in this study exhibited a modest range in AV/TV and a relatively small but significant measurement error in ρ_m compared to the HA and BCt samples. Percent change in ρ_m between successive AV/TV groups reached as high as 3.4% and the maximum percent change was 5.6%. Given these results, trabecular bone core ρ_m differences between 3% and 5% should be carefully interpreted. It is important to bear this in mind since clinically relevant ρ_m changes, as measured by ash fraction or other independent methods, may be 5% or less [61, 99, 103].

Although the measurements in this study were completed across a smaller sample size range than that previously reported in Mulder et al. [24], the relative size differences of the HA and BCt samples were still large relative to typical pre-clinical studies. As a result, we were unable to document how small size-related error can be (or alternatively, how different in bone mass two groups must be to engender a significant difference in ρ_m). Future studies should compare size-related ρ_m measurement error across many specimens with smaller size and smaller size/bone mass differences between successive samples [e.g., ²⁸]. The outcomes of those studies will improve upon the initial guidelines provided here for the measurement of ρ_m with μCT. Nevertheless, the HA data in this study may provide a glimpse into the outcome of those studies. The apparent non-linearity of the curve in Figure 2 and its steepening slope between 3 and 7 mm suggests that small bone mass differences will still lead to large errors in ρ_m in this size range. Our own recent observations with liquid phantoms (K₂HPO₄) appear to corroborate this pattern.

In conclusion, this study documents the influence of specimen size/bone mass on μCT-based measurements of ρ_m and notes the presence of accuracy error as well. The sign and strength of the size-related error will be primarily dependent on the object structure and BHC choice. This study makes clear that a critical step in reducing the size-related error in ρ_m measurements is the choice of the BHC prior to initiating the analysis. If, for example, a 200 mg HA/cm³ BHC is used on bone samples whose true tissue density is above 500 mg/cm³, then significant error could be introduced to a comparison of two experimental groups that differ in the amount of bone in the samples. Our results and interpretations are potentially limited to the μCT system we used but Prevrhal et al [28] also reported size-related errors in equivalent ρ_m measurements of cortical bone with medical CT. Based on the maximum errors in our cortical bone and porous foams (when appropriate BHC is used), we currently suggest cautious interpretation of ρ_m differences up to 12% in pre-clinical studies of metaphyseal bone (or cortical bone cores) and up to 5% in studies of isolated trabecular bone cores.

The use of polychromatic μCT to quantify ρ_m is relatively new and is only now beginning to receive appropriate scrutiny. Decades of research have documented the limitations of medical CT and DXA yet these modalities have proven to be invaluable clinical and research tools. It is important that research investigating the accuracy of μCT-based measurement of ρ_m continue since this imaging tool is broadly used in pre-clinical trials that are the foundation for advancing experiments on therapeutic agents to larger pre-clinical models and eventually human trials.