Do humans make good decisions?

Abstract

Human performance on perceptual classification tasks approaches that of an ideal observer, but economic decisions are often inconsistent and intransitive, with preferences reversing according to the local context. We discuss the view that suboptimal choices may result from the efficient coding of decision-relevant information, a strategy that allows expected inputs to be processed with higher gain than unexpected inputs. Efficient coding leads to ‘robust’ decisions that depart from optimality but maximise the information transmitted by a limited-capacity system in a rapidly-changing world. We review recent work showing that when perceptual environments are variable or volatile, perceptual decisions exhibit the same suboptimal context-dependence as economic choices, and propose a general computational framework that accounts for findings across the two domains.

Good or bad decisions?

Consider a footballer deciding whether to angle a penalty shot into the left or right corner of the goal, a medical practitioner diagnosing a chest pain of mysterious origin, or a politician deliberating over whether or not to take the country to war. All of these decisions, however different in scope and seriousness, require information to be collected, evaluated, and combined before commitment is made to a course of action. To date, however, the biological and computational mechanisms by which we make decisions have been hard to pin down. One major stumbling block is that it remains unclear whether human choices are optimised to account for prior beliefs and uncertainty in the environment, or whether humans are fundamentally biased and irrational. In other words, do we make good decisions, or not?

Optimal perceptual integration

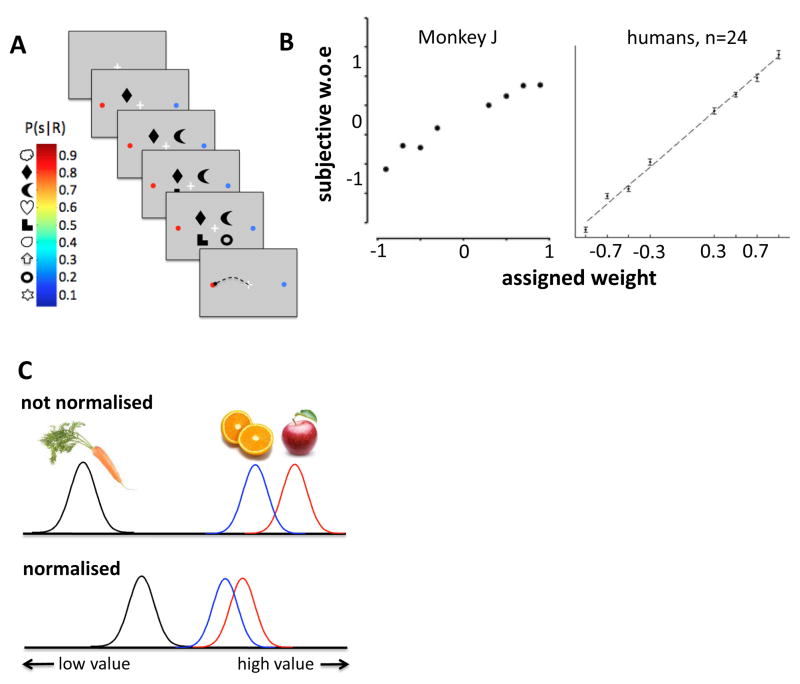
Although behavioural scientists continue to debate what might constitute a good decision (Box 1), optimal behaviour is usually limited only by the level of noise (or uncertainty) in the environment. Consider a doctor diagnosing a patient who is experiencing vice-like chest pains. Optimal binary decisions are determined by the likelihood ratio, that is, the relative probability of the evidence (chest pains) given one hypothesis (incipient cardiac arrest) or another (gastric reflux). When decision-relevant information arises from multiple sources, evidence must be combined to make the best decision. For binary choices, decisions are optimised by sequential summation of log-likelihood ratio, expressing the relative likelihood that information was drawn from one category or the other [1, 2]. An observer who views a sequence of probabilistic cues (‘samples’) before making one of two responses (e.g. the shapes in Fig. 1a) will make the best decision by considering all samples equivalently, i.e. in proportion to the evidence they convey. In other words, the “subjective weight of evidence” for each sample will depend linearly on the weight assigned by the experimenter. Well-trained monkeys and humans seem to weight information optimally in this way (Fig. 1b) [3, 4]. When some cues are more trustworthy than others, the best decisions are made by adding up information weighted by its reliability. Again, observers seem to do just this – giving less credence to features or modalities that the experimenter has corrupted with noise, for example when combining information from across different senses [5–7]. Thus, the footballer alluded to in the opening sentence will most likely strike the ball with great precision towards a spot which is just out of the goalkeeper’s reach – factoring in uncertainty due to the weather conditions and his or her own bodily fatigue.

Box 1. What makes a good decision?

Behavioural scientists have often disagreed about what constitutes a good decision. For example, in the absence of overt financial incentives, experimental psychologists usually define good decisions as those that elicit “correct” feedback, given the predetermined structure of their task. In experiments where stimuli are noisy or outcomes are uncertain, a theoretical upper limit can be placed on performance, by estimating how an “ideal” agent would perform – one who is most likely to be right, given the levels of uncertainty in the stimulus. However, it is not always clear whether humans have the same motives, or are imbued with the same preconceptions, as an ideal observer [51]. For example, humans often make erroneous assumptions about the nature of the task they are performing. For example, in a decision-making task, if participants believe that the values of prospects are changeable when really they are stationary, then they will learn “superstitiously” from recent outcomes [52]. Moreover, although many human volunteers are strongly motivated to maximise feedback, others might instead try to minimize the time spent performing a boring or disagreeable task.

Behavioural economists argue that good decisions maximise expected utility over the short or long term [53]. However, behavioural ecologists emphasise that organisms need to maximise their fitness, in order to survive and reproduce [54]. Often these definitions align, but sometimes they diverge. For example, temporal discount functions that overweight short-term reward might deter an animal from an investment strategy that maximises long-term income. However, if current resources are insufficient to survive over the near-term, steep temporal discounting may be the best insurance against an untimely end [55]. The subjective nature of utility has led theorists to define a series of axioms that are necessary (but not sufficient) for optimal decisions [56]. These rational axioms guarantee that an agent’s preferences – as revealed by overt choices – are internally coherent and consistent with a stable, context-independent utility function [57]. Because human behaviour is at systematic odds with rational axioms [14, 44], psychologists used non-normative frameworks to describe human behaviour [49, 58]. These approaches, despite their descriptive adequacy, have failed to explain why choice processes are irrational. By contrast, the efficient coding hypothesis and analogous frameworks, which consider the computational costs the brain faces while making decisions, promise to offer a normatively motivated account of irrationalities in human choice.

Figure 1. Optimal perceptual classification and irrational economic decisions.

A. Schematic depiction of the ‘weather prediction’ task used in [3]. On each trial, 4 shapes appeared in succession. Each shape was associated with a given probability of reward (red/blue colourbar), conditioned on an eye movement to one of two targets (red and blue dots). In [4], a similar task was used but each shape was replaced on the screen by its successor. B. Subjective weight of evidence associated with each shape for a monkey ([3]) and the average of 24 humans ([4]). In both cases, dots fall on a straight line, suggesting that each sample is weighed in proportion to its objective probability. C. In [14], participants choose between a preferred snack (e.g. apple) and a dispreferred snack (e.g., orange); their (uncertain) value is represented by red and blue Gaussian distributions. Because neural value signals are normalised by the total outcome associated with all stimuli, the introduction of a yet more inferior option (e.g., carrot; black Gaussian) brings the value estimates of the preferred and dispreferred options closer together, increasing the probability that the dispreferred option (orange) will be chosen.

Irrational economic decisions

By contrast, humans choosing among economic alternatives are often unduly swayed by irrelevant contextual factors, leading to inconsistent or intransitive decisions which fail to maximise potential reward [8]. For example, consumers will bid higher for a house whose initial price tag has been deliberately inflated, as if their valuation is “anchored” by the range of possible market prices [9]. Similarly, human participants undervalue risky prospects when most offers consisted of low-value gambles but overvalued the same prospects when the majority of offers consisted of high-value gambles [10]. Anchoring by an irrelevant, low-value third alternative can also disrupt choices between two higher-valued prospects, leading to systematic reversals of preference [11]. For example, the probability that a hungry participant will choose a preferred snack item A over another item B (rather than vice versa) is often reduced in the presence of a yet more inferior option C, in particular when C resembles B in value [12] (Fig. 1c).

Irrational economic behaviour can arise if the brain computes and represents stimulus value relative to the context provided by other previously [13] or currently available options [14, 15]. Changing the context of a decision by adding other alternatives (even if they are rapidly withdrawn, or so inferior as to be irrelevant) can alter the way that choice-relevant options A and B are valued, biasing the choice between them. For example, the pattern of data described in Fig. 1c can be explained by a simple computational model in which the value of each alternative is normalised by the total value of all those available (Fig. 1c). As the value of C grows, distributions representing noisy value estimates of A and B exhibit more overlap, increasing the probability that the inferior option B is mistakenly chosen over A (although in other circumstances, increasing the value of C may lead B to be selected less often, and rival models have been proposed to account for this alternative finding [16, 17]). Indeed, single-cell recordings from macaques making choices among juice or food rewards suggest that neural encoding of value in the parietal and orbitofrontal cortices is scaled by the context provided by the range of possible options [18]. When one measures the scaling factor (or ‘gain’) that quantifies how subjective value (e.g. drops of juice) is mapped onto neuronal activity (e.g. spike rates) in these brain regions, it is found to vary according to the range of values on offer. This ensures that average firing rates remain in a roughly constant range across blocks or even trials with variable offers [19–21].

Efficient coding

Why might the brain have evolved to compute value on a relative, rather than an absolute scale? One compelling answer to this question, first put forward by Horace Barlow [22] and known as the “efficient coding hypothesis”, appeals to the limited capacity of neuronal information processing systems and their consequent need for efficiency [23, 24]. Efficient systems are those that minimise the level of redundancy in a neural code, for example by transmitting a signal with a minimal number of spikes. Efficiency of neural coding is maximised when sensitivity is greatest to those sensory inputs or features that are most diagnostic for the decision at hand. In some situations, the most diagnostic features will be those that are most likely to occur, given the statistics of the natural environment or the local context. For example, an efficient system will become most sensitive to high-valued stimuli when they are abundant, and to low-valued stimuli during times of scarcity [12, 18]. Formally, this strategy maximises the information that a neuronal system can encode and transmit, thereby optimising processing demands to match the available resources [25].

By contrast, encoding absolute input values is an inefficient strategy. For example, if a hypothetical neuron were to linearly signal the value of goods with widely disparate economic worth (for example, a cappuccino and a holiday in Hawaii), then only a very limited portion of its dynamic firing range could be devoted to those alternatives any given value. This would make it very hard for the neuron to signal consistently that the cappuccino was preferred over (say) a cup of tea. Normalisation of neural signals (for example, via lateral inhibition) is one operation that permits efficient information coding in sensory systems [26]. For example the sensitivity of cells in the early visual system is adjusted over the diurnal cycle, ensuring that neurons with limited dynamic range can continue to encode information even as the strength of ambient illumination varies over many orders of magnitude [27]. When input signals are transformed in this way, choices can vary as a function of context provided by recent stimulation, potentially leading to preference reversals and other deviations from optimal behaviour.

The efficient coding hypothesis thus implies that economic choices are irrational because they are overly susceptible to variation in the local context. By the same token, it could be that perceptual classification judgments tend towards optimal because psychophysical experiments usually involve repeated choices made in a single, unvarying context. This prompts a prediction: that perceptual judgments made in variable or volatile environments will deviate from optimal in ways that resemble economic decision-making.

Robust perceptual decision-making

In the task described in Fig. 2a, humans are asked to categorise the average colour of 8 elements (samples) as ‘red’ vs. ‘blue’ (or the average shape as ‘square’ vs. ‘circle’). This paradigm is similar to the ‘weather prediction’ task shown in Fig. 1a, except that the samples arrive all at once, and their predictive value is conveyed by a continuously-varying visual feature (e.g. degree of redness vs. blueness; we refer to this as feature value). An ideal observer should thus add up equally weighted feature values (which are proportional to the log-likelihood ratios) and compare them to an internal category boundary (in this case, red versus blue or square versus circle), thereby using the same policy as the experimenter to decide which response is correct.

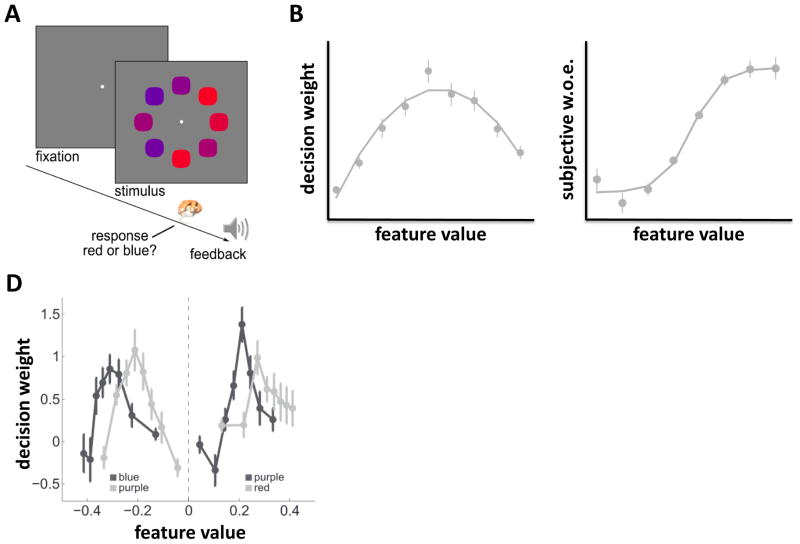
Figure 2. Robust averaging of variable feature information.

A. In [28], participants judged the average colour (shown) or shape of an array of 8 items, receiving feedback after each response. B. Decision weights (calculated via logistic regression) associated with item ranks (e.g. sorted by most red to most blue) have an inverted-u profile, indicating that outlying elements (furthest from category boundary) carried less influence in decisions. C. Decision weights associated with each portion of feature space, multiplied by that feature value, reveal the subjective w.o.e. Note that the shape is different to that in Fig. 1b. D. Decision weights (similar to B) for two experiments in which participants separately judged whether the array was more blue versus more purple (left curves; negative feature values) or more red vs. more purple (right curves; positive feature values). Features that are outlying with respect to the relevant category boundary are downweighted. Light and dark gray lines show weights for items drawn for the two respective categories.

However, this is not what humans do [28, 29]. The relative weight associated with each feature value can be calculated by using a logistic regression model to predict choices on the basis of the feature values present in each array. The resulting weights form an inverted u-shape over the space of possible features (Fig. 2b), indicating that humans give more credence to inlying samples – those that lie close to the category boundary (e.g., purple) – than to outlying samples (e.g. extreme red or blue). Another way of visualising this effect is by plotting these weights multiplied by their corresponding feature values, thereby revealing the psychophysical “transfer” function that transduces inputs into response probabilities. For an ideal observer, this function would be linear. Empirically, however, it is sigmoidal (Fig. 2c). One way of understanding this behaviour is that when feature information is variable or heterogeneous, humans integrate information in a ‘robust’ fashion, discounting outlying evidence, much as a statistician might wish to eliminate aberrant data points from an analysis. Interestingly, the effect remains after extensive training with fully informative feedback, and equivalent effects are obtained when observers average other features over multiple elements, such as shape [28, 29].

Efficient perceptual classification

From the viewpoint of the researcher, this robust averaging behaviour is suboptimal. However, because the distribution of features viewed over the course of the experiment in Gaussian, inlying features occur more frequently than outlying features. Thus, humans are exhibiting greatest sensitivity to those visual features that are most likely to occur – an efficient coding strategy. The sigmoidal transfer function ensures that for inlying features, a small change in feature information leads to a large change in the probability of one response over another. Interestingly, this notion that inputs are transformed in this way suggests an explanation for classical ‘magnet’ effects that characterise categorical perception, whereby observers are more sensitive to information that lies close to a category boundary [30], and for natural biases in perception, such as heightened sensitivity to contours falling close to the cardinal axes of orientation [31]. Note that these effects arise because information is sampled or encoded in a biased fashion; it may still be read out via Bayesian prinicples [32].

Efficient coding is an appealing explanation for the down-weighting of outliers during perceptual averaging, but an alternative culprit could be nonlinearities in feature space, such as hardwired boundaries in human perception of red and blue hues. One way to rule out this possibility is to systematically vary the range of features over which judgments are made, so that previously inlying elements (e.g. purple during blue-red discrimination) becoming outlying elements (e.g. during blue-purple or red-purple discrimination). Under this manipulation, those features that fall far from the category boundary are down-weighted, irrespective of their physical properties (Fig. 2d). In other words, feature values are evaluated differently according to the range of information available, as predicted by the efficient coding hypothesis. Computationally, this finding can be explained if the sigmoidal “transfer” function linking inputs to outputs migrates across feature space in such a way that its inflection point remains aligned with the modal feature in the visual environment [28].

In the neuroeconomics literature, a key question pertains to the timescale over which value signals are normalised [18, 33]. Perceptual classification has typically been measured in stationary environments, but when category statistics change rapidly over time, participants depart from optimality and use instead a memory-based heuristic that updates category estimates to their last known value, suggesting that rapid updating is at play [34]. But can we measure the timescale over which adaptive gain control occurs during perceptual decision-making?

Rapidly adapting gain control during decision-making

The results of one recent study imply that the gain of processing of decision information can adapt very rapidly even within – the timeframe of a single trial [35]. Participants viewed a stream of 8 tilted gratings occurring at 4Hz, and were asked to judge whether, on average, the orientations fell closer to the cardinal (0 or 90°) or diagonal (45 or −45°) axes (Fig. 3a). Firstly, this allowed the authors to estimate the impact of each sample position on choice – for example, to ask whether early samples (primacy bias) or late samples (recency bias) were weighted most heavily [36]. Secondly, the authors calculated how the impact of each sample varied according to whether it was consistent or inconsistent with the average decision information viewed thus far. According to the efficient coding hypothesis, neural coding should adapt so that expected inputs – i.e. those consistent with the stream average – should carry more impact than inconsistent information.

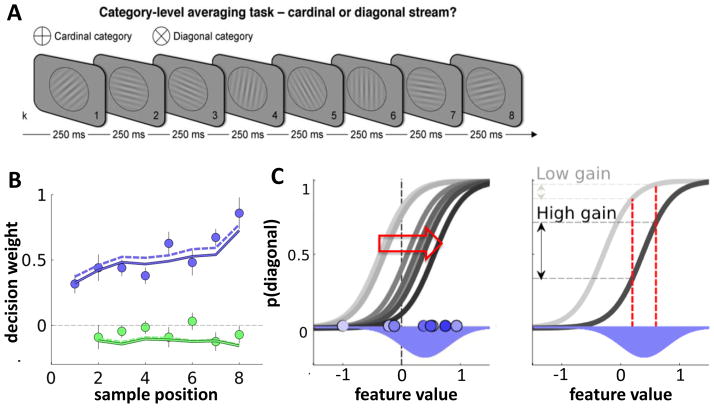
Figure 3. Adaptive gain control during sequential integration.

A. Cardinal-diagonal categorisation task. Participants viewed a sequence of 8 tilted gratings occurring at 4Hz. Each sample was associated with a decision update DU reflecting whether it was tilted at the cardinal axes (DU = −1) or diagonal axes (DU = +1) or in between (−1 < DU < 1). Participants received positive feedback for correctly classifying the sum of DU as >0 or <0, i.e. for indicating whether the orientations were on average closer to the cardinal or diagonal axes. In this task, DU is orthogonal to the perceptual input [50]. B. Blue dots show decision weights (regression coefficients) for each of the 8 samples, as a function of sequence position. Participants showed a recency bias. Green dots: modulation of decision weights for each sample by disparity to previous sample. Dots are negative, indicating that unexpected samples were downweighted. Lines show fits of the adaptive gain model using two separate fitting procedures. C. Illustration of the adaptive gain model. Left panel: grey curves show the theoretical transfer function from feature values to the probability of responding ‘diagonal’. As successive samples are presented (light->dark blue dots) drawn from a category distribution (blue Gaussian), the function mapping inputs onto outputs adjusts towards the mode of the generative distribution. Right panel: two possible positions of the transfer function. Initially, the transfer function is misaligned with the generative distribution, so that p(diagonal) only changes slightly with two nearby samples (light grey). Later, when the transfer function is aligned with the generative distribution, a small change in feature value has a large impact on response. The gradual alignment of the transfer function with the true distribution also explains the recency bias displayed by humans (B).

Human observers exhibited a recency bias, but they also displayed a tendency to weight consistent samples more heavily than inconsistent samples (consistency bias) when choosing their response (Fig. 3b) Perceptual and decision information are orthogonal in this task, so the latter is not merely a perceptual priming effect. Both the recency and the consistency bias were explained by a computational model in which the sigmoidal transfer function was gradually adjusted towards the modal feature information occurring on that trial – i.e. towards ‘cardinal’ when samples were closer on average to cardinal, and towards ‘diagonal’ when evidence favoured diagonal. This had the effect of bringing the linear portion of the transfer function – where sensitivity is greatest – in line with the mode of distribution of samples experienced thus far (Fig. 3c). In other words, observers processed information that was most likely to occur (conditioned on the sequence of samples in that trial) with higher gain, in keeping with the efficient coding hypothesis. Interestingly, this model also predicts that when evidence arrives in sequence, the consistency bias replaces an overall downweighting of outliers. This may help explain why previous studies have shown roughly linear decision weights (Fig. 1b). A bias towards consistency in perceptual classification was also demonstrated in a recent study that asked participants to make successive judgments about visual angle [37]. This work builds upon earlier demonstrations that the second of two successive judgments about a visual feature is biased by the first, in a fashion that indicates the most sensitive encoding of the most informative feature information [38–40].

The heightened gain for consistent (relative to inconsistent) information was also reflected in measures of physiological and neural actvity. Pupil diameter, thought to be a crude proxy for the gain of cortical processing [41], covaried with the available decision information more sharply when samples were consistent than when they were inconsistent. Similar effects were observed for EEG activity recorded from electrodes situated over central and parietal zones, and BOLD signals localised to the parietal cortex, dorsomedial prefrontal cortex, and anterior insula [35]. A population coding model in which tuning sharpens to expected features provides a more detailed framework for understanding these effects (see Box 2).

Box 2. Expectation as sharpening.

The efficient coding hypothesis states that we become most sensitive to those features that are most likely to occur in the environment. One implication of this view is that the receptive fields of neurons tuned to expected inputs become sharper – better enabling observers to detect or discriminate these features. The data described in Fig. 3b can also be accounted for with a population coding model in which incoming feature information excites sensory neurons with bell-shaped tuning curves (Fig. I). These in turn drive “integration” neurons whose activity level depends on their accumulated inputs [59]. The state of the integration neurons drives the level of local inhibition, leading to a sharpening of tuning curves at sensory neurons coding for expected features (see below). For a more detailed explanation, see [34].

Figure I.

Top panel. Consider a task in which continuously-valued feature information (e.g. tilt: cardinal vs. diagonal; x-axis) is drawn successively from one of two categories (grey Gaussian distributions). The most likely feature of the forthcoming sample (blue arrow) can be inferred from the history of samples drawn thus far (blue dots). An efficient system will maximise sensitivity to expected information. Lower panel. Population coding model for expectation as sharpening. The model consists of input neurons (blue circles) and integration neurons (green circles). The input neurons are inhibited by local interneurons (grey circles). Sensory information (e.g. the tilt of a grating) is fed forward from input neurons to integration neurons, where it is linearly accumulated. The integration neurons excite the interneurons in proportion to the current level of integrated evidence. This ensures that the tuning curves of neurons for expected features become sharper.

An established theory – known as the feature-similarity gain hypothesis – states that the gain of neuronal responses depends on the degree of similarity between an observed feature and an internal standard to which it is being compared [60]. However, in psychophysical detection tasks, base rates of occurrence of a target feature (e.g. a vertical grating) are typically found to bias responses in an additive fashion rather than increasing sensitivity measured by d’ [61]. Nevertheless, recent evidence using psychophysical reverse correlation has revealed that observers show heightened sensitivity to expected features [62]. Moreover, a recent fMRI study has found that although expected gratings elicit globally reduced BOLD signals, their angle of orientation can be more accurately decoded from multivoxel patterns in visual cortex [63].

Priming by variance

Another recent study provides evidence that perceptual decisions are influenced by the context furnished by local environmental statistics [42]. Observers judged the average feature (colour or shape) in a ring of coloured shapes similar to that shown in figure 2a, with feature values (e.g., red versus blue hues) drawn from Gaussian distributions with differing dispersion. When each target array was immediately preceded by a task-irrelevant “prime” array whose feature variance was also high or low, performance depended not only on the consistency between the mean feature information (e.g., were the prime and target on average both red?) but also on their variability (e.g., were the prime and target arrays both highly variable?), with faster response times for prime-target pairs with consistent levels of feature variability. This result held even if the prime and target array were drawn from different categories (e.g., red versus blue). One explanation for this curious finding is that the space over which inferences about the target array are made is shaped by the range of feature information available in the prime array – with the slope of the sigmoidal transfer function adapting according to the dispersion of feature information in the prime array. A similar mechanism has been reported in the visual system of the fly during adaptation to dynamic motion variability [43].

Value psychophysics

Taken together, these studies imply that unexpected or outlying inputs are downweighted when observers judge feature information with respect to a category boundary. However, seemingly contradictory results have been obtained from a different averaging experiment, in which observers view two streams of numbers and are asked to pick the stream with the higher tally [44]. When the numbers were drawn from two streams with differing variance, observers exhibited a strong bias to choose the more variable of the two streams – as if they were giving more credence to outlying samples (e.g. the higher number in the pair) during integration. So why do observers seem to overweight inlying relative to outlying elements during categorisation, but do the reverse when comparing two streams of information?

Recall that an efficient neural coding scheme maximises sensitivity to those features that are most informative for the decision. When the task is to compare two currently-available sources of information, it is the outlying, rather than the inlying samples that are most diagnostic for choice [45], just as during fine discriminations, where the “off-channel” features (e.g. exaggerated versions of the features in each category) carry most information [40, 46]. This is particularly the case in the number comparison experiment, where the absolute average of features fluctuates unpredictably from trial to trial and choices must rely on local comparisons between the two streams. Thus, when comparing two streams, the one with the larger mean payoff will more likely have a larger number on a given pair, and the latter is highly diagnostic of the former. Interestingly, in the value comparison task, the direction of outlier overweighting was dependent on the instructions – when observers were asked which stream they preferred, high values were overweighted; when they were asked to choose which stream they dispreferred, low values were more impactful – even though these two framings are logically equivalent. This finding is reminiscent of classic violations of description invariance in economic judgments tasks, and is consistent with a qualitative theory known as reason-based decision-making [47], in which advantages loom larger when participants are asked which of two prospects they would like to accept, whereas disadvantages drive decisions that are framed as a rejection. Thus, faced with the choice between an extravagant holiday (say, to Bali) and a more modest trip (to Bournemouth), people choose to accept Bali (because it is exciting) but will reject Bali (because it is expensive) in alternate framings of the choice [48].

Robust decisions and heuristics

Discarding outliers in categorisation tasks and overweighting winners in comparison tasks are thus both examples of ‘robust’ decision-making – involving coding strategies that focus processing resources on the most informative features. Interestingly, extreme versions of these policies both reduce to ‘counting’ strategies – for example, an observer might tally up the number of ‘winners’ in the stream of paired numbers, or count the number of samples that favour red vs. blue. Strategies such as counting that involve reliance on propositional rules or approximations, rather than statistical inference, are often proposed as alternatives to optimal behaviour [49]. As such, efficient coding provides a space of decision policies that lie on a continuum between heuristic choices and full statistical optimality.

Concluding Remarks

In the end, is the quality of human decision-making good, bad, or indifferent? There is no doubt that in some situations, humans deviate strongly from statistical optimality in their judgments, and exhibit inconsistent or irrational preferences. However, we argue that human choices can be understood if information is encoded efficiently, with maximal sensitivity to decision-relevant evidence that is likely to occur. Classic economic biases, including framing and anchoring effects, as well as the range-dependence of neural value encoding – are explained by a model in which the gain of neural processing adapts to the local environmental context. When sensory input is rendered variable, volatile, or otherwise heterogenous, perceptual classification judgments come to exhibit a similar sub-optimal context-dependence, consistent with the notion that efficient coding of information is a general-purpose constraint on human decision-making. Conversely, optimal behaviour may emerge when repeated decisions are made in stationary environments, such as when psychophysical observers repeatedly attempt to detect a visual stimulus embedded in noise. In terms of the computational framework outlined above, during these judgments the transfer function becomes aligned so that all features fall in the linear portion of the sigmoid, where inputs are transduced without loss and decisions are optimal. Efficient coding is likely to have evolved as the best strategy in a rapidly-changing, unpredictable world in which optimal inference over all possible eventualities is computationally intractable.

Highlights.

• Perceptual and economic decisions approach optimality when the environment is stable

• Humans making decisions about variable visual information use suboptimal strategies

• Visual feature information may be represented efficiently during categorization

• Efficient coding may explain departures from optimality in variable environments