Viral ssRNAs Are Indeed Compact

DNA is the genetic material of all living things, except for viruses, most of which have genomes that are RNA—not DNA. Further, the majority of viral RNA genomes are single-stranded (ss) rather than duplex chains. The simplest of these ssRNA viruses, whether infecting bacteria, plants, or animals, involve a single copy of their genome, protected (packaged) by a single-molecule-thick spherical shell (capsid) of protein, which is typically smaller than 25 nm in radius. The small size is advantageous for minimizing the amount of viral protein needed for each viral particle (virion) and for maximizing the number of these infectious units that can be made by each host cell. Finally, and perhaps most remarkably, many ssRNA viruses can be spontaneously self-assembled by simply mixing their genome and capsid protein. These facts suggest that a single-stranded RNA viral genome should be as compact a three-dimensional object as possible.

The double-stranded DNA genomes of many viruses, by contrast, are packaged into preformed capsids by extremely powerful motor proteins (1), resulting in essentially close-packed densities of nucleotides (nts). More explicitly, the DNA is, on average, organized with local hexagonal symmetry with an interaxial distance as small as 2.5 nm between neighboring strands, well into the repulsive regime of DNA-DNA interaction (2,3). For the ∼50,000 basepair genome of bacteriophage λ, for instance, whose inner capsid radius is ∼27 nm, this amounts to an average volume per nucleotide of ν ≈ 0.8 nm³.

On the other hand, no motor needs to be involved in the packaging of a single-stranded RNA genome into its capsid: the virus assembly is a cooperative process involving both the RNA genome and the capsid proteins (albeit with the size of the capsid being dominated by the preferred curvature of its constituent proteins). And yet, even without the help of a motor protein, the average density of RNA nucleotides inside the capsid is as much as one-half that of DNA nucleotides in phage capsids. In the case of (the tripartite) cowpea chlorotic mottle virus (CCMV), for example, ∼3000 nucleotides are packaged in each of three identical capsids whose inner radius is 10.5 nm, implying ν ≈ 1.6 nm³ for the volume per nucleotide in the capsid. How does this high density of nucleotides arise spontaneously?

Note that ssRNA genomes need to be thousands of nucleotides long because they code for several genes. Their contour lengths, L (∼0.5 nm per nucleotide), are therefore ∼1000 nm. Neglecting for a moment the secondary structure that results from the large extent of intramolecular basepairing (i.e., self-complementarity), we can treat the genome as an ideal linear polymer—a string of nucleotides—with a persistence length (ξ) equal to that of ssRNA, i.e., a few nanometers (4). Then its three-dimensional size, e.g., radius of gyration, can be estimated as

$$R_g\simeq {\left(L\xi \right)}^{1/2}\approx {\left[\left(1000\text{nm}\right)\left(3\text{nm}\right)\right]}^{1/2}\approx 55\text{nm},$$

which is several times larger than the internal radius of the viral capsid.

What brings the RNA down-to-size is that its secondary structure, which we have temporarily neglected, gives rise to a high degree of effective branching. This is appreciated most directly through the mapping of RNA secondary structures onto tree-type graphs by associating each single-stranded loop with a vertex and each double-stranded portion (RNA duplex) with a line connecting each pair of neighboring vertices (5). For viral-length RNAs, a large number of branch points is always present—i.e., vertices from which three or more duplexes emanate. It is this branching that compactifies ssRNA, allowing ssRNA viral genomes to be coassembled into still smaller volumes with their capsid protein.

Due to its confinement inside the capsid’s interior and its electrostatic interactions with the inner capsid walls, the secondary and tertiary structures of the genomic RNA in the capsid will in general differ from those of the free RNA in solution. It is nevertheless reasonable to assume that sizeable energetic and entropic penalties would be involved in packaging the genome if its linear dimensions were significantly larger than the capsid’s diameter. Indeed, recent cryoelectron microscopy studies, complemented by small-angle x-ray scattering (radius of gyration) measurements (6), demonstrate that the naked viral RNA in solution is only 25% larger than the virion, and that naked viral RNAs are smaller than nonviral sequences of the same length. Similar results (7) are obtained from diffusion coefficient (hydrodynamic radius) measurements by fluorescence correlation spectroscopy.

Several years earlier, Yoffe et al. (8) had carried out a comprehensive theoretical study revealing that viral RNAs are indeed smaller than random RNA sequences of identical length and base composition. The metric introduced in these analyses is the average maximum ladder distance, 〈MLD〉. The ladder distance between any two nucleotides along the RNA backbone denotes the number of basepairs (i.e., ladder rungs) between them (9), and the MLD is the largest of these, i.e., the number of basepairs crossed along the trajectory between the two most distant hairpin loops. The 〈MLD〉 is the Boltzmann average over the energetically low-lying secondary structures. An example demonstrating the difference between the minimum free energy secondary structures and the MLDs of a viral and a random sequence of nucleotides is shown in Fig. 1. The viral RNA is the 3200-nt molecule of the brome mosaic virus (BMV) genome, and the random sequence is of the same length, with equal numbers of the four nucleotides. The MLD of the viral RNA is 207 whereas that of the random sequence is 354.

Figure 1.

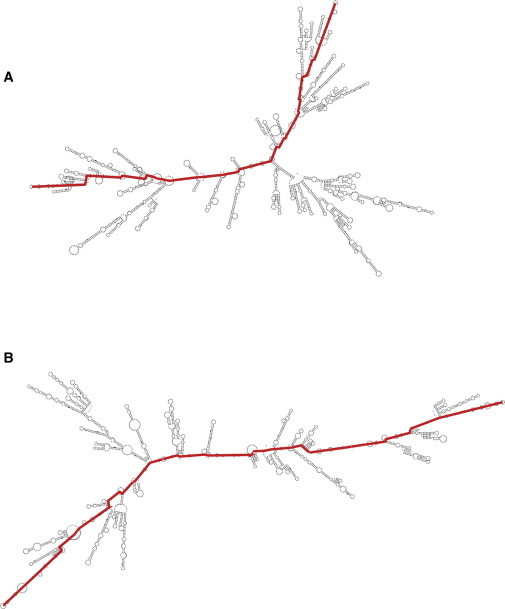
Minimum free energy secondary structures of (A) the 3200-nt RNA molecule of the brome mosaic virus (BMV); and (B) a random 3200-nt RNA sequence with equal proportions of the four bases. The MLD paths of the two structures (colored red) are 207 and 354, respectively.

Yoffe et al. (8) suggested that the relative sizes of different long—and hence highly-branched—RNA molecules could be estimated by describing them as ideal linear polymers whose effective contour lengths are given by their average MLDs. It follows that 〈MLD〉^1/2 can be regarded as a measure of the radius of gyration of the branched RNA molecule, i.e., R_g ≃ 〈MLD〉^1/2 (8). Decisive support for this conjecture is obtained by mapping the secondary structure onto a tree graph and (again, assuming ideal behavior) calculating its R_g value using Kramer’s exact formula (10). For random sequences comprising N ≃ 10²–10⁴ nucleotides, both methods yield the same scaling relation between the radius of gyration and the overall RNA length, R_g ∼ N^1/3, or equivalently, 〈MLD〉 ∼ N^2/3. (Note that randomly-branched ideal polymers are more compact than ideal RNAs, obeying R_g ∼ N^1/4 scaling (11), and recall that both calculations ignore excluded volume interactions.) Further, the 〈MLD〉 values (equivalently the R_g values) of all the icosahedral—as distinguished from rodlike—viruses analyzed are significantly smaller than those of random sequences of equal length and base composition.

In an elegant article appearing in this issue of the Biophysical Journal, Tubiana et al. (12) have significantly advanced the notion that viral RNA genomes have evolved to be exceptionally compact. The authors establish a firmer biological basis for this idea by comparing the MLDs of many viral RNA genomes to the MLDs of nucleotide sequences resulting from synonymous mutations of the wild-type sequences. Their analysis reveals very convincingly that while preserving the genetic information encoded by the wild-type genomes, successive synonymous mutations—whose sequence space is, by definition, far smaller than that of random permutations—quickly (already after just ∼5% of the mutation vocabulary) lead to larger 〈MLD〉 values, essentially identical to those of random sequences of equal length and nucleotide composition.

While it is reasonable to assume that the exceptional compactness of the viral RNA in solution facilitates its spontaneous coassembly with the capsid proteins, experimental verification of this hypothesis is still lacking, and thus called for. Rather surprising, and so far unclear, are the results of recent in vitro measurements (13) of the relative packaging efficiencies of equal-length RNAs by CCMV capsid proteins, showing that CCMV RNA1 is outcompeted by the RNA1 of a closely-related bromovirus, BMV. What is there about the effective size and nature of branching in one RNA that makes it a better competitor for one capsid protein than another?

Arguably, in comparison to nonviral sequences, the compactness of viral RNAs is enhanced by the higher degree of branching in their Boltzmann ensemble of secondary structures, and specifically the presence of high-order vertices around the center of the structure. Indeed, a recent study (14) indicates that the key difference in the distributions of orders of vertices associated with the secondary structure ensembles of viral and nonviral sequences of equal length is the rare, but significant, presence of higher-order (≥4) multiloops in the viral case. Are there life-cycle consequences of viral RNA compactness other than its role in efficient packaging by capsid protein? In addition to puzzling biological questions of this kind there are also fundamental questions of physical and mathematical interest. For instance, how does the branching pattern of random RNA sequences differ from that of (ideal) randomly-branched polymers, e.g., what is behind their R_g ∼ N^1/3 (versus R_g ∼ N^1/4) scaling when treated as (ideal) tree graphs (10), or as follows from their MLD (8)?