Abstract
Fibrin is a biopolymer that gives thrombi the mechanical strength to withstand the forces imparted on them by blood flow. Importantly, fibrin is highly extensible, but strain hardens at low deformation rates. The density of fibrin in clots, especially arterial clots, is higher than that in gels made at plasma concentrations of fibrinogen (3–10 mg/mL), where most rheology studies have been conducted. Our objective in this study was to measure and characterize the elastic regimes of low (3–10 mg/mL) and high (30–100 mg/mL) density fibrin gels using shear and extensional rheology. Confocal microscopy of the gels shows that fiber density increases with fibrinogen concentration. At low strains, fibrin gels act as thermal networks independent of fibrinogen concentration. Within the low-strain regime, one can predict the mesh size of fibrin gels by the elastic modulus using semiflexible polymer theory. Significantly, this provides a link between gel mechanics and interstitial fluid flow. At moderate strains, we find that low-density fibrin gels act as nonaffine mechanical networks and transition to affine mechanical networks with increasing strains within the moderate regime, whereas high-density fibrin gels only act as affine mechanical networks. At high strains, the backbone of individual fibrin fibers stretches for all fibrin gels. Platelets can retract low-density gels by >80% of their initial volumes, but retraction is attenuated in high-density fibrin gels and with decreasing platelet density. Taken together, these results show that the nature of fibrin deformation is a strong function of fibrin fiber density, which has ramifications for the growth, embolization, and lysis of thrombi.
Introduction
Fibrin is one of the most extensively studied biopolymers in terms of rheological properties on both the single-fiber and network scales (1–11). Fibrin is extraordinarily extensible and shows nonlinear rheological behaviors such as strain hardening and negative normal stresses under shear strain (1–14). Most studies of fibrin gel rheology have been conducted on gels derived from fibrinogen concentrations equal to or near that of human plasma (∼3 mg/mL) (1,2,10,15–17). These low-density (fibers/volume) fibrin gels have fiber volume fractions of <5%. Yet, thrombi formed in vivo, fibrin glues used for surgical wounds, and tissue-engineering matrices can have fiber volume fractions of 10–50% (18–21). Our objective in this study was to measure the rheology of high-density fibrin gels (defined as those derived from >10 mg/mL fibrinogen) and to relate the mechanics of these gels to their network structure.
Thrombi formed under flow contain a higher density of fibrin than gels formed under static conditions at plasma concentrations of fibrinogen. For example, thrombi retrieved from patients with myocardial infarctions have a solid volume fraction of fibrin fibers of ∼0.5 (18). This high density appears to be partially due to the effect of blood flow on fibrin deposition. Fibrin gels formed under flow on procoagulant surfaces have a 5-fold higher fibrin density than static gels formed at 3 mg/mL fibrinogen (21). Platelet retraction can reduce the volume of low-density fibrin gels (2 mg/mL fibrinogen) by as much as 90%, thereby yielding a much denser network of fibers (22). The magnitude of platelet contractile forces imparted to a substrate increases with increasing stiffness of the substrate (23); however, whether platelets have the ability to retract high-density fibrin gels is unknown. Thus, the rheology of high-density fibrin gels is important because it will determine, in part, whether the stresses imparted by blood flow will cause the clot to deform reversibly or irreversibly, or to embolize, as well as the degree of platelet-mediated retraction.
In addition to its role in mechanics, the density of fibrin partly determines the fluid and solute transport into and out of a thrombus. In vitro (24), in vivo (25), and computational (26–28) studies suggest that the hindered transport of coagulation enzymes and platelet agonists in the interstitial space between platelets and fibrin fibers is a mechanism that contributes to thrombus arrest. Specifically, the transport of coagulation enzymes from the injured vessel wall through the porous clot may regulate the late stages of clot growth (29). Moreover, the transport of fibrinolytic agents (e.g., tissue plasminogen activator) into a thrombus regulates the rate of its dissolution (30). In vivo, it is more difficult to measure transport properties such as hydraulic permeability and diffusion coefficients than mechanical properties, which can be estimated by ultrasound and other imaging modalities (31). As such, providing a link between thrombi mechanics and transport should prove useful for developing therapeutic approaches for thrombosis.
Low-density fibrin gels have a strain-dependent rheology characterized by several elastic regimes. These regimes are categorized as networks undergoing either entropic, thermal fluctuations or enthalpic, mechanical deformation. Mechanical deformation is further divided into affine and nonaffine models. Affine models assume that fibers deform such that the strain of individual fibers is identical to that of the macroscopic strain; a Poisson’s ratio of one-half (i.e., incompressibility) is also assumed. Nonaffine models account for deviations on the microscopic scale from the affine assumption (32). Nonlinearity in nonaffine networks originates from network reorganization that leads to a transition from fiber bending/buckling to fiber stretching (33). For sufficiently large strains, fiber buckling may even lead to a decrease in shear modulus (32,34). At low strains, low-density fibrin gels have been shown to behave as networks of semiflexible polymers where the elasticity is dominated by thermal fluctuations and entropic resistance to stretching; however, at high strains, the nonlinear response of fibrin deviates from the entropic model (35). At higher strains, low-density fibrin gels undergo nonaffine deformation (32,36) and exhibit Poisson ratios above the incompressible value of 0.5 (i.e., they lose mass upon deformation) (17,37).
In this report, we use shear and extensional rheology and platelet retraction to characterize the mechanical properties of low- and high-density fibrin gels (3–100 mg/mL) and determine how these properties relate to network structure. All gels act as thermal, affine networks at low strains. This allows one to predict the mesh size from the elastic modulus, and thus provides a link between mechanics and fluid and solute transport. Nonaffine behavior is apparent in low-density, but not high-density, fibrin gels at moderate strains. Platelet retraction of fibrin gels is attenuated by increasing fibrin density.
Materials and Methods
Materials
For details regarding the materials used in this work, see Supporting Material.
Preparation of fibrin gels
For details regarding the preparation of fibrin gels, see Supporting Material.
Small-strain dynamic shear rheology
Shear and normal stresses were measured with a DHR-3 rheometer from TA Instruments (New Castle, DE) using a parallel plate (d = 20 mm, stainless steel) and solvent trap to prevent evaporation. Recalcified fibrinogen (161.5 μL) was pipetted on the bottom plate. Thrombin (8.5 μL) was added to the fibrinogen solution and the top plate was quickly (∼3 s) lowered to a gap height of 500 μm while being spun freely at ∼60 rpm to induce mixing. Each sample was subjected to four tests: 1) shear storage (G′) and loss (G″) moduli were measured at 1% strain and at 1 Hz for 3000 s to monitor gelation (samples were assumed to have reached their steady state if G′ did not change by greater than ±5% over the time period of 2700–3000 s); 2) an oscillation sweep with strains of 0.01–1% at 1 Hz was conducted; 3) a frequency sweep from 0.01 to 3 Hz at 1% strain was conducted; and 4) shear storage (G′) and loss (G″) moduli were again measured at 1% strain and at 1 Hz, but for 300 s, to detect changes greater than ±10% in the gel induced by test 2 or 3. If changes greater than ±10% occurred, the sample was discarded.
Shear and normal stresses under a strain ramp
Using an identical sample preparation and gelation test (step 1 above), the gel was deformed at a strain rate of 0.01 s−1 until each sample broke. The shear and normal stresses and the shear modulus (G) were recorded (38).
Extensional rheology
Glass slides (50 mm × 75 mm) were coated with 25% Triton X-100 in Tris-buffered saline (TBS) to prevent the fibrin from adhering to the glass. Fibrin gels (30, 50, and 100 mg/mL) were formed between two glass slides separated by a 450 μm (l = 50 mm, w = 10 mm, thickness = 0.45 mm) polypropylene spacer, and 10 mg/mL fibrin gels were formed between two glass slides separated by three 450 μm spacers stacked on each other (total thickness = 1.35 mm). To be able to handle samples with a low fibrinogen concentration without deforming them, we used thicker samples. The sample thickness varied by <1% across the sample. Gels were allowed to form in a humidified chamber for 50 min. Gel samples (l = 20 mm and w = 3–6 mm) were cut from each casting with a razor blade for tensile testing on an ARES-G2 rheometer (TA Instruments, New Castle, DE) with the Sentmanat Extensional Rheometer (SER) fixture (39) with rough-textured drums. Samples were stretched at 10 mm/min (17). We determined the elastic modulus, E(γ), defined as the slope of the stress-strain curve at each value of γ, by fitting a fifth-degree polynomial to the stress-strain data using the MATLAB (The MathWorks, Natick, MA) function polyfit and then taking the first derivative of the polynomial (Fig. S1).
Platelet retraction of fibrin gels
We performed platelet-mediated retraction of fibrin gels using a modified version of previously reported protocols (40). Nonsiliconized glass vials (Alltech Associates, Deerfield, IL) were incubated with 5 mg/mL bovine serum albumin in modified Tyrode’s buffer for 1 h at room temperature, rinsed with deionized water, and dried with an air brush. Whole blood was collected by venipuncture into a syringe containing 3.8% sodium citrate. The first 5 mL of blood was discarded. Acid-citrate-dextrose was then added to the blood in a 1:10 ratio. The anticoagulated blood was centrifuged at 200 g for 20 min. Then supernatant platelet-rich plasma (PRP) was removed, and PGI2 (1.3 μM) was added to inhibit platelet activation. The PRP was centrifuged at 1000 g for 10 min and the platelet-poor plasma (PPP) was decanted off the platelet plug, which was immediately resuspended in modified Tyrode’s buffer. After repeating the same washing step, we enumerated the resuspended platelets using a Z1 Coulter Counter (Beckman Coulter, Brea, CA). Platelet concentrations of 2 × 104 and 2 × 105 platelets/μL in 500 μL of 3, 10, and 30 mg/mL fibrinogen were placed in glass vials, followed by the addition of MgCl2 and CaCl2 at 3.75 mM and 7.5 mM, respectively. Finally, clotting was induced with 10 nM α-thrombin. Clot retraction was recorded for 5 h at 37°C. After retraction, the entire system (clot + liquid + glass) was weighed. Next, the retracted clot was removed and the remaining liquid and glass were weighed. Finally, the mass of the dried glass vial was measured and the volume of the expelled liquid was calculated assuming a liquid density of 1.01 mg/mL. The percent retraction (PR) is reported as the volume of the expelled liquid relative to the initial volume of the clot.
| (1) |
where Vtot is the total clot volume, mg+l is the mass of the glass vial plus the liquid, mg is the mass of the glass vial, and ρl is the density of the liquid. The calculated mass of the clot (mc+g+l – mg+l) was used to confirm that the total mass of the system did not change over the course the experiment.
Theory
We used two theoretical models of fibrous networks (the thermal network model and the mechanical network model) to interpret the bulk rheology experimental data in the context of single-fiber mechanics and network structure.
Calculation of mesh size
We determined the mesh size, ξ, of fibrin gels by measuring the hydraulic permeability, k, using previously reported methods (41):
| (2) |
The square root of the permeability is a hydrodynamic screening length for flow-through fibrous media that is used to estimate the distance between fibers in hydrogels (42,43).
Predicting the mesh size from the elasticity of thermal affine networks
The shear modulus (G) of a thermal affine elastic network can be connected to the mesh size of the network by
| (3) |
where κB is the bending modulus of a fibrin fiber (see Supporting Material for calculation), kB is Boltzmann’s constant, T is the absolute temperature, and Lc is the length of a fiber in the network (44). The length of each fiber was taken to be 2 μm, within the range of 2.86 ± 2.51 μm as measured by Kim et al. (45). Ryan et al. (46) reported that the fiber length is roughly independent of fibrinogen concentration from 0.5–6 mg/mL. The bending modulus, κB, was estimated to be 4.5 × 10−24 N m2 by assuming that fibrin fibers are bundles of coupled protofibrils (47), with each protofibril having a persistence length of 500 nm (7) (see Supporting Material for calculation).
Using negative normal stresses to categorize fibrin gels at moderate strain
Fibrin’s nonlinear elastic response has been described by two models: 1) the thermal network model, which considers the gel fibers to have nonlinear force elongations that arise from thermal fluctuations (48); and 2) the mechanical network model, which considers the gel fibers to be mechanical rods with linear force-elongation relations whereby nonlinearity arises from nonaffine deformation and a shift from fiber bending to stretching at high strains (38).
The ratio of the negative first normal stress to shear stress (−σN/σS) as a function of strain can distinguish between the two models. Both models show a small-strain regime characterized by σN ≈ γS2 and σS ≈ γS, where γS is the shear strain. The range of strains that the small-strain regime scaling holds increases with increasing fiber density (number of fibers per unit volume) for the mechanical network model, whereas in the thermal network the range decreases with increasing fiber density (14,49). Accordingly, if the small-strain regime increases with increasing fiber density, the thermal network model is supported, and if it decreases, the mechanical model is more appropriate. Additionally, within the mechanical model, a peak where the normal stresses exceed the shear stresses at small strains is indicative of fibers that are softer to bending than to stretching (49). This behavior, where the ratio of normal stress to shear stress is greater than unity, is inconsistent with a purely thermal model (38).
Distinguishing between nonaffine and affine mechanical networks
Mechanical networks can be categorized as nonaffine or affine depending on their bending (κB) and stretching (μ) moduli and fiber length (50–52). A distinguishing feature of these networks is the relationship between the shear modulus (G) and the elastic modulus (E). Purely affine networks are dominated by stretching modes, have a Poisson’s ratio (ν = E/2G − 1) of 0.5 (52), and are described by
| (4) |
Nonaffine networks have elastic regimes dominated by bending modes and show deviations from Eq. 4 as predicted by elasticity theory (53). The transition from affine to nonaffine deformation is shown in a depression of G (53,54). As the affine linear modulus serves as the upper bound for G at moderate strains, a depression in G results in an increased ratio of E/G for increasingly nonaffine networks. These high values of E/G, by definition, result in an elevated Poisson’s ratio (ν > 0.5). Thus, volume is not conserved, but rather decreases upon stretching, a phenomenon that is observed in fibrin gels as mass loss during extensional strain (17,37).
Results
Verification of fibrinogen conversion to fibrin
Fibrin gels were formed from 3, 10, 30, 50, and 100 mg/mL fibrinogen and 10 and 100 nM thrombin. The density of the fibers increased with increasing fibrinogen concentration (Fig. 1). A stock solution of fibrinogen (12.9 mg/mL) was concentrated by centrifugation to 130–160 mg/mL. Absorbance measurements at 450 nm showed that the fibrinogen in the concentrated retentate remained soluble at room temperature (Supporting Material and Fig. S2). This concentrated solution was found to contain no aggregates as measured by dynamic light scattering. The measured particle diameter of the concentrated fibrinogen solution was 30 nm with a dispersity of 0.2, identical to the values reported by the vendor (Enzyme Research Laboratory). All fibrinogen appeared to be converted to fibrin. No fibrinogen was present in the excess TBS. The excess TBS solution did not form a gel, but remained liquid when the extent of reaction was tested, and no excess fibrinogen was detected by the modified Clauss assay (see Supporting Material). Factor XIII was present in the stock fibrinogen solution. SDS-PAGE analysis showed that 3–50 mg/mL fibrinogen gels were completely cross-linked, as indicated by the absence of γ monomers and presence of γ dimers (Fig. S3). In addition, 100 mg/mL fibrinogen gels were partially cross-linked, as both γ monomers and dimers were present.
Figure 1.
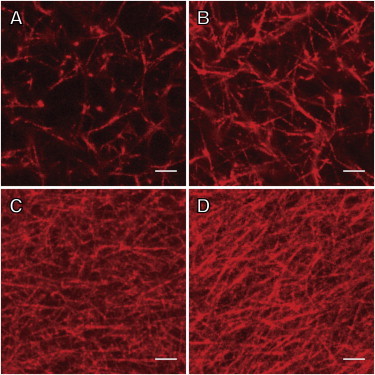
(A–D) Laser scanning confocal microscopy images of fibrin gels derived from (A) 3 mg/mL, (B) 10 mg/mL, (C) 30 mg/mL, and (D) 50 mg/mL fibrinogen and 10 nM thrombin. Scale bar = 5 μm. To see this figure in color, go online.
Fibrin gels are linearly viscoelastic for all fibrinogen concentrations at low strains
After monitoring gelation with step 1 for 3000 s (Fig. S4), we conducted amplitude sweeps over strains of 0.01%–1% at 1 Hz to confirm linear viscoelastic behavior. There was a <5% change in G′ and G″ for all gels over this range of strains, suggesting linear viscoelastic behavior. At a strain of 1%, gelation was confirmed by a plateau in G′ during low-frequency sweeps (0.01 Hz to 3 Hz) and linear viscoelasticity (Fig. 2) (55). G′ was roughly independent of frequency at all fibrinogen concentrations, indicating the absence of relaxation mechanisms at these frequencies for a strain of 1%. G′ was more strongly dependent on fibrinogen concentration than on thrombin concentration. G″ showed a modest increase with increasing frequency at all fibrinogen concentrations, indicating a relaxation mechanism whose reciprocal time constant exists above the experimental range of the frequencies measured. This trend suggests that fibrin acts as a viscous liquid only on long timescales. For all gels tested, the dynamic shear storage modulus dominated the mechanical response: gels showed tan δ (G″/G′) values of 0.05 ± 0.01 independently of fibrinogen or thrombin concentrations. G′ and G″ increased rapidly with fibrinogen concentrations of 3–30 mg/mL and were less sensitive from 30 to 100 mg/mL (Table S1).
Figure 2.
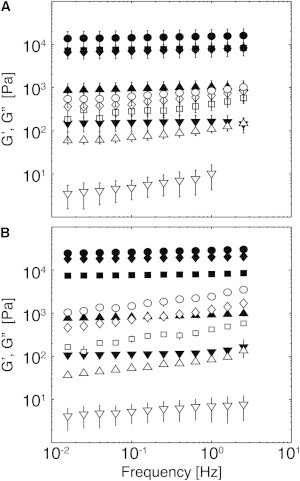
Dynamic shear rheology of fibrin gels at small strains. G′ (solid symbols) and G″ (open symbols) of fibrin gels formed at fibrinogen concentrations of (▼) 3 mg/mL, (▲)10 mg/mL, (▪) 30 mg/mL, (♦) 50 mg/mL, and (●) 100 mg/mL as a function of frequency at a strain of 0.01. (A and B) Gels formed with 10 nM (A) and 100 nM (B) thrombin. Data are presented as the mean and standard deviation (SD; n = 3).
Strain hardening under shear is attenuated in high-density fibrin gels
The shear modulus (G) of fibrin gels formed with 10 nM thrombin was measured as a function of strain during a constantly increasing deformation test at a strain rate of 0.01 s−1 over strains of 10−3 to 1 (Fig. 3). At low strains (γ = 10−3), the G value was similar to the measured dynamic storage modulus (G′) value. This was as expected, as G′ was frequency independent and much greater than G″ for all gels. G ranged from ∼100 Pa to 20,000 Pa as fibrinogen concentration was increased from 3–100 mg/mL, with most of the change occurring over the range of 3–30 mg/mL. Given the viscoelastic nature of the gels, it should be recognized that the strain hardening is expected to be ramp-rate dependent. At the selected ramp rate, low-density fibrin gels (3 and 10 mg/mL) showed significantly greater strain hardening than high-density fibrin gels (30, 50, and 100 mg/mL) at strains of 0.1–1. Fibrin gels formed at 3 and 10 mg/mL had roughly an order of magnitude increase in G for γ > 0.05. Gels formed at 30–100 mg/mL either remained relatively constant at moderate strains or showed a very slight degree of strain softening below strains of 0.2 and a modest degree of strain hardening at higher strains.
Figure 3.
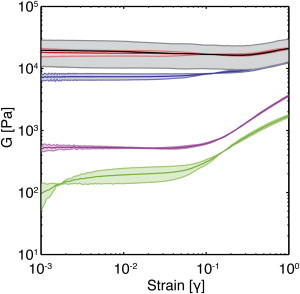
Strain hardening in low- and high-density fibrin gels. The shear moduli, G, of fibrin gels formed with 10 nM thrombin and 3 (green), 10 (magenta), 30 (blue), 50 (red), and 100 mg/mL (black) fibrinogen are shown as a function of strain. The shaded region represents the SD (n = 3). Note that the 50 and 100 mg/mL lines overlap, so it is difficult to discriminate them from each other; the gray shading corresponds to the SD of the 100 mg/mL gel. To see this figure in color, go online.
Extensional rheology reveals two strain-hardening regimes
Similar to what was observed for shear rheology, the stress-strain relationship in biaxial extension of fibrin gels was weakly dependent on thrombin concentration compared with fibrinogen concentration (Table S2; Fig. 4, A and B). Note that 3 mg/mL gels were not tested, because they were unable to support their own weight in the SER fixture. Stress-strain curves of all gels ≥10 mg/mL showed two regions of strain hardening (Fig. 4, C and D). The first region occurred at strains of 0.01 < γ < 0.25. This is similar to the strain hardening seen under shear stress in Fig. 3. The second region occurred at strains of γ > 0.75. At strains of 0.25 < γ < 0.75, E(γ) remained relatively constant. The stress at break increased from 3.2 × 104 Pa to 39 × 104 Pa with increasing fibrinogen concentration. The strain at break was 1.0–1.6 for all gels, with no apparent trend for different fibrinogen concentrations. For reasons discussed below, the first strain-hardening regime is likely caused by network rearrangement, and the second regime is likely caused by fiber stretching.
Figure 4.
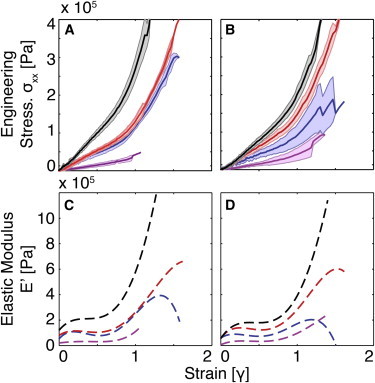
(A and B) Biaxial extensional stress-strain data for fibrin gels formed with 100 nM (A) and 10 nM (B) thrombin and 10 (magenta), 30 (blue), 50 (red), and 100 mg/mL (black) fibrinogen. The shaded region represents the SD (n = 5–8). (C and D) The corresponding elastic moduli were found by taking the first derivative of a fifth-order polynomial fit to the stress-strain data for gels formed with 100 nM (C) and 10 nM thrombin (D). To see this figure in color, go online.
High-density fibrin gels act as thermal affine networks at small strains based on mesh size scaling
The shear modulus (G) of thermal affine networks scales with mesh size according to Eq. 3. The mesh size of fibrin networks was independently estimated by Eq. 2 using measurements of hydraulic permeability (41) and by Eq. 3 using the measured G values at low strains (γ = 0.01) for fibrin gels formed with 10 nM and 100 nM thrombin. There is good agreement between the estimates of mesh size based on permeability and G (Fig. 5, A and B). The predicted mesh size ranges from 300–400 nm in 3 mg/mL gels to 20–30 nm in 100 mg/mL gels. The largest change in mesh size occurred over the range of 3–30 mg/mL fibrinogen. There was only a modest change in mesh size at higher fibrinogen concentrations.
Figure 5.
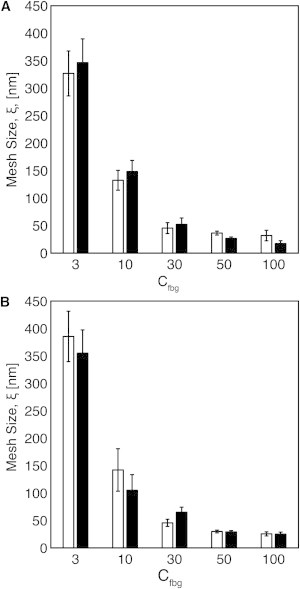
(A and B) Mesh size, ξ, of fibrin gels formed with (A) 10 nM thrombin and (B) 100 nM thrombin as calculated by measurements of G′ (Eq. 3; white bars) and permeability (Eq. 2; black bars) for fibrin gels formed with 3–100 mg/mL fibrinogen.
Negative normal stresses show that fibrin gels act as mechanical networks at moderate strains
The ratio between negative normal stress and shear stress (−σN/σS) at strains greater than 0.01 is characteristic of a network of mechanical elastic rods for all fibrinogen concentrations (Fig. 6, A–E). The −σN/σS ratios show initial large increases with strain before reaching maximums between strains of 0.15–0.25, and then decreasing at higher strains. All gels showed a small strain regime with scaling of σN ≈ γS2 and σS ≈ γS. This scaling held for larger strains with increasing fibrinogen concentration, strongly suggesting a mechanical network. The flatter shape of the −σN/σS curve and reduced peak with increasing fibrinogen concentrations suggests that gels with higher fiber density are more susceptible to fiber stretching than to bending. This feature might be expected as mesh size decreases and the length between strand-supporting junctions decreases. These results are consistent with models of mechanical networks, which predict that fibers will become less susceptible to bending as the maximum of the curve becomes smaller (38,49).
Figure 6.
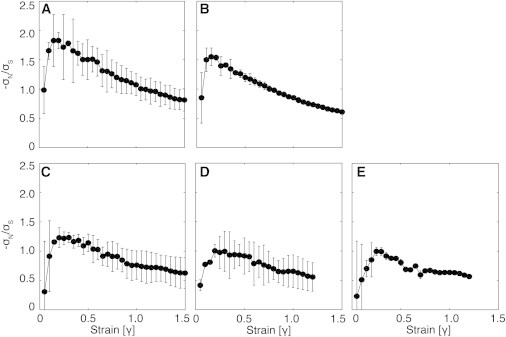
(A–E) Negative normal stress to shear stress ratio plotted versus strain for fibrin gels formed with 10 nM thrombin and (A) 3 mg/mL, (B) 10 mg/mL, (C) 30 mg/mL, (D) 50 mg/mL, and (E) 100 mg/mL fibrinogen.
Affine and nonaffine mechanical networks as a function of fibrin density
The ratio of elastic modulus to shear modulus, E(γ)/G(γ), can be used to characterize affine and nonaffine mechanical deformation. Using data from shear and extensional rheology (Figs. 3 and 4), we compared the ratio of the material functions E(γ)/G(γ) as a function of strain for 10–100 mg/mL gels (Fig. 7). At low strain (γ < 0.003), E(γ)/G(γ) was ∼3, which is the affine prediction (Eq. 4). As strain was increased, E(γ)/G(γ) of all gels increased, reaching local maximums at strains of 0.1–0.3, and with the strain at maximum increasing with increasing fibrinogen concentration. As strain was further increased, E(γ)/G(γ) of all gels decreased to local minimums at strains of 0.6–0.7. Finally, the E(γ)/G(γ) ratio of all gels increased again as strain was further increased above 0.7. The E(γ)/G(γ) ratio of the 10 mg/mL gel reached a maximum value of 48 at a strain of 0.15 before decreasing to a local minimum of 19 at a strain of 0.6. The E(γ)/G(γ) ratios of the 30, 50, and 100 mg/mL gels were less sensitive to strain, and all reached local maxima of ∼10 at strains of 0.2, 0.25, and 0.3 before decreasing to values of 3, 5, and 9 at strains of 0.7, 0.65, and 0.6, respectively. The decrease in E(γ)/G(γ) toward the affine limit as strain was increased from 0.15 to 0.6 indicates that fibrin gels become more affine with increasing strain.
Figure 7.
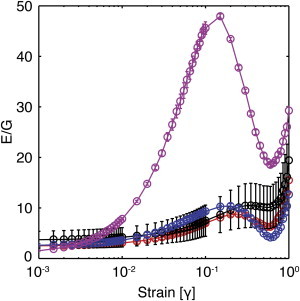
Ratio of elastic moduli, E(γ), to shear moduli, G(γ), of fibrin gels formed with 10 nM thrombin and 10 (magenta), 30 (blue), 50 (red), and 100 mg/mL fibrinogen (black) as a function of strain. The error bars represent the propagated error (shear n = 3, extensional n = 5–8). To see this figure in color, go online.
Platelet retraction of fibrin gels depends on both platelet and fibrin density
Fibrin gels derived from 3, 10, and 30 mg/mL fibrinogen and 10 nM thrombin were created with the inclusion of 2 × 104 and 2 × 105 platelets/μL and allowed to retract for 5 h at 37°C. The majority of the retraction occurred in the first hour and there was little change in gel volumes after 2 h (Movie S1). Gels formed with 2 × 105 platelets/μL showed final retraction values of 97.5% ± 0.1%, 89.3% ± 1.0%, and 39.0% ± 2.9% for 3, 10, and 30 mg/mL gels, respectively (Fig. 8). Gels formed with 3 and 10 mg/mL fibrinogen and 2 × 104 platelets/μL retracted by 75.1% ± 10.5% and 23.4% ± 0.8%, respectively (Fig. 8). There was no measurable retraction for gels formed with 30 mg/mL fibrinogen and 2 × 104 platelets/μL. Due to the reduction in clot volume resulting from retraction, gels formed with 2 × 105 platelets/μL resulted in gels with final fibrin concentrations of 119 ± 0.1 mg/mL, 93 ± 1.1 mg/mL, and 49 ± 3.7 mg/mL for gels with initial concentrations of 3, 10, and 30 mg/mL, respectively. Gels formed with 2 × 104 platelets/μL resulted in clots with fibrin concentrations of 12 ± 1.7 mg/mL and 13 ± 0.5 mg/mL for gels with initial concentrations of 3 and 10 mg/mL, respectively. The degree of retraction could be slightly overestimated due to the collapse of fibrin gels during removal from the tube. The contractile force of a platelet is 4 nN on a substrate with an elasticity of ∼10 kPa, which is comparable to the elasticity of a 30 mg/mL gel (Fig. 2) (23). Using this force, we estimated that a platelet could bend a fibrin fiber 2 nm and stretch a fiber 64 nm in a 30 mg/mL gel (see Supporting Material for calculation of bending and stretching displacement). The same force could bend a fiber 770 nm and stretch a fiber 64 nm in a 3 mg/mL gel. Although these calculations assume that fiber bending and stretching moduli are independent of fiber density, they suggest that platelet-mediated retraction in high-density fibrin gels may be limited to fiber stretching, which would be consistent with affine deformation.
Figure 8.
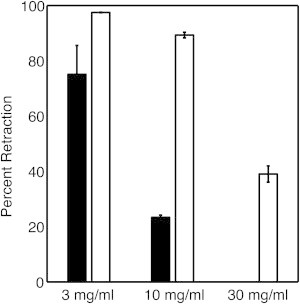
Percent retraction of fibrin-platelet gels formed with 2 × 105 platelets/μL (white bars) and 2 × 104 platelets/μL (black bars) for fibrin gels formed with 3–30 mg/mL fibrinogen. Data represent the mean and SD (n = 3).
Fibrin rheology state diagram
Results from shear and extensional rheology experiments show that low- and high-density fibrin gels are characterized by strain-dependent network rearrangement and fiber stretching regimes. Fig. 9 shows a proposed state diagram of these different regimes. The evidence supporting this state diagram is summarized below.
Figure 9.
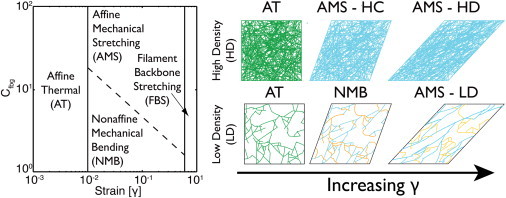
Proposed state diagram of the elastic regime of fibrin gels as a function of fibrinogen concentration and strain. In the affine thermal (AT) regime, at strains of less than a few percent, network elasticity is dominated by entropic restrictions of thermally fluctuating fibers (green) for all gel concentrations. As strain is increased, fibrin gels transition into a regime where elasticity is mechanically dominated. High-density (HD) gels transition directly to an affine mechanical stretching (AMS) regime in which fibers are mechanically stretched (blue). Low-density (LD) gels transition to a nonaffine mechanical bending (NMB) regime in which bent fibers (orange) allow for network rearrangement. Eventually, network rearrangement results in fibers that effectively span the network and stretch, causing the LD gels to transition into the AMS regime. In the filament backbone stretching (FBS) regime, at strains >60–70% the filament backbone is stretched due to protein unfolding or other mechanisms.
At low strains (γ < 0.01), all fibrin gels exhibit an initial linear regime where elasticity is determined by thermal fluctuations of the fibrin fibers that undergo affine deformation regardless of fiber density. Fibrin elasticity in this low-strain linear regime is well described by the thermal affine model, Eq. 3, and the mesh size for fibrin gels as measured by elasticity and permeability show good agreement over the entire range of concentrations tested. Furthermore, the E/G ratio is close to the affine limit for all gels at low strains. These results are in agreement with previous measurements of low-density fibrin gels at low strains (35). Here, we find that this model also holds for high-density fibrin gels. We find that with increasing strain, all fibrin gels transition away from the linear regime at γ ∼ 0.01, as indicated by the deviation of E(γ)/G(γ) from the affine predictions (Fig. 7). This agrees with the results of Piechocka and colleagues (35), who found that the thermal slack is pulled out of fibrin fiber at strains of 0.01 for fibrin gels formed with 3–8 mg/mL fibrinogen.
At moderate strains (0.01 < γ < 0.6), elasticity is determined by mechanical network deformations. The scaling in the small-strain regime, where σN ≈ γS2 and σS ≈ γS with fibrinogen concentration, and the shape of the −σN/σS curve, where the values of the ratio trend toward 0.5 with increasing strain, with a possible peak at lower strains, are characteristic of mechanical networks. Whether network deformation is dominated by nonaffine fiber bending or affine fiber stretching depends on the fiber density and strain.
Gels formed from 3 and 10 mg/mL fibrinogen appear to first transition into a nonaffine, bending-dominated deformation regime before ultimately reaching an affine, stretching-dominated regime at higher strains. Evidence of nonaffine mechanical bending is provided by the high E(γ)/G(γ) ratios, which indicate a strong deviation from the affine assumption. The peak in the E(γ)/G(γ) ratio shows that the maximum nonaffine deformation occurs at a strain of ∼0.15 before deformations become more affine (E(γ)/G(γ) decreasing) as strain is increased to 0.6. Furthermore, sharp peaks in the −σN/σS ratios at strains of 0.1–0.2 are characteristic of the nonaffine, bending regime (38,49). Microrheology measurements in low-density fibrin gels show a peak of nonaffine deformation at slightly lower strains (0.02), but show a similar trend toward affine deformation at increasing strain (36). At increased strain, the −σN/σS ratios of all gels approach the same value of ∼0.5, indicating a weak dependence on bending and a stretching-dominated regime (38,49).
Gels formed from 30, 50, and 100 mg/mL fibrinogen transition from affine thermal fluctuations directly into a predominantly affine, stretching-dominated regime. This conclusion is based on E(γ)/G(γ) ratios that deviate only slightly from the affine prediction. High-concentration gels also show a less pronounced peak in the −σN/σS ratios before decreasing to approach the same value of ∼0.5, indicating more stretching-dominated deformations over the entire range of strains. Using criteria developed by Broedersz and colleagues (51), we can estimate the transition from nonaffine to affine mechanical deformations using the ratio of fiber length (Lc) to critical length (λNA), which is a function of mesh size (see Supporting Material for calculation). Gels formed with 30–100 mg/mL fibrinogen have Lc/λNA >> 1, suggesting that the deformation regime of these gels is stretching dominated and largely affine (Table S3). Gels formed at 3 and 10 mg/mL fibrinogen have Lc/λNA on the order of unity, suggesting that these gels do not deform with purely affine modes, and instead have some degree of nonaffine bending.
At high strains (γ > 0.6), all fibrin gels again strain harden. Based on previous reports (10,15,35), we assume that the strain hardening in this regime is due to unfolding of fibrin molecules. However, other mechanisms may be present simultaneously.
Discussion
Our objective in this study was to measure and characterize the mechanical properties of fibrin gels over a range of fibrinogen concentrations that are representative of arterial thrombi, fibrin surgical glues, and tissue-engineering scaffolds. Our results show that fibrin undergoes a variety of elastic deformations as a function of strain, in agreement with previous reports (7,12,56,57). Here, we show that there are unique features that distinguish low- and high-density fibrin gels. A notable finding is that low-density fibrin gels appear to undergo both affine stretching and nonaffine mechanical bending at moderate strains, whereas high-density fibrin gels undergo primarily affine mechanical stretching. This difference was also apparent in platelet retraction assays: retraction was significantly reduced in high-density fibrin gels, where fiber bending presumably is limited. The network mechanics of high-density fibrin gels are only weakly dependent on fibrinogen concentration, suggesting that fibrin monomers contribute more to changes in the internal structure of fibers than to the network structure above a certain fibrinogen concentration.
The only previous rheological study of high-density fibrin gels that we are aware of comes from Weigandt and colleagues (57). They measured the mechanics and structure of high-density fibrin gels by neutron scattering coupled with shear rheology for fibrin gels derived from fibrinogen solutions of 1–40 mg/mL. Our results from dynamic shear rheology and strain ramp in shear deformation are in good agreement with their results. In particular, strain hardening at moderate strains was attenuated by increasing fibrinogen concentration. The degree of strain softening at strains ∼0.1 that they observed for high-density fibrin gels was more pronounced than our observations. This difference could be explained by the different solvents used (water versus deuterated water) and the relatively high salt concentration (0.5 M NaCl) used in their study.
The observed trend of a transition from thermal semiflexible fibers to mechanical fibers for all fibrin gels is consistent with the observations of Piechocka et al. (35). They report that fibrin gels from 0.06–8 mg/mL fibrinogen have linear mechanics described by thermal fluctuations of fibers at very low strains, but that strains of only a few percent are adequate to remove any thermal slack from the fibers and to force the fibers to mechanically deform. One notable difference is that our results suggest that low-density fiber gels transition from a bending-controlled nonaffine regime into a mostly affine stretching-dominated regime at higher strains, as is evident from the ratio of E(γ)/G(γ) with increasing strains. This nonaffine regime is further supported by measurements of the negative normal to shear stress ratio as a function of strain and the direct observation of nonaffine deformations. Wen and colleagues (36) used fluorescent microscopy to track the displacement of beads embedded in a 2.5 mg/mL fibrin gel and showed that fibrin gels deform nonaffinely, with a sharp increase in nonaffine behavior up to a strain of 0.02 and then a decrease in nonaffine behavior at higher strains. The existence of a nonaffine regime caused by the fibers’ susceptibility to bending and buckling and resulting network ultracompressibility also explains the observed water loss of gels formed with lower fibrinogen concentrations (9). The affine deformations characteristic of high-density fibrin gels may explain their strain softening, since compressive forces generated on fibers oriented 135° away from the horizontal axis during shear would be great enough to cause fiber buckling, and the collapsed fibers would no longer contribute to elasticity (33,34). Moreover, the absence of a transition from bending to stretching likely reduces strain hardening at moderate strains (33).
The differences between nonaffine bending-dominated elasticity in low-density fibrin gels and affine stretching-dominated elasticity in high-density fibrin gels may have physiological implications for the volume and stability of thrombi formed in vivo. In particular, it appears that the degree of platelet contraction depends on the fiber density. The contractile force of an individual platelet increases with increasing substrate stiffness, suggesting that a platelet would pull on higher-density fibrin gels with a force of up to ∼79 nN (23). Despite this increased force, clot retraction was still attenuated in high-concentration fibrin gels, presumably due to the affine stretching-dominated deformation of the higher-concentration gel. Platelets at concentrations representative of those found in blood were able to retract low-density fibrin gels by >90%, in agreement with previous reports (22). However, platelets were only able to retract a high-density fibrin gel by 40%. Retraction of low-density fibrin gels could be due to the ability of platelets to induce nonaffine, bending deformations of fibers and fiber rearrangement. Based on the estimated bending modulus and using the mesh size as a characteristic length, the force generated by a single platelet is sufficient to cause bending deformations of almost 1 μm in 3 mg/mL gels, but only negligible bending deformation relative to stretching deformation in 30 mg/mL gels. A complementary or alternative explanation is that at mesh sizes of <100 nm, it may be difficult for the platelet to extend filopodia into the dense fibrous network during retraction assays. These observations may be most relevant in venous thrombi, which contain high-solid fractions of fibrin and low-solid fractions of platelets. It is possible that the increased platelet density associated with flow-formed arterial clots can produce sufficient force to retract even the most highly concentrated fibrin gels.
The physical properties of low- and high-density fibrin gels show a significant difference in their dependence on fibrinogen concentration. Both interstitial fluid flow, as measured by permeability, and elasticity, as measured by shear and extensional rheology, show a strong dependence on fibrinogen concentrations over the range of 3–30 mg/mL. At higher concentrations, the changes in these properties are modest up to 100 mg/mL. The strong dependence of elasticity on fibrinogen concentration at low fibrinogen concentrations can be attributed to the change in mesh size and thus fiber density, as previously reported (41,46). This relationship is also evident in confocal microscopy images of low- and high-density fibrin gels. The weak dependence at higher fibrinogen concentrations suggests that the excess fibrin(ogen) may lead to denser fibers. This reasoning is supported by neutron scattering studies that showed that the solid volume fraction within fibers scales with increasing fibrinogen concentration (57). We hypothesize that these denser fibers have different mechanical properties at high strains; however, to date, there are no single-fiber measurements to support this hypothesis.
Regardless of fiber density, fibrin gels act as thermal affine networks at low strains. Here, we used this feature in combination with semiflexible polymer theory to estimate the mesh size from elasticity measurements. We found good agreement between mesh sizes measured by two independent methods (permeability and shear elasticity), and agreement between mesh sizes estimated at 3 mg/mL (∼350 nm) and measured directly by scanning electron microscopy at 2.5 mg/mL (200–500 nm) (36). In these calculations, we assumed a constant fiber length, which is consistent with measurements of low-density fibrin gels (45,46). However, to our knowledge, the fiber lengths in high-density fibrin gels have not yet been measured. This structure-property relationship serves as a link that can be used to estimate difficult-to-measure, structure-related properties (e.g., permeability and hindered diffusion) from noninvasive, in vivo rheology measurements (e.g., ultrasound) or in vitro measurements of clot mechanics (e.g., thromboelastograms) (31,58). Such measurements are potentially useful for guiding mechanical and fibrinolytic strategies.
Conclusions
In this study, we measured the mechanical properties of fibrin gels formed over the range of fibrinogen concentrations found in clots formed in vivo, and used in fibrin glues and tissue-engineering scaffolds. Shear and extensional rheology measurements show differences in the elastic regimes of gels formed at 3–10 mg/mL and 30–100 mg/mL fibrinogen. Interpretation of these results with deformation theories of fibrous networks suggests distinct network structures for these two types of fibrin gels.
Acknowledgments
This work was supported by a Grant-in-Aid award from the American Heart Association, a National Science Foundation CAREER Award (K.B.N.), the National Institutes of Health (R21NS082933 and R01HL120728), NSF Research Experience for Undergraduates Award EEC-1156745, and the Army Research Office (DURIP W911NF-11-1-030).
Supporting Material
Supporting Citations
References (59–63) appear in the Supporting Material.
References
- 1.Roberts W.W., Kramer O., Ferry J.D. Rheology of fibrin clots. I. Dynamic viscoelastic properties and fluid permeation. Biophys. Chem. 1974;1:152–160. doi: 10.1016/0301-4622(74)80002-5. [DOI] [PubMed] [Google Scholar]
- 2.Gerth C., Roberts W.W., Ferry J.D. Rheology of fibrin clots. II. Linear viscoelastic behavior in shear creep. Biophys. Chem. 1974;2:208–217. doi: 10.1016/0301-4622(74)80046-3. [DOI] [PubMed] [Google Scholar]
- 3.Nelb G.W., Gerth C., Ferry J.D. Rheology of fibrin clots. III. Shear creep and creep recovery of fine ligated and coarse unligated closts. Biophys. Chem. 1976;5:377–387. doi: 10.1016/0301-4622(76)80050-6. [DOI] [PubMed] [Google Scholar]
- 4.Rosser R.W., Roberts W.W., Ferry J.D. Rheology of fibrin clots. IV. Darcy constants and fiber thickness. Biophys. Chem. 1977;7:153–157. doi: 10.1016/0301-4622(77)80008-2. [DOI] [PubMed] [Google Scholar]
- 5.Nelb G.W., Kamykowski G.W., Ferry J.D. Rheology of fibrin clots. V. Shear modulus, creep, and creep recovery of fine unligated clots. Biophys. Chem. 1981;13:15–23. doi: 10.1016/0301-4622(81)80020-8. [DOI] [PubMed] [Google Scholar]
- 6.Janmey P.A., Amis E.J., Ferry J.D. Rheology of fibrin clots. VI. Stress relaxation, creep, and differential dynamic modulus of fine clots in large shearing deformations. J. Rheol. 1983;27:135–153. [Google Scholar]
- 7.Storm C., Pastore J.J., Janmey P.A. Nonlinear elasticity in biological gels. Nature. 2005;435:191–194. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- 8.Hudson N.E., Houser J.R., Falvo M.R. Stiffening of individual fibrin fibers equitably distributes strain and strengthens networks. Biophys. J. 2010;98:1632–1640. doi: 10.1016/j.bpj.2009.12.4312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brown A.E.X., Litvinov R.I., Weisel J.W. Forced unfolding of coiled-coils in fibrinogen by single-molecule AFM. Biophys. J. 2007;92:L39–L41. doi: 10.1529/biophysj.106.101261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Averett R.D., Menn B., Guthold M. A modular fibrinogen model that captures the stress-strain behavior of fibrin fibers. Biophys. J. 2012;103:1537–1544. doi: 10.1016/j.bpj.2012.08.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Falvo M.R., Gorkun O.V., Lord S.T. The molecular origins of the mechanical properties of fibrin. Biophys. Chem. 2010;152:15–20. doi: 10.1016/j.bpc.2010.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen D.T.N., Wen Q., Yodh A.G. Rheology of soft materials. Annu. Rev. Condens. Matter Phys. 2010;1:301–322. [Google Scholar]
- 13.Liu W., Jawerth L.M., Guthold M. Fibrin fibers have extraordinary extensibility and elasticity. Science. 2006;313:634. doi: 10.1126/science.1127317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Janmey P.A., McCormick M.E., MacKintosh F.C. Negative normal stress in semiflexible biopolymer gels. Nat. Mater. 2007;6:48–51. doi: 10.1038/nmat1810. [DOI] [PubMed] [Google Scholar]
- 15.Helms C.C., Ariëns R.A.S., Guthold M. α-α Cross-links increase fibrin fiber elasticity and stiffness. Biophys. J. 2012;102:168–175. doi: 10.1016/j.bpj.2011.11.4016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Collet J.-P., Shuman H., Weisel J.W. The elasticity of an individual fibrin fiber in a clot. Proc. Natl. Acad. Sci. USA. 2005;102:9133–9137. doi: 10.1073/pnas.0504120102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Brown A.E.X., Litvinov R.I., Weisel J.W. Multiscale mechanics of fibrin polymer: gel stretching with protein unfolding and loss of water. Science. 2009;325:741–744. doi: 10.1126/science.1172484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Silvain J., Collet J.-P., Weisel J.W. Composition of coronary thrombus in acute myocardial infarction. J. Am. Coll. Cardiol. 2011;57:1359–1367. doi: 10.1016/j.jacc.2010.09.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gibble J.W., Ness P.M. Fibrin glue: the perfect operative sealant? Transfusion. 1990;30:741–747. doi: 10.1046/j.1537-2995.1990.30891020337.x. [DOI] [PubMed] [Google Scholar]
- 20.Albala D.M., Lawson J.H. Recent clinical and investigational applications of fibrin sealant in selected surgical specialties. J. Am. Coll. Surg. 2006;202:685–697. doi: 10.1016/j.jamcollsurg.2005.11.027. [DOI] [PubMed] [Google Scholar]
- 21.Onasoga-Jarvis A.A., Puls T.J., Neeves K.B. Thrombin generation and fibrin formation under flow on biomimetic tissue factor-rich surfaces. J. Thromb. Haemost. 2014;12:373–382. doi: 10.1111/jth.12491. [DOI] [PubMed] [Google Scholar]
- 22.Osdoit S., Rosa J.P. Fibrin clot retraction by human platelets correlates with α (IIb)β(3) integrin-dependent protein tyrosine dephosphorylation. J. Biol. Chem. 2001;276:6703–6710. doi: 10.1074/jbc.M008945200. [DOI] [PubMed] [Google Scholar]
- 23.Lam W.A., Chaudhuri O., Fletcher D.A. Mechanics and contraction dynamics of single platelets and implications for clot stiffening. Nat. Mater. 2011;10:61–66. doi: 10.1038/nmat2903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hathcock J.J., Nemerson Y. Platelet deposition inhibits tissue factor activity: in vitro clots are impermeable to factor Xa. Blood. 2004;104:123–127. doi: 10.1182/blood-2003-12-4352. [DOI] [PubMed] [Google Scholar]
- 25.Stalker T.J., Traxler E.A., Brass L.F. Hierarchical organization in the hemostatic response and its relationship to the platelet-signaling network. Blood. 2013;121:1875–1885. doi: 10.1182/blood-2012-09-457739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fogelson A.L., Tania N. Coagulation under flow: the influence of flow-mediated transport on the initiation and inhibition of coagulation. Pathophysiol. Haemost. Thromb. 2005;34:91–108. doi: 10.1159/000089930. [DOI] [PubMed] [Google Scholar]
- 27.Leiderman K., Fogelson A.L. Grow with the flow: a spatial-temporal model of platelet deposition and blood coagulation under flow. Math. Med. Biol. 2011;28:47–84. doi: 10.1093/imammb/dqq005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Xu Z., Lioi J., Alber M. A multiscale model of venous thrombus formation with surface-mediated control of blood coagulation cascade. Biophys. J. 2010;98:1723–1732. doi: 10.1016/j.bpj.2009.12.4331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Leiderman K., Fogelson A.L. The influence of hindered transport on the development of platelet thrombi under flow. Bull. Math. Biol. 2013;75:1255–1283. doi: 10.1007/s11538-012-9784-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Diamond S.L., Anand S. Inner clot diffusion and permeation during fibrinolysis. Biophys. J. 1993;65:2622–2643. doi: 10.1016/S0006-3495(93)81314-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Mfoumou E., Tripette J., Cloutier G. Time-dependent hardening of blood clots quantitatively measured in vivo with shear-wave ultrasound imaging in a rabbit model of venous thrombosis. Thromb. Res. 2014;133:265–271. doi: 10.1016/j.thromres.2013.11.001. [DOI] [PubMed] [Google Scholar]
- 32.Wen Q., Basu A., Yodh A.G. Non-affine deformations in polymer hydrogels. Soft Matter. 2012;8:8039–8049. doi: 10.1039/c2sm25364j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Onck P.R., Koeman T., van der Giessen E. Alternative explanation of stiffening in cross-linked semiflexible networks. Phys. Rev. Lett. 2005;95:178102. doi: 10.1103/PhysRevLett.95.178102. [DOI] [PubMed] [Google Scholar]
- 34.Chaudhuri O., Parekh S.H., Fletcher D.A. Reversible stress softening of actin networks. Nature. 2007;445:295–298. doi: 10.1038/nature05459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Piechocka I.K., Bacabac R.G., Koenderink G.H. Structural hierarchy governs fibrin gel mechanics. Biophys. J. 2010;98:2281–2289. doi: 10.1016/j.bpj.2010.01.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wen Q., Basu A., Janmey P.A. Local and global deformations in a strain-stiffening fibrin gel. New J. Phys. 2007;9:428. [Google Scholar]
- 37.Lai V.K., Lake S.P., Barocas V.H. Mechanical behavior of collagen-fibrin co-gels reflects transition from series to parallel interactions with increasing collagen content. J. Biomech. Eng. 2012;134:011004. doi: 10.1115/1.4005544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kang H., Wen Q., MacKintosh F.C. Nonlinear elasticity of stiff filament networks: strain stiffening, negative normal stress, and filament alignment in fibrin gels. J. Phys. Chem. B. 2009;113:3799–3805. doi: 10.1021/jp807749f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sentmanat M.L. Miniature universal testing platform: from extensional melt rheology to solid-state deformation behavior. Rheol. Acta. 2004;43:657–669. [Google Scholar]
- 40.Flevaris P., Stojanovic A., Du X. A molecular switch that controls cell spreading and retraction. J. Cell Biol. 2007;179:553–565. doi: 10.1083/jcb.200703185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wufsus A.R., Macera N.E., Neeves K.B. The hydraulic permeability of blood clots as a function of fibrin and platelet density. Biophys. J. 2013;104:1812–1823. doi: 10.1016/j.bpj.2013.02.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Howells I.D. Drag due to the motion of a Newtonian fluid through a sparse random array of small fixed rigid objects. J. Fluid Mech. 1974;64:449–476. [Google Scholar]
- 43.Johnson E.M., Berk D.A., Deen W.M. Hindered diffusion in agarose gels: test of effective medium model. Biophys. J. 1996;70:1017–1023. doi: 10.1016/S0006-3495(96)79645-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gardel M.L., Shin J.H., Weitz D.A. Elastic behavior of cross-linked and bundled actin networks. Science. 2004;304:1301–1305. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 45.Kim E., Kim O.V., Alber M. Correlation between fibrin network structure and mechanical properties: an experimental and computational analysis. Soft Matter. 2011;7:4983. [Google Scholar]
- 46.Ryan E.A., Mockros L.F., Lorand L. Structural origins of fibrin clot rheology. Biophys. J. 1999;77:2813–2826. doi: 10.1016/S0006-3495(99)77113-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bathe M., Heussinger C., Frey E. Cytoskeletal bundle mechanics. Biophys. J. 2008;94:2955–2964. doi: 10.1529/biophysj.107.119743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.MacKintosh F.C., Käs J., Janmey P.A. Elasticity of semiflexible biopolymer networks. Phys. Rev. Lett. 1995;75:4425–4428. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
- 49.Conti E., Mackintosh F.C. Cross-linked networks of stiff filaments exhibit negative normal stress. Phys. Rev. Lett. 2009;102:088102. doi: 10.1103/PhysRevLett.102.088102. [DOI] [PubMed] [Google Scholar]
- 50.Broedersz C.P., Mao X., MacKintosh F.C. Criticality and isostaticity in fibre networks. Nat. Phys. 2011;7:983–988. [Google Scholar]
- 51.Broedersz C.P., Sheinman M., Mackintosh F.C. Filament-length-controlled elasticity in 3D fiber networks. Phys. Rev. Lett. 2012;108:078102. doi: 10.1103/PhysRevLett.108.078102. [DOI] [PubMed] [Google Scholar]
- 52.Head D.A., Levine A.J., MacKintosh F.C. Distinct regimes of elastic response and deformation modes of cross-linked cytoskeletal and semiflexible polymer networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;68:061907. doi: 10.1103/PhysRevE.68.061907. [DOI] [PubMed] [Google Scholar]
- 53.Bai M., Missel A.R., Levine A.J. The mechanics and affine–nonaffine transition in polydisperse semiflexible networks. Soft Matter. 2011;7:907. doi: 10.1103/PhysRevE.82.041907. [DOI] [PubMed] [Google Scholar]
- 54.Missel A.R., Bai M., Levine A.J. Affine-nonaffine transition in networks of nematically ordered semiflexible polymers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;82:041907. doi: 10.1103/PhysRevE.82.041907. [DOI] [PubMed] [Google Scholar]
- 55.Zuidema J.M., Rivet C.J., Morrison F.A. A protocol for rheological characterization of hydrogels for tissue engineering strategies. J. Biomed. Mater. Res. B Appl. Biomater. 2014;102:1063–1073. doi: 10.1002/jbm.b.33088. [DOI] [PubMed] [Google Scholar]
- 56.Shah J.V., Janmey P.A. Strain hardening of fibrin gels and plasma clots. Rheol. Acta. 2013;36:262–268. [Google Scholar]
- 57.Weigandt K.M., Pozzo D.C., Porcar L. Structure of high density fibrin networks probed with neutron scattering and rheology. Soft Matter. 2009;5:4321. [Google Scholar]
- 58.Bernal M., Gennisson J.-L., Tanter M. Shear wave elastography quantification of blood elasticity during clotting. Ultrasound Med. Biol. 2012;38:2218–2228. doi: 10.1016/j.ultrasmedbio.2012.08.007. [DOI] [PubMed] [Google Scholar]
- 59.Smith E.L., Cardinali B., Philippou H. Elimination of coagulation factor XIII from fibrinogen preparations. J. Thromb. Haemost. 2013;11:993–995. doi: 10.1111/jth.12174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Marder V.J., Shulman N.R., Carroll W.R. High molecular weight derivatives of human fibrinogen produced by plasmin. I. Physicochemical and immunological characterization. J. Biol. Chem. 1969;244:2111–2119. [PubMed] [Google Scholar]
- 61.Larsson U. Polymerization and gelation of fibrinogen in D2O. Eur. J. Biochem. 1988;174:139–144. doi: 10.1111/j.1432-1033.1988.tb14073.x. [DOI] [PubMed] [Google Scholar]
- 62.Laemmli U.K. Cleavage of structural proteins during the assembly of the head of bacteriophage T4. Nature. 1970;227:680–685. doi: 10.1038/227680a0. [DOI] [PubMed] [Google Scholar]
- 63.Shulman S. The size and shape of bovine fibrinogen. Studies of sedimentation, diffusion and viscosity. J. Am. Chem. Soc. 1953;75:5846–5852. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


