Estimating Orientation Factors in the FRET Theory of Fluorescent Proteins: The TagRFP-KFP Pair and Beyond

Abstract

The orientation factor κ², one of the key parameters defining Förster resonance energy transfer efficiency, is determined by the transition dipole moment orientations of the donor and acceptor species. Using the results of quantum chemical and quantum mechanical/molecular mechanical calculations for the chromophore-containing pockets in selected colored proteins of the green fluorescent protein family, we derived transition dipole moments corresponding to the S_0,min → S₁ excitation for green fluorescent protein, red fluorescent protein (TagRFP), and kindling fluorescent protein, and the S_1,min → S₀ emission for TagRFP. These data allowed us to estimate κ² values for the TagRFP-linker-kindling fluorescent protein tetrameric complex required for constructing novel sensors.

Introduction

Förster resonance energy transfer (FRET) is a radiationless process that occurs between a donor molecule in the excited state and an acceptor molecule in the ground state. The importance of FRET in modern biomolecular research is hard to overestimate (1–6). For this work, we concentrate on the application of FRET to the colored protein systems of the green fluorescent protein (GFP) family, well-known molecular markers used in living cells (7–9). More specifically, we are interested in theoretical evaluation of the FRET parameters in these systems, which can be used when constructing novel sensors (10–12), as well as in the interpretation of complicated spectral features of fluorescent proteins.

FRET parameters can be referred to individual properties of donor and acceptor species, namely, absorption and emission band shapes, extinction coefficients, quantum yields, and fluorescence lifetimes, as well as to quantities that are defined by donor and acceptor interactions, including R, the distance between the donor and acceptor, and the orientation factor, κ². The latter quantity is the only parameter defining the Förster radius R₀ (the distance at which 50% of the energy is transferred to the acceptor) that cannot be determined experimentally. In turn, the transfer efficiency E is directly related to R and R₀

$$E=1/\left[1+{\left(R/R_{\mathrm{0}}\right)}^6\right].$$

To estimate κ² the following formula is applied

$${\mathit{\kappa }}^2={\left[\mathbf{d}\cdot \mathbf{a}-3\left(\mathbf{d}\cdot {\mathbf{r}}_{\text{da}}\right)\left(\mathbf{a}\cdot {\mathbf{r}}_{\text{da}}\right)\right]}^2,$$ (1)

where d and a are transition dipole moments of the donor and acceptor, respectively, and r_da is a normalized vector connecting the two dyes. The value of κ² can range between 0 and 4, and a strongly simplified approach used to estimate this value is to average the donor and acceptor orientations of freely rotated dyes, leading to a mean value κ² = 2/3. However, this approximation may be inappropriate for the chromophores trapped inside protein barrels of fluorescent proteins.

To evaluate κ² accurately, using electronic structure principles, one must optimize the ground- and excited-state equilibrium geometry parameters of relevant models, and then calculate the transition dipole moment (TDM). The practical realization of this strategy requires considerable effort: large molecular model systems mimicking chromophore-containing pockets should be considered, optimizing excited-state geometry parameters is an especially difficult task, and calculating electronic transition properties to a reasonable level of accuracy is an issue of debate.

The primary goal of this study was to calculate TDMs to compute the κ² parameters of a specific FRET system, composed of two colored proteins in the GFP family, red fluorescent protein (TagRFP) and kindling fluorescent protein (KFP), connected by a flexible peptide linker. KFP, serving as an acceptor partner in this pair, is the Ala-143-Gly mutant of natural chromoprotein asFP595 from Anemonia sulcata (13–15). Brightly fluorescent TagRFP is the donor in this particular FRET pair, and is a genetic construct derived from the wild-type protein found in the sea anemone Entacmaea quadricolor (16,17). Employing FRET between these two proteins (connected by an appropriate peptide linker) opens new avenues for monitoring biological and physiological mechanisms. Recently, a FRET system composed of TagRFP and KFP connected by a linker built from 23 amino acids was studied experimentally as a promising novel diagnostic tool (12). Proteolic cleavage of the linker between brightly fluorescent donor TagRFP and dark acceptor KFP resulted in a substantial increase of donor fluorescence intensity and lifetime. The TagRFP-linker-KFP fusion contains the caspase-3 recognition site DEVD, which is cleaved upon caspase-3 activation.

By analyzing the results of quantum chemical (QC) and quantum mechanical/molecular mechanical (QM/MM) approaches for the corresponding chromophores within their protein environments, we deduce that the TDMs for S_0,min → S₁ in the KFP transition and S_1,min → S₀ in the TagRFP transition are characterized by similar orientations relative to the chromophore. Ansbacher et al. (18) have hypothesized a similar assumption by considering bare chromophores extracted from their protein matrices. Combining this fairly simple rule with knowledge of protein structure allows us to interpret the FRET efficiency for the tetrameric TagRFP-linker-KFP system and the dimeric KillerRed variant.

Materials and Methods

Molecular models of the chromophore-containing pockets of fluorescent proteins from the GFP family were constructed for this work based on available Protein Data Bank (PDB) crystal structures. The following members were considered: GFP (the relevant crystal structure PDB ID 1EMA (19)), KFP (PDB ID 1XQM (14)), and TagRFP (PDB ID 3M22 (17)). The chemical formulae of the corresponding chromophore molecules in the anionic protonation state are presented in Fig. 1.

Figure 1.

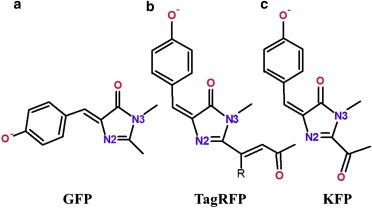
Chemical structures of the chromophores from the fluorescent proteins: (a) GFP, (b) TagRFP, (c) KFP. Only the oxygen and nitrogen atoms are designated. To see this figure in color, go online.

The GFP chromophore shown in Fig. 1 a represents the cis conformer, whereas the TagRFP and KFP chromophores (Fig. 1, b and c) are shown in the trans conformation, as they occur in their protein matrices.

In all cases, fairly large model systems composed of molecular groups from crystal structures were selected for equilibrium geometry parameter calculations. After addition of hydrogen atoms, assuming a customary assignment of protons to the polar residues of Asp, Glu (negatively charged), Lys and Arg (positively charged), optimization of coordinates in model systems was performed using either QM/MM or QC methods. The QM/MM approach was applied to model systems that included almost the entire protein and the QC approach to systems mimicking chromophore-containing pockets. In the latter case, the coordinates of the outermost atoms at the periphery of the clusters were kept frozen, as they were in the corresponding crystal structures.

Minimum-energy, ground-state equilibrium geometry parameters in the lowest singlet electronic state S₀ were calculated using density functional theory (DFT) approaches in quantum subsystems.

In the case of TagRFP model systems, the following approaches were applied. For the QC calculations, we constructed a model cluster (called the GS-cluster) composed of the chromophore, the side chains of Leu-13, Gln-39, Ala-59 Thr-60, Ser-61, Phe-62, Ser-66, Arg-67, Arg-92, Gln-106, Tyr-117, Asn-143, Glu-145, Ser-158, Met-160, Phe-174, His-197, Leu-199, Gln-213, and Glu-215, and 11 water molecules. After adding hydrogen atoms, the system included 326 atoms in total. Optimization of geometry coordinates was performed in the B3LYP/6-31G^∗ approximation while keeping the C_α atoms of the involved residues frozen. For QM/MM ground state geometry optimization, the protein system was subdivided into QM and MM parts. The QM subsystem included the chromophore, the nearest water molecules, and the side chains of Arg-67, Arg-92, Asn-143, Glu-145, Ser-158, His-197, and Glu-215, whereas the rest of the protein was treated as the MM subsystem. The DFT approach, with functional PBE0 and cc-pVDZ basis sets, was applied in QM, whereas AMBER force field parameters were applied in MM.

For KFP, the QM subsystem included the chromophore, the nearest water molecules, and the side chains of Lys-67, Arg-92, Glu-145, Ser-158, His-197, and Glu-215; the rest of the protein was treated as a MM subsystem. The DFT approach, with functional PBE0 and cc-pVDZ basis sets, was applied for calculations in QM, and AMBER force field parameters in MM.

The model system mimicking GFP was constructed following motifs of the crystal structure PDB ID 1EMA (19). This entry corresponds to the protein with a point mutation Ser-65-Thr compared to the wild-type GFP. The structure was augmented by hydrogen atoms, and the side chain of the residue at position 65 was set to Ser, as in the wild-type. The atomic coordinates of the model system were then optimized by the QM/MM technique, using the flexible effective fragment potential method (20,21) with PBE0/6-31G^∗ in the QM part and the AMBER force field parameters in the MM part. The chromophore and the side chains of Glu-222, Arg-96, Ser-205, and His-148, as well as the two nearest water molecules were assigned to the quantum subsystem. This model structure refers to the so-called I-form of GFP (22).

Excited state (S₁) geometry coordinates for TagRFP models were optimized using the configuration interaction singles (CIS) approximation and the complete active space self-consistent field (CASSCF) approach. To find coordinates of the minimum energy structures in the S₁ excited state, we carried out QC calculations for molecular clusters that were constructed as follows. First, the model GS-cluster was reduced and its coordinates optimized for the second singlet S₁ state using the CIS/6-31G^∗ approximation. We designated the corresponding 241-atom system ES-cluster1. Another model, ES-cluster2, was constructed by taking the coordinates of the QM/MM ground state structure, i.e., removing the MM part from the QM/MM model. Optimization of excited-state geometry parameters was carried out using the CASSCF procedure, keeping frozen the coordinates of the outermost atoms in the cluster. More specifically, we applied the CASSCF(6/6) method by distributing six electrons over six orbitals, and obtained a true solution for the second root in the corresponding configuration interaction expansion (in other words, the state-specific CASSCF solution was constructed). To select the active orbitals we first performed CIS calculations and choose the π-orbitals whose population changed upon the S₀ → S₁ excitation. In this particular case three double occupied and three vacant orbitals in the ground state were included to the active space.

TDMs for the S_0,min → S₁ transitions in GFP, TagRFP, and KFP, and for the S_1,min → S₀ transition in TagRFP were computed using ab initio CIS or semiempirical ZINDO (23) approximations. We also report the ZINDO results for the vertical transition energies and the corresponding optical band maxima wavelengths. We previously showed (24–29) that such a computational strategy, namely, estimating transition energies at the ZINDO level using a chromophore’s coordinates optimized by DFT calculations, yields results that are in remarkably good agreement with experimental data.

QC calculations were carried out using Gaussian-03 (30), Firefly (31), and ORCA (32) programs. QM/MM calculations were performed using the NWChem program (33), as well as a combination of the GAMESS(US) (34) and TINKER (35) software packages, as described in (20,21). Additional details are presented below, with the results from each system.

Results

Structures, absorption, and emission spectra of the TagRFP model systems

Geometry configurations of the chromophore-containing pockets in TagRFP were optimized in the ground electronic state in QC calculations for a model cluster and in QM/MM calculations for a larger model encompassing the entire protein. Remarkably, both approaches resulted in very close equilibrium configurations of the chromophore and in indistinguishable orientations of the TDM.

A view of the most important part of the model cluster, showing the chromophore and the nearest residues in the chromophore environment, is illustrated in Fig. 2. We specify several key intermolecular distances obtained from our calculations (top and middle values in Fig. 2) to show that a good agreement with the parent crystal structure PDB ID 3M22 (bottom values), solved to 2.2 Å resolution (17), is obtained. Specific equilibrium geometry parameters of the chromophore molecule in the ground electronic state are provided in Table S1 in the Supporting Material. The chromophore structure is essentially nonplanar in the protein matrix.

Figure 2.

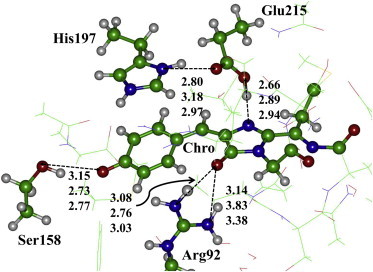
A part of the molecular cluster for the chromophore-containing pocket of TagRFP. Selected distances between heavy atoms (in Å) are arranged as follows: QC cluster model (top), QM/MM model (middle), and crystal structure PDB ID 3M22 (bottom). In this and forthcoming figures, carbon atoms are colored in green, oxygen in red, and nitrogen in blue. To see this figure in color, go online.

The experimental absorption band maximum for TagRFP corresponds to excitation energy of 2.23 eV or a wavelength of 555 nm (16,17). The computational results, using ZINDO at the DFT-optimized geometry for the GS-cluster model, are 2.25 eV and 551 nm; the results of the QM/MM model are 2.41 eV and 515 nm.

The equilibrium geometry parameters of the chromophore molecule in the S₁ excited state are provided in Table S2.

The experimental emission band maximum for TagRFP corresponds to an energy of 2.12 eV or a wavelength of 584 nm (16,17). Computational results (ZINDO) for the ES-cluster1 model are 2.21 eV and 559 nm, and 2.19 eV and 565 nm for the ES-cluster2 model.

Fig. 3 illustrates computed TDM directions for S_0,min → S₁ absorption (upper graph) and for S_1,min → S₀ emission (lower graph). Remarkably, the sets of different theoretical models used in this work (QM/MM and GS-cluster for the ground state, and ES-cluster1 and ES-cluster2 for the excited state) resulted in practically indistinguishable predictions for TDM directions. As seen in Fig. 3, absorption and emission TDMs can be viewed as vectors connecting the phenolic oxygen (O) and the imidazolinone nitrogen (N3). The absorption and emission transition dipole moments can often be considered to be colinear. In particular, similarities in absorption and emission TDM directions in fluorescent proteins were discussed in (36) by analyzing results from experiments on crystals.

Figure 3.

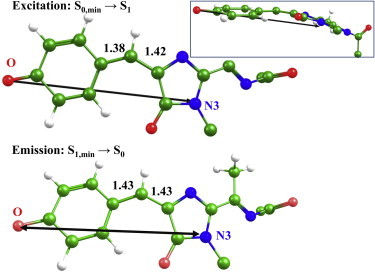
Structures of the TagRFP chromophore and TDM orientations. Upper graph refers to the S₀ minimum and the S_0,min → S₁ transition; bottom graph refers to the S₁ minimum and the S_1,min → S₀ transition. Distances (in Å) illustrate the bond-length changes at the methylene bridge upon excitation. TDM vectors connecting the phenolic O and N3 are indicated by double-arrow lines. The inset in the upper-right corner illustrates that the chromophore is essentially nonplanar. To see this figure in color, go online.

A final comment in this subsection refers to the heuristic rule for guessing the TDM direction in fluorescent proteins, as formulated by Ansbacher et al. (18). Apparently, an imaginary line connecting the two farthest atoms in the π-conjugated system of the molecule suggested in (18) deviates here from our prediction: in our calculations the TDM vector connects the O and N3 atomic centers, but not the two farthest oxygen atoms (Fig. 3). However, it should be noted that the authors of (18) considered mainly the cis form of chromophores; here, the chromophore is in the trans configuration.

Structure and absorption spectra of KFP and GFP model systems

A view of the most important part of the model cluster, showing the chromophore and the key residues in the chromophore environment, is illustrated in Fig. 4. Equilibrium geometry parameters of the chromophore molecule are provided in Table S3. Similar to TagRFP, the chromophore structure is essentially nonplanar in the protein matrix.

Figure 4.

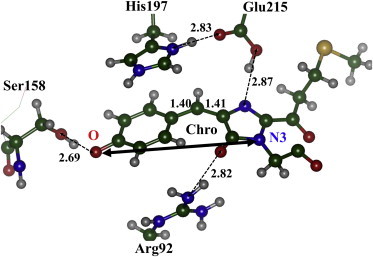
A part of the molecular cluster that includes the chromophore-containing domain of KFP. Selected distances between heavy atoms are given in Å. The TDM direction for the S_0,min → S₁ excitation is shown as a solid, double-arrow line. To see this figure in color, go online.

The experimental absorption band maximum in KFP corresponds to excitation energy of 2.18 eV or a wavelength of 568 nm (13). Computational results (ZINDO at the DFT-optimized geometry) for this QM/MM model are 2.31 eV or 535 nm.

The computed TDM direction for the S_0,min → S₁ excitation in KFP is also shown in Fig. 4; apparently, it is practically the same as that calculated for TagRFP (Fig. 3).

Finally, we considered the parent member of this protein family, GFP itself, with the anionic chromophore. We illustrate this model as Fig. S1, and Table S4 lists the Cartesian coordinates of the GFP chromophore. As in all previous examples, we estimated the TDM at the equilibrium geometry configuration by using ZINDO at the DFT-optimized geometry.

In this particular case, we were able to directly compare our computational data (Fig. 5) with the TDM calculation results for the bare fluorescent protein chromophores reported in (18). The authors suggested characterizing the TDM direction by a deviation angle from the carbonyl group of the imidazolinone ring. This direction for the anionic GFP chromophore, estimated in (18) as 70°, is plotted in Fig. 5 (dashed, double-arrow line). Our TDM calculations again revealed a vector between the phenolic O and the N3 of the chromophore (solid black line). At a glance (Fig. 5), both theoretical approaches result in fairly consistent conclusions.

Figure 5.

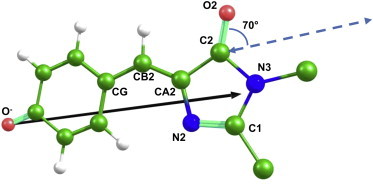
Computed TDM for GFP with the anionic chromophore. The result of our approach is shown as a solid black vector. The vector estimated in (18) is indicated by a dashed, double-arrow line. To see this figure in color, go online.

The following two subsections illustrate applications of the proposed rule to orient the TDM in fluorescent protein chromophores in the O-N3 direction for the complex TagRFP-linker-KFP and KillerRed systems.

Orientation factors for the tetrameric TagRFP-linker-KFP system

The model considered in (12) for the tetrameric TagRFP-linker-KFP system was constructed using molecular docking as a tool to arrange eight protein barrels linked by peptide chains. Analysis of the conformational flexibility of such a system is beyond the scope of this work (see (12)). Of importance, the model described in (12) did not take into account the orientation factors of donor and acceptor chromophores when estimating FRET efficiency; an averaged value of κ² = 2/3 was used. Here, we calculated specific orientation factors using the established rule to orient TDMs in the corresponding O-N3 directions. Because TagRFP species are located symmetrically around the core KFP tetramer complex, we considered a reduced system composed of single TagRFP species connected to a KFP tetramer by a flexible linker (Fig. 6). After photoexcitation, the TagRFP donor (D) can either fluoresce or transfer energy to one of four acceptors (A_i).

Figure 6.

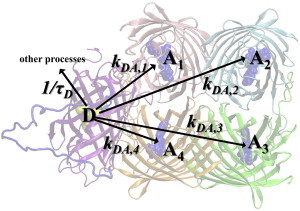
Structure of the TagRFP-linker-KFP (tetramer) complex. The chromophores of the donor, D (from TagRFP), and four acceptors, A_i (from KFP), are represented by the solid balls. To see this figure in color, go online.

Table 1 shows distances, computed orientation factors, and FRET rate constants corresponding to all possible pairs. We can describe processes occurring after TagRFP energy absorption in terms of parallel reactions: energy can be either transferred to one of four acceptors or emitted from TagRFP with the corresponding rate constants k_DA,i (i = 1 ÷ 4) or 1/τ_D. The probability of occurrence of each pathway of energy transfer is proportional to the corresponding reaction rate constant; therefore probability (or efficiency) of FRET is estimated as follows:

$$E=\frac{{\sum }_{i=1}^4{k}_{DA,i}}{{\sum }_{i=1}^4{k}_{DA,i}+1/{\tau }_D}.$$

Application of this formula leads to the calculated FRET efficiency for this particular system as 86%. The latter value indicates, first, that the conformation presented in (12) is not the major one for this sensor, and second, a high efficiency in this particular conformation is due to individual properties of donor and acceptor species despite the relatively low orientation factors κ². Therefore, a proper modification of the linker may affect a distance distribution between donor and acceptor molecules resulting in enhancement of sensor properties.

Table 1.

Interchromophore distances (R), computed orientation factors (κ²), and rate constants (k_DA,i) for the TagRFP-linker-KFP (tetramer) complex shown in Fig. 6

Parameter	D-A1	D-A2	D-A3	D-A4
R, Å	38.5	63.1	57.8	37.7
κ2	0.89	0.62	0.02	0.06
kDAi, ns−1	2.33	0.09	<0.01	0.20

Evaluating the data shown in Table 1 immediately makes it clear that contributions to FRET efficiency are not only due to differences in distances, but also due to different orientation factors. We reiterate that an estimated κ² value, 2/3 = 0.67, is typically used when evaluating FRET efficiency.

Orientation factor for the KillerRed dimer

An increased interest in one of the genetically derived red fluorescent proteins, KillerRed (37), is explained by its cytotoxicity in living cells. A series of structural and spectral studies of this protein has been completed, among which the recent work described in (38) is worth particular attention. The authors designed a Val-44-Ala mutant of KillerRed and noticed that its composition as a dimer demonstrated an intradimeric FRET effect between neutral (green) and anionic (blue) chromophores. The authors assume that the green emission peak may be explained by FRET and point to the interesting head-to-tail orientation of two chromophores in the dimer (Fig. 7).

Figure 7.

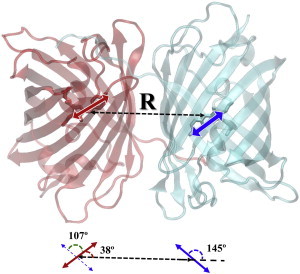
Dimeric structure of the Val-44-Ala mutant of KillerRed by motifs of PDB ID 4B30 (38). TDM directions are indicated by solid, double-arrow lines. The inset at the bottom shows the orientation angles of the TDM vectors of the crystal geometry. To see this figure in color, go online.

We applied a heuristic rule to orient the TDM (from O to N3) in both chromophores in the model system, based on the crystal structure of the dimer (PDB ID 4B30), and calculated the κ² for such a construct. The resulting κ² value of 2.69 far exceeds the averaged 2/3 = 0.67 estimate, which, in conjunction with the short distance between chromophores, explains the observed considerably FRET efficiency.

Discussion

Despite the structural similarities between colored proteins in the GFP family, it is far from obvious that they should share a common TDM orientation. In fact, the chromophores of these proteins are not identical; they are characterized by varying numbers of conjugated π-bonds and noticeable differences in geometry configurations, including, in particular, the cis and trans isomers (Scheme 1). However, the calculations presently used, as well as the recent work by Ansbacher et al. (18), encourage us to assume that fairly simple rules may provide reasonably good estimates for TDM orientations within this protein family. The authors of (18) used the time-dependent (TD)-DFT method to calculate the TDM in S₀-S₁ absorption for several fluorescent protein chromophores for gas phase and solution conditions (in the latter case, within the polarized continuum model). They borrowed the starting coordinates of the chromophore molecules from the corresponding crystal structures and reoptimized the coordinates within the DFT B3LYP/6-31G^∗ approach in vacuo. As expected, the ground-state geometry structures of the chromophores turned out to be planar. Next, TDMs were computed by using the B3LYP/6-31+G^∗ approach in TD-DFT. For GFP, the only system considered here and in (18), and for which direct comparison is possible, the results are consistent.

To our knowledge, novel features of our work are related to 1), modeling entire chromophore-containing pockets, not just bare chromophores (i.e., a realistic protein environment is considered, resulting in nonplanar geometry structures); 2), using other electronic structure theory methods beyond TD-DFT; and 3), calculating the S₁-S₀ transition moment directly for emission in TagRFP.

For obtaining fairly simple TDM direction estimates for absorption and emission, our recommendation is to consider the vector connecting the phenolic O and the N3 of the chromophore (Scheme 1). Applying this rule, we are able to explain the efficient FRET observed in the tetrameric TagRFP-linker-KFP system (12) and in the dimeric form of a variant of the KillerRed protein (38).

Conclusions

We report the TDM and orientation factor calculation results for TagRFP-KFP, the pair of fluorescent proteins required for construction of fusion proteins with enhanced FRET efficiency. The QM/MM and QC approaches for large molecular clusters allowed us to compute the properties of the chromophores in the protein environment. On the basis of these calculations, we deduced that TDMs for the S_0,min-S₁ and S_1,min-S₀ transitions in fluorescent proteins of the GFP family have similar orientations relative to the chromophore: the TDM direction can be estimated accurately as the vector between the phenolic O and N3 of the chromophore. Application of this simple rule to the chromophores in the tetrameric TagRFP-linker-KFP system and in the dimeric KillerRed variant allowed us to provide an interpretation of their FRET efficiencies.