Physical Modeling of Chromosome Segregation in Escherichia coli Reveals Impact of Force and DNA Relaxation

Abstract

The physical mechanism by which Escherichia coli segregates copies of its chromosome for partitioning into daughter cells is unknown, partly due to the difficulty in interpreting the complex dynamic behavior during segregation. Analysis of previous chromosome segregation measurements in E. coli demonstrates that the origin of replication exhibits processive motion with a mean displacement that scales as t^0.32. In this work, we develop a model for segregation of chromosomal DNA as a Rouse polymer in a viscoelastic medium with a force applied to a single monomer. Our model demonstrates that the observed power-law scaling of the mean displacement and the behavior of the velocity autocorrelation function is captured by accounting for the relaxation of the polymer chain and the viscoelastic environment. We show that the ratio of the mean displacement to the variance of the displacement during segregation events is a critical metric that eliminates the compounding effects of polymer and medium dynamics and provides the segregation force. We calculate the force of oriC segregation in E. coli to be ∼0.49 pN.

Introduction

Numerous biological processes hinge on dynamic rearrangement of the massive genomic DNA strand within the crowded cellular environment. After replication, daughter strands must be disentangled from parent DNA, and kilobase-length segments of DNA must be organized to form large regulatory complexes. Megabase-scale DNA looping events are required for recombination to occur. In the model bacterium Escherichia coli, the motion of chromosomal DNA between replication events exhibits complex dynamic behavior. A single DNA locus moves along a stochastic trajectory with zero mean displacement (MD) and a power-law mean-square displacement (MSD) with time (1–4). The observed MSD has a subdiffusive scaling (i.e., power-law exponent <1) (1–3), and the measured MSD and velocity autocorrelation function reveal a memory signature that implicates both the polymer relaxation and environmental viscoelasticity as the major determinants of the observed behavior (1,5,6). The amplitude of the random forces driving this stochastic motion are ATP-dependent (7), suggesting that biological activity within the nucleoid acts as an additional driving force for motion, beyond the thermal fluctuations alone. Despite this complication, a simple polymer model captures this in vivo behavior (5,6).

In stark contrast to eukaryotic mitosis, newly replicated chromosomal DNA in E. coli is continuously segregated, i.e., shortly after a DNA locus is replicated, the two copies move toward opposite cell poles in a concerted manner (nonzero MD) with stochastic fluctuations in each trajectory (2,3,8–12). This process of organizational flux is distinct from the steady-state behavior between replication events, and it is not clear how the physical mechanisms responsible for the stochastic motion between replication events impact the concerted motion during the segregation process. Furthermore, the physical mechanism by which E. coli drives segregation is still a mystery, although several models propose spatial crowding (13,14) or some active biological mechanism (e.g., filament depolymerization (15) or interaction with a membrane-protein gradient (16)) as possible drivers. Identification of the segregation mechanism requires a clear interpretation of the dynamic behavior, accounting for both the driving force and the relaxation of the viscoelastic environment and the DNA polymer.

In this article, we leverage a simple model for active segregation to analyze the motion of the E. coli origin of replication (oriC), one of the first genetic loci to have its copies partitioned. We model the DNA as a flexible polymer in a viscoelastic environment, which accurately captures the stochastic behavior of chromosomal DNA between replication events (1,5,6). Thus, we assume that the physical properties of the cellular environment and the DNA strand during segregation remain relatively unchanged from the properties between replication events. We model the concerted motion toward the cell poles as a constant force applied to a single chain segment (i.e., an active biological driving force at a DNA locus). Our approach aims to illustrate the competing physical effects using the simplest possible model to result in concerted polymer motion. Despite its simplicity, our model provides a quantitatively accurate prediction of the in vivo motion during segregation.

Materials and Methods

Polymer model

We consider a flexible polymer in a viscoelastic environment. The time-dependent polymer conformation is defined by the space curve $\overrightarrow{r}\left(n,t\right)$, where n is a contour variable that runs from zero to the chain length N (number of Kuhn lengths) and t is the time. The polymer chain has Kuhn length b and is subjected to an external force $f\hat{x}$ at its end. The viscoelastic response to segmental motion is captured by a viscoelastic drag coefficient ξ and a memory kernel K(t) = (2 – α)(1 – α)|t|^−α. This single power-law kernel results in a single power-law MSD (i.e., MSD ∼ t^α) for a particle undergoing Brownian diffusion in this environment, and is commonly used to describe fractional Brownian motion (17,18). The choice of memory kernel K(t) is based on the experimentally observed in vivo motion of both an RNA-protein particle (19) and a chromosomal locus (1,6,7) in E. coli having a single power-law MSD over the reported timescales. In this treatment, b, ξ, and K(t) have no spatial or contour position dependence, and are assumed to remain approximately the same throughout the segregation process. We stress that this homogeneous model is intended to describe a local region in the Ori macrodomain and not the entire chromosome (locus diffusivity can vary significantly between macrodomains (4).

The dynamic motion of this fractional-Langevin-motion polymer chain is governed by the Langevin equation

$$\xi {\int }_0^{t}d{t}^{\prime }K\left(t-t^{\prime }\right)\frac{\partial \overrightarrow{r}\left(n,t^{\prime }\right)}{\partial t}=\frac{3k_{\text{B}}T}{b^2}\frac{{\partial }^2\overrightarrow{r}\left(n,t\right)}{\partial n^2}+{\overrightarrow{f}}^{\left(B\right)}\left(n,t\right),$$ (1)

where the left-hand side represents a drag force whose magnitude and orientation is dependent on all previous values of the monomer velocity weighted by the memory kernel. The first term on the right-hand side represents the elastic forces between neighboring monomers, which are assumed to behave like Hookean springs with a spring constant 3k_BTb⁻². We have employed the continuum approximation to describe the distance between neighboring monomers, as is commonly used in analytical treatments for very long polymer chains (20). The Brownian force ${\overrightarrow{f}}^{\left(B\right)}\left(n,t\right)$ obeys the fluctuation-dissipation theorem, which states that

$$\begin{array}{l}\langle {\overrightarrow{f}}^{\left(B\right)}\left(n,t\right)\rangle =0\text{and}\hfill \\ \langle {\overrightarrow{f}}^{\left(B\right)}\left(n,t\right){\overrightarrow{f}}^{\left(B\right)}\left(n^{\prime },t^{\prime }\right)\rangle =\xi k_{\text{B}}TK\left(t-t^{\prime }\right)\delta \left(n-n^{\prime }\right)\mathbf{I}\hfill \end{array}$$

(5). The boundary conditions at the chain ends are

$${\frac{3k_{\text{B}}T}{b^2}\frac{\partial \overrightarrow{r}\left(n,t\right)}{\partial n}|}_{n=N}+f\hat{x}=\overrightarrow{0}\text{and}\overrightarrow{r}\left(n=0,t\right)=\overrightarrow{0},$$ (2)

introducing the external force f into the model. The external force drives the model out of its steady-state conformation, resulting in a nontrivial change to its dynamic behavior that is not described in our previous steady-state treatments (1,5,6).

Our model contains several simplifications that neglect features that exist within a bacterial cell. However, the physical behavior at the length and timescales of interest in this work are not affected by these simplifications. For instance, in our model the chain is assumed to be linear, and the force is subjected to the end bead. This choice of representation is inspired by the concept of the external force pulling on the oriC region while the replisome stays fixed at the mid-cell position (21). Fig. 1 A shows a schematic representation of segregation within E. coli, demonstrating the observed trajectory of the origin of replication within the circular chromosome of this species. Escherichia coli positions oriC at the cell midplane between segregation events, and ∼10 min after its replication (3), each oriC copy migrates to opposite quarter-cell positions (Fig. 2, A and B). This specific scenario could be captured by modeling ring polymers with appropriate forces and anchors. We have tested these specific cases and found that the response of a single locus to an external force is identical in all scenarios, provided the timescale of observation is much shorter than the relaxation time of the intervening DNA segments. More generally, this model neglects hydrodynamic interactions between different segments of the chain, because such interactions would be screened due to the concentrated macromolecular environment of the cellular cytoplasm (5,20).

Figure 1.

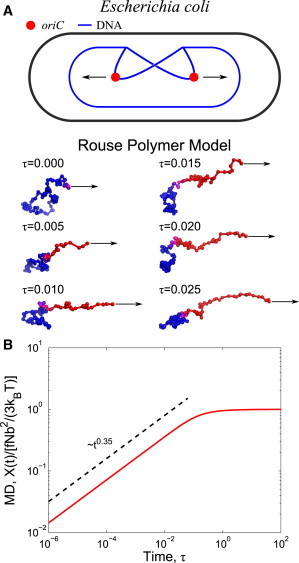
(A) Schematic of our model for the segregation of the oriC locus as the Rouse chain being extended from its steady-state configuration. The red segments highlight the portions of the polymer chain to which stress has propagated from the force applied at the end bead. (B) MD = X(t)/[fNb²/3k_BT] of the end bead pulled by an external force for a fractional-Langevin-motion polymer versus dimensionless time τ = t/t_R, where t_R = [N²b²ξ/(k_BT)]^1/α for α = 0.7. To see this figure in color, go online.

Figure 2.

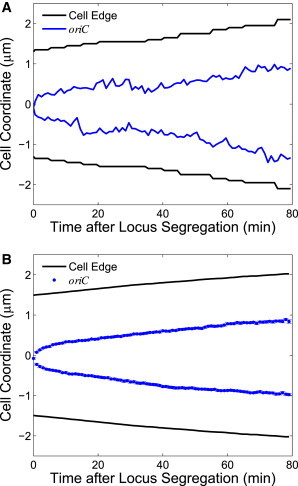
oriC locus trajectories and longitudinal cell edges for (A) a single representative trajectory pair and (B) an ensemble average of trajectory pairs. Error bars in (B) for oriC are standard error of the mean.

We also neglect the influence of the confining cell wall in our model. Simulations of a single polymer chain within a confinement predict that the motion is dominated by the Rouse relaxation modes for timescales less than the relaxation time for the cell-length wavemode (5). Furthermore, we do not include the self-interaction of the chain that introduces entanglement in concentrated polymer solutions (20). For simulations of a single self-interacting polymer within a confinement, no signatures of reptation are evident (e.g., distinct scaling regimes within the primitive path) and the Rouse relaxation modes appear to be largely unaffected (5). A biological justification for neglecting polymer self-interaction is that the activity of Topoisomerase IV in E. coli can cross DNA strands through one another and resolve entanglements (22). The effects of supercoiling and chain rigidity contribute to relaxation timescales in the range of milliseconds, which are substantially below the timescales of observation (>1 s) (23). Because the in vivo segregation exhibits a single power law for MD, we assume the local influence of rigidity and supercoiling has sufficiently relaxed.

The concerted motion of the forced segment is predicted using Eq. 1 to find $X\left(t\right)=\hat{x}\cdot \langle \overrightarrow{r}\left(n=N,t\right)\rangle$, resulting in the expression

$$X\left(t\right)=\frac{fN{b}^2}{3k_{\text{B}}T}-\sum _{p=1}^{\infty }\frac{2Nf}{k_p}{E}_{\alpha ,1}\left[-\frac{k_p{t}^{\alpha }}{\xi N\text{Γ}\left(3-\alpha \right)}\right],$$ (3)

where

$$k_p=\left[3{\pi }^2{k}_{\text{B}}T/\left(N{b}^2\right)\right]{\left(p-1/2\right)}^2$$

and E_α,β(x) is the generalized Mittag-Leffler function

$$E_{\alpha ,\beta }\left(z\right)={\sum }_{j=0}^{\infty }\frac{z^j}{\text{Γ}\left(\beta +\alpha j\right)}$$

(5). Tracking of fluorescent mRNA-protein particles in live E. coli reveals that α ≈ 0.7 (1,19). When this value for α is plugged into Eq. 3, the forced segment is predicted to have an MD ∼t^0.35 before the polymer’s steady-state extension is reached (Fig. 1 B).

The physical justification for the short-time behavior of the forced monomer is determined from a scaling analysis. The pth normal mode of the polymer corresponds to a wavelength λ = bN/p, and each term in the summation in Eq. 3 represents the contribution of the normal mode to the mean displacement. We identify a timescale t_λ at which the pth mode becomes correlated (5).

We find

$$t_{\lambda }\sim {\left(\frac{{\lambda }^2\xi }{k_{\text{B}}T}\right)}^{\frac{1}{\alpha }}\text{or}\lambda \sim {\left(\frac{k_{\text{B}}T}{\xi }\right)}^{1/2}{t}_{\lambda }^{\frac{\alpha }{2}}$$ (4)

by setting the argument of the Mittag-Leffler function within the pth term to order unity.

At the timescale t_λ, sections of chain at lengths shorter than λ away from the end monomer move in a coordinated fashion in response to the external force. Thus, the end monomer feels an effective drag coefficient ξ ∼ ξλ/b at time t_λ. The resulting MD at time t_λ scales as

$$X\sim \frac{f}{{\xi }_{\lambda }}{t}_{\lambda }^{\alpha }\sim fb{\left(\frac{1}{k_{\text{B}}T\xi }\right)}^{1/2}{t}_{\lambda }^{\frac{\alpha }{2}}$$ (5)

or in dimensionless form, we write

$$\frac{X}{Nb}\sim \frac{fb}{k_{\text{B}}T}{\tau }^{\frac{\alpha }{2}},$$ (6)

where τ = t/t_R with the Rouse relaxation time t_R =[b²N²ξ/(k_BT)]^1/α. We note that this scaling is consistent with a previous treatment derived for a Rouse polymer with α = 1 (24,25). This treatment also shows that this type of Rouse polymer extension model is valid for f < f_c = 3K_BT/b, beyond which individual Kuhn segments would reach full extension (24).

Nucleoid expansion model

During the process of chromosome replication and segregation, the cell continues to grow in size, and the nucleoid expands with it (26). To account for the motion of chromosome loci due to cell growth, we use a simple affine expansion model. This model assumes that locus motion, purely due to the expansion of the nucleoid, would not change the locus position relative to the total cell length (11). We therefore subtract-off this prediction from the total motion of the locus due to other forces. This model also assumes that, on average, the nucleoid expands like the cell length in an affine manner. In this scenario, locus dynamics are described by the differential equation

$$\frac{d{x}^{\left(T\right)}}{dt}=\frac{dx}{dt}+\frac{x^{\left(T\right)}}{L}\frac{dL}{dt}.$$ (7)

The first term represents rate of change of the observed total position of the locus x^(T), the second term is the rate of change of the locus position due to external forcing, and the third term is the predicted rate of motion due to the change in cell length L. Because locus tracking measurements are made at discrete time points, we approximate Eq. 7 as the difference equation

$$x_i^{\left(T\right)}-x_{i-1}^{\left(T\right)}=x_i-x_{i-1}+\frac{1}{2}\left(\frac{x_i^{\left(T\right)}}{L_i}+\frac{x_{i-1}^{\left(T\right)}}{L_{i-1}}\right)\left(L_i-L_{i-1}\right),$$ (8)

where the growth-corrected displacement of the locus x_i can be determined for each time point using the observed locus positions x_i^(T), cell length measurements L_i, and x₀^(T) = x₀ = 0 (11). Locus trajectory data from Kuwada et al. (3) were analyzed using custom MATLAB software (The MathWorks, Natick, MA). See Kuwada et al. (3) for details of experimental methods and data acquisition.

Results and Discussion

Analysis of locus displacement statistics

We will now compare our theoretical predictions to recently published experimental data from Kuwada et al. (3) for the movement of the oriC locus in E. coli during chromosome segregation. We include the 199 trajectory pairs for which the splitting of the oriC locus into two loci is clearly observed, and use Eq. 8 to remove the contribution from cell growth to the motion of the locus. Because Kuwada et al. (3) observed that the average longitudinal motion of oriC loci appears to be symmetric about the cell center (also see Fig. 2 B), we combine trajectories from both cell halves in our subsequent analysis. We calculate that the growth-corrected MD of the oriC locus scales as a power law over nearly two decades of time during segregation. Fig. 3 A plots the average locus displacement during segregation, for both the observed and growth-corrected locus measurements. We note that the observed MD and the growth-corrected MD are virtually indistinguishable for times <10 min. Fitting the growth-corrected MD curve to a power-law function over the first 60 min reveals that α/2 = 0.32 ± 0.02, slightly lower than our theoretical prediction.

Figure 3.

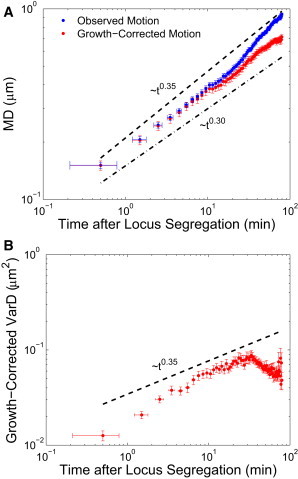
(A) Mean displacement of the oriC locus in E. coli (from Kuwada et al. (3)) over time for observed (blue) and growth-corrected (red) motion. (Vertical error bars) Standard error of the mean. (Horizontal error bars) Standard deviation representing the uncertainty in each time point due to the uncertainty in the true segregation start time. (Dashed black line) Predicted MD scaling of t^0.35; (dot-dashed line) scaling of t^0.3. (B) The variance of the displacement for growth-corrected trajectories. (Dashed black line) Predicted VarD scaling of t^0.35.

Locus tracking in one dimension gives

$$\text{MD}\left(t\right)=\langle X\left(t\right)-X\left(0\right)\rangle =v_{\text{app}}{t}^{\alpha /2}$$

and the variance in displacement

$$\text{VarD}\left(t\right)=\langle {\left[X\left(t\right)-X\left(0\right)-MD\left(t\right)\right]}^2\rangle =2D_{\text{app}}{t}^{\frac{\alpha }{2}},$$

where D_app is the apparent diffusivity and v_app is the apparent velocity. Our definition of VarD gives the time-dependent variance from the mean displacement to remove the processive contribution to motion. Note that if there is no average processive motion of the locus, then MD = 0 and VarD would become equivalent to the MSD. Fitting the VarD curve in Fig. 3 B to a power law between 2 and 30 min produces a scaling of α/2 = 0.38, slightly higher than our theoretical prediction, and consistent with previous locus MSD measurements (1,4). The first two time points are excluded from the fit because they are much smaller than would be predicted, possibly due to the uncertainty in the start time of segregation. Measurements after 30 min are excluded because of the sudden decline in the variance, likely due to loci transitioning to a stay-at-home phase upon reaching its destination at the quarter-cell position (3). Our model does not address this change in dynamics, because we are only interested in modeling the migration period of the oriC loci.

Segregation force calculation

Using our polymer model and the fluctuation-dissipation theorem, we determine the ratio of MD to VarD for the pulled monomer to be

$$\frac{\text{MD}\left(t\right)}{\text{VarD}\left(t\right)}=\frac{f}{2k_{\text{B}}T}.$$ (9)

This simple result arises from the complex polymer and medium relaxation processes contributing to both the MD and the VarD in an identical manner, thus canceling their contributions in the ratio and providing a direct measure of force. This also predicts that for a constant force, the ratio of the MD to the VarD should be approximately constant, which is observed in Fig. 4. The first two ratio measurements appear slightly higher than the rest because the two values of the VarD are smaller than predicted.

Figure 4.

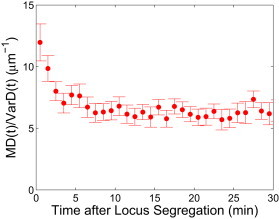
The ratio of the ensemble-averaged MD to the VarD for corresponding observation times. Error bars are standard error of the mean, calculated using a linear-order Taylor expansion to calculate the propagation of uncertainty. To see this figure in color, go online.

Using the MD and VarD measurements with Eq. 9, the force can be calculated to be 0.07 ± 0.02 pN for T = 30°C. However, k_BT does not reflect the true level of background fluctuations, which exhibit an elevated value due to the activity of ATP-dependent enzymes (7). This manifests as a change in the measured value of D_app, but not of α/2, indicating the locus statistics can be described by fractional Brownian motion. This enables us to calculate the effective temperature T^∗ using the observable D_app, and to define a nonequilibrium fluctuation-dissipation relation

$$\langle {\overrightarrow{f}}^{\left(B^{\ast }\right)}\left(n,t\right){\overrightarrow{f}}^{\left(B^{\ast }\right)}\left(n^{\prime },t^{\prime }\right)\rangle =\xi k_{\text{B}}{T}^{\ast }K\left(t-t^{\prime }\right)\delta \left(n-n^{\prime }\right)\mathbf{I},$$

where ${\overrightarrow{f}}^{\left(B^{\ast }\right)}$ would replace ${\overrightarrow{f}}^{\left(B\right)}$ in Eq. 1 (27). We acknowledge that much work remains to be done to fully understand nonequilibrium fluctuations and the effective temperature. We employ this simple correction method to obtain a better estimate of the force. Comparison of the D_app during segregation $\left(D_{\text{app}}^{\left(\text{Seg}\right)}=1.14\times {10}^{-2}\mu {\text{m}}^2{\text{min}}^{-0.38}\right)$ to D_app between segregation events $\left(D_{\text{app}}^{\left(\text{Int}\right)}=0.66\times {10}^{-2}\mu {\text{m}}^2{\text{min}}^{-0.38}\right)$ and with depletion of ATP ($D_{\text{app}}^{\left(\text{Int}\right)}/D_{\text{app}}^{\left(\text{ATP}-\text{Dep}\right)}\approx 1.5$ at T = 30°C (7)) can be used to estimate T^∗. Because D_app ∼ (k_BT)^0.5 for a segment of a Rouse polymer (5), T^∗ can be calculated using

$$T^{\ast }=T{\left(\frac{D_{\text{app}}^{\left(\text{Seg}\right)}}{D_{\text{app}}^{\left(\text{Int}\right)}}\frac{D_{\text{app}}^{\left(\text{Int}\right)}}{D_{app}^{\left(\text{ATP}-\text{Dep}\right)}}\right)}^2.$$ (10)

This correction to the temperature results in a predicted force of f = 0.49 pN. We calculate f_c = 0.84 pN for b = 100 nm, showing that f < f_c, and thus in a regime consistent with the setup of our model.

A segregation force of this magnitude could be generated by proteins bound near oriC interacting with an established protein gradient or a spindlelike apparatus, using the nucleoid as scaffolding (15,16). The magnitudes of these calculated forces are substantially smaller than those of canonical eukaryotic molecular motors, resulting in a smaller segregation driving force that is more difficult to discern from random fluctuations. This calculated force is substantially larger than a previous estimate of ∼0.01 pN made using the oriC locus drift velocity and Einstein relation for a particle. This demonstrates the importance of including the viscoelastic properties of the cytoplasm and the DNA polymer and the role of the superthermal, ATP-dependent fluctuations in estimating forces from dynamic measurements.

Velocity autocorrelation analysis

If the motion of the oriC locus in E. coli is truly due to a combination of random motion due to Brownian-like fluctuations and processive motion due to an external force, then such a combination of modes should be made apparent by examining the velocity autocorrelation in the locus trajectories. The velocity autocorrelation function has the form

$$C_v\left(t\right)=\langle v_x\left(t\right)v_x\left(0\right)\rangle ,$$

where

$$v_x\left(t\right)=\frac{dX\left(t\right)}{dt}$$

is the x-component velocity. For discrete time intervals δ between monomer-position measurements, the velocity autocorrelation function is defined as

$$C_v^{\left(\delta \right)}\left(t\right)=\frac{1}{{\delta }^2}\langle \left[X\left(t+\delta \right)-X\left(t\right)\right]\left[X\left(\delta \right)-X\left(0\right)\right]\rangle .$$ (11)

When we average the monomer position over the ensemble of trajectories for given time points, Brownian forces average out to zero and what remains is the contribution of processive motion due to f. This processive velocity autocorrelation is predicted to behave as

$$C_{v,P}^{\left(\delta \right)}\left(t\right)=\frac{v_{\text{app}}^2}{{\delta }^2}\left[{\left(t+\delta \right)}^{\frac{\alpha }{2}}-t^{\frac{\alpha }{2}}\right]{\delta }^{\frac{\alpha }{2}}.$$ (12)

When this velocity autocorrelation function is used, it accurately predicts the processive motion of the ensemble average of oriC trajectories (Fig. 5 A). The velocity autocorrelation function for the effects of Brownian motion is found to be (5,6)

$$C_{v,B}^{\left(\delta \right)}\left(t\right)=\frac{D_{\text{app}}}{{\delta }^2}\left[{\left(t+\delta \right)}^{\frac{\alpha }{2}}+{\left|t-\delta \right|}^{\frac{\alpha }{2}}-2t^{\frac{\alpha }{2}}\right].$$ (13)

In Fig. 5 b, we subtract-off the processive velocity autocorrelation from the total velocity autocorrelation and find excellent agreement with the prediction from Eq. 13. This indicates that the motion of the oriC locus during segregation can be adequately described as a combination of processive motion and Brownian fluctuations. We emphasize that the theoretical predictions in Fig. 5 use no fitting parameters to the velocity autocorrelation data, and that only the parameter α/2 is determined by power-law fits to the MD or VarD measurements.

Figure 5.

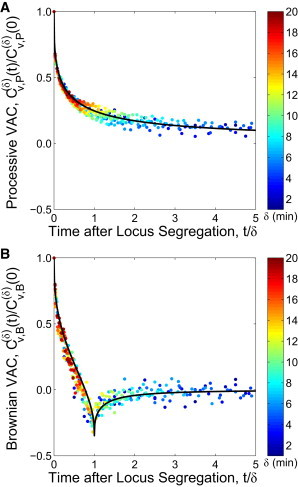
Velocity autocorrelation (VAC) of the oriC locus over time (t) for different values of δ (color gradient, min). (A) Processive VAC $C_{v,P}^{\left(\delta \right)}\left(t\right)/C_{v,P}^{\left(\delta \right)}\left(0\right)$. (Black line) Analytical prediction based on Eq. 12 for α/2 = 0.32. (B) Brownian VAC $C_{v,B}^{\left(\delta \right)}\left(t\right)/C_{v,B}^{\left(\delta \right)}\left(0\right)$. (Black line) Analytical prediction based on Eq. 13 for α/2 = 0.38.

Conclusions

Our results suggest that the motion of the oriC locus is consistent with application of an external, nonthermal force applied during the initiation of segregation. Using our analytical theory and statistics from in vivo locus tracking measurements, we are able to estimate the force during oriC segregation. Given how weak this force is compared to the force scale of canonical eukaryotic molecular motors, it is not surprising that the movement of single trajectories appear dominated by random Brownian motion. There are potentially large-scale structural changes to the nucleoid during the segregation process that our theory does not account for, such as the snapping phenomena seen at particular points during segregation in certain strains (14,26), but our data is from a strain for which these behaviors were not observed as a component of the segregation process (3).

While the biochemical mechanism of segregation is still unknown, our results allow us to comment on previously proposed models and possible mechanisms. The nature of the directed motion we observe and the propensity for oriC to colocalize with the structural maintenance of chromosome complex MukBEF (28) would suggest that entropic demixing is not the main driving force for this initial stage of chromosome segregation. The motion we observe could be generated by protein gradients that interact with DNA, and use the nucleoid itself as scaffolding. One example of such a system is the ParA-type ATPase, which has been shown to be able to generate forces via a burnt-bridge diffusion-ratchet mechanism (29). As of this writing, this mechanism was very recently measured to exert a force of ∼0.012 pN on DNA-covered particles in an in vitro system (30). The biasing force could alternatively be measured using a burnt-bridge lattice random walk model for molecular motors if the relevant step size and bridge-burning probability parameters could be elucidated (31). A similar-acting mechanism would make a good candidate for the constant force behavior we observe, and the forces generated by protein gradients can be larger depending on the kinetic and physical parameters of the segregation machinery (32). It has also been suggested that the oscillations of MinD could help drive chromosome segregation, because it interacts weakly with DNA (16). However, the measurements from Kuwada et al. (3) were taken at 1-min intervals, whereas MinD oscillations have a period of approximately 15 seconds, so we are unable to comment further on this mechanism without more data.

Analysis of existing locus tracking measurements for the origin of replication locus, ori, in Caulobacter crescentus reveals similar behavior to what we observe in E. coli. In this organism, ori is positioned at the cell pole, and one copy becomes the first genomic region to be translocated to the other cell pole (33,34). Analysis of the MD of the ori locus during the first 15 min of its segregation reveal that motion of the translocating copy scales as a power law in time with α/2 = 0.37 (33). The MSD between segregation events in the same strain under almost identical experimental conditions scales as a power law in time with α/2 = 0.39 (1). Dividing the MD by the MSD (in place of the VarD) from these sources and using T = 30°C estimates a force of 1.1 pN. This likely underestimates the actual force of segregation on ori, because there are not yet any measurements on locus dynamics in ATP-depleted Caulobacter, which are necessary to estimate the effective temperature. Chromosome segregation in this organism is driven by the ParABS-mediated DNA partitioning system, which is hypothesized to use a burnt-bridge diffusion-ratchet mechanism along a depolymerizing ParA filament (15,29,30).

A very recent study (as of this writing) presented evidence for an alternative mechanism involving the relay of the ParB-DNA complex between DNA-bound ParA dimers (35). Using parameters extracted from locus tracking measurements based on a particle model, the authors estimated the segregation force to be 0.1 pN (35). This estimate is an order-of-magnitude less than ours; however, Lim et al. (35) do not include the effects of subdiffusion or the polymeric nature of the chromosome in their analysis. Comparing these results from Caulobacter to our analysis for oriC would suggest that similar-acting but weaker mechanisms could be at work in E. coli.

Our simple theoretical model illustrates several important effects that are critical for interpreting in vivo processes. The dynamic response to a constant force does not result in a MD value that scales linearly with time, as is the case for a particle in a simple Newtonian fluid. Environmental and molecular relaxation processes leads to memory effects that alter the MD to a power-law scaling with time. Our model demonstrates that these confounding effects contribute equally to both the active transport (measured using MD) and passive diffusive motion (measured using VarD). Thus, the ratio of MD to VarD cancels these effects and results in an indirect determination of the force using observation of locus position alone. Our theoretical model provides evidence that some in vivo physical processes can be analyzed by observation of both active and passive transport processes, as is the case in conventional polymeric systems. Therefore, the analytical framework presented in this article exhibits great promise for interpreting a wide range of scenarios involving processive translocation of chromosome loci, including plasmid segregation (36) and homologous recombination mediated by RecA filaments (37).