Abstract
Knowledge about the global translational and rotational motion of proteins under crowded conditions is highly relevant for understanding the function of proteins in vivo. This holds in particular for human αB-crystallin, which is strongly crowded in vivo and inter alia responsible for preventing cataracts. Quantitative information on translational and rotational diffusion is not readily available, and we here demonstrate an approach that combines pulsed-field-gradient NMR for translational diffusion and proton T1ρ/T2 relaxation-time measurements for rotational diffusion, thus overcoming obstacles encountered in previous studies. The relaxation times measured at variable temperature provide a quantitative measure of the correlation function of protein tumbling, which cannot be approximated by a single exponential, because two components are needed for a minimal and adequate description of the data. We find that at high protein concentrations, rotational diffusion is decoupled from translational diffusion, the latter following the macroscopic viscosity change almost quantitatively, resembling the behavior of spherical colloids. Analysis of data reported in the literature shows that well-packed globular proteins follow a scaling relation between the hydrodynamic radius and the molar mass, Rh ∼ M1/d, with a fractal dimension of d ∼ 2.5 rather than 3. Despite its oligomeric nature, Rh of αB-crystallin as derived from both NMR methods is found to be fully consistent with this relation.
Introduction
In a living cell, proteins exist and function in a rather concentrated solution of a wide range of different solutes. In comparison with dilute conditions, such crowding can significantly alter the protein behavior (1,2). The most important parameters in describing protein overall Brownian motion are the translational and rotational diffusion coefficients. Obviously, crowding increases the viscosity of the solution and slows down protein diffusion. However, this differs from a simple increase of the solution viscosity by adding, for instance, glycerol (3). Intermolecular protein interactions and their influence on Brownian diffusion are rather complicated in nature, which cannot be effectively described by increased viscosity alone. The complex changes of the protein dynamics at high protein concentrations, and the key factors determining these changes, are largely unclear at present. Experimental data on this topic are still rather sparse. Some results even contradict each other; for example, fluorescence data demonstrate that upon increasing protein concentration, translational diffusion is slowed down to a larger extent than rotational diffusion (4), whereas NMR experiments yield the opposite conclusion (3).
The interior of the vertebrate eye lens is a typical example of a crowded protein solution. Here, a highly concentrated mixture of short-range ordered (5) α-, β-, and γ-crystallins provides a high refractive index and lens transparency without protein metabolism (6,7). The main constituent of this protein mixture is α-crystallin, which comprises ∼35% (w/w) of the lens crystallins (8). α-crystallin consists of two homologous proteins, αA- and αB-crystallin, which have a monomer molecular mass of ∼20 kDa each. They form oligomeric associations with a molecular mass distribution from 500 to >1000 kDa and an average mass of ∼800 kDa (9). Besides maintaining the high refractive index, α-crystallin acts as a molecular chaperone, preventing protein aggregation that causes cataracts to form (10,11).
Although αΒ-crystallin has been studied quite intensively over the last decades (for reviews, see Narberhaus (12), Horwitz (13), Augusteyn (14), and Andley (15)), its dynamics, especially at high concentrations, has not been investigated in much detail. Delaye et al. concluded that α-crystallin acts as a good model system for colloids with an effective hard-sphere radius that is not dependent on concentration (16,17), with translational self-diffusion coefficients (SDCs) that closely follow the macroscopic viscosity (18). Conversely, another report indicated that α-crystallin does not form a compact sphere at all (17) but has a dynamic quaternary structure (19).
Here, we present a detailed comparative study of the rotational and translational diffusion of αB-crystallin as a function of concentration. The translational and rotational dynamics of αB-crystallin were studied by pulsed-field-gradient (PFG) NMR and proton NMR relaxation-time measurements, respectively. PFG NMR provides an objective and robust measure of the SDC, even at high concentrations where dynamic light-scattering (DLS) experiments are challenged by the appearance of a slow mode and the necessary conversion of a cooperative diffusion coefficient into an SDC (20). Due to its large aggregate size, the resonances of the rigid core of αΒ-crystallin are broadened beyond detection (9) and thus cannot be studied by conventional high-resolution NMR techniques. We rely instead on low-resolution 1H NMR relaxation-time measurements at various concentrations and temperatures, which in fact allows us to address potential ambiguities related to the common use of the NMR T1/T2 relaxation-time ratio as a measure of rotational diffusion. For the relaxation measurements, we rely on an integration of the whole proton spectrum, thus analyzing the integral signal from all protein protons. We present a consistent and quantitative treatment of relaxation data in terms of a bicomponent rotational autocorrelation function. Our analysis reveals a progressive decoupling of translational and rotational motion upon an increase in concentration.
Materials and Methods
Sample preparation
Protein expression and purification of human αB-crystallin
The human αB cDNA (construct kindly provided by Prof. Wilbert Boelens, Nijmegen Centre for Molecular Life Sciences, Gelderland, The Netherlands) was cloned into a modified, His-tag-free pET16b vector and expressed in Escherichia coli BL21(DE3). Protein expression and purification were performed as described in Mainz et al. (21), with minor modifications including autoinduction media (ZYM 5052) instead of minimal media (M9), microfluidizer instead of French press, an additional DNA digestion step after cell lysis, and different column materials: in place of Q-Sepharose and Superose 6, TMAE and Superdex 200, respectively, were used. The lyophilized sample was dissolved in 50 mM Na-phosphate buffer, 50 mM NaCl, and 0.002% NaN3 D2O buffer, pD 7.6, with prior minimization of labile protons to lower the water signal and so as not to have an impact on the solvent viscosity via isotope effects. For more details, see the Supporting Material. Hen egg white lysozyme was delivered from Sigma-Aldrich (St. Louis, MO). Similar to αB-crystallin, lysozyme was dissolved in D2O, lyophilized, and dissolved in D2O again for maximal removal of residual water protons.
Viscosity
Steady-shear viscosities were measured at high shear rates (1000 s−1/2000 s−1) using the microfluid viscometer-rheometer on chip (m-VROC, Rheosense, San Ramon, CA), which determines the sample viscosity by analyzing the pressure gradient inside of a capillary (d = 50 μm). The samples for the viscosity measurements were also prepared using D2O buffer instead of H2O.
NMR experiments
Translational diffusion and T1ρ measurements were conducted on a Bruker Avance II spectrometer (Billerica, MA) with a 1H resonance frequency for protons of 400 MHz equipped with a Diff60 probehead. T1ρs were measured at spin-lock frequencies of 20, 40, and 60 kHz; the latter was measured using a resonance offset of the spin-lock field with angle θ between the B0 and B1e fields fixed to 42°. T2 measurements were performed on a Bruker Minispec mq20 at 20 MHz 1H resonance frequency. The low-resonance frequency for T2 experiments was chosen to avoid T2 shortening due to the chemical exchange of protein protons, which may significantly affect T2 values at high resonance frequencies (22). For the relaxation measurements, in all cases, we employ single short-pulse excitation and a sufficiently large spectral width of 50 kHz, thus assuring that all types of protons (rigid and mobile) in the protein contribute equally to the integral signal. In all cases, the accuracy of the temperature calibration and stabilization was ±1°C. For more details, see the Supporting Material.
Translational SDCs were obtained from the PFG NMR diffusion decays using the well-known formula (23)
| (1) |
where A(g) is the signal intensity, g is the field gradient strength, γ is the proton gyromagnetic ratio, Δ is the diffusion time, δ is the duration of the field gradient pulse, and D is the SDC.
Rotational correlation times were obtained by analyzing NMR relaxation times. These are determined by the spectral density function, which is the Fourier transformation of the rotational autocorrelation function (RACF). The RACF of protein motion in solution is complicated in nature. For its unambiguous determination from experimental data, multiple measurements of relaxation times at different resonance frequencies are required, since each relaxation time reflects molecular dynamics only within the frequency domain around the circular (i.e., multiplied by 2π) resonance frequency. Because of the high molecular mass of the αB-crystallin oligomer, its Brownian tumbling is very slow, and thus, the often employed T1 relaxation times are not useful for studying such a slow motion since they provide information on (sub)nanosecond-timescale motions, which is much faster than the αB-crystallin tumbling. For this reason, we used T1ρ proton relaxation times, which enable one to shift the sampling frequency of motions down to the 10–100 kHz range. Specifically, we measured the temperature dependences of T1ρ values at spin-lock frequencies (the analog of the resonance frequency for T1) of 20, 40, and 60 kHz, the latter values being measured using the resonance offset of spin-lock irradiation (see the Supporting Material). We stress that measuring relaxation times at different temperatures is important for a reliable data analysis, since the slope of the temperature dependence is more informative than the absolute value of the relaxation time measured at one temperature in correctly determining the rotational correlation time. In addition to T1ρ values, we also measured the proton T2, which provides the low-frequency limit of the spectral density function. The relaxation is governed by the homonuclear (1H-1H) dipole-dipole mechanism; all other mechanisms are negligible in this case. The equations for the homonuclear dipolar T1, T2, and T1ρ relaxation times are well known (24). However, since we measured off-resonance T1ρ, for the data analysis, we should use a general expression defining relaxation times T1 and T1ρ at arbitrary off-resonance angle. Such an expression was derived a long time ago by Jones (25). In a more compact form, applying the approximation ω0 >> ω1e, this expression reads (26)
| (2) |
where
| (3) |
| (4) |
Here, θ is the off-resonance angle (the angle between the static field B0 and effective spin-lock field B1e), J(ω) is the spectral density function, KHH is the squared effective proton-proton dipolar coupling (second moment), and ω0/2π and ω1e/2π are the resonance and spin-lock frequencies, respectively. At θ = 0° and 90°, Eq. 2 converts to the standard expressions for T1 and T1ρ, respectively. Relaxation time T2 corresponds to the case θ = 90° and ω1e = 0. Note that these equations are valid not only in the fast-motion limit, but for slow motions as well (27). For the case of the relaxation of protein protons, the effective KHH can be expressed as
| (5) |
where N is the number of protons in a protein, ħ is the Planck constant, γ is the proton gyromagnetic ratio, and rij is the distance between the ith and jth protons in the protein. Although summation in Eq. 5 formally extends over all protons in the protein, because of the r−6 dependence, the dominant contribution to the coupling for each proton is attributable to the two to three nearest neighbors, and proton-proton interactions with more distant neighbors are practically negligible.
Since an integral proton signal was detected in the relaxation experiments, the spectral density function J(ω) in Eqs. 2–4 is the average spectral density of all protons in the protein:
| (6) |
The same is true for the RACF:
| (7) |
Each individual RACF can be written as a product of the correlation functions of the overall Brownian tumbling and internal local motion (28),
| (8) |
where Ct(t) is the overall tumbling RACF and and τli are the order parameter and correlation time of the internal motion for the ith proton. Since Ct(t) is the same for all protons, Eq. 7 can be rewritten as
| (9) |
where . Then, the spectral density function is
| (10) |
where Jt(ω) is the Fourier transform of Ct(t). In our analysis, we assume that all values of τli are much smaller than the correlation time of the overall protein tumbling. Then, the second term in Eq. 10 can be neglected. This formalism is very similar to that applied in the analysis of field-cycling T1 relaxation data of protein protons in D2O solutions (29).
The key point of our analysis is an assumption of a biexponential overall tumbling RACF Ct(t). Even in relatively dilute protein solutions, long-range electrostatic intermolecular protein interactions give rise to a local anisotropy that renders the so-called normal Brownian tumbling somewhat anisotropic (30,31). Thus, the RACF decays not to zero, but to a certain value that we denote as the rotational order parameter, . Its physical meaning is similar to that of the order parameter of the internal motions (28): both are measures of the anisotropy of rotational motion of the overall tumbling and internal mobility, respectively. In infinitely dilute solutions, = 0, and it increases with increasing concentration, as interprotein interactions become stronger and Brownian tumbling thus becomes more anisotropic. Since proteins diffuse relative to each other, the local anisotropy has a finite lifetime; hence, Ct(t) finally decays to zero, but on a longer timescale than for normal Brownian tumbling. Therefore, Ct(t) can be presented as a sum of two components,
| (11) |
where τrot is the correlation time of Brownian rotation and τS is the correlation time of the slow component of Ct(t), i.e., the lifetime of local anisotropy. The apparent slow contribution to protein Brownian tumbling has been observed experimentally and computationally in a number of independent works (for a review, see Krushelnitsky (31)).
The corresponding spectral density function reads
| (12) |
For typical protein concentrations of high-resolution NMR samples (a few mM), is very low, less than a few percent (31). Hence, T1 relaxation times are not sensitive to the slow component. However, T2s are quite sensitive to it because of the spectral density function at zero frequency:
| (13) |
Despite the fact that << 1, the two terms in Eq. 13 are comparable, since τS >> τrot. For this reason, using the T1/T2 ratio for determination of the tumbling correlation time, τrot, can provide imprecise results. The higher the concentration, the less correct is the value of τrot obtained from the T1/T2 ratio. Thus, the assumption of a biexponential form of Ct(t) is a prerequisite for the correct analysis of the relaxation data at different concentrations.
In fitting the temperature dependences of the relaxation times, we assume an Arrhenius dependence of the correlation times,
| (14) |
where ES,rot is the activation energy of the τS/τrot correlation times and R is the universal gas constant. Thus, the fitting parameters in the analysis were two correlation times, two activation energies, the order parameter (separate sets for each concentration), and the product of the rigid-lattice second moment, KHH (which for rigid globular proteins has an approximate value of ∼1.3 × 1010 s−2 (32)), and the order parameter :
| (15) |
where is the motionally averaged second moment of the protein protons; we assume it to be the same for all concentrations. The overall number of the fitting parameters for all four concentrations was 21: five parameters for each concentration (see above) and one parameter shared between all concentrations. For the fitting, we used Eqs. 2–4, replacing J(ω) and KHH by Jt(ω) and , respectively. A similar approach was taken previously by Bertini et al. (29), stressing the use of as a qualitative indicator of internal rigidity. For simplicity, we assume to be temperature-independent and we neglect the distribution of sizes. Strictly speaking, this is not absolutely true, yet it has only a minor effect on the analysis, as demonstrated in Fig. S8. is also assumed to be temperature-independent. Within the temperature range of our experiments, the temperature dependence of is rather weak (32,33). Simply assuming a reasonable temperature dependence, however, has practically no influence on the results (see Table S2).
The fitting procedure was based upon a minimization of the root mean-square deviation,
| (16) |
where Tsim and Texp are the simulated (according to the current set of the fitting parameters) and experimental relaxation times (T1ρ or T2), respectively, and N is the number of all relaxation times measured at all temperatures and concentrations. For the minimization procedure, we used the Metropolis algorithm.
Results
Translational diffusion and viscosity
Typical examples of the PFG NMR intensity decays (signal intensity versus strength of the pulsed field gradient) are shown in Fig. 1. In the representation log(I) versus g2, a deviation of the intensity decay from a straight line reflects an SDC dispersion, i.e., a distribution of molecular mass. Fig. 1 likewise demonstrates that this distribution is somewhat wider for a higher concentration; the normalized (relative) RMSDs of the diffusion coefficients from their average, as estimated from a bicomponent decomposition of the decays, are 0.2, 0.2, 0.25, and 0.35 for the concentrations 35, 80, 113, and 185 mg/mL, respectively, in qualitative agreement with DLS data (20). In this analysis we did not quantify the distribution, instead defining the mean SDC, which corresponds to the initial slope of the decay. Practically, we fitted the decay with a sum of two components as a minimal but sufficient model and then calculated the mean SDC as
| (17) |
where P1,2 and D1,2 are the intensities and SDCs, respectively, of the two components. The specific values of D1 and D2 depend on the weighting factor; these values taken separately have no physical meaning, yet the average diffusion coefficient is well-defined and reliable. Note that the subunit exchange between α-crystallin oligomers occurs on a timescale of minutes (34); thus, the observed SDC is not the exchange-averaged value of SDCs of oligomers and mono(di)mers. In fact, the amount of α-crystallin mono(di)meric subunits in solution is very low; otherwise, we would see a corresponding fast component in the PFG intensity decays.
Figure 1.
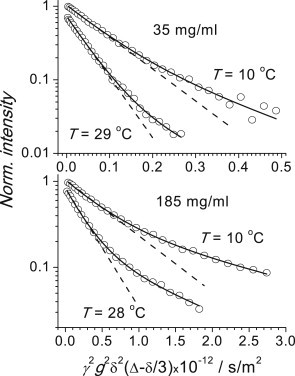
Typical examples of diffusion-dependent PFG NMR decays of αB-crystallin at two different concentrations and two different temperatures. The experimental error corresponds to the size of the symbols in the initial part of the decays. Solid red lines are bicomponent fits of the decays and dashed lines denote the initial slope of the decays corresponding to the mean SDC.
Fig. 2 a presents the temperature dependences of mean SDCs at four different concentrations of αB-crystallin in an Arrhenius representation. It is useful to analyze these data in comparison with lysozyme (M = 14.3 kDa). At acidic pH, lysozyme forms no dimers or oligomers and retains its rigid native structure over a wide range of concentrations and temperatures (35). This comparison shows that the slope of the SDC temperature dependences (i.e., the activation energy of translational diffusion) for αB-crystallin at all concentrations is quite similar to that of lysozyme. This indicates that at all concentrations, the mean molecular mass of the αB-crystallin assemblies is independent of temperature. Fig. 2 b presents the macroscopic viscosity, along with data for pure D2O. In the Arrhenius plot, given the improved data quality of the viscosity measurements compared to those of translational diffusion, a slight curvature of the viscosity can be seen, indicating that the glassy dynamics related to the solvent can be described by a Vogel-Fulcher relationship (36). A slightly stronger deviation from the Arrhenius behavior is observed for the highest concentrations, pointing to the increasing relevance of studying the glassy dynamics of confined/bound water.
Figure 2.
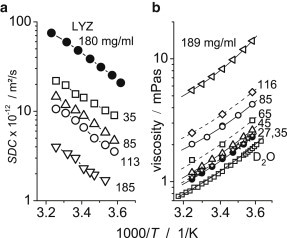
Translational self-diffusion coefficients and viscosity of αB-crystallin. In both graphs, the size of the symbols corresponds to the experimental uncertainty. (a) Temperature dependences of the mean SDCs at four different concentrations of αB-crystallin (open symbols). For comparison, SDCs of a lysozyme solution (concentration 180 mg/mL, pD 3.5) are shown (solid symbols). (b) Temperature dependence of the viscosity at seven concentrations of αB-crystallin (symbols), displaying a Vogel-Fulcher relationship (solid lines). The solid line for the D2O viscosity represents literature data as recalculated (48) from the viscosity of water (49).
At the smallest concentration (35 mg/mL), the protein SDC concentration dependence is weak (37), and thus, intermolecular protein interactions have almost no influence on the SDC. This allows us to estimate the size of αB-crystallin using the Stokes-Einstein relationship and the experimental viscosity data. This gives a temperature-independent value (see Fig. S7) of RH = (95 ± 3) Å, which exactly matches the value obtained from the DLS experiments by Licinio et al. (20). Note that those authors were studying α-crystallin from calf lenses, which are oligomers composed of a mixture of αA- and αB-crystallins.
Rotational diffusion
Fig. 3 depicts the relaxation times and fitting curves for different concentrations of αB-crystallin. Fitting a single-component correlation function for the protein Brownian rotation (i.e., assuming = 0) results in a pronounced mismatch, confirming the invalidity of the one-component model. The fitting results are summarized in Table 1.
Figure 3.
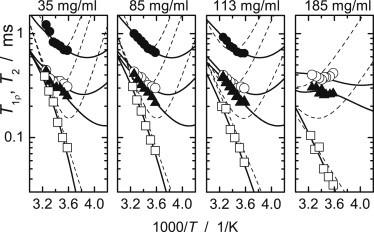
Proton T1ρ and T2 for αB-crystallin solutions at different concentrations. The experimental error corresponds to the size of the symbols. Information is provided for relaxation times T2 (open squares), T1ρ at the spin-lock frequency, 20 kHz (solid triangles), T1ρ at 40 kHz (open circles), and off-resonance T1ρ at 60 kHz (solid circles) (the latter parameter was not measured for 185 mg/mL). Solid lines show the best fits for double-exponential correlation functions, and dashed lines correspond to the best fit assuming = 0, i.e., a single-exponential correlation function.
Table 1.
Dynamic parameters obtained from the data fitting
| c/mg/mL | τrot/μs at 20°C | τS/μs at 20°C | τS/μs at 20°C | Erot/kJ/mol | Es/kJ/mol | |
|---|---|---|---|---|---|---|
| 35 | 0.90 ± 0.02 | <0.03 | >30 | 0.64 ± 0.02 | 16 ± 1 | 66 ± 2 |
| 85 | 0.96 ± 0.02 | <0.03 | >30 | 0.83 ± 0.02 | 18 ± 1 | 51 ± 2 |
| 113 | 1.03 ± 0.03 | <0.03 | >80 | 1.36 ± 0.03 | 17 ± 1 | 40 ± 2 |
| 185 | 1.04 ± 0.03 | 0.22 ± 0.02 | 17 ± 1 | 3.70 ± 0.06 | 10 ± 1 | 30 ± 1 |
(Eq. 15) was found to be (4.2 ± 0.2) × 109 s−2 by a shared fit of all data sets. Since is very small, the parameters and τS cannot be determined separately at low concentrations; only the product τS could be reliably obtained from the fitting. For details, see Krushelnitsky (31).
The absolute value of the rotational correlation time for the lowest concentration investigated in this study, 35 mg/mL, is 0.9 μs. Applying the Stokes-Einstein-Debye law with the experimentally determined viscosity of this sample, these values correspond to an αB-crystallin radius of ∼82 Å. This value is somewhat less than 95 Å, as obtained from the translational diffusion data (see above). This may indicate that the Stokes-Einstein-Debye law does not hold for the rotational diffusion, and that the macroscopic viscosity should not be used to determine rotational correlation time (see below). If, instead of the solution viscosity, the viscosity of a pure solvent (D2O) is used in the Stokes-Einstein-Debye equation, then the calculated αB-crystallin radius reaches 89 Å. Given the overall experimental accuracy, the discrepancy between 89 Å and 95 Å can be considered as negligible. Note that the activation energy of the Brownian tumbling Erot corresponds quite well to that of the viscous flow of pure water, which is ∼19 kJ/mol (38). The decrease of Erot to 10 kJ/mol at a concentration of 185 mg/mL is obviously an apparent effect associated with the increased distribution of molecular masses and the probably more complex form of the Ct(t).
Discussion
The impact of crowding: rotational diffusion is less hindered than translational diffusion
Since the rotational diffusion is described by the two-component overall tumbling RACF Ct(t), we define, as in the case of translational diffusion, a mean rotational diffusion rate equal to the initial slope of the rotational correlation function:
| (18) |
Since and τS are poorly defined at low concentrations there is a certain ambiguity in defining the rotational diffusion rate at low concentrations. However, since the second term in Eq. 18 is much smaller than the first, this ambiguity is obviously negligible.
Fig. 4 presents the central result of this work, the comparative retardation of translational and rotational diffusion relative to macroscopic viscosity with increasing concentration. It is seen that the trend of the translational diffusion nicely corresponds to that of viscosity, which confirms previous findings by Licinio and Delaye (18). Thus, the Stokes-Einstein law appears to be valid even at high concentrations. This in turn shows that the mean size of αB-crystallin under our conditions does not depend on concentration.
Figure 4.
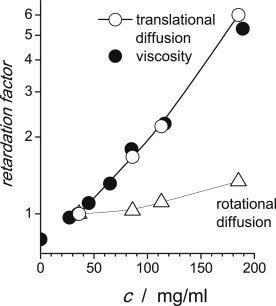
Retardation of the translational (open circles) and rotational diffusion (open triangles) as a function of αB-crystallin concentration as compared to the normalized macroscopic viscosity (solid circles). The retardation factor was defined as the ratio of the translational (rotational) diffusion rate to the value at 35 mg/mL, taken as a reference for the higher concentrations. The viscosity was normalized in the same way. The size of the symbols reflects the experimental error, and the solid line simply guides the eye.
On the other hand, these results clearly demonstrate a significant difference between translational and rotational diffusion of αB-crystallin at high concentrations, far beyond all the assumptions and uncertainties of the data analysis. We also stress that fitting the relaxation data with a fixed ratio of the correlation times, τrot, at different concentrations after the known increase in viscosity (and thus the slow-down of translational diffusion) results in a strong mismatch with the experimental data (see Fig. S10).
Interestingly, a similar conclusion regarding the limited applicability of the Stokes-Einstein-Debye law for high αB-crystallin concentrations can be deduced from recently published data on Brownian tumbling of this protein obtained by field-cycling relaxometry of the water protons (39). At a single concentration of 100 mg/mL, T = 25°C in 80% H2O and 20% glycerol solvent, the correlation time, τrot, of αB-crystallin was found to be 1.4 μs. Using our viscosity data for this protein concentration and temperature, and taking into account the correction factor for viscosity between D2O and 80% H2O and 20% glycerol solvents, we estimated the apparent radius of αB-crystallin to be 68 Å. This value is obviously too small, in accordance with our finding that rotational diffusion is less hindered than expected by the increase of viscosity.
Similar concentration dependences of rotational and translational protein diffusion have been reported previously (4), but this is the first time, to our knowledge, that such a large quantitative difference has been observed in a protein system. The effect of less hindered rotations compared to the translational self-diffusion goes far beyond a pure viscosity effect resulting from the difference in local microviscosity around the protein and the bulk viscosity. Increasing the bulk viscosity with ethylene glycol by a factor of 6 (corresponding to a retardation factor of 6 in Fig. 4) results in retardation of translation diffusion and rotational diffusion by factors of 5.5 and 4, respectively, for a small globular protein (40). The less hindered rotation at high protein concentrations can be easily understood in terms of the cage effect, which is well known for the case of spherical colloids (41,42). For translational diffusion, each probe molecule needs to escape a cage formed by the surrounding particles (α-relaxation) and thus has to interact with its neighboring proteins, which represent obstacles to translational motion. For rotational diffusion, proteins may rotate rather freely within a cage (β-relaxation); hence, intermolecular protein interactions can be expected to have an appreciably smaller effect on it. Note that the effect of decoupling between translational and rotational diffusion has been observed not only in experimental studies, but also in numerical simulations of protein diffusion at high concentrations (43). However, we refrain from extrapolating the findings of this work to other proteins and experimental conditions. The acquired data are obviously not sufficient to make generalizations, and more experimental work is required to further advance our knowledge in this area.
Fractal structure: αB-crystallin behaves like a normal globular protein
Further information on αB-crystallin properties can be obtained by comparing the absolute values of the diffusion constants with those of other proteins. Although such data have been published, at least for translational diffusion (see, e.g., the work of Delaye and colleagues (16,18,20)), the comparison has apparently not yet been made. The SDC is inversely proportional to the linear size of the Brownian particle, whereas the rotational correlation time is proportional to its volume. To minimize the influence of intermolecular protein interactions, we compared the diffusion parameters only for the dilute αB-crystallin solution. If the average protein density is the same for proteins of different molecular mass, M, one might expect that SDC ∼ M−0.33 and τrot ∼ M, but this is not the case. Computer analysis of a large number of 3D protein structures (44,45) demonstrates that V ∼ Rd, where V is the van der Waals (or solvent-accessible) volume of the protein directly proportional to the molecular mass, which is connected to the linear size, R (more specifically, the radius of gyration) of the protein molecule by a scaling exponent, d, of ∼2.5. Such a relation between size and volume reflects a fractal nature of the protein packing, which has generated increased interest over the last few years (see the review by Banerji and Ghos (46)). The fractal dimension d < 3 indicates that the protein density decreases with increasing M (47). If V ∼ M, then the SDC is ∼M−1/d and τrot ∼ M3/d.
Fig. 5 a shows a collection of data from the literature on SDCs as a function of M for many proteins and includes the αB-crystallin results from this work. Two important points must be mentioned. First, the slope of the SDC versus M dependence matches reasonably well the value of d obtained by Liang and Dill (44). To our knowledge, this is the first experimental confirmation of this fractal dependence based on diffusion data, reporting on the hydrodynamic radius Rh. Second, the αB-crystallin SDC is located close to this line, which indicates that it has no specific features, as compared to other globular proteins, and is just as compact as might be expected based on the fractal scaling law, Rh ∼ M1/d, and its high molecular mass.
Figure 5.
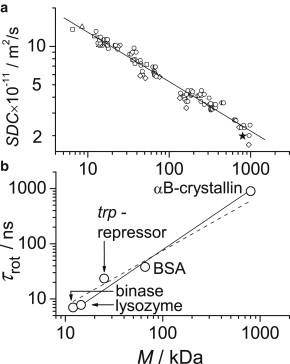
(a) SDCs for different proteins as a function of M at 20°C. Literature data are either taken directly from Tyn and Gusek (50) and Ilyina et al. (51) (open circles and triangles) or recalculated from the hydrodynamic radii reported in Wilkins et al. (52) and Armstrong et al. (53) (open squares and diamonds). Proteins too anisotropic in shape or that are intrinsically disordered were not taken into account. The αB-crystallin SDC as obtained in this study is indicated by the solid star. The αB-crystallin SDC was measured at a concentration of 10 mg/mL and multiplied by 1.25 to account for the viscosity difference between H2O (literature data of H2O solutions) and D2O (this work). The solid line is a best fit to the data, with a slope (power-law exponent) of 0.39 ± 0.03. (b) Rotational correlation time τrot at 20°C for five different proteins as a function of molecular weight. The solid line presents the dependence τrot ∼ M1.2. For comparison, the dashed line shows the dependence τrot ∼ M.
A similar dependence can likewise be plotted for rotational diffusion. Many studies have been published on protein dynamics in solution over the last 20 to 30 years. However, in most of these, the rotational correlation time was determined from the NMR T1/T2 relaxation-time ratio assuming only a single-component RACF or, at best, a more complex form of it accounting for the anisotropic shape of the protein. We again stress that this is quantitatively not correct (see above). The amplitude of the slow component of the RACF depends on many parameters (concentration, ionic strength, pH, and electrostatic properties of a protein) and hence is different for different experiments. This induces a spread of τrot values that makes it difficult to reliably define the power-law exponent of M (see Fig. S11). Therefore, for comparison, we took the data of only four proteins, binase, lysozyme, trp-repressor, and bovine serum albumin, as described in Krushelnitsky (31). In that study, τrot was determined according to the same protocol as in this work, so the correlation times can be compared directly.
Fig. 5 b presents τrot as a function of M for five proteins, including αB-crystallin. Despite the poor statistics, it can be clearly seen that rotational diffusion also confirms the findings of Liang and Dill (44). The largest deviation from the solid line in Fig. 5 b is observed for trp-repressor. This can be explained by the fact that trp-repressor is a symmetric dimer with two long (12 residues each) unstructured chains exposed to the solvent. Thus, the trp-repressor is not a completely rigid protein, and an apparently increased τrot is easily understood. Note that the rotational diffusion of αB-crystallin again reveals no evident specificity in comparison with other globular proteins.
Conclusions
In this study, we have provided an accurate determination of the translational and rotational diffusion of αB-crystallin over a wide range of concentrations. Our data allowed us to draw three important conclusions. First, our main finding was that upon increasing the protein concentration, the translational diffusion of αB-crystallin nicely followed the trend measured for the inverse solution viscosity, whereas the rotational diffusion was found to be affected by the concentration increase to a much smaller extent. This could be explained on the basis of the cage effect typical for spherical colloids. The temperature dependence of all observables was found to be largely governed by the flow activation energy of pure water, with deviations visible only at the largest concentrations. Second, despite its large size and oligomeric structure, αB-crystallin in dilute solution behaves like a normal rigid globular protein, showing no specificity in Brownian dynamics compared to other, even much smaller, proteins. Third, both the translational and rotational diffusion data (reporting on the hydrodynamic radius, Rh) confirm the fractal scaling law, V ∼ M ∼ Rd, with d ∼ 2.5 instead of d ∼3 for a variety of protein structures of different size, R. This finding is in agreement with previous statistical analyses of protein packing density.
The methodological approach presented here, in particular addressing the autocorrelation function of the overall protein tumbling by a bimodal analysis of NMR relaxation times measured at different frequencies and temperatures, provides an efficient and reliable tool for studying the effect of crowding on Brownian dynamics. Application of this approach to the αB-crystallin study enabled a qualitative step forward in the description of protein mobility at high concentrations. We expect that the use of this approach for other proteins and protein mixtures will help in constructing a detailed and consistent general picture of protein dynamics under crowding conditions.
Acknowledgments
We thank Wilbert Boelens for the plasmid for αB crystallin and Qi Zhang for the expression clone.
Funding for this work was provided by the Deutsche Forschungsgemeinschaft (DFG) in the framework of the collaborative research center SFB-TRR 102 (project A08). We also acknowledge significant investments in our NMR facility by the European Regional Development Fund (ERDF) of the European Union.
Contributor Information
Alexey Krushelnitsky, Email: krushelnitsky@physik.uni-halle.de.
Kay Saalwächter, Email: kay.saalwaechter@physik.uni-halle.de.
Supporting Material
References
- 1.Zimmerman S.B., Minton A.P. Macromolecular crowding: biochemical, biophysical, and physiological consequences. Annu. Rev. Biophys. Biomol. Struct. 1993;22:27–65. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 2.Ellis R.J. Macromolecular crowding: obvious but underappreciated. Trends Biochem. Sci. 2001;26:597–604. doi: 10.1016/s0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
- 3.Wang Y., Li C., Pielak G.J. Effects of proteins on protein diffusion. J. Am. Chem. Soc. 2010;132:9392–9397. doi: 10.1021/ja102296k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zorrilla S., Hink M.A., Lillo M.P. Translational and rotational motions of proteins in a protein crowded environment. Biophys. Chem. 2007;125:298–305. doi: 10.1016/j.bpc.2006.09.003. [DOI] [PubMed] [Google Scholar]
- 5.Delaye M., Tardieu A. Short-range order of crystallin proteins accounts for eye lens transparency. Nature. 1983;302:415–417. doi: 10.1038/302415a0. [DOI] [PubMed] [Google Scholar]
- 6.Bloemendal H. The vertebrate eye lens. Science. 1977;197:127–138. doi: 10.1126/science.877544. [DOI] [PubMed] [Google Scholar]
- 7.Bloemendal H., de Jong W., Tardieu A. Ageing and vision: structure, stability and function of lens crystallins. Prog. Biophys. Mol. Biol. 2004;86:407–485. doi: 10.1016/j.pbiomolbio.2003.11.012. [DOI] [PubMed] [Google Scholar]
- 8.Pierscionek B., Augusteyn R.C. Protein distribution patterns in concentric layers from single bovine lenses: changes with development and ageing. Curr. Eye Res. 1988;7:11–23. doi: 10.3109/02713688809047015. [DOI] [PubMed] [Google Scholar]
- 9.Carver J.A. Probing the structure and interactions of crystallin proteins by NMR spectroscopy. Prog. Retin. Eye Res. 1999;18:431–462. doi: 10.1016/s1350-9462(98)00027-5. [DOI] [PubMed] [Google Scholar]
- 10.Horwitz J. Alpha-crystallin can function as a molecular chaperone. Proc. Natl. Acad. Sci. USA. 1992;89:10449–10453. doi: 10.1073/pnas.89.21.10449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Derham B.K., Harding J.J. α-Crystallin as a molecular chaperone. Prog. Retin. Eye Res. 1999;18:463–509. doi: 10.1016/s1350-9462(98)00030-5. [DOI] [PubMed] [Google Scholar]
- 12.Narberhaus F. α-Crystallin-type heat shock proteins: socializing minichaperones in the context of a multichaperone network. Microbiol. Mol. Biol. Rev. 2002;66:64–93. doi: 10.1128/MMBR.66.1.64-93.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Horwitz J. α-Crystallin. Exp. Eye Res. 2003;76:145–153. doi: 10.1016/s0014-4835(02)00278-6. [DOI] [PubMed] [Google Scholar]
- 14.Augusteyn R.C. α-Crystallin: a review of its structure and function. Clin. Exp. Optom. 2004;87:356–366. doi: 10.1111/j.1444-0938.2004.tb03095.x. [DOI] [PubMed] [Google Scholar]
- 15.Andley U.P. Crystallins in the eye: function and pathology. Prog. Retin. Eye Res. 2007;26:78–98. doi: 10.1016/j.preteyeres.2006.10.003. [DOI] [PubMed] [Google Scholar]
- 16.Delaye M., Gromiec A. Mutual diffusion of crystallin proteins at finite concentrations: a light-scattering study. Biopolymers. 1983;22:1203–1221. doi: 10.1002/bip.360220413. [DOI] [PubMed] [Google Scholar]
- 17.Tardieu A., Laporte D., Delaye M. Colloidal dispersions of α-crystallin proteins. 1. Small-angle x-ray analysis of the dispersion structure. J. Phys. (Paris) 1987;48:1207–1215. [Google Scholar]
- 18.Licinio P., Delaye M. Mutual and self-diffusion in concentrated α-crystallin protein dispersion. A dynamic light-scattering study. J. Phys. (Paris) 1988;49:975–981. [Google Scholar]
- 19.Haley D.A., Horwitz J., Stewart P.L. The small heat-shock protein, αB-crystallin, has a variable quaternary structure. J. Mol. Biol. 1998;277:27–35. doi: 10.1006/jmbi.1997.1611. [DOI] [PubMed] [Google Scholar]
- 20.Licinio P., Delaye M., Leger L. Colloidal dispersions of α-crystallin proteins. 2. Dynamics: a maximum-entropy analysis of photon-correlation spectroscopy data. J. Phys. (Paris) 1987;48:1217–1223. [Google Scholar]
- 21.Mainz A., Jehle S., Reif B. Large protein complexes with extreme rotational correlation times investigated in solution by magic-angle-spinning NMR spectroscopy. J. Am. Chem. Soc. 2009;131:15968–15969. doi: 10.1021/ja904733v. [DOI] [PubMed] [Google Scholar]
- 22.Luz Z., Meiboom S. Nuclear magnetic resonance study of protolysis of trimethylammonium ion in aqueous solution: order of reaction with respect to solvent. J. Chem. Phys. 1963;39:366–370. [Google Scholar]
- 23.Stejskal E.O., Tanner J.E. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys. 1965;42:288–292. [Google Scholar]
- 24.Kimmich R., Anoardo E. Field-cycling NMR relaxometry. Prog. NMR Spectrosc. 2004;44:257–320. [Google Scholar]
- 25.Jones G.P. Spin-lattice relaxation in rotating frame: weak-collision case. Phys. Rev. 1966;148:332–335. [Google Scholar]
- 26.Krushelnitsky A., Reichert D. Response of lysozyme internal dynamics to hydration probed by C-13 and H-1 solid-state NMR relaxation. Appl. Magn. Reson. 2004;27:501–518. [Google Scholar]
- 27.Goldman M. Formal theory of spin-lattice relaxation. J. Magn. Reson. 2001;149:160–187. doi: 10.1006/jmre.2000.2239. [DOI] [PubMed] [Google Scholar]
- 28.Lipari G., Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- 29.Bertini I., Gupta Y.K., Schwalbe H. NMR spectroscopic detection of protein protons and longitudinal relaxation rates between 0.01 and 50 MHz. Angew. Chem. Int. Ed. 2005;44:2223–2225. doi: 10.1002/anie.200462344. [DOI] [PubMed] [Google Scholar]
- 30.Krushelnitsky A.G., Fedotov V.D. Overall and internal protein dynamics in solution studied by the nonselective proton relaxation. J. Biomol. Struct. Dyn. 1993;11:121–141. doi: 10.1080/07391102.1993.10508713. [DOI] [PubMed] [Google Scholar]
- 31.Krushelnitsky A. Intermolecular electrostatic interactions and Brownian tumbling in protein solutions. Phys. Chem. Chem. Phys. 2006;8:2117–2128. doi: 10.1039/b517448a. [DOI] [PubMed] [Google Scholar]
- 32.Krushelnitsky A.G., Fedotov V.D., Straka J. Dynamic structure of proteins in solid state. 1H and 13C NMR relaxation study. J. Biomol. Struct. Dyn. 1996;14:211–224. doi: 10.1080/07391102.1996.10508110. [DOI] [PubMed] [Google Scholar]
- 33.Blears D.J., Danyluk S.S. Proton wide-line nuclear magnetic resonance spectra of hydrated proteins. Biochim. Biophys. Acta. 1968;154:17–27. doi: 10.1016/0005-2795(68)90254-7. [DOI] [PubMed] [Google Scholar]
- 34.Bova M.P., Ding L.-L., Fung B.K.-K. Subunit exchange of αA-crystallin. J. Biol. Chem. 1997;272:29511–29517. doi: 10.1074/jbc.272.47.29511. [DOI] [PubMed] [Google Scholar]
- 35.Sedgwick H., Kroy K., Poon W.C. Non-equilibrium behavior of sticky colloidal particles: beads, clusters and gels. Eur Phys J E Soft Matter. 2005;16:77–80. doi: 10.1140/epje/e2005-00009-x. [DOI] [PubMed] [Google Scholar]
- 36.Strobl G. 3rd ed. Springer; Berlin-Heidelberg: 2007. The Pyhsics of Polymers. [Google Scholar]
- 37.Nesmelova I.V., Skirda V.D., Fedotov V.D. Generalized concentration dependence of globular protein self-diffusion coefficients in aqueous solutions. Biopolymers. 2002;63:132–140. doi: 10.1002/bip.10023. [DOI] [PubMed] [Google Scholar]
- 38.Horne R.A., Courant R.A., Margosian F.F. The activation energy of viscous flow of pure water and sea water in the temperature region of maximum density. J. Phys. Chem. 1965;69:3988–3991. [Google Scholar]
- 39.Ravera E., Parigi G., Luchinat C. Experimental determination of microsecond reorientation correlation times in protein solutions. J. Phys. Chem. B. 2013;117:3548–3553. doi: 10.1021/jp312561f. [DOI] [PubMed] [Google Scholar]
- 40.Zeeb M., Jacob M.H., Balbach J. 15N relaxation study of the cold shock protein CspB at various solvent viscosities. Biomol. NMR. 2003;27:221–234. doi: 10.1023/a:1025449611201. [DOI] [PubMed] [Google Scholar]
- 41.Doliwa B., Heuer A. Cage effect, local anisotropies, and dynamic heterogeneities at the glass transition: a computer study of hard spheres. Phys. Rev. Lett. 1998;80:4915–4918. [Google Scholar]
- 42.Pusey P.N. Colloidal glasses. J. Phys. Condens. Matter. 2008;20:494202. [Google Scholar]
- 43.Mereghetti P., Wade R.C. Atomic detail Brownian dynamics simulations of concentrated protein solutions with a mean field treatment of hydrodynamic interactions. J. Phys. Chem. B. 2012;116:8523–8533. doi: 10.1021/jp212532h. [DOI] [PubMed] [Google Scholar]
- 44.Liang J., Dill K.A. Are proteins well-packed? Biophys. J. 2001;81:751–766. doi: 10.1016/S0006-3495(01)75739-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Moret M.A., Santana M.C., Zebende G.F. Protein chain packing and percolation threshold. Physica A. 2006;361:250–254. [Google Scholar]
- 46.Banerji A., Ghosh I. Fractal symmetry of protein interior: what have we learned? Cell. Mol. Life Sci. 2011;68:2711–2737. doi: 10.1007/s00018-011-0722-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Fischer H., Polikarpov I., Craievich A.F. Average protein density is a molecular-weight-dependent function. Protein Sci. 2004;13:2825–2828. doi: 10.1110/ps.04688204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Harris K.R., Woolf L.A. Temperature and volume dependence of the viscosity of water and heavy water at low temperatures. J. Chem. Eng. Data. 2004;49:1064–1069. [Google Scholar]
- 49.Kestin J., Sokolov M., Wakeham W.A. Viscosity of liquid water in range −8°C to 150°C. J. Phys. Chem. Ref. Data. 1978;7:941–948. [Google Scholar]
- 50.Tyn M.T., Gusek T.W. Prediction of diffusion coefficients of proteins. Biotechnol. Bioeng. 1990;35:327–338. doi: 10.1002/bit.260350402. [DOI] [PubMed] [Google Scholar]
- 51.Ilyina E., Roongta V., Mayo K.H. A pulsed-field gradient NMR study of bovine pancreatic trypsin inhibitor self-association. Biochemistry. 1997;36:3383–3388. doi: 10.1021/bi9622229. [DOI] [PubMed] [Google Scholar]
- 52.Wilkins D.K., Grimshaw S.B., Smith L.J. Hydrodynamic radii of native and denatured proteins measured by pulse field gradient NMR techniques. Biochemistry. 1999;38:16424–16431. doi: 10.1021/bi991765q. [DOI] [PubMed] [Google Scholar]
- 53.Armstrong J.K., Wenby R.B., Fisher T.C. The hydrodynamic radii of macromolecules and their effect on red blood cell aggregation. Biophys. J. 2004;87:4259–4270. doi: 10.1529/biophysj.104.047746. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


