Abstract
We developed a multiscale model to bridge neuropeptide receptor-activated signaling pathway activity with membrane electrophysiology. Typically, the neuromodulation of biochemical signaling and biophysics have been investigated separately in modeling studies. We studied the effects of Angiotensin II (AngII) on neuronal excitability changes mediated by signaling dynamics and downstream phosphorylation of ion channels. Experiments have shown that AngII binding to the AngII receptor type-1 elicits baseline-dependent regulation of cytosolic Ca2+ signaling. Our model simulations revealed a baseline Ca2+-dependent response to AngII receptor type-1 activation by AngII. Consistent with experimental observations, AngII evoked a rise in Ca2+ when starting at a low baseline Ca2+ level, and a decrease in Ca2+ when starting at a higher baseline. Our analysis predicted that the kinetics of Ca2+ transport into the endoplasmic reticulum play a critical role in shaping the Ca2+ response. The Ca2+ baseline also influenced the AngII-induced excitability changes such that lower Ca2+ levels were associated with a larger firing rate increase. We examined the relative contributions of signaling kinases protein kinase C and Ca2+/Calmodulin-dependent protein kinase II to AngII-mediated excitability changes by simulating activity blockade individually and in combination. We found that protein kinase C selectively controlled firing rate adaptation whereas Ca2+/Calmodulin-dependent protein kinase II induced a delayed effect on the firing rate increase. We tested whether signaling kinetics were necessary for the dynamic effects of AngII on excitability by simulating three scenarios of AngII-mediated KDR channel phosphorylation: (1), an increased steady state; (2), a step-change increase; and (3), dynamic modulation. Our results revealed that the kinetics emerging from neuromodulatory activation of the signaling network were required to account for the dynamical changes in excitability. In summary, our integrated multiscale model provides, to our knowledge, a new approach for quantitative investigation of neuromodulatory effects on signaling and electrophysiology.
Introduction
Neuromodulators are integral to the control of intrinsic neuronal excitability, synaptic integration, and neural network function (1–3). Neuromodulators typically interact with specific G protein-coupled receptors (GPCRs) to activate biochemical signaling pathways and alter the metabolism, transcriptional activity, and electrophysiological responsiveness of the postsynaptic cell (4–7). However, the biochemical signaling and electrophysiological responses to neuromodulators have typically been examined separately in computational studies (8). The integration of signaling with electrophysiology in computational models of nonneuronal excitable cells has yielded important mechanistic insights to the diverse fields including cardiovascular physiology (9,10), platelet biology (11), and insulin metabolism (12,13). Our objective for this study was to integrate computational models of signaling pathway activation with those of electrophysiology to study the mechanistic underpinnings of neuromodulation.
We investigated neuromodulatory mechanisms of intracellular signaling and excitability responses to Angiotensin II (AngII) in brainstem neurons. AngII is a peptide neuromodulator involved in the regulation of autonomic nervous system activity via its actions within central autonomic nuclei (6,14–18). Neuromodulatory effects of AngII are primarily stimulated by the binding of AngII to the type-1 angtiotensin receptor (AT1R) and by eliciting G-protein mediated pathways (19). In brainstem autonomic neurons, AngII influences the inotropic and chronotropic drive of the heart (20,21). Neurons in autonomic nuclei such as the nucleus of the solitary tract participate in control of cardiovascular regulation at a beat-to-beat timescale and at the level of long-term arterial pressure setpoint control (22). Importantly, aberrations of AngII signaling in the brainstem have been implicated in the pathology underlying neurogenic hypertension (23–26). Thus, deciphering the mechanisms of AngII-mediated regulation of neuronal state is central to our understanding of cardiovascular homeostasis and diseases thereof.
Studies of AngII-mediated changes in cytosolic Ca2+ levels have shown contrasting effects of AT1R activation on intracellular Ca2+ levels, in which both stimulatory and suppressive effects have been reported (27–29). In cultured rat stellate ganglion neurons, it has been demonstrated that this divergence in Ca2+ responses was related to the Ca2+ baseline level. Suppressive effects were found in neurons with higher Ca2+ baseline levels and stimulatory effects were observed in neurons with relatively lower Ca2+ baseline levels (27). However, the mechanisms underlying such divergent Ca2+ baseline-dependent responses to AngII have not been elucidated. Similarly, it is unclear how this baseline-dependent regulation impacts neuronal excitability. Concomitant with the fluctuations of intracellular Ca2+ levels, application of AngII to cultured brainstem neurons in vitro results in an AT1R-dependent increase in action-potential (AP) firing rate (30–34). Electrophysiological studies have shown that AngII-stimulated protein kinase C (PKC) and Ca2+/Calmodulin-dependent protein kinase II (CaMKII) activation leads to the phosphorylation of delayed rectifier potassium (KDR) channels, which results in decreased channel conductance and increased firing rate (35–39). The relative contributions of PKC and CaMKII to firing rate response dynamics have not been studied. Our study addresses mechanistic questions regarding the biochemical basis for divergent Ca2+ responses and the molecular contributions to the biophysical consequences of AngII stimulation.
The effects of AngII-mediated neuromodulation result from nonlinear interactions involving numerous elements, thus necessitating a computational approach to unravel the dynamic mechanisms (40,41). We employed a multiscale modeling approach to quantitatively study AngII-mediated neuromodulation (42–44). We developed an integrated model to bridge GPCR signaling (19) with membrane electrophysiology (45) through an apparently new biochemical model of ion channel phosphorylation. We examined the molecular contributions to the dynamics of neuromodulation through targeted in silico manipulations. Our model incorporated AngII stimulation via Gq receptor activation of the signaling network. Bridging temporal scales from signaling (10 s) to electrophysiology (10−3 s) enabled us to investigate AngII/AT1R-mediated effects upon the following: 1) intracellular Ca2+ dynamics; 2) PKC and CaMKII activity and their distinct contributions to downstream neuronal firing; and 3) contributions of dynamic ion channel phosphorylation to firing rate modulation.
Our results revealed that controlling the rate of Ca2+ transport to endoplasmic reticulum (ER) generated the dichotomy in Ca2+ baseline-dependent responses. Examining relative contributions of PKC and CaMKII to excitability changes showed nonlinear interactions among distinct kinase contributions to the dynamics of AngII-mediated neuromodulation. We investigated the importance of dynamic AngII-mediated KDR channel phosphorylation by simulating multiple scenarios of altering KDR channel conductance. We found that the kinetics of channel phosphorylation were necessary for capturing the dynamics of neuronal excitability. To our knowledge, our multiscale modeling study provides a novel approach to quantitatively investigate the AngII neuromodulatory effects on signaling and electrophysiology, and revealed putative mechanisms underlying the regulation of Ca2+ responses, KDR conductance, and neuronal excitability. Understanding the dynamical interactions associated with AngII effects on different Ca2+ baseline states and elucidating the differential modulatory effects of kinases on neuronal properties have larger impact in understanding physiology of blood pressure control and pathophysiology of hypertension development (34,46,47).
Materials and Methods
An integrated model of neuronal cell signaling and electrophysiology was implemented as a set of ordinary differential equations solved using the ODE15s solver in the software MATLAB (The MathWorks, Natick, MA). The signaling reactions were modeled with either mass-action or Michaelis-Menten kinetics and ion channel electrophysiology was modeled according to the Hodgkin-Huxley formalism. These models were initially validated against their respective data domains independently and were then integrated to develop a multiscale model of signaling and electrophysiology. The model code in MATLAB format and instructions to reproduce the key results are available through accession No. 156830 in the ModelDB resource (48) at http://senselab.med.yale.edu/ModelDB/ShowModel.asp?model=156830.
Modeling AngII-mediated signaling network dynamics
AngII-activated AT1R stimulates phospholipase C (PLCβ) and triggers phosphoinositide (IP) hydrolysis, which releases IP3 and DAG, followed by Ca2+ mobilization from internal stores and activation of Ca2+-dependent enzymes including PKC and CaMKII (6). To construct a model of the AngII-mediated signaling network, we started with reaction pathways from an established cellular signaling database (DOQCS, doqcs.ncbs.res.in, accession No. 31). We employed a model of GPCR-mediated PLCβ activation, IP3 metabolism, Ca2+ release by the IP3 receptor (IP3R) in ER, and activation of signaling kinases PKC and CaMKII (19) as the basis for our biochemical model. A total of 13 signaling pathways from DOQCS were merged to build the AngII-mediated signaling network (see Table S1 in the Supporting Material). Our integrated model is comprised of 13 signaling pathways, a biochemical model of ion-channel phosphorylation, and an electrophysiological model containing six ion channels. A schematic of the integrated model topology including signaling network is shown in Fig. 1 A.
Figure 1.
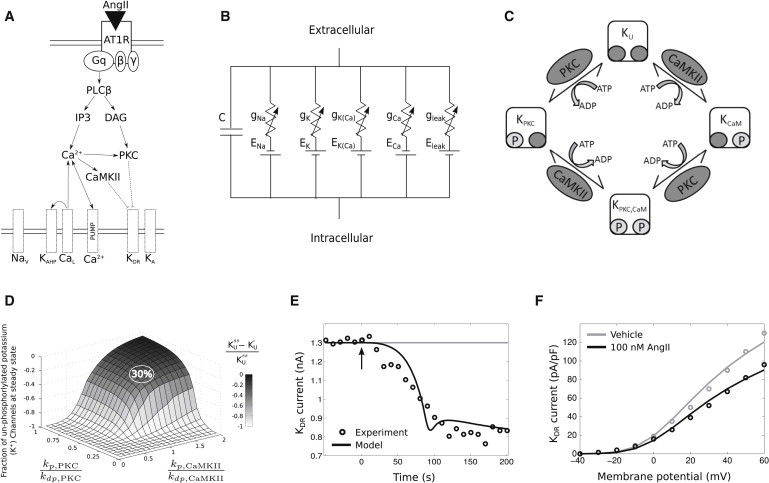
Integrated model of the intracellular signaling and electrophysiology. (A) An overview of the integrated model topology, showing AngII activation eliciting multiple signaling pathways and subsequently modulating membrane electrophysiology. (B) Circuit diagram of the electrophysiology model. (C) Schematic depicting the phosphorylation reactions underlying the AngII-mediated reduction of KDR conductance. (D) Plot showing the fractional reduction of unphosphorylated KDR channels as a function of phosphorylation/dephosphorylation reaction rate ratios (kp/kdp for both PKC and CaMKII). Data correspond to simulations in which KUss indicates the fraction of unphosphorylated KDR channels after 100 nM AngII at steady state and KUi refers to the fraction of unphosphorylated KDR channels before the application of AngII. The relative phosphorylation and dephosphorylation rates were set to yield ∼30% reduction in unphosphorylated channels to fit the experimental data in (E) (see Table S4 for reaction details). (E) Model fit to dynamic KDR current data after the application of 100 nM AngII to cultured brainstem neurons (37). (F) I-V relations for KDR from experiments (37) and simulations under baseline conditions and after 100 nM AngII application to cultured brainstem neurons.
We modified the initially collated signaling network in three distinct ways:
-
1.
The DOQCS model of Gq pathway activation was based on metabotropic glutamate receptor (mGluR) signaling. We replaced the mGluR kinetics with those of AT1R. The forward rate constant for binding of AngII to AT1R was estimated based on experiments from Yang et al. (49). The corresponding backward reaction kinetics, obtained from Mishra and Bhalla (19), were assumed to be similar to those of mGluR. The total AT1R concentration in the model was based on Ouali et al. (50). The majority of the parameters were initially taken from the DOQCS resource, because these parameters were tuned based on brain tissue data (19).
-
2.
We compartmentalized the Ca2+ dynamics in the model into three sections: the intracellular (cytosolic), the ER (sequestered), and the perimembrane space adjacent to calcium channels (extracellular). Cytosolic Ca2+ could be either free or buffered and the IP3 receptor regulated its transport from the ER. Reaction details and parameter values for the Ca2+ regulation model are shown in Table S2. Parameters corresponding to nonoscillatory Ca2+ response were modified to match the experimental data from neurons (27,29). Table S2 also shows reactions and/or equations for all of submodules of calcium dynamics, except for the CaL type ion-channel, which are reported in Table S3.
-
3.
We augmented the Ca2+ regulation module to include the sodium-calcium exchanger (NCX). Electrodiffusion of NCX, characterized by the influx of three Na+ ions for the efflux of every Ca2+ ion, was modeled based on the Goldman-Hodgkin-Katz equation (51). The chemical flux component of the exchanger was modeled with a PKC-dependent regulatory component (52,53), which also incorporated Michaelis-Menten kinetics for allosteric activation by Ca2+ (54) (see NCX module in Table S2 for details).
Modeling the neuronal membrane electrical activity dynamics
Neuronal electrophysiology was modeled using a modified Hodgkin and Huxley formalism (55). We modeled an electrical circuit (Fig. 1 B) containing multiple ionic currents balanced across the membrane (see Section S2 in the Supporting Material for details). The channel conductance and current expressions for the sodium channel (Na+), delayed rectifier potassium channel (KDR), A-type potassium channel (KA), L-type calcium channel (CaL2+), hyperpolarized calcium-dependent potassium channel (KAHP), and a nonspecific leak channel are described in Table S3.
The initial parameters of the electrical model were based on a model of cardiorespiratory brainstem neurons (45). The model parameters were modified to match experimental observations of increased firing rates, reduced KDR currents, and increased intracellular Ca2+ concentration after AngII application. The following constraints were imposed on the model based on AngII experimental data:
-
1.
The maximal conductances of the different channel types were adopted from Rybak et al. (45). This ensured a brainstem neuronal phenotype exhibiting the physiological firing rate at nominal conditions (38).
-
2.
The steady-state activation variables of the KDR and KA currents (i.e., and in Table S3) were chosen to provide a good fit to whole-cell, patch-clamp data (35,39).
Modeling ion-channel phosphorylation to bridge signaling pathways and electrical activity
We considered the macroscopic conductance of KDR channel as dependent on phosphorylation by PKC and CaMKII. An apparently new kinetic model was constructed based on mass action kinetics (Fig. 1 C). Experimental data show that phosphorylation of KDR channels results in a substantial reduction in current (50–90% (56)). We assumed that phosphorylated KDR channels could be completely inhibited at saturating levels of channel phosphorylation (i.e., = 0). The KDR conductance was obtained by multiplying basal maximal conductance by the fraction of unphosphorylated channels. The phosphorylation reactions were modeled with first-order kinetics as
| (1) |
| (2) |
| (3) |
where KT represents the total fraction of potassium channels with n phosphorylation sites (KT = 1), KU represents the fraction of unphosphorylated channels, and KP represents the fraction of phosphorylated channels. The levels of phosphorylated channels represent aggregate of channels phosphorylated by PKC, CaMKII, or both. Kinases were assumed to act independently on distinct phosphorylation sites on these channels. The parameter n = 4 was set for simplification under the assumption that each of the four channel subunits can be phosphorylated. In our integrated model, PKC and CaMKII both phosphorylated KDR (see Table S4 for details).
To simulate phosphorylation-mediated reduction of KDR current, we weighted the peak conductance by the fraction of unphosphorylated channels in Table S3 (KU = 1 before AngII stimulation):
| (4) |
To occlude the phosphorylation reactions of a kinase in silico, we set kp,CAMKII and/or kp,PKC in Table S4 to zero.
Results
Bridging the signaling network with the electrophysiology model
Bidirectional interactions between the signaling and electrophysiological domains arise due to kinases PKC and CaMKII phosphorylating the KDR channel, the dependence of NCX on membrane potential, the contribution of voltage-dependent Ca2+ channels to Ca2+ regulation, and the effects of Ca2+ level on Ca2+-dependent potassium channel conductance (KAHP). The signaling network model was modified to incorporate the membrane potential as a dynamic state variable in the NCX description. The maximal conductance of KDR was dependent on the state variables corresponding to active PKC and CaMKII as detailed above. The remaining key interactions involved Ca2+ dynamics due to release from cytosolic stores in the signaling model and flux through ion channel currents in the electrical model.
Simulations indicated that the Ca2+ levels affecting KAHP had to be considered separately from the levels of free cytosolic Ca2+. Otherwise, large increase in cytosolic Ca2+ levels after AngII stimulation activated the KAHP current to saturation and prevented any neuronal firing activity. The hypothesis that there exists a perimembrane Ca2+ compartment distinct from bulk cytosolic Ca2+ is supported by experimental data (57) and is typically considered as such in neuronal modeling studies (58). To address this issue, Ca2+ dynamics were compartmentalized in the model such that the KAHP and CaL channels were assumed to be closely situated with local Ca2+ buffering and were uninfluenced by bulk cytosolic Ca2+.
Integrated AngII signaling and electrophysiology model accounts for the dynamics of KDR channel phosphorylation
Our integrated model quantitatively simulated AngII/AT1R-mediated neuromodulation by recapitulating experimental findings from brainstem neurons. To fit the electrophysiological data with that of signaling network interactions, we varied the ratio of (KDR) phosphorylation to dephosphorylation rate constants (kp/kdp) for PKC and CaMKII (Fig. 1 D). The model was calibrated to account for the 30% reduction in KDR current observed after application of 100 nM AngII (37). Evidence suggests that this current reduction is attributable to KDR channel phosphorylation (37). We then tuned the kp and kdp parameters for PKC and CaMKII to render a 30% reduction in the fraction of unphosphorylated KDR channels. This calibration recapitulated the kinetics of KDR current reduction after the application of 100 nM AngII (Fig. 1 E), as well as the shift in the KDR current-voltage relation observed in voltage-clamp data (Fig. 1 F) (37). Our results showed that the combined effects of PKC and CaMKII were required to attain the experimental results. The fitted CaMKII rate constants were equal for phosphorylation and dephosphorylation, and the PKC dephosphorylation rate constant was twice that of the PKC phosphorylation rate constant. Our integrated model with known signaling network interactions, when appropriately tuned with channel phosphorylation kinetics, accounted for the experimentally observed dynamics of excitability changes in response to AngII stimulation.
Ca2+ baseline-dependent bifurcation of signaling responses to AngII
AngII application resulted in a dose-dependent AT1R-signaling pathway response, including regulation of PKC and CaMKII by Ca2+. Cytosolic Ca2+ levels in neurons are maintained by chemical and electrochemical fluxes due to L-type Ca2+ channels (CaL), the sodium-calcium exchanger (NCX), and plasma membrane Ca2+ pumps (EPump) (see Fig. 2 A). Excess intracellular Ca2+ is stored in the ER until the buffer reaches its saturating limit, and is released after IP3R binding. Experimental observations have shown that AngII elicits divergent neuronal responses depending on Ca2+ baseline levels (see insets in Fig. 2, D and F) (27). To determine why such divergent responses occur, we individually varied all of the parameters in the Ca2+ regulation module to search for variations that could reproduce this nonlinear behavior. We found that reducing the rate of Ca2+ transport into the ER increased the cytosolic Ca2+ baseline levels at steady state without AngII (Fig. 2 B), thus instantiating the high baseline Ca2+ condition. Reduction in this rate constant (from 3600 to 36 μM−2 s−1) initiates an efflux of all stored Ca2+ from the ER to the cytosol. This efflux resulted in an empty ER buffer in the high Ca2+ baseline condition (Fig. 2 C). This is because the decreased influx rate of Ca2+ into the ER induced an imbalance in Ca2+ flux between ER and cytosol. Because the outward rate (3125 μM−1 s−1) remained the same, the increase in rate difference (outward versus inward) introduced a driving force that favored Ca2+ extrusion from the ER (see Section S1 in the Supporting Material). At steady state, the ER Ca2+ buffer transferred all of its sequestered Ca2+ into the cytosolic region, resulting in an increase in the intracellular Ca2+ baseline level. Thus, due to a change in the amount of Ca2+ available in ER stored for different Ca2+ baseline conditions, application of AngII led to a divergence in cytosolic Ca2+ and buffer responses to AngII.
Figure 2.
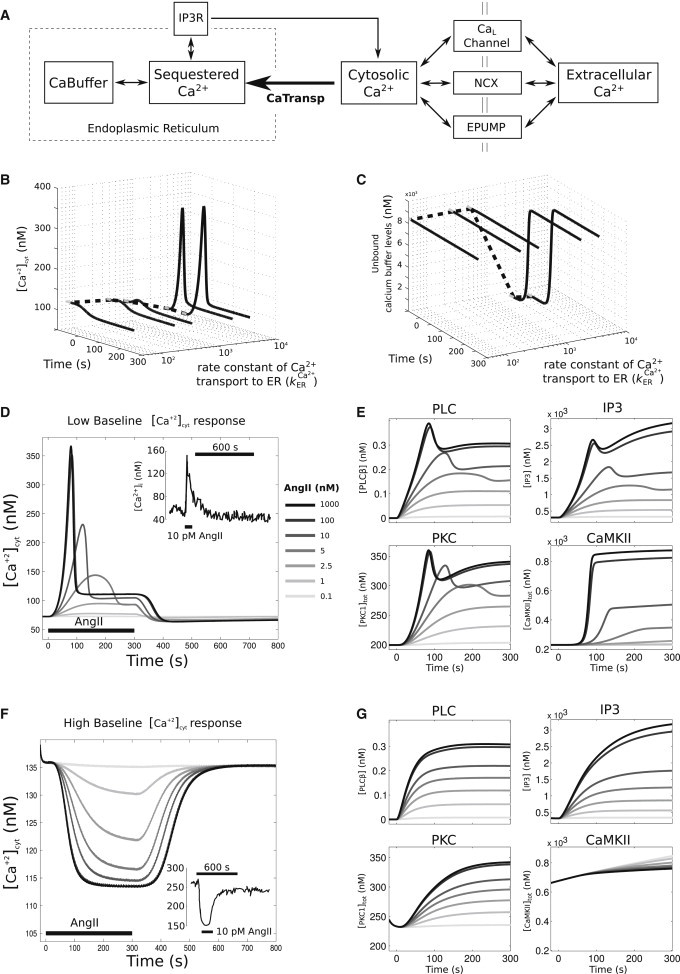
Nonlinear baseline Ca2+-dependent response to AngII stimulus, in which low cytosolic Ca2+ baseline levels resulted in an increase in cytosolic Ca2+ and high cytosolic Ca2+ levels resulted in a decrease in cytosolic Ca2+ levels. (A) Schematic of Ca2+ regulatory dynamics. (B) Dynamic traces of cytosolic Ca2+ as a function of change in the rate constant of a Ca2+ transport into the ER . (Solid lines) Time period where 100 nM AngII was applied; (shaded lines) steady-state levels preceding AngII application. Decreasing the from 3600 to 36 μm−2 s−1 increases the Ca2+ baseline levels from ∼72 to 136 nM (dotted line). (C) Dynamic traces of unbound calcium buffer levels as a function of change in . For plot details, see (B). Decrease in drains out all stored Ca2+ in the buffer before AngII application (total capacity of the saturated buffer = 9091 nM). (D) AngII dose-dependence of cytosolic Ca2+ response for low cytosolic Ca2+ baseline condition. (Inset, top right) Intracellular calcium tracing from primary cultures of neonatal rat sympathetic neurons when exposed to 3 min AngII pulses (10 pM) for low baseline condition (27). (E) Upstream responses of PLCβ and IP3, and downstream kinase responses of PKC and CaMKII for the low Ca2+ baseline condition. (F) AngII dose-dependence of cytosolic Ca2+ response for high cytosolic Ca2+ baseline condition. (Inset, bottom-right panel) Intracellular calcium tracings taken from cells (see D for details) with a higher baseline (>200 nM). (G) High Ca2+ baseline condition upstream responses of PLCβ and IP3, and downstream kinase responses of PKC and CaMKII.
We applied AngII to a neuronal state that was characterized by a higher rate of Ca2+ transport into ER, or the corresponding low cytosolic Ca2+ baseline condition. Our simulations resulted in an increase in cytosolic Ca2+ level followed by a response adaptation. The Ca2+ level returned to the initial baseline state after withdrawal of AngII (Fig. 2 D). The peak Ca2+ response increased nonlinearly as a function of AngII dose (Fig. 2 D). The time point of the initial Ca2+ peak after stimulation was observed within ∼45 s in stellate ganglion cells (27). Our simulation results showed an initial peak within 50–120 s and thus provided a good match to these data in terms of the observed temporal response. The absolute peak values were comparable in both experimental data sets and were matched well by the model. For AngII concentrations up to 1 nM the Ca2+ response was negligible, although the response increases sigmoidally for AngII >1 nM (see Fig. S2 A). The dynamics of PLCβ, IP3, PKC, and CaMKII exhibited saturating responses with distinct amplitudes and kinetics (Fig. 2 E). PLCβ and IP3 showed peak responses followed by either sustained or transient adaptation, respectively. PKC showed a peak response followed by adaptation, whereas CaMKII, which is activated solely by Ca2+, showed a relatively delayed increase without adaptation. The CaMKII responses showed initial kinetics and a dose-response relation similar to that of Ca2+, while other species showed a markedly reduced kinetics and cooperativity (Fig. 3). These results are in agreement with experimental results from Zhu et al. (59). Simulations with a higher Ca2+ baseline indicated that Ca2+ decreased significantly after AngII stimulation, but returned to the initial steady-state levels after withdrawal of AngII (Fig. 2 F). For high baseline condition, PLCβ, IP3, and PKC showed increases in their levels after AngII stimulation but showed saturated response at high AngII doses (Fig. 2 G). The CaMKII response, however, displayed a decrease in levels because it was activated solely by intracellular Ca2+.
Figure 3.
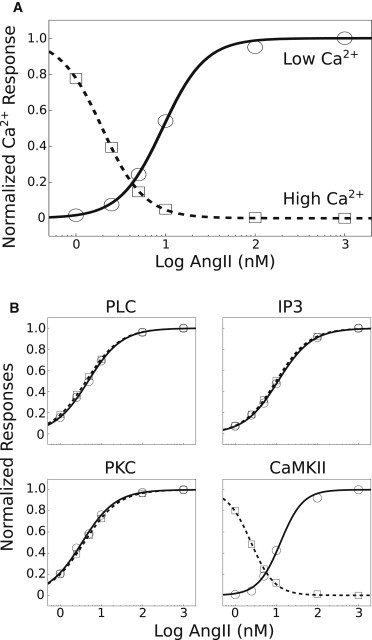
AngII dose-dependence of divergent Ca2+ responses. (A) Baseline-subtracted peak deflections were normalized and plotted for high and low Ca2+ baseline phenotypes. Dose-response data were fitted with the Hill equation: . Fit results indicate that the high Ca2+ baseline phenotype is more sensitive to AngII as compared to that of the low Ca2+ baseline phenotype (K0.5 = 2.0 nM and K0.5 = 9.3 nM, respectively). However, the cooperativity coefficients were nearly identical (nH = 1.85, 1.82). (B) Steady-state responses (t = 300 s) of PLC, IP3, PKC, and CaMKII were baseline-subtracted, normalized, and fitted as described above. Dose-response relations for PLC, IP3, and PKC were nearly identical for the high- and low-Ca2+ baseline phenotypes (see Table S4 for all fit parameters). Because CaMKII is activated by cytosolic Ca2+, active CaMKII levels decrease along with Ca2+ in the high baseline condition. The AngII-dependence of the CaMKII response is pronounced in the high baseline phenotype relative to the low Ca2+ baseline condition (K0.5 = 2.4 nM and K0.5 = 12.6 nM, respectively), while the cooperativity coefficients were similar (nH = 1.52, 1.59). Dose response relations for peak responses yielded similar trends (see Table S4).
We examined the dose-dependency of the AngII-mediated peak Ca2+ response for the high and low Ca2+ baseline conditions. Hill equation fits for the high Ca2+ baseline condition yielded a lower K0.5 value compared to that of the low Ca2+ baseline (Fig. 3 A). This suggests that there is differential sensitivity to AngII for the high versus low Ca2+ baseline. We fitted Hill equations to both peak and steady state (t = 300 s) AngII dose-response relations for PLCβ, IP3, PKC, and CaMKII (Fig. 3 B and see Table S5). The results showed similar dose response profiles for PLCβ, IP3, and PKC in the high and low Ca2+ baseline conditions. This similarity trend was obtained for both the peak and steady-state responses of PLCβ, IP3, and PKC (see Table S5). In contrast, the deactivation of CaMKII after AngII application to the high Ca2+ baseline condition had a lower K0.5 value compared to the low baseline condition.
This suggests that the deactivation of CaMKII in the high Ca2+ baseline condition is more sensitive to AngII concentration when compared to the activation of CaMKII in the low Ca2+ baseline condition. Although active PKC levels were elevated in the high Ca2+ baseline condition, the responsiveness of PKC to AngII stimulation was similar in both Ca2+ baseline conditions. However, while the changes in CaMKII levels were relatively small in the high Ca2+ baseline condition, the AngII dose-dependence of CaMKII deactivation relation was left-shifted compared to the low Ca2+ baseline condition. Further, we found that the baseline firing rate was elevated in the high Ca2+ baseline state (see Fig. S2). This increase in baseline firing rate was due to increase in baseline CaMKII levels, and application of AngII induced a slow and small change in excitability, resulting in an electrophysiological state comparable to that of the low Ca2+ baseline state (see details in Section S3 in the Supporting Material).
Distinct dynamic contributions of CaMKII and PKC to AngII-mediated changes in neuronal excitability
To examine the relative contributions of PKC- and CaMKII-mediated phosphorylation of KDR channels to AngII-mediated firing rate responses, we simulated in silico blockade of each phosphorylation mechanism by removing the corresponding reactions from the model individually and in combination (Fig. 4 A). Such scenarios are biologically plausible if the phosphorylation sites are unavailable due to genetic polymorphisms (60). The wild-type simulation (Fig. 4 B, condition 1) showed an excitability increase after AngII stimulation that exhibited adaptation in the continuous presence of AngII. Occluding PKC-dependent channel modulation (Fig. 4 B, condition 2) significantly altered the response to result in a faster, but delayed, increase in firing rate without adaptation. Blocking CaMKII-dependent phosphorylation (Fig. 4 B, condition 3) had an effect on overall gain but not on the pattern of neuronal adaptation. Blocking modulation by both kinases (Fig. 4 B, condition 4) abrogated the AngII-mediated increase in neuronal excitability. These results indicate that NCX alone does not influence the neuronal firing rate under the conditions of our simulations, whereas CaMKII and PKC have distinctive effects on the dynamics of neuronal firing rate responses to AngII stimulation. Both conditions of kinase phosphorylation occlusion resulted in similar steady-state firing rates that were ∼75% of the wild-type response, indicating a nonlinear interaction among kinases.
Figure 4.
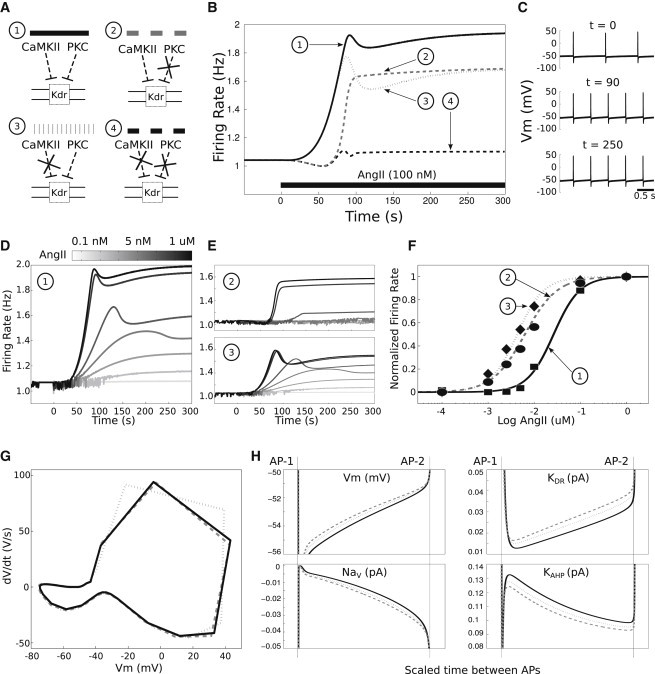
Distinct dynamic contributions of PKC and CaMKII to AngII-mediated excitability changes. (A) The neuronal response to AngII was simulated in four conditions: 1), the wild-type reference simulation; 2), occluding PKC phosphorylation of KDR; 3), occluding CaMKII phosphorylation of KDR; and 4), occluding both CaMKII and PKC-mediated phosphorylation of KDR. (B) Firing rate responses to 100 nM AngII (starting at t = 0 s) are shown for all four conditions. (C) Membrane potential time-series at t = 0, 90, 250 s showing increases in excitability after AngII application to the wild-type model (1). (D and E) Responses at a range of AngII input levels are shown for the wild-type and single kinase phosphorylation occlusion conditions (conditions 1–3). (F) Baseline-subtracted firing rate responses at steady state (t = 300 s) are plotted as a function of AngII concentration for conditions 1–3. Each relation was fitted with a Hill equation: . (G) Phase-space representations of APs at the times of peak responses to AngII for conditions 1–3 (same legend as in B and F). (H) Interspike interval biophysical properties of conditions 1–3 at times of peak responses to AngII. Abbreviations: Vm = membrane potential, NaV = Na+ current, KDR = KDR current, and KAHP = KAHP current.
We next investigated the dose-response effects of AngII on excitability (Fig. 4, D–F). We applied a range of AngII doses and fitted Hill equations to the rate versus dose relations at peak and at steady state (see Table S6). The results for steady-state fits showed that the wild-type phenotype (condition 1) had a reduced sensitivity to AngII when compared to the individual in silico blockade conditions (1,2), both of which showed similar sensitivities to AngII (Fig. 4 F). These results suggest that pronounced reductions in the activity of either kinase individually will reduce the excitability response amplitude but increase the sensitivity to AngII. Results for fits to peak firing rates showed similar trends (see Table S6 and Fig. S4). Although firing rates were different at the times of peak responses in conditions 1–3, AP waveforms were similar, indicating the absence of KDR phosphorylation effects on AP threshold or repolarization (Fig. 4 G). To interrogate the electrophysiological basis for observed effects, we examined the ionic contributions to the AngII firing rate responses in conditions 1–3 at times of peak AngII responses in each respective condition. The results showed that occluding phosphorylation of KDR led to subtle changes in Na+, KAHP, and KDR currents during interspike intervals (Fig. 4 H). This suggests that differences in KDR phosphorylation, as determined by the relative contributions of PKC and CaMKII, alter the contributions of other ionic conductances and thereby modify the overall electrophysiological response to AngII stimulus.
Kinetic channel modulation is required to account for the dynamics of AngII-mediated excitability changes
We hypothesized that the kinetics of AngII signaling pathway activation are required to shape the dynamic response profile. To test this hypothesis, we evaluated the electrophysiological response under three distinct KDR phosphorylation conditions:
-
1.
Higher steady-state phosphorylation,
-
2.
Step change to instantaneously increased phosphorylation, and
-
3.
Signaling kinase-mediated dynamic changes in phosphorylation (Fig. 5 A).
The results showed that a steady-state reduction of KDR conductance produced a constant firing rate (Fig. 5 B). A step reduction in KDR conductance produced a transient excitability increase followed by a constant firing rate. The dynamic profile of the firing rate change due to kinetic signaling activity was strikingly different from those elicited by steady state and as step changes in KDR phosphorylation (Fig. 5 B). Hence, we conclude that the signaling kinase-mediated phosphorylation of KDR is required to reproduce the dynamics of the experimentally observed neuronal response to AngII stimulation (Fig. 1 E).
Figure 5.
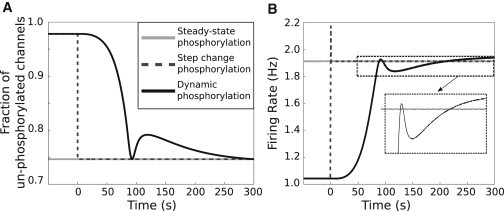
Dynamic KDR channel modulation emerging from signaling activities is necessary to account for the dynamics of AngII-induced neuronal excitability. (A) Simulated fractions of unphosphorylated KDR channels for three scenarios describing AngII-mediated KDR channel phosphorylation: (1), a steady-state increase (2), a step-change increase, and (3), dynamic modulation. (B) AngII-induced firing rate responses (100 nM starting at t = 0 s) for the three simulated scenarios. (Inset) Distinct effects of dynamic phosphorylation corresponding to Scenario 3 as compared to those of nondynamic phosphorylation (Scenarios 1 and 2).
Discussion
Neuromodulation is a subject under intense investigation in experimental and computational neuroscience, given its role in a plethora of physiological, behavioral, and cognitive functions of the central/peripheral nervous systems in health and disease (1–3,61–63). This work integrates a large-scale biochemical signaling network with a detailed Hodgkin-Huxley-like model of membrane electrophysiology to study dynamic neuromodulation. While biochemically detailed models have been developed that incorporate neuromodulator-induced signaling influences on specific ion channels, these models do not contain a cadre of ion channels sufficient for suprathreshold membrane potential dynamics and AP firing (64–66). Models have been developed that integrate temporal and spatial scales of calcium dynamics and multiple channels in dendrites to investigate mechanisms underlying synaptic plasticity (42–44,67–69). Some models of cardiac physiology incorporated GPCR-mediated modulation of signaling cascades (9,10), while others either do not include GPCRs or else simulate their effects as steady-state parameter changes (70–72). In addition, the majority of the published neuromodulation models have simulated the modulatory influences on electrophysiology with steady-state parameter variations, whereas only some models have included kinetics based on coarse-grained abstractions of the underlying cell signaling pathways (8). A quantitative study of neuromodulation, therefore, must integrate GPCR-neuropeptide interactions, biochemical signaling pathways, calcium dynamics, and membrane electrophysiology to thoroughly interrogate the underlying dynamical interactions (40,41). Because signaling events evolve over seconds and electrophysiological dynamics span milliseconds, integrative modeling of neuromodulation necessitates the bridging of timescales. It also entails signaling events that span multiple spatial components, from organelle to cell. Thus, we developed a multiscale modeling approach to study neuromodulation in the context of AngII-mediated influences on brainstem neurons.
Our model captured two distinct experimentally observed divergent AngII-mediated response patterns. AngII elicits a cytosolic Ca2+ increase at low baseline Ca2+ levels and a Ca2+ decrease at high baseline Ca2+ levels (27). Effects of intracellular Ca2+ diffusion, particularly during transport to and from ER, have been noted in oscillatory Ca2+ releases (73). However, Ca2+ diffusion within the cell cytoplasm is much slower compared to the intracellular release due to second messenger activation such as IP3 (74). Because our model contains nonoscillatory Ca2+ mobilization, we considered that the flux due to Ca2+ diffusion has minimal effect in comparison to the fluxes of channels/pumps, and ignored the former component in this model. Further analysis of the simulation results revealed that the decrease in cytosolic Ca2+ can be explained by reducing the rate constant of Ca2+ flux into the ER. These results suggest that the signaling system is recalibrated in conditions of high Ca2+ such that the ER Ca2+ stores are completely eliminated. This finding indicated that the augmentation of Ca2+ baseline levels elevated baseline neuronal firing frequency but diminished the changes in AngII-induced excitability. These observations are consistent with data showing that repeated applications of AngII lead to tachyphylaxis (75,76). The Ca2+ baseline-dependence of AngII-mediated responses is also consistent with the observation that AngII elicits divergent effects on blood pressure in vivo via actions within the rostral brainstem (77). Such alterations of Ca2+ responses may have important implications for AngII-mediated effects on gene expression and gene regulatory influences on autonomic control of cardiovascular physiology (78,79).
Pharmacological studies have implicated a definitive role of PKC and CaMKII in the modulation of various ion channels. In particular, the delayed rectifier potassium (KDR) current decreases upon AT1R activation by AngII in brainstem neurons (35–39). The inhibition of KDR current is believed to occur after direct phosphorylation of Kv2.2 subunits (35,36). Although it is still unclear whether direct phosphorylation of Kv2.2 occurs, Kv2.1 channels have been shown to be directly phosphorylated (80). Inhibition of KA has also been shown to occur after direct phosphorylation of the Kv1.4a subunit at putative PKC and CaMKII sites (81). However, we found that inhibition of KA current did not alter firing rate significantly relative to changes in KDR conductance in our model. Hence, we did not simulate kinase-mediated phosphorylation reactions with KA channels. Our assessments of the relative contributions of PKC and CaMKII to AngII-mediated modulation of firing rate showed that these kinases reduced the neuronal sensitivity to AngII. The steady-state excitability response to saturating AngII doses is largely intact in the complete absence of either of the kinases, suggesting a high degree of redundancy in the dual kinase system within our model. The kinetic contributions of each kinase is also distinct such that PKC determines the initial response kinetics and firing rate adaptation, whereas CaMKII contributes exclusively to firing rate gain while reducing the extent of adaptation. Overall, our simulations suggest that PKC and CaMKII fine-tunes the degree, timing, and adaptation of excitability responses to AngII. Our simulation results could be experimentally tested via targeted perturbations of these kinases in brainstem cardiac control regions, which could ameliorate the aberrant effects of AngII on sympathetic overdrive observed in conditions such as hypertension and heart failure (21).
Molecular neuronal pathways elicited by AngII binding to AT1R in brainstem neurons are involved in the regulation of blood pressure and development of hypertension (14,82–84). These activated pathways include those that trigger short-term increase in neuronal firing rate as well as those that affect gene expressions and protein levels for longer-term effects leading to sustained changes in neuronal activities (6,33,85,86). Our model-based results connect the alteration in Gq-mediated signaling to the short-term implications on electrophysiological behavior by linking it through activation of PKC and CaMKII, in consistency with experimental findings (6,33). Our results predict that each of the two signaling kinases provide distinct regulatory influence on neuronal excitability, suggesting a differential pathway-specific sensitivity of the neuronal circuit controlling blood pressure. Experimentally observed aberrations in the kinase activities in pathophysiological conditions can be interpreted through our model-based approach to understand the effects of AngII on the balance between excitatory and inhibitory effects on sympathetic neurons (34,46,47). Opportunities exist for an unbiased approach to identify key sensitivities in the integrated multiscale network, for example, utilizing global sensitivity analysis and decision trees (78). AngII effects on overall cardiovascular physiology are difficult to predict due to the involvement of AngII signaling in multiple cell types in the control circuit, leading to the push-pull hypothesis of AngII action (77). Our integrated model can be extended across multiple cell types to explore the network balances in computationally testing the push-pull hypothesis toward explaining the nonlinear effects of AngII on sympathoexcitation as well as sympathoinhibition (20,21,87).
A key characteristic of our model is the inclusion of a highly detailed signaling cascade, validated with experimental data from neurons (19). Building on models that consider instantaneous parameter perturbations to simulate the effects of neuromodulators on downstream targets, we examined the effects of signaling kinetics on firing rate dynamics. Simulations support the hypothesis that dynamic neuromodulation is critical for AngII-mediated excitability dynamics, which cannot be captured by simulating neuromodulation as steady-state or step reductions of the KDR conductance. Overall, our modeling work suggests that the dynamic interplay among neuromodulatory influences, ionic conductances, and membrane potential determine neuromodulator response in a nonlinear fashion.
Our modeling approach can be expanded to address several physiological questions. Simulations of subthreshold membrane dynamics and synaptic integration can be performed to study the neuromodulation of excitatory and inhibitory input processing. Neuromodulator effects on neural circuits can be studied using our model as a basis for simulating individual cells. The combination of signaling pathway activity with electrophysiology can be integrated into morphologically detailed neuronal models that incorporate experimentally determined spatial variations in channel distributions (88,89). Our model can also be integrated with AngII-signaling-induced transcriptional regulatory networks to bridge neuromodulation of signaling and electrophysiology with gene expression (78). In the context of autonomic regulation of cardiovascular control, our model could be expanded to study the mechanisms and consequences of aberrant AngII signaling in brainstem neurons from hypertensive rats, based on extensive data on signaling activity and electrophysiological responses to AngII in spontaneously hypertensive rats (47,90–92). Hence, our multiscale model of integrated signaling and electrophysiology offers broader utility as a platform for studies of neuromodulatory mechanisms underlying physiological function.
Acknowledgments
This study was supported by National Institute of General Medical Sciences grant No. R01 GM083108 and National Heart, Lung, and Blood Institute grant No. R01 HL111621.
Footnotes
Hirenkumar K. Makadia, Warren D. Anderson, and Dirk Fey contributed equally to this work.
Supporting Material
Supporting Citations
Reference (93) appears in the Supporting Material.
References
- 1.Marder E. Neuromodulation of neuronal circuits: back to the future. Neuron. 2012;76:1–11. doi: 10.1016/j.neuron.2012.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Levitan I.B. Modulation of ion channels by protein phosphorylation and dephosphorylation. Annu. Rev. Physiol. 1994;56:193–212. doi: 10.1146/annurev.ph.56.030194.001205. [DOI] [PubMed] [Google Scholar]
- 3.Finkel L.H. Neuroengineering models of brain disease. Annu. Rev. Biomed. Eng. 2000;2:577–606. doi: 10.1146/annurev.bioeng.2.1.577. [DOI] [PubMed] [Google Scholar]
- 4.Lu D., Yang H., Raizada M.K. Angiotensin II regulation of neuromodulation: downstream signaling mechanism from activation of mitogen-activated protein kinase. J. Cell Biol. 1996;135:1609–1617. doi: 10.1083/jcb.135.6.1609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lu D., Yang H., Raizada M.K. Regulation of angiotensin II-induced neuromodulation by MARCKS in brain neurons. J. Cell Biol. 1998;142:217–227. doi: 10.1083/jcb.142.1.217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sumners C., Fleegal M.A., Zhu M. Angiotensin AT1 receptor signaling pathways in neurons. Clin. Exp. Pharmacol. Physiol. 2002;29:483–490. doi: 10.1046/j.1440-1681.2002.03660.x. [DOI] [PubMed] [Google Scholar]
- 7.Temporal S., Desai M., Golowasch J. Neuromodulation independently determines correlated channel expression and conductance levels in motor neurons of the stomatogastric ganglion. J. Neurophysiol. 2012;107:718–727. doi: 10.1152/jn.00622.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fellous J.M., Linster C. Computational models of neuromodulation. Neural Comput. 1998;10:771–805. doi: 10.1162/089976698300017476. [DOI] [PubMed] [Google Scholar]
- 9.Saucerman J.J., Brunton L.L., McCulloch A.D. Modeling β-adrenergic control of cardiac myocyte contractility in silico. J. Biol. Chem. 2003;278:47997–48003. doi: 10.1074/jbc.M308362200. [DOI] [PubMed] [Google Scholar]
- 10.Tao T., Paterson D.J., Smith N.P. A model of cellular cardiac-neural coupling that captures the sympathetic control of sinoatrial node excitability in normotensive and hypertensive rats. Biophys. J. 2011;101:594–602. doi: 10.1016/j.bpj.2011.05.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dolan A.T., Diamond S.L. Systems modeling of Ca2+ homeostasis and mobilization in platelets mediated by IP3 and store-operated Ca2+ entry. Biophys. J. 2014;106:2049–2060. doi: 10.1016/j.bpj.2014.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fridlyand L.E., Philipson L.H. Coupling of metabolic, second messenger pathways and insulin granule dynamics in pancreatic β-cells: a computational analysis. Prog. Biophys. Mol. Biol. 2011;107:293–303. doi: 10.1016/j.pbiomolbio.2011.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Salvucci M., Neufeld Z., Newsholme P. Mathematical model of metabolism and electrophysiology of amino acid and glucose stimulated insulin secretion: in vitro validation using a β-cell line. PLoS ONE. 2013;8:e52611. doi: 10.1371/journal.pone.0052611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Touyz R.M., Pu Q., Viel E. Effects of low dietary magnesium intake on development of hypertension in stroke-prone spontaneously hypertensive rats: role of reactive oxygen species. J. Hypertens. 2002;20:2221–2232. doi: 10.1097/00004872-200211000-00022. [DOI] [PubMed] [Google Scholar]
- 15.McCubbin J.W., DeMoura R.S., Olmsted F. Arterial hypertension elicited by subpressor amounts of angiotensin. Science. 1965;149:1394–1395. doi: 10.1126/science.149.3690.1394. [DOI] [PubMed] [Google Scholar]
- 16.Hogarty D.C., Speakman E.A., Phillips M.I. The role of angiotensin, AT1 and AT2 receptors in the pressor, drinking and vasopressin responses to central angiotensin. Brain Res. 1992;586:289–294. doi: 10.1016/0006-8993(92)91638-u. [DOI] [PubMed] [Google Scholar]
- 17.Phillips M.I., Sumners C. Angiotensin II in central nervous system physiology. Regul. Pept. 1998;78:1–11. doi: 10.1016/s0167-0115(98)00122-0. [DOI] [PubMed] [Google Scholar]
- 18.Ferguson A.V., Washburn D.L., Latchford K.J. Hormonal and neurotransmitter roles for angiotensin in the regulation of central autonomic function. Exp. Biol. Med. (Maywood) 2001;226:85–96. doi: 10.1177/153537020122600205. [DOI] [PubMed] [Google Scholar]
- 19.Mishra J., Bhalla U.S. Simulations of inositol phosphate metabolism and its interaction with InsP3-mediated calcium release. Biophys. J. 2002;83:1298–1316. doi: 10.1016/S0006-3495(02)73901-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Accorsi-Mendonca D., Machado B. Synaptic transmission of baro- and chemoreceptors afferents in the NTS second order neurons. Autonom. Neurosci. 2013;175:3–8. doi: 10.1016/j.autneu.2012.12.002. [DOI] [PubMed] [Google Scholar]
- 21.Guyenet P.G. The sympathetic control of blood pressure. Nat. Rev. Neurosci. 2006;7:335–346. doi: 10.1038/nrn1902. [DOI] [PubMed] [Google Scholar]
- 22.Thrasher T.N. Arterial baroreceptor input contributes to long-term control of blood pressure. Curr. Hypertens. Rep. 2006;8:249–254. doi: 10.1007/s11906-006-0058-z. [DOI] [PubMed] [Google Scholar]
- 23.Shan Z., Zubcevic J., Raizada M.K. Chronic knockdown of the nucleus of the solitary tract AT1 receptors increases blood inflammatory-endothelial progenitor cell ratio and exacerbates hypertension in the spontaneously hypertensive rat. Hypertension. 2013;61:1328–1333. doi: 10.1161/HYPERTENSIONAHA.111.00156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zubcevic J., Jun J.Y., Shan Z. Nucleus of the solitary tract (pro)renin receptor-mediated antihypertensive effect involves nuclear factor-κB-cytokine signaling in the spontaneously hypertensive rat. Hypertension. 2013;61:622–627. doi: 10.1161/HYPERTENSIONAHA.111.199836. [DOI] [PubMed] [Google Scholar]
- 25.Cuadra A.E., Shan Z., Raizada M.K. A current view of brain renin-angiotensin system: is the (pro)renin receptor the missing link? Pharmacol. Ther. 2010;125:27–38. doi: 10.1016/j.pharmthera.2009.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Paton J.F., Wang S., Kasparov S. Signaling across the blood brain barrier by angiotensin II: novel implications for neurogenic hypertension. J. Mol. Med. 2008;86:705–710. doi: 10.1007/s00109-008-0324-4. [DOI] [PubMed] [Google Scholar]
- 27.Fernandez S.F., Huang M.H., Izzo J.L., Jr. Modulation of angiotensin II responses in sympathetic neurons by cytosolic calcium. Hypertension. 2003;41:56–63. doi: 10.1161/01.hyp.0000047513.75459.7e. [DOI] [PubMed] [Google Scholar]
- 28.Fernandez S.F., Huang M.H., Izzo J.L., Jr. Mechanisms of angiotensin II-mediated decreases in intraneuronal Ca2+ in calcium-loaded stellate ganglion neurons. Hypertension. 2005;45:276–282. doi: 10.1161/01.HYP.0000153320.13842.43. [DOI] [PubMed] [Google Scholar]
- 29.Monck J.R., Williamson R.E., Williamson J.R. Angiotensin II effects on the cytosolic free Ca2+ concentration in N1E-115 neuroblastoma cells: kinetic properties of the Ca2+ transient measured in single fura-2-loaded cells. J. Neurochem. 1990;54:278–287. doi: 10.1111/j.1471-4159.1990.tb13312.x. [DOI] [PubMed] [Google Scholar]
- 30.Li Y.W., Guyenet P.G. Angiotensin II decreases a resting K+ conductance in rat bulbospinal neurons of the C1 area. Circ. Res. 1996;78:274–282. doi: 10.1161/01.res.78.2.274. [DOI] [PubMed] [Google Scholar]
- 31.Zhu M., Neubig R.R., Sumners C. Modulation of K+ and Ca2+ currents in cultured neurons by an angiotensin II type 1a receptor peptide. Am. J. Physiol. 1997;273:C1040–C1048. doi: 10.1152/ajpcell.1997.273.3.C1040. [DOI] [PubMed] [Google Scholar]
- 32.Richards E.M., Raizada M.K., Sumners C. Angiotensin II type 1 receptor-modulated signaling pathways in neurons. Mol. Neurobiol. 1999;19:25–41. doi: 10.1007/BF02741376. [DOI] [PubMed] [Google Scholar]
- 33.Sun C., Sumners C., Raizada M.K. Chronotropic action of angiotensin II in neurons via protein kinase C and CaMKII. Hypertension. 2002;39:562–566. doi: 10.1161/hy0202.103057. [DOI] [PubMed] [Google Scholar]
- 34.Wong L.F., Polson J.W., Kasparov S. Genetic and pharmacological dissection of pathways involved in the angiotensin II-mediated depression of baroreflex function. FASEB J. 2002;16:1595–1601. doi: 10.1096/fj.02-0099com. [DOI] [PubMed] [Google Scholar]
- 35.Gelband C.H., Warth J.D., Sumners C. Angiotensin II type 1 receptor-mediated inhibition of K+ channel subunit kv2.2 in brain stem and hypothalamic neurons. Circ. Res. 1999;84:352–359. doi: 10.1161/01.res.84.3.352. [DOI] [PubMed] [Google Scholar]
- 36.Pan S., Sumners C., Gelband C. Kv1.4 underlies angiotensin II-mediated inhibition of neuronal A-type K+ current. Biophys. J. 2000;78:450A. [Google Scholar]
- 37.Pan S.J., Zhu M., Gelband C.H. ANG II-mediated inhibition of neuronal delayed rectifier K+ current: role of protein kinase C-α. Am. J. Physiol. Cell Physiol. 2001;281:C17–C23. doi: 10.1152/ajpcell.2001.281.1.C17. [DOI] [PubMed] [Google Scholar]
- 38.Wang D., Gelband C.H., Posner P. Mechanisms underlying the chronotropic effect of angiotensin II on cultured neurons from rat hypothalamus and brain stem. J. Neurophysiol. 1997;78:1013–1020. doi: 10.1152/jn.1997.78.2.1013. [DOI] [PubMed] [Google Scholar]
- 39.Wang D., Sumners C., Gelband C.H. A-type K+ current in neurons cultured from neonatal rat hypothalamus and brain stem: modulation by angiotensin II. J. Neurophysiol. 1997;78:1021–1029. doi: 10.1152/jn.1997.78.2.1021. [DOI] [PubMed] [Google Scholar]
- 40.Blackwell K.T., Jedrzejewska-Szmek J. Molecular mechanisms underlying neuronal synaptic plasticity: systems biology meets computational neuroscience in the wilds of synaptic plasticity. Wiley Interdiscip. Rev. Syst. Biol. Med. 2013;5:717–731. doi: 10.1002/wsbm.1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bhalla U.S. Understanding complex signaling networks through models and metaphors. Prog. Biophys. Mol. Biol. 2003;81:45–65. doi: 10.1016/s0079-6107(02)00046-9. [DOI] [PubMed] [Google Scholar]
- 42.Ferrante M., Blackwell K.T., Ascoli G.A. Computational models of neuronal biophysics and the characterization of potential neuropharmacological targets. Curr. Med. Chem. 2008;15:2456–2471. doi: 10.2174/092986708785909094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ajay S.M., Bhalla U.S. A role for ERKII in synaptic pattern selectivity on the time-scale of minutes. Eur. J. Neurosci. 2004;20:2671–2680. doi: 10.1111/j.1460-9568.2004.03725.x. [DOI] [PubMed] [Google Scholar]
- 44.Bhalla U.S. Signaling in small subcellular volumes. II. Stochastic and diffusion effects on synaptic network properties. Biophys. J. 2004;87:745–753. doi: 10.1529/biophysj.104.040501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rybak I.A., Paton J.F., Schwaber J.S. Modeling neural mechanisms for genesis of respiratory rhythm and pattern. I. Models of respiratory neurons. J. Neurophysiol. 1997;77:1994–2006. doi: 10.1152/jn.1997.77.4.1994. [DOI] [PubMed] [Google Scholar]
- 46.Seyedabadi M., Goodchild A.K., Pilowsky P.M. Differential role of kinases in brain stem of hypertensive and normotensive rats. Hypertension. 2001;38:1087–1092. doi: 10.1161/hy1101.096054. [DOI] [PubMed] [Google Scholar]
- 47.Sun C., Du J., Raizada M.K. PI3-kinase inhibitors abolish the enhanced chronotropic effects of angiotensin II in spontaneously hypertensive rat brain neurons. J. Neurophysiol. 2003;90:3155–3160. doi: 10.1152/jn.00222.2003. [DOI] [PubMed] [Google Scholar]
- 48.Hines M.L., Morse T., Shepherd G.M. MODELDB: a database to support computational neuroscience. J. Comput. Neurosci. 2004;17:7–11. doi: 10.1023/B:JCNS.0000023869.22017.2e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yang H., Lu D., Raizada M.K. Involvement of MAP kinase in angiotensin II-induced phosphorylation and intracellular targeting of neuronal AT1 receptors. J. Neurosci. 1997;17:1660–1669. doi: 10.1523/JNEUROSCI.17-05-01660.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ouali R., Berthelon M.C., Saez J.M. Angiotensin II receptor subtypes AT1 and AT2 are down-regulated by angiotensin II through AT1 receptor by different mechanisms. Endocrinology. 1997;138:725–733. doi: 10.1210/endo.138.2.4952. [DOI] [PubMed] [Google Scholar]
- 51.Athanasiades A., Clark J.W., Jr., Bidani A. An ionic current model for medullary respiratory neurons. J. Comput. Neurosci. 2000;9:237–257. doi: 10.1023/a:1026583620467. [DOI] [PubMed] [Google Scholar]
- 52.Iwamoto T., Wakabayashi S., Shigekawa M. Growth factor-induced phosphorylation and activation of aortic smooth muscle Na+/Ca2+ exchanger. J. Biol. Chem. 1995;270:8996–9001. doi: 10.1074/jbc.270.15.8996. [DOI] [PubMed] [Google Scholar]
- 53.Iwamoto T., Watano T., Shigekawa M. A novel isothiourea derivative selectively inhibits the reverse mode of Na+/Ca2+ exchange in cells expressing NCX1. J. Biol. Chem. 1996;271:22391–22397. doi: 10.1074/jbc.271.37.22391. [DOI] [PubMed] [Google Scholar]
- 54.Philipson K.D., Nicoll D.A., Qiu Z. The Na+/Ca2+ exchange molecule: an overview. Ann. N. Y. Acad. Sci. 2002;976:1–10. doi: 10.1111/j.1749-6632.2002.tb04708.x. [DOI] [PubMed] [Google Scholar]
- 55.Hodgkin A.L., Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Peretz T., Levin G., Lotan I. Modulation by protein kinase C activation of rat brain delayed-rectifier K+ channel expressed in Xenopus oocytes. FEBS Lett. 1996;381:71–76. doi: 10.1016/0014-5793(96)00085-3. [DOI] [PubMed] [Google Scholar]
- 57.Fakler B., Adelman J.P. Control of KCa channels by calcium nano/microdomains. Neuron. 2008;59:873–881. doi: 10.1016/j.neuron.2008.09.001. [DOI] [PubMed] [Google Scholar]
- 58.Taylor A.L., Goaillard J.M., Marder E. How multiple conductances determine electrophysiological properties in a multicompartment model. J. Neurosci. 2009;29:5573–5586. doi: 10.1523/JNEUROSCI.4438-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zhu M., Gelband C.H., Sumners C. Angiotensin II decreases neuronal delayed rectifier potassium current: role of calcium/calmodulin-dependent protein kinase II. J. Neurophysiol. 1999;82:1560–1568. doi: 10.1152/jn.1999.82.3.1560. [DOI] [PubMed] [Google Scholar]
- 60.Shieh C.C., Coghlan M., Gopalakrishnan M. Potassium channels: molecular defects, diseases, and therapeutic opportunities. Pharmacol. Rev. 2000;52:557–594. [PubMed] [Google Scholar]
- 61.Hille B. Modulation of ion-channel function by G-protein-coupled receptors. Trends Neurosci. 1994;17:531–536. doi: 10.1016/0166-2236(94)90157-0. [DOI] [PubMed] [Google Scholar]
- 62.Dayan P. Twenty-five lessons from computational neuromodulation. Neuron. 2012;76:240–256. doi: 10.1016/j.neuron.2012.09.027. [DOI] [PubMed] [Google Scholar]
- 63.Nadim F., Bucher D. Neuromodulation of neurons and synapses. Curr. Opin. Neurobiol. 2014;29C:48–56. doi: 10.1016/j.conb.2014.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Suh B.-C., Horowitz L.F., Hille B. Regulation of KCNQ2/KCNQ3 current by G protein cycling: the kinetics of receptor-mediated signaling by Gq. J. Gen. Physiol. 2004;123:663–683. doi: 10.1085/jgp.200409029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Hille B., Dickson E., Falkenburger B. Dynamic metabolic control of an ion channel. Prog. Mol. Biol. Transl. Sci. 2014;123:219–247. doi: 10.1016/B978-0-12-397897-4.00008-5. [DOI] [PubMed] [Google Scholar]
- 66.Zhou J., Shapiro M.S., Hille B. Speed of Ca2+ channel modulation by neurotransmitters in rat sympathetic neurons. J. Neurophysiol. 1997;77:2040–2048. doi: 10.1152/jn.1997.77.4.2040. [DOI] [PubMed] [Google Scholar]
- 67.Blackwell K.T. Approaches and tools for modeling signaling pathways and calcium dynamics in neurons. J. Neurosci. Methods. 2013;220:131–140. doi: 10.1016/j.jneumeth.2013.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Kotaleski J.H., Blackwell K.T. Modeling the molecular mechanisms of synaptic plasticity using systems biology approaches. Nat. Rev. Neurosci. 2010;11:239–251. doi: 10.1038/nrn2807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Bhalla U.S. Multiscale interactions between chemical and electric signaling in LTP induction, LTP reversal and dendritic excitability. Neural Netw. 2011;24:943–949. doi: 10.1016/j.neunet.2011.05.001. [DOI] [PubMed] [Google Scholar]
- 70.Cortassa S., Aon M.A., Winslow R.L. A computational model integrating electrophysiology, contraction, and mitochondrial bioenergetics in the ventricular myocyte. Biophys. J. 2006;91:1564–1589. doi: 10.1529/biophysj.105.076174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Saucerman J.J., Bers D.M. Calmodulin mediates differential sensitivity of CaMKII and calcineurin to local Ca2+ in cardiac myocytes. Biophys. J. 2008;95:4597–4612. doi: 10.1529/biophysj.108.128728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Grandi E., Pandit S.V., Bers D.M. Human atrial action potential and Ca2+ model: sinus rhythm and chronic atrial fibrillation. Circ. Res. 2011;109:1055–1066. doi: 10.1161/CIRCRESAHA.111.253955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Jafri M.S., Keizer J. On the roles of Ca2+ diffusion, Ca2+ buffers, and the endoplasmic reticulum in IP3-induced Ca2+ waves. Biophys. J. 1995;69:2139–2153. doi: 10.1016/S0006-3495(95)80088-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Stutzmann G.E., Mattson M.P. Endoplasmic reticulum Ca2+ handling in excitable cells in health and disease. Pharmacol. Rev. 2011;63:700–727. doi: 10.1124/pr.110.003814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Sharpe L.G., Swanson L.W. Drinking induced by injections of angiotensin into forebrain and mid-brain sites of the monkey. J. Physiol. 1974;239:595–622. doi: 10.1113/jphysiol.1974.sp010584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Ma X., Bielefeldt K., Chapleau M.W. Dual mechanisms of angiotensin-induced activation of mouse sympathetic neurones. J. Physiol. 2006;573:45–63. doi: 10.1113/jphysiol.2006.106716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Dampney R.A.L., Tan P.S.P., Horiuchi J. Cardiovascular effects of angiotensin II in the rostral ventrolateral medulla: the push-pull hypothesis. Curr. Hypertens. Rep. 2007;9:222–227. doi: 10.1007/s11906-007-0040-4. [DOI] [PubMed] [Google Scholar]
- 78.Miller G.M., Ogunnaike B.A., Vadigepalli R. Robust dynamic balance of AP-1 transcription factors in a neuronal gene regulatory network. BMC Syst. Biol. 2010;4:171. doi: 10.1186/1752-0509-4-171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Clark A.J., Balla T., Catt K.J. Stimulation of early gene expression by angiotensin II in bovine adrenal glomerulosa cells: roles of calcium and protein kinase C. Mol. Endocrinol. 1992;6:1889–1898. doi: 10.1210/mend.6.11.1336125. [DOI] [PubMed] [Google Scholar]
- 80.Misonou H., Mohapatra D.P., Trimmer J.S. Regulation of ion channel localization and phosphorylation by neuronal activity. Nat. Neurosci. 2004;7:711–718. doi: 10.1038/nn1260. [DOI] [PubMed] [Google Scholar]
- 81.Hagiwara K., Nunoki K., Yanagisawa T. Differential inhibition of transient outward currents of Kv1.4 and Kv4.3 by endothelin. Biochem. Biophys. Res. Commun. 2003;310:634–640. doi: 10.1016/j.bbrc.2003.09.062. [DOI] [PubMed] [Google Scholar]
- 82.Allen A.M., Dampney R.A., Mendelsohn F.A. Angiotensin receptor binding and pressor effects in cat subretrofacial nucleus. Am. J. Physiol. 1988;255:H1011–H1017. doi: 10.1152/ajpheart.1988.255.5.H1011. [DOI] [PubMed] [Google Scholar]
- 83.Averill D.B., Tsuchihashi T., Ferrario C.M. Losartan, nonpeptide angiotensin II-type 1 (AT1) receptor antagonist, attenuates pressor and sympathoexcitatory responses evoked by angiotensin II and L-glutamate in rostral ventrolateral medulla. Brain Res. 1994;665:245–252. doi: 10.1016/0006-8993(94)91344-7. [DOI] [PubMed] [Google Scholar]
- 84.Hirooka Y., Potts P.D., Dampney R.A.L. Role of angiotensin II receptor subtypes in mediating the sympathoexcitatory effects of exogenous and endogenous angiotensin peptides in the rostral ventrolateral medulla of the rabbit. Brain Res. 1997;772:107–114. doi: 10.1016/s0006-8993(97)00861-5. [DOI] [PubMed] [Google Scholar]
- 85.Khan R.L., Vadigepalli R., Schwaber J.S. Dynamic transcriptomic response to acute hypertension in the nucleus tractus solitarius. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2008;295:R15–R27. doi: 10.1152/ajpregu.00152.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Park J., Brureau A., Vadigepalli R. Inputs drive cell phenotype variability. Genome Res. 2014;24:930–941. doi: 10.1101/gr.161802.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Sheriff M.J., Fontes M.A.P., Dampney R.A.L. Blockade of AT1 receptors in the rostral ventrolateral medulla increases sympathetic activity under hypoxic conditions. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2006;290:R733–R740. doi: 10.1152/ajpregu.00410.2005. [DOI] [PubMed] [Google Scholar]
- 88.Ascoli G.A., Brown K.M., Barrionuevo G. Quantitative morphometry of electrophysiologically identified CA3b interneurons reveals robust local geometry and distinct cell classes. J. Comp. Neurol. 2009;515:677–695. doi: 10.1002/cne.22082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Ascoli G.A., Gasparini S., Migliore M. Local control of postinhibitory rebound spiking in CA1 pyramidal neuron dendrites. J. Neurosci. 2010;30:6434–6442. doi: 10.1523/JNEUROSCI.4066-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Matsuura T., Kumagai H., Saruta T. Rostral ventrolateral medulla neurons of neonatal Wistar-Kyoto and spontaneously hypertensive rats. Hypertension. 2002;40:560–565. doi: 10.1161/01.hyp.0000032043.64223.87. [DOI] [PubMed] [Google Scholar]
- 91.Sun C., Zubcevic J., Raizada M.K. Shift to an involvement of phosphatidylinositol 3-kinase in angiotensin II actions on nucleus tractus solitarii neurons of the spontaneously hypertensive rat. Circ. Res. 2009;105:1248–1255. doi: 10.1161/CIRCRESAHA.109.208926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Kumagai H., Oshima N., Saruta T. Importance of rostral ventrolateral medulla neurons in determining efferent sympathetic nerve activity and blood pressure. Hypertens. Res. 2012;35:132–141. doi: 10.1038/hr.2011.208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Huguenard J.R., Prince D.A. Slow inactivation of a TEA-sensitive K current in acutely isolated rat thalamic relay neurons. J. Neurophysiol. 1991;66:1316–1328. doi: 10.1152/jn.1991.66.4.1316. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


