Abstract
Recent experiments have investigated the response of smooth muscle cells to transient stretch-compress (SC) and compress-stretch (CS) maneuvers. The results indicate that the transient SC maneuver causes a sudden fluidization of the cell while the CS maneuver does not. To understand this asymmetric behavior, we have built a biomechanical model to probe the response of stress fibers to the two maneuvers. The model couples the cross-bridge cycle of myosin motors with a viscoelastic Kelvin-Voigt element that represents the stress fiber. Simulation results point to the sensitivity of the myosin detachment rate to tension as the cause for the asymmetric response of the stress fiber to the CS and SC maneuvers. For the SC maneuver, the initial stretch increases the tension in the stress fiber and suppresses myosin detachment. The subsequent compression then causes a large proportion of the myosin population to disengage rapidly from actin filaments. This leads to the disassembly of the stress fibers and the observed fluidization. In contrast, the CS maneuver only produces a mild loss of myosin motors and no fluidization.
Introduction
Conventional wisdom, informed by polymer physics, holds that stretching causes cells to stiffen. Known as the “reinforcement effect”, the stiffening is manifested by increase of one or more of the following experimentally measured properties: the elastic modulus of the cytoskeleton (1), cell stiffness probed by microbead displacement (2), traction force on deformable substrate (3), and formation of new focal adhesion sites (4). More recent experiments (5–7), on the other hand, have demonstrated an apparently opposite response known as “fluidization”, indicated by a drastic decrease of the elastic modulus and disintegration of the cytoskeleton of the cells.
To rationalize this apparent contradiction, several studies have compared different modes of imposing mechanical deformation. In a stretch-hold (SH) maneuver, the cell is stretched to a prescribed strain and then held at the deformed state. This mode of deformation engenders no controversy; all studies reported cell stiffening similar to a polymer network under external stress (8). In a stretch-compress (SC) maneuver, the cell is stretched to a prescribed strain ε0 and then compressed so as to yield a net strain of zero. After such a maneuver, the cell stiffness is seen to drop by a considerable amount, ∼50% for ε0 ∼ 0.1 (5,6). This is fluidization. Afterwards, the cell gradually recovers its equilibrium stiffness over some 5 min. Gavara et al. (3) and Chen et al. (6) further demonstrated that the fluidization happens during the compression stage of the maneuver; the initial stretch in fact increases cell stiffness as in the SH maneuver. Remarkably, a compress-stretch (CS) maneuver, where a cell is first compressed and then returned to zero strain, does not elicit fluidization (6).
Taken together, these studies have established a history-dependence of the mechanical response of the cell. But what is its mechanism? Is it purely mechanical, akin to the thixotropy of complex fluids? Or is it unique to biological cells, arising from biochemical signals that direct structural remodeling? What causes the stark asymmetry between the CS and SC maneuvers in fluidizing the cell?
One expects the mechanical response, be it stiffening or fluidization, to be directly related to structural changes in the cytoskeleton. The most prominent entity in these adherent cells is the stress fibers, which are bundles of actin filaments cross-linked by myosin, α-actinin, and other cross-linkers, frequently emanating from focal adhesions. Earlier experiments (9–11) have shown that compression of a large enough strain causes stress fibers to buckle and disintegrate, in accord with the fragility of actin filaments under compression (12). This suggests that the disassembly of the stress fibers causes fluidization. In support of this idea, Chen et al. (6) reported disassembly of the cytoskeleton during the compression phase of the SC maneuver. Besides, cyclic stretch-unstretch deformation of cells causes disassembly of stress fibers oriented along the direction of deformation, and their prevalence in the orthogonal direction (7,13–15). However, how does this mechanism discriminate between SC and CS maneuvers? Why is the initial stretch prerequisite to subsequent disassembly of the stress fibers during compression?
To our knowledge, two models have appeared on cell fluidization, both based on the dynamics of semiflexible polymer networks:
-
1.
Morozov and Pismen (8,16) showed that mechanical stretching may cause an anisotropic redistribution of myosin in the actin network, thereby lowering its modulus and causing fluidization. However, this argument based on anisotropic prestress does not distinguish between the SC and CS maneuvers, and thus does not speak to the dependence of fluidization on deformation history. Besides, the mechanism of disassembly for actin filaments is rupture under high tension. This differs from the conventional view of buckling under compression (6,9,12).
-
2.
Wolff et al. (17) built a wormlike-chain model to explain the rheology of reconstituted actomyosin networks under large-strain oscillatory shear. The network is predicted to stiffen after the first cycle of strain, and then gradually soften with subsequent cycles due to breaking of transient bonds between polymer chains. This bears some resemblance to cell fluidization. But the latter happens after a single SC cycle (6,7). There is also no discussion of the contrast between SC and CS maneuvers.
Models of cyclic stretching of cells (7,13–15) are also potentially relevant to cell fluidization. These typically attribute stress fiber disassembly to the detachment of myosin motors, with a probability based on the sliding velocity of the motors on the actin cable and the tensile force in it (14). This predicts disassembly of the stress fibers during the stretching phase of the cycle, as opposed to the compression phase (3,6). Chen et al. (6) also suggested an analogy between cell fluidization and the behavior of catch bonds (15,18), whose lifetime increases under stretching. Although common in focal adhesions, catch bonds have never been reported in the cytoskeleton (6), and, as of this writing, its molecular basis is unclear.
The objective of this article is to explain the dependence of cell fluidization on the stretching protocol, more specifically the contrast between the SC and CS maneuvers. We couple a simple mechanical model for the stress fiber with the cross-bridge cycle of the myosin motors, and demonstrate that in the SC maneuver, the initial stretching produces a condition in which a subsequent compression causes a large fraction of the myosin to detach from the actin filaments. This is taken as the precursor to the disassembly of the stress fiber and the cytoskeleton, i.e., fluidization. The CS maneuver, on the other hand, does not produce the same condition.
Model formulation
Despite the various puzzles mentioned above, one fact seems well established by experiments: the fluidization corresponds to the disassembly of the cytoskeleton (1,5–7). This is the physical entity underlying all previously used measures of fluidization—losses in cell modulus, traction forces on the substrate, and focal adhesions. Following the spirit of numerous prior studies (13–15), we will focus on the dynamics of a single stress fiber (SF). Such a dramatic simplification, down from the complexities of the actomyosin network or even the whole cell, allows us to capture the essential features of the fluidization process in a minimalist fashion. Such an SF model should capture three key effects: 1) the SF is a viscoelastic solid, which sustains a finite prestress in equilibrium (8,19); 2) the SF has a myosin contractile element, which imposes the prestress in equilibrium; and 3) The myosin crossbridge exhibits a powerstroke, which will be discussed shortly.
During mechanical deformation, the myosin apparatus should provide a relaxation mechanism that adjusts the unloaded reference length of the stress fiber (19). The first two considerations have led us to the Kelvin-Voigt-Myosin (KVM) model depicted in Fig. 1, with the myosin unit in series with the spring-dashpot assembly.
Figure 1.
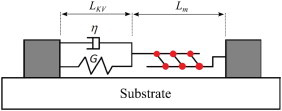
Our model for the stress fiber has a Kelvin-Voigt element connected in series to a myosin apparatus. The two ends of the stress fiber are attached to the substrate through focal adhesions, which are assumed permanent in our model. To see this figure in color, go online.
The KVM model is based on previous models for the SF (15,19–22,) and smooth muscle cells and strips (23,24). Strictly speaking, it only represents one sarcomeric unit of the SF. As is usually done (15), we tacitly assume that all sarcomere units are activated simultaneously. Besser and Schwarz (20) used a Kelvin-Voigt element in parallel with a myosin apparatus to study the dynamic coupling between the stress fiber and the focal adhesion. Laser ablation of stress fibers, however, argues against a parallel configuration in favor of one with the elastic and myosin elements in series (21). Later, the series configuration was used to study the dynamics of SF under cyclic stretch (19,22). To reflect the viscoelasticity of the SF (25), we have further added a viscous element to this model to arrive at the KVM configuration of Fig. 1. A similar model has been used by Chen et al. (15) to study SF reorientation under cyclic stretch. Thus, the total length of the stress fiber is L = LKV + Lm, with LKV and Lm being the lengths of the Kelvin-Voigt element and the myosin element, respectively. The myosin and Kelvin-Voigt elements share the same tension, which is also the tension of the SF as a whole,
| (1) |
where G is the elastic modulus and η is the viscosity of the Kelvin-Voigt element, and L0 is the resting length of the Kelvin-Voigt element; for L, the dot indicates time derivative.
Myosin plays a key role in our model, partly because its detachment en masse from the actin filament will be taken to mark the onset of disassembly of the stress fiber, which leads to fluidization of the cell. The experimental evidence for such a criterion for SF disassembly has been reviewed by Kaunas and Deguchi (13). In particular, Trepat et al. (1) and Chen et al. (6) have ascribed the disruption of the cytoskeleton to the breakage of cross-linkers, especially the detachment of the myosin crossbridge. Gavara et al. (3) attributed cell fluidization after the SC maneuver to “a fall in active contractile tension caused by stretch-induced actomyosin detachment”. Matsui et al. (26,27) showed that high levels of MgATP reduce the number of actomyosin crossbridges, and promote rapid disassembly of the SF. Furthermore, there exists a clear connection between the loss of tension in the SF and its disassembly (28). Compression of SFs reduces the tensile prestress in them, and causes the SF to disassemble, or if the strain rate is sufficiently high, to buckle (9–12). These ideas inform the third component of our model, the cycle of the myosin crossbridge. Our goal is to show that the SC maneuver generates a loss of tension in the KVM model of the stress fiber, such that myosin motors detach from the actin filaments and cause disassembly of the stress fiber. A CS maneuver, on the other hand, will not have the same effect.
To capture the kinetics of the myosin motors, we start from the well-known swinging cross-bridge model (Fig. 2 a) (29). Initially, myosin carrying an ADP and a phosphate binds to an actin filament in the configuration marked with m1. Release of the phosphate prompts the light-chain-binding region of myosin to swing through an angle, providing a working stroke of 5–15 nm. This motion, known as the power-stroke, is where the mechanical work of contraction is done. Next, the ADP is released, and the binding of a fresh ATP causes the myosin to detach from the actin filament. Hydrolysis of the ATP then returns the myosin to the cocked conformation and primes it for the next cycle. For our purpose, we represent the swinging cross-bridge cycle by three steps connecting three distinct myosin states: the detached state, the attached prestroke state, and the attached poststroke state (Fig. 2 b). This can be viewed as a simplified version of the popular cross-bridge model for smooth muscle cells (30–34), with the unphosphorylated myosin motors disregarded. Myosin amounts for each of the states are indicated as m0, m1, and m2, respectively. Neglecting reverse reactions, we can describe the myosin kinetics by the equations
| (2) |
| (3) |
and
| (4) |
where k01, k12, and k20 are the rate constants. We assume that k01 and k12 remain constant during the cross-bridge cycle. The rate of myosin detachment k20, on the other hand, is known to decrease with mechanical load on the motor (35–37). In particular, a myosin motor may stall on an actin filament when the tensile force σ reaches a critical stalling force σ0. Following Veigel et al. (35,36), we assume an exponential form for k20:
| (5) |
This relationship will prove to be important to our model, inasmuch as it represents the sensitivity of the myosin duty ratio to external forcing on the stress fiber.
Figure 2.
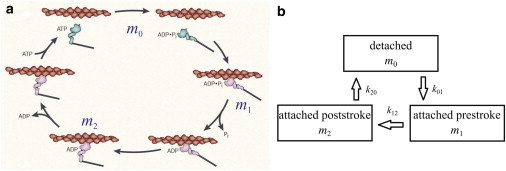
(a) The swinging cross-bridge model adapted from Spudlich (29). (b) A simplified three-stage model represents the interaction between the myosin and actin filaments, with m0, m1, and m2 denoting myosin in the detached state, attached prestroke state, and attached poststroke state. These states correspond roughly to those marked in panel a. To see this figure in color, go online.
Similar to the models of Kaunas and Deguchi (13) and Kaunas et al. (19), our myosin apparatus actively regulates the length of the stress fiber. In equilibrium, the myosin motors walk until the elastic tension in the SF equals its stalling force σ0. Further stretching or compression will cause the motors to slide or walk in an attempt to return the SF to tensional homeostasis (19,38). The relationship between the contractile speed of the myosin apparatus and the mechanical load is commonly represented by Hill’s law (23,39,40). In SF models, however, a linearized version is often used to avoid algebraic complexity (15,19,21,41–43), here shown as
where Vm is the upper bound of myosin speed attained under zero load. Furthermore, the external load not only changes the myosin speed directly as above, but also indirectly by modifying the myosin duty ratio, and therefore the fraction of myosin motors that are actively walking and contributing to the velocity v. To account for this effect, we modify the velocity-load relationship as
| (6) |
This modification is based on two considerations:
-
1.
During the cross-bridge cycle (29), only attached prestroke motors (m1) are capable of producing contraction. After the power-stroke, the myosin molecules are stuck in the rigor state pending arrival of the next ATP, which will cause them to detach. Therefore, it seems reasonable to make v proportional to m1.
-
2.
Warshaw et al. (44) have designed an in vitro motility assay in which a fraction of the myosin motors have an unphosphorylated light chain and hence remain inactive. They found that the unphosphorylated myosin motors do not generate force but act as a load to slow down the contraction that is driven by the cycling phosphorylated myosin motors. Drawing an analogy with our model, we consider the motors not actively walking, i.e., m2 and m0, to act as dampers to the contraction. Hence we have put the total myosin number mt in the denominator. Warshaw et al. (44) suggested a sigmoidal dependence of the sliding speed on the fraction of phosphorylated myosin. We adopt a linear relationship for simplicity. Note that our model assumes the total number of myosin on the stress fiber mt to be fixed. Micropipette aspiration experiments (45–47) suggest that external forcing may recruit myosin motors from the cytoplasm to the actomyosin cortex. Our simple model disregards such spatial transport.
Equations 1–6 form a complete description of our model stress fiber. When a prescribed deformation is imposed on the total length L, these equations can be time-stepped for the evolution of the tension σ; the myosin population in each of the three states m0, m1, and m2; and the lengths of the KV and myosin elements. One feature of this model might be counterintuitive. The instantaneous tension σ(t) is not directly given by the number of attached myosin molecules. The latter controls the sliding or walking velocity of the myosin apparatus, which then modulates the relaxation of the KV element. It is through these two intermediaries that myosin controls the tension σ.
Model parameters
To introduce the parameters of the problem, it is convenient to consider first the equilibrium or homeostatic state of the KVM apparatus. Given any total length L for the apparatus, the myosin element will contract (by substall walking) or expand (by superstall sliding) to adjust its length and the length of the KV element such that in the equilibrium state, the tension in the apparatus is exactly the stalling force σ0. This determines the prestrain of the KV element to be εp = σ0/(GL0). In equilibrium, the myosin in different states can be easily calculated from Eqs. 2–4:
| (7) |
| (8) |
and
| (9) |
Note that the equilibrium myosin length Lm and total length L are not unique but depend on the total strain imposed on the KVM apparatus. As Lm enters the dynamics only through (compare to Eq. 6), we set Lm = 0 at the equilibrium state without losing generality. For this reason, the strain for the subsequent deformation is given in terms of the resting length L0 instead of L.
Starting from equilibrium, the SC maneuver is imposed by stretching the KVM model at a constant speed to a prescribed total extension of L0ε0, and then compressed at the same constant speed to the original length. Denoting the duration of SC maneuver by T, the maneuver can be represented by the stretching velocity:
| (10) |
This amounts to a triangular wave form of the strain. The CS maneuver is the reverse of the above.
Table 1 lists all the parameters of the problem, their values as adopted here, and their sources (48–57). The determination of several of the parameters requires some explanation. We define the duty ratio γ as the fraction of time that a myosin motor spends being attached to the actin filament during a cross-bridge cycle in equilibrium (48,49). Thus, Eqs. 8 and 9 give us
| (11) |
In Table 1, we have adopted the duty ratio γ = 0.8 appropriate for the myosin IIB isoform. For the IIA isoform, the duty ratio is much lower, at ∼ γ = 0.1 (49). Myosin IIB binds to actin filaments for a much longer time under resistant stress (37), and is thus more effective in maintaining tension in the stress fibers and more sensitive to mechanical strains (50). While both myosin IIA and IIB contribute to stress fibers in adherent nonmigrating cells (58), they assume spatially polarized patterns in migrating cells. IIB is concentrated at the rear of the cell in the contractile stress fibers, whereas IIA is predominantly found in the protrusive actin structures at the leading edge (59,60). This suggests distinct functions of IIA and IIB in forming different actomyosin structures. For its prominent role in maintaining the contractile stress fibers at the rear of migrating cells (60,61), IIB appears more relevant to the stress fibers considered here, and hence its duty ratio is used.
Table 1.
Parameters for the KVM stress-fiber model
| Parameters | Meaning | Value | References |
|---|---|---|---|
| γ | Myosin duty ratio | 0.8 | (48,49) |
| k01 | Myosin attachment rate | 4 s−1 | — |
| k12 | Phosphate release rate | 1.5 s−1 | (48,50) |
| Koff | Myosin detachment rate | 3 s−1 | (35,37,48,50) |
| k | Mechanical sensitivity (Eq. 5) | 0.6 nN−1 | (37,51–53) |
| L0 | Resting length of KV unit | 1 μm | (54) |
| G | Elastic modulus | 50 nN/μm | (15,20,25,52) |
| η | Viscosity | 200 nN · s/μm | (15,25) |
| εp | Prestrain | 0.1 | (9,55) |
| σ0 | Myosin stall force | 5 nN | (52) |
| Vm | Characteristic contractile velocity | 0.075 μm/s | (15,19,26,56,57) |
Using measured values of k12, Koff, and γ, Eq. 11 allows us to determine the myosin attachment rate to be k01 = 4 s−1. Thus, in the equilibrium state, the myosin motors are distributed in the three states as m0 = 0.2mt, m1 = 0.533mt, and m2 = 0.267mt. The mechanical sensitivity parameter k is determined from the measurement of Kovács et al. (37) on a single myosin head and an estimation of the number of myosin motors in a stress fiber (51,52).
The characteristic contractile velocity Vm is estimated from the contraction rate of isolated, load-free SFs (26,56,57). In our model, the distribution of myosin motors under zero load is such that m1/mt = 0.714. Through Eq. 6, the measured SF contraction rate of 0.01–0.2 s−1 corresponds to 0.014 ≤ Vm ≤ 0.28 μm/s. Vm = 0.075 μm/s is chosen as a representative value. As discussed later, this choice is also based partly on fitting the experimental data later in Fig. 7 (see also Fig. S1 in the Supporting Material). Thus, Vm is the sole fitting parameter of the model.
Figure 7.
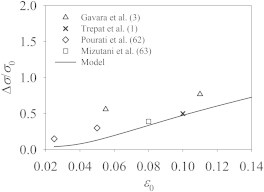
Comparison of the excess tension, upon cessation of stretch, between the model prediction and experimental data.
The system of ordinary differential equations is solved by using a fourth-order Runga-Kutta scheme in the software MATLAB (The MathWorks, Natick, MA). Each simulation starts from the equilibrium state with a prestrain of εp = 0.1. The time step is set to be Δt = 0.004 s. Numerical tests show that this ensures sufficient temporal resolution; refining Δt further brings negligible changes to the results.
Results and Discussion
Responses to the SC and CS maneuvers
To study cell responses to the stretch-compress (SC) and compress-stretch (CS) maneuvers, Chen et al. (6) applied a strain magnitude of ε0 = 0.1 over T = 4 s, with a strain rate of s−1. The SC maneuver induces cell fluidization, while the CS maneuver does not. In our simulation, we similarly apply the two maneuvers at ε0 = 0.1 and s−1. The rest of the parameters are as listed in Table 1.
For the SC maneuver (Fig. 3 a), the tension σ jumps up at the start, inasmuch as the finite strain rate instantaneously elicits a finite force from the viscous element. Then σ continues to increase thanks to the stretching of the elastic spring. The rate itself increases in time. This is because the stretch reduces the number of myosin motors m1 and thus the sliding speed of the myosin element (compare to Eq. 6). Consequently, the KV element is forced to increase its rate of stretching. Hence the faster rise of σ. Because the stretching is reversed at t/T = 0.5, the tension σ abruptly drops due to the reversal in the viscous force, to a negative value in this case. Then σ recovers in time to a positive value that is roughly 40% its initial equilibrium value.
Figure 3.
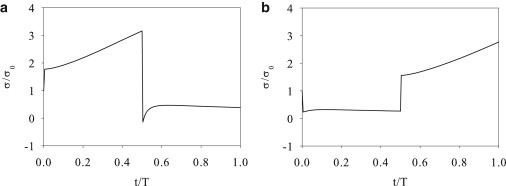
Tension in the stress fiber under the SC (a) and CS (b) maneuvers.
Upon starting the CS maneuver (Fig. 3 b), the tension σ drops instantaneously due to sudden imposition of a negative strain rate. It then maintains a roughly constant level through the whole compression phase. In this process, the myosin motors walk at a more or less constant speed, and the KV element sustains a roughly constant rate of compression. The tension σ reflects mostly the viscous contribution, similar to the compression stage of the SC maneuver. At the start of the subsequent stretching phase, the tension suddenly jumps up and then gradually increases due to elongation of the Kelvin-Voigt element. For the parameters used, our model predicts that the SC maneuver produces a negative (compressive) force within the stress fiber while the CS maneuver does not.
Now we can examine the evolution of the three myosin populations during the SC and CS maneuvers. For the SC maneuver (Fig. 4), the rising tension during the stretch phase lowers the myosin off-rate k20 (compare to Eq. 5) and suppresses myosin detachment from actin filaments. This causes accumulation of myosin in the m2 stage and depletes the m1 population (Fig. 4 a). But the total number of attached myosin ma = m1 + m2 increases moderately during the stretch phase (Fig. 4 b). At the end of stretch (t = 0.5T), m2 myosin makes up ∼90% of all the myosin motors. More importantly, the low level of m1 means that now the myosin element has a very slow walking speed. Upon reversal of the deformation, the myosin element cannot contract quickly enough to absorb the compression imposed on the entire stress fiber. Thus, the negative strain rate is mostly sustained by the KV element, which produces the negative σ of Fig. 3 a. The compressive force significantly increases the off-rate k20 and results in a rapid detachment of m2 myosin. The total number of attached myosin ma = m1 + m2 undergoes a sharp drop as well (Fig. 4 b). This scenario corresponds to the loss of tension that is the immediate trigger for stress-fiber disassembly in prior experiments and models (9,10,28). In our model, the newly detached m0 motors reattach at the fixed rate k01, and thus ma recovers to some extent during the compression (Fig. 4 b). In reality, the cytoskeleton rapidly disintegrates, and only reforms several minutes after the SC maneuver has been completed (6).
Figure 4.
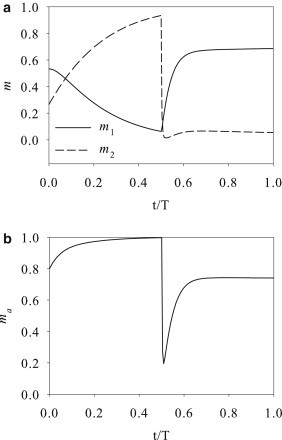
Evolution of myosin populations under the SC maneuver: (a) m1 and m2; (b) the total attached myosin ma = m1 + m2.
The reaction of the myosin populations to the CS maneuver is entirely different. Upon the start of compression, m2 rapidly decreases while m1 increases moderately (Fig. 5 a). The increasing m1 enhances the walking speed of the attached myosin and the relaxation rate of the myosin apparatus, which helps to alleviate the compression being sustained by the KV element. Consequently, the drop in the tension σ is much smaller than in the compression part of the SC maneuver (Fig. 3). In particular, it remains tensile throughout the compression phase. As a result, the compression only causes a moderate loss of m2 and an even smaller drop in the total attached myosin ma (Fig. 5 b). The subsequent stretching recruits more myosin onto the actin filaments, elevating m2 and ma and raising the tensile force σ. Note that the contrast between SC and CS maneuvers illustrated above depends on the high duty ratio of myosin IIB. When the low duty ratio of IIA is used, the SC-CS difference is much reduced, and the force in the stress fiber stays tensile in both cases.
Figure 5.
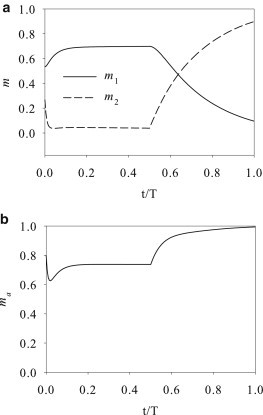
Evolution of myosin populations under the CS maneuver: (a) m1 and m2; (b) the total attached myosin ma = m1 + m2.
At the end of the SC maneuver (t = T), the force σ recovers instantaneously to a value slightly above the stalling force σ0 (not shown in Fig. 3). This can be rationalized as follows. The compression phase enjoys a larger m1 population than the stretching phase (Fig. 4 a), and thus faster myosin walking (Eq. 6). As a result, the elastic element has compressed less than it has expanded, ending up in a stretched state (LKV > L0) that produces a tension >σ0. This relaxes toward the equilibrium state in time, falling within 1% of σ0 in 1.5T. Similarly, the end of the CS maneuver sees an abrupt drop of σ to a level above σ0, followed by a gradual relaxation toward equilibrium.
In summary, our model accounts for the distinct reaction of the stress fiber to SC and CS maneuvers from the dynamics of the different myosin populations. Essentially, the stretching in SC causes a great number of myosin motors that have completed the power stroke to stay attached onto actin filaments. Furthermore, this myosin distribution reduces the speed at which the myosin element can relax. Both factors conspire to produce the rapid detachment of a large fraction of the myosin motors when the compression phase starts. The consequence is disassembly of the stress fiber. Thus, the stretching establishes a precondition for the subsequent detachment of myosin upon compression. For the CS maneuver, such a precondition is absent. As a result, the initial compression produces a much milder loss of attached myosin and no fluidization.
The SC-CS asymmetry discussed above is quite robust and insensitive to certain model assumptions. For example, it still arises if the Kelvin-Voigt element is replaced by a Maxwell element, as long as the stretch puts a large enough force on the myosin apparatus that markedly reduces the myosin sliding velocity. Similarly, if the nonlinear Hill’s law is used in place of the linear velocity-force relationship (Eq. 6), a slower sliding velocity prevails under superstall forcing. Thus, during the stretching phase, the myosin apparatus will sustain a larger force. This accumulates a larger number of attached myosin motors, which will subsequently detach en masse upon start of the compression phase. Hence, the Hill model will accentuate the fluidization response. Finally, the SC-CS asymmetry can be produced as long as the myosin velocity increases with the proportion of attached myosin m1/mt. Thus, the myosin apparatus becomes more rigid during the stretching phase, with the depletion of m1, setting up the condition for the loss of tension upon reversal of the strain rate. The linear dependence on m1/mt in Eq. 6 is not essential but adopted for its simplicity.
SH maneuver
The stiffening of the cell in response to a stretch-hold (SH) maneuver has been demonstrated in several experiments (1,3,62,63). All experiments have reported the same general features. The tensile force σ rises during the stretching. Upon cessation of stretching, σ experiences a prompt decrease followed by a more gradual relaxation toward σ0. Individual studies differ in quantitative details. For instance, Pourati et al. (62) applied strains of 2.5 and 5% in a short time period (<10 s) on adherent endothelial cells, and recorded a 15 and 30% increase in cell stiffness within 70 s of the cessation of the stretch. Mizutani et al. (63) have reported a roughly 40% increase in Young’s modulus for fibroblasts after an 8% stretch. Then the modulus decreases gradually in the following 2 h. Trepat et al. (1) applied a 10% stretch on human airway smooth muscle cells over 2 s, and reported a 50% increase in their stiffness immediately afterwards. In the ensuing hold, it took >10 min for the cell to relax to its original stiffness. Gavara et al. (3) observed apparently stronger effects than the other groups, documenting an increase of 56 and 77% in cell-substrate traction after a 5.5 and 11% stretch, respectively. The increased traction was measured within 2 min of holding the stretch, but they did not hold the stretch longer to explore the long-term relaxation toward equilibrium.
Inspired by these experiments, we have carried out stretch-hold simulations using our KVM model. The stretch is implemented at a constant rate for a time T/2 (compare to Eq. 10), and then the stretched state is maintained indefinitely. Fig. 6 shows the model prediction of the tension σ(t) using the same parameters as in the SC maneuver (Fig. 3 a). As expected, reaction to the initial stretch is identical to that in the SC maneuver, with the tension increase in time to ∼3.2σ0 at t/T = 0.5. After the stretch stops, the tension abruptly drops to ∼1.5σ0 due to loss of the viscous force. Afterwards, σ gradually relaxes toward the homeostatic level σ0. The viscoelastic response observed here is comparable to that of fibroblast in uniaxial stretching (64), where a similar Kelvin model is used to interpret the data. Two quantities of interest are Δσ, the excess tension above the homeostatic level immediately after the cessation of stretch, and the half-life td for the subsequent relaxation, the time for the excess tension to drop by 50%. These will be compared with experimental values in the following.
Figure 6.
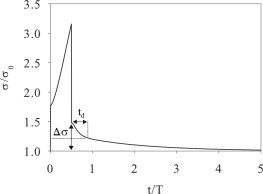
Evolution of the tension σ during an SH maneuver modeled after the experiment of Trepat et al. (1): a 10% strain is applied over T/2 = 2 s and then maintained indefinitely. The characteristic time T = 4 s. The value Δσ is the excess tension after cessation of the stretch, and td is the time for Δσ to relax by 50%.
Fig. 7 compares Δσ as a function of the strain magnitude with experimental data (1,3,62,63). Two caveats must be noted:
-
1.
Only Trepat et al. (1) managed to capture the cell stiffness more or less immediately upon cessation of stretching, thanks to their optical magnetic twisting cytometry technique. The other experiments recorded such data for only a short time, roughly 1–2 min, afterwards. Thus, only Trepat et al. (1) is strictly comparable with our model prediction.
-
2.
Most of the experiments measured cell modulus by microrheometry and magnetic twisting cytometry.
Inasmuch as the elastic modulus of biological cells is proportional to the contractile force in the actomyosin network (65), the percentage excessive modulus is comparable with the percentage excess tension. With these in mind, Fig. 7 shows that all the experimental data lie close to the model prediction using Vm = 0.075 μm/s. In particular, there is quantitative agreement with the result of Trepat et al. (1). Our model also captures the rising trend in the data; a larger strain ε0 causes the elastic element to extend more at the end of stretching.
Unfortunately, the model fails to capture the timescale of the subsequent relaxation of the excess tension. The calculation in Fig. 6 matches the experimental conditions of Trepat et al. (1) in that a 10% strain is applied linearly over 2 s. The relaxation has a half-life of td = 1.9 s, and as a whole lasts ∼16 s. Experimentally, on the other hand, td is ∼400 s and the whole relaxation lasts ∼17 min. Thus, the relaxation is too fast in the simulation by two orders of magnitude. One possible explanation is that Trepat et al. (1) measured whole-cell relaxation while the model deals with a single SF. Thus, slow diffusive processes of reequilibrating a large number of SFs are missing from the model. Besides, the model uses a linear force-velocity relation (Eq. 6) instead of the more realistic hyperbolic Hill’s law (39,51). Under superstall force, the former predicts a much larger sliding velocity than the latter. Inasmuch as the SH maneuver resides entirely in the superstall regime, the relaxation would proceed much more rapidly than in reality.
Aside from the SH maneuver, several experiments have explored the reaction of adherent cells to the stretch-compress (3,5,6), compress-hold (9–11), and cyclic stretch (13,14,19,22,66,67) maneuvers. The most salient feature of these experiments is the critical conditions for the buckling and disassembly of the stress fibers. It is possible to compare model predictions quantitatively with the measured critical strains and strain rates, and we report such comparisons in the Supporting Material.
Conclusions
The response of cells to external strain is a complex process. Prior experiments have explored its various aspects, and the results are not always in agreement. Therefore, we have chosen a well-defined feature of the process for theoretical modeling: the sensitivity of cell fluidization to strain history. More specifically, cells fluidize after a SC maneuver but not after a CS maneuver of the same strain magnitude and strain rate. Logically, our model is based on the following chain of reasoning, each step being supported by experimental evidence explained in the preceding sections: 1) cell fluidization is due to disassembly of the cytoskeletal network, and in particular the stress fibers; 2) the stress fibers disintegrate as a result of the detachment of myosin motors en masse from the actin filaments; 3) the detachment of myosin motors is due to loss of tensile force in the stress fibers; and 4) the loss of tension and appearance of a compressive force actually stem from the external strain being imposed on the cell.
To elucidate the dependence of fluidization on strain history, we have focused on modeling a single stress fiber undergoing the various protocols of stretching and compression. The model does not account for the actual disintegration of the cytoskeleton, nor the subsequent resolidification. Chemical signaling has been neglected.
Coupling the myosin crossbridge with a viscoelastic Kelvin-Voigt element, the model demonstrates a striking contrast between the SC and CS maneuvers. In SC, the initial stretching leaves most of the myosin motors in a post-power-stroke attached state, which rapidly disengage at the start of the compression stage, once the tension is lost. This is taken to be the precursor of fluidization. In CS of the same magnitude, on the other hand, the initial compression has a much milder effect on the myosin population, and no fluidization results. In the Supporting Material, we further explore the critical strain and strain rate for fluidization in SC, CS, and compress-hold maneuvers and compare the model prediction with experiments. There is qualitative and even semiquantitative agreement. The main contribution of this work, therefore, is a mechanical explanation of how adherent cells react differently according to the history of the external strain.
The Kelvin-Voigt-Myosin model proposed here is arguably the simplest model that allows one to describe the viscosity, elasticity, and contractility of a stress fiber, and to capture the mechanism of strain-history dependence. For this reason, it must be viewed as only one ingredient in a more comprehensive description of the process of fluidization and resolidification. Several important factors are left out.
For example, we take the loss of tension as marking the onset of fluidization. The subsequent events of stress-fiber buckling and disassembly and depolymerization of the actin filaments are not explicitly accounted for.
Moreover, resolidification—the longer-term recovery of cell stiffness—presents interesting mechanical and biological questions that we have not attempted to address. Experiments suggest that the slow recovery of filamentous actin and actin-myosin connectivity is ATP-driven and regulated by signal pathways, with zyxin being a potentially key player (5,6). Due to the model’s simplicity, it cannot capture the timescale for the relaxation of cell modulus after a SH maneuver, nor can it reflect the effect of substrate stiffness, which influences the mechanosensing and cytoskeletal remodeling of adherent cells.
Finally, the model ignores a potentially important mechanism for redistributing myosin motors from the cytoplasm to the cytoskeleton under external forcing (45–47). In this context, this model should be seen as a preliminary effort at formulating and rationalizing the response of cells to mechanical forcing.
Acknowledgments
We thank Graham Donovan, Jeff Fredberg, Rama Krishnan, Len Pismen, and Chun Seow for helpful discussion.
The study was supported by the Natural Sciences and Engineering Research Council of Canada, the Canada Research Chair program, and the Canada Foundation for Innovation. Part of the work was done while J.J.F. was a visitor at the Kavli Institute for Theoretical Physics, Santa Barbara, and he acknowledges support by the National Science Foundation (NSF No. PHY11-25915). T.W. acknowledges partial support by the Chinese Government Award for Outstanding Self-Financed Students Abroad.
Supporting Material
Supporting Citations
Refs. (68–71) appear in the Supporting Material.
References
- 1.Trepat X., Deng L., Fredberg J.J. Universal physical responses to stretch in the living cell. Nature. 2007;447:592–595. doi: 10.1038/nature05824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Matthews B.D., Overby D.R., Ingber D.E. Cellular adaptation to mechanical stress: role of integrins, Rho, cytoskeletal tension and mechanosensitive ion channels. J. Cell Sci. 2006;119:508–518. doi: 10.1242/jcs.02760. [DOI] [PubMed] [Google Scholar]
- 3.Gavara N., Roca-Cusachs P., Navajas D. Mapping cell-matrix stresses during stretch reveals inelastic reorganization of the cytoskeleton. Biophys. J. 2008;95:464–471. doi: 10.1529/biophysj.107.124180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Giannone G., Jiang G., Sheetz M.P. Talin1 is critical for force-dependent reinforcement of initial integrin-cytoskeleton bonds but not tyrosine kinase activation. J. Cell Biol. 2003;163:409–419. doi: 10.1083/jcb.200302001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Krishnan R., Park C.Y., Fredberg J.J. Reinforcement versus fluidization in cytoskeletal mechanoresponsiveness. PLoS ONE. 2009;4:e5486. doi: 10.1371/journal.pone.0005486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen C., Krishnan R., Fredberg J.J. Fluidization and resolidification of the human bladder smooth muscle cell in response to transient stretch. PLoS ONE. 2010;5:e12035. doi: 10.1371/journal.pone.0012035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Krishnan R., Canović E.P., Stamenović D. Fluidization, resolidification, and reorientation of the endothelial cell in response to slow tidal stretches. Am. J. Physiol. Cell Physiol. 2012;303:C368–C375. doi: 10.1152/ajpcell.00074.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Morozov K.I., Pismen L.M. Cytoskeleton fluidization versus resolidification: prestress effect. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;83:051920. doi: 10.1103/PhysRevE.83.051920. [DOI] [PubMed] [Google Scholar]
- 9.Costa K.D., Hucker W.J., Yin F.C.P. Buckling of actin stress fibers: a new wrinkle in the cytoskeletal tapestry. Cell Motil. Cytoskeleton. 2002;52:266–274. doi: 10.1002/cm.10056. [DOI] [PubMed] [Google Scholar]
- 10.Sato K., Adachi T., Tomita Y. Quantitative evaluation of threshold fiber strain that induces reorganization of cytoskeletal actin fiber structure in osteoblastic cells. J. Biomech. 2005;38:1895–1901. doi: 10.1016/j.jbiomech.2004.08.012. [DOI] [PubMed] [Google Scholar]
- 11.Sato K., Adachi T., Tomita Y. Measurement of local strain on cell membrane at initiation point of calcium signaling response to applied mechanical stimulus in osteoblastic cells. J. Biomech. 2007;40:1246–1255. doi: 10.1016/j.jbiomech.2006.05.028. [DOI] [PubMed] [Google Scholar]
- 12.Soares e Silva M., Depken M., Koenderink G.H. Active multistage coarsening of actin networks driven by myosin motors. Proc. Natl. Acad. Sci. USA. 2011;108:9408–9413. doi: 10.1073/pnas.1016616108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kaunas R., Deguchi S. Multiple roles for myosin II in tensional homeostasis under mechanical loading. Cell. Mol. Bioeng. 2011;4:182–191. [Google Scholar]
- 14.Tondon A., Hsu H.-J., Kaunas R. Dependence of cyclic stretch-induced stress fiber reorientation on stretch waveform. J. Biomech. 2012;45:728–735. doi: 10.1016/j.jbiomech.2011.11.012. [DOI] [PubMed] [Google Scholar]
- 15.Chen B., Kemkemer R., Gao H. Cyclic stretch induces cell reorientation on substrates by destabilizing catch bonds in focal adhesions. PLoS ONE. 2012;7:e48346. doi: 10.1371/journal.pone.0048346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Morozov K.I., Pismen L.M. Strain dependence of cytoskeleton elasticity. Soft Matter. 2012;8:9193–9199. [Google Scholar]
- 17.Wolff L., Fernández P., Kroy K. Resolving the stiffening-softening paradox in cell mechanics. PLoS ONE. 2012;7:e40063. doi: 10.1371/journal.pone.0040063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Marshall B.T., Long M., Zhu C. Direct observation of catch bonds involving cell-adhesion molecules. Nature. 2003;423:190–193. doi: 10.1038/nature01605. [DOI] [PubMed] [Google Scholar]
- 19.Kaunas R., Hsu H.-J., Deguchi S. Sarcomeric model of stretch-induced stress fiber reorganization. Cell Health Cytoskel. 2011;3:13–22. [Google Scholar]
- 20.Besser A., Schwarz U.S. Coupling biochemistry and mechanics in cell adhesion: a model for inhomogeneous stress fiber contraction. New J. Phys. 2007;9:425. [Google Scholar]
- 21.Russell R.J., Xia S.L., Lele T.P. Sarcomere mechanics in capillary endothelial cells. Biophys. J. 2009;97:1578–1585. doi: 10.1016/j.bpj.2009.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hsu H.J., Lee C.F., Kaunas R. Stretch-induced stress fiber remodeling and the activations of JNK and ERK depend on mechanical strain rate, but not FAK. PLoS ONE. 2010;5:e12470. doi: 10.1371/journal.pone.0012470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bates J., Bullimore S., Lauzon A. Transient oscillatory force-length behavior of activated airway smooth muscle. Am. J. Physiol.-. Lung C. 2009;297:L362–L372. doi: 10.1152/ajplung.00095.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Brook B.S. Emergence of airway smooth muscle mechanical behavior through dynamic reorganization of contractile units and force transmission pathways. J. Appl. Physiol. 2014;116:980–997. doi: 10.1152/japplphysiol.01209.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kumar S., Maxwell I.Z., Ingber D.E. Viscoelastic retraction of single living stress fibers and its impact on cell shape, cytoskeletal organization, and extracellular matrix mechanics. Biophys. J. 2006;90:3762–3773. doi: 10.1529/biophysj.105.071506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Matsui T.S., Ito K., Deguchi S. Actin stress fibers are at a tipping point between conventional shortening and rapid disassembly at physiological levels of MgATP. Biochem. Biophys. Res. Commun. 2010;395:301–306. doi: 10.1016/j.bbrc.2010.03.150. [DOI] [PubMed] [Google Scholar]
- 27.Matsui T.S., Kaunas R., Deguchi S. Non-muscle myosin II induces disassembly of actin stress fibers independently of myosin light chain dephosphorylation. Interface Focus. 2011;1:754–766. doi: 10.1098/rsfs.2011.0031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pirentis A.P., Peruski E., Stamenović D. A model for stress fiber realignment caused by cytoskeletal fluidization during cyclic stretching. Cell. Mol. Bioeng. 2011;4:67–80. doi: 10.1007/s12195-010-0152-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Spudich J.A. The myosin swinging cross-bridge model. Nat. Rev. Mol. Cell Biol. 2001;2:387–392. doi: 10.1038/35073086. [DOI] [PubMed] [Google Scholar]
- 30.Hai C.M., Murphy R.A. Cross-bridge phosphorylation and regulation of latch state in smooth muscle. Am. J. Physiol. 1988;254:C99–C106. doi: 10.1152/ajpcell.1988.254.1.C99. [DOI] [PubMed] [Google Scholar]
- 31.Mijailovich S.M., Butler J.P., Fredberg J.J. Perturbed equilibria of myosin binding in airway smooth muscle: bond-length distributions, mechanics, and ATP metabolism. Biophys. J. 2000;79:2667–2681. doi: 10.1016/S0006-3495(00)76505-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chin L., Yue P., Seow C.Y. Mathematical simulation of muscle cross-bridge cycle and force-velocity relationship. Biophys. J. 2006;91:3653–3663. doi: 10.1529/biophysj.106.092510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wang I., Politi A.Z., Sneyd J. A mathematical model of airway and pulmonary arteriole smooth muscle. Biophys. J. 2008;94:2053–2064. doi: 10.1529/biophysj.107.113977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Donovan G.M. Modeling airway smooth-muscle passive length adaptation via thick-filament length distributions. J. Theor. Biol. 2013;333:102–108. doi: 10.1016/j.jtbi.2013.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Veigel C., Molloy J.E., Kendrick-Jones J. Load-dependent kinetics of force production by smooth muscle myosin measured with optical tweezers. Nat. Cell Biol. 2003;5:980–986. doi: 10.1038/ncb1060. [DOI] [PubMed] [Google Scholar]
- 36.Veigel C., Schmitz S., Sellers J.R. Load-dependent kinetics of myosin-V can explain its high processivity. Nat. Cell Biol. 2005;7:861–869. doi: 10.1038/ncb1287. [DOI] [PubMed] [Google Scholar]
- 37.Kovács M., Thirumurugan K., Sellers J.R. Load-dependent mechanism of nonmuscle myosin 2. Proc. Natl. Acad. Sci. USA. 2007;104:9994–9999. doi: 10.1073/pnas.0701181104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Brown R.A., Prajapati R., Eastwood M. Tensional homeostasis in dermal fibroblasts: mechanical responses to mechanical loading in three-dimensional substrates. J. Cell. Physiol. 1998;175:323–332. doi: 10.1002/(SICI)1097-4652(199806)175:3<323::AID-JCP10>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 39.Hill A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. 1938;126:136–195. [Google Scholar]
- 40.Seow C.Y. Hill’s equation of muscle performance and its hidden insight on molecular mechanisms. J. Gen. Physiol. 2013;142:561–573. doi: 10.1085/jgp.201311107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wei Z., Deshpande V.S., Evans A.G. Analysis and interpretation of stress fiber organization in cells subject to cyclic stretch. J. Biomech. Eng. 2008;130:031009. doi: 10.1115/1.2907745. [DOI] [PubMed] [Google Scholar]
- 42.Stachowiak M.R., O’Shaughnessy B. Recoil after severing reveals stress fiber contraction mechanisms. Biophys. J. 2009;97:462–471. doi: 10.1016/j.bpj.2009.04.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Colombelli J., Besser A., Stelzer E.H. Mechanosensing in actin stress fibers revealed by a close correlation between force and protein localization. J. Cell Sci. 2009;122:1665–1679. doi: 10.1242/jcs.042986. [DOI] [PubMed] [Google Scholar]
- 44.Warshaw D.M., Desrosiers J.M., Trybus K.M. Smooth muscle myosin cross-bridge interactions modulate actin filament sliding velocity in vitro. J. Cell Biol. 1990;111:453–463. doi: 10.1083/jcb.111.2.453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Luo T., Mohan K., Robinson D.N. Understanding the cooperative interaction between myosin II and actin cross-linkers mediated by actin filaments during mechanosensation. Biophys. J. 2012;102:238–247. doi: 10.1016/j.bpj.2011.12.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Luo T., Mohan K., Robinson D.N. Molecular mechanisms of cellular mechanosensing. Nat. Mater. 2013;12:1064–1071. doi: 10.1038/nmat3772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Shin J.-W., Buxboim A., Discher D.E. Contractile forces sustain and polarize hematopoiesis from stem and progenitor cells. Cell Stem Cell. 2014;14:81–93. doi: 10.1016/j.stem.2013.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rosenfeld S.S., Xing J., Sweeney H.L. Myosin IIb is unconventionally conventional. J. Biol. Chem. 2003;278:27449–27455. doi: 10.1074/jbc.M302555200. [DOI] [PubMed] [Google Scholar]
- 49.Conti M.A., Kawamoto S., Adelstein R.S. Non-muscle myosin II. In: Ridley A.J., Frampton J., editors. Vol. 7. Springer; Berlin: 2008. pp. 223–264. (Proteins and Cell Regulation). [Google Scholar]
- 50.Wang F., Kovács M., Sellers J.R. Kinetic mechanism of non-muscle myosin IIB: functional adaptations for tension generation and maintenance. J. Biol. Chem. 2003;278:27439–27448. doi: 10.1074/jbc.M302510200. [DOI] [PubMed] [Google Scholar]
- 51.Debold E.P., Patlak J.B., Warshaw D.M. Slip sliding away: load-dependence of velocity generated by skeletal muscle myosin molecules in the laser trap. Biophys. J. 2005;89:L34–L36. doi: 10.1529/biophysj.105.072967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Deguchi S., Ohashi T., Sato M. Tensile properties of single stress fibers isolated from cultured vascular smooth muscle cells. J. Biomech. 2006;39:2603–2610. doi: 10.1016/j.jbiomech.2005.08.026. [DOI] [PubMed] [Google Scholar]
- 53.Wang Q., Feng J.J., Pismen L.M. A cell-level biomechanical model of Drosophila dorsal closure. Biophys. J. 2012;103:2265–2274. doi: 10.1016/j.bpj.2012.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Sanger J.W., Sanger J.M., Jockusch B.M. Differences in the stress fibers between fibroblasts and epithelial cells. J. Cell Biol. 1983;96:961–969. doi: 10.1083/jcb.96.4.961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lu L., Feng Y., Yin F.C.P. Actin stress fiber pre-extension in human aortic endothelial cells. Cell Motil. Cytoskeleton. 2008;65:281–294. doi: 10.1002/cm.20260. [DOI] [PubMed] [Google Scholar]
- 56.Katoh K., Kano Y., Fujiwara K. Isolation and contraction of the stress fiber. Mol. Biol. Cell. 1998;9:1919–1938. doi: 10.1091/mbc.9.7.1919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Katoh K., Kano Y., Fujiwara K. Rho-kinase—mediated contraction of isolated stress fibers. J. Cell Biol. 2001;153:569–584. doi: 10.1083/jcb.153.3.569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kolega J. Cytoplasmic dynamics of myosin IIA and IIB: spatial ‘sorting’ of isoforms in locomoting cells. J. Cell Sci. 1998;111:2085–2095. doi: 10.1242/jcs.111.15.2085. [DOI] [PubMed] [Google Scholar]
- 59.Kolega J. Asymmetric distribution of myosin IIB in migrating endothelial cells is regulated by a rho-dependent kinase and contributes to tail retraction. Mol. Biol. Cell. 2003;14:4745–4757. doi: 10.1091/mbc.E03-04-0205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Vicente-Manzanares M., Zareno J., Horwitz A.F. Regulation of protrusion, adhesion dynamics, and polarity by myosins IIA and IIB in migrating cells. J. Cell Biol. 2007;176:573–580. doi: 10.1083/jcb.200612043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Vicente-Manzanares M., Koach M.A., Horwitz A.F. Segregation and activation of myosin IIB creates a rear in migrating cells. J. Cell Biol. 2008;183:543–554. doi: 10.1083/jcb.200806030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Pourati J., Maniotis A., Wang N. Is cytoskeletal tension a major determinant of cell deformability in adherent endothelial cells? Am. J. Physiol. 1998;274:C1283–C1289. doi: 10.1152/ajpcell.1998.274.5.C1283. [DOI] [PubMed] [Google Scholar]
- 63.Mizutani T., Haga H., Kawabata K. Cellular stiffness response to external deformation: tensional homeostasis in a single fibroblast. Cell Motil. Cytoskeleton. 2004;59:242–248. doi: 10.1002/cm.20037. [DOI] [PubMed] [Google Scholar]
- 64.Thoumine O., Ott A. Time-scale-dependent viscoelastic and contractile regimes in fibroblasts probed by microplate manipulation. J. Cell Sci. 1997;110:2109–2116. doi: 10.1242/jcs.110.17.2109. [DOI] [PubMed] [Google Scholar]
- 65.Wang N., Tolić-Nørrelykke I.M., Stamenović D. Cell prestress. I. Stiffness and prestress are closely associated in adherent contractile cells. Am. J. Physiol. Cell Physiol. 2002;282:C606–C616. doi: 10.1152/ajpcell.00269.2001. [DOI] [PubMed] [Google Scholar]
- 66.Kaunas R., Nguyen P., Chien S. Cooperative effects of Rho and mechanical stretch on stress fiber organization. Proc. Natl. Acad. Sci. USA. 2005;102:15895–15900. doi: 10.1073/pnas.0506041102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kaunas R., Hsu H.-J. A kinematic model of stretch-induced stress fiber turnover and reorientation. J. Theor. Biol. 2009;257:320–330. doi: 10.1016/j.jtbi.2008.11.024. [DOI] [PubMed] [Google Scholar]
- 68.Discher D.E., Janmey P., Wang Y.-L. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 69.Guo W.-H., Frey M.T., Wang Y.-L. Substrate rigidity regulates the formation and maintenance of tissues. Biophys. J. 2006;90:2213–2220. doi: 10.1529/biophysj.105.070144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Tee S.-Y., Fu J., Janmey P.A. Cell shape and substrate rigidity both regulate cell stiffness. Biophys. J. 2011;100:L25–L27. doi: 10.1016/j.bpj.2010.12.3744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Jannat R.A., Dembo M., Hammer D.A. Traction forces of neutrophils migrating on compliant substrates. Biophys. J. 2011;101:575–584. doi: 10.1016/j.bpj.2011.05.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


