Abstract
The concept of positional information is central to our understanding of how cells determine their location in a multicellular structure and thereby their developmental fates. Nevertheless, positional information has neither been defined mathematically nor quantified in a principled way. Here we provide an information-theoretic definition in the context of developmental gene expression patterns and examine the features of expression patterns that affect positional information quantitatively. We connect positional information with the concept of positional error and develop tools to directly measure information and error from experimental data. We illustrate our framework for the case of gap gene expression patterns in the early Drosophila embryo and show how information that is distributed among only four genes is sufficient to determine developmental fates with nearly single-cell resolution. Our approach can be generalized to a variety of different model systems; procedures and examples are discussed in detail.
Keywords: development, patterning, positional information, precision
CENTRAL to the formation of multicellular organisms is the ability of cells with identical genetic material to acquire distinct cell fates according to their position in a developing tissue (Lawrence 1992; Kirschner and Gerhart 1997). While many mechanistic details remain unsolved, there is a wide consensus that cells acquire knowledge about their location by measuring local concentrations of various form-generating molecules, called “morphogens” (Turing 1952; Wolpert 1969). In most cases, these morphogens directly or indirectly control the activity of other genes, often coding for transcription factors, resulting in a regulatory network whose successive layers produce refined spatial patterns of gene expression (von Dassow et al. 2000; Tomancak et al. 2007; Fakhouri et al. 2010; Jaeger 2011). The systematic variation in the concentrations of these morphogens with position defines a chemical coordinate system, used by cells to determine their location (Nüsslein-Volhard 1991; St. Johnston and Nüsslein-Volhard 1992; Grossniklaus et al. 1994). Morphogens are thus said to contain “positional information,” which is processed by the genetic network, ultimately giving rise to cell fate assignments that are very re-producible across the embryos of the same species (Wolpert 2011).
The concept of positional information has been widely used as a qualitative descriptor and has had an enormous success in shaping our current understanding of spatial patterning in developing organisms (Wolpert 1969; Tickle et al. 1975; French et al. 1976; Driever and Nüsslein-Volhard 1988a,b; Meinhardt 1988; Struhl et al. 1989; Reinitz et al. 1995; Schier and Talbot 2005; Ashe and Briscoe 2006; Jaeger and Reinitz 2006; Bökel and Brand 2013; Witchley et al. 2013). Mathematically, however, positional information has not been rigorously defined. Specific morphological features during early development have been studied in great detail and shown to occur reproducibly across wild-type embryos (Gierer 1991; Gregor et al. 2007a; Gregor et al. 2007b; Okabe-Oho et al. 2009; Dubuis et al. 2013a; Liu et al. 2013), while perturbations to the morphogen system resulted in systematic shifts of these same features (Driever and Nüsslein-Volhard 1988a,b; Struhl et al. 1989; Liu et al. 2013). This established a causal—but not quantitative—link between the positional information encoded in the morphogens and the resulting body plan.
In Drosophila, the body plan along the major axis of the future adult fly is established by a hierarchical network of interacting genes during the first 3 hr of embryonic development (Nüsslein-Volhard and Wieschaus 1980; Akam 1987; Ingham 1988; Spradling 1993; Papatsenko 2009). The hierarchy is composed of three layers: long-range protein gradients that span the entire long axis of the egg (Driever and Nüsslein-Volhard, 1988a), gap genes expressed in broad bands (Jaeger 2011), and pair-rule genes that are expressed in a regular seven-striped pattern (Lawrence and Johnston 1989). Positional information is provided to the system solely via the first layer, which is established from maternally supplied and highly localized messenger RNAs (mRNAs) that act as protein sources for the maternal gradients (Nüsslein-Volhard 1991; St. Johnston and Nüsslein-Volhard 1992; Ferrandon et al. 1994; Anderson 1998; Little et al. 2011). The network uses these inputs to specify a blueprint for the segments of the adult fly in the form of gene expression patterns that circumferentially span the embryo in the transverse direction to the anterior–posterior axis. These patterns define distinct single-nucleus wide segments with nuclei expressing the downstream genes in unique and distinguishable combinations (Gergen et al. 1986; Gregor et al. 2007a; Dubuis et al. 2013a,b).
It is remarkable that such precision can be achieved in such a short amount of time, using only a few handfuls of genes. Gene expression is subject to intrinsic fluctuations, which trace back to the randomness associated with regulatory interactions between molecules present at low absolute copy numbers (van Kampen 2011; Tsimring 2014). Moreover, there is random variability not only within, but also between, embryos, for instance in the strength of the morphogen sources (Bollenbach et al. 2008). These biophysical limitations—e.g., in the number of signaling molecules, the time available for morphogen readout, and the reproducibility of initial and environmental conditions—place severe constraints on the ability of the developmental system to generate reproducible gene expression patterns (Gregor et al. 2007a; Tkačik et al. 2008).
Given these constraints, how precisely can gene expression levels encode information about position in the embryo? To address this question rigorously, we need to be able to make quantitative statements about the positional information of spatial gene expression profiles without presupposing which features of the profile (e.g., sharpness of the boundary, size of the domains, position-dependent variability, etc.) encode the information. Here we make the case that the relevant measure for positional information is the mutual information I—a central information-theoretic quantity (Shannon 1948)—between expression profiles of the gap genes and position in the embryo. We show how positional information puts mathematical limits on the ability with which cells in the developing Drosophila embryo can infer their position along the major axis by simultaneously reading the concentrations of multiple gap gene proteins. This framework allows us (i) to quantitatively determine how many truly distinct and meaningful levels of gene expression are generated by the Drosophila gap gene system, (ii) to assess how many distinguishable cell fates such a system can support, and (iii) to ask how variability across embryos impedes the ability of the patterning system to transmit positional information.
This study builds on two previously published articles. In Dubuis et al. (2013a), the general data acquisition and error analysis frameworks were presented with a subset of the data analyzed here (referred to as data set A below); here we analyze roughly eight times as many samples, to assess the experimental reproducibility of the results and perform tests that would be impossible with the original small sample. In Dubuis et al. (2013b), data set A was used to estimate positional information and positional error, as outlined in greater detail here. The study aimed at understanding positional information in the Drosophila gap gene network, but the treatment of the conceptual and data analysis frameworks was very cursory. In the present methodological article, we provide a full account of both frameworks and include a number of previously unreported results, relating to (i) the mathematical connection between positional error and information, (ii) different estimators of information from data, (iii) various data normalization techniques, (iv) combining data from multiple experiments, and (v) the validity of various approximation schemes. We report on these techniques in detail and benchmark them on real data to prepare our approach for a straightforward generalization to other developmental systems.
Results
Theoretical foundations
In this section we establish the information-theoretic framework for positional information carried by spatial patterns of gene expression. To develop an intuition, we start with a one-dimensional toy example of a single gene, which will be generalized later to a many-gene system. We present scenarios where positional information is stored in different qualitative features of gene expression patterns. To capture that intuition mathematically, we give a precise definition of positional information for one and for multiple genes. Finally, we show how a quantitative formulation of positional information is related to “decoding,” i.e., the ability of the nuclei to infer their position in the embryo.
Positional information in spatial gene expression profiles:
Let us consider the simplest possible example where the expression of a single gene G(x) varies with position x along the axis of a one-dimensional embryo. We choose units of length such that x = 0 and x = 1 correspond to the anterior and posterior poles of the embryo, respectively. Suppose we are able to quantitatively measure the profile of such a gene along the anterior–posterior axis in embryos, labeled with an index . Such measurements of the light intensity profile of fluorescently labeled antibodies against a particular gene product yield G(μ)(x), where G is the quantitative readout in embryo μ of the gene expression level. From a collection of embryos—after suitable data processing steps described later—we can then extract two statistics: the position-dependent “mean profile,” capturing the prototypical gene expression pattern, and the position-dependent variance across embryos, which measures the degree of embryo-to-embryo variability or the reproducibility of the mean profile. We can transform the measurements G(x) into profiles g(x) with rescaled units, such that the mean profile is normalized to 1 at the maximum and to 0 at the minimum along x. After these steps, our description of the system consists of the mean profile, and the variance in the profile,
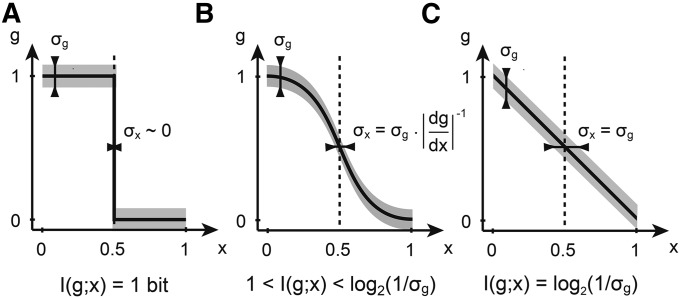
How much can a nucleus learn about its position if it expresses a gene at level g? We compare three idealized cases, where we pick the shape of by hand and assume, for the start, that the variance is constant, The first case is illustrated in Figure 1A, where a step-like profile in splits the embryo into two domains of gene expression: an anterior “on” domain, where for x < x0, and an “off” domain in the posterior, x > x0, where This arrangement has an extremely precise, indeed infinitely sharp, boundary at x0; if we think that the sharpness of the boundary is the biologically relevant feature in this system, this arrangement would correspond to an ideal patterning gene. But how much information can nuclei extract from such a profile? If x0 were 1/2, the boundary would reproducibly split the embryo into two equal domains: based on reading out the expression of g, the nucleus could decide whether it is in the anterior or the posterior, a binary choice that is equally likely prior to reading out g. As we will see, the positional information needed (and provided by such a sharp profile!) to make a clear two-way choice between two a priori equally likely possibilities = 1 bit.
Figure 1.
Positional information encoded by a single gene. Shown are three hypothetical mean gene expression profiles as a function of position x, with spatially constant variability σg (shaded area). (A) A step function carries (at most) 1 bit of positional information, by perfectly distinguishing between “off” (not induced, posterior) and “on” (fully induced, anterior) states. (B) The boundary of the sigmoidal g(x) function is now wider, but the total amount of encoded positional information can be >1 bit because the transition region itself is distinguishable from the on and off domains. (C) A linear gradient has no well-defined boundary, but nevertheless provides a further increase in information—if σg is low enough—by being equally sensitive to position at every x.
Can a profile of a different shape do better? Figure 1B shows a somewhat more realistic sigmoidal shape that has a steep, but not infinitely sharp, transition region. If the variance is small enough, this profile can be more informative about the position. Nuclei far at the anterior still have (full induction or the on state), while nuclei at the posterior still have (the off state). But the graded response in the middle defines new expression levels in g that are significantly different from both 0 and 1. A nucleus with g ≈ 0.5 will thus “know” that it is neither in the anterior nor in the posterior. This system will therefore be able to provide more positional information than the sharp boundary that is limited by 1 bit. Clearly, this conclusion is valid only insofar as the variance is low enough; if it gets too big, the intermediate levels of expression in the transition region can no longer be distinguished and we are back to the 1-bit case.
In contrast to the infinitely sharp gradient, a linear gradient, as depicted in Figure 1C, has already been proposed as efficient in encoding positional information (Wolpert 1969). By extending the argument for sigmoidal shapes above, if is not a function of position, the linear gradient is in fact the optimal choice. Consider starting at the anterior and moving toward the posterior: as soon as we move far enough in x that the change in is above σg, we have created one more distinguishable level of expression in g and thus a group of nuclei that, by measuring g, can differentiate themselves from their anteriorly positioned neighbors. Finally, this reasoning gives us a hint about how to generalize to the case where the variance depends on position, x. What is important is to count, as x covers the range from anterior to posterior, how much changes in units of the local variability, σg(x)—it will turn out that this is directly related to the mutual information between g and position.
Thus a sharp and reproducible boundary can correspond to a profile that does not encode a lot of positional information, and a linear profile where the boundary is not even well defined can encode a high amount of positional information. Ultimately, whether or not there are intermediate distinguishable levels of gene expression depends on the variability in the profile. Therefore, any measure of positional information must be a function of both and
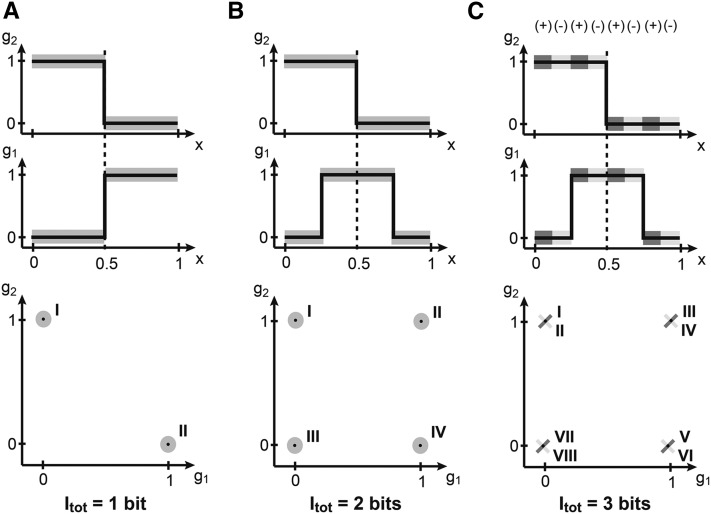
Does the ability of the nuclei to infer their position automatically improve if they can simultaneously read out the expression levels of more than one gene? Figure 2A shows the case where two genes, g1 and g2, do not provide any more information than each one of them provides separately, because they are completely redundant. Redundant does not mean equal—indeed, in Figure 2A the profiles are different at every x—but they are perfectly correlated (or dependent): knowing the expression level of g1, one knows exactly the level of g2, so g2 cannot provide any additional new information about the position. In general, redundancy can help compensate for detrimental effects of noise when noise is significant, but this is not the case in the toy example at hand.
Figure 2.
(A–C) Positional information encoded by two genes. Spatial gene expression profiles are shown at the top; an enumeration of all distinguishable combinations of gene expression (roman numerals) across the embryo is shown at the bottom. (A) Step function profiles of g1, g2 each encode 1 bit of information, but are perfectly redundant, jointly encoding only two distinguishable states and thus 1 bit of positional information, the same as each gene alone. (B) The mean profiles of g1, g2 have been displaced, removing the redundancy and bringing the total information to 2 bits (four distinct states of joint gene expression). (C) If in addition to the mean profile shape the downstream layer can read out the (correlated) fluctuations of g1, g2, a further increase in information is possible. In this toy example, fluctuations are correlated (+) and anticorrelated (−) in various spatially separated regions, which allows the embryo to use this information along with the mean profile shape to distinguish eight distinct regions, bringing the total encoded information to 3 bits.
The situation is completely different if the two profiles are shifted relative to each other by, say, 25% embryo length. Note that none of the individual profile properties have changed; however, the two genes now partition the embryo into four different segments: the posteriormost domain that is combinatorially encoded by the gene expression pattern the third domain with the second domain with and the anteriormost domain with Upon reading out g1 and g2, a nucleus, a priori located in any of the four domains, can unambiguously decide on a single one of the four possibilities. This is equivalent to making two binary decisions and, as we will later show, to 2 bits of positional information.
Finally, the most subtle case is depicted in Figure 2C. Here, the mean profiles have exactly the same shapes as in Figure 2B. What is different, however, is the correlation structure of the fluctuations. In certain areas of the embryo the two genes are strongly positively correlated, while in the others they are strongly negatively correlated. If these areas are overlaid appropriately on top of the domains defined by the mean expression patterns, an additional increase in positional information is possible. In the admittedly contrived but pedagogical example of Figure 2C, the mean profiles and the correlations together define eight distinguishable domains of expression, combinatorially encoded by two genes. Nuclei, having simultaneous access to the concentrations of the two genes, can compute which of the eight domains they reside in, although it might not be easy to implement such a computation in molecular hardware. Picking one of eight choices corresponds to making three binary decisions, and thus to 3 bits of positional information. Note that in this case, each gene considered in isolation still carries 1 bit as before, so that the system of two genes carries more information than the sum of its parts—such a scheme is called synergistic encoding.
In sum, we have shown that the mean shapes of the profiles, as well as their variances and correlations, can carry positional information. Extrapolating to three or more genes, we see that the number of pairwise correlations increases and in addition higher-order correlation terms start appearing. Formally, positional information could be encoded in all of these features, but would become progressively harder to extract using plausible biological mechanisms. Nevertheless, a principled and assumption-free measure should combine all statistical structure into a single number, a scalar quantity measured in bits, that can “count” the number of distinguishable expression states (and thus positions), as illustrated in the examples above.
Defining positional information:
Determining the number of “distinguishable states” of gene expression is more complicated in real data sets than in our toy models: the mean profiles have complex shapes and their (co)variability depends on position. In the ideal case we can measure joint expression patterns of N genes {gi}, i = 1, … , N (for example N = 4 for four gap genes in Drosophila) in a large set of embryos. In such a scenario the position dependence of the expression levels can be fully described with a conditional probability distribution P({gi}|x). Concretely, for every position x in the embryo we construct an N-dimensional histogram of expression levels across all recorded embryos, which (when normalized) yields the desired P({gi}|x). This distribution contains all the information about how expression levels vary across embryos in a position-dependent fashion. For instance,
| (1) |
| (2) |
| (3) |
are the mean profile of gene gi, the variance across embryos of gene gi, and the covariance between genes gi and gj, respectively. In principle, the conditional distribution contains also all higher-order moments that we can extract by integrating over appropriate sets of variables. Realistically, we are often limited in our ability to collect enough samples to construct P({gi}|x) by histogram counts, especially when considering several genes simultaneously; the number of samples needed grows exponentially with the number of genes. However, estimating the mean profiles on the left-hand sides of Equations 1–3 can often be achieved from data directly. A reasonable first step (but one that has to be independently verified) is to assume that the joint distribution P({gi}|x) of N expression levels {gi} at a given position x is Gaussian, which can be constructed using the measured mean values and covariances:
| (4) |
We emphasize that the Gaussian approximation is not required to theoretically define positional information, but it will turn out to be practical when working with experimental data; in the cases of one or two genes it is often possible to proceed without making this approximation, which provides a convenient check for its validity.
While the conditional distribution, P({gi}|x), captures the behavior of gene expression levels at a given x, establishing how much information, in total, the expression levels carry about position requires us to know also how frequently each combination of gene expression levels, {gi}, is used across all positions. Recall, for instance, that our arguments related to the information encoded in patterns in Figure 2 rested on counting how often a pair of genes will be found in expression states 00, 01, 10, and 11 across all x. This global structure is encoded in the total distribution of expression levels, which can be obtained by averaging the conditional distribution over all positions,
| (5) |
where 〈⋅〉x denotes averaging over x. Note that we can think of Equation 5 as a special case of averaging with a position-dependent weight,
| (6) |
where Px(x) is chosen to be uniform. As we shall see, in the case of Drosophila anterior–posterior (AP) patterning, Px(x) will be the distribution of possible nuclear locations along the AP axis, which indeed is very close to uniform.
When formulated in the language of probabilities, the relationship between the position x and the gene expression levels can be seen as a statistical dependency. If we knew this dependency were linear, we could measure it using, e.g., a linear correlation analysis between x and {gi}. Shannon (1948) has shown that there is an alternative measure of total statistical dependence (not just of its linear component), called the mutual information, which is a functional of the probability distributions Px(x) and P({gi}|x), and is defined by
| (7) |
This positive quantity, measured in bits, tells us how much one can know about the gene expression pattern if one knows the position, x. It is not hard to convince oneself that the mutual information is symmetric; i.e., I({gi} → x) = I(x → {gi}) = I({gi}; x). This is very attractive: we do the experiments by sampling the distribution of expression levels given position, while the nuclei in a developing embryo implicitly solve the inverse problem—knowing a set of gene expression levels, they need to infer their position. A fundamental result of information theory states that both problems are quantified by the same symmetric quantity, the information I({gi}; x). Furthermore, mutual information is not just one out of many possible ways of quantifying the total statistical dependency, but rather the unique way that satisfies a number of basic requirements, for example that information from independent sources is additive (Shannon 1948; Cover and Thomas 1991).
The definition of mutual information in Equation 7 can be rewritten as a difference of two entropies,
| (8) |
where S[p(x)] is the standard entropy of the distribution p(x) measured in bits (hence log base 2):
| (9) |
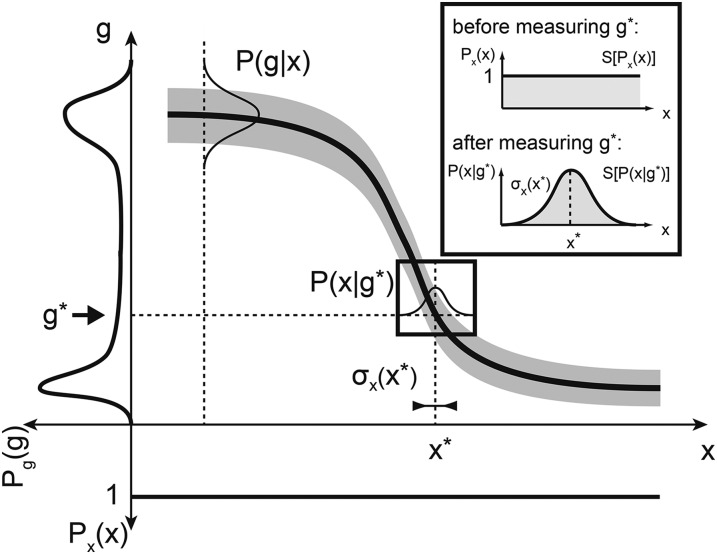
Equation 8 provides an alternative interpretation of the mutual information I({gi}; x), which is illustrated in Figure 3. In the case of a single gene g, the “total entropy” S[Pg(g)], represented on the left, measures the range of gene expression available across the whole embryo. This total entropy, or dynamic range, can be written as the sum of two contributions. One part is due to the systematic modulation of g with position x, and this is the useful part (the “signal”) or the mutual information I({gi}; x). The other contribution is the variability in g that remains even at constant position x; this represents pure “noise” that carries no information about position and is formally measured by the average entropy of the conditional distribution (the noise entropy), 〈S[P(g|x)]〉x. Positional information carried by g is thus the difference between the total and noise entropies, as expressed in Equation 8.
Figure 3.
The mathematics of positional information and positional error for one gene. The mean profile of gene g (thick solid line) and its variability (shaded envelope) across embryos are shown. Nuclei are distributed uniformly along the AP axis; i.e., the prior distribution of nuclear positions Px(x) is uniform (shown at the bottom). The total distribution of expression levels across the embryo, Pg(g), is determined by averaging P(g|x) over all positions and is shown on the left. The positional information I(g; x) is related to these two distributions as in Equation 8. Inset shows decoding (i.e., estimating) the position of a nucleus from a measured expression level g*. Prior to the “measurement” all positions are equally likely. After observing the value g*, the positions consistent with this measured values are drawn from P(x|g*). The best estimate of the true position, x*, is at the peak of this distribution, and the positional error, σx(x), is the distribution’s width. Positional information I(g; x) can equally be computed from Px(x) and P(x|g) by Equation 10.
Mutual information is theoretically well founded and is always nonnegative, being 0 if and only if there is no statistical dependence of any kind between the position and the gene expression level. Conversely, if there are I bits of mutual information between the position and the expression level, there are distinguishable gene expression patterns that can be generated by moving along the AP axis, from the head at x = 0 to the tail at x = 1. This is precisely the property we require from any suitable measure of positional information. We therefore suggest that, mathematically, positional information should be defined as the mutual information between expression level and position, I({gi}; x).
Defining positional error:
Thus far we have discussed positional information in terms of the statistical dependency and the number of distinguishable levels of gene expression along the position coordinate. To present an alternative interpretation, we start by using the symmetry property of the mutual information and rewrite I({gi}; x) as
| (10) |
i.e., the difference between the (uniform) distribution over all possible positions of a cell in the embryo and the distribution of positions consistent with a given expression level. Here, P(x|{gi}) can be obtained using Bayes’ rule from the known quantities:
| (11) |
The total entropy of all positions, S[Px(x)] in Equation 10, is independent of the particular regulatory system—it simply measures the prior uncertainty about the location of the cells in the absence of knowing any gene expression level. If, however, the cell has access to the expression levels of a particular set of genes, this uncertainty is reduced, and it is hence possible to localize the cell much more precisely; the reduction in uncertainty is captured by the second term in Equation 10. This form of positional information emphasizes the decoding view, that is, that cells can infer their positions by simultaneously reading out protein concentrations of various genes (Figure 3).
Positional information is a single number: it is a global measure of the reproducibility in the patterning system. Is there a local quantity that would tell us, position by position, how well cells can read out their gene expression levels and infer their location? Is positional information “distributed equally” along the AP axis or is it very nonuniform, such that cells in some regions of the embryo are much better at reproducibly assuming their roles?
The optimal estimator of the true location x of a cell, once we (or the cell) measure the gene expression levels is the maximum a posteriori (MAP) estimate, In cases like ours, where the prior distribution Px(x) is uniform, this equals the maximum-likelihood (ML) estimate,
| (12) |
thus, for each expression level readout, this “decoding rule” gives us the most likely position of the cell, x*. The inset in Figure 3 illustrates the decoding in the case of one gene.
How well can this (optimal) rule perform? The expected error of the estimated x* is given by where brackets denote averaging over This error is a function of the gene expression levels; however, we can also evaluate it for every x, since we know the mean gene expression profiles, for every x. Thus, we define a new quantity, the positional error σx(x), which measures how well cells at a true position x are able to estimate their position based on the gene expression levels alone. This is the local measure of positional information that we were aiming for.
Independently of how cells actually read out the concentrations mechanistically, it can be shown that σx(x) cannot be lower than the limit set by the Cramer–Rao bound (Cover and Thomas 1991),
| (13) |
where is the Fisher information given by
| (14) |
Despite its name, the Fisher information ℐ is not an information-theoretic quantity, and unlike the mutual information I, the Fisher information depends on position. Is there a connection between the positional error, σx(x), and the mutual information I({gi}; x)? Below we sketch the derivation, following Brunel and Nadal (1998), demonstrating the link for the case of one gene, g.
Let us assume that the Gaussian approximation of Equation 4 holds and that the distribution of the levels of a single gene at a given position is
| (15) |
We can use the Gaussian distribution to compute the Fisher information in Equation 14. We find that
| (16) |
where (⋅)′ denotes a derivative with respect to position, x. Information about position is thus carried by the change in mean profile with position, as well as the change in the variability itself with position. If the noise is small, then typically it will be the case that (a potentially important issue arises when the profiles and their variability are estimated from noisy sampled data; in this case one needs to be careful about spurious contributions to Fisher information due to noise-induced gradients of the profiles and the variability). If we formally require we can retain only the first term to obtain a bound on positional error:
| (17) |
This result is intuitively straightforward: it is simply the transformation of the variability in gene expression, into an effective variance in the position estimate, and the two are related by slope of the input/output relation,
A crucial next step is to think of x as determining gene expressions gi probabilistically, and the x* as being a function of these gene expression levels—that is, when computing x* neither we nor the nuclei have access to the true position. This forms a dependency chain, x → {gi} → x*. Since each of these steps is probabilistic, it can only lose information, such that by information-processing inequality (Cover and Thomas 1991) we must have I({gi}; x) ≥ I(x*; x). The mutual information between the true location and its estimate is given by
| (18) |
Under weak assumptions, the first term in our case is approximately the entropy of a uniform distribution. While we do not know the full distribution P(x*|x) and thus cannot compute its entropy directly, we know its variance, which is just the square of the positional error, Regardless of what the full distribution is, its entropy must be less or equal to the entropy of the Gaussian distribution of the same variance, which is bits. Putting everything together, we find that
| (19) |
Therefore, positional information I({gi}; x) puts an upper bound to the average ability of the cells to infer their locations, that is, to the smallness of the positional error σx(x). In a straightforward generalization of a single-gene case, the Fisher information for a multivariate Gaussian distribution, written for compactness in matrix notation, yields
| (20) |
Under the same assumptions we made for the case of a single gene, we retain only the first term, so that the expression for positional error, written out explicitly in the component notation, reads
| (21) |
where Cij is the covariance matrix of the profiles, as defined in Equation 3. This extends the fundamental connection, Equation 19, between the positional information and positional error, to the case of multiple genes. Importantly, all quantities—the mean profiles and their covariance—in Equation 21 can be obtained from experimental data, so σx(x) is a quantity that can be estimated directly.
Interpretation in a spatially discrete (cellular) system:
In the setup presented above, gene expression levels carry information about a continuous position variable, x. But in a real biological system, there exists a minimal spatial scale—the scale of individual nuclei (or cells)—below which the concept of gene expression at a position is no longer well defined. This is particularly the case in systems that interpret molecular concentrations to make decisions that determine cell fates: such interpretations have no meaning at the spatial scale of a molecule, but only at cellular scales. How should positional information be interpreted in such a context?
When noise is small enough and the distribution of positions consistent with observed gene expression levels, P(x|{gi}) of Equation 11 is nearly Gaussian, and Equations 19 and 21 become tight bounds. In this case we can apply Equation 10 directly. In developmental systems, cells or nuclei are often distributed in space such that the intercellular (or internuclear) spacings are, to a good approximation, equal: at least in systems we are studying, there are no significant local rarefactions or overabundances of cells or nuclei. Mathematically, this amounts to assuming that Px(x) = 1/L (where L is the linear spatial extent over which the cells or nuclei are distributed). This assumption of uniformity is not crucial for any calculation in this article and can be easily relaxed, but it makes the equations somewhat simpler to display and interpret. Using a uniform distribution for Px(x), the information is
| (22) |
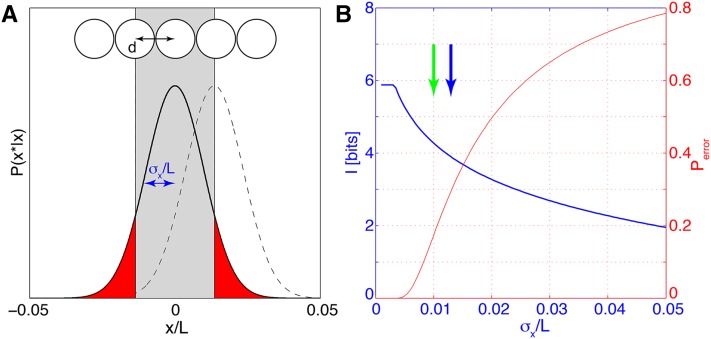
Note that in the problem setup we have normalized the spatial axis so that the length L = 1 in the formula above (or, if we restrict the attention to some section of the embryo, the fractional size of that section). For any real data set one needs to verify that the approximations leading to this result are warranted (see below). Assuming that, Equation 22 further illustrates the connection between positional error and positional information. Consider a one-dimensional row of nuclei spaced by internuclear distance d along the AP axis, as illustrated in Figure 4. To determine its position along the AP axis, each nucleus has to generate an estimate x* of its true position x by reading out gap gene expression levels. In the simplest case, the errors of these estimates are independent, normally distributed, with a mean of zero and a variance Given these parameters, there is some probability Perror that the positional estimate deviates by more than the lattice spacing d, in which case the nucleus would be assigned to the wrong position, and perfectly unique, nucleus-by-nucleus identifiability would be impossible. Figure 4 shows how the positional information of Equation 22 and the probability of fate misassignment, Perror, vary as functions of σx. Importantly, even when σx < d, that is, the positional error is smaller than the internuclear spacing (as in Figure 4A), there is still some probability of nuclear misidentification and therefore the positional information has not yet saturated. Only when the positional error is sufficiently small that the probability weight in the tails of the Gaussian distribution is negligible (at σx ≪ d), can each of the Nn nuclei be perfectly identified and the information saturates at log2(Nn) bits.
Figure 4.
Positional information, error, and perfect identifiability. (A) Nuclei, separated by distance d, decode their position from gap gene expression levels (top). The probability P(x*|x) for the estimated position x* is Gaussian (solid black line for the central nucleus and dashed line for the right next nucleus); its width is the positional error σx. The probability Perror that the central nucleus is assigned to the wrong lattice position is equal to the integral of the tails |x*| > d of the distribution P(x*|x) (red area). (B) Positional information (blue) and probability of false assignment (red) as a function of positional error σx. Blue arrow indicates the value of positional error σx = d used for the toy example in A; specifically we used Nn = 59 nuclei uniformly tightly packing the central 80% of the AP axis (L = 0.8 and thus d = L/Nn). In comparison, the 1% positional error inferred from data in Dubuis et al. (2013b) corresponds to the green arrow. The information is computed using Equation 22 and made to saturate at Imax = log2(Nn) bits (perfect identifiability). All parameters are chosen to roughly match the results of the Drosophila gap gene analysis.
In sum, we have shown that a rigorous mathematical framework of positional information can quantify the reproducibility of gene expression profiles in a global manner. By framing the cells’ problem of finding their location in the embryo in terms of an estimation problem, we have shown that the same mathematical framework of positional information places precise constraints on how well the cells can infer their positions by reading out a set of genes. These constraints are universal: regardless of how complex the mechanistic details of the cells’ readout of the gene concentration levels are, the expression level variability prevents the cells from decreasing the positional error below σx. The concept of positional error easily generalizes to the case of multiple genes and is diagnostic about how positional information is distributed along the AP axis.
Estimation methodology
There are a number of technical details that need to be fulfilled when applying the formalisms of positional information and positional error to real data sets. Estimating information theoretic quantities from finite data is generally challenging (Paninski 2003; Slonim et al. 2005). In practice it involves combining general theory and algorithms for information estimation with problem-specific approximations. Here we present the information content of the four major gap genes in early Drosophila embryos as a test case. First, we briefly recapitulate our experimental and data-processing methods (for details, see Dubuis et al. 2013a). Next, we present the statistical techniques necessary to consistently merge data from separate pairwise gap gene immunostaining experiments into a single data set. Then we estimate mutual information directly from data for one gene, using different profile normalization and alignment methods. Finally, we introduce the Gaussian noise approximation and an adaptive Monte Carlo integration scheme to extract the information carried jointly by pairs of genes and by the full set of four genes.
Extracting expression level profiles from imaging data:
Drosophila embryos were fixed and simultaneously immunostained for the four major gap genes hunchback (hb), Krüppel (Kr), knirps (kni), and giant (gt), using fluorescent antibodies with minimal spectral overlap, as described in Dubuis et al. (2013a). We present an analysis of four data sets (A, B, C, and D): data sets A–C have been processed simultaneously, but imaged in different sessions; data set D has been processed and imaged independently from the other data sets. Hence these datasets are well suited to assess the dependence of our measurements and calculations on the experimental processing. Dataset A has been presented and analyzed previously in Dubuis et al. (2013a,b) and Krotov et al. (2013).
Fluorescence intensities were measured using automated laser scanning confocal microscopy, processing hundreds of embryos in one imaging session. Cross-sectional images of multicolor-labeled embryos were taken with an imaging focus at the midsagittal plane, the center plane of the embryo with the largest circumference. Intensity profiles of individual embryos were extracted along the outer edge of the embryos, using custom software routines (MATLAB; MathWorks, Natick, MA) as described in Houchmandzadeh et al. (2002) and Dubuis et al. (2013a). The results in the following sections are presented using exclusively dorsal intensity profiles, and we report their projection onto the AP axis in units normalized by the total length L of the embryo, yielding a fractional coordinate between 0 (anterior) and 1 (posterior). The dorsal edge was chosen for its smaller curvature, which limits geometric distortions of the profiles when projecting the intensity onto the AP axis. The AP axis was uniformly divided into 1000 bins, and the average profile intensity in each bin is reported. This procedure results in a raw data matrix that lists, for each embryo and for each of the four gap genes, one intensity value for each of the 1000 equally spaced spatial positions along the AP axis. Unless specified differently, all our results are reported for the middle 80% of the AP axis (from x = 0.1 to x = 0.9), consistent with Dubuis et al. (2013b); at the embryo poles geometric distortion is large, and patterning mechanisms are distinct from the middle.
For any successful information-theoretic analysis, the dominant source of observed variability in the data set must be due to the biological system and not due to the measurement process, requiring tight control over systematic measurement errors. Gap gene expression levels critically depend on the developmental stage and on the imaging orientation of the embryo. Therefore we applied strict selection criteria on developmental timing and orientation angle (see Dubuis et al. 2013a). In this article we restrict our analysis to a time window of ∼10 min, 38–48 min into nuclear cycle 14. During this time interval the mean gap gene expression levels peak and overall temporal changes are minimal. A careful analysis of residual variabilities due to measurement error (i.e., age determination, orientation, imaging, antibody nonspecificity, spectral crosstalk, and focal plane determination) reveals that the estimated fraction of observed variance in the gap gene profiles due to systematic and experimental error is <20% of the total variance in the pool of profiles; i.e., >80% of the variance is due to the true biological variability (Dubuis et al. 2013a), satisfying the condition for the information-theoretic analysis to yield true biological insight.
In most cases expression profiles need to be normalized before they can be compared or aggregated across embryos. Careful experimental design and imaging conditions can make normalization steps essentially superfluous (Dubuis et al. 2013a), but such control may not always be possible. To deal with experimental artifacts, we introduce three possible types of normalizations, which we call Y alignment, X alignment, and T alignment. In Y alignment, the recorded intensity of immunostaining for each profile of a given gap gene, G(μ)(x) recorded from embryo μ is assumed to be linearly related to the (unknown) true concentration profile g(μ)(x) by an additive constant αμ and an overall scale factor βμ (to account for the background and staining efficiency variations from embryo to embryo, respectively), so that G(μ)(x) = αμ + βμg(μ)(x). We wish to minimize the total deviation χ2 of the concentration profiles from the mean across all embryos. The objective function is
| (23) |
where denotes an average concentration profile across all embryos. The parameters {αμ, βμ} are chosen to minimize the and thus maximize alignment, and since the cost function is quadratic, this optimization has a closed-form solution (Gregor et al. 2007a; Dubuis et al. 2013a).
Additionally, one can perform the X alignment, where all gap gene profiles from a given embryo can be translated along the AP axis by the same amount; this introduces one more parameter γi per embryo (not per expression profile), which can be again determined using χ2 minimization, similar to the above. (In practice, one first carries out the tractable Y alignment, followed by a joint minimization of χ2 for α, β, γ, which needs to be carried out numerically.) There are two candidate sources of variability that can be compensated for by X alignments: (i) our error in the exact determination of the AP axis, i.e., in the exact end points of the embryo, due to image processing; and (ii) real biological variability that would result in all the nuclei within the embryo being rigidly displaced by a small amount along the long axis of the embryo relative to the egg boundary.
Finally, the T alignment attempts to compensate for the fraction of observed variability that is due to the systematic change in gene profiles with embryo age even within the chosen 10-min time bracket. We can use our knowledge of how the mean profiles evolve with time and detrend the entire data set in a given time window by this evolution of the mean profile. We follow the procedure outlined in Dubuis et al. (2013a) to carry out this alignment.
In sum, each of the three alignments, X, Y, and T, subtracts from the total variance the components that are likely to have an experimental origin and do not represent properly either the intrinsic noise within an embryo or natural variability between the embryos; since the total variance will be lower after alignment, successive alignment procedures should lead to increases in positional information. Strictly speaking, the lower bound on positional information would be obtained by estimating it using raw data, without any alignment, thus ascribing all variability in the recorded profiles to the true biological variability in the system, but unless the control over experimental variability is excellent, this lower bound might be far below the true value. For instance, if embryos cannot be stained and imaged in a single session, it would be very hard to guarantee that there are no embryo-to-embryo variabilities in the antibody staining and imaging background. For that reason, we view the Y alignment as the minimal procedure that should be performed unless staining and imaging variability is shown to be negligible in dedicated control experiments. The choice of performing alignments beyond Y depends on system-specific knowledge about the plausible sources of experimental vs. biological variability. For these reasons, all the results in this article are based on the minimal Y alignment procedure (unless explicitly specified otherwise), thus yielding conservative information estimates, but we also explore how these estimates would increase for single genes and the quadruplet in the case of the other alignments.
Once the desired alignment procedure has been carried out, we can define the mean expression across the embryos, for every gap gene i = 1, … , 4, and choose the units for the profiles such that the minimum value of each mean profile across the AP axis is 0, and the maximal value is 1. This is the final, aligned and normalized, set of profiles on which we carry out all subsequent analyses and from which we compute the covariance matrix Cij(x) of Equation 3.
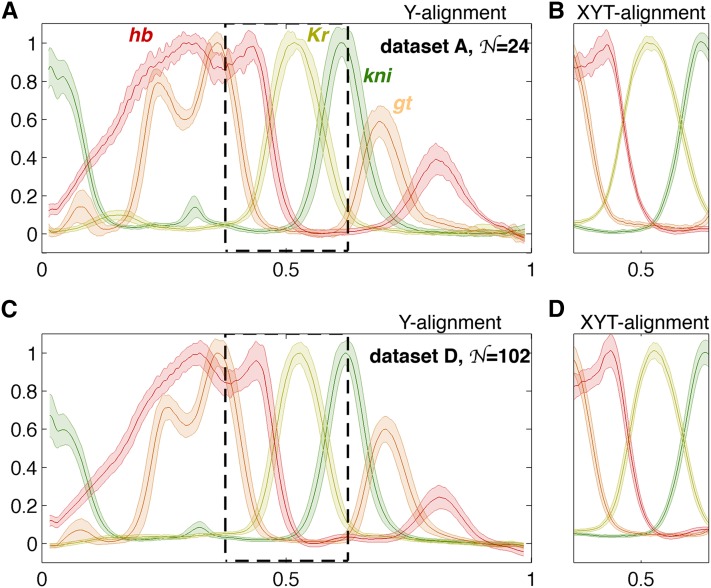
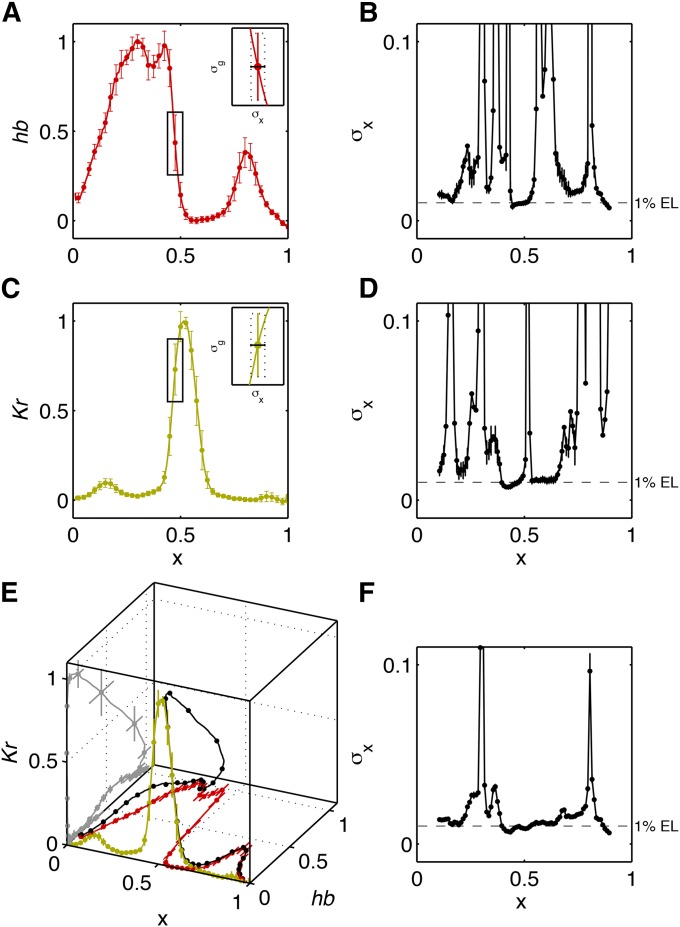
Applying the described selection criteria to the four mentioned data sets yields embryo counts of (A), (B), (C), and (D). Figure 5 shows the mean profiles and their variability for two of the data sets, using either the minimal (Y) or the full (XYT) alignment.
Figure 5.
Simultaneous measurements of gap gene expression levels and profile alignment. (A) The mean profiles (thick lines) of gap genes Hunchback, Giant, Knirps, and Krüppel (color coded as indicated) and the profile variability (shaded region = ±1 SD envelope) across 24 embryos in data set A, normalized using the Y alignment procedure. (B) The same profiles have been aligned using the full (XYT) procedure. Shown is the region that corresponds to the dashed rectangle in A to illustrate the substantially reduced variability across the profiles. (C and D) Plots analogous to A and B showing the profiles and their variability for data set D.
Estimating information with limited amounts of data:
Measuring positional information from a finite number of embryos is challenging due to estimation biases. Good estimators are more complicated than the naive approach, which consists of estimating the relevant distributions by counting and using Equation 7 for mutual information directly. Nevertheless, the naive approach can be used as a basis for an unbiased information estimator, following the so-called direct method (Strong et al. 1998; Slonim et al. 2005).
The easiest way to obtain a naive estimate for P({gi}, x) is to convert the range of continuous values for gi and x into discrete bins of size ΔN × Δ. On this discrete domain, we can estimate the distribution empirically by creating a normalized histogram. To this end, we treat our data matrix of (4 gap genes) × ( embryos) × (1000 spatial bins) as containing samples from the joint distribution of interest. A naive estimate of the positional information, is
| (24) |
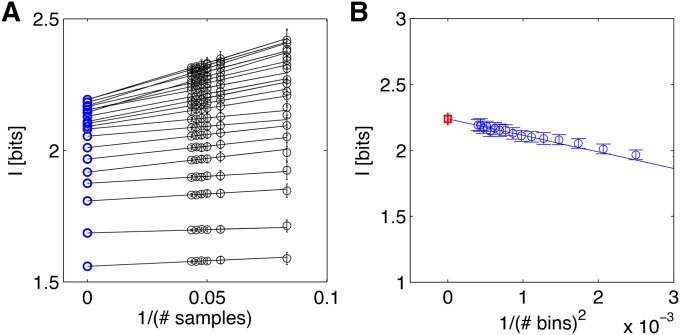
where the subscripts indicate the explicit dependence on sample size M and bin size Δ. It is known that naive estimators suffer from estimation biases that scale as 1/M and ΔN+1. Following Strong et al. (1998) and Slonim et al. (2005), we can obtain a direct estimate of the mutual information by first computing a series of naive estimates for a fixed value of Δ and for fractions of the whole data set. Concretely, we pick fractions of the total number of embryos, At each fraction, we randomly pick m embryos 100 times and compute (where averages are taken across 100 random embryo subsets). This gives us a series of data points that can be extrapolated to an infinite data limit by linearly regressing vs. 1/m (Figure 6A). The intercept of this linear model yields , and we can repeat this procedure for a set of ever smaller bin sizes Δ. To extrapolate the result to very small bin sizes, Δ → 0, we use the previously computed for various choices of decreasing Δ, and extrapolate to Δ → 0 as shown in Figure 6B. At the end of this procedure we obtain the final estimate called direct estimate (DIR) of positional information (red square in Figure 6B). While no prior knowledge about the shape of the distribution P({gi}, x) is assumed by the direct estimation method, a potential disadvantage is the amount of data required, which grows exponentially in the number of gap genes. In practice, our current data sets suffice for the direct estimation of positional information carried simultaneously by one or at most two gap genes.
Figure 6.
Direct estimation for the positional information carried by Hunchback. (A) Extrapolation in sample size for different bin sizes Δ, starting with 10 bins for the bottom line and increasing to 50 bins for the top line in increments of 2. Black points are averages of naive estimates over 100 random choices of m embryos (error bars = SD), plotted against 1/m on the x-axis. Lines and blue circles represent extrapolations to the infinite data limit, m → ∞. (B) The extrapolations to the infinite data limit (blue points from A) are plotted as a function of the bin size, and the second regression is performed (blue line) to find the extrapolation of Δ → 0. The final estimate, represented by the red square, is IDIR(hb; x) = 2.26 ± 0.04 bits; the error bar is the statistical uncertainty in the extrapolated value due to limited sample size.
To extend this method tractably to more than two genes, one needs to resort to approximations for P({gi}|x), the simplest of which is the so-called Gaussian approximation, shown in Equation 4. In this case, we can write down the entropy of P({gi}|x) analytically. For a single gene we get
| (25) |
while the straightforward generalization to the case of N genes is given by
| (26) |
where |C(x)| is the determinant of the covariance matrix Cij(x). From Equation 8 we know that I(g; x) = S[P(g)] − 〈S[P(g|x)]〉x. Here the second term (“noise entropy”) is therefore easily computable from Equation 25, for a discretized version of the distribution, using the (co)variance estimate of gene expression levels alone. The first term (total entropy) can be estimated as above by the direct method, i.e., by making an empirical estimate of for various sample sizes M and bin sizes Δ and extrapolating M → ∞ and Δ → 0. This combined procedure, where we evaluate one term in the Gaussian approximation and the other one directly, has two important properties. First, the total entropy is usually much better sampled than the noise entropy, because it is based on the values of g pooled together over every value of x; it can therefore be estimated in a direct (assumption-free) way even when the noise entropy cannot be. Second, by making the Gaussian approximation for the second term, we are always overestimating the noise entropy and thus underestimating the total positional information, because the Gaussian distribution is the maximum entropy distribution with a given mean and variance. Therefore, in a scenario where the first term in Equation 25 is estimated directly, while the second term is computed analytically from the Gaussian ansatz, we always obtain a lower bound on the true positional information. We call this bound (which is tight if the conditional distributions really are Gaussian) the first Gaussian approximation (FGA).
For three or more gap genes the amount of data can be insufficient to reliably apply either the direct estimate or FGA, and one needs to resort to yet another approximation, called the second Gaussian approximation (SGA). As in the FGA, for the second Gaussian approximation we also assume that is Gaussian, but we make another assumption in that Pg({gi}), obtained by integrating over these Gaussian conditional distributions, is a good approximation to the true Pg({gi}). The total distribution we use for the estimation is therefore a Gaussian mixture:
| (27) |
For each position, the noise entropy in Equation 26 is proportional to the logarithm of the determinant of the covariance matrix, whose bias scales as 1/M if estimated from a limited number M of samples. We therefore estimate the information for fractions of the whole data set and then extrapolate for M → ∞.
Figure 7 compares the three methods for computing the positional information carried by single gap genes in the 10–90% egg length segment. Across all four gap genes and all four data sets the methods agree within the estimation error bars. This provides implicit evidence that, at least on the level of single genes, the Gaussian approximation holds sufficiently well for our estimation methods.
Figure 7.
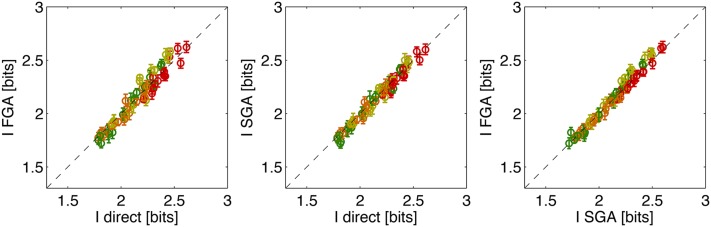
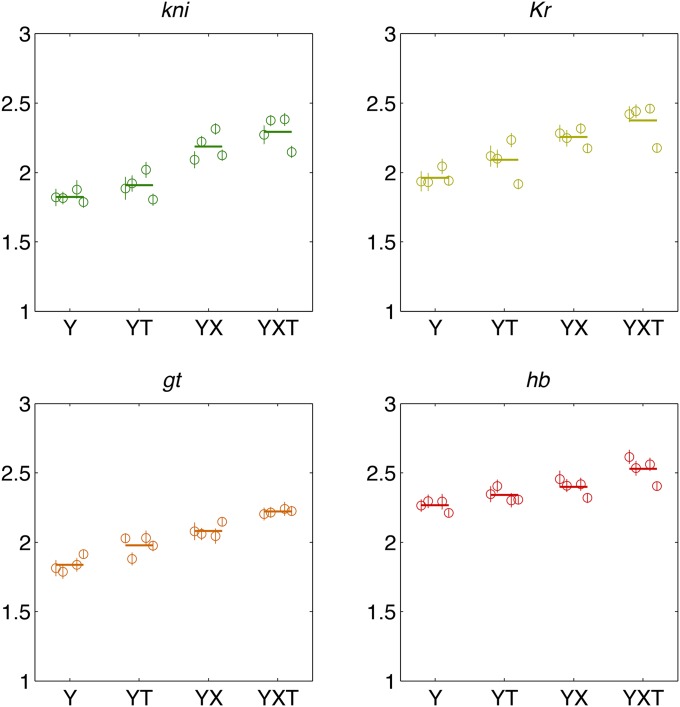
Comparing estimation methods for positional information carried by single gap genes. Shown are the estimates for four gap genes (color coded as in Figure 5), using four data sets (data sets A, B, C, and D) and four different alignment methods (Y, YT, XY, and XYT), for 64 total points per plot. Dashed line shows equality. Different alignment methods result in a spread of information values for the same gap gene, as shown explicitly in Figure 8.
Figure 8 compares the estimation results across data sets and the alignment methods. With the exception of data set D data under T alignments, the information estimates are consistent across data sets. As expected, successive alignment procedures remove systematic variability and increase the information by comparable amounts, so that the maximal differences (between the minimal Y alignment and the maximal XYT alignment) are ∼25%, 21%, 21%, and 11% for kni, Kr, gt, and hb, respectively, when averaged across data sets.
Figure 8.
Consistency across data sets and a comparison of alignment methods for positional information carried by single gap genes. Direct estimates with estimation error bars are shown for four gap genes (color coded as in Figure 5) in separate panels. On each panel, different alignment methods (Y, YT, XY, and XYT) are arranged on the horizontal axis, and for every alignment method we report the estimation results using data sets A, B, C, and D (successive plot symbols from left to right) and their average (thick horizontal line).
Merging data from different experiments:
To compute positional information carried by multiple genes from our data, using the second Gaussian approximation, we need to measure N mean profiles, and the N × N covariance matrix, Cij(x). While measuring is a standard technique, estimating the covariance matrix, Cij(x), requires the simultaneous labeling of all N gap genes in each embryo, using fluorescent probes of different colors. While simultaneous immunostainings of two genes are not unusual, it is not easy to scale the method up to more genes while maintaining a quantitative readout. While for data sets A–D we succeeded in doing a simultaneous four-way stain, in general this is not always feasible, so we developed an estimation technique for inferring a consistent N × N covariance matrix based on multiple collections of pairwise stained embryos.
Estimating a joint covariance matrix from pairwise staining experiments is nontrivial for two reasons. First, each diagonal element of the covariance matrix, i.e., the variance of an individual gap gene, is measured in multiple experiments, but the obtained values might vary due to measurement errors. Second, true covariance matrices are positive definite, i.e., det(C(x)) > 0, a property that is not guaranteed by naively filling in different terms of the matrix by computing them across sets of embryos collected in different experiments. This is a consequence of small sampling errors that can strongly influence the determinant of the matrix. We therefore need a principled way to find a single best and valid covariance matrix from multiple partial observations, a problem that has considerable history in statistics and finance (see, e.g., Stein 1956; Newey and West 1986).
We start by considering a number of embryos that have been costained for the pair of gap genes (i, j). Let the full data set consist of all such pairwise stainings: for N gap genes, this is a total of pairwise experiments, where i, j = 1, … , N and i < j. Thus, in the case of the four major gap genes in Drosophila embryos, kni, Kr, gt, and hb, the total number of recorded embryos is where the sum is across all six pairwise measurements: (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4). These pairwise measurements give us estimates of the mean profile and the 2 × 2 covariance matrices for each pair (i, j),
For four gap genes and six pairwise experiments, we will get six 2 × 2 partial covariance matrices and 6 × 2 estimates of the mean profile Our task is to find a single set of four mean profiles and a single 4 × 4 covariance matrix Cij(x) that fits all pairwise experiments best. In the next paragraphs, we show how this can be computed for the arbitrary case of N gap genes.
To infer a single set of mean profiles and a single consistent N × N covariance matrix Cij(x), we use maximum-likelihood inference. We assume that at each position x our data are generated by a single N-dimensional Gaussian distribution of Equation 4 with unknown mean values and an unknown covariance matrix, which we wish to find, but we can observe only two of the mean values and a partial covariance in each experiment; the other variables are integrated over in the likelihood.
Following this reasoning, the log likelihood of the data for pairwise staining (i, j) at position x is
| (28) |
where the log-likelihood ℒ as well as the mean profiles, covariance elements, and the measurements all depend on x; index μ enumerates all the embryos recorded in a pairwise experiment (i, j).
Since all pairwise experiments are independent measurements, the total likelihood at a given position x is the sum of the individual likelihoods After some algebraic manipulation, the total log likelihood can be written in terms of the empirical estimates for the mean profiles and covariances of the separate pairwise experiments:
For each position x, we search for and Cij(x) that maximize Before proceeding, however, we have to guarantee that the search can take place only in the space of positive semidefinite matrices Cij(x) (i.e., det C ≥ 0). We enforce this constraint by spectrally decomposing Cij and parameterizing it in its eigensystem (Pinheiro and Bates 2007). To this end, we write C(x) = PDPT, where D is a diagonal matrix parameterized with the variables α1, … , αN that determine the diagonal elements in D; i.e., Dii = exp(αi). The orthonormal matrix P is decomposed as a product of the N(N − 1)/2 rotation matrices in N dimensions: where Rk(ϕk) is a Euclidean rotation matrix for angle ϕk acting in each pair of dimensions indexed by k.
In the spectral representation, the likelihood is a function of N values N parameters αi, and N(N − 1)/2 angles ϕk at each x. In the case of four gap genes, this is a total of 14 parameters that need to be computed by maximizing at each location x.
There is no guarantee that there is a unique minimum for the log likelihood; moreover, there could exist sets of covariance matrices that all lead to essentially the same value for or, even more dangerously, the maximum-likelihood solution could favor matrices with vanishing determinants, especially when estimating from a small number of samples. To address these issues, we regularize the problem by replacing D → D + λI, where I is the identity matrix and λ is the regularization parameter. Larger values of λ will favor more “spherical” distributions, while small values will allow distributions that can be very squeezed in some directions. We thus maximize to find the best set of parameters given the value of the regularizer (which is assumed to be the same for every x). To set λ we use cross-validation: the maximum-likelihood fit is performed for various choices of λ not over all available data (embryos), but only over a training subset. The remaining embryos constitute a test subset. Parameter fits for different λ obtained on the training data can be assessed and compared by evaluating their likelihood over test data and selecting the value of λ that maximizes the model likelihood over the testing set.
To compute and Cij(x), we initialize to the mean profile across all pairwise experiments (i, j); we initialize αi to the mean of the log of the diagonal terms and we initialize all rotation angles ϕk = 0. The Nelder–Mead simplex method is used to maximize (Lagarias et al. 1998). Finally, we compute C(x) from αi and ϕk.
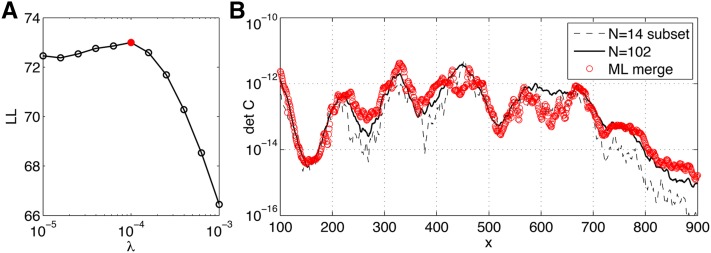
Finally, we use our quadruple-stained data sets to test our pairwise merging procedure. We partition the 102 embryos from data set D into six disjoint subsets of 14 embryos each (while retaining 18 embryos for validation), and in each subset we consider only one of the six possible pairs of gap gene data; that is, in every subset for a pair of genes (i, j), we measured the mean expression profiles and the 2 × 2 covariance matrix Cij(x), the inputs to the maximum-likelihood merging procedure. Note that this benchmark uses real data from data set D, by simply “blacking out” certain measured values so that for every embryo, only one pair of gap genes remains visible to the merging procedure. The inferred 4 × 4 covariance matrix can be compared to the covariance matrix estimated from the complete data set. The results of this procedure are shown in Figure 9, demonstrating that pairwise measurements can be merged into a consistent covariance matrix, whose determinant matches well with the determinant extracted from the complete data set. Note that determinants are compared because they are very sensitive to the inferred parameters and enter directly into the expressions for positional information and positional error. Importantly, filling in the covariance matrix naively, or skipping the regularization, results in either non-positive-definite matrices or matrices whose determinants are close to singular at multiple values of position x. The presented maximum-likelihood merging procedure will allow our framework to be applied to model systems where simultaneous gap gene measurements are hard to obtain, but pairwise stains are feasible.
Figure 9.
Merging data sets using maximum-likelihood reconstruction. Dataset D (102 embryos) is used to simulate six pairwise staining experiments with 14 unique embryos per experiment. (A) The log likelihood of the merged model on 18 test embryos (not used in model fitting), as a function of regularization parameter λ; λ = 10−4 is the optimal choice for this synthetic data set. (B) The comparison of the determinant of the 4 × 4 inferred covariance matrix (red) as a function of position x, compared to the determinant of the full data set (black solid line) or the determinant of a subset of 14 embryos (black dashed line), where small sample effects are noticeable.
Monte Carlo integration of mutual information:
Another technical challenge in applying the second Gaussian approximation for positional information to three or more gap genes lies in computing the entropy of the distribution of expression levels, S[Pg({gi})]. This is a Gaussian mixture obtained by integrating P({gi}|x) over all x as prescribed by Equation 27. In one or two dimensions one can evaluate this integral numerically in a straightforward fashion by partitioning the integration domain into a grid with fine spacing Δ in each dimension, evaluating the conditional distribution P({gi}|x) on the grid for each x and averaging the results over x to get Pg({g}), from which the entropy can be computed using Equation 9. Unfortunately, for three genes or more this is infeasible because of the curse of dimensionality for any reasonably fine-grained partition.
To address this problem we make use of the fact that over most of the integration domain Pg({gi}) is very small if the variability over the embryos is small. This means that most of the probability weight is concentrated in the small volume around the path traced out in N-dimensional space by the mean gene expression trajectory, as x changes from 0 to 1. We designed a method that partitions the whole integration domain adaptively into volume elements such that the total probability weight in every box is approximately the same, ensuring fine partition in regions where the probability weight is concentrated, while simultaneously using only a tractable number of partitions.
The following algorithm was used to compute the total entropy, S[Pg({gi})]:
The whole domain for {gi} is recursively divided into boxes such that no box contains >1% of the total domain volume.
For each box i with volume ωi, we use Monte Carlo sampling to randomly select t = 1, … , T points gt in the box and approximate the weight of the box i as ; we explore different choices for T in Figure 11.
Analogously, we evaluate the approximate total weight of each box π(i), by pooling Monte Carlo sampled points across all x.
π(i|x) and π(i) are renormalized to ensure for every x and
The conditional and total entropies are computed as and
The positional information is estimated as I({gi}; x) = Stot − Snoise.
The box i* = argmaxiπ(i) with the highest probability weight π(i*) is split into two smaller boxes of equal volume ω(i*)/2, and the estimation procedure is repeated by returning to step 2. Additional Monte Carlo sampling needs to be done only within the newly split box; for the other boxes old samples can be reused.
The algorithm terminates when the positional information achieves desired convergence or at a preset number of box partitions.
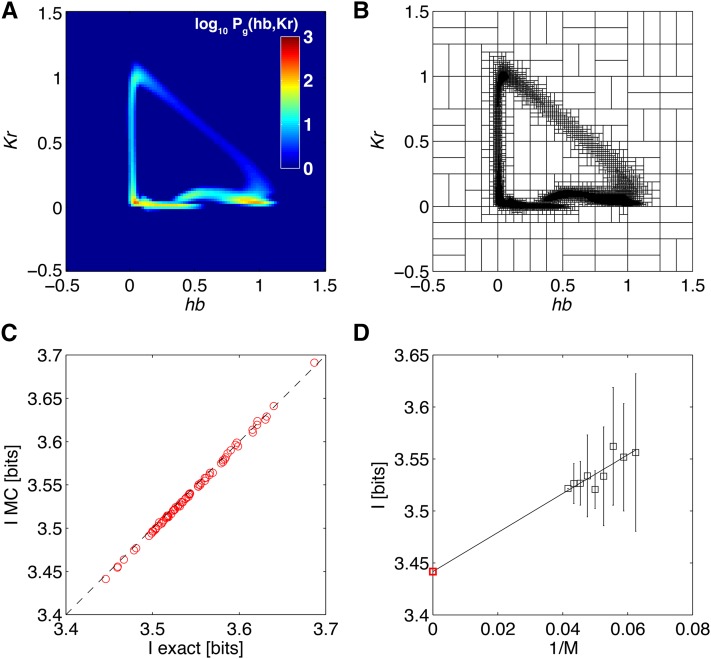
Figure 10, A and B, shows how the algorithm works for a pair of genes ({hb, Kr}) for which the joint probability distribution is easy to visualize. To get the final SGA estimate of positional information that the two genes jointly carry about position, extrapolation to infinite data size is performed in Figure 10D.
Figure 10.
Monte Carlo integration of information for a pair of genes. (A) The (log) distribution of gene expression levels, Pg(hb, Kr), obtained by numerically averaging the conditional Gaussian distributions for the pair over all x (data set A). For two genes this explicit construction of Pg is tractable and can be used to evaluate the total entropy, S[Pg]. (B) As an alternative, one can use the Monte Carlo procedure (with T = 100) outlined in the text, which uses adaptive partitioning of the domain, shown here. The boxes, here 104, are dense where the distribution contains a lot of weight. (C) The comparison between MC evaluated positional information carried by the hb/Kr pair and the exact numerical calculation as in A, over different random subsets of m = 16, … , 24 embryos, with 10 random subsets at every m. The MC integration underestimates the true value by 0.1% on average, with a relative scatter of 4 × 10−4. (D) To debias the estimate of the information due to the finite sample size used to estimate the covariance matrix, a SGA extrapolation m → ∞ is performed on the estimates from C, to yield a final estimate of I({hb, Kr}; x) = 3.44 ± 0.02 bits.
Figure 11 shows the MC estimate of the positional information carried by the quadruplet of gap genes and its dependence on the parameter T (the number of MC samples per box per position) and the refinement of the adaptive partition. When T is too small (e.g., T = 100), we obtain a biased estimate of the information, presumably because the evaluation of the distribution over boxes is poor, leading to suboptimal recursive partitioning. When T is increased to T ≥ 200, the estimates for different T start converging as the number of adaptive boxes is increased, and the final estimates (after extrapolation to an infinitely fine partition) for different T agree to within a few percent.
Figure 11.
Monte Carlo integration of mutual information for the gap gene quadruplet. The estimation uses data set A embryos, without correcting for the finite number of embryos (i.e., the empirical covariance matrix is taken to be the ground truth for this analysis). Shown are the mean and 1-SD scatter over 10 independent MC estimations, for each choice of T (number of samples per box). The information can then be linearly regressed against the inverse number of boxes for last 2000 partitions and extrapolated to an infinitely fine partition; for each T, these extrapolations are shown at right (crosses).
Application to the Drosophila gap gene system
Information in single gap genes and gap gene pairs:
Information carried by single genes is reported in Table 1. The values are estimated using the direct method, which agrees closely with the alternative estimation methods (FGA and SGA; cf. Figure 7). Measured across four independent experiments, the information values are consistent to within the estimated error bars, indicating that not only embryo-to-embryo experimental variability can be brought under control as described in Dubuis et al. (2013a), but also experiment-to-experiment variability is small.
Table 1. Information (in bits) carried by single genes.
| Data set | kni | Kr | gt | hb |
|---|---|---|---|---|
| A | 1.82 ± 0.06 | 1.94 ± 0.07 | 1.81 ± 0.06 | 2.26 ± 0.04 |
| B | 1.81 ± 0.04 | 1.93 ± 0.06 | 1.79 ± 0.05 | 2.29 ± 0.05 |
| C | 1.88 ± 0.07 | 2.04 ± 0.05 | 1.84 ± 0.05 | 2.19 ± 0.05 |
| D | 1.79 ± 0.04 | 1.94 ± 0.04 | 1.91 ± 0.03 | 2.21 ± 0.03 |
| Mean | 1.83 ± 0.04 | 1.96 ± 0.05 | 1.84 ± 0.05 | 2.24 ± 0.05 |
For each data set, we report the direct estimate of positional information. Error bars are the estimation errors. The bottom row contains the (mean ± SD) over data sets.
Single genes carry substantially more than 1 bit of positional information, sometimes even more than 2 bits, thus clearly providing more information about position than would be possible with binary domains of expression. How is this information combined across genes? We can look at the (fractional) redundancy of K genes coding for position together,
| (29) |
by comparing the sum of individual positional informations to the information encoded jointly by pairs (K = 2) of gap genes. Note that R = 1 for a totally redundant pair, R = 0 for a pair that codes for the position independently, and R = −1 for a totally synergistic pair where individual genes carry zero information about position.
At the level of pairs, information is always redundantly encoded, R > 0, although redundancy is relatively small (∼20%), as shown in Figure 12. Such a low degree of redundancy is expected because gap genes are often expressed in complementary regions of the embryo in nontrivial combinations and will thus mostly convey new information about position. Unlike in our toy examples in the Introduction, real gene expression levels are continuous and noisy, and some degree of redundancy might be useful in mitigating the effects of noise, as has been shown for other biological information processing systems (Tkačik et al. 2010). Overall, with the addition of the second gene, positional information increases well above the 0.5 bits that would be expected theoretically for fully redundant gene profiles. The increase is also larger than the theoretical maximum for nonredundant (but noninteracting) genes, where the increase for the second gap gene would be limited to 1 bit (Tkačik et al., 2009). The ability to generate nonmonotonic profiles of gene expression (e.g., bumps) is therefore crucial for high information transmissions achieved in the Drosophila gap gene network (Walczak et al. 2010).
Figure 12.
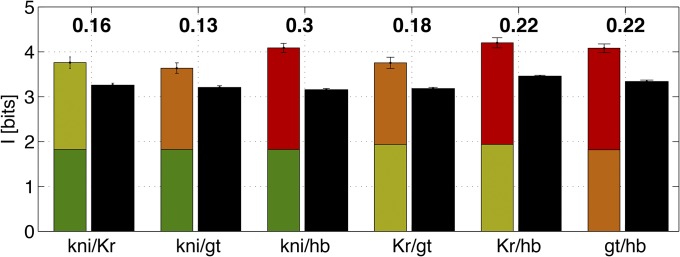
Positional information carried by pairs of gap genes and their redundancy. For each gene pair (horizontal axis) the first bar represents the sum of individual positional informations (color coded as in Figure 5), using the direct estimate. The second (black) bar represents the positional information carried jointly by the gene pair, estimated using SGA with direct numerical evaluation of the integrals. Fractional redundancy R (Equation 29) is reported above the bar.
Information in the gap gene quadruplet:
How much information about position is carried by the four gap genes together, referred to as the gap gene quadruplet? Figure 13 shows the estimation of positional information, using MC integration for all four data sets. The average positional information across four data sets is I = 4.3 ± 0.07 bits, and this value is highly consistent across the data sets. Notably, the information content in the quadruplet displays a high degree of redundancy: the sum of single-gene positional information values is substantially larger than the information carried by the quadruplet, with the fractional redundancy of Equation 29 being R = 0.84. Possible implications of such a redundant representation are addressed in the Discussion.
Figure 13.
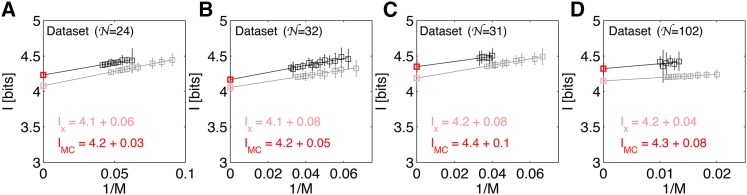
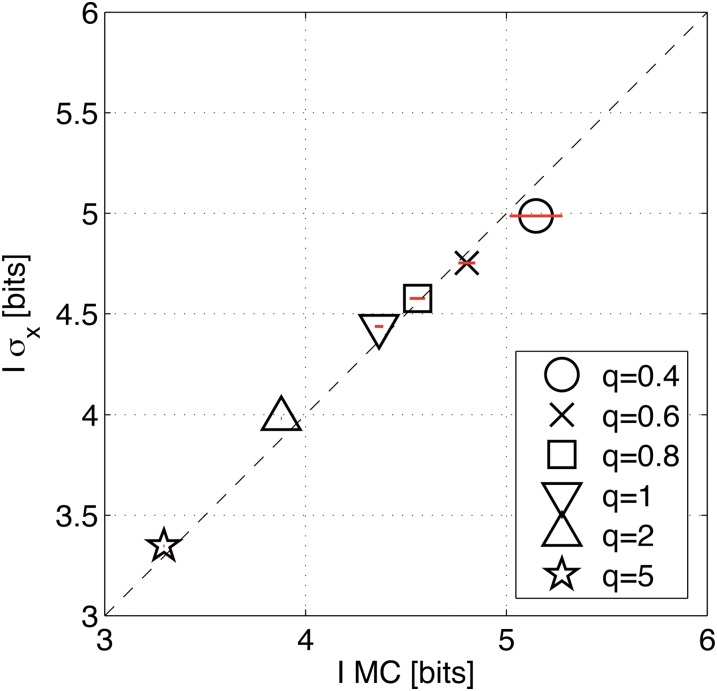
Positional information carried by the quadruplet, {kni, Kr, gt, hb}, of gap genes. The four panels correspond to the four data sets. Shown is the extrapolation to the infinite data limit (M → ∞) for SGA estimates using Monte Carlo integration (black plot symbols and dark red extrapolated value in bits), as well as for estimation of positional information from positional error (gray plot symbols and light red extrapolated value in bits). For MC estimation, 25 subsets of embryos were analyzed per subset size. For estimation from positional error, 100 estimates at each subsample size (data fractions f = 0.5, 0.55, … , 0.85, 0.9) were performed. In the MC estimation, where MC sampling contributes to the error on the extrapolated information value, the error on the final estimate is taken to be the SD of the estimates over 25 subsets at the highest data fraction (smallest 1/M). For estimation from positional error that does not use a stochastic estimation procedure, the error estimate on the final extrapolation is the variance due to small number of samples, estimated as 2−1/2 times the SD over 100 estimates at half the data fraction.
To assess the importance of correlations in the expression profiles and their contribution to the total information, we start with the covariance matrices Cij(x) of data set A, which we artificially diagonalize by setting the off-diagonal elements to zero at every x. This manipulation destroys the correlations between the genes, making them conditionally independent (mechanistically, off-diagonal elements in the covariance matrix could arise as a signature in gene expression noise of the gap gene cross interactions). With these matrices in hand we performed the information estimation, using Monte Carlo integration, analogous to the analysis in Figure 13. Surprisingly, we find a minimal increase in information from I = 4.2 ± 0.03 bits to I = 4.4 ± 0.02 bits when the correlations are removed. This indicates that gap gene cross interactions play a minor role in reshaping the gene expression variability, at least insofar as that influences the total positional information.
We also evaluated the importance of the alignment procedure for estimating total information. Again we use data set A to recompute the MC information estimates with YT, XY, and XYT alignments and compare these with the Y alignment procedure used in Figure 13. The positional information encoded by the quadruplet is I = 4.3 ± 0.03 (for YT), I = 4.7 ± 0.06 (for XY), and I = 4.8 ± 0.06 (for XYT), respectively. This shows that the temporal (T) alignment does not change the information much, probably because our stringent initial selection cutoff on the depth of the membrane furrow canal has picked out the profiles that are sufficiently localized in time around their stable shapes. In contrast, X alignment emerges as important, generating an extra half bit of positional information. This suggests that either our determination of the AP axis used to assign a coordinate to every gene expression has a random embryo-to-embryo error (which is unlikely given the visual inspection of microscopy images and extracted AP axes) or the gap gene expression pattern is intrinsically variable in that it shifts rigidly from embryo to embryo relative to the egg boundary. This would imply that correlated readout errors that the nuclei might make are less harmful than uncorrelated errors. If two neighboring nuclei are positioned both toward the left or both toward the right of the “true” pattern with some positional error σx, this is very different from each of the nuclei randomly perturbing its position with noise of magnitude σx: in the first case, the rank order of the nuclear identities is preserved, while in the second case it need not be, possibly leading to a detrimental spatial mixing of the cell fates.
Decoding information and the resulting positional error:
Positional information is a single aggregate, or global, measure that quantifies the performance of the patterning system, but we can also ask about such performance position by position, using the positional error of Equation 21.
We start by looking at a single gene g, for which we compute the positional error (for equally spaced positions along the AP axis), using Equation 17. Figure 14 shows that by reading out single gap genes (hb or Kr) the nuclei can already achieve positional errors of <1.5% egg length in specific regions of the embryo, yet fail to do so in other regions. Positional error is smaller in the regions of high profile slope, where the variations in gene expression are reliably translated into variations in position. Conversely, the error formally diverges at the peaks and troughs of the profiles where small variations in gene expression cannot efficiently map to changes in position. Were the noise much higher, this conclusion would not hold—in that regime one could distinguish solely between, e.g., a domain of minimal and a domain of maximal expression, and the positional information would correspond better to the intuitive picture of gap genes that define on and off domains.
Figure 14.
Positional error for a single gene and a pair of genes. (A) The mean hb profile and standard deviation across embryos of data set A, as a function of fractional egg length. The inset shows a close-up with the positional error σx determined geometrically from the mean and the variability σg of the profiles. (B) Positional error for hb, computed using Equation 17 (dashed line corresponds to σx = 0.01). Error bars are obtained by bootstrapping 10 times over embryo subsets. (C and D) Plots analogous to A and B for Kr. (E) Three-dimensional representation of hb and Kr profiles from A and C as a function of position x. The mean and standard deviations of the gene expression levels are shown in the {hb, Kr} plane in a gray curve with error bars; cf. the joint distribution of hb and Kr expression levels in Figure 11A. The black curve that extends through the cube volume shows the average expression “trajectory” as a function of position x. (F) Positional error computed using Equation 21 for the {hb, Kr} pair.
An important advantage of using positional error is that it can be naturally generalized to quantify the precision of local position readout, using more than one morphogen gradient. In Figure 14, E and F, we analyze the positional error given the joint readout of the {hb, Kr} pair. The results show that the optimal positional decoding performed with several genes (e.g., N = 2) at a given x does not correspond to the positional error carried by the most informative gene at that position; the combined error can be smaller than the individual errors due to the noise averaging by the N readouts, as well as due to the correlation structure in the variability of the N profiles.
Finally, using the gap gene quadruplet simultaneously, the positional error can reach an average value of ∼ 1%, while never exceeding a few percent, as shown for all four data sets in Figure 15. This shows that the gap genes establish a convenient “chemical coordinate system,” in which it is in principle possible to position any feature along the entire length of the AP axis with roughly 1% precision; the uniform coverage of the AP axis is a sign of efficient encoding of positional information (Dubuis et al. 2013b). Note that 1% positional error still does not correspond to perfect nuclear identifiability, as shown in Figure 4: the error probability of switching the identities of two nearest neighbor nuclei remains ∼16% (and the positional information is ∼1.5 bits below that needed for perfect identifiability). This precision might be sufficient for development, as suggested by the matching precision of downstream markers (Dubuis et al. 2013b). Alternatively, the positional errors of neighboring nuclei are correlated, in which case the gap genes could have sufficient information to uniquely determine the order of nuclear identities (but not their absolute position), despite 1% positional error. In either case, the consequences of gene expression variability are truly small and we expect that the approximation to the positional information using positional error, given by Equation 22, could hold.
Figure 15.
Positional error for the gene quadruplet. Positional error has been estimated using Equation 21 and extrapolated to large sample size. Error bars are bootstrap error estimates. Different colors denote different data sets (inset).
To systematically check whether the gene quadruplet system really is within the small noise limit where expressions of Equations 17, 21, and 22 should hold, we perform the analysis summarized in Figure 16. We systematically scale the measured gene variability in data set A up or down by a factor q to generate synthetic data sets and compare the positional information computed directly, using MC integration on these synthetic data with the approximation of Equation 22, computed using the positional error. Across the range of q (extending from times the observed noise to times the observed noise), the difference between both estimates of positional information is <3%. For small q, the information for the synthetic data (which is Gaussian by construction) should be equal to the information derived from positional error computed using the full expression for the Fisher information given by Equation 20. In fact, Figure 16 shows that simple approximations to the Fisher information leading to Equations 17 and 21 are sufficient for a very good match. Even when the noise is increased for q > 1, the approximation remains surprisingly good.
Figure 16.
The validity of the small noise approximation. Synthetic data were generated from data set A by keeping the mean profiles as inferred from the data, forcing the covariance matrix to be diagonal (by zeroing out the off-diagonal terms), and multiplying the variances by a tunable factor q (see inset); q = 1 corresponds to measured variances in the data and q < 1 (q > 1) corresponds to decreasing (increasing) amount of variability. For each q, positional information was estimated using Equation 21 (vertical axis) or using Monte Carlo integration (horizontal axis). Error bars are SD across 10 independent Monte Carlo integrations for every q.
The agreement between the Monte Carlo estimate of positional information and its approximation based on positional error, observed in a controlled setting of Figure 16, is reflected in the analogous comparison on the real data highlighted in Figure 13. Here the Monte Carlo estimate is by ∼0.1 bit larger than the estimate from positional error, corresponding to a relative difference of ∼2.5%, and formally still within the error bars of both estimates. Both analyses suggest that the gap gene quadruplet truly is in the small noise regime (note that this might not be true for single genes or gene pairs) and that tractable approximations to positional information are therefore available.
Discussion
To generate a differentiated body plan during the development of a multicellular organism, cells with identical genetic material need to reproducibly acquire distinct cell fates, depending on their position in the embryo. The mechanisms of establishment and acquisition of such positional information have been widely studied, but the concept of positional information itself has, surprisingly, eluded formal definition. Here we have provided a mathematical framework for positional information and positional error based on information theory. These are principled measures for quantifying how much knowledge cells can gain about their absolute location in the embryo—and thus how precisely they can commit to correct cell fates—by locally reading out noisy gene expression profiles of (possibly multiple) morphogen gradients. From this broad perspective, our framework is a mathematical realization of the classic ideas put forth by Wolpert almost 50 years ago (Wolpert 1969).
An information-theoretic formulation of positional information has a number of very attractive features. First and foremost, it is mechanism independent. Many plausible mechanisms exist for the establishment of spatial gene expression patterns, involving the processes of gene regulation, signaling, controlled degradation, etc. In particular, these mechanisms could involve spatial coupling, e.g., by diffusion (Little et al. 2013). The spatial aspect of the problem seemingly suggests that our definition of positional information that considers gene expression locally—separately at each spatial location x—is insufficient or incomplete. However, irrespective of the mechanisms involved, what ultimately matters for positional information is the final pattern at the local scale, where nuclei make decisions; specifically, what matters are the mean profile shapes and their (co)variability. This thinking forces us to make a clear distinction between the mechanistic processes that generate expression profiles and the positional information that these profiles carry.
Our definition of positional information is also free of assumptions of what specific geometric features of the expression profiles—boundaries, domains, slopes, etc.—“carry” or encode the information. Much prior work has focused on the sharpness of an expression boundary as a proxy for positional information (Meinhardt 1983; Crauk and Dostatni 2005; Dahmann et al. 2011; Lopes et al. 2012; Zhang et al. 2012). It is unclear, however, how to generalize this approach to systems with more than one expression boundary, and, even more profoundly, we show that the boundary sharpness is not the feature that actually maximizes positional information. In contrast, the information-theoretic framework makes it clear in what particular way profile shapes and their (co)variabilities need to be combined into an appropriate measure of positional information. This measure and the associated positional error naturally generalize to systems with an arbitrary number of gene gradients.
Furthermore, positional information inherits all the attractive features of mutual information. The numerical value of mutual information can be interpreted in terms of the number of distinguishable states or, in the developmental context, as the number of distinguishable positions and cell fates. Information is reparameterization invariant: its value does not depend on what units, or what scale, e.g., log vs. linear, the expression levels are measured. To estimate the information, carefully worked out estimation procedures exist and can be adapted to the developmental context. Finally, as experimental variability can only decrease the information, the computed values will always be conservative lower-bound estimates of the information that approach the true value from below as experimental techniques advance.
Methodologically, we have provided enough detail to make this framework applicable to different systems and experimental setups. In particular, we have shown how data can be aligned and normalized if necessary; how different partial stainings can be merged into a consistent data set; and how analysis methods, including inference from data, numerical computation, and information estimation, should be performed on real experimental data. Importantly, we have proposed how information can be estimated in the small noise regime (which is likely applicable in different systems) and how the consistency of these estimates can be validated.
An important shortcoming of the proposed analysis framework is the assumption that positional information can be read out from steady-state expression patterns. Expression patterns of the gap gene system are highly dynamic even within a given nuclear cycle. While they appear most stable in the particular time class during nuclear cycle 14 that we chose for our analysis, whether that constitutes a true steady state has been debated (Bergmann et al. 2007; Siggia 2008). There exist other systems, e.g., the segmentation clock in vertebrate somite formation (Pourquie 2001), which are intrinsically dynamic. While it is possible that positional information in all of these systems is encoded in the expression levels in particular time windows, it could (at least in principle) also be encoded in full gene expression trajectories, i.e., the temporal sequences of gene expression levels. Extending the information-theoretic approach presented here to include such a temporal aspect will be an important direction of future research.
A significant drawback of the current experiments is their restriction to extracting expression profiles from below the dorsal embryo surface. The resulting analyses—including this one—therefore confound the expression levels of neighboring nuclei with the levels in the interstitial cytoplasmic space, while the only expression levels that are meaningful for regulating downstream genes are the nuclear ones. Ideally a data set would contain expression levels on a nucleus-by-nucleus basis (Myasnikova et al. 2001, 2009; Surkova et al. 2008), possibly encompassing all nuclei in three-dimensional (3D) reconstructed embryos (Fowlkes et al. 2008). While the analysis methods presented here can be easily extended and applied to data sets containing discrete nuclear expression levels, collecting the large data sets needed to estimate profile covariances is a challenge for current nuclear and 3D experimental setups.
The application of our methods to the Drosophila gap gene system has generated several results beyond those reported in Dubuis et al. (2013b), which we now highlight. First, the results are consistent across four different data sets, with fractional deviations in information estimates of <5%. This is comparable to the estimation errors on single data sets, indicating the extremely high biological reproducibility, as well as very stringent control over the experiment and data analysis. Second, the analysis of positional error explicitly shows that information is encoded in the parts of the expression profile that have high slopes (spatial derivatives), further weakening the interpretation of gap genes as providing sharp boundaries between expression domains. Third, we find that at the level of the gene quadruplet, the information is represented very redundantly. This opens up the possibility where such redundancy could be used for robustness to different external perturbations or mutations, by allowing a measure of “error correction” in the downstream layer (Gierer 1991). Finally, the difference between information estimates with and without X alignment implies that a noticeable fraction of biological variability across the embryos consists of rigid shifts of the full gap gene expression pattern along the AP axis. This suggests that the biological system cares less about the absolute position of each nucleus in the embryo and more about their relative positions (i.e., order along the AP axis). This is a topic of our future research.
Footnotes
Communicating editor: G. D. Stormo
Literature Cited
- Akam M., 1987. The molecular basis for metameric pattern in the Drosophila embryo. Development 101: 1–22. [PubMed] [Google Scholar]
- Anderson K. V., 1998. Pinning down positional information: dorsal-ventral polarity in the Drosophila embryo. Cell 95: 439–442. [DOI] [PubMed] [Google Scholar]
- Ashe H. L., Briscoe J., 2006. The interpretation of morphogen gradients. Development 133: 385–394. [DOI] [PubMed] [Google Scholar]
- Bergmann S., Sandler O., Sbarro H., Shnider S., Schejter E., et al. , 2007. Pre-steady-state decoding of the bicoid morphogen gradient. PLoS Biol. 5: e46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bökel C., Brand M., 2013. Generation and interpretation of FGF morphogen gradients in vertebrates. Curr. Opin. Genet. Dev. 23: 415–422. [DOI] [PubMed] [Google Scholar]
- Bollenbach T., Pantazis P., Kicheva A., Bÿokel C., Gonzalez-Gaitan M., et al. , 2008. Precision of the Dpp gradient. Development 135: 1137–1146. [DOI] [PubMed] [Google Scholar]
- Brunel N., Nadal J. P., 1998. Mutual information, Fisher information, and population coding. Neural Comput. 10: 1731–1757. [DOI] [PubMed] [Google Scholar]
- Cover T. M., Thomas J. A., 1991. Elements of Information Theory. John Wiley & Sons, New York. [Google Scholar]
- Crauk O., Dostatni N., 2005. Bicoid determines sharp and precise target gene expression in the Drosophila embryo. Curr. Biol. 15: 1888–1898. [DOI] [PubMed] [Google Scholar]
- Dahmann C., Oates A. C., Brand M., 2011. Boundary formation and maintenance in tissue development. Nat. Rev. Genet. 12: 43–55. [DOI] [PubMed] [Google Scholar]
- Driever W., Nüsslein-Volhard C., 1988a A gradient of Bicoid protein in Drosophila embryos. Cell 54: 83–93. [DOI] [PubMed] [Google Scholar]
- Driever W., Nüsslein-Volhard C., 1988b The Bicoid protein determines position in the Drosophila embryo in a concentration-dependent manner. Cell 54: 95–104. [DOI] [PubMed] [Google Scholar]
- Dubuis J. O., Samanta R., Gregor T., 2013a Accurate measurements of dynamics and reproducibility in small genetic networks. Mol. Syst. Biol. 9: 639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubuis J. O., Tkačik G., Wieschaus E. F., Gregor T., Bialek W., 2013b Positional information, in bits. Proc. Natl. Acad. Sci. USA 110: 16301–16308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fakhouri W. D., Ay A., Sayal R., Dresch J., Dayringer E., et al. , 2010. Deciphering a transcriptional regulatory code: modeling short-range repression in the Drosophila embryo. Mol. Syst. Biol. 6: 341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrandon D., Elphick L., Nüsslein-Volhard C., St Johnston D., 1994. Staufen protein associates with the 3′UTR of bicoid mRNA to form particles that move in a microtuble-dependent manner. Cell 79: 1221–1232. [DOI] [PubMed] [Google Scholar]
- Fowlkes C. C., Hendriks C. L. L., Keränen S. V. E., Weber G. H., Rübel O., et al. , 2008. A quantitative spatiotemporal atlas of gene expression in the Drosophila blastoderm. Cell 133: 364–374. [DOI] [PubMed] [Google Scholar]
- French V., Bryant P. J., Bryant S. V., 1976. Pattern regulation in epimorphic fields. Science 193: 969–981. [DOI] [PubMed] [Google Scholar]
- Gergen, J. P., D. Coulter, and E. F. Wieschaus, 1986 Segmental pattern and blastoderm cell identities, pp. 195–220 in Gametogenesis and The Early Embryo, edited by J. G. Gall. Alan R. Liss, New York. [Google Scholar]
- Gierer A., 1991. Regulation and reproducibility of morphogenesis. Semin. Dev. Biol. 2: 83–93. [Google Scholar]
- Gregor T., Tank D. W., Wieschaus E. F., Bialek W., 2007a Probing the limits to positional information. Cell 130: 153–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregor T., Wieschaus E. F., McGregor A. P., Bialek W., Tank D. W., 2007b Stability and nuclear dynamics of the bicoid morphogen gradient. Cell 130: 141–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossniklaus U., Cadigan K. M., Gehring W. J., 1994. Three maternal coordinate systems cooperate in the patterning of the Drosophila head. Development 120: 3155–3171. [DOI] [PubMed] [Google Scholar]
- Houchmandzadeh B., Wieschaus E., Leibler S., 2002. Establishment of developmental precision and proportions in the early Drosophila embryo. Nature 415: 798–802. [DOI] [PubMed] [Google Scholar]
- Ingham P. W., 1988. The molecular genetics of embryonic pattern formation in Drosophila. Nature 335: 25–34. [DOI] [PubMed] [Google Scholar]
- Jaeger J., 2011. The gap gene network. Cell. Mol. Life Sci. 68: 243–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaeger J., Reinitz J., 2006. On the dynamic nature of positional information. BioEssays 28: 1102–1111. [DOI] [PubMed] [Google Scholar]
- Kirschner M., Gerhart J., 1997. Cells, Embryos and Evolution. Blackwell Science, Malden, MA. [Google Scholar]
- Krotov D., Dubuis J. O., Gregor T., Bialek W., 2013. Morphogenesis at criticality. Proc. Natl. Acad. Sci. USA 111: 6301–6308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagarias J. C., Reeds J. A., Wright M. H., Wright P. E., 1998. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J. Optim. 9: 112–147. [Google Scholar]
- Lawrence P. A., 1992. The Making of a Fly: The Genetics of Animal Design. Blackwell Scientific, Oxford. [Google Scholar]
- Lawrence P. A., Johnston P., 1989. Pattern formation in the Drosophila embryo: allocation of cells to parasegments by even-skipped and fushi tarazu. Development 105: 761–767. [DOI] [PubMed] [Google Scholar]
- Little S. C., Tkačik G., Kneeland T. B., Wieschaus E. F., Gregor T., 2011. The formation of the bicoid morphogen gradient requires protein movement from anteriorly localized mRNA. PLoS Biol. 9: e1000596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little S. C., Tikhonov M., Gregor T., 2013. Precise developmental gene expression arises from globally stochastic transcriptional activity. Cell 154: 789–800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu F., Morrison A. H., Gregor T., 2013. Dynamic interpretation of maternal inputs by the Drosophila segmentation gene network. Proc. Natl. Acad. Sci. USA 110: 6724–6729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopes F. J., Spirov A. V., Bisch P. M., 2012. The role of Bicoid cooperative binding in the patterning of sharp borders in Drosophila melanogaster. Dev. Biol. 370: 165–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinhardt H., 1983. A boundary model for pattern formation in vertebrate limbs. J. Embryol. Exp. Morphol. 76: 115–137. [PubMed] [Google Scholar]
- Meinhardt H., 1988. Models for maternally supplied positional information and the activation of segmentation genes in Drosophila embryogenesis. Development 104: 95–110. [Google Scholar]
- Myasnikova E., Samsonova A., Kozlov K., Samsonova M., Reinitz J., 2001. Registration of the expression patterns of Drosophila segmentation genes by two independent methods. Bioinformatics 17: 3–12. [DOI] [PubMed] [Google Scholar]
- Myasnikova E., Surkova S., Panok L., Samsonova M., Reinitz J., 2009. Estimation of errors introduced by confocal imaging into the data on segmentation gene expression in Drosophila. Bioinformatics 25: 346–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newey, W. K., and K. D. West, 1986 A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. NBER Technical Working Paper N 55. National Bureau of Economic Research, Cambridge, MA.
- Nüsslein-Volhard C., 1991. Determination of the embryonic axes of Drosophila. Development 1(Suppl): 1–10. [PubMed] [Google Scholar]
- Nüsslein-Volhard C., Wieschaus E. F., 1980. Mutations affecting segment number and polarity in Drosophila. Nature 287: 795–801. [DOI] [PubMed] [Google Scholar]
- Okabe-Oho Y., Murakami H., Oho S., Sasai M., 2009. Stable, precise, and reproducible patterning of bicoid and hunchback molecules in the early Drosophila embryo. PLoS Comput. Biol. 5: e1000486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paninski L., 2003. Estimation of entropy and mutual information. Neural Comput. 15: 1191–1253. [Google Scholar]
- Papatsenko D., 2009. Stripe formation in the early fly embryo: principles, models, and networks. BioEssays 31: 1172–1180. [DOI] [PubMed] [Google Scholar]
- Pinheiro J. C., Bates D. M., 2007. Unconstrained parametrizations for variance-covariance matrices. Stat. Comput. 6: 289–296. [Google Scholar]
- Pourquie O., 2001. The vertebrate segmentation clock. J. Anat. 199: 169–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinitz J., Mjolsness E., Sharp D. H., 1995. Model for cooperative control of positional information in Drosophila by bicoid and maternal hunchback. J. Exp. Zool. 271: 47–56. [DOI] [PubMed] [Google Scholar]
- Schier A. F., Talbot W. S., 2005. Molecular genetics of axis formation in zebrafish. Annu. Rev. Genet. 39: 561–613. [DOI] [PubMed] [Google Scholar]
- Shannon, C. E., 1948 A mathematical theory of communication. Bell Syst. Tech. J. 27: 379–423, 623–656.
- Siggia E. D., 2008. Developmental regulatory bits. Mol. Syst. Biol. 4: 226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slonim, N., G. S. Atwal, G. Tkačik, and W. Bialek, 2005 Estimating mutual information and multi–information in large networks. arXiv.org: cs.IT/0502017.
- Spradling A., 1993. The Development of Drosophila melanogaster, edited by Arias M. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY. [Google Scholar]
- Stein, C., 1956 Some problems in multivariate analysis, part I. Technical Report 6. Department of Statistics, Stanford University, Stanford, CA.
- St. Johnston D., Nüsslein-Volhard C., 1992. The origin of pattern and polarity in the Drosophila embryo. Cell 68: 201–219. [DOI] [PubMed] [Google Scholar]
- Strong S. P., Koberle R., de Ruyter van Steveninck R. R., Bialek W., 1998. Entropy and information in neural spike trains. Phys. Rev. Lett. 80: 197–200. [Google Scholar]
- Struhl G., Struhl K., Macdonald P. M., 1989. The gradient morphogen Bicoid is a concentration-dependent transcriptional activator. Cell 57: 1259–1273. [DOI] [PubMed] [Google Scholar]
- Surkova S., Kosman D., Kozlov K., Manu, E. Myasnikova et al, 2008. Characterization of the Drosophila segment determination morphome. Dev. Biol. 313: 844–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tickle C., Summerbell D., Wolpert L., 1975. Positional signaling and specification of digits in chick limb morphogenesis. Nature 254: 199–202. [DOI] [PubMed] [Google Scholar]
- Tkačik G., Callan C. G., Jr, Bialek W., 2008. Information flow and optimization in transcriptional regulation. Proc. Natl. Acad. Sci. USA 105: 12265–12270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tkačik G., Walczak A. M., Bialek W., 2009. Optimizing information flow in small genetic networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 80: 031920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tkačik G., Prentice J. S., Balasubramanian V., Schneidman E., 2010. Optimal population coding by noisy spiking neurons. Proc. Natl. Acad. Sci. USA 107: 14419–14424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomancak P., Berman B., Beaton A., Weiszmann R., Kwan E., et al. , 2007. Global analysis of patterns of gene expression during Drosophila embryogenesis. Genome Biol. 8: R145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsimring L. S., 2014. Noise in biology. Rep. Prog. Phys. 77: 026601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turing A. M., 1952. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 237: 37–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Kampen N., 2011. Stochastic Processes in Physics and Chemistry, Ed. 3 North Holland, Amsterdam. [Google Scholar]
- von Dassow G., Meir E., Munro E. M., Odell G. M., 2000. The segment polarity network is a robust developmental module. Nature 406: 188–192. [DOI] [PubMed] [Google Scholar]
- Walczak A. M., Tkačik G., Bialek W., 2010. Optimizing information flow in small genetic networks. II. Feed-forward interactions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 81: 041905. [DOI] [PubMed] [Google Scholar]
- Witchley J. N., Mayer M., Wagner D. E., Owen J. H., Reddien P. W., 2013. Muscle cells provide instructions for planarian regeneration. Cell Rep. 4: 633–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolpert L., 1969. Positional information and the spatial pattern of cellular differentiation. J. Theor. Biol. 25: 1–47. [DOI] [PubMed] [Google Scholar]
- Wolpert L., 2011. Positional information and patterning revisited. J. Theor. Biol. 269: 359–365. [DOI] [PubMed] [Google Scholar]
- Zhang L., Radtke K., Zheng L., Cai A. Q., Schilling T. F., et al. , 2012. Noise drives sharpening of gene expression boundaries in the zebrafish hindbrain. Mol. Syst. Biol. 8: 613. [DOI] [PMC free article] [PubMed] [Google Scholar]