Endogeneity in High Dimensions

Abstract

Most papers on high-dimensional statistics are based on the assumption that none of the regressors are correlated with the regression error, namely, they are exogenous. Yet, endogeneity can arise incidentally from a large pool of regressors in a high-dimensional regression. This causes the inconsistency of the penalized least-squares method and possible false scientific discoveries. A necessary condition for model selection consistency of a general class of penalized regression methods is given, which allows us to prove formally the inconsistency claim. To cope with the incidental endogeneity, we construct a novel penalized focused generalized method of moments (FGMM) criterion function. The FGMM effectively achieves the dimension reduction and applies the instrumental variable methods. We show that it possesses the oracle property even in the presence of endogenous predictors, and that the solution is also near global minimum under the over-identification assumption. Finally, we also show how the semi-parametric efficiency of estimation can be achieved via a two-step approach.

1. Introduction

In high-dimensional models, the overall number of regressors p grows extremely fast with the sample size n. It can be of order exp(n^α), for some α ∈ (0, 1). What makes statistical inference possible is the sparsity and exogeneity assumptions. For example, in the linear model

$$Y={\mathbf{X}}^T{\mathit{\beta }}_0+\epsilon ,$$ (1.1)

it is assumed that the number of elements in S = {j : β_0j ≠ 0} is small and EεX = 0, or more stringently

$$E(\epsilon |\mathbf{X})=E(Y-{\mathbf{X}}^T{\mathit{\beta }}_0|\mathbf{X})=0.$$ (1.2)

The latter is called “exogeneity”. One of the important objectives of high-dimensional modeling is to achieve the variable selection consistency and make inference on the coefficients of important regressors. See, for example, Fan and Li (2001), Hunter and Li (2005), Zou (2006), Zhao and Yu (2006), Huang, Horowitz and Ma (2008), Zhang and Huang (2008), Wasserman and Roeder (2009), Lv and Fan (2009), Zou and Zhang (2009), Städler, Bühlmann and van de Geer (2010), and Bühlmann, Kalisch and Maathuis (2010). In these papers, (1.2) (or EεX = 0) has been assumed either explicitly or implicitly¹. Condition of this kind is also required by the Dantzig selector of Candès and Tao (2007), which solves an optimization problem with constraint ${max}_{j\le p}|\frac{1}{n}{\sum }_{i=1}^n{X}_{ij}(Y_i-{\mathbf{X}}_i^T\mathit{\beta })|<C\sqrt{\frac{logp}{n}}$ for some C > 0.

In high-dimensional models, requesting that ε and all the components of X be uncorrelated as (1.2), or even more specifically

$$E(Y-{\mathbf{X}}^T{\mathit{\beta }}_0)X_j=0,\forall j=1,\dots ,p,$$ (1.3)

can be restrictive particularly when p is large. Yet, (1.3) is a necessary condition for popular model selection techniques to be consistent. However, violations to assumption either (1.2) or (1.3) can arise as a result of selection biases, measurement errors, autoregression with autocorrelated errors, omitted variables, and from many other sources (Engle, Hendry and Richard 1983). They also arise from unknown causes due to a large pool of regressors, some of which are incidentally correlated with the random noise Y−X^Tβ₀. For example, in genomics studies, clinical or biological outcomes along with expressions of tens of thousands of genes are frequently collected. After applying variable selection techniques, scientists obtain a set of genes Ŝ that are responsible for the outcome. Whether (1.3) holds, however, is rarely validated. Because there are tens of thousands of restrictions in (1.3) to validate, it is likely that some of them are violated. Indeed, unlike low-dimensional least-squares, the sample correlations between residuals ∊̂, based on the selected variables X_Ŝ, and predictors X, are unlikely to be small, because all variables in the large set Ŝ^c are not even used in computing the residuals. When some of those are unusually large, endogeneity arises incidentally. In such cases, we will show that Ŝ can be inconsistent. In other words, violation of assumption (1.3) can lead to false scientific claims.

We aim to consistently estimate β₀ and recover its sparsity under weaker conditions than (1.2) or (1.3) that are easier to validate. Let us assume that ${\mathit{\beta }}_0={({\mathit{\beta }}_{0S}^T,0)}^T$ and X can be partitioned as $\mathbf{X}={({\mathbf{X}}_S^T,{\mathbf{X}}_N^T)}^T$. Here X_S corresponds to the nonzero coefficients β_0S, which we call important regressors, and X_N represents the unimportant regressors throughout the paper, whose coefficients are zero. We borrow the terminology of endogeneity from the econometric literature. A regressor is said to be endogenous when it is correlated with the error term, and exogenous otherwise. Motivated by the aforementioned issue, this paper aims to select X_S with probability approaching one and making inference about β_0S, allowing components of X to be endogenous. We propose a unified procedure that can address the problem of endogeneity to be present in either important or unimportant regressors, or both, and we do not require the knowledge of which case of endogeneity is present in the true model. The identities of X_S are unknown before the selection.

The main assumption we make is that, there is a vector of observable instrumental variables W such that

$$E[\epsilon |\mathbf{W}]=0.$$ (1.4)

²

Briefly speaking, W is called an “instrumental variable” when it satisfies (1.4) and is correlated with the explanatory variable X. In particular, as noted in the footnote, W = X_S is allowed so that the instruments are unknown but no additional data are needed. Instrumental variables (IV) have been commonly used in the literature of both econometrics and statistics in the presence of endogenous regressors, to achieve identification and consistent estimations (e.g., Hall and Horowitz 2005). An advantage of such an assumption is that it can be validated more easily. For example, when W = X_S, one needs only to check whether the correlations between ∊̂ and X_Ŝ are small or not, with X_Ŝ being a relatively low-dimensional vector, or more generally, the moments that are actually used in the model fitting such as (1.5) below hold approximately In short, our setup weakens the assumption (1.2) to some verifiable moment conditions.

What makes the variable selection consistency (with endogeneity) possible is the idea of over identification. Briefly speaking, a parameter is called “over-identified” if there are more restrictions than those are needed to grant its identifiability (for linear models, for instance, when the parameter satisfies more equations than its dimension). Let (f₁,…, f_p) and (h₁,…, h_p) be two different sets of transformations, which can be taken as a large number of series terms, e.g., B-splines and polynomials. Here each f_j and h_j are scalar functions. Then (1.4) implies

$$E(\epsilon f_j(\mathbf{W}))=E(\epsilon h_j(\mathbf{W}))=0,j=1,\dots ,p.$$

Write F = (f₁(W),…, f_p(W))^T, and H = (h₁(W),…, h_p(W))^T. We then have EεF = EεH = 0. Let S be the set of indices of important variables, and let F_S and H_S be the subvectors of F and H corresponding to the indices in S. Implied by EεF = EεH = 0, and $\epsilon =Y-{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}$, there exists a solution β_S = β_0S to the over-identified equations (with respect to β_S) such as

$$E(Y-{\mathbf{X}}_S^T{\mathit{\beta }}_S){\mathit{F}}_S=0\text{and}E(Y-{\mathbf{X}}_S^T{\mathit{\beta }}_S){\mathit{H}}_S=0.$$ (1.5)

In (1.5), we have twice as many linear equations as the number of unknowns, yet the solution exists and is given by β_S = β_0S. Because β_0S satisfies more equations than its dimension, we call β_0S to be over-identified. On the other hand, for any other set S̃ of variables, if S ⊄ S̃, then the following 2|S̃| equations (with |S̃| = dim(β_S̃) unknowns)

$$E(Y-{\mathbf{X}}_{\stackrel{\sim }{S}}^T{\mathit{\beta }}_{\stackrel{\sim }{S}}){\mathbf{F}}_{\stackrel{\sim }{S}}=0\text{and}E(Y-{\mathbf{X}}_{\stackrel{\sim }{S}}^T{\mathit{\beta }}_{\stackrel{\sim }{S}}){\mathit{H}}_{\stackrel{\sim }{S}}=0$$ (1.6)

have no solution as long as the basis functions are chosen such that F_S̃ ≠ H _S̃.³ The above setup includes W = X_S with F = X and H = X² as a specific example (or H = cos(X) + 1 if X contain many binary variables).

We show that in the presence of endogenous regressors, the classical penalized least squares method is no longer consistent. Under model

$$Y={\mathbf{X}}_S^T{\mathit{\beta }}_{0S}+\epsilon ,E(\epsilon |\mathbf{W})=0,$$

we introduce a novel penalized method, called focused generalized method of moments (FGMM), which differs from the classical GMM (Hansen 1982) in that the working instrument V(β) in the moment functions $n^{-1}{\sum }_{i=1}^n(Y_i-{\mathbf{X}}_i^T\mathit{\beta })\mathbf{V}(\mathit{\beta })$ for FGMM also depends irregularly on the unknown parameter β (which also depends on (F, H), see Section 3 for details). With the help of over identification, the FGMM successfully eliminates those subset S̃ such that S ⊄ S̃. As we will see in Section 3, a penalization is still needed to avoid over-fitting. This results in a novel penalized FGMM.

We would like to comment that FGMM differs from the low-dimensional techniques of either moment selection (Andrews 1999, Andrews and Lu 2001) or shrinkage GMM (Liao 2013) in dealing with mis-specifications of moment conditions and dimension reductions. The existing methods in the literature on GMM moment selections cannot handle high-dimensional models. Recent literature on the instrumental variable method for high-dimensional models can be found in, e.g., Belloni et al. (2012), Caner and Fan (2012), García (2011). In these papers, the endogenous variables are in low dimensions. More closely related work is by Gautier and Tsybakov (2011), who solved a constrained minimization as an extension of Dantzig selector. Our paper, in contrast, achieves the oracle property via a penalized GMM. Also, we study a more general conditional moment restricted model that allows nonlinear models.

The remainder of this paper is as follows: Section 2 gives a necessary condition for a general penalized regression to achieve the oracle property. We also show that in the presence of endogenous regressors, the penalized least squares method is inconsistent. Sections 3 constructs a penalized FGMM, and discusses the rationale of our construction. Section 4 shows the oracle property of FGMM. Section 5 discusses the global optimization. Section 6 focuses on the semi-parametric efficient estimation after variable selection. Section 7 discusses numerical implementations. We present simulation results in Section 8. Finally, Section 9 concludes. Proofs are given in the appendix.

Notation

Throughout the paper, let λ_min(A) and λ_max(A) be the smallest and largest eigenvalues of a square matrix A. We denote by ‖A‖_F, ‖A‖ and ‖A‖_∞ as the Frobenius, operator and element-wise norms of a matrix A respectively, defined respectively as ‖A‖_F = tr^1/2(A^T A), $\Vert \mathbf{A}\Vert ={\lambda }_{max}^{1/2}({\mathbf{A}}^T\mathbf{A})$, and ‖A‖_∞ = max_i,j ‖A_ij‖. For two sequences a_n and b_n, write a_n ≪ b_n (equivalently, b_n ≫ a_n) if a_n = o(b_n). Moreover, |β|₀ denotes the number of nonzero components of a vector β. Finally, $P_n^{\prime }(t)$ and $P_n^{″}(t)$ denote the first and second derivatives of a penalty function P_n(t), if exist.

2. Necessary Condition for Variable Selection Consistency

2.1. Penalized regression and necessary condition

Let s denote the dimension of the true vector of nonzero coefficients β_0S. The sparse structure assumes that s is small compared to the sample size. A penalized regression problem, in general, takes a form of:

$$\underset{\beta \in {ℝ}^p}{min}{L}_n(\mathit{\beta })+\sum _{j=1}^p{P}_n(|{\beta }_j|),$$

where P_n(·) denotes a penalty function. There are relatively less attentions to the necessary conditions for the penalized estimator to achieve the oracle property. Zhao and Yu (2006) derived an almost necessary condition for the sign consistency, which is similar to that of Zou (2006) for the least squares loss with Lasso penalty. To the authors' best knowledge, so far there has been no necessary condition on the loss function for the selection consistency in the high-dimensional framework. Such a necessary condition is important, because it provides us a way to justify whether a specific loss function can result in a consistent variable selection.

Theorem 2.1 (Necessary Condition)

Suppose:

1. L_n(β) is twice differentiable, and

   $$\underset{1\le l,j\le p}{max}\left|\frac{{\partial }^2{L}_n({\mathit{\beta }}_0)}{\partial {\beta }_l\partial {\beta }_j}\right|=O_p(1).$$

2. There is a local minimizer β̂ = (β̂_S, β̂_N)^T of

   $$L_n(\mathit{\beta })+\sum _{j=1}^p{P}_n(|{\beta }_j|)$$

   such that P(β̂_N = 0) → 1, and √s ‖β̂ − β₀‖ = o_p(1).

3. The penalty satisfies: P_n(·) ≥ 0, P_n(0) = 0, $P_n^{\prime }(t)$ is non-increasing when t ∈ (0, u) for some u > 0, and ${lim}_{n\to \infty }{lim}_{t\to 0^{+}}{P}_n^{\prime }(t)=0$. Then for any l ≤ p,

$$\left|\frac{\partial L_n({\mathit{\beta }}_0)}{\partial {\beta }_l}\right|{\to }^{p}0.$$ (2.1)

The implication (2.1) is fundamentally different from the “irrepresentable condition” in Zhao and Yu (2006) and that of Zou (2006). It imposes a restriction on the loss function L_n(·), whereas the “irrepresentable condition” is derived under the least squares loss and E(εX) = 0. For the least squares, (2.1) reduces to either $n^{-1}{\sum }_{i=1}^n{\epsilon }_i{X}_{il}=o_p(1)$ or EεX_l = 0, which requires a exogenous relationship between ε and X. In contrast, the irrepresentable condition requires a type of relationship between important and unimportant regressors and is specific to Lasso. It also differs from the Karush-Kuhn-Tucker (KKT) condition (e.g., Fan and Lv 2011) in that it is about the gradient vector evaluated at the true parameters rather than at the local minimizer.

The conditions on the penalty function in condition (iii) are very general, and are satisfied by a large class of popular penalties, such as Lasso (Tibshirani 1996), SCAD (Fan and Li 2001) and MCP (Zhang 2010), as long as their tuning parameter λ_n → 0. Hence this theorem should be understood as a necessary condition imposed on the loss function instead of the penalty.

2.2. Inconsistency of least squares with endogeneity

As an application of Theorem 2.1, consider a linear model:

$$Y={\mathbf{X}}^T{\mathit{\beta }}_0+\epsilon ={\mathbf{X}}_S^T{\mathit{\beta }}_{0S}+\epsilon ,$$ (2.2)

where we may not have E(εX) = 0.

The conventional penalized least squares (PLS) problem is defined as:

$$\underset{\mathit{\beta }}{min}\frac{1}{n}\sum _{i=1}^n{(Y_i-{\mathbf{X}}_i^T\mathit{\beta })}^2+\sum _{j=1}^p{P}_n(|{\beta }_j|).$$

In the simpler case when s, the number of nonzero components of β₀, is bounded, it can be shown that if there exist some regressors correlated with the regression error ε, the PLS does not achieve the variable selection consistency. This is because (2.1) does not hold for the least squares loss function. Hence without the possibly ad-hoc exogeneity assumption, PLS would not work any more, as more formally stated below.

Theorem 2.2 (Inconsistency of PLS)

Suppose the data are i.i.d., s = O(1), and X has at least one endogenous component, that is, there is l such that |E(X_lε)| > c for some c > 0. Assume that $E{X}_l^4<\infty$, Eε⁴ < ∞, and P_n (t) satisfies the conditions in Theorem 2.1. If $\stackrel{\sim }{\mathit{\beta }}={({\stackrel{\sim }{\mathit{\beta }}}_S^T,{\stackrel{\sim }{\mathit{\beta }}}_N^T)}^T$, corresponding to the coefficients of (X_S, X_N), is a local minimizer of

$$\frac{1}{n}\sum _{i=1}^n{(Y_i-{\mathbf{X}}_i^T\mathit{\beta })}^2+\sum _{j=1}^p{P}_n(|{\beta }_j|),$$

then either ‖β̃_S – β_0S ‖ = o_p(1), or lim sup_n→∞ P(β̃_N = 0) < 1.

The index l in the condition of the above theorem does not have to be an index of an important regressor. Hence the consistency for penalized least squares will fail even if the endogeneity is only present on the unimportant regressors.

We conduct a simple simulated experiment to illustrate the impact of endogeneity on the variable selection. Consider

$$\begin{array}{c}Y={\mathbf{X}}^T{\mathit{\beta }}_0+\epsilon ,\epsilon ~N(0,1),\\ {\mathit{\beta }}_{0S}=(5,-4,7,-2,1.5);{\beta }_{0j}=0,\text{for}6\le j\le p.\\ X_j=Z_j\text{for}j\le 5,X_j=(Z_j+5)(1+∊),\text{for}6\le j\le p.\\ Z~N_p(0,\sum ),\text{independent of}\epsilon ,\text{with}{(\sum )}_{ij}={0.5}^{|i-j|}.\end{array}$$

In the design, the unimportant regressors are endogenous. The penalized least squares (PLS) with SCAD-penalty was used for variable selection. The λ's in the table represent the tuning parameter used in the SCAD-penalty. The results are based on the estimated ${({\widehat{\mathit{\beta }}}_S^T,{\widehat{\mathit{\beta }}}_N^T)}^T$, obtained from minimizing PLS and FGMM loss functions respectively (we shall discuss the construction of FGMM loss function and its numerical minimization in detail subsequently). Here β̃_S and β̂_N represent the estimators for coefficients of important and unimportant regressors respectively.

From Table 1, PLS selects many unimportant regressors (FP). In contrast, the penalized FGMM performs well in both selecting the important regressors and eliminating the unimportant ones. Yet, the larger MSE_S of β̂_S by FGMM is due to the moment conditions used in the estimate. This can be improved further in Section 6. Also, when endogeneity is present on the important regressors, PLS estimator will have larger bias (see additional simulation results in Section 8.)

Table 1.

Performance of PLS and FGMM over 100 replications. p = 50, n = 200

	PLS				FGMM
	λ = 0.05	λ = 0.1	λ = 0.5	λ = 1	λ = 0.05	λ = 0.1	λ = 0.2
MSES	0.145 (0.053)	0.133 (0.043)	0.629 (0.301)	1.417 (0.329)	0.261 (0.094)	0.184 (0.069)	0.194 (0.076)
MSEN	0.126 (0.035)	0.068 (0.016)	0.072 (0.016)	0.095 (0.019)	0.001 (0.010)	0 (0)	0.001 (0.009)
TP	5 (0)	5 (0)	4.82 (0.385)	3.63 (0.504)	5 (0)	5 (0)	5 (0)
FP	37.68 (2.902)	35.36 (3.045)	8.84 (3.334)	2.58 (1.557)	0.08 (0.337)	0 (0)	0.02 (0.141)

MSE_S is the average of ‖β̂_S − β_0S‖ for nonzero coefficients. MSE_N is the average of ‖β̂_N − β_0N‖ for zero coefficients. TP is the number of correctly selected variables, and FP is the number of incorrectly selected variables. The standard error of each measure is also reported.

3. Focused GMM

3.1. Definition

Because of the presence of endogenous regressors, we introduce an instrumental variable (IV) regression model. Consider a more general nonlinear model:

$$E[g(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S})|\mathbf{W}]=0,$$ (3.1)

where Y stands for the dependent variable; g :ℝ × ℝ → ℝ is a known function. For simplicity, we require g be one-dimensional, and should be thought of as a possibly nonlinear residual function. Our result can be naturally extended to a multi-dimensional g function. Here W is a vector of observed random variables, known as instrumental variables.

Model (3.1) is called a conditional moment restricted model, which has been extensively studied in the literature, e.g., Newey (1993), Donald et al. (2009), Kitamura et al (2004). The high-dimensional model is also closely related to the semi/nonparametric model estimated by sieves with a growing sieve dimension, e.g., Ai and Chen (2003). Recently van de Geer (2008) and Fan and Lv (2011) considered generalized linear models without endogeneity. Some interesting examples of the generalized linear model that fit into (3.1) are:

• linear regression, g(t₁, t₂) = t₁ − t₂;

• logit model, g(t₁, t₂) = t₁ − exp(t₂)/(1 + exp(t₂));

• probit model, g(t₁, t₂) = t₁ − Φ(t₂) where Φ(·) denotes the standard normal cumulative distribution function.

Let (f₁, …, f_p) and (h₁,…, h_p) be two different sets of transformations of W, which can be taken as a large number of series basis, e.g., B-splines, Fourier series, polynomials (see Chen 2007 for discussions of the choice of sieve functions). Here each f_j and h_j are scalar functions. Write F = (f₁(W),…, f_p(W))^T, and H = (h₁(W),…, h_p(W))^T. The conditional moment restriction (3.1) then implies that

$$E[g(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{F}}_S]=0,\text{and}E[g(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{H}}_S]=0,$$ (3.2)

where F_S and H_S are the subvectors of F and H whose supports are on the oracle set S = {j ≤ p : β_0j ≠ 0}. In particular, when all the components of X_S are known to be exogenous, we can take F = X and H = X² (the vector of squares of X taken coordinately), or H = cos(X) + 1 if X is a binary variable. A typical estimator based on moment conditions like (3.2) can be obtained via the generalized method of moments (GMM, Hansen 1982). However, in the problem considered here, (3.2) cannot be used directly to construct the GMM criterion function, because the identities of X_S are unknown.

Remark 3.1

One seemingly working solution is to define V as a vector of transformations of W, for instance V = F, and employ GMM to the moment condition E[g(Y, X^T β₀)V] = 0. However, one has to take dim(V) ≥ dim(β) = p to guarantee that the GMM criterion function has a unique minimizer (in the linear model for instance). Due to p ≫ n, the dimension of V is too large, and the sample analogue of the GMM criterion function may not converge to its population version due to the accumulation of high-dimensional estimation errors.

Let us introduce some additional notation. For any β ∈ ℝ^p/{0}, and i = 1, …, n, define r = |β|₀-dimensional vectors

F_i(β) = (f_l1(W_i),…, f_lr(W_i))^T and H_i(β) = (h_l1(W_i),…, h_lr(W_i))^T, where (l₁, …, l_r) are the indices of nonzero components of β. For example, if p = 3 and β = (−1, 0, 2)^T, then F_i(β) = (f₁(W_i), f₃(W_i))^T, and H_i(β) = (h₁(W_i), h₃(W_i))^T, i ≤ n.

Our focused GMM (FGMM) loss function is defined as

$$L_{\text{FGMM}}(\mathit{\beta })=\sum _{j=1}^p{I}_{({\beta }_j\ne 0)}\{w_{j1}{[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta })f_j({\mathbf{W}}_i)]}^2+w_{j2}{[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta })h_j({\mathbf{W}}_i)]}^2\},$$ (3.3)

where w_j1 and w_j2 are given weights. For example, we will take $w_{j1}=1/\widehat{var}(f_j(\mathbf{W}))$ and $w_{j2}=1/\widehat{var}(h_j(\mathbf{W}))$ to standardize the scale (here $\widehat{var}$ represents the sample variance). Writing in the matrix form, for V_i(β) = (F_i(β^T,H _i(β)^T)^T,

$$L_{\text{FGMM}}(\mathit{\beta })={[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{V}}_i(\mathit{\beta })]}^T\mathbf{J}(\mathit{\beta })[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{V}}_i(\mathit{\beta })],$$

where J(β) = diag{w_l11, …, w_lr1, w_l12, …, w_lr2}.⁴

Unlike the traditional GMM, the “working instrumental variables” V(β) depend irregularly on the unknown β. As to be further explained, this ensures the dimension reduction, and allows to focus only on the equations with the IV whose support is on the oracle space, and is therefore called the focused GMM or FGMM for short.

We then define the FGMM estimator by minimizing the following criterion function:

$$Q_{\text{FGMM}}(\mathit{\beta })=L_{\text{FGMM}}(\mathit{\beta })+\sum _{j=1}^p{P}_n(|{\beta }_j|).$$ (3.4)

Sufficient conditions on the penalty function P_n(|β_j|) for the oracle property will be presented in Section 4. Penalization is needed because otherwise small coefficients in front of unimportant variables would be still kept in minimizing L_FGMM (β). As to become clearer in Section 6, the FGMM focuses on the model selection and estimation consistency without paying much effort to the efficient estimation of β_0S.

3.2. Rationales behind the construction of FGMM

3.2.1. Inclusion of V(β)

We construct the FGMM criterion function using

$$\mathbf{V}(\mathit{\beta })={(\mathbf{F}{(\mathit{\beta })}^T,\mathbf{H}{(\mathit{\beta })}^T)}^T.$$

A natural question arises: why not just use one set of IV's so that V(β) = F(β)? We now explain the rationale behind the inclusion of the second set of instruments H(β). To simplify notation, let F_ij = f_j(W_i) and H_ij = h_j(W_i) for j ≤ p and i ≤ n. Then F_i = (F_i1,…, F_ip) and H_i = (H_i1,…, H_ip). Also write F_j = f_j (W) and H_j = h_j (W) for j ≤ p.

Let us consider a linear regression model (2.2) as an example. If H(β) were not included and V(β) = F(β) had been used, the GMM loss function would have been constructed as

$$L_v(\mathit{\beta })={\Vert \frac{1}{n}\sum _{i=1}^n(Y_i-{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{F}}_i(\mathit{\beta })\Vert }^2,$$ (3.5)

where for the simplicity of illustration, J(β) is taken as an identity matrix. We also use the L₀-penalty P_n(|β_j|) = λ_nI_(|βj|≠0) for illustration. Suppose that the true ${\mathit{\beta }}_0={({\mathit{\beta }}_{0S}^T,0,\dots ,0)}^T$ where only the first s components are nonzero and that s > 1. If we, however, restrict ourselves to β_p = (0, …, 0, β_p), the criterion function now becomes

$$Q_{\text{FGMM}}({\mathit{\beta }}_p)={[\frac{1}{n}\sum _{i=1}^n(Y_i-X_{ip}{\beta }_p)F_{ip}]}^2+{\lambda }_n.$$

It is easy to see its minimum is just λ_n. On the other hand, if we optimize Q_FGMM on the oracle space $\mathit{\beta }={({\mathit{\beta }}_S^T,0)}^T$, then

$$\underset{\mathit{\beta }={({\mathit{\beta }}_S^T,0)}^T,{\mathit{\beta }}_{S,j}\ne 0}{min}{Q}_{\text{FGMM}}(\mathit{\beta })\ge s{\lambda }_n.$$

As a result, it is inconsistent for variable selection.

The use of L₀-penalty is not essential in the above illustration. The problem is still present if the L₁-penalty is used, and is not merely due to the biasedness of L₁-penalty. For instance, recall that for the SCAD penalty with hyper parameter (a, λ_n), P_n(·) is non-decreasing, and $P_n(t)=\frac{(a+1)}{2}{\lambda }_n^2$ when t ≥ aλ_n. Given that min_j∈S|β_0j|≫λ_n,

$$Q_{\text{FGMM}}({\mathit{\beta }}_0)\ge \sum _{j\in S}{P}_n(|{\beta }_{0j}|)\ge s{P}_n(\underset{j\in S}{min}|{\beta }_{0j}|)=\frac{(a+1)}{2}{\lambda }_n^{2}s.$$

On the other hand, $Q_{\text{FGMM}}({\mathit{\beta }}_p^{\ast })=P_n(|{\beta }_p^{\ast }|)\le \frac{(a+1)}{2}{\lambda }_n^2$ which is strictly less than Q_FGMM(β₀). So the problem is still present when an asymptotically unbiased penalty (e.g., SCAD, MCP) is used.

Including an additional term H(β) in V(β) can overcome this problem. For example, if we still restrict to β_p = (0,…, β_p) but include an additional but different IV H_ip, the criterion function then becomes, for the L₀ penalty:

$$Q_{\text{FGMM}}({\mathit{\beta }}_p)={[\frac{1}{n}\sum _{i=1}^n(Y_i-X_{ip}{\beta }_p)F_{ip}]}^2+{[\frac{1}{n}\sum _{i=1}^n(Y_i-X_{ip}{\beta }_p)H_{ip}]}^2+{\lambda }_n.$$

In general, the first two terms cannot achieve o_p(1) simultaneously as long as the two sets of transformations {f_j(·)} and {h_j(·)} are fixed differently. so long as n is large and

$${(E{X}_p{F}_p)}^{-1}E(Y{F}_p)\ne {(E{X}_p{H}_p)}^{-1}E(Y{H}_p).$$ (3.6)

As a result, Q_FGMM(β_p) is bounded away from zero with probability approaching one.

To better understand the behavior of Q_FGMM (β), it is more convenient to look at the population analogues of the loss function. Because the number of equations in

$$E[(Y-{\mathbf{X}}^T\mathit{\beta })\mathbf{F}(\mathit{\beta })]=0\text{and}E[(Y-{\mathbf{X}}^T\mathit{\beta })\mathbf{H}(\mathit{\beta })]=0$$ (3.7)

is twice as many as the number of unknowns (nonzero components in β), if we denote S̃ as the support of β, then (3.7) has a solution only when ${(E{\mathbf{F}}_{\stackrel{\sim }{S}}{\mathbf{X}}_{\stackrel{\sim }{S}}^T)}^{-1}E(Y{\mathbf{F}}_{\stackrel{\sim }{S}})={(E{\mathbf{H}}_{\stackrel{\sim }{S}}{\mathbf{X}}_{\stackrel{\sim }{S}}^T)}^{-1}E(Y{\mathbf{H}}_{\stackrel{\sim }{S}})$, which does not hold in general unless S̃ = S, the index set of the true nonzero coefficients. Hence it is natural for (3.7) to have a unique solution β = β₀. As a result, if we define

$$G(\mathit{\beta })={\Vert E(Y-{\mathbf{X}}^T\mathit{\beta })\mathbf{F}(\mathit{\beta })\Vert }^2+{\Vert E(Y-{\mathbf{X}}^T\mathit{\beta })\mathbf{H}(\mathit{\beta })\Vert }^2,$$

the population version of L_FGMM, then as long as β is not close to β₀, G should be bounded away from zero. Therefore, it is reasonable for us to assume that for any δ > 0, there is γ(δ) > 0 such that

$$\underset{{\Vert \mathit{\beta }-{\mathit{\beta }}_0\Vert }_{\infty }>\delta ,\mathit{\beta }\ne 0}{inf}G(\mathit{\beta })>\gamma (\delta ).$$ (3.8)

On the other hand, $E(\epsilon |\mathbf{W})=E(Y-{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}|\mathbf{W})=0$ implies G(β₀) = 0.

Our FGMM loss function is essentially a sample version of G(β), so minimizing L_FGMM(β) forces the estimator to be close to β₀, but small coefficients in front of unimportant but exogenous regressors may still be allowed. Hence a concave penalty function is added to L_FGMM to define Q_FGMM.

3.2.2. Indicator function

Another question readers may ask is that why not define L_FGMM(β) to be, for some weight matrix J,

$${[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{V}}_i]}^T\mathbf{J}[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{V}}_i],$$ (3.9)

that is, why not replace the irregular β-dependent V(β) with V, and use the entire 2p-dimensional V = (F^T, H^T)^T as the IV? This is equivalent to the question why the indicator function in (3.3) cannot be dropped.

The indicator function is used to prevent the accumulation of estimation errors under the high dimensionality. To see this, rewrite (3.9) to be:

$$\sum _{j=1}^p\frac{1}{\widehat{var}(F_j)}{(\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta })F_{ij})}^2+\frac{1}{\widehat{var}(H_j)}{(\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta })H_{ij})}^2.$$

Since dim(V_i) = 2p ≫ n, even if each individual term evaluated at β = β₀ is $O_p\left(\frac{1}{n}\right)$, the sum of p terms would become stochastically unbounded. In general, (3.9) does not converge to its population analogue when p ≫ n because the accumulation of high-dimensional estimation errors would have a non-negligible effect.

In contrast, the indicator function effectively reduces the dimension and prevents the accumulation of estimation errors. Once the indicator function is included, the proposed FGMM loss function evaluated at β₀ becomes:

$$\sum _{j\in S}\frac{1}{\widehat{var}(F_j)}{(\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T{\mathit{\beta }}_0)F_{ij})}^2+\frac{1}{\widehat{var}(H_j)}{(\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T{\mathit{\beta }}_0)H_{ij})}^2,$$

which is small because E[g(Y, X^Tβ₀)F_S] = E[g(Y, X^Tβ₀)H_S] = 0 and that there are only s = |S|₀ terms in the summation.

Recently, there has been growing literature on the shrinkage GMM, e.g., Caner (2009), Caner and Zhang (2013), Liao (2013), etc, regarding estimation and variable selection based on a set of moment conditions like (3.2). The model considered by these authors is restricted to either a low-dimensional parameter space or a low-dimensional vector of moment conditions, where there is no such a problem of error accumulations.

4. Oracle Property of FGMM

FGMM involves a non-smooth loss function. In the appendix, we develop a general asymptotic theory for high-dimensional models to accommodate the non-smooth loss function.

Our first assumption defines the penalty function we use. Consider a similar class of folded concave penalty functions as that in Fan and Li (2001).

For any β = (β₁,…, β_s)^T ∈ ℝ^s, and |β_j| ≠ 0, j = 1,…, s, define

$$\eta (\mathit{\beta })=\underset{∊\to 0^{+}}{limsup}\underset{j\le s}{max}\underset{\begin{array}{c}{t}_1<t_2\\ (t_1,t_2)\in (|{\beta }_j|-∊,|{\beta }_j|+∊)\end{array}}{sup}-\frac{P_n^{\prime }(t_2)-P_n^{\prime }(t_1)}{t_2-t_1},$$ (4.1)

which is ${max}_{j\le s}-P_n^{″}(|{\beta }_j|)$ if the second derivative of P_n is continuous. Let

$$d_n=\frac{1}{2}min\{|{\beta }_{0j}|:{\beta }_{0j}\ne 0,j=1,\dots ,p\}$$

represent the strength of signals.

Assumption 4.1

The penalty function P_n(t) : [0, ∞) → ℝ satisfies:

1. P_n(0) = 0

2. P_n(t) is concave, non-decreasing on [0, ∞), and has a continuous derivative $P_n^{\prime }(t)$ when t > 0.

3. $\sqrt{s}{P}_n^{\prime }(d_n)=o(d_n)$.

4. There exists c > 0 such that sup_{β∈B(β0S,cdn)} η(β) = o(1).

These conditions are standard. The concavity of P_n(·) implies that η(β) ≥ 0 for all β ∈ ℝ^s. It is straightforward to check that with properly chosen tuning parameters, the L_q penalty (for q ≤ 1), hard-thresholding (Antoniadis 1996), SCAD (Fan and Li 2001), and MCP (Zhang 2010) all satisfy these conditions. As thoroughly discussed by Fan and Li (2001), a penalty function that is desirable for achieving the oracle properties should result in an estimator with three properties: unbiasedness, sparsity and continuity (see Fan and Li 2001 for details). These properties motivate the needs of using a folded concave penalty.

The following assumptions are further imposed. Recall that for j ≤ p, F_j = f_j (W) and H_j = h_j (W).

Assumption 4.2

1. The true parameter β₀ is uniquely identified by E(g(Y, X^T β₀)|W) = 0.

2. (Y₁, X₁₎,…, (Y_n, X_n) are independent and identically distributed.

Remark 4.1

Condition (i) above is standard in the GMM literature (e.g., Newey 1993, Donald et al. 2009, Kitamura et al. 2004). This condition is closely related to the “over-identifying restriction”, and ensures that we can always find two sets of transformations F and H such that the equations in (3.2) are uniquely satisfied by β_S = β_0S. In linear models, this is a reasonable assumption, as discussed in Section 3.2. In nonlinear models, however, requiring the identifiability from either E(g(Y, X^Tβ₀)|W) = 0 or (3.2) may be restrictive. Indeed, Dominguez and Lobato 2004) showed that the identification condition in (i) may depend on the marginal distributions of W. Furthermore, in nonparametric regression problems as in Bickel et al. (2009) and Ai and Chen (2003), the sufficient condition of Condition (i) is even more complicated, which also depends on the conditional distribution of X|W, and is known to be statistically untestable (see Newey and Powell 2003, Canay et al 2013).

Assumption 4.3

There exist b₁, b₂, b₃ > 0 and r₁, r₂, r₃ > 0 such that for any t > 0,

1. P(|g(Y, X^Tβ₀)| > t) ≤ exp(−(t/b₁)^r₁),

2. max_l≤p P(|F_l| > t) ≤ exp(−(t/b₂)^r₂), max_l≤p P(|H_l > t) ≤ exp(−(t/b₃)^r₃).

3. min_j∈S var(g(Y, X^T β₀)F_j) and min_j∈S var(g(Y, X^T β₀)H_j) are bounded away from zero.

4. var(F_j) and var(H_j) are bounded away from both zero and infinity uniformly in j = 1,…, p and p ≥ 1.

We will assume g(·,·) to be twice differentiable, and in the following assumptions, let

$$m(t_1,t_2)=\frac{\partial g(t_1,t_2)}{\partial t_2},q(t_1,t_2)=\frac{{\partial }^{2}g(t_1,t_2)}{\partial t_2^2},{\mathbf{V}}_S=\left(\begin{array}{c}{\mathbf{F}}_S\\ {\mathbf{H}}_S\end{array}\right).$$

Assumption 4.4

1. g(·,·) is twice differentiable.

2. sup_{t1, t2} |m(t₁, t₂)| < ∞, and sup_{t1, t2} |q(t₁, t₂)| <∞.

It is straightforward to verify Assumption 4.4 for linear, logistic and probit regression models.

Assumption 4.5

There exist C₁ > 0 and C₂ > 0 such that

$$\begin{array}{c}{\lambda }_{max}[(Em(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{X}}_S{\mathbf{V}}_S^T){(Em(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{X}}_S{\mathbf{V}}_S^T)}^T]<C_1.\\ {\lambda }_{min}[(Em(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{X}}_S{\mathbf{V}}_S^T){(Em(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{X}}_S{\mathbf{V}}_S^T)}^T]<C_2;\end{array}$$

These conditions require that the instrument V_S be not weak, that is, V_S should not be weakly correlated with the important regressors. In the generalized linear model, Assumption 4.5 is satisfied if proper conditions on the design matrices are imposed. For example, in the linear regression model and probit model, we assume the eigenvalues of $(E{\mathbf{X}}_S{\mathbf{V}}_S^T){(E{\mathbf{X}}_S{\mathbf{V}}_S^T)}^T$ and $(E\varphi ({\mathbf{X}}^T{\mathit{\beta }}_0){\mathbf{X}}_S{\mathbf{V}}_S^T){(E\varphi ({\mathbf{X}}^T{\mathit{\beta }}_0){\mathbf{X}}_S{\mathbf{V}}_S^T)}^T$ are bounded away from both zero and infinity respectively, where ϕ(·) is the standard normal density function. Conditions in the same spirit are also assumed in, e.g., Bradic et al. (2011), and Fan and Lv (2011).

Define

$$\mathbf{\Upsilon }=var(g(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{V}}_S).$$ (4.2)

Assumption 4.6

1. For some c > 0, λ_min(ϒ) > c.

2. $s{P}_n^{\prime }(d_n)+s\sqrt{(logp)/n}+s^3(logs)/n=o(P_n^{\prime }(0^{+}))$, $P_n^{\prime }(d_n)s^2=O(1)$, and $s\sqrt{(logp)/n}=o(d_n)$.

3. $P_n^{\prime }(d_n)=o(1/\sqrt{ns})$ and sup_{‖β − β0S ‖≤dn/4}η(β)=o((s log p)^−1/2).

4. ${max}_{j\notin S}\Vert Em(y,{\mathbf{X}}^T{\mathit{\beta }}_0)X_j{\mathbf{V}}_S\Vert \sqrt{(logs)/n}=o(P_n(0^{+}))$.

This assumption imposes a further condition jointly on the penalty, the strength of the minimal signal and the number of important regressors. Condition (i) is needed for the asymptotic normality of the estimated nonzero coefficients. When either SCAD or MCP is used as the penalty function with a tuning parameter λ_n, $P_n^{\prime }(d_n)={sup}_{\Vert \mathit{\beta }-{\mathit{\beta }}_{0S}\Vert \le d_n/4}\eta (\mathit{\beta })=0$ and $P_n^{\prime }(0^{+})={\lambda }_n$ when λ_n = o(d_n). Thus Conditions (ii)-(iv) in the assumption are satisfied as long as $s\sqrt{logp/n}+s^{3}logs/n\ll {\lambda }_n\ll d_n$. This requires the signal d_n be strong and s be small compared to n. Such a condition is needed to achieve the variable selection consistency.

Under the foregoing regularity conditions, we can show the oracle property of a local minimizer of Q_FGMM (3.4).

Theorem 4.1

Suppose s³ log p = o(n). Under Assumptions 4.1-4.6, there exists a local minimizer $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_S^T,{\widehat{\mathit{\beta }}}_N^T)}^T$ of Q_FGMM(β) with β̂_S and β̂_N being sub-vectors of β̂ whose coordinates are in S and S^c respectively, such that:

1. $$\sqrt{n}{\mathit{\alpha }}^T{\mathbf{\Gamma }}^{-1/2}\sum ({\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}){\to }^{d}N(0,1),$$

   for any unit vector α ∈ ℝ^s, ‖α‖ = 1, where $\mathbf{A}=Em(Y,{\mathbf{X}}^T{\mathit{\beta }}_0){\mathbf{X}}_S{\mathbf{V}}_S^T$,

   $$\mathbf{\Gamma }=4\mathbf{A}\mathbf{J}({\mathit{\beta }}_0)\mathbf{\Upsilon }\mathbf{J}({\mathit{\beta }}_0){\mathbf{A}}^T,\mathit{\text{and}}\sum =2\mathbf{A}\mathbf{J}{\mathit{\beta }}_0){\mathbf{A}}^T.$$
2. $$\underset{n\to \infty }{lim}P({\widehat{\mathit{\beta }}}_N=0)=1.$$

   In addition, the local minimizer β̂ is strict with probability at least 1 – δ for an arbitrarily small δ > 0 and all large n.

3. Let Ŝ = {j ≤ p : β̂_j ≠ 0}. Then

   $$P(\widehat{S}=S)\to 1.$$

Remark 4.2

As was shown in an earlier version of this paper Fan and Liao (2012), when it is known that E[g(Y, X^Tβ₀)|X_S] = 0 but likely E[g(Y, X^Tβ₀)|X] ≠ 0, we can take V = (F^T, H^T)^T to be transformations of X that satisfy Assumptions 4.3-4.6. In this way, we do not need an extra instrumental variable W, and Theorem 4.1 still goes through, while the traditional methods (e.g., penalized least squares in the linear model) can still fail as shown by Theorem 2.2. In the high-dimensional linear model, compared to the classical assumption: E(ε|X) = 0, our condition E(ε| X_S) = 0 is relatively easier to validate as X_S is a low-dimensional vector.

Remark 4.3

We now explain our required lower bound on the signal $s\sqrt{logp/n}=o(d_n)$. When a penalized regression is used, which takes the form ${min}_{\mathit{\beta }}{L}_n(\mathit{\beta })+{\sum }_{j=1}^p{P}_n(|{\beta }_j|)$, it is required that if L_n (β) is differentiable, ${max}_{j\notin S}|\partial L_n({\mathit{\beta }}_0)/\partial {\beta }_j|=o(P_n^{\prime }(0^{+}))$. This often leads to a requirement of the lower bound of d_n. Therefore, such a lower bound of d_n depends on the choice of both the loss function L_n(β) and the penalty. For instance, in the linear model when least squares with a SCAD penalty is employed, this condition is equivalent to $\sqrt{logp/n}=o(d_n)$. It is also known that the adaptive lasso penalty requires the minimal signal to be significantly larger than $\sqrt{logp/n}$(Huang, Ma and Zhang 2008). In our framework, the requirement $s\sqrt{logp}/n=o(d_n)$ arises from the use of the new FGMM loss function. Such a condition is stronger than that of the least squares loss function, which is the price paid to achieve variable selection consistency in the presence of endogeneity. This condition is still easy to satisfy as long as s grows slowly with n.

Remark 4.4

Similar to the “irrpresentable condition” for Lasso, the FGMM requires important and unimportant explanatory variables not be strongly correlated. This is fulfilled by Assumption 4.6(iv). For instance, in the linear model and V_S contains X_S as in our earlier version, this condition implies ${max}_{j\notin S}\Vert E{X}_j{\mathbf{X}}_S\Vert \sqrt{logs/n}=o({\lambda }_n)$. Strong correlation between (X_S, X_N) is also ruled out by the identifiability condition Assumption 4.2. To illustrate the idea, consider a case of perfect linear correlation: ${\mathbf{X}}_S^T\mathit{\alpha }-{\mathbf{X}}_N^T\mathit{\delta }=0$ for some (α, δ) with δ ≠ 0. Then, ${\mathbf{X}}^T{\mathit{\beta }}_0={\mathbf{X}}_S^T({\mathit{\beta }}_{0S}-\mathit{\alpha })+{\mathbf{X}}_N^T\mathit{\delta }$. As a result, the FGMM can be variable selection inconsistent because β₀ and (β_0S − α, δ) are observationally equivalent, violating Assumption 4.2.

5. Global minimization

With the over identification condition, we can show that the local minimizer in Theorem 4.1 is nearly global. To this end, define an l_∞ ball centered at β₀ with radius δ:

$${\mathrm{\Theta }}_{\delta }=\{\mathit{\beta }\in {\mathbb{R}}^p:|{\beta }_i-{\beta }_{0i}|<\delta ,i=1,\dots ,p\}.$$

Assumption 5.1 (over-identification)

For any δ > 0, there is γ > 0 such that

$$\underset{n\to \infty }{lim}P(\underset{\mathit{\beta }\notin {\mathrm{\Theta }}_{\delta }\cup \{0\}}{inf}{\Vert \frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{V}}_i(\mathit{\beta })\Vert }^2>\gamma )=1.$$

This high-level assumption is hard to avoid in high-dimensional problems. It is the empirical counterpart of (3.8). In classical low-dimensional regression models, this assumption has often been imposed in the econometric literature, e.g., Andrews (1999), Chernozhukov and Hong (2003), among many others. Let us illustrate it by the following example.

Example 5.1

Consider a linear regression model of low dimensions: $E(Y-{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}|\mathbf{W})=0$, which implies $E[(Y-{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{F}}_S]=0$ and $E[(Y-{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{H}}_S]=0$ where p is either bounded or slowly diverging with n. Now consider the following problem:

$$\underset{\mathit{\beta }\ne 0}{min}G(\mathit{\beta })\equiv \underset{\mathit{\beta }\ne 0}{min}{\Vert E(Y-{\mathbf{X}}^T\mathit{\beta })\mathbf{F}(\mathit{\beta })\Vert }^2+{\Vert E(Y-{\mathbf{X}}^T\mathit{\beta })\mathbf{H}(\mathit{\beta })\Vert }^2.$$

Once ${[E{\mathbf{F}}_{\stackrel{\sim }{S}}{\mathbf{X}}_{\stackrel{\sim }{S}}^T]}^{-1}E[{\mathbf{F}}_{\stackrel{\sim }{S}}Y]\ne {[E{\mathbf{H}}_{\stackrel{\sim }{S}}{\mathbf{X}}_{\stackrel{\sim }{S}}^T]}^{-1}E[{\mathbf{H}}_{\stackrel{\sim }{S}}Y]$ for all index set S̃ ≠ S, the objective function is then minimized to zero uniquely by β = β₀. Moreover, for any δ > 0 there is γ > 0 such that when β ∉ Θ_δ ∪ {0}, we have G(β) > γ > 0. Assumption 5.1 then follows from the uniform weak law of large number: with probability approaching one, uniformly in (β ∉ Θ_δ ∪ {0},

$${\Vert \frac{1}{n}\sum _{i=1}^n{\mathbf{F}}_i(\mathit{\beta })(Y_i-{\mathbf{X}}_i^T\mathit{\beta })\Vert }^2+{\Vert \frac{1}{n}\sum _{i=1}^n{\mathbf{H}}_i(\mathit{\beta })(Y_i-{\mathbf{X}}_i^T\mathit{\beta })\Vert }^2>\gamma /2.$$

When p is much larger than n, the accumulation of the fluctuations from using the law of large number is no longer negligible. It is then challenging to show that ‖E[g(Y_i, X^Tβ)V(β)] ‖ is close to $\Vert \frac{1}{n}{\sum }_{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{V}}_i(\mathit{\beta })\Vert$ uniformly for high-dimensional β's, which is why we impose Assumption 5.1 on the empirical counterpart instead of the population.

Theorem 5.1

Assume ${max}_{j\in S}{P}_n^{\prime }(|{\beta }_{0j}|)=o(s^{-1})$. Under Assumption 5.1 and those of Theorem 4.1, the local minimizer β̂ in Theorem 4.1 satisfies: for any δ > 0, there exists γ > 0,

$$\underset{n\to \infty }{lim}P(Q_{\mathbf{\text{FGMM}}}(\widehat{\mathit{\beta }})+\gamma <\underset{\mathit{\beta }\notin {\mathrm{\Theta }}_{\delta }\cup \{0\}}{inf}{Q}_{\mathit{\text{FGMM}}}(\mathit{\beta }))=1.$$

The above theorem demonstrates that β̂ is a nearly global minimizer. For SCAD and MCP penalties, the condition ${max}_{j\in S}{P}_n^{\prime }(|{\beta }_{0j}|)=o(s^{-1})$ holds when λ_n = o(s⁻¹), which is satisfied if s is not large.

Remark 5.1

We exclude the set {0} from the searching area in both Assumption 5.1 and Theorem 5.1 because we do not include the intercept in the model so X(0) = 0 by definition, and hence Q_FGMM(0) = 0. It is reasonable to believe that zero is not close to the true parameter, since we assume there should be at least one important regressor in the model. On the other hand, if we always keep X₁ = 1 to allow for an intercept, there is no need to remove {0} in either Assumption 5.1 or the above theorem. Such a small change is not essential.

Remark 5.2

Assumption 5.1 can be slightly relaxed so that γ is allowed to decay slowly at a certain rate. The lower bound of such a rate is given by Lemma D.2 in the appendix. Moreover, Theorem 5.1 is based on an over-identification assumption, which is essentially different from the global minimization theory in the recent high-dimensional literature, e.g., Zhang (2010), Bühlmann and van de Geer (2011, ch 9), and Zhang and Zhang (2012).

6. Semi-parametric efficiency

The results in Section 5 demonstrate that the choice of the basis functions {f_j, h_j}_j≤p forming F and H influences the asymptotic variance of the estimator. The resulting estimator is in general not efficient. To obtain a semi-parametric efficient estimator, one can employ a second step post-FGMM procedure. In the linear regression, a similar idea has been used by Belloni and Chernozhukov (2013).

After achieving the oracle properties in Theorem 4.1, we have identified the important regressors with probability approaching one, that is,

$$\widehat{S}=\{j:{\widehat{\beta }}_j\ne 0\},{\widehat{\mathbf{X}}}_S=(X_j:j\in \widehat{S}),P(\widehat{S}=S)\to 1.$$

This reduces the problem to a low-dimensional problem. For simplicity, we restrict s = O(1). The problem of constructing semi-parametric efficient estimator (in the sense of Newey (1990) and Bickel et al. (1998)) in a low-dimensional model

$$E[g(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S})|\mathbf{W}]=0$$

has been well studied in the literature (see, for example, Chamberlain (1987), Newey (1993)). The optimal instrument that leads to the semi-parametric efficient estimation of β_0S is given by D(W)σ(W)⁻², where

$$\mathbf{D}(\mathbf{W})=E(\frac{\partial g(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S})}{\partial {\mathit{\beta }}_S}|\mathbf{W}),\sigma {(\mathbf{W})}^2=E(g{(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S})}^2|\mathbf{W}).$$

Newey (1993) showed that the semi-parametric efficient estimator of β_0S can be obtained by GMM with the moment condition:

$$E[g(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S})\sigma {(\mathbf{W})}^{-2}\mathbf{D}(\mathbf{W})]=0.$$ (6.1)

In the post-FGMM procedure, we replace X_S with the selected X̂_S obtained from the first-step penalized FGMM. Suppose there exist consistent estimators D̂(W) and σ̂ (W)² of D(W) and σ(W)². Let us assume the true parameter ‖β_0S‖_∞ < M for a large constant M > 0. We then estimate β_0S by solving

$${\rho }_n({\mathit{\beta }}_S)=\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\widehat{\mathbf{X}}}_{iS}^T{\mathit{\beta }}_S)\widehat{\sigma }{({\mathbf{W}}_i)}^{-2}\widehat{\mathbf{D}}({\mathbf{W}}_i)=0,$$ (6.2)

on {β_S : ‖β_0S‖_∞ ≤ M}, and the solution is assumed to be unique.

Assumption 6.1

1. There exist C₁ > 0 and C₂ > 0 so that

   $$C_1<\underset{\mathbf{w}\in \chi }{inf}\sigma {(\mathbf{w})}^2\le \underset{\mathbf{w}\in \chi }{sup}\sigma {(\mathbf{w})}^2<C_2.$$

   In addition, there exist σ̂(w)² and D̂ (w) such that

   $$\underset{\mathbf{w}\in \chi }{sup}|\widehat{\sigma }{(\mathbf{w})}^2-\sigma {(\mathbf{w})}^2|=o_p(1),\mathit{\text{and}}\underset{\mathbf{w}\in \chi }{sup}\Vert \widehat{\mathbf{D}}(\mathbf{w})-\mathbf{D}(\mathbf{w})\Vert =o_p(1)$$

   where χ is the support of W.

2. $$E({sup}_{{\Vert \mathit{\beta }\Vert }_{\infty }\le M}g{(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_S)}^4)<\infty .$$

The consistent estimators for D(w) and σ(w)² can be obtained in many ways. We present a few examples below.

Example 6.1 (Homoskedasticity)

Suppose $Y=h({\mathbf{X}}_S^T{\mathit{\beta }}_{0S})+\epsilon$ for some nonlinear function h(·). Then σ(w)² = E(ε²|W = w) = σ², which does not depend on w under homoskedasticity. In this case, equations (6.1) and (6.2) do not depend on σ².

Example 6.2 (Simultaneous linear equations)

In the simultaneous linear equation model, X_S linearly depends on W as:

$$g(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_S)=Y-{\mathbf{X}}_S^T{\mathit{\beta }}_S,{\mathbf{X}}_S=\mathbf{\Pi }\mathbf{W}+\mathbf{u}$$

for some coefficient matrix Π, where u is independent of W. Then D(w) = E(X_S|W = w) = Πw. Let X̂ = (X̂_S1, …, X̂_Sn), W̄ = (W₁, …, W_n). We then estimate D(w) by Π̂w, where Π̂ = (X̂W̄^T)(W̄W̄)⁻¹.

Example 6.3 (Semi-nonparametric estimation)

We can also assume a semi-parametric structure on the functional forms of D(w) and σ(w)²:

$$\mathbf{D}(\mathbf{w})=\mathbf{D}(\mathbf{w};{\theta }_1),\sigma {(\mathbf{w})}^2={\sigma }^2(\mathbf{w};{\theta }_2),$$

where D(·;θ₁) and σ²(·;θ₂) are semi-parametric functions parameterized by θ₁ and θ₂. Then D(w) and σ(w)² are estimated using a standard semi-parametric method. More generally, we can proceed by a pure nonparametric approach via respectively regressing $\partial g(Y,{\widehat{\mathbf{X}}}_S^T{\widehat{\mathit{\beta }}}_S)/\partial {\mathit{\beta }}_S$ and $g{(Y,{\widehat{\mathbf{X}}}_S^T{\widehat{\mathit{\beta }}}_S)}^2$ on W, provided that the dimension of W is either bounded or growing slowly with n (see Fan and Yao, 1998).

Theorem 6.1

Suppose s = O(1), Assumption 6.1 and those of Theorem 4.1 hold. Then

$$\sqrt{n}({\widehat{\mathit{\beta }}}_S^{\ast }-{\mathit{\beta }}_{0S}){\to }^{d}N(0,{[E(\sigma {(\mathbf{W})}^{-2}\mathbf{D}(\mathbf{W})\mathbf{D}{(\mathbf{W})}^T)]}^{-1}),$$

and [E(σ(W)⁻²D(W)D(W)^T)]^–1 is the semi-parametric efficiency bound in Chamberlain (1987).

7. Implementation

We now discuss the implementation for numerically minimizing the penalized FGMM criterion function.

7.1. Smoothed FGMM

As we previously discussed, including an indicator function benefits us in dimension reduction. However, it also makes L_FGMM unsmooth. Hence, minimizing Q_FGMM(β) = L_FGMM(β)+Penalty is generally NP-hard.

We overcome this discontinuity problem by applying the smoothing technique as in Horowitz (1992) and Bondell and Reich (2012), which approximates the indicator function by a smooth kernel K : (−∞,∞) → ℝ that satisfies

1. 0 ≤ K(t) < M for some finite M and all t ≥ 0.

2. K(0) = 0 and lim_|t|→∞ K(t) = 1.

3. lim sup_|t|→∞ |K′(t)t| = 0, and lim sup_|t|→∞ |K″(t)t²| < ∞.

We can set $K(t)=\frac{F(t)-F(0)}{1-F(0)}$, where F(t) is a twice differentiable cumulative distribution function. For a pre-determined small number h_n, L_FGMM is approximated by a continuous function L_K(β) with the indicator replaced by $K({\beta }_j^2/h_n)$. The objective function of the smoothed FGMM is given by

$$Q_K(\mathit{\beta })=L_K(\mathit{\beta })+\sum _{j=1}^p{P}_n(|{\beta }_j|).$$

As h_n→0⁺, $K({\beta }_j^2/h_n)$ converges to I_(βj≠0), and hence L_K(β) is simply a smoothed version of L_FGMM (β). As an illustration, Figure 1 plots such a function.

Fig 1. $K\left(\frac{t^2}{h_n}\right)=\frac{exp(t^2/h_n)-1}{exp(t^2/h_n)+1}$ as an approximation to I_(t≠0).

Smoothing the indicator function is often seen in the literature on high-dimensional variable selections. Recently, Bondell and Reich (2012) approximate I_(t≠0) by $\frac{(h_n+1)t}{h_n+t}$ to obtain a tractable non-convex optimization problem. Intuitively, we expect that the smoothed FGMM should also achieve the variable selection consistency. Indeed, the following theorem formally proves this claim.

Theorem 7.1

Suppose $h_n^{1-\gamma }=o(d_n^2)$ for a small constant γ ∈ (0, 1). Under the assumptions of Theorem 4.1 there exists a local minimizer β̂′ of the smoothed FGMM Q_K(β) such that, for ${\widehat{S}}^{\prime }=\{j\le p:{\widehat{\beta }}_j^{\prime }\ne 0\}$,

$$P({\widehat{S}}^{\prime }=S)\to 1.$$

In addition, the local minimizer β̂′ is strict with probability at least 1 − δ for an arbitrarily small δ > 0 and all large n.

The asymptotic normality of the estimated nonzero coefficients can be established very similarly to that of Theorem 4.1, which is omitted for brevity.

7.2. Coordinate descent algorithm

We employ the iterative coordinate algorithm for the smoothed FGMM minimization, which was used by Fu (1998), Daubechies et al. (2004), Fan and Lv (2011), etc. The iterative coordinate algorithm minimizes one coordinate of β at a time, with other coordinates kept fixed at their values obtained from previous steps, and successively updates each coordinate. The penalty function can be approximated by local linear approximation as in Zou and Li (2008).

Specifically, we run the regular penalized least squares to obtain an initial value, from which we start the iterative coordinate algorithm for the smoothed FGMM. Suppose β^(l) is obtained at step l. For k ∈ {1, …, p}, denote by ${\mathit{\beta }}_{(-k)}^{(l)}$ a (p − 1)-dimensional vector consisting of all the components of (β^(l) but ${\beta }_k^{(l)}$. Write $({\mathit{\beta }}_{(-k)}^{(l)},t)$ as the p-dimensional vector that replaces ${\beta }_k^{(l)}$ with t. The minimization with respect to t while keeping ${\mathit{\beta }}_{(-k)}^{(l)}$ fixed is then a univariate minimization problem, which is not difficult to implement. To speed up the convergence, we can also use the second order approximation of $L_K({\mathit{\beta }}_{(-k)}^{(l)},t)$ along the kth component at ${\beta }_k^{(l)}$:

$$L_K({\mathit{\beta }}_{(-k)}^{(l)},t)\approx L_K({\mathit{\beta }}^{(l)})+\frac{\partial L_K({\mathit{\beta }}^{(l)})}{\partial {\beta }_k}(t-{\beta }_k^{(l)})+\frac{1}{2}\frac{{\partial }^2{L}_K({\mathit{\beta }}^{(l)})}{\partial {\beta }_k^2}{(t-{\beta }_k^{(l)})}^2\equiv L_K({\mathit{\beta }}^{(l)})+{\widehat{L}}_K({\mathit{\beta }}_{(-k)}^{(l)},t),$$ (7.1)

where ${\widehat{L}}_K({\mathit{\beta }}_{(-k)}^{(l)},t)$ is a quadratic function of t. We solve for

$$t^{\ast }=arg\underset{t}{min}{\widehat{L}}_K({\mathit{\beta }}_{(-k)}^{(l)},t)+P_n^{\prime }(|{\beta }_k^{(l)}|)|t|,$$ (7.2)

which admits an explicit analytical solution, and keep the remaining components at step l. Accept t* as an updated kth component of β^(l) only if $L_K({\mathit{\beta }}^{(l)})+{\sum }_{j=1}^p{P}_n(|{\mathit{\beta }}_j^{(l)}|)$ strictly decreases. The coordinate descent algorithm runs as follows.

1. Set l = 1. Initialize β⁽¹⁾ = β̂*, where β̂* solves

   $$\underset{\mathit{\beta }\in {\mathbb{R}}^p}{min}\frac{1}{n}\sum _{i=1}^n{[g(Y_i,{\mathbf{X}}_i^T\mathit{\beta })]}^2+\sum _{j=1}^p{P}_n(|{\beta }_j|)$$

   using the coordinate descent algorithm as in Fan and Lv (2011).

2. Successively for k = 1, …, p, let t* be the minimizer of

   $$\underset{t}{min}{\widehat{L}}_K({\mathit{\beta }}_{(-k)}^{(l)},t)+P_n^{\prime }(|{\beta }_k^{(l)}|)|t|.$$

   Update ${\beta }_k^{(l)}$ as t* if

   $$L_K({\mathit{\beta }}_{(-k)}^{(l)},t^{\ast })+P_n(|t^{\ast }|)<L_K({\mathit{\beta }}^{(l)})+P_n(|{\beta }_k^{(l)}|).$$

   Otherwise set ${\beta }_k^{(l)}={\beta }_k^{(l-1)}$. Increase l by one when k = p.

3. Repeat Step 2 until | Q_K(β^(l))−Q_K (β^(l+1))| < ε, for a pre-determined small ε.

When the second order approximation (7.1) is combined with SCAD in Step 2, the local linear approximation of SCAD is not needed. As demonstrated in Fan and Li (2001), when P_n(t) is defined using SCAD, the penalized optimization of the form ${min}_{\beta \in \mathbb{R}}\frac{1}{2}{(z-\beta )}^2+\mathrm{\Lambda }{P}_n(|\beta |)$ has an analytical solution.

We can show that the evaluated objective values {Q_K(β^(l))}_l≥1 is a bounded Cauchy sequence. Hence for an arbitrarily small ε > 0, the above algorithm stops after finitely many steps. Let M(β) denote the map defined by the algorithm from β^(l) to β^(l+1). We define a stationary point of the function Q_K(β) to be any point β at which the gradient vector of Q_K(β) is zero. Similar to the local linear approximation of Zou and Li (2008), we have the following result regarding the property of the algorithm.

Theorem 7.2

The sequence {Q_K (β^(l))}_l≥1 is a bounded non-increasing Cauchy sequence. Hence for any arbitrarily small ε > 0, the coordinate descent algorithm will stop after finitely many iterations. In addition, if Q_K (β) = Q_K (M(β)) only for stationary points of Q_K(·) and if β* is a limit point of the sequence {(β^(l)) _l≥1, then β* is a stationary point of Q_K (β).

Theoretical analysis of non-convex regularization in the recent decade has focused on numerical procedures that can find local solutions (Hunter and Li 2005, Kim et al. 2008, Brehenry and Huang 2011). Proving that the algorithm achieves a solution that possesses the desired oracle properties is technically difficult. Our simulated results demonstrate that the proposed algorithm indeed reaches the desired sparse estimator. Further investigation along the lines of Zhang and Zhang (2012) and Loh and Wainwright (2013) is needed to investigate the statistical properties of the solution to non-convex optimization problems, which we leave as future research.

8. Monte Carlo Experiments

8.1. Endogeneity in both important and unimportant regressors

To test the performance of FGMM for variable selection, we simulate from a linear model:

$$Y={\mathbf{X}}^T{\mathit{\beta }}_0+\epsilon ,({\beta }_{01},\dots ,{\beta }_{05})=(5,-4,7,-2,1.5);{\beta }_{0j}=0,\text{for}6\le j\le p$$

with p = 50 or 200. Regressors are classified as being exogenous (independent of ε) and endogenous. For each component of X, we write $X_j=X_j^e$ if X_j is endogenous, and $X_j=X_j^x$ if X_j is exogenous, and $X_j^e$ and $X_j^x$ are generated according to:

$$X_j^e=(F_j+H_j+1)(3\epsilon +1),X_j^x=F_j+H_j+u_j,$$

where {ε, u₁, …, u_p} are independent N(0, 1). Here F = (F₁, …, F_p)^T and H = (H₁, …, H_p)^T are the transformations (to be specified later) of a three-dimensional instrumental variable W = (W₁, W₂, W₃)^T ∼ N₃(0, I₃). There are m endogenous variables (X₁, X₂, X₃, X₆, …, X_2+m)^T, with m = 10 or 50. Hence three of the important regressors (X₁, X₂, X₃) are endogenous while two are exogenous (X₄, X₅).

We apply the Fourier basis as the working instruments:

$$\begin{array}{c}\mathbf{F}=\sqrt{2}\{sin(j\pi W_1)+sin(j\pi W_2)+sin(j\pi W_3):j\le p\},\\ \mathbf{H}=\sqrt{2}\{cos(j\pi W_1)+cos(j\pi W_2)+cos(j\pi W_3):j\le p\}.\end{array}$$

The data contain n = 100 i.i.d. copies of (Y, X, F, H). PLS and FGMM are carried out separately for comparison. In our simulation we use SCAD with pre-determined tuning parameters of λ as the penalty function. The logistic cumulative distribution function with h = 0.1 is used for smoothing:

$$F(t)=\frac{exp(t)}{1+exp(t)},K\left(\frac{{\beta }_j^2}{h}\right)=2F\left(\frac{{\beta }_j^2}{h}\right)-1.$$

There are 100 replications per experiment. Four performance measures are used to compare the methods. The first measure is the mean standard error (MSE_S) of the important regressors, determined by the average of ‖β̂_S − β_0S‖ over the 100 replications, where S = {1, …, 5}. The second measure is the average of the MSE of unimportant regressors, denoted by MSE_N. The third measure is the number of correctly selected non-zero coefficients, that is, the true positive (TP), and finally, the fourth measure is the number of incorrectly selected coefficients, the false positive (FP). In addition, the standard error over the 100 replications of each measure is also reported. In each simulation, we initiate β⁽⁰⁾ = (0,…, 0)^T, and run a penalized least squares (SCAD(λ)) for λ = 0.5 to obtain the initial value for the FGMM procedure. The results of the simulation are summarized in Table 2, which compares the performance measures of PLS and FGMM.

Table 2. Endogeneity in both important and unimportant regressors, n = 100.

	PLS			FGMM
	λ = 1	λ =3	λ = 4	λ = 0.08	λ = 0.1	λ = 0.3	post-FGMM
				p = 50 m = 10
MSES	0.190 (0.102)	0.525 (0.283)	0.491 (0.328)	0.106 (0.051)	0.097 (0.043)	0.102 (0.037)	0.088 (0.026)
MSEN	0.171 (0.059)	0.240 (0.149)	0.183 (0.149)	0.090 (0.030)	0.085 (0.035)	0.048 (0.034)
TP	5 (0)	5 (0)	4.97 (0.171)	5 (0)	5 (0)	5 (0)
FP	27.69 (6.260)	14.63 (5.251)	10.37 (4.539)	3.76 (1.093)	3.5 (1.193)	1.63 (1.070)
				p = 200 m = 50
MSES	0.831 (0.787)	0.966 (0.595)	1.107 (0.678)	0.111 (0.048)	0.104 (0.041)	0.231 (0.431)	0.092 (0.032)
MSEN	1.286 (1.333)	0.936 (0.799)	0.828 (0.656)	0.062 (0.018)	0.063 (0.021)	0.053 (0.075)
TP	5 (0)	4.9 (0.333)	4.73 (0.468)	5 (0)	5 (0)	4.94 (0.246)
FP	86.760 (27.41)	42.440 (15.08)	35.070 (13.84)	4.726 (1.358)	4.276 (1.251)	2.897 (2.093)

m is the number of endogenous regressors. MSE_S is the average of ‖β̂_S − β_0S‖ for nonzero coefficients. MSE_N is the average of ‖β̂_N − β_0N‖ for zero coefficients. TP is the number of correctly selected variables; FP is the number of incorrectly selected variables, and m is the total number of endogenous regressors. The standard error of each measure is also reported.

PLS has non-negligible false positives (FP). The average FP decreases as the magnitude of the penalty parameter increases, however, with a relatively large MSE_S for the estimated nonzero coefficients, and the FP rate is still large compared to that of FGMM. The PLS also misses some important regressors for larger λ. It is worth noting that the larger MSE_S for PLS is due to the bias of the least squares estimation in the presence of endogeneity. In contrast, FGMM performs well in both selecting the important regressors, and in correctly eliminating the unimportant regressors. The average MSE_S of FGMM is significantly less than that of PLS since the instrumental variable estimation is applied instead. In addition, after the regressors are selected by the FGMM, the post-FGMM further reduces the mean squared error of the estimators.

8.2. Endogeneity only in unimportant regressors

Consider a similar linear model but only the unimportant regressors are endogenous and all the important regressors are exogenous, as designed in Section 2.2, so the true model is as the usual case without endogeneity. In this case, we apply (F, H) = (X, X²) as the working instruments for FGMM with SCAD(λ) penalty, and need only data X and Y = (Y₁, …, Y_n). We still compare the FGMM procedure with PLS. The results are reported in Table 3.

Table 3. Endogeneity only in unimportant regressors, n = 200.

	PLS			FGMM
	λ = 0.1	λ = 0.5	λ = 1	λ = 0.05	λ = 0.1	λ = 0.2
	p = 50
MSES	0.133 (0.043)	0.629 (0.301)	1.417 (0.329)	0.261 (0.094)	0.184 (0.069)	0.194 (0.076)
MSEN	0.068 (0.016)	0.072 (0.016)	0.095 (0.019)	0.001 (0.010)	0 (0)	0.001 (0.009)
TP	5 (0)	4.82 (0.385)	3.63 (0.504)	5 (0)	5 (0)	5 (0)
FP	35.36 (3.045)	8.84 (3.334)	2.58 (1.557)	0.08 (0.337)	0 (0)	0.02 (0.141)
	p = 300
MSES	0.159 (0.054)	0.650 (0.304)	1.430 (0.310)	0.274 (0.086)	0.187 (0.102)	0.193 (0.123)
MSEN	0.107 (0.019)	0.071 (0.023)	0.086 (0.027)	5 × 10−4(0.006)	0 (0)	5 × 10−4(0.005)
TP	5 (0)	4.82 (0.384)	3.62 (0.487)	5 (0)	5 (0)	4.99 (0.100)
FP	210.47 (11.38)	42.78 (11.773)	7.94 (5.635)	0.11 (0.37)	0 (0)	0.01 (0.10)

It is clearly seen that even though only the unimportant regressors are endogenous, however, the PLS still does not seem to select the true model correctly. This illustrates the variable selection inconsistency for PLS even when the true model has no endogeneity. In contrast, the penalized FGMM still performs relatively well.

8.3. Weak minimal signals

To study the effect on variable selection when the strength of the minimal signal is weak, we run another set of simulations with the same data generating process as in Design 1 but we change β₄ = −0.5 and β₅ = 0.1, and keep all the remaining parameters the same as before. The minimal nonzero signal becomes |β₅| = 0.1. Three of the important regressors are endogenous as in Design 1. Table 4 indicates that the minimal signal is so small that it is not easily distinguishable from the zero coefficients.

Table 4. FGMM for weak minimal signal β₄ = −0.5, β₅ = 0.1.

	p = 50	m = 10		p = 200	m = 50
	λ = 0.05	λ = 0.1	λ = 0.5	λ = 0.05	λ = 0.1	λ = 0.5
MSES	0.128 (0.020)	0.107 (0.000)	0.118 (0.056)	0.138 (0.061)	0.125 (0.074)	0.238 (0.154)
MSEN	0.155 (0.054)	0.097 (0.000)	0.021 (0.033)	0.134 (0.052)	0.108 (0.043)	0.084 (0.062)
TP	4.12 (0.327)	4 (0)	4 (0)	4.04 (0.281)	3.98 (0.141)	3.8 (0.402)
FP	4.93 (1.578)	5 (0)	2.08 (0.367)	4.72 (1.198)	4.3 (0.948)	1.95 (1.351)

9. Conclusion and Discussion

Endogeneity can arise easily in the high-dimensional regression due to a large pool of regressors, which causes the inconsistency of the penalized least-squares methods and possible false scientific discoveries. Based on the over-identification assumption and valid instrumental variables, we propose to penalize an FGMM loss function. It is shown that FGMM possesses the oracle property, and the estimator is also a nearly global minimizer.

We would like to point out that this paper focuses on correctly specified sparse models, and the achieved results are “pointwise” for the true model. An important issue is the uniform inference where the sparse model may be locally misspecified. While the oracle property is of fundamental importance for high-dimensional methods in many scientific applications, it may not enable us to make valid inference about the coefficients uniformly across a large class of models (Leeb and Pötscher 2008, Belloni et al. 2013)⁵. Therefore, the “post-double-selection” method with imperfect model selection recently proposed by Belloni et al. (2013) is important for making uniform inference. Research along that line under high-dimensional endogeneity is important and we shall leave it for the future agenda.

Finally, as discussed in Bickel et al. (2009) and van de Geer (2008), high-dimensional regression problems can be thought of as an approximation to a nonparametric regression problem with a “dictionary” of functions or growing number of sieves. Then in the presence of endogenous regressors, model (3.1) is closely related to the non-parametric conditional moment restricted model considered by, e.g., Newey and Powell (2003), Ai and Chen (2003), and Chen and Pouzo (2008). While the penalization in the latter literature is similar to ours, it plays a different role and is introduced for different purposes. It will be interesting to find the underlying relationships between the two models.

Appendix A: Proofs for Section 2

Throughout the Appendix, C will denote a generic positive constant that may be different in different uses. Let sgn(·) denote the sign function.

A.1. Proof of Theorem 2.1

Proof. When β̂ is a local minimizer of Q_n(β), by the Karush-Kuhn-Tucker (KKT) condition, ∀l ≤ p,

$$\frac{\partial L_n(\widehat{\mathit{\beta }})}{\partial {\beta }_l}+v_l=0,$$

where $v_l=P_n^{\prime }(|{\widehat{\beta }}_l|)sgn({\widehat{\beta }}_l)$ if β̂_l ≠ 0; $v_l\in [-P_n^{\prime }(0^{+}),P_n^{\prime }(0^{+})]$ if β̂_l = 0, and we denote $P_n^{\prime }(0^{+})={lim}_{t\to 0^{+}}{P}_n^{\prime }(t)$. By the monotonicity of $P_n^{\prime }(t)$, we have $|\partial L_n(\widehat{\mathit{\beta }})/\partial {\beta }_l|\le P_n^{\prime }(0^{+})$. By Taylor expansion and the Cauchy-Schwarz inequality, there is β̃ on the segment joining β̂ and β₀ so that, on the event β̂_N = 0, (β̂_j − β_0j = 0 for all j ∉ S)

$$|\frac{\partial L_n(\widehat{\mathit{\beta }})}{\partial {\beta }_l}-\frac{\partial L_n({\mathit{\beta }}_0)}{\partial {\beta }_l}|=|\sum _{j=1}^p\frac{{\partial }^2{L}_n(\stackrel{\sim }{\mathit{\beta }})}{\partial {\beta }_l\partial {\beta }_j}({\widehat{\beta }}_j-{\beta }_{0j})|=|\sum _{j\in S}\frac{{\partial }^2{L}_n(\stackrel{\sim }{\mathit{\beta }})}{\partial {\beta }_l\partial {\beta }_j}({\widehat{\beta }}_j-{\beta }_{0j})|.$$

The Cauchy-Schwarz inequality then implies that max_l≤p |∂L_n(β̂)/∂β_l − ∂L_n(β₀)/∂β_l| is bounded by

$$\underset{l,j\le p}{max}\left|\frac{{\partial }^2{L}_n(\stackrel{\sim }{\mathit{\beta }})}{\partial {\beta }_l\partial {\beta }_j}\right|{\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert }_1\le \underset{l,j\le p}{max}\left|\frac{{\partial }^2{L}_n(\stackrel{\sim }{\mathit{\beta }})}{\partial {\beta }_l\partial {\beta }_j}\right|\sqrt{s}\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert .$$

By our assumption, √s‖β̂_S − β _0S‖ = o_p(1). Because P(β̂_N = 0) → 1,

$$\underset{l\le p}{max}|\frac{\partial L_n(\widehat{\mathit{\beta }})}{\partial {\beta }_l}-\frac{\partial L_n({\mathit{\beta }}_0)}{\partial {\beta }_l}|{\to }^{p}0.$$ (A.1)

This yields that ∂L_n(β₀)/∂β_l = o_p(1).

A.2. Proof of Theorem 2.2

Proof. Let ${\{X_{il}\}}_{i=1}^n$ be the i.i.d. data of X_l where X_l is an endogenous regressor. For the penalized LS, $L_n(\mathit{\beta })=\frac{1}{n}{\sum }_{i=1}^n{(Y_i-{\mathbf{X}}_i^T\mathit{\beta })}^2$. Under the theorem assumptions, by the strong law of large number ${\partial }_{{\beta }_l}{L}_n({\mathit{\beta }}_0)=-\frac{2}{n}{\sum }_{i=1}^n{X}_{il}(Y_i-{\mathbf{X}}_i^T{\mathit{\beta }}_0)\to -2E(X_l\epsilon )$ almost surely, which does not satisfy (2.1) of Theorem 2.1.

Appendix B: General Penalized Regressions

We present some general results for the oracle properties of penalized regressions. These results will be employed to prove the oracle properties for the proposed FGMM. Consider a penalized regression of the form:

$$\underset{\mathit{\beta }\in {ℝ}^p}{min}{L}_n(\mathit{\beta })+\sum _{j=1}^p{P}_n(|{\beta }_j|),$$

Lemma B.1

Under Assumption 4.1, if (β = (β₁,…, β_s)^T is such that max_j≤s |β_j − β_0S,j| ≤ d_n, then

$$|\sum _{j=1}^s{P}_n(|{\beta }_j|)-P_n(|{\beta }_{0S,j}|)|\le \Vert \mathit{\beta }-{\mathit{\beta }}_{0S}\Vert \sqrt{s}{P}_n^{\prime }(d_n).$$

Proof. By Taylor's expansion, there exists β* ( ${\mathit{\beta }}_j^{\ast }\ne 0$ for each j) lying on the line segment joining β and β_0S, such that

$$\sum _{j=1}^s(P_n(|{\beta }_j|)-P_n(|{\beta }_{0S,j}|)={(P_n^{\prime }(|{\beta }_1^{\ast }|)sgn({\beta }_1^{\ast }),\dots ,P_n^{\prime }(|{\beta }_s^{\ast }|)sgn({\beta }_s^{\ast }))}^T(\mathit{\beta }-{\mathit{\beta }}_{0S})\le \Vert \mathit{\beta }-{\mathit{\beta }}_{0S}\Vert \sqrt{s}\underset{j\le s}{max}{P}_n^{\prime }(|{\beta }_j^{\ast }|).$$

Then $min\{|{\beta }_j^{\ast }|:j\le s\}\ge min\{|{\beta }_{0S,j}|:j\le s\}-{max}_{j\le s}|{\beta }_j^{\ast }-{\beta }_{0S,j}|\ge 2d_n-d_n=d_n$.

Since $P_n^{\prime }$ is non-increasing (as P_n is concave), $P_n^{\prime }(|{\beta }_j^{\ast }|)\le P_n^{\prime }(d_n)$ for all j ≤ s. Therefore ${\sum }_{j=1}^s(P_n(|{\beta }_j|)-P_n(|{\beta }_{0S,j}|)\le \Vert \mathit{\beta }-{\mathit{\beta }}_{0S}\Vert \sqrt{s}{P}_n^{\prime }(d_n)$.

In the theorems below, with S = {j : β_0j ≠ 0}, define a so-called “oracle space” ℬ = {β ∈ ℝ^p : β_j = 0 if j ∉ S}. Write L_n(β_S, 0) = L_n(β) for $\mathit{\beta }={({\mathit{\beta }}_S^T,0)}^T\in ℬ$. Let β_S = (β_S1,…, β_Ss) and

$${\nabla }_S{L}_n({\mathit{\beta }}_S,0)={(\frac{\partial L_n({\mathit{\beta }}_S,0)}{\partial {\beta }_{S1}},\dots ,\frac{\partial L_n({\mathit{\beta }}_S,0)}{\partial {\beta }_{Ss}})}^T.$$

Theorem B.1 (Oracle Consistency)

Suppose Assumption 4.1 holds. In addition, suppose L_n(β_S, 0) is twice differentiable with respect to β_S in a neighborhood of β_0S restricted on the subspace ℬ, and there exists a positive sequence a_n = o(d_n) such that:

1. $$\Vert {\nabla }_S{L}_n({\mathit{\beta }}_{0S},0)\Vert =O_p(a_n).$$

2. For any ε > 0, there is C_ε > 0 so that for all large n,

   $$P({\lambda }_{min}({\nabla }_S^2{L}_n({\mathit{\beta }}_{0S},0))>C_{\epsilon })>1-\epsilon .$$ (B.1)

3. For any ε > 0, δ > 0, and any nonnegative sequence α_n = o(d_n), there is N > 0 such that when n > N,

   $$P(\underset{\Vert {\beta }_S-{\beta }_{0S}\Vert \le {\alpha }_n}{sup}{\Vert {\nabla }_S^2{L}_n({\mathit{\beta }}_S,0)-{\nabla }_S^2{L}_n({\mathit{\beta }}_{0S},0)\Vert }_F\le \delta )>1-\epsilon .$$ (B.2)

Then there exists a local minimizer $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_S^T,0)}^T$ of

$$Q_n({\mathit{\beta }}_S,0)=L_n({\mathit{\beta }}_S,0)+\sum _{j\in S}{P}_n(|{\beta }_j|)$$

such that $\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert =O_p(a_n+\sqrt{s}{P}_n^{\prime }(d_n))$. In addition, for an arbitrarily small ε > 0, the local minimizer β̂ is strict with probability at least 1 − ε, for all large n.

Proof. The proof is a generalization of the proof of Theorem 3 in Fan and Lv (2011). Let $k_n=a_n+\sqrt{s}{P}_n^{\prime }(d_n)$. It is our assumption that k_n = o(1). Write Q₁(β_S) = Q_n(β_S, 0), and L₁(β_S) = L_n(β_S, 0). In addition, write

$$\nabla L_1({\mathit{\beta }}_S)=\frac{\partial L_n}{\partial {\mathit{\beta }}_S}({\mathit{\beta }}_S,0),\text{and}{\nabla }^2{L}_1({\mathit{\beta }}_S)=\frac{{\partial }^2{L}_n}{\partial {\mathit{\beta }}_S{\mathit{\beta }}_S^T}({\mathit{\beta }}_S,0).$$

Define 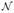_τ = {β ∈ ℝ^s : ‖ β − β_0S‖ ≤k_nτ} for some τ > 0. Let ∂ _τ denote the boundary of _τ. Now define an event

$$H_n(\tau )=\{Q_1({\mathit{\beta }}_{0S})<\underset{{\mathit{\beta }}_S\in \partial {\mathcal{N}}_{\tau }}{min}{Q}_1({\mathit{\beta }}_S)\}.$$

On the event H_n(τ), by the continuity of Q₁, there exists a local minimizer of Q₁ inside _τ. Equivalently, there exists a local minimizer ${({\widehat{\mathit{\beta }}}_S^T,0)}^T$ of Q_n restricted on $ℬ=\{\mathit{\beta }={({\mathit{\beta }}_S^T,0)}^T\}$ inside $\{\mathit{\beta }={({\mathit{\beta }}_S^T,0)}^T:{\mathit{\beta }}_S\in {\mathcal{N}}_{\tau }\}$. Therefore, it suffices to show that ∀ε > 0, there exists τ > 0 so that P(H_n(τ)) > 1 − ε for all large n, and that the local minimizer is strict with probability arbitrarily close to one.

For any β_S ∈ ∂ _τ, which is ‖β_S − β_0S‖ = k_nτ, there is β* lying on the segment joining β_S and β_0S such that by the Taylor's expansion on L₁ (β_S):

$$Q_1({\mathit{\beta }}_S)-Q_1({\mathit{\beta }}_{0S})={({\mathit{\beta }}_S-{\mathit{\beta }}_{0S})}^T\nabla L_1({\mathit{\beta }}_{0S})+\frac{1}{2}{({\mathit{\beta }}_S-{\mathit{\beta }}_{0S})}^T{\nabla }^2{L}_1({\mathit{\beta }}^{\ast })({\mathit{\beta }}_S-{\mathit{\beta }}_{0S})+\sum _{j=1}^s[P_n(|{\beta }_{Sj}|)-P_n(|{\beta }_{0S,j}|)].$$

By Condition (i) ‖∇L₁(β_0S)‖ = O_p(a_n), for any ε > 0, there exists C₁ > 0, so that the event H₁ satisfies P(H₁) > 1 − ε/4 for all large n, where

$$H_1=\{{({\mathit{\beta }}_S-{\mathit{\beta }}_{0S})}^T\nabla L_1({\mathit{\beta }}_{0S})\ge -C_1\Vert {\mathit{\beta }}_S-{\mathit{\beta }}_{0S}\Vert a_n\}.$$ (B.3)

In addition, Condition (ii) yields that there exists C_ε > 0 such that the following event H₂ satisfies P(H₂) ≥ 1 − ε/4 for all large n, where

$$H_2=\{{({\mathit{\beta }}_S-{\mathit{\beta }}_{0S})}^T{\nabla }^2{L}_1({\mathit{\beta }}_{0S})({\mathit{\beta }}_S-{\mathit{\beta }}_{0S})>C_{\epsilon }{\Vert {\mathit{\beta }}_S-{\mathit{\beta }}_{0S}\Vert }^2\}.$$ (B.4)

Define another event H₃ = {‖∇²L₁(β_0S) − ∇²L₁(β*)‖_F < C_ε/4}. Since ‖β_S − β_0S‖ = k_nτ, by Condition (B.2) for any τ > 0, P(H₃) > 1 — ε/4 for all large n. On the event H₂ ∩ H₃, the following event H₄ holds:

$$H_4=\{{({\mathit{\beta }}_S-{\mathit{\beta }}_{0S})}^T{\nabla }^2{L}_1({\mathit{\beta }}^{\ast })({\mathit{\beta }}_S-{\mathit{\beta }}_{0S})>\frac{3C_{\epsilon }}{4}{\Vert {\mathit{\beta }}_S-{\mathit{\beta }}_{0S}\Vert }^2\}.$$

By Lemma B.1, ${\sum }_{j=1}^s[P_n(|{\beta }_{Sj}|)-P_n(|{\beta }_{0S,j}|)]\ge -\sqrt{s}{P}_n^{\prime }(d_n)\Vert {\mathit{\beta }}_S-{\mathit{\beta }}_{0S}\Vert$. Hence for any β_S ∈ ∂ _τ, on H₁ ∩ H₄,

$$Q_1({\mathit{\beta }}_S)-Q_1({\mathit{\beta }}_{0S})\ge k_n\tau (\frac{3k_n\tau C_{\epsilon }}{8}-C_1{a}_n-\sqrt{s}{P}_n^{\prime }(d_n)).$$

For $k_n=a_n+\sqrt{s}{P}_n^{\prime }(d_n)$, we have $C_1{a}_n+\sqrt{s}{P}_n^{\prime }(d_n)\le (C_1+1)k_n$. Therefore, we can choose τ > 8(C₁ + 1)/(3C_ε) so that Q₁(β_S)−Q₁(β_0S) ≥ 0 uniformly for β ∈ ∂ _τ. Thus for all large n, when τ > 8(C₁ + 1)/(3C_ε),

$$P(H_n(\tau ))\ge P(H_1\cap H_4)\ge 1-\epsilon .$$

It remains to show that the local minimizer in _τ (denoted by β̂_S) is strict with a probability arbitrarily close to one. For each h ∈ ℝ/{0}, define

$$\psi (h)=\underset{\epsilon \to 0^{+}}{lim\; sup}\underset{\underset{(t_1,t_2)\in (|h|-\epsilon ,|h|+\epsilon )}{t_1<t_2}}{sup}-\frac{P_n^{\prime }(t_2)-P_n^{\prime }(t_1)}{t_2-t_1}.$$

By the concavity of P_n(·), ψ(·) ≥ 0. We know that L₁ is twice differentiable on ℝ^s. For β_S ∈ _τ Let A(β_S) = ∇²L₁(β_S) − diag{ψ(β_S1), …, ψ(β_Ss)}. It suffices to show that A(β̂_S) is positive definite with probability arbitrarily close to one. On the event H₅ = {η(β̂_S) ≤ sup_{β∈B(β0S,cdn)} η(β)} (where cd_n is as defined in Assumption 4.1(iv)),

$$\underset{j\le s}{max}\psi ({\widehat{\beta }}_{S,j})\le \eta ({\widehat{\mathit{\beta }}}_S)\le \underset{\beta \in B({\beta }_{0S},c{d}_n)}{sup}\eta (\mathit{\beta })\}.$$

Also define events H₆ = {‖∇²L₁(β_S) − ∇²L₁(β_0S)‖_F < C_ε/4} and H₇ = {λ_min(∇²L₁(β_0S)) > C_ε. Then on H₅∩H₆∩H7, for any α ∈ ℝ^s satisfying ‖α‖ = 1, by Assumption 4.1(iv),

$${\mathit{\alpha }}^T\mathbf{A}({\widehat{\mathit{\beta }}}_S)\mathit{\alpha }\ge {\mathit{\alpha }}^T{\nabla }^2{L}_1({\mathit{\beta }}_{0S})\mathit{\alpha }-|{\mathit{\alpha }}^T({\nabla }^2{L}_1({\widehat{\mathit{\beta }}}_S)-{\nabla }^2{L}_1({\mathit{\beta }}_{0S}))\mathit{\alpha }|-\underset{j\le s}{max}\psi ({\widehat{\beta }}_{S,j})\ge 3C_{\epsilon }/4-\underset{\beta \in B({\beta }_{0S},d_n)}{sup}\eta (\mathit{\beta })\ge C_{\epsilon }/4$$

for all large n. This then implies λ_min(A(β̂_S)) ≥ C_ε/4 for all large n.

We know that P(λ_min[∇²L₁(β_0S)] > C_ε) > 1 − ε. It remains to show that P(H₅ ∩ H₆) > 1 — ε for arbitrarily small ε. Because k_n = o(d_n), for an arbitrarily small ε > 0, P(H₅) > P(β̂_S ∈ B(β_0S, cd_n)) ≥ 1 − ε/2 for all large n. Finally,

$$P(H_6^c)\le P(H_6^c,\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert \le k_n)+P(\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert >k_n)\le P(\underset{\Vert {\beta }_S-{\beta }_{0S}\Vert \le k_n}{sup}{\Vert {\nabla }^2{L}_1({\mathit{\beta }}_S)-{\nabla }^2{L}_1({\mathit{\beta }}_{0S})\Vert }_F\ge C_{\epsilon }/4)+\epsilon /4=\epsilon /2.$$

The previous theorem assumes that the true support S is known, which is not practical. We therefore need to derive the conditions under which S can be recovered from the data with probability approaching one. This can be done by demonstrating that the local minimizer of Q_n restricted on ℬ is also a local minimizer on ℝ^p. The following theorem establishes the variable selection consistency of the estimator, defined as a local solution to a penalized regression problem on ℝ^p.

For any β ∈ ℝ^p, define the projection function

$$\mathbb{T}\mathit{\beta }={({\beta }_1^{\prime },{\beta }_2^{\prime },\dots ,{\beta }_p^{\prime })}^T\in ℬ,{\beta }_j^{\prime }=\{\begin{array}{cc}{\beta }_j& \text{if}j\in S\\ 0,& \text{if}j\notin S\end{array}.$$ (B.5)

Theorem B.2(Variable selection)

Suppose L_n : ℝ^p → ℝ satisfies the conditions in Theorem B.1, and Assumption 4.1 holds. Assume the following Condition A holds:

Condition A: With probability approaching one, for β̂_S in Theorem B.1, there exists a neighborhood ℋ ⊂ ℝ^p of ${({\widehat{\mathit{\beta }}}_S^T,0)}^T$, such that for all $\mathit{\beta }={({\mathit{\beta }}_S^T,{\mathit{\beta }}_N^T)}^T\in \mathscr{H}$ but β_N ≠ 0,

$$L_n(\mathbb{T}\mathit{\beta })-L_n(\mathit{\beta })<\sum _{j\notin S}{P}_n(|{\beta }_j|).$$ (B.6)

Then (i) with probability approaching one, $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_S^T,0)}^T$ is a local minimizer in ℝ^p of

$$Q_n(\mathit{\beta })=L_n(\mathit{\beta })+\sum _{i=1}^p{P}_n(|{\beta }_i|)$$

(ii) For an arbitrarily small ε > 0, the local minimizer β̂ is strict with probability at least 1 − ε, for all large n.

Proof. Let $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_S^T,0)}^T$ with β̂_S being the local minimizer of Q₁(β_S) as in Theorem B.1. We now show: with probability approaching one, there is a random neighborhood of β̂, denoted by ℋ, so that ∀β = (β_S, β_N) ∈ ℋ with β_N ≠ 0, we have Q_n(β̂) < Q_n(β). The last inequality is strict.

To show this, first note that we can take ℋ sufficiently small so that Q₁(β̂) ≤ Q₁(β_S) because β̂_S is a local minimizer of Q₁(β_S) from Theorem B.1. Recall the projection defined to be $\mathbb{T}\mathit{\beta }={({\mathit{\beta }}_S^T,0)}^T$, and Q_n( β) = Q₁(β_S) by the definition of Q₁. We have Q_n(β̂) = Q₁(β̂_S) ≤ Q₁(β_S) = Q_n( β). Therefore, it suffices to show that with probability approaching one, there is a sufficiently small neighborhood of ℋ of β ^, so that for any $\mathit{\beta }={({\mathit{\beta }}_S^T,{\mathit{\beta }}_N^T)}^T\in \mathscr{H}$ with β_N ≠ 0, Q_n( β) < Q_n(β).

In fact, this is implied by Condition (B.6):

$$Q_n(\mathbb{T}\mathit{\beta })-Q_n(\mathit{\beta })=L_n(\mathbb{T}\mathit{\beta })-L_n(\mathit{\beta })-(\sum _{j=1}^p{P}_n({\beta }_j)-\sum _{j=1}^s{P}_n(|{(\mathbb{T}\mathit{\beta })}_j|))<0.$$ (B.7)

The above inequality, together with the last statement of Theorem B.1 implies part (ii) of the theorem.

Appendix C: Proofs for Section 4

Throughout the proof, we write F_iS = F_i(β_0S), H_iS = H_i(β_0S) and ${\mathbf{V}}_{iS}={({\mathbf{F}}_{iS}^T,{\mathbf{H}}_{iS}^T)}^T$.

Lemma C.1

1. ${max}_{l\le p}|\frac{1}{n}{\sum }_{i=1}^n{(F_{ij}-{\overline{F}}_j)}^2-var(F_j)|=o_p(1).$

2. ${max}_{l\le p}|\frac{1}{n}{\sum }_{i=1}^n{(H_{ij}-{\overline{H}}_j)}^2-var(H_j)|=o_p(1).$

3. sup_β∈ℝ^p λ_max(J(β)) = O_p(1), and λ_min(J(β₀)) is bounded away from zero with probability approaching one.

Proof. Parts (i)(ii) follow from an application of the standard large deviation theory by using Bernstein inequality and Bonferroni's method. Part (iii) follows from the assumption that var(F_j) and var(H_j) are bounded uniformly in j ≤ p.

C.1. Verifying conditions in Theorems B.1, B.2

C.1.1. Verifying conditions in Theorem B.1

For any β ∈ℝ^p, we can write $\mathbb{T}\mathit{\beta }={({\mathit{\beta }}_S^T,0)}^T$. Define

$${\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_S)={[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_S){\mathbf{V}}_{iS}]}^T\mathbf{J}({\mathit{\beta }}_0)[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_S){\mathbf{V}}_{iS}].$$

Then L̃_FGMM (β_S) = L_FGMM(β_S, 0).

Condition (i)

$\nabla {\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})=2{\mathbf{A}}_n({\mathit{\beta }}_{0S})\mathbf{J}({\mathit{\beta }}_0)[\frac{1}{n}{\sum }_{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S}){\mathbf{V}}_{iS}]$, where

$${\mathbf{A}}_n({\mathit{\beta }}_S)\equiv \frac{1}{n}\sum _{i=1}^{n}m(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_S){\mathbf{X}}_{iS}{\mathbf{V}}_{iS}^T.$$ (C.1)

By Assumption 4.5, ‖A_n(β₀)‖ = O_p(1). In addition, the elements in J(β₀) are uniformly bounded in probability due to Lemma C.1. Hence $\Vert \nabla {\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})\Vert \le O_p(1)\Vert \frac{1}{n}{\sum }_{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S}){\mathbf{V}}_{iS}\Vert$. Due to $Eg(Y,{\mathbf{X}}_s^T{\mathit{\beta }}_{0S}){\mathbf{V}}_S=0$, using the exponential-tail Bernstein inequality with Assumption 4.3 plus Bonferroni inequality, it can be shown that there is C > 0 such that for any t > 0,

$$P(\underset{l\le p}{max}|\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S})F_{li}|>t)<P(\underset{l\le p}{max}P(|\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S})F_{li}|>t)\le exp(logp-C{t}^2/n),$$

which implies ${max}_{l\le p}|\frac{1}{n}{\sum }_{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S})F_{li}|=O_p(\sqrt{\frac{logp}{n}})$. Similarly, ${max}_{l\le p}|\frac{1}{n}{\sum }_{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S})H_{li}|=O_p(\sqrt{\frac{logp}{n}})$. Hence $\Vert \nabla {\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})\Vert =O_p(\sqrt{(slogp)/n})$.

Condition (ii)

Straightforward but tedious calculation yields

$${\nabla }^2{\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})=\sum ({\mathit{\beta }}_{0S})+\mathbf{M}({\mathit{\beta }}_{0S}),$$

where Σ(β_0S) = 2A_n(β_0S)J(β₀)A_n(β_0S)^T, and M(β_0S) = 2Z(β_0S)B(β_0S), with (suppose X_iS = (X_il1, …, X_ils)^T)

$$\mathbf{Z}({\mathit{\beta }}_{0S})=\frac{1}{n}\sum _{i=1}^n{q}_i(Y_i,{\mathbf{X}}_{iS}{\mathit{\beta }}_{0S})(X_{i{l}_1}{\mathbf{X}}_{iS},\dots ,X_{i{l}_s}{\mathbf{X}}_{iS}){\mathbf{V}}_{iS}^T,\mathbf{B}({\mathit{\beta }}_{0S})=\mathbf{J}({\mathit{\beta }}_0)\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S}){\mathbf{V}}_{iS}.$$

It is not hard to obtain ${\Vert \mathbf{B}({\mathit{\beta }}_{0S})\Vert }_F=O_p(\sqrt{slogp/n})$, and ‖Z(β_0S)‖_F = O_p(s), and hence ${\Vert \mathbf{M}({\mathit{\beta }}_{0S})\Vert }_F=O_p(s\sqrt{slogp/n})=o_p(1)$.

Moreover, there is a constant C > 0, $P({min}_{j\in S}\widehat{var}{(X_j)}^{-1}>C)>1-\epsilon$ and $P({min}_{j\le p}\widehat{var}{(X_j^2)}^{-1}>C)>1-\epsilon$ for all large n and any ε > 0. This then implies P(λ_min[J(β₀)] > C) > 1 − ε. Recall Assumption 4.5 that λ_min(EA_n(β_0S)EA_n(β_0S)^T) > C₂ for some C₂ > 0. Define events

$$G_1=\{{\lambda }_{min}[\mathbf{J}({\mathit{\beta }}_0)]>C\},G_2=\{\Vert \mathbf{M}({\mathit{\beta }}_{0S})\Vert <C_{2}C/5\}{G}_3=\{\Vert {\mathbf{A}}_n({\mathit{\beta }}_{0S}){\mathbf{A}}_n{({\mathit{\beta }}_{0S})}^T-E{\mathbf{A}}_n({\mathit{\beta }}_{0S})E{\mathbf{A}}_n{({\mathit{\beta }}_{0S})}^T)\Vert <C_2/5\}.$$

Then on the event ${\cap }_{i=1}^3{G}_i$,

$${\lambda }_{min}[{\nabla }^2{\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})]\ge 2{\lambda }_{min}(\mathbf{J}({\mathit{\beta }}_0)){\lambda }_{min}({\mathbf{A}}_n({\mathit{\beta }}_{0S}){\mathbf{A}}_n{({\mathit{\beta }}_{0S})}^T)-{\Vert \mathbf{M}({\mathit{\beta }}_{0S})\Vert }_F\ge 2C[{\lambda }_{min}(E{\mathbf{A}}_n({\mathit{\beta }}_{0S})E{\mathbf{A}}_n{({\mathit{\beta }}_{0S})}^T)-C_2/5]-C_{2}C/5\ge 7C{C}_2/5.$$

Note that $P({\cap }_{i=1}^3{G}_i)\ge 1-{\sum }_{i=1}^{3}P(G_i^c)\ge 1-3\epsilon$. Hence Condition (B.1) is then satisfied.

Condition (iii)

It can be shown that for any nonnegative sequence α_n = o(d_n) where d_n = min_k∈S |β_0k|/2, we have

$$P(\underset{\Vert {\beta }_S-{\beta }_{0S}\Vert \le {\alpha }_n}{sup}{\Vert \mathbf{M}({\mathit{\beta }}_S)-\mathbf{M}({\mathit{\beta }}_{0S})\Vert }_F\le \delta )>1-\epsilon .$$ (C.2)

holds for any ε and δ > 0. As for Σ(β_S), note that for all β_S such that ‖β_S − β_0S‖ < d_n/2, we have β_S,k ≠ 0 for all k ≤ s. Thus J(β_S) = J(β_0S). Then P(sup_{‖βS−β0S‖<αn}‖Σ(β_S) − Σ(β_0S)‖_F ≤ δ) > 1 − ε holds since P(sup_{‖βS−β0S‖<αn}‖A_n(β_S) − A_n(β_0S)‖_F ≤ δ) > 1 − ε.

C.1.2. Verifying conditions in Theorem B.2

Proof. We verify Condition A of Theorem B.2, that is, with probability approaching one, there is a random neighborhood ℋ of $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_S^T,0)}^T$, such that for any $\mathit{\beta }={({\beta }_{\mathit{S}}^T,{\mathit{\beta }}_N^T)}^T\in \mathscr{H}$ with β_N ≠ 0, condition (B.6) holds.

Let F( β) = {F_l : l ∈ S, β_l ≠ 0} and H( β) = {H_l: l ∈ S, β_l ≠ 0} for any fixed $\mathit{\beta }={({\mathit{\beta }}_S^T,{\mathit{\beta }}_N^T)}^T$. Define

$$\mathrm{\Xi }(\mathit{\beta })={[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{F}}_i(\mathbb{T}\mathit{\beta })]}^T{\mathbf{J}}_1(\mathbb{T}\mathit{\beta })[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{F}}_i(\mathbb{T}\mathit{\beta })]+{[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{H}}_i(\mathbb{T}\mathit{\beta })]}^T{\mathbf{J}}_2(\mathbb{T}\mathit{\beta })[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{H}}_i(\mathbb{T}\mathit{\beta })]$$

where J₁( β) and J₂( β) are the upper-|S|₀ and lower-|S|₀ sub matrices of J( β). Hence L_FGMM( (β)) = Ξ( β). Then L_FGMM(β) − Ξ(β) equals

$$\sum _{l\notin S,{\beta }_l\ne 0}[w_{l1}{(\frac{1}{n}\sum _{i=1}^{n}g(y_i,{\mathbf{X}}_i^T\mathit{\beta })F_{il})}^2+w_{l2}{(\frac{1}{n}\sum _{i=1}^{n}g(y_i,{\mathbf{X}}_i^T\mathit{\beta })H_{il})}^2],$$

where w_l1 = 1/var̂(F_l and w_l2 = 1/var̂(H_l. So L_FGMM(β) ≥ Ξ(β). This then implies L_FGMM( β) − L_FGMM(β) ≤ Ξ( β) − Ξ(β). By the mean value theorem, there exists λ ∈ (0,1), for $\mathbf{h}={({\mathit{\beta }}_S^T,-\lambda {\mathit{\beta }}_N^T)}^T$,

$$\mathrm{\Xi }(\mathbb{T}\mathit{\beta })-\mathrm{\Xi }(\mathit{\beta })=\sum _{l\notin S,{\beta }_l\ne 0}{\beta }_l{[\frac{1}{n}\sum _{i=1}^n{X}_{il}m(Y_i,{\mathbf{X}}_i^T\mathbf{h}){\mathbf{F}}_i(\mathbb{T}\mathit{\beta })]}^T{\mathbf{J}}_1(\mathbb{T}\mathit{\beta })[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathbf{h}){\mathbf{F}}_i(\mathbb{T}\mathit{\beta })]+\sum _{l\notin S,{\beta }_l\ne 0}{\beta }_l{[\frac{1}{n}\sum _{i=1}^n{X}_{il}m(Y_i,{\mathbf{X}}_i^T\mathbf{h}){\mathbf{H}}_i(\mathbb{T}\mathit{\beta }]}^T{\mathbf{J}}_2(\mathbb{T}\mathit{\beta })[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathbf{h}){\mathbf{H}}_i(\mathbb{T}\mathit{\beta })]\equiv \sum _{l\notin S,{\beta }_l\ne 0}{\beta }_l(a_l(\mathit{\beta })+b_l(\mathit{\beta })).$$

Let ℋ be a neighborhood of $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_S^T,0)}^T$ (to be determined later). We have shown that Ξ ( β) − Ξ (β) = Σ_{l∉S,βl≠0} β_l(a_l(β) + b_l(β)), for any β ∈ ℋ,

$$a_l(\mathit{\beta })={[\frac{1}{n}\sum _{i=1}^n{X}_{il}m(Y_i,{\mathbf{X}}_i^T\mathbf{h}){\mathbf{F}}_i(\mathbb{T}\mathit{\beta })]}^T{\mathbf{J}}_1(\mathbb{T}\mathit{\beta })[\frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathbf{h}){\mathbf{F}}_i(\mathbb{T}\mathit{\beta })],$$

and b_l(β) is defined similarly based on H. Note that h lies in the segment joining β and β, and is determined by β, hence should be understood as a function of β. By our assumption, there is a constant M, such that |m(t₁, t₂) | and |q(t₁, t₂)|, the first and second partial derivatives of g, and $E{X}_l^2{F}_k^2$ are all bounded by M uniformly in t₁, t₂ and l, k ≤ p. Therefore the Cauchy-Schwarz and triangular inequalities imply

$${\Vert \frac{1}{n}\sum _{i=1}^n{X}_{il}m(Y_i,{\mathbf{X}}_i^T\mathbf{h}){\mathbf{F}}_i(\mathbb{T}\mathit{\beta })\Vert }^2\le M^2\underset{l\le p}{max}|\frac{1}{n}\sum _{i=1}^n{\Vert X_{il}{\mathbf{F}}_{iS}\Vert }^2-E{\Vert X_l{\mathbf{F}}_S\Vert }^2|+M^2\underset{l\notin S}{max}E{\Vert X_l{\mathbf{F}}_S\Vert }^2.$$

Hence there is a constant M₁ such that if we define the event (again, keep in mind that h is determined by β)

$$B_n=\{\underset{\beta \in \mathscr{H}}{sup}\Vert \frac{1}{n}\sum _{i=1}^n{X}_{il}m(Y_i,{\mathbf{X}}_i^T\mathbf{h}){\mathbf{F}}_i(\mathbb{T}\mathit{\beta })\Vert <\sqrt{s}{M}_1,\underset{\beta \in \mathscr{H}}{sup}\Vert {\mathbf{J}}_1(\mathbb{T}\mathit{\beta })\Vert <M_1\},$$

then P(B_n) → 1. In addition with probability one,

$$\Vert \frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathbf{h}){\mathbf{F}}_i(\mathbb{T}\mathit{\beta })\Vert \le \underset{\beta \in \mathscr{H}}{sup}\Vert \frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{F}}_{iS}\Vert \le \underset{\beta \in \mathscr{H}}{sup}\Vert \frac{1}{n}\sum _{i=1}^n[g(Y_i,{\mathbf{X}}_i^T\mathit{\beta })-g(Y_i,{\mathbf{X}}_i^T\widehat{\mathit{\beta }})]{\mathbf{F}}_{iS}\Vert +\Vert \frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\widehat{\mathit{\beta }}){\mathbf{F}}_{iS}\Vert \equiv Z_1+Z_2,$$

where, $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_S^T,0)}^T$. For some deterministic sequence r_n (to be determined later), we can define the above ℋ to be dddd

$$\mathscr{H}=\{\mathit{\beta }:\Vert \mathit{\beta }-\widehat{\mathit{\beta }}\Vert <r_n/p\}$$

then sup_β∈ℋ‖β − β̂‖₁ < r_n. By the mean value theorem and Cauchy Schwarz inequality, there is β̃:

$$Z_1=\underset{\beta \in \mathscr{H}}{sup}\Vert \frac{1}{n}\sum _{i=1}^{n}m(Y_i,{\mathbf{X}}_i^T\stackrel{\sim }{\mathit{\beta }}){\mathbf{F}}_{iS}{\mathbf{X}}_i^T(\mathit{\beta }-\widehat{\mathit{\beta }})\Vert \le \sqrt{s}\underset{\beta \in \mathscr{H}}{sup}{\Vert \frac{1}{n}\sum _{i=1}^{n}m(Y_i,{\mathbf{X}}_i^T\stackrel{\sim }{\mathit{\beta }}){\mathbf{F}}_{iS}{\mathbf{X}}_i^T\Vert }_{\infty }{r}_n\le M\sqrt{s}\underset{k\in S,l\le p}{max}|\frac{1}{n}\sum _{i=1}^n{(F_{ik}{X}_{il})}^2{|}^{1/2}{r}_n.$$

Hence there is a constant M₂ such that P(Z₁ < M₂√sr_n) → 1.

Let ${\epsilon }_i=g(Y_i,{\mathbf{X}}_i^T{\mathit{\beta }}_0)$. By the triangular inequality and mean value theorem, there are h̃ and $\stackrel{\sim }{\stackrel{\sim }{\mathbf{h}}}$ lying in the segment between β̂ and β₀ such that

$$Z_2\le \Vert \frac{1}{n}\sum _{i=1}^n{\epsilon }_i{\mathbf{F}}_{iS}\Vert +\Vert \frac{1}{n}\sum _{i=1}^{n}m(Y_i,{\mathbf{X}}_i^T\stackrel{\sim }{\mathbf{h}}){\mathbf{F}}_{iS}{\mathbf{X}}_{iS}^T({\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S})\Vert \le \sqrt{s}\underset{j\le p}{max}|\frac{1}{n}\sum _{i=1}^n{\epsilon }_i{F}_{ij}|+\Vert \frac{1}{n}\sum _{i=1}^{n}m(Y_i,{\mathbf{X}}_i^T{\mathit{\beta }}_0){\mathbf{F}}_{iS}{\mathbf{X}}_{iS}^T({\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S})\Vert +\Vert \frac{1}{n}\sum _{i=1}^{n}q(Y_i,{\mathbf{X}}_i^T\stackrel{\sim }{\stackrel{\sim }{\mathbf{h}}}){\mathbf{X}}_{iS}^T({\mathit{\beta }}_{0S}-{\stackrel{\sim }{\mathbf{h}}}_S){\mathbf{F}}_{iS}{\mathbf{X}}_{iS}^T({\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S})\Vert \le O_p(\sqrt{slogp/n})+(o_p(1)+\Vert Em(Y,{\mathbf{X}}^T{\mathit{\beta }}_0){\mathbf{F}}_S{\mathbf{X}}_S^T\Vert )\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert {(\frac{1}{n}\sum _{i=1}^n{\Vert q(Y_i,{\mathbf{X}}_i^T\stackrel{\sim }{\stackrel{\sim }{\mathbf{h}}}){\mathbf{X}}_{iS}\Vert }^2)}^{1/2}{(\frac{1}{n}\sum _{i=1}^n{\Vert {\mathbf{X}}_{iS}\Vert }^2{\Vert {\mathbf{F}}_{iS}\Vert }^2)}^{1/2}{\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert }^2,$$

where we used the assumption that $\Vert Em(Y,{\mathbf{X}}^T{\mathit{\beta }}_0){\mathbf{X}}_S{\mathbf{F}}_S^T\Vert =O(1)$. We showed that $\Vert \nabla {\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})\Vert =O_p(\sqrt{(slogp)}/n)$ in the proof of verifying conditions in Theorem B.1. Hence by Theorem B.1, $\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert =O_p(\sqrt{slogp/n}+\sqrt{s}{P}_n^{\prime }(d_n))$. Thus

$$Z_2=O_p(\sqrt{\frac{slogp}{n}}+\sqrt{s}{P}_n^{\prime }(d_n)+\frac{s^2\sqrt{s}logs}{n}+s^2\sqrt{s}{P}_n^{\prime }{(d_n)}^2)\equiv O_p({\xi }_n).$$

By the assumption $\sqrt{s}{\xi }_n=o(P_n^{\prime }(0^{+}))$, hence $P(Z_2<P_n^{\prime }(0^{+})/(8\sqrt{s}{M}_1^2))\to 1$, where M₁ is defined in the event B_n. Consequently, if we define an event $D_n=\{Z_1<M_2\sqrt{s}{r}_n,Z_2<P_n^{\prime }(0^{+})/(8\sqrt{s}{M}_1^2)\}$, then P(B_n ∩ D_n → 1, and on the event B_n ∩ D_n,

$$\underset{\beta \in \mathscr{H}}{sup}|a_l(\mathit{\beta })|\le M_1^2\sqrt{s}(M_2\sqrt{s}{r}_n+P_n^{\prime }(0^{+}))/(8\sqrt{s}{M}_1^2)=M_1^2{M}_{2}s{r}_n+P_n^{\prime }(0^{+})/8.$$

We can $r_n<P_n^{\prime }(0^{+})/(8M_1^2{M}_{2}s)$, and thus ${sup}_{\beta \in \mathscr{H}}|a_l(\mathit{\beta })|\le P_n^{\prime }(0^{+})/4$.

On the other hand, Because ( 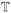β)_j = β_j for either j ∈ S or β_j = 0, there exists λ₂ ∈ (0,1),

$$\sum _{j=1}^p(P_n(|{\beta }_j|)-P_n(|{(\mathbb{T}\mathit{\beta })}_j|)=\sum _{j\notin S}{P}_n(|{\beta }_J|)=\sum _{l\notin S,{\beta }_l\ne 0}|{\beta }_l|P_n^{\prime }({\lambda }_2|{\beta }_l|).$$

For all l ∉ S, |β_l| ≤ ‖β − β₀‖₁ < r_n. Due to the non-increasingness of $P_n^{\prime }(t)$, ${\sum }_{l\notin S}{P}_n(|{\beta }_l|)\ge {\sum }_{l\notin S,{\beta }_l\ne 0}|{\beta }_l|P_n^{\prime }(r_n)$. We can make r_n further smaller so that $P_n^{\prime }(r_n)\ge P_n^{\prime }(0^{+})/2$ which is satisfied for example, when r_n < λ_n if SCAD(λ_n) is used as the penalty. Hence

$$\sum _{l\notin S}{\beta }_l{a}_l(\mathit{\beta })\le \sum _{l\notin S}|{\beta }_l|\frac{P_n^{\prime }(0^{+})}{4}\le \sum _{l\notin S}|{\beta }_l|\frac{P_n^{\prime }(r_n)}{2}\le \frac{1}{2}\sum _{l\notin S}{P}_n(|{\beta }_l|).$$

Using the same argument we can show ${\sum }_{l\notin S}{\beta }_l{b}_l(\mathit{\beta })\le \frac{1}{2}{\sum }_{l\notin S}{P}_n(|{\beta }_l|)$. Hence L_FGMM( 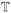β) − L_FGMM(β) < Σ_{l∉S,βl≠0} β_l (a_l(β)+b_l(β)) ≤ Σ_l∉S P_n(|β_l|) for all β ∈ {β : ‖β − β̂‖₁ < r_n} under the event B_n ∩ D_n. Here r_n is such that $r_n<P_n^{\prime }(0^{+})/(8M_1^2{M}_{2}s)$ and $P_n^{\prime }(r_n)\ge P_n^{\prime }(0^{+})/2$. This proves Condition A of Theorem B.2 due to P(B_n ∩ D_n) → 1.

C.2. Proof of Theorem 4.1: parts (ii) (iii)

We apply Theorem B.2 to infer that with probability approaching one, $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_S^T,0)}^T$is a local minimizer of Q_FGMM(β). Note that under the event that ${({\widehat{\mathit{\beta }}}_S^T,0)}^T$ is a local minimizer of Q_FGMM (β), we then infer that Q_n (β) has a local minimizer ${({\widehat{\mathit{\beta }}}_S^T,{\widehat{\mathit{\beta }}}_N^T)}^T$such that β̂_N = 0. This reaches the conclusion of part (ii). This also implies P(Ŝ ⊂ S) → 1.

By Theorem B.1, and $\Vert \nabla {\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})\Vert =O_p(\sqrt{(slogp)/n})$ as proved in verifying conditions in Theorem B.1, we have ‖β_0S − β̂_S‖ = o_p(d_n). So

$$P(S\not\subset \widehat{S})=P(\exists j\in S,{\widehat{\beta }}_j=0)\le P(\exists j\in S,|{\beta }_{0j}-{\widehat{\beta }}_j|\ge |{\beta }_{0j}|)\le P(\underset{j\in S}{max}|{\beta }_{0j}-{\widehat{\beta }}_j|\ge d_n)\le P(\Vert {\mathit{\beta }}_{0S}-{\widehat{\mathit{\beta }}}_S\Vert \ge d_n)=o(1)$$

This implies P(S ⊂ Ŝ) → 1. Hence P(Ŝ = S) → 1.

C.3. Proof of Theorem 4.1: part (i)

Let $P_n^{\prime }(|{\widehat{\mathit{\beta }}}_S|)={(P_n^{\prime }(|{\widehat{\beta }}_{S1}|),\dots ,P_n^{\prime }(|{\widehat{\beta }}_{Ss}|))}^T$.

Lemma C.2

Under Assumption 4.1,

$$\Vert P_n^{\prime }(|{\widehat{\mathit{\beta }}}_S|)\circ sgn({\widehat{\mathit{\beta }}}_S)\Vert =O_p(\underset{\Vert {\mathit{\beta }}_S-{\mathit{\beta }}_{0S}\Vert \le d_n/4}{max}\eta (\mathit{\beta })\sqrt{slogp/n}+\sqrt{s}{P}_n^{\prime }(d_n)),$$

where ∘ denotes the element-wise product.

Proof. Write $P_n^{\prime }(|{\widehat{\mathit{\beta }}}_S|)\circ sgn({\widehat{\mathit{\beta }}}_S)={(v_1,\dots ,v_s)}^T$, where $v_i=P_n^{\prime }(|{\widehat{\beta }}_{Si}|)sgn({\widehat{\beta }}_{Si})$. By the triangular inequality and Taylor expansion,

$$|v_i|\le |P_n^{\prime }(|{\widehat{\beta }}_{Si}|)-P_n^{\prime }(|{\beta }_{0S,i}|)|+P_n^{\prime }(|{\beta }_{0S,i}|)\le \eta ({\mathit{\beta }}^{\ast })|{\widehat{\beta }}_{Si}-{\beta }_{0S,i}|+P_n^{\prime }(d_n)$$

where β* lies on the segment joining β̂_S and β_0S. For any ε > 0 and all large n,

$$P(\eta ({\mathit{\beta }}^{\ast })>\underset{\Vert {\mathit{\beta }}_S-{\mathit{\beta }}_{0S}\Vert \le d_n/4}{max}\eta (\mathit{\beta }))\le P(\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert >d_n/4)<\epsilon .$$

This implies η(β*) = O_p(max‖_{βS−β0S‖<dn/4} η(β)). Therefore, ${\Vert P_n^{\prime }(|{\widehat{\mathit{\beta }}}_S|)\circ sgn({\widehat{\mathit{\beta }}}_S)\Vert }^2={\sum }_{i=1}^s{v}_j^2$ is upper-bounded by

$$2\underset{\Vert {\mathit{\beta }}_S-{\mathit{\beta }}_{0S}\Vert \le d_n/4}{max}\eta {(\mathit{\beta })}^2{\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert }^2+2s{P}_n^{\prime }{(d_n)}^2,$$

which implies the result since $\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert =O_p(\sqrt{slogp/n}+\sqrt{s}{P}_n^{\prime }(d_n))$.

Lemma C.3

Let Ω_n = √nΓ^−1/2. Then for any unit vector α ∈ℝ^s,

$${\mathit{\alpha }}^T{\mathbf{\Omega }}_n\nabla {\stackrel{\sim }{L}}_{\mathit{\text{FGMM}}}({\mathit{\beta }}_{0S}){\to }^{d}N(0,1).$$

Proof. We have ∇L̃_FGMM(β_0S) = 2A_n(β_0S)J(β₀)B_n, where ${\mathbf{B}}_n=\frac{1}{n}{\sum }_{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S}){\mathbf{V}}_{iS}$. We write $\mathbf{A}=Em(Y,{\mathbf{X}}_s^T{\mathit{\beta }}_{0S}){\mathbf{X}}_S{\mathbf{V}}_S^T$, $\mathbf{\Upsilon }=var(\sqrt{n}{\mathbf{B}}_n)=var(g(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{V}}_S)$ and Γ = 4AJ(β₀)ϒJ(β₀)^TA^T.

By the weak law of large number and central limit theorem for iid data,

$$\Vert {\mathbf{A}}_n({\mathit{\beta }}_{0S})-\mathbf{A}\Vert =o_p(1),\sqrt{n}{\stackrel{\sim }{\mathit{\alpha }}}^T{\mathbf{\Upsilon }}^{-1/2}{\mathbf{B}}_n{\to }^{d}N(0,1).$$

for any unit vector α̃∈ℝ^2s. Hence by the Slutsky's theorem,

$$\sqrt{n}{\mathit{\alpha }}^T{\mathbf{\Gamma }}^{-1/2}\nabla {\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S}){\to }^{d}N(0,1).$$

Proof of Theorem 4.1: part (i)

Proof. The KKT condition of β̂_S gives

$$-P_n^{\prime }(|{\widehat{\mathit{\beta }}}_S|)\circ sgn({\widehat{\mathit{\beta }}}_S)=\nabla {\stackrel{\sim }{L}}_{\text{FGMM}}({\widehat{\mathit{\beta }}}_S),$$ (C.3)

By the mean value theorem, there exists β* lying on the segment joining β_0S and β̂_S such that

$$\nabla {\stackrel{\sim }{L}}_{\text{FGMM}}({\widehat{\mathit{\beta }}}_S)=\nabla {\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})+{\nabla }^2{\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}^{\ast })({\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}).$$

Let D = (∇²L̃_FGMM(β*) − ∇²L̃_FGMM(β_0S))(β̂_S − β_0S). It then follows from (C.3) that for ${\mathbf{\Omega }}_n=\sqrt{n}{\mathbf{\Gamma }}_n^{-1/2}$, and any unit vector α,

$${\mathit{\alpha }}^T{\mathbf{\Omega }}_n{\nabla }^2{\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})({\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S})=-{\mathit{\alpha }}^T{\mathbf{\Omega }}_n[P_n^{\prime }(|{\widehat{\mathit{\beta }}}_S|)\circ sgn({\widehat{\mathit{\beta }}}_S)+\nabla {\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})+\mathbf{D}].$$

In the proof of Theorem 4.1, condition (ii), we showed that ∇²L̃_FGMM(β_0S) = Σ + O_p(1). Hence by Lemma C.3, it suffices to show ${\mathit{\alpha }}^T{\mathbf{\Omega }}_n[P_n^{\prime }(|{\widehat{\mathit{\beta }}}_S|)\circ sgn({\widehat{\mathit{\beta }}}_S)+\mathbf{D}]=o_p(1)$.

By Assumptions 4.5 and 4.6(i), λ_min(Γ_n)⁻¹/² = O_p(1).Thus ‖ α^TΩ_n‖ = O_p(√n). Lemma C.2 then implies ${\lambda }_{max}({\mathbf{\Omega }}_n)\Vert P_n^{\prime }(|{\widehat{\mathit{\beta }}}_S|)\circ sgn({\widehat{\mathit{\beta }}}_S)\Vert$ is bounded by $O_p(\sqrt{n})({max}_{\Vert {\mathit{\beta }}_S-{\mathit{\beta }}_{0S}\Vert \le d_n/4}\eta (\mathit{\beta })\sqrt{slogp/n}+\sqrt{s}{P}_n^{\prime }(d_n))=o_p(1)$.

It remains to prove ‖D‖ = o_p(n^−1/2), and it suffices to show that

$$\Vert {\nabla }^2{\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}^{\ast })-{\nabla }^2{\stackrel{\sim }{L}}_{\text{FGMM}}({\mathit{\beta }}_{0S})\Vert =o_p({(slogp)}^{-1/2})$$ (C.4)

due to $\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert =O_p(\sqrt{slogp/n}+\sqrt{s}{P}_n^{\prime }(d_n))$, and Assumption 4.6 that $\sqrt{ns}{P}_n^{\prime }(d_n)=o(1)$. Showing (C.4) is straightforward given the continuity of ∇²L̃_FGMM.

Appendix D: Proofs for Sections 5 and 6

The local minimizer in Theorem 4.1 is denoted by $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_S^T,{\widehat{\mathit{\beta }}}_N^T)}^T$ and P(β̂_N) → 1. Let ${\widehat{\mathit{\beta }}}_G={({\widehat{\mathit{\beta }}}_S^T,0)}^T$.

D.1. Proof of Theorem 5.1

Lemma D.1

$$L_{\mathit{\text{FGMM}}}({\widehat{\mathit{\beta }}}_G)=O_p(slogp/n+s{P}_n^{\prime }{(d_n)}^2)$$

Proof. We have, $L_{\text{FGMM}}({\widehat{\mathit{\beta }}}_G)\le {\Vert \frac{1}{n}{\sum }_{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\widehat{\mathit{\beta }}}_S){\mathbf{V}}_{iS}\Vert }^2{O}_p(1)$. By Taylor expansion, with some β̂ in the segment joining β_0S and β̂_S,

$$\Vert \frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\widehat{\mathit{\beta }}}_S){\mathbf{V}}_{iS}\Vert \le \Vert \frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S}){\mathbf{V}}_{iS}\Vert +\Vert \frac{1}{n}\sum _{i=1}^{n}m(Y_i,{\mathbf{X}}_{iS}^T{\stackrel{\sim }{\mathit{\beta }}}_S){\mathbf{X}}_{iS}{\mathbf{V}}_{iS}^T\Vert \Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert \le O_p(\sqrt{slogp/n})+\Vert \frac{1}{n}\sum _{i=1}^{n}m(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S}){\mathbf{X}}_{iS}{\mathbf{V}}_{iS}^T\Vert \Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert +\frac{1}{n}\sum _{i=1}^n|m(Y_i,{\mathbf{X}}_{iS}^T{\stackrel{\sim }{\mathit{\beta }}}_S)-m(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_{0S})|\Vert {\mathbf{X}}_{iS}{\mathbf{V}}_{iS}^T\Vert \Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert .$$

Note that $\Vert Em(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_{0S}){\mathbf{X}}_S{\mathbf{V}}_S\Vert$ is bounded due to Assumption 4.5. Apply Taylor expansion again, with some β̂*, the above term is bounded by

$$O_p(\sqrt{slogp/n})+O_p(1)\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert +\frac{1}{n}\sum _{i=1}^n|q(Y_i,{\mathbf{X}}_{iS}^T{\stackrel{\sim }{\mathit{\beta }}}_S^{\ast })|\Vert {\mathbf{X}}_{iS}\Vert \Vert {\stackrel{\sim }{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert \Vert {\mathbf{X}}_{iS}{\mathbf{V}}_{iS}^T\Vert \Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert .$$

Note that sup_t1,t2| q(t₁, t₂)| < ∞ by Assumption 4.4. The second term in the above is bounded by $C\frac{1}{n}{\sum }_{i=1}^n\Vert {\mathbf{X}}_{iS}\Vert \Vert {\mathbf{X}}_{iS}{\mathbf{V}}_{iS}^T\Vert {\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert }^2$. Combining these terms, $\Vert \frac{1}{n}{\sum }_{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\widehat{\mathit{\beta }}}_S){\mathbf{V}}_{iS}\Vert$ is bounded by $O_p(\sqrt{slogp/n}+\sqrt{s}{P}_n^{\prime }(d_n))+O_p(s\sqrt{s}){\Vert {\widehat{\mathit{\beta }}}_S-{\mathit{\beta }}_{0S}\Vert }^2=O_p(\sqrt{slogp/n}+\sqrt{s}{P}_n^{\prime }(d_n))$.

Lemma D.2

Under the theorem's assumptions

$$Q_{\mathit{\text{FGMM}}}({\widehat{\mathit{\beta }}}_G)=O_p(\frac{slogp}{n}+s{P}_n^{\prime }{(d_n)}^2+s\underset{j\in S}{max}{P}_n(|{\beta }_{0j}|)+P_n^{\prime }(d_n)s\sqrt{\frac{logs}{n}}).$$

Proof. By the foregoing lemma, we have

$$Q_{\text{FGMM}}({\widehat{\mathit{\beta }}}_G)=O_p(\frac{slogp}{n}+s{P}_n^{\prime }{(d_n)}^2)+\sum _{j=1}^s{P}_n(|{\beta }_{Sj}|).$$

Now, for some β̃_Sj in the segment joining β̂_Sj and β_0j,

$$\sum _{j=1}^s{P}_n(|{\beta }_{Sj}|)\le \sum _{j=1}^s{P}_n(|{\beta }_{0S,j}|)+\sum _{j=1}^s{P}_n^{\prime }(|{\stackrel{\sim }{\mathit{\beta }}}_{Sj}|)|{\mathit{\beta }}_{Sj}-{\mathit{\beta }}_{0S,j}|\le s\underset{j\in S}{max}{P}_n(|{\beta }_{0j}|)+\sum _{j=1}^s{P}_n^{\prime }(d_n)|{\beta }_{Sj}-{\beta }_{0S,j}|\le s\underset{j\in s}{max}{P}_n(|{\beta }_{0j}|)+P_n^{\prime }(d_n)\Vert {\widehat{\beta }}_S-{\beta }_{0S}\Vert \sqrt{s}.$$

The result then follows.

Note that ∀δ > 0,

$$\underset{\mathit{\beta }\notin {\mathrm{\Theta }}_{\delta }\cup \left\{0\right\}}{inf}{Q}_{\text{FGMM}}(\mathit{\beta })\ge \underset{\mathit{\beta }\notin {\mathrm{\Theta }}_{\delta }\cup \left\{0\right\}}{inf}{L}_{\text{FGMM}}(\mathit{\beta })\ge \underset{\mathit{\beta }\notin {\mathrm{\Theta }}_{\delta }\cup \left\{0\right\}}{inf}{\Vert \frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_i^T\mathit{\beta }){\mathbf{V}}_i(\mathit{\beta })\Vert }^2\underset{j\le p}{min}\{\widehat{var}(X_j),\widehat{var}(X_j^2)\}.$$

Hence by Assumption 5.1, there exists γ > 0,

$$P(\underset{\mathit{\beta }\notin {\mathrm{\Theta }}_{\delta }\cup \left\{0\right\}}{inf}{Q}_{\text{FGMM}}(\mathit{\beta })>2\gamma )\to 1.$$

On the other hand, by Lemma D.2, Q_FGMM(β̂_G) = o_p(1). Therefore,

$$P(Q_{\text{FGMM}}(\widehat{\mathit{\beta }})+\gamma >\underset{\mathit{\beta }\notin {\mathrm{\Theta }}_{\delta }\cup \left\{0\right\}}{inf}{Q}_{\text{FGMM}}(\mathit{\beta }))P(Q_{\text{FGMM}}({\widehat{\mathit{\beta }}}_G)+\gamma >\underset{\mathit{\beta }\notin {\mathrm{\Theta }}_{\delta }\cup \left\{0\right\}}{inf}{Q}_{\text{FGMM}}(\mathit{\beta }))+o(1)\le P(Q_{\text{FGMM}}({\widehat{\mathit{\beta }}}_G)+\gamma >2\gamma )+P(\underset{\mathit{\beta }\notin {\mathrm{\Theta }}_{\delta }\cup \left\{0\right\}}{inf}{Q}_{\text{FGMM}}(\mathit{\beta })<2\gamma )+o(1)\le P(Q_{\text{FGMM}}({\widehat{\mathit{\beta }}}_G)>\gamma )+o(1)=o(1).$$

Q.E.D.

D.2. Proof of Theorem 6.1

Lemma D.3

Define $\rho ({\mathit{\beta }}_S)=E[g(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_S)\sigma {(\mathbf{W})}^{-2}\mathbf{D}(\mathbf{W})]$. Under the theorem assumptions, sup_{βS ∈ Θ} ‖ρ(β_S) − ρ_n(β_S)‖ = o_p(1).

Proof. We first show three convergence results:

$$\underset{{\mathit{\beta }}_S\in \mathrm{\Theta }}{sup}\frac{1}{n}\sum _{i=1}^n\Vert g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_S)(\mathbf{D}({\mathbf{W}}_i)-\widehat{\mathbf{D}}({\mathbf{W}}_i))\widehat{\sigma }{({\mathbf{W}}_i)}^{-2}\Vert =o_p(1),$$ (D.1)

$$\underset{{\mathit{\beta }}_S\in \mathrm{\Theta }}{sup}\frac{1}{n}\sum _{i=1}^n\Vert g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_S)\mathbf{D}({\mathbf{W}}_i)(\widehat{\sigma }{({\mathbf{W}}_i)}^{-2}-\sigma {({\mathbf{W}}_i)}^{-2})\Vert =o_p(1),$$ (D.2)

$$\underset{{\mathit{\beta }}_S\in \mathrm{\Theta }}{sup}\Vert \frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_S)\mathbf{D}({\mathbf{W}}_i)\sigma {({\mathbf{W}}_i)}^{-2}-Eg(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_S)\mathbf{D}(\mathbf{W})\sigma {(\mathbf{W})}^{-2}\Vert =o_p(1),$$ (D.3)

Because both sup_w ‖D̂ (w) − D(w)‖ and sup_w |σ̂(w)² − σ(w)²| are o_p(1), proving (D.1) and (D.2) is straightforward. In addition, given the assumption that $E({sup}_{\Vert \mathit{\beta }\Vert \infty \le M}g{(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_S)}^4)<\infty$, (D.3) follows from the uniform law of large number. Hence we have,

$$\underset{{\mathit{\beta }}_S\in \mathrm{\Theta }}{sup}\Vert \frac{1}{n}\sum _{i=1}^{n}g(Y_i,{\mathbf{X}}_{iS}^T{\mathit{\beta }}_S)\widehat{\mathbf{D}}({\mathbf{W}}_i)\widehat{\sigma }{({\mathbf{W}}_i)}^{-2}-Eg(Y,{\mathbf{X}}_S^T{\mathit{\beta }}_S)\mathbf{D}(\mathbf{W})\sigma {(\mathbf{W})}^{-2}\Vert =o_p(1).$$

In addition, the event X_S = X̂_S occurs with probability approaching one, given the selection consistency P(Ŝ = S) → 1 achieved in Theorem 4.1.

The result then follows because ${\rho }_n({\mathit{\beta }}_S)=\frac{1}{n}{\sum }_{i=1}^{n}g(Y_i,{\widehat{\mathbf{X}}}_{iS}^T{\mathit{\beta }}_S)\widehat{\sigma }{({\mathbf{W}}_i)}^{-2}\widehat{\mathbf{D}}({\mathbf{W}}_i)$.

Given Lemma D.3, Theorem 6.1 follows from a standard argument for the asymptotic normality of GMM estimators as in Hansen (1982) and Newey and McFadden (1994, Theorem 3.4). The asymptotic variance achieves the semi-parametric efficiency bound derived by Chamberlain (1987) and Severini and Tripathi (2001). Therefore, β̂* is semi-parametric efficient.

Appendix E: Proofs for Section 7

The proof of Theorem 7.1 is very similar to that of Theorem 4.1, which we leave to the online supplementary material, downloadable from http://terpconnect.umd.edu/∼yuanliao/high/supp.pdf

Proof of Theorem 7.2

Proof. Define $Q_{l,k}=L_K({\mathit{\beta }}_{(-k)}^{(l)},{\mathit{\beta }}_k^{(l)})+{\sum }_{j\le k}{P}_n(|{\mathit{\beta }}_j^{(l)}|)+{\sum }_{j>k}{P}_n(|{\mathit{\beta }}_j^{(l-1)}|)$. We first show Q_l,k ≤ Q_l,k−1 for 1 < k ≤ p and Q_l+1,1 ≤ Q_l,p. For 1 < k ≤ p, Q_l,k − Q_l,k−1 equals

$$L_K({\mathit{\beta }}_{(-k)}^{(l)},{\mathit{\beta }}_k^{(l)})+P_n(|{\mathit{\beta }}_k^{(l)}|)-[L_K({\mathit{\beta }}_{(-(k-1))}^{(l)},{\mathit{\beta }}_{k-1}^{(l)})+P_n(|{\mathit{\beta }}_k^{(l-1)}|)].$$

Note that the difference between $({\mathit{\beta }}_{(-k)}^{(l)},{\mathit{\beta }}_k^{(l)})$ and $({\mathit{\beta }}_{(-(k-1))}^{(l)},{\mathit{\beta }}_{k-1}^{(l)})$ only lies on the kth position. The kth position of $({\mathit{\beta }}_{(-k)}^{(l)},{\mathit{\beta }}_k^{(l)})$ is ${\beta }_k^{(l)}$ while that of $({\mathit{\beta }}_{(-(k-1))}^{(l)},{\beta }_{k-1}^{(l)})$ is ${\beta }_k^{(l-1)}$. Hence by the updating criterion, Q_l,k ≤ Q_l,k−1 for k ≤ p.

Because $({\mathit{\beta }}_{(-1)}^{(l+1)},{\beta }_1^{(l+1)})$ is the first update in the l + 1th iteration, $({\mathit{\beta }}_{(-1)}^{(l+1)},{\beta }_1^{(l+1)})=({\mathit{\beta }}_{(-1)}^{(l)},{\beta }_1^{(l+1)})$. Hence

$$Q_{l+1,1}=L_K({\mathit{\beta }}_{(-1)}^{(l)},{\beta }_1^{(l+1)})+P_n(|{\beta }_1^{(l+1)}|)+\sum _{j>1}{P}_n(|{\beta }_j^{(l)}|).$$

On the other hand, for ${\mathit{\beta }}^{(l)}=({\mathit{\beta }}_{(-p)}^{(l)},{\beta }_p^{(l)})$,

$$Q_{l,p}=L_K({\mathit{\beta }}^{(l)})+\sum _{j>1}{P}_n(|{\beta }_j^{(l)}|)+P_n(|{\mathit{\beta }}_1^{(l)}|).$$

Hence $Q_{l+1,1}-Q_{l,p}=L_K({\mathit{\beta }}_{(-1)}^{(l)},{\beta }_1^{(l+1)})+P_n(|{\beta }_1^{(l+1)}|)-[L_K({\mathit{\beta }}^{(l)})+P_n(|{\mathit{\beta }}_1^{(l)}|)]$. Note that $({\mathit{\beta }}_{(-1)}^{(l)},{\beta }_1^{(l+1)})$ differs β^(l) only on the first position. By the updating criterion, Q_l+1,1 − Q_l,p ≤ 0.

Therefore, if we define {L_m}_m≥1 = {Q_1,1, …,Q₁,_p, Q_2,1, …,Q₂,_p, …}, then we have shown that {L_m}_m≥1 is a non-increasing sequence. In addition, L_m ≥ 0 for all m ≥ 1. Hence L_m is a bounded convergent sequence, which also implies that it is Cauchy. By the definition of Q_K(β^(l)), we have Q_K(β^(l)) = Q_l,p, and thus {Q_K(β^(l))}_l≥1 is a sub-sequence of {L_m}. Hence it is also bounded Cauchy. Therefore, for any ε > 0, there is N > 0, when l₁, l₂ > N, | Q_K(β^(l₁)) − Q_K(β^(l₂))| < ε, which implies that the iterations will stop after finite steps.

The rest of the proof is similar to that of the Lyapunov's theorem of Lange (1995, Prop. 4). Consider a limit point β* of {β^(l)} _l≥1 such that there is a subsequence lim_k→∞ β^(lk) = β*. Because both Q_K(·) and M(·) are continuous, and Q_K(β^(l)) is a Cauchy sequence, taking limits yields

$$Q_K(M({\mathit{\beta }}^{\ast }))=\underset{k\to \infty }{lim}{Q}_K(M({\mathit{\beta }}^{(l_k)}))=\underset{k\to \infty }{lim}{Q}_K({\mathit{\beta }}^{(l_k)})=Q_K({\mathit{\beta }}^{\ast }).$$

Hence β* is a stationary point of Q_K(β).