Learning Modifies Odor Mixture Processing to Improve Detection of Relevant Components

Abstract

Honey bees have a rich repertoire of olfactory learning behaviors, and they therefore are an excellent model to study plasticity in olfactory circuits. Recent behavioral, physiological, and molecular evidence suggested that the antennal lobe, the first relay of the olfactory system in insects and analog to the olfactory bulb in vertebrates, is involved in associative and nonassociative olfactory learning. Here we use calcium imaging to reveal how responses across antennal lobe projection neurons change after association of an input odor with appetitive reinforcement. After appetitive conditioning to 1-hexanol, the representation of an odor mixture containing 1-hexanol becomes more similar to this odor and less similar to the background odor acetophenone. We then apply computational modeling to investigate how changes in synaptic connectivity can account for the observed plasticity. Our study suggests that experience-dependent modulation of inhibitory interactions in the antennal lobe aids perception of salient odor components mixed with behaviorally irrelevant background odors.

Introduction

Learning and memory are essential brain functions that enable animals to survive in diverse and constantly changing environments. The insect olfactory system has been a canonical model for understanding the fundamental mechanisms of learning and memory due to its smaller size, easier access for different experimental approaches, and several kinds of behavioral plasticity toward odors. For instance, honey bees forage on different types of flowers that rapidly come into and go out of bloom and whose occurrence may vary drastically depending on geographical and seasonal variables. In this context, honey bees have been shown to adapt, thanks to a keen ability to detect and discriminate a wide range of olfactory stimuli and to a rich repertoire of olfactory learning behaviors that include nonassociative learning as well as classical and operant conditioning (Menzel, 1990; Farooqui et al., 2003; Smith et al., 2006; Fernandez et al., 2009; Locatelli et al., 2013).

In insects, the mushroom bodies are primary brain sites for olfactory learning and memory formation (Cassenaer and Laurent, 2007; Keene and Waddell, 2007; Okada et al., 2007; Busto et al., 2010; Strube-Bloss et al., 2011). However, recent studies have revealed systematic changes in the spatiotemporal patterns that encode odors at the antennal lobe (AL) as a consequence of different olfactory learning tasks (Faber et al., 1999; Sandoz, 2003; Sandoz et al., 2003; Yu et al., 2004; Fernandez et al., 2009; Rath et al., 2011; Locatelli et al., 2013). Additional lines of evidence have also pointed to the AL as an important site for olfactory learning and memory. For example, biogenic amines, such as octopamine and dopamine, are released in the AL by neurons that convey information about appetitive and aversive reinforcements, where they merge with sensory input that represent the conditioned odor (Hammer, 1993; Schwaerzel et al., 2003; Yu et al., 2004; Riemensperger et al., 2005; Farooqui, 2007; Aso et al., 2010; Sinakevitch et al., 2011, 2013). Recently, we have found that octopaminergic neurons have varicose-like fibers that invade the glomeruli of the AL, where olfactory sensory neurons interact with local neurons (LNs) and projection neurons (PNs) (I. Sinakevitch, J.-Y.C., M.B., B.H.S., unpublished observation). In addition, blockade of octopamine receptors (AmOA1) in the honey bee AL prevents associative olfactory learning (Farooqui et al., 2003).

The AL is also an important site for nonassociative olfactory learning (Das et al., 2011; Locatelli et al., 2013). In Drosophila, olfactory habituation, a reduction of the animal's olfactory response induced by repeated exposure to the same odor, was found to be regulated by glomerulus-specific synaptic plasticity at local inhibitory synapses (i.e., connections from LNs to PNs) (Das et al., 2011). It was shown that activity occurring at glomerulus-specific PNs is necessary and sufficient to launch olfactory habituation and that a subset of local inhibitory synapses (i.e., LN-PN) is strengthened during prolonged postsynaptic PN activity (Sudhakaran et al., 2012).

In the current study, we combine optical recordings from PNs with behavioral and computational analyses to characterize how synaptic plasticity can alter odor representations in the AL after associative olfactory learning in the honey bee. We found that the spatiotemporal responses to binary mixtures across PNs in the AL became more similar to a learned component and less similar to a nonlearned component after associative learning with appetitive reward. A conductance-based computational model of the honeybee AL revealed that the plasticity at inhibitory synapses connecting LNs and PNs is essential and might be sufficient for olfactory learning. We conclude that plasticity on synaptic inhibition into the PNs enhances salient features of complex odor mixtures while it simultaneously depresses less informative components.

Materials and Methods

Experiments

Animals.

Honey bee (Apis mellifera) pollen foragers (all females) were collected at the entrance of two regular hives located at the Campus of the University of Buenos Aires (34° 32′ S; 58° 6′ W). The bees were briefly cooled and restrained in individual stages (Galizia and Vetter, 2004). After recovery from cooling, bees were fed 5 μl of a 1.0 m sucrose solution and remained undisturbed until feeding ad libitum in the evening. At the laboratory, the bees were kept in a humid box at room temperature (20°C–24°C) on a 12:12 h light:dark cycle. Training and testing sessions were performed between 10:00 A.M. and 4:00 P.M. All experiments started 1 d after capture.

Odor stimulation.

Odors used were 1-hexanol and acetophenone (both TCI America). A total of 100 μl of pure odor was loaded into 5 ml glass vials before the experiments. The saturated headspace inside the vials was used as the odor sample for stimulation. To generate samples, a defined volume of the headspace was transferred into the syringe. When pure odors were used, a 1 ml syringe was loaded first with 0.5 ml of the headspace from the odor vial and that sample was combined with 0.5 ml of clean air inside the syringe. To obtain the mixture, 0.5 ml of headspace from the 1-hexanol vial and 0.5 ml from the acetophenone vial were sequentially loaded into the syringe; thus, both headspaces were mixed inside the syringe before using it for stimulation. Different syringes were used for 1-hexanol, acetophenone, and the mixture to avoid contamination. To apply the odor to the honey bee, the syringe was inserted into a computer-controlled device, the odorgun, which pushed the plunger of the syringe at a constant speed of 1 ml/s. The content of the syringe was injected into a charcoal-filtered air stream with a flow rate of 9 ml/s. Thus, the final odor concentration delivered to the bee resulted in 1/20 of the saturated headspace sample originally taken from the vials. The onset and offset of the odor were synchronized with imaging from the imaging acquisition software (TillVision, Till Photonics). During periods without odor stimulation, the charcoal-filtered air stream ventilated continuously the antennae. An exhaust 10 cm behind the bee removed the odors from the experimental area. The same procedure for odor delivery was used in training, testing, and imaging sessions.

Olfactory conditioning.

Bees were subjected to appetitive olfactory conditioning using the Proboscis Extension Response conditioning procedure (Bitterman et al., 1983). All training sessions consisted of 10 conditioning trials (see Fig. 2). During each trial, a honey bee was positioned facing toward the odorgun. Twenty seconds later, the odor started and lasted 1 s. The reward was applied coincident with the odor offset, which was indicated to the experimenter by an LED that was not visible to the honey bee. In this moment, the antennae were touched with 2.0 m sucrose solution, which elicits the proboscis extension. The sucrose solution was rapidly moved to the proboscis, and the bee was allowed to ingest 0.4 μl delivered with a Gilmont micrometer syringe. Twenty seconds after the reward was consumed, the honey bee was returned to a resting container until the next trial. The intertrial interval was 10 min. During training trials, the response of each subject was recorded as positive if the subject extended its proboscis during the stimulation with the odor and before stimulation with sucrose. The 1 s delay between odor onset and reward allowed determination of learning performance during the training session. No reward was presented during the test session or during calcium imaging.

Figure 2.

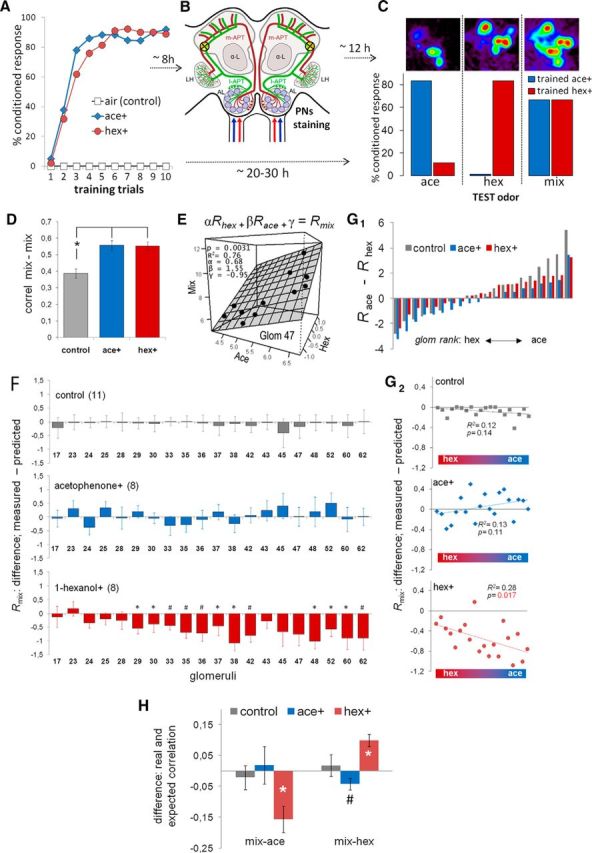
Changes in the responses to the mixture after appetitive olfactory conditioning. A, Three groups of bees were trained using appetitive conditioning. Each bee received 10 trials with 2 m sucrose solution separated by 10 min intertrial intervals. Control bees received the reward paired with clean air provided by the odorgun. The other two groups received 1-hexanol or acetophenone as conditioned odor. Learning performance was recorded during conditioning as percentage of animals that extended the proboscis upon stimulation with odor. B, Eight hours after conditioning, projection neurons were stained bilaterally using fura-dextran targeted to where the l-APT enters the lateral calyces of the mushroom bodies (yellow circles). m-APT, Medial antenno-protocerebal tract; l-APT, lateral antenno-protocerebral tract; LH, lateral horn; α-L, alpha lobe. C, On the next day, the bees were prepared for calcium imaging of odor-induced signals on the dorsal side of the antennal lobe (top). Activity patterns were measured three times each to 1-hexanol, acetophenone, and the binary mixture, presented in random order separated by 1 min intervals. A set of trained bees not stained for imaging was used to determine the strength of olfactory memory and odor discrimination (bottom). All honey bees underwent three test trials without reward using: (1) the conditioned odor (1-hexanol or acetophenone), (2) a different odor that they have not experienced before (1-hexanol or acetophenone), and (3) the binary mixture containing both odors in same proportion. Bar colors represent the odor used for conditioning. The order of the three odors was randomized across animals (1-hexanol-trained bees, n = 20; acetophenone-trained bees, n = 18). Control bees are not shown because they did not evoke any conditioned response. D, Average ± SEM of the correlation coefficients between mixture-elicited activation patterns across bees. The correlation was calculated between bees from the same training group: control (gray), ace⁺ (blue), and hex⁺ (red), ANOVA: F_(2,108) < 0.0001. *p < 0.001 (post hoc contrasts). E, A best fit linear equation was obtained for each glomerulus to estimate the response of the mixture as a function of the responses to 1-hexanol and acetophenone. Graph represents an example of the best-fit linear equation (plane) of glomerulus 47 derived from 11 data points (11 control bees). F, Average ± SEM of the difference between the measured and the predicted response to the mixture for each glomerulus in the three different groups of bees. The numbers in the abscissa indicate the identification of the glomeruli. The differences shown in the graph were calculated as the measured response minus the predicted response. *p < 0.05, between measured and predicted values (paired t test). ^#p < 0.01, between measured and predicted values (paired t test). From top down, control group (n = 11), ace⁺ group (n = 8), and hex⁺ group (n = 8). G₁, Glomeruli were ranked according to the difference of the average response to 1-hexanol and acetophenone in control bees. The ranking was made by subtracting the response to 1-hexanol (R_hex) from the response to acetophenone (R_ace). G₂, The points in these plots correspond to the data (R_mix: measured − predicted) shown in F, but reorganized along the abscissa according to the ranking derived from G₁. The red/blue color bar at the bottom of each plot represents the ranking of glomeruli from hexanol responders to acetophenone responders. The results of a linear regression analysis are displayed in each plot. H, The predicted responses to the mixture for each glomerulus were arranged to establish a predicted response pattern to the mixture. The correlation between patterns elicited by the pure odors and the predicted pattern to the mixture were designated predicted correlations. The figure shows the average ± SEM of the differences between the real and the predicted correlation between responses to the mixture and responses to the pure odors (mix-ace, mix-hex) in the three groups of bees (control, ace⁺, hex⁺). *p < 0.001, between real and predicted correlation (paired t test). ^#p = 0.06, in the case of correlation mix-hex after conditioning with acetophenone.

Projection neuron staining.

The head of the bee was fixed to the stage with soft dental wax (Kerr Sybron Dental Specialties). A window was cut in the head capsule dorsal to the joints of the antennae and ventral to the medial ocellus. The glands were carefully moved aside until the α-lobes were visible, which serve as spatial reference for staining. PNs were stained by backfilling with the calcium sensor dye Fura-dextran (potassium salt, 10,000 MW; Invitrogen). To do that instead of it, the tip of a glass microelectrode coated with dye was inserted into both sides of the protocerebrum, dorsolateral of the α-lobes where the antenno-protocerebral tracts enter the lateral calyces of the mushroom bodies (see Fig. 2) (Kirschner et al., 2006). The dye bolus dissolved into the tissue in 3–5 s. The window was closed using the same piece of cuticle that had been previously removed, and it was sealed with eicosane (Sigma-Aldrich). Twenty minutes after staining, the bees were fed with 1.0 m sucrose solution and left undisturbed until the next day. Before imaging, the antennae were immobilized pointing forward using eicosane. The head capsule was opened, and the brain was rinsed with Ringer's solution (in mm as follows): NaCl, 130; KCl, 6; MgCl₂, 4; CaCl₂, 5; sucrose, 160; glucose, 25; and HEPES, 10; pH 6.7, 500 mOsmol (all chemicals from Sigma-Aldrich). Glands and trachea covering the ALs were removed. Only ALs that presented homogeneous staining of all visually accessible glomeruli were used for imaging. Only one AL per animal was used for imaging. Body movements were prevented by gently compressing the abdomen and thorax with a piece of foam. A second hole in the head capsule was cut between the antennae and the mandibles, and the compact structure of muscles, esophagus, and supporting chitin was lifted and put under slight tension (Mauelshagen, 1993). Finally, the brain was covered with Kwik-sil (WPI). After preparation, bees were mounted in the microscope and were allowed to recover for 20 min before starting with imaging.

Imaging.

Calcium imaging was done using an EMCCD iXon camera (ANDOR) mounted on an upright fluorescence microscope (Olympus BX-50WI) equipped with a 20× dip objective, NA 0.95 (Olympus). Filter- and mirror-set: 505 DRLPXR dichroic mirror and 515 nm LP filter (Till Photonics). Excitation light was provided by a Polychrome V (Till Photonics), which alternated between 340 and 380 nm for excitation light. Acquisition protocols were written using TillVision software (Till Photonics). Sampling rate was 8 Hz. Spatial resolution was 125 × 125 pixels binned on a chip of 1000 × 1000 pixels. The intensity of the fluorescence lamp was controlled from the imaging acquisition software to get exposure times of 20 and 5 ms for 340 and 380 nm, respectively. Each imaging session consisted of 9 measurements of odor-elicited activity in the AL (3 measurements with 1-hexanol, 3 with acetophenone, and 3 with the mixture). The 3 odors were presented in random order and separated by 1 min intervals. Each measurement lasted 10 s, and the odor lasted from 4 to 5 s. The three measurements of each odor were averaged for the analysis.

Imaging analysis.

Imaging analysis was done using software written in IDL (Research Systems) by Giovanni Galizia (Universtity Konstanz, Germany) and in R by Emiliano Marachlian. Each measurement consisted of two sequences of 80 fluorescence images each, obtained by alternating 340 and 380 nm excitation light (Fi₃₄₀, Fi₃₈₀, where i is the number of the image from 1 to 80). For each pair of images Fi, we calculated pixel-wise the ratio Ri = (Fi_{340 nm}/Fi_{380 nm}) × 100 and subtracted the background Rb, obtained by averaging the Ri values 1 s before odor onset [Rb = 1/8 (R₁₆ + … + R₂₃)]. The resulting values (ΔR in figures) represent the change of fluorescence from the reference window and are proportional to the changes in the intracellular calcium concentration. The analysis of odor-induced activation patterns in the present study was based on signals from 20 glomeruli that were identified on the basis of their morphology and position using a published atlas of the honey bee AL (Flanagan and Mercer, 1989; Galizia et al., 1999). Glomeruli are visible in the raw fluorescence images at 380 nm excitation light after backfilling the PNs with FURA (see Fig. 1B). In addition, we used a tool written in IDL by Mathias Ditzen (Freie Universität Berlin, Germany) that segments the image based on the degree of correlated activity between neighboring pixels. Pixels stemming from the same glomerulus are highly correlated. This provides images in which glomeruli are discrete units separated by dark boundaries (see Fig. 1B). The glomerular activation was calculated by averaging activity in a square area of 7 × 7 pixels that correspond to 23 × 23 μm and fit within the limits of the glomeruli. The temporal detail of the activity was collapsed averaging the ΔR from 250 to 750 ms after odor onset.

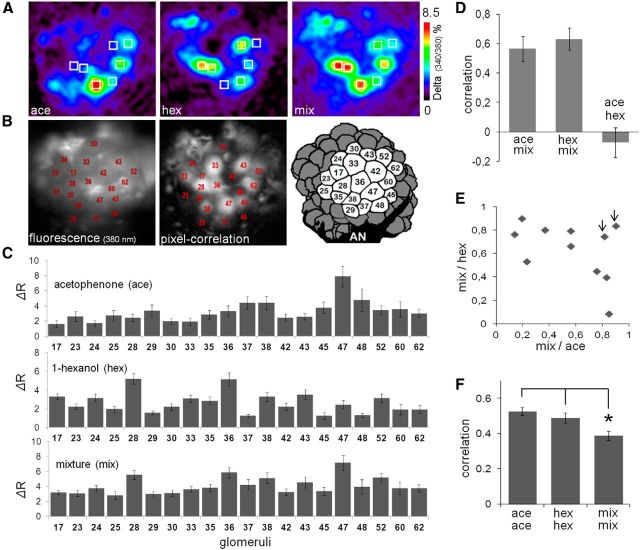
Figure 1.

Imaging of odor elicited calcium signals in projection neurons. A, Color-coded calcium images represent the average of odor responses from 250 to 750 ms after odor onset. From left to right, Images are responses to acetophenone, 1-hexanol, and their mixture (10:10) in the same honey bee. The seven squares represent the same seven glomeruli in different odor responses to aid visualization of the differences between patterns. B, Left, Basal fluorescence image observed with 380 nm excitation light and LP510 emission filter after staining the PNs with FURA-dextran. The glomeruli were identified according to size, shape, and position by comparison with the honey bee AL atlas (Flanagan and Mercer, 1989; Galizia et al., 1999). Middle, Pixel-correlation image (see Materials and Methods) used as an additional tool to aid glomeruli identification. Dark glomeruli do not mean lack of staining; these glomeruli were not activated by the odors and consequently produce low correlation values between neighboring pixels. Right, Schema of the dorsal view of the AL showing the 20 glomeruli used in our analyses. AN, Antennal nerve. C, Quantitative evaluation of the odor responses via change of fluorescence from the reference window (ΔR) from 250 to 750 ms after odor onset in 20 glomeruli. Average ± SEM of odor responses from 11 control bees (top to down: acetophenone, 1-hexanol, and mixture). Numbers in the abscissa correspond to the identity of the glomeruli. D, Pearson's correlation coefficients between response patterns were used to evaluate similarity between odor patterns. The correlation coefficients of three different pairs (ace-mix, hex-mix, ace-hex) were calculated in each control bee. Data are average ± SEM of 11 control bees. E, Scatter plot of the correlation coefficients between mixture and either pure components (hexanol or acetophenone). Each point represents one control bee. Two arrowheads indicate two bees with the highest correlation coefficients between the pure components. F, Correlation coefficients between patterns elicited by the same odor in different bees. Vertical bars represent average ± SEM from a total 55 correlation values that result from arranging 11 controls bees in pairs. The representation of mixture was less conserved across animals than the representation of the pure odors. *p < 0.01 contrasts after ANOVA (F_(2,162) = 6 0.97; p = 0.001).

Response patterns analysis.

It has been proven that odor coding in the antennal lobe (input and output) (Sachse et al., 1999; Sachse and Galizia, 2002) relies on a population coding scheme rather than on activation of odor-specific glomeruli or neurons. Therefore, the analysis performed along this study was based on neuronal activation patterns as a whole. The odor-elicited activation patterns used for analysis consisted of vectors of 20 elements that represent the activity measured in 20 identified glomeruli during a time window from 250 to 750 ms after odor onset. The analysis was based on Pearson′s correlation coefficients between pairs of patterns to describe and compare the degree of similarity between the neural representation of the same odor in different bees or between the representation of different odors in the same bee. The correlation between odor representations in different bees was used as a measure of variability across bees. For this aim, the pattern obtained from each bee was correlated against the patterns from all other bees from the same treatment group. Thus, in case of the untrained group, we calculated 55 correlation values that were obtained from pairing the patterns from 11 untrained bees; and in case of the trained bees (acetophenone and 1-hexanol), we calculated 28 correlation values in each group that were obtained from pairing patterns from 8 bees in each trained group. Figures 1F and 2D show the average and SEM of the correlation values that characterize the variability within the group of odor patterns indicated in the graphs. For statistical purposes, all Pearson's correlation values were subjected to Fisher z-transformation and the transformed data were analyzed using ANOVA.

The analysis of the effect of training was based on within animal comparisons, in which the pattern elicited by the mixture was compared with a “predicted pattern” that was calculated for each individual animal and represented the pattern expected for an untrained bee. The first step to obtain the predicted pattern for the mixture was to calculate the response of each glomerulus to the mixture. The algorithm used to predict the response of each glomerulus to the mixture was made by fitting the data from untrained bees to a linear equation of the form, αRg_hex +βRg_ace + γ = Rg_mix, where Rg represents the response measured in the g glomerulus upon stimulation with 1-hexanol, acetophenone, and the mixture. A set of parameters (α, β, and γ) was obtained for each glomerulus. The 20 fitted planes were in all cases highly significant (p < 0.001 in all cases). Afterward, the linear fits were used to calculate the predicted response to the mixture for each glomerulus in untrained and trained bees. Figure 2F shows the average of the difference between the measured and the predicted response to the mixture in each glomerulus. The statistical analysis was based on paired comparisons between the measured and the predicted response in each bee (paired t test for each column in the graphs; n_control = 11; n_ace+ = 8; n_hex+ = 8). Afterward, the predicted glomerular responses were combined to generate a predicted pattern elicited by the mixture. We calculated in each bee the Pearson's correlation coefficient between the patterns elicited by each one of the components and the pattern elicited by the mixture and called it “real correlation.” In addition, we calculated the correlations between the patterns elicited by each one of the components and the “predicted pattern” to the mixture and called it “predicted correlations.” Real and predicted correlations between the mixture and the components were compared to determine whether the mixture was as similar to the components as it was expected or whether the representations of the mixture were biased toward the representation of one component. Figures 2H and 3C show the difference between real and predicted correlations between the mixture and each one of the components. For statistical purposes, the correlation values were corrected using the Fisher's z-transformation, and the analysis was based on paired t test of the z-transformed real and predicted correlation values of each bee (n_control = 11; n_hex+ = 8; n_ace+ = 8).

Figure 3.

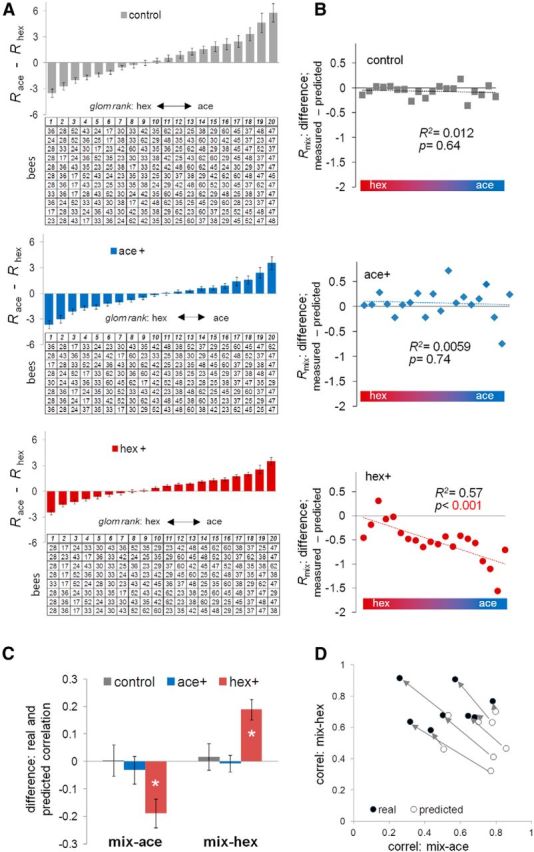
Changes of correlation between the responses to the mixture and the pure odors based on individual bee response profiles. A, Glomeruli were ranked according to the difference of response to acetophenone and 1-hexanol in each individual bee. Three groups of bees (from top down: 11 control bees; 8 ace⁺ bees; 8 hex⁺ bees) are shown. In the tables: each row represents one bee, each column represents one category, and the numbers in the table indicate the identity of the glomeruli. The graphs (bars) show the average ± SEM of the difference between the responses to acetophenone and 1-hexanol in each group of bees along the ranking category (1–20). B, For each group of bees, the average of the difference between measured and predicted response to the mixture was plotted along the ranked categories (1–20). C, The average ± SEM of the differences between real and predicted correlation coefficients between the mixture and either pure components were calculated in each group of bees. *p < 0.001 (paired t test). D, For hex⁺ group, a scatter plot showing the predicted and real correlation coefficient between the mixture and the pure components. The eight open circles represent predicted correlation coefficients of eight bees in the hex⁺ group; the eight filled circles represent the real correlation coefficient in the same eight bees. The arrows indicate the shift from the predicted correlation to the real correlation of the same bee.

Computational model

Network geometry.

The honey bee antennal lobe model contains 20 glomeruli. Each glomerulus consists of 12 local neurons (lateral inhibition) and 5 projection neurons. In addition, there are 40 local neurons contributing to global inhibition. Overall, the neural network model of AL consists of eight types of connection (see Fig. 4A; Table 1). Each connection is set up randomly based on the probability listed in Table 1. In this AL model, totally, there are 28,719 synapses between LNs, 12,629 synapses from LNs to PNs, and 11,245 synapses from PNs to LNs.

Figure 4.

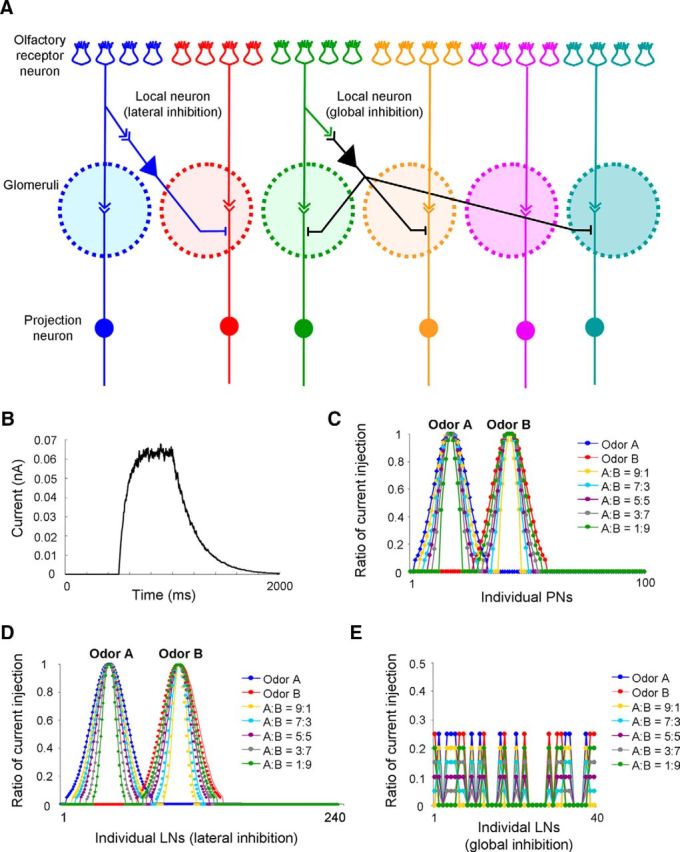
Settings of AL network model and odor stimulation. A, Structure of the AL network model (for details, see Table 1). B, The temporal pattern of full current injection (ratio = 1) in each stimulation cycle (2 s). C, The spatial patterns of odor stimuli (current injections), including odor A, odor B, and their binary mixtures (A:B = 9:1, 7:3, 5:5, 3:7, 1:9) to 100 PNs. D, The spatial patterns of current injection across 240 LNs (lateral inhibition). E, The spatial patterns of current injection across 40 LNs (global inhibition).

Table 1.

Types of connection and connecting probability in the antennal lobe neural network model

Source unit	Target unit	Connecting probability
LN–lateral inhibition	LN–lateral inhibition (belong to the same GL)	0
	LN–lateral inhibition (belong to different GL)	0.4
	Any LN–global inhibition	0.3
	PN–belong to the same GL	0
	PN–belong to different GL	0.5
LN–global inhibition	Any LN–lateral inhibition	0.4
	Any LN–global inhibition	0.1
	Any PN	0.3
PN	Any LN–lateral inhibition	0.4
	Any LN–global inhibition	0.4

Model of individual neurons.

Each PN and LN was modeled by a single compartment that included voltage or Ca²⁺-dependent currents described by Hodgkin–Huxley kinetics (Hodgkin and Huxley, 1952). The membrane potentials of PN and LN are governed by the following ordinary differential equations:

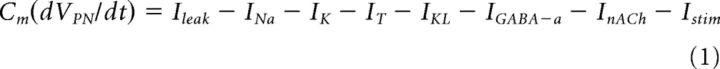For PNs, C_m = 2.9 × 10⁻⁴ μF, g_KL = 0.012 mS/cm², and E_KL = −95 mV. For LNs, C_m = 1.43 × 10⁻⁴ μF, g_KL = 0.018 mS/cm², and E_KL = −95 mV. For LNs, the nonspecific leakage current (mixed Na⁺, K⁺, Cl⁻) is I_leak = g_leak (V − E_leak), where g_leak = 0.05 mS/cm² and E_leak = −70 mV. For PNs, the g_leak = 0.01 mS/cm² and E_leak = −70 mV.

The intrinsic currents, including a fast sodium current, I_Na, a fast potassium current, I_K, a low threshold transient Ca²⁺ current, I_T, a transient potassium A-current, I_A, and a hyperpolarization-activated cation current, I_h, are described by Equation 3 as follows:

where the maximal conductances for PNs are g_Na = 100 mS/cm², g_K = 10 mS/cm², g_T = 2 mS/cm², g_A = 10 mS/cm², and g_h = 0.02 mS/cm². For LNs, g_Na = 100 mS/cm², g_K = 10 mS/cm², and g_T = 1.75 mS/cm². For all cells, E_Na = 50 mV, E_K = −95 mV, and E_Ca = 140 mV. For PNs, E_h = −40 mV. The gating variables 0 ≤ m(t), h(t) ≤ 1 satisfy the following:

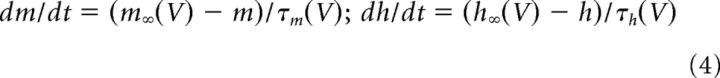where m_∞(V), τ_m(V), h_∞(V), and τ_h(V) are nonlinear function of V derived from experimental recordings of ionic currents. Details of these nonlinear functions are given in Table 2. For all cells, intracellular Ca²⁺ dynamics were described by a simple first-order model as follows:

where [Ca] _∞ = 2.4 × 10⁻⁴ mm is the equilibrium intracellular Ca²⁺ concentration, A = 0.518 × 10⁻⁴ mm · cm²/(ms · μA), and τ = 5 ms.

Table 2.

Current dynamics I = g m^Mh^N(V − E) used in antennal lobe neural network model

Cell	Currents	Current dynamics
PN and LN	INa	M = 3; N = 1;
		α1 = 0.32 × (− 37 − V)/(exp((13 − (V + 50))/4) − 1);
		β1 = 0.28 × (V + 10)/(exp(((V + 50) − 40)/5) − 1);
		m∞ = α1/(α1 + β1);
		τm = 1/(α1 + β1);
		α2 = 0.128 × exp((17 − (V + 50))/18);
		β2 = 4/(exp((40 − (V + 50))/5) + 1);
		h∞ = α2/(α2 + β2);
		τh = (α2 + β2)
PN and LN	IK	M = 4; N = 0;
		α1 = 0.032 × (− 35 − V)/(exp((− 35 − V)/5) − 1);
		β1 = 0.5 × exp((− 40 − V)/40);
		m∞ = α1/(α1 + β1);
		τm = 1/(α1 + β1)
PN	IT	M = 2; N = 1;
		m∞ = 1/(1 + exp(−(V + 59)/6.2));
		τm = (1/(exp(−(V + 131.6)/16.7) + exp((V + 16.8)/18.2)) + 0.612)/4.5738;
		h∞ = 1/(1 + exp((V + 83)/4));
		τh = (30.8 + (211.4 + exp((V + 115.2)/5))/(1 + exp((V + 86)/3.2)))/3.7372
PN	IA	M = 4; N = 1;
		m∞ = 1.0/(1 + exp(−(V + 60)/8.5));
		τm = (1.0/( exp((V + 35.82)/19.69) + exp(−(V + 79.69)/12.7)) + 0.37)/3.9482;
		h∞= 1.0/(1 + exp((V + 78)/6));
		If V < −63
		τh = 1.0/((exp((V + 46.05)/5) + exp(−(V + 238.4)/37.45)))/3.9482;
		If V ≥ −63
		τh = 19.0/3.9482
PN	Ih	Voltage dependence (C indicates close state; O indicates open state):
		$C\underset{\beta }{\overset{\alpha }{\leftrightarrow }}O$
		h∞= 1/(1 + exp((V + 75)/5.5));
		τs = (20 + 1000/(exp((V + 71.5)/14.2) + exp(−(V + 89)/11.6)));
		α = h∞/τs
		β = (1 − h∞)/τs
		Calcium dependence (P0 indicates unbound form; P1 indicates bound form; OL implies locked state):
		P0 + 2Ca $\underset{k2}{\overset{k1}{\iff }}$; P1; O + P1 $\underset{k4}{\overset{k3}{\iff }}$ OL;
		k1 = 2.5 × 107 mm−4, k2 = 4 × 10−4 ms−1, k3 = 0.1 ms−1, and k4 = 0.001 ms−1
LN	IT	M = 2; N = 1;
		m∞ = 1/(1 + exp(−(V + 52)/7.4));
		τm = (3 + 1/(exp((V + 27)/10) + exp(−(V + 102)/15)))/6.8986;
		h∞ = 1/(1 + exp((V + 80)/5));
		τh = (85 + 1/(exp((V + 48)/4) + exp(−(V + 407)/50)))/3.7372

Synaptic currents.

Fast GABA and cholinergic synaptic currents are given by the following equation:

where the reversal potential is E_nACh = 0 mV for cholinergic receptors and E_GABA = −70 mV for fast GABA receptors. The fraction of open channels [O] is calculated according to Equation 7 as follows:

For cholinergic synapses:

and for GABAergic synapses as follows:

In Equation 8, H(x) is the Heaviside (step-) function, t₀ is the instant of receptor activation, A = 0.5, and t_max = 0.3 ms. In Equation 9, V₀ = −20 mV and σ = 1.5. The rate constants, α and β, are α = 10 ms⁻¹ and β = 0.2 ms⁻¹ for GABA synapses and α = 1 ms⁻¹ and β = 0.2 ms⁻¹ for cholinergic synapses. The peak synaptic conductance was g_{GABA (LN-LN)} = 0.02 μS; g_{GABA (LN-PN)} = 0.02 μS; g_{nACh (PN-LN)} = 0.3 μS.

We have tested models with different baseline connectivity strength between AL neurons and found the network dynamics to be qualitatively similar to the results reported in the paper. We have also tested the model dynamics for different connectivity patterns (probability of connections) to ensure that the results of our simulations are structurally stable.

Olfactory stimulation.

To mimic olfactory stimulation, stimulus-specific patterns of current pulses were applied to the PNs and LNs based on the same approach as in our previous studies (Bazhenov et al., 2001a, b, 2005). The temporal profile of a full current pulse is illustrated in Figure 4B. It starts with a rising exponential function at 500 ms with a time constant = 100 ms, and followed by a decaying exponential function (starting at 1000 ms) with a time constant = 200 ms. Random current fluctuation was varied between 5% and 10%. Each cycle of odor stimulation is 2 s.

The spatial profile of an odor stimulus was characterized by a Gaussian distribution (see Fig. 4C–E). In our study, different odors and their various binary mixtures were used. To maintain overall mixture concentration similar to individual components, the spatial patterns representing individual components within a mixture were proportionally reduced (see Fig. 4C,D) based on our previous results (Assisi et al., 2007; Ito et al., 2009). Moreover, the spatial patterns of the stimulus across LNs providing global inhibition were tuned to randomly selected odor, and the ratio was also proportionally reduced to maintain overall mixture concentration (see Fig. 4E).

Synaptic plasticity.

A simple phenomenological model was used to describe the facilitation of inhibitory connections (from LNs to PNs and from LNs to LNs) during olfactory learning. Accordingly, the maximum synaptic conductance was multiplied by a facilitation variable, F. Here, F = 1 + 1/2(F_i + dF_pre − 1) × exp(− (t − t_i)/τ_pre) + 1/2(F_i + dF_post − 1) × exp(− (t − t_i)/τ_post), where dF was the facilitating rate (dF_pre = 0.15, dF_post = 0 for presynaptic facilitation; dF_pre = 0, dF_post = 0.2 for postsynaptic facilitation), τ_pre = τ_post = 10 ms was the time constant of recovery, F_i was the value of F immediately before the i^th spiking event (initial F_i = 1), and (t − t_i) was the time after i^th spiking event. The initial value of the GABA conductance was 0.02 μS. Presynaptic facilitation was based on the spiking events occurring in presynaptic neurons. On the other hand, the postsynaptic facilitation was based on the spiking events occurring in postsynaptic neurons. The updated synaptic weights at the end of the last learning cycle (at 6000 ms) were used as the new synaptic weights during testing phase.

Principal component analysis (PCA).

The response trajectory of the entire PN population to a specific input was constructed by binning PN spike trains in 20 ms bins and shifting the time bin with 5 ms steps. To visualize PN responses, the 100 dimensional space of all PN activities was then reduced to 3D olfactory space via PCA.

Correlation coefficient between odor responses.

Correlations between odor responses were calculated based on spike count profile across all 100 PNs for a single trial (2 s). The correlation coefficients were calculated before learning and compared with those after olfactory learning. The changes of the correlation coefficients before/after learning were used to compare simulation results with the experimental data.

Results

Variability in odor-elicited activation patterns in the AL

In the present work, we evaluated how associative learning modifies the way in which the antennal lobe network processes olfactory information contained in odor mixtures. For this aim, we performed calcium imaging of spatiotemporal activity patterns elicited by two pure odors, 1-hexanol and acetophenone, and their binary mixture across PN dendrites. The recorded patterns correspond to the output of the AL and represent olfactory information that is conveyed to the mushroom bodies and lateral horn through the lateral antenno-protocerebral tract (Galizia and Rössler, 2010). The odors 1-hexanol and acetophenone were selected for these experiments because they show minimal overlap of the activity patterns elicited in the AL and because they are comparable in terms of the amplitude and the number of glomeruli that are recruited. Figure 1A shows false-color pictures of the activation patterns elicited by the pure odors and the mixture in a representative honey bee. The figures correspond to the average of the activity between 250 and 750 ms after odor onset. This time interval was selected for analysis because it includes the time point at which odor patterns reach maximal separation after odor onset and because it is the time interval during which olfactory-based behavioral decisions occur in honey bees (Ditzen et al., 2003; Fernandez et al., 2009). The analysis performed along the imaging section is based on the responses measured from 20 specific glomeruli that could be identified across all honey bees (Fig. 1B). Raw fluorescence and pixel-correlation images shown in Figure 1B were used to aid in identification of glomeruli by comparison with the honey bee AL atlas (Flanagan and Mercer, 1989; Galizia et al., 1999) (see Materials and Methods). Figure 1C shows the average responses to acetophenone, 1-hexanol, and the mixture in the 20 identified glomeruli across 11 control bees.

Pearson's correlation coefficients between response patterns were used to evaluate similarity between patterns elicited by the pure odors and the mixture. Figure 1D shows no correlation between the pure odors (ace-hex), as might be expected from the low overlap between their respective patterns (Fig. 1A,C). On the other hand, the correlations between the pure odors and the mixture (ace-mix; hex-mix) were significantly higher, consistent with the fact that the pure odors and the mixture share many active glomeruli. However, pooling the correlation coefficients obtained from different bees, as in Figure 1D, occludes the high variability that exists across animals. Figure 1E shows the correlation values between each pure odor and the mixture for individual honey bees. The correlation is highly variable from animal to animal, ranging from 0.13 to 0.90 for acetophenone versus mixture (abscissa), and from 0.08 to 0.89 for 1-hexanol versus mixture (ordinate). This analysis indicates that the contribution of the pure odors to the representation of the mixture is not necessarily balanced. Indeed, the higher the correlation between the mixture and one component, the lower the correlation between the mixture and the other component. Only two bees (Fig. 1E, two arrows) showed high and balanced correlation coefficients between the mixture and either pure odors, but it turned out that these two bees had also the highest correlation values between the two pure odors (0.28 and 0.71). In summary, we found pronounced variability across animals in regard to the relative weight of the components in the representation of the mixture. As a measure of the variability of the activation patterns across honey bees, we determined the correlation coefficient among response patterns evoked by the same odors across control honey bees that did not receive any olfactory training, with the exception of the experience they acquired during foraging before they were captured. Figure 1F shows the average and SEM of correlation values between patterns elicited by the same three odors across 11 control bees. The results show that the pattern elicited by the mixture is more variable than the patterns elicited by the pure odors (ANOVA, F_(2,162) = 6.76; p = 0.001; p < 0.01 post hoc contrasts). We hypothesized that part of this variability might be caused by different olfactory experiences that had shaped the AL network during foraging. Thus, in the next section, we evaluate whether olfactory conditioning affects this variability as well as the contribution of the components to the representation of the mixture.

Appetitive conditioning shifts the representation of the mixture toward the rewarded component

Figure 2A shows the learning curves of bees that were trained using 1-hexanol or acetophenone and were later used for imaging. The conditioning protocol consisted of 10 reinforced trials separated by 10 min intertrial intervals. Groups of honey bees conditioned to odors reached peak (∼90%) response levels by 5 or 6 conditioning trials. A group of untrained bees that served as control was handled simultaneously and received the same manipulation and reward as trained groups but was not stimulated with odors. After conditioning, honey bees from the two trained groups and from the untrained group were further divided into two subgroups (Fig. 2A–C). One subgroup was used for imaging odor responses in the AL. For this aim, PNs were backfilled with calcium sensor dye Fura-dextran 8 h after conditioning (Fig. 2B) and odor responses were imaged between 12 and 16 h after staining (Fig. 2C, top). The other subgroup of bees was left intact and was used to confirm olfactory memory retention at a time interval consistent with the imaging experiment. As shown in Figure 2C (bottom), the conditioning protocol supports strong memory retention after 24 h. The conditioned response was highly specific; no conditioned response was evoked by 1-hexanol in bees conditioned to acetophenone, and almost no conditioned response was elicited by acetophenone in bees conditioned to 1-hexanol.

Next, we tested whether conditioning with a component changes the representation of the mixture in a way that facilitates the perception of the component in the mixture. As shown in the previous section, we found a high variability in the correlation between the mixture and the pure components (Fig. 1E). We hypothesized that this variability might be a consequence of different individual experiences that had shaped the AL network of the foragers before they were captured. Because the conditioned bees were obtained simultaneously from the same pool of animals as the control bees, similar variability should be expected across the conditioned bees, unless the additional olfactory experience provided by the training induced changes in the AL that shape the representation of the mixture. Thus, we compared the variability of the activation patterns within each group of bees by measuring the correlation among the patterns elicited by the mixture across bees that had the same treatment. Figure 2D shows the average and SEM of the correlation coefficients between pairs of patterns elicited by the mixture across control bees, acetophenone-trained bees, and 1-hexanol-trained bees. The correlation (ANOVA: F_(2,108) = 11.52, p < 0.0001; p < 0.001, post hoc contrasts) was higher between patterns elicited by the mixture in animals that received olfactory conditioning with 1-hexanol or acetophenone compared with the correlation value among patterns measured from control bees, suggesting that olfactory conditioning shaped the representation of the mixture.

We then evaluated the nature of the changes in the representation of the mixture caused by conditioning. The impossibility of doing paired comparisons between patterns obtained from the same animal before and after conditioning and the variability described in the previous section demanded an analysis that is sensitive to the effects caused by training on top of the interindividual differences. The rationale behind the analysis was based on the observation that general aspects of the pattern elicited by the mixture can be predicted based on the patterns elicited by the pure components and that part of the variability in the representation of the mixture reflected the variability in the representation of the pure components. Thus, we analyzed whether conditioning caused the mixture pattern to deviate from the pattern that can be expected based on the representations of the components. For this analysis, we do not analyze whether the patterns elicited by the pure odors were affected by training. We focus instead on whether training modifies the way in which the representations of the components are summed in the mixture. The analysis first focused on data from the control bees and used it to establish algorithms that allow accurate prediction of the pattern elicited by the mixture in each animal based on the patterns elicited by the pure components in the same animal. Second, we applied the prediction algorithms derived from control bees to the data from trained bees to evaluate whether olfactory conditioning changes the way the representations of the components are summed in the mixture. On a first approach, the data from all bees were analyzed according to the identification of the glomeruli. Considering that response versus concentration curves (and thus the summation of the activities elicited by each component) may follow different dynamics in each particular glomerulus, the following calculation was made independently for each of the 20 glomeruli. For each glomerulus in each honey bee, we had values of calcium responses for 1-hexanol (R_hex), acetophenone (R_ace), and the binary mixture (R_mix). Using the data from the control bees, we fitted a linear equation of the form of αR_hex +βR_ace + γ = R_mix, which provided a plane for each glomerulus. Thus, we calculated a set of parameters (α, β, γ) that makes the best fit of the data points representing different control honey bees. An example of the plane fitted for glomerulus 47 based on the data points from the control honey bees is shown in Figure 2E. We calculated 20 sets of parameters α, β, and γ, and each set represents one plane specific for one glomerulus. R² values of the 20 planes ranged between 0.68 and 0.95 (average = 0.86), and p values of the fitted planes were in all cases <0.01 (average of p values = 0.001).

Afterward, the linear fits were used to predict for each glomerulus the response elicited by the mixture on the basis of the responses elicited by the pure components. Then, we compared the predicted and the measured response elicited by the mixture in each glomerulus. Figure 2F shows the average of the difference between the measured and the predicted responses to the mixture for each glomerulus. The difference was calculated by subtracting the predicted activity from the measured activity. Positive values imply glomeruli in which the activity elicited by the mixture was higher than expected, and negative values indicate glomeruli in which the activity elicited by the mixture was lower than expected. Figure 2F (top) shows how accurate the predictions were for the control bees. The relatively small differences between predicted and measured activity indicate that mixture response can indeed be predicted accurately from the responses to the individual components using the calculated linear fits. Subsequently, the linear fits calculated from the control bees were used to predict glomerular responses to the mixture in conditioned bees. Figure 2F (middle) shows the results from honey bees conditioned with acetophenone. Although there is no statistically significant difference between measured and predicted responses, the results show more tendencies to underestimations and overestimations than in the control group. Finally, Figure 2F (bottom) shows the results from the bees trained with 1-hexanol. Twelve of 20 glomeruli show significant differences between the predicted and the measured responses (* and # for p < 0.05 and p < 0.01 respectively, paired t test). In summary, the linear model calculated for control honey bees could not predict the mixture pattern in trained honey bees, which suggests that the systematic deviations can be explained by changes induced by training.

Next, to analyze whether the differences in the glomerular activity represent a change in favor of one of the components, we evaluated whether the changes differentially involve glomeruli that are recruited by one or other component. For this aim, the 20 glomeruli were ranked according to their responses to 1-hexanol and acetophenone. For each glomerulus, we subtracted the average response to 1-hexanol from the average response to acetophenone (R_ace − R_hex) across control bees. Figure 2G₁ shows the distribution of the 20 glomeruli along this ranking, including control and trained honey bees. The left side of the distribution corresponds to the glomeruli that show strong responses to 1-hexanol and weak or no response to acetophenone, whereas the right side corresponds to glomeruli with strong responses to acetophenone and weak or no responses to 1-hexanol. Glomeruli that have similar responses to both odors fell in the middle region as the glomeruli that are not activated by either of the two odors. Subsequently, the ranking was used in Figure 2G₂ to reorganize the data from Figure 2F, but this time in relation to the response profile of the glomeruli. The trend line and the results of a linear regression inserted in the figure were calculated to evaluate whether the difference between measured and predicted responses to the mixture depends on the response profile of the glomeruli. The regression was significant for the honey bees trained with 1-hexanol. Although there was a general decrease in the response of almost all glomeruli, the decrease is pronounced and significant in the glomeruli that encode acetophenone. Thus, at least for bees trained with 1-hexanol, the glomeruli that show more robust responses to acetophenone than 1-hexanol were found to be less activated in the mixture than expected. The regression was not significant in the other two groups of honey bees, although an opposite tendency was observed for honey bees trained with acetophenone (Fig. 2G₂, middle).

Finally, to determine whether the changes constitute a net bias in the representation of the mixture as a whole, we compared, within each bee, the correlation between the patterns elicited by the components and that elicited by the mixture with the correlation between the patterns elicited by the components and the pattern expected for the mixtures. We called the first one “real correlation coefficient” and the second one “predicted correlation coefficient.” Figure 2H shows the average of the difference between the real and the predicted correlation coefficients. In honey bees that were conditioned to 1-hexanol, the difference between both types of correlations reveals that the mixture was less similar to acetophenone (negative red column on the left) and more similar to 1-hexanol (positive red column on the right) than the predicted mixture. In control honey bees, there were no differences between the predicted and real correlations. For honey bees that were trained with acetophenone, there was only a minor tendency for the mixture pattern to be less similar to 1-hexanol than expected (negative blue column on the right).

The analysis described so far was entirely based on the identity of the glomeruli used as the criterion to pool the data from different honey bees and fit the linear equations used to predict the responses to the mixture based on the responses to the pure odors. We noticed, however, that the response profile of each glomerulus to the pure components was not strictly conserved across honey bees. For example, glomerulus 28 was the most prominent activated glomerulus in the pattern elicited by 1-hexanol in 5 of 11 control bees, but it was the second one in 4 of them, and it was in fourth or 17th positions in two bees. A similar kind of divergence was observed for the remaining glomeruli (Fig. 3, tables).

The origin of this variability could be due to differential foraging experiences that shaped the response profile of the glomeruli before the forager bees were captured for the experiment. This argument supports the view that the behavior of each glomerulus might be more accurately predicted on the basis of its response profile rather than on the basis of the anatomical location. Therefore, we repeated the same analysis as before, but instead of using the anatomical identification of the glomeruli as the criterion for pooling the data and fit the linear equations, we pooled them on the basis of their functional profile. Thus, we ranked the 20 glomeruli within each honey bee from responders to 1-hexanol to responders to acetophenone and created 20 categories (Fig. 3A, tables). In each bee, category 1 was assigned to the glomerulus with the highest negative value after the subtraction R_ace − R_hex, and category 20 was assigned to the glomerulus with the highest positive value. The tables displayed in Figure 3A show the ranking of the glomeruli for each individual bee and for the three groups of bees. Then, we used the data from the glomeruli in the same category of the control group to calculate the linear equation that fits the response to 1-hexanol, acetophenone, and the mixture in one plane as in the previous section. R² values ranged from 0.96 to 0.54 (average = 0.84) and p values were in all cases <0.04 (average = 0.003). Based on the linear equations derived from the control honey bees and on the response elicited by the pure odors in each individual, we calculated the predicted response to the mixture for each glomerulus in each individual bee in all groups.

Figure 3B summarizes the difference between the measured and the predicted response for all glomeruli along the ranking. In the control group (Figure 3, top), the predictions were accurate and there was no dependence on the category of the glomeruli. In the 1-hexanol trained group (Figure 3, bottom), there was a general decrease in the response elicited by the mixture, and the difference between measured and predicted mixture response was related to the categories of the glomeruli. Glomeruli that encode acetophenone were lower than expected. Associative learning using acetophenone as the conditioned odor failed to show any tendency in this analysis. As before, the predicted glomerular responses to the mixture were used to generate a predicted pattern to the mixture in each bee. The predicted pattern was compared with the measured pattern on the basis of the correlations that they have with the patterns elicited by the pure components. Figure 3C shows the effect of conditioning in regard to the real and predicted correlation values between the mixture and the components. Similar to Figure 2H, the associative learning of 1-hexanol produced a bias in the representation of the mixture that makes it more similar to the representation of 1-hexanol and less similar to the representation of acetophenone than expected in controls. Finally, Figure 3D expresses the results for each individual honey bee from the 1-hexanol conditioned group, showing how the representation of the mixture shifted from its predicted position to its measured position in regard to the correlation coefficients between the mixture and the pure components.

Unlike the honey bees trained with 1-hexanol, honey bees trained with acetophenone did not show a clear shift in the representation of the mixture (data not shown). We found differences between the predicted and the measured pattern to the mixture, which suggests again that training modifies the way in which the components are summed in the representation of the mixture. However, the changes in the glomerular activity did not make the pattern of the mixture more similar to acetophenone than what was expected. Possible explanations are that only a portion of the AL is sampled with the imaging technique that we used (20 of 160 glomeruli in the present work), and we may have missed the glomeruli that make the difference. It is also possible that network interactions are not completely symmetrical between the elements that encode acetophenone and 1-hexanol. Such asymmetry would be consistent with our results in which conditioning with hexanol reduces the expression of acetophenone in the mixture, but conditioning with acetophenone does not reduce the expression of hexanol in the mixture pattern. Finally, conditioning with acetophenone might have modified the representation of acetophenone itself, as it is expected on the basis of previous studies that showed changes in coding of the conditioned odor after training (Sandoz et al., 2003; Daly et al., 2004; Yu et al., 2004; Rath et al., 2011). In this case, changes in the representation of the pure odor produce changes in the representation of the mixture that are predicted by our model and thus are not detected by the analysis. In summary, the results indicate that, after appetitive conditioning with 1-hexanol, the response to the mixture became more similar to 1-hexanol (the conditioned odor) and less similar to the pattern for acetophenone (the background odor).

Odor stimulation triggers oscillatory and odor-specific responses in the AL model

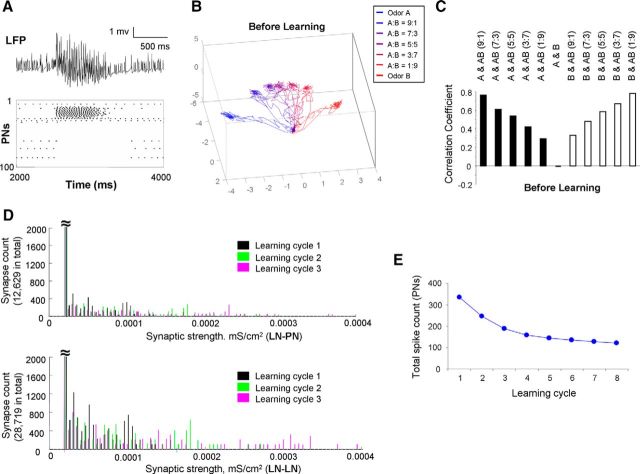
To explore potential mechanisms behind the experimental results, we designed a honey bee AL model, including populations of conductance-based excitatory PNs and inhibitory local interneurons (LNs) (detailed model and simulation settings are illustrated in Materials and Methods; Fig. 4; Tables 1 and 2). Before learning, the AL model response to odor A is displayed in Figure 5A. Figure 5A (top) shows a trace of local field potential (LFP), which is derived from the average of membrane potential across all PNs in the network. Figure 5A (bottom) is a rastergram representing the spiking activities across the entire population of PNs during a stimulating cycle (2 s). The odor response lasted for ∼1 s and then decayed to the baseline level of spontaneous activity. To characterize the entire network response, we calculated all PN spikes in 20 ms bins and plotted it as a trajectory in 3D space via principal component analysis (i.e., the first three principal components). Figure 5B shows PN responses to two single distinct odors (A and B) and several binary mixtures that were made by combining A and B in different proportions (A:B = 9:1, 7:3, 5:5, 3:7, 1:9; Fig. 4C–E). In all cases, the olfactory trajectories started from the same origin representing the baseline activity. It then quickly projected out during the initial phase of the odor response to reach a quasi-stationary state. After that, it returned to the origin during the offset phase of the stimulation. Similar dynamics have been reported previously in the locust (Stopfer et al., 2003) and honey bee (Fdez Galán et al., 2004; Fernandez et al., 2009). Consistent with previous experimental observation (Fernandez et al., 2009), the trajectories were sequentially ordered according to the mixture ratios from one extreme to the other.

Figure 5.

Olfactory responses in AL before learning and after learning modified by presynaptic facilitation. A, Before learning, the LFP in AL and the rastergram across whole population of PNs in responding to odor A are displayed. B, Before learning, spatiotemporal patterns of two pure odor and five mixture odor responses across all PNs are displayed in a PCA space. A smooth transition of trajectories along mixture ratios is observed. C, Before learning, the correlation coefficients between two pure odors and between pure odor and mixture odors are shown. D, During learning of odor A, the synaptic strength of LN-PN and LN-LN was facilitated based on presynaptic spiking activities in LN. These two histogram plots show distribution of synaptic weights of 12,629 LN-PN synapses (top) and 28,719 LN-LN synapses (bottom) during the first three learning cycles indicated by different colors. E, Total PNs' spike count dropped mainly during the first few learning cycles.

Figure 5C shows the correlation coefficients between patterns elicited by single odors and mixture odors based on the response profiles across all PNs (i.e., the spike count profile across all PNs during one odor stimulating trial). These values (correlation coefficients) are consistent with the order of the different trajectories shown in Figure 5B. The response to a pure odor had higher correlation with the response of the mixture odor that contains a higher concentration of that pure odor (i.e., correlation coefficient between A and AB 9:1 = 0.767, and correlation coefficient between B and AB 1:9 = 0.784). The correlation between responses to the pure odors A and B was the lowest (−0.0006) and the correlation among pure odors and the balanced mixture 5:5 was ∼0.6, which is similar to the value obtained from the experiments for the pure odors acetophenone or 1-hexanol with the mixture 10:10 (Fig. 1D).

Appetitive associative learning increases response similarity between mixture odor and learned odor

Next, we investigated how plasticity in the AL may change the odor responses and how these changes correspond to our experimental observations. Because release of octopamine is needed for appetitive olfactory learning (Hammer, 1993; Farooqui et al., 2003), and a large fraction of the octopamine receptor AmOA1 was found to be expressed in inhibitory LNs in the honey bee AL (Sinakevitch et al., 2011, 2013), we simulated the appetitive conditioning by increasing the synaptic weights of LN-PN and LN-LN synapses as the presynaptic LN was activated by the conditioned odor. The synaptic facilitation based on activity of the presynaptic inhibitory LNs represents the situation of coincidental activation by the conditioned and the unconditioned pathways. The activation of octopamine receptors in LNs together with odor induced activity causes a rise in Ca²⁺ that primes adenylyl cyclase to enhance cAMP and cAMP-dependent protein kinase activation that further regulates synaptic plasticity (Capogna et al., 1995; Han et al., 1998; Muller, 2002; Antonov et al., 2003). Thus, during appetitive conditioning, the LNs are able to merge the signals from the conditioned stimulus and the unconditioned stimulus pathways.

In Figure 5D, the distributions of synaptic weights during different training cycles with conditioned odor A are plotted. During this appetitive learning process, some LN-PN synapses and some LN-LN synapses gradually increased their weights due to the spiking activities occurring at their presynaptic LNs. Because learning causes an overall increase of inhibition in the AL network, many PNs reduced their firing rate as a result of olfactory learning, whereas some of them maintained their firing activities. Overall, we found a decrease of activity in the AL network along learning cycles (Fig. 5E) as observed in experiments (Fig. 2F,G₂).

After training involving three cycles of conditioning to odor A, pure odors (odor A and odor B) and their binary mixtures were tested again to evaluate the impact of learning on the olfactory responses in AL. In Figure 6A, we found a significant shift of the mixture trajectories toward the trajectory of the pure odor that was use as the conditioned stimulus. Thus, after training based on presynaptic activity-dependent facilitation on both LN-PN and LN-LN synapses, the spatiotemporal patterns for the mixture became more similar to the pattern of the learned odor, odor A. This observation was further confirmed by the correlation coefficient analysis shown in Figure 6B. The value of the correlation coefficients between odor A and all mixtures increased after learning of odor A (i.e., Fig. 6B, positive black bars). On the other hand, the correlation coefficients between odor B and all mixtures reduced (i.e., Fig. 6B, negative white bars).

Figure 6.

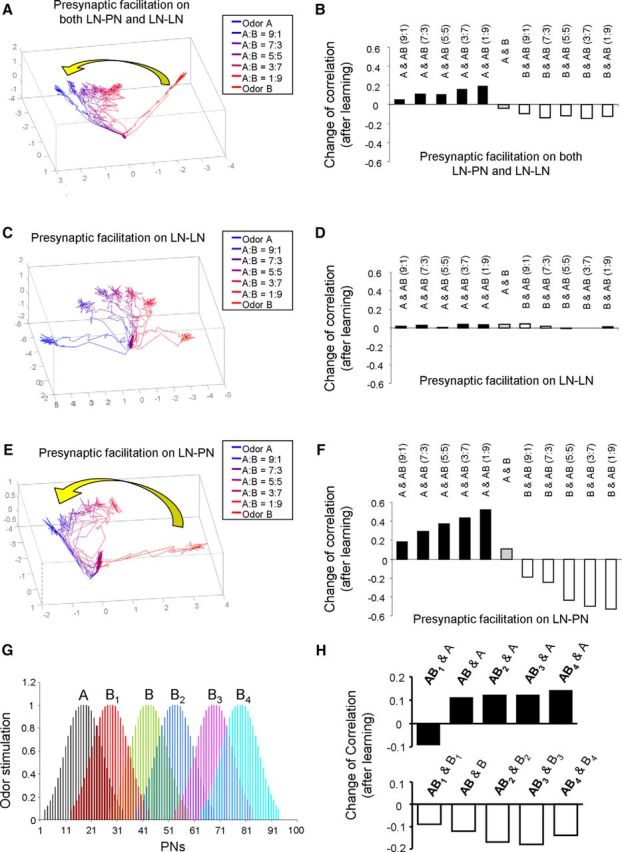
Changes of odor responses in AL after learning based on presynaptic facilitation. A, After learning of odor A manipulated by presynaptic facilitation in both LN-PN and LN-LN synapses, the dynamic trajectories of odor responses based on activities across all PNs are presented in 3D PCA space. The trajectories of mixtures were found to shift closer to the trajectory of learned odor, odor A. B, Corresponding to A, the change of correlation coefficient derived before and after olfactory learning was also calculated. It was found that, after learning of odor A, the correlation coefficient between odor A and mixture odors increased. On the other hand, the correlation coefficient between odor B and mixture odors reduced. C, In the second setting, the presynaptic facilitation mechanism was installed in LN-LN synapses only. In PCA space, the trajectories of mixture odors stay at the middle between the trajectories of odor A and odor B after learning without obvious shift toward either pure odor component. D, Corresponding to C, the change of correlation coefficient between odor responses was quite small after learning. E, In the third setting, the presynaptic facilitation mechanism was installed in LN-PN synapses only. The trajectories of mixture odors in PCA space were found to move toward the learned odor, odor A. F, Corresponding to E, the correlation coefficients between odor A and mixture odors were increased significantly after learning. On the other hand, the correlation coefficients between odor B and mixture odors were decreased. G, The spatial patterns of alterative odor B (including B₁, B₂, B₃, and B₄) were plotted. These alternative odors were also used to test the impact of presynaptic facilitation on olfactory responses. H, Following G, the degree of similarity between pure odor and mixture odor (5:5) responses was evaluated by correlation coefficients across PNs. Top, The correlation between mixture odors and odor A increased after learning of odor A, except one of the mixture odors, AB₁. Bottom, The correlations between all mixture odors and odor B reduced after learning of odor A.

Next, to distinguish the contribution of different types of synapses (LN-PN or LN-LN) to the observed change, we implemented the presynaptic facilitation mechanism at only one type of synapse (Fig. 6C–F). In Figure 6C, D, presynaptic facilitation was implemented exclusively in LN-LN synapses, and the strength of LN-PN synapses was kept unchanged. We found that the trajectories representing responses to the mixture of odors stayed at the middle of the pure odor trajectories (Fig. 6C). Consistently, the changes of the correlation coefficient between odor responses were close to 0 (Fig. 6D). In contrast, when presynaptic facilitation was implemented only in LN-PN synapses and the strength of LN-LN synapses was kept unchanged, the trajectories of the mixtures moved toward the learned odor A (Fig. 6E). The correlation coefficients between the response of odor A and the mixtures were largely increased (Fig. 6F, positive black bars), and the correlation coefficients between the response of odor B and the mixture odors were mainly reduced (Fig. 6F, negative white bars). These results are consistent with the results from the appetitive conditioning experiments shown in previous sections when bees showed conditioning to 1-hexanol (Fig. 3D). Our simulation results suggest that the effect of appetitive olfactory conditioning may depend on the facilitation of the inhibitory synapses from active LNs to PNs in the AL.

It has been shown that different odor stimuli could evoke different spatial patterns of odor response across glomeruli with different degrees of overlap (Sachse et al., 1999). To test whether the observation of shift of mixture odor responses induced by the mechanism of synaptic facilitation is widely held with a variety of odor stimuli, next, we extended the previous computational experiments to pairs of odors that have different degrees of overlap in their representation in AL. In new simulation studies, odor B was replaced by odors B₁, B₂, B₃, or B₄, which have different spatial response patterns across LNs and PNs and different degrees of overlap with odor A (Fig. 6G). By repeating the same training procedures (i.e., setting up presynaptic facilitation on both LN-PN and LN-LN), the similarity of odor response patterns between the pure odor and the mixture (5:5) was evaluated by calculating the change of correlation coefficient, and the results are plotted in Figure 6H. We found that the response pattern of mixture (5:5) became more similar to the learned odor, odor A, except in the case of odor B₁, whose input pattern and activity pattern was very close to odor A (Fig. 6G,H). On the other hand, the correlation coefficients between mixture and components B_i (i = 1–4) were all reduced after learning of odor A (Fig. 6H, bottom).

Nonassociative learning decreases response similarity between mixture odor and exposed odor

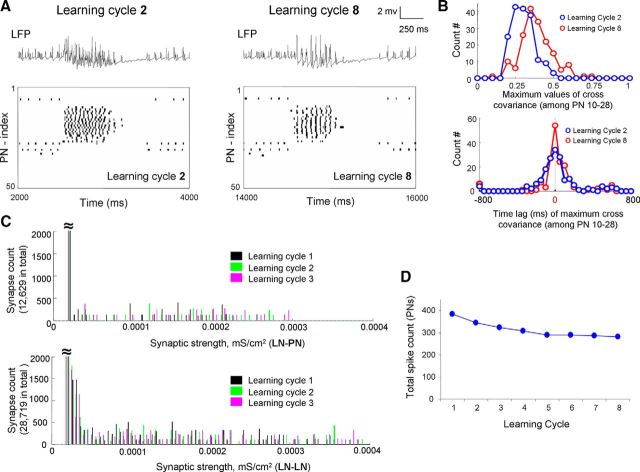
Our previous experimental and modeling study of the nonassociative olfactory learning in the honey bee revealed that, after multiple presentations of the same pure odor without any reward, which decreases subsequent learning of that odor (Chandra et al., 2010), the AL response pattern to the odor mixture became less like the pure odor responses presented during training (Locatelli et al., 2013). A related cellular mechanism has been reported in Drosophila during olfactory habituation (Das et al., 2011; Sudhakaran et al., 2012). These studies revealed that glomerulus-specific inhibitory facilitation of LN-PN synapses occurred during odor habituation and that this facilitation could be driven by the postsynaptic activities of LN-PN synapses (Das et al., 2011; Sudhakaran et al., 2012). We then explored the hypothesis that, in contrast to appetitive olfactory learning, nonassociative olfactory learning is manipulated by the synaptic facilitation that depends on the postsynaptic activities of the AL neurons. In our model, Figure 7A shows a representative example of the response to odor A across PNs during early and late stage of learning. In this modeling experiment, synaptic plasticity was solely dependent on the postsynaptic neuron activities; the strength of inhibitory LN-PN and LN-LN synapses was facilitated when a spiking event was detected in the postsynaptic neuron during training phase. First, it was found that increase of inhibition led to more synchronous PN responses that were reflected in the large amplitude LFP oscillations (Fig. 7A). In Figure 7B, the level of synchronization across PNs was evaluated by cross-covariance analysis across PN pairs. Along the training, the distribution of the peak amplitudes of the cross-covariance function became narrower (Fig. 7B, top) and the width of the distribution of the time lags to the peak decreased (Fig. 7B, bottom), indicating an increase in synchrony across PNs. In Figure 7C, the changes of synaptic weight distribution (Fig. 7C, top, LN-PN; Fig. 7C, bottom: LN-LN) during the first three learning cycles are shown. Along the learning cycles, the total PN spike count dropped over the first 4 or 5 cycles (Fig. 7D). These results are consistent with our previous modeling results (Bazhenov et al., 2005) and associated experimental studies (Stopfer and Laurent, 1999) of fast odor learning in the locust AL.

Figure 7.

Results of olfactory learning manipulated by postsynaptic facilitation. A, As the postsynaptic facilitation mechanism was effective in both LN-PN and LN-LN, the trace of LFP and the rastergram of all PNs obtained from learning cycle 2 (left panel) and cycle 8 (right panel) are exhibited. It was noticed that, after experiencing several learning cycles, the firing activities became more synchronous across PNs (comparing cycle 8 with cycle 2 here). B, Corresponding to A, the level of synchronization across active PNs (PN 10-PN 28) was further evaluated by cross-covariance analysis. After several cycles of learning, the PNs' firing patterns became more synchronous indicated by larger values of maximum cross-covariance (top, red distribution) and overall shorter time lag to the main peak (bottom, red distribution). C, Changes of synaptic strength distribution during the first three cycles of learning of odor A in the model with postsynaptic facilitation in LN-PN and LN-LN. D, The total spike number in PNs along learning cycles modified by postsynaptic facilitation in LN-PN and LN-LN. Decrease of total spike number (mostly the first 3 or 4 cycles) was observed.

We then tested and compared the effect of postsynaptic facilitation in the AL network using three different model settings, including the following: (1) installing postsynaptic facilitation mechanism in both LN-PN and LN-LN types of synapses, (2) installing postsynaptic facilitation mechanism in LN-LN synapses only, and (3) installing postsynaptic facilitation mechanism in LN-PN synapses only. We found that, when postsynaptic facilitation involved both LN-PN and LN-LN synapses, response to the odor mixture moved away from the exposed odor, odor A, and toward the novel odor component in the mixture (i.e., odor B here) (Fig. 8A). Moreover, postsynaptic facilitation implemented in LN-PN synapses alone was sufficient to obtain this network dynamics (Fig. 8E), whereas postsynaptic facilitation implemented in LN-LN synapses alone produced no shift (Fig. 8C). These results were further confirmed by the correlation coefficient analysis (Fig. 8B,D,F).

Figure 8.

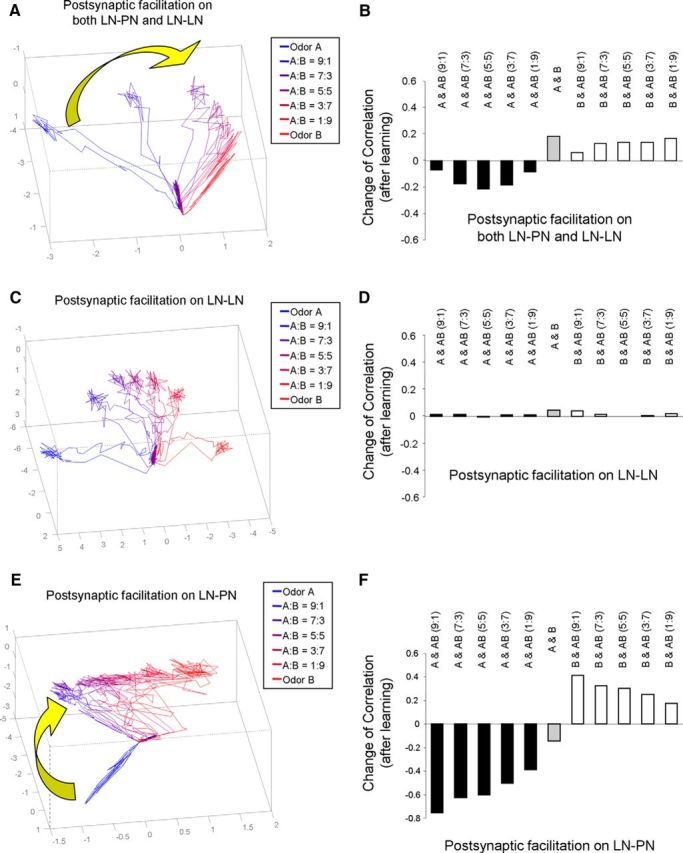
Changes of odor responses after learning manipulated by postsynaptic facilitation. A, After learning of odor A via manipulation of postsynaptic facilitation in both LN-PN and LN-LN, the trajectories of mixture odor responses moved toward the unlearned odor, odor B, in PCA space. B, Corresponding to A, after learning of odor A, the correlation coefficient between odor A and mixture odors reduced. On the other hand, the correlation coefficient between odor B and mixture odors increased. C, After learning of odor A manipulated by postsynaptic facilitation in LN-LN synapses only, the mixture odors stayed at middle between odor A and odor B in PCA space. D, Corresponding to C, the changes of correlation coefficient among odor responses are small. E, When postsynaptic facilitation was set up at LN-PN synapses only, the trajectories of mixture odors were found to move toward the unlearned odor, odor B. F, Corresponding to E, the correlation coefficients between odor A and mixture odors reduced. At the same time, the correlation coefficients between odor B and mixture odors increased.

Our results are consistent with experimental data (Locatelli et al., 2013). After repeated exposure of the same single odor (hexanol or octanone) with no reward, the spatiotemporal pattern of the mixture odor response in AL became more similar to the odor component, which was not exposed previously. Thus, our study suggests that nonassociative olfactory learning in the AL could be regulated by facilitation of the inhibitory LN-PN synapses dependent on the postsynaptic cell activity.

Discussion

The primary goal of our study was to understand the changes of the odor representation in the AL after learning. Results from our previous report (Fernandez et al., 2009) and other studies (Linster and Smith, 1997; Sandoz, 2003; Sandoz et al., 2003; Rath et al., 2011) agreed that the changes might serve in part to increase the separation between the spatiotemporal patterns for reinforced versus unreinforced odors, thus making odors with different outcomes perceptually more distinct. In the present study, we have considered another ecologically relevant situation in which experience-dependent modifications in odor perception could help odor-guided behaviors. Monomolecular pure odors rarely occur as olfactory stimuli in nature. Instead, natural odors with either learned or innate predictive value are blends of several components that are presented with changing and different background odors. Thus, one hypothesis for the role of plasticity in odor coding is that it adjusts the sensitivity of the olfactory system to detect meaningful stimuli and filter out background (Smith, 1996). Consistent with this idea, we have recently reported that the representation of uninformative components is reduced in a mixture thereby improving the perception of novel components (Locatelli et al., 2013). In the present work, we tested the complementary idea: Do meaningful learned odors have a clearer representation in the mixture in a way that improves its perception against background odors? We set up an appetitive conditioning experiment combined with optical recordings of PN activity. We measured the activation patterns elicited by two pure odors and the binary mixture in three groups of bees: a control group (without olfactory conditioning) and two groups that underwent appetitive conditioning using the pure odors. The pattern of the mixture included glomeruli showing hypoadditive effects, synergisms, and cases of suppressions (Deisig et al., 2006, 2010; Silbering and Galizia, 2007). We found that control bees showed a wide range of variability in the representation of the mixture. Most of the variability in the mixture could be predicted based on the representation of the pure odors, suggesting that a high proportion of the variability was not inherent to the mixture but transferred from variability in the representation of the pure odors. Indeed, the linear fit provided accurate prediction of the representation of the mixture from the responses to the components for the control group. Decomposition of mixture responses into its component responses has been previously used to study representation of mixtures in mitral cells of the rat olfactory bulb (Giraudet et al., 2002) and in projection neurons of the locust AL (Shen et al., 2013). We found that the algorithms based on control bees were less accurate for predicting a glomerular response to the mixture in trained bees. This indicates that the way in which the patterns of the components are summed in the mixture differs between control and trained bees, and it suggests that conditioning modifies interactions between the components in the mixture.

Further analysis showed that the pattern for the mixture favored the representation of the rewarded odor in 1-hexanol trained bees and reduced the representation of acetophenone when it was the background odor. The shift in the pattern was caused by a reduction in the activity of glomeruli that encode the background odor. There was no increase in the activity of glomeruli that encode the rewarded odor. These changes constitute a decrease of the global activity elicited by the mixture in the trained animals that is consistent with the prediction from our computational model. In contrast to bees trained with hexanol, training with acetophenone did not shift the representation of the mixture in the direction of any of the pure odors. This raises the question if the effect reported here after olfactory conditioning solely occurs for hexanol. However, this is very unlikely because several previous reports are consistent with ours in that olfactory conditioning produces changes in the representation of odors in the AL, and this has been proven for different odors (Faber et al., 1999; Sandoz et al., 2003; Yu et al., 2004; Rath et al., 2011). In this context, training could have modified the representation of acetophenone itself. If this change is in turn transferred to the representation of the mixture, such change is predicted by our linear algorithm and is not detected by the analysis. Thus, the results presented here in regard to plasticity in mixture coding in PNs may represent only part of the mechanisms through which plasticity in the AL optimizes the perception of relevant cues.

A major question that remains to be answered is what cellular mechanisms could be responsible for the changes of the spatiotemporal pattern of the odor responses. Studies regarding associative olfactory learning have revealed that biogenic amines play an important role in transmitting appetitive or aversive reinforcement during olfactory learning and memory formation (Hammer, 1993; Hammer and Menzel, 1998; Schwaerzel et al., 2003; Riemensperger et al., 2005; Unoki et al., 2005; Aso et al., 2010). In honey bees, the neuroanatomical pathway conveying the appetitive reward consists of an octopaminergic neuron called VUMmx1 (Hammer, 1993), which arborizes in multiple neuropils of the olfactory pathway, including the AL, the lateral protocerebrum, and the mushroom body calyces (Hammer, 1993; Schröter et al., 2007). Stimulation of VUMmx1, application of sucrose solution to the antenna and proboscis, or injection of octopamine into the mushroom bodies or AL coincident with odor stimulation each results in appetitive learning (Hammer, 1993; Kreissl et al., 1994; Hammer and Menzel, 1998; Farooqui et al., 2003; Schwaerzel et al., 2003; Schroll et al., 2006; Farooqui, 2007).

The octopamine receptor AmOA1 is expressed in GABAergic LNs in the honey bee AL (Sinakevitch et al., 2011, 2013), and recent studies have shown that octopamine modulates odor representation in PN by regulating inhibitory and disinhibitory elements in the AL network (Rein et al., 2013). In addition, it is known that activation of AmOA1 induces Ca²⁺ release and increase in cAMP levels (Grohmann et al., 2003). This evidence supports a model in which the action of octopamine coincident with odor stimulation may promote synaptic facilitation in active LNs (Antonov et al., 2003; Farooqui, 2007; Shakiryanova et al., 2011).

We tested this hypothesis using a conductance-based computational network model of the honey bee AL. We found that the inhibitory synapses between LNs and PNs play an essential role in altering the dynamic pattern of odor responses across PNs. When stimulus-dependent enhancement of LN-PN synapses was driven by LN activity, the correlation coefficient between the odor mixture and the rewarded odor increased after learning. At the same time, the representation of the odor mixture in the high-dimensional space of PN responses shifted toward representation of the rewarded odor. This outcome is consistent with results from our calcium imaging experiments. In addition, to investigate impact of synaptic plasticity on appetitive olfactory conditioning, we tested the effect of increase of local neuron excitability to the network dynamics. We found that activity-dependent increase of intrinsic LN excitability during training does not lead to the shift of the mixture response as we observed in the model with synaptic changes. Although intrinsic and synaptic changes seem to be largely equivalent in our model, they may affect network dynamics differently depending on specific connectivity within local neuronal circuits.

Repeated or prolonged exposure to a stimulus without any reinforcement reduces the behavioral response to that stimulus, which is called habituation (Thompson and Spencer, 1966; Bazhenov et al., 2013). When odors do not elicit innate responses, habituation becomes evident when the odor is subsequently used as the conditioned stimulus in classical conditioning. Under these conditions, animals require more conditioning trials to learn and express the conditioned response. Latent inhibition to odors has been characterized in honey bees (Chandra et al., 2001, 2010). Using Ca²⁺ imaging, we have compared spatiotemporal patterns of PN activities before and after a training protocol that induces latent inhibition, and we found that the representation of mixtures moves away from the habituated components and toward the novel components that were not exposed previously (Locatelli et al., 2013).

Recent studies in the fruit fly AL using transgenic lines revealed that habituation arose from glomerulus-specific (i.e., odorant-selective) facilitation of inhibitory synapses from LNs to PNs (Larkin et al., 2010; Das et al., 2011; Sudhakaran et al., 2012) and that glomerulus-specific inhibitory facilitation can be driven by postsynaptic activities in PNs (Sudhakaran et al., 2012). We adopted the results from flies and honey bees into our computational network model to understand the mechanisms that change the pattern of neural activities across PNs after nonassociative learning. This time, synaptic facilitation was implemented to depend on the postsynaptic activity of PNs and LNs during odor responses. By comparing the odor responses before and after training, we found that the inhibitory LN-PN synapses play a major role in modulating the spatiotemporal patterns of AL activity. After repeated exposure of single odor, the synaptic strength was enhanced in an odor-specific manner, and response to the odor mixture became less correlated to the response to exposed odor in agreement with our experimental data (Locatelli et al., 2013).

Our present experimental study of conditioned (supervised) learning and our past results on nonassociative (unsupervised) learning (Locatelli et al., 2013) in the honey bee AL revealed ways that the AL circuitry can modify information flow from olfactory receptors to the downstream brain areas. The model presented in the current work consolidates experimental evidence from several previous studies, as well as our new experimental results. The model revealed that stimulus-specific changes in synaptic inhibition are sufficient to explain experimental results. It predicted that facilitation of the different sets of inhibitory synapses, either tagged by presynaptic or postsynaptic activation during odor stimulation, can differentiate between associative and nonassociative learning. Our results led to important questions of how a specific form of plasticity operating at the early olfactory circuits (in the AL) interacts with plastic changes taking place at the downstream levels of olfactory processing (mushroom bodies) to provide optimal odor learning. These findings now provide hypotheses for further experimental and modeling efforts.