Abstract
Models have been developed to explain double-peaked plasma concentration-time profiles using mechanisms such as variable absorption and enterohepatic recirculation. Interruption of gastric emptying has also been shown to produce double-peaks, and this work proposes models for analysis of such data. In the presence of levodopa, gastric emptying is interrupted at times associated with double-peaks in pharmacokinetic profiles. Data from a simultaneous scintigraphy and paracetamol absorption study with levodopa was obtained, and models with compartments for stomach, intestine, central and peripheral tissue were developed to describe levodopa and paracetamol pharmacokinetics, including the double-peak phenomenon. The empirical model uses two gastric emptying parameter rates which are applied over separate time periods to describe the varying gastric emptying rate. The semi-mechanistic model uses a feedback mechanism acting via an effect compartment to link the plasma concentration of levodopa to the rate of gastric emptying, allowing levodopa pharmacokinetics to vary the rate of gastric emptying and give rise to a multiple-peaked plasma pharmacokinetic profile. The models were applied to plasma levodopa and paracetamol pharmacokinetic data with and without simultaneous analysis of scintigraphy data, in both cases giving a good fit and in the absence of scintigraphy data adequately predicting the stomach profile. For the semi-mechanistic model, the first-order constant governing gastric emptying was shown to switch between fast and slow values at a critical levodopa effect compartment concentration. New models have thus been proposed for analysis of plasma concentration profiles that exhibit double-peak phenomenon and applied successfully to levodopa data.
KEY WORDS: double-peak, gastric emptying, levodopa, modelling, paracetamol, scintigraphy
INTRODUCTION
In pharmacokinetics (PK), plasma concentration-time profiles for many drugs are defined by a single peak following a single oral administration: a rise to the peak due to rapid absorption is followed by exponential decay due to elimination of the drug. However, for some drugs, the plasma-concentration-time profile is characterised by one or more secondary peaks. For drugs with double-peaked profiles, the second peak may go unobserved due to the chosen sampling scheme. Causes of secondary peaks in PK have been classified into physicochemical and formulation factors and physiological factors (1). Physicochemical and formulation factors include solubility-limited absorption, complexation due to formation of poorly soluble bile salt micelles and modified-release formulation (1). Physiological factors on the other hand include enterohepatic recirculation, gastric emptying (GE), site-specific absorption, gastric secretion-enteral reabsorption and anaesthesia and surgery (1,2). Some of these factors have received attention in the past, but in this work, attention will be focused on secondary peaks due to GE using levodopa (LDOPA) data as a case study.
LDOPA remains the most widely used and therapeutically effective agent available for the treatment of Parkinson’s disease. Parkinson’s disease is a degenerative central nervous system disorder associated with movement-related problems such as shaking, rigidity and walking. It usually occurs in the elderly and in most cases after the age of 50. Due to its low bioavailability, LDOPA is often given in combination with catechol-O-methyl transferase inhibitors (such as tolcapone and entacopone) and decarboxylase inhibitors in the treatment of Parkinson’s disease (3–6). GE is very important in the treatment of Parkinson’s disease for a number of reasons. Firstly, as Parkinson’s disease is a disorder associated with ageing, the delayed GE that occurs as a pathophysiological change with age will have implications for the PK of LDOPA. It has been reported that the systemic availability of LDOPA is inversely related to the GE times in Parkinson’s disease patients, and this is also associated with poor therapeutic response in some patients (7). Goetze et al. (8) investigated the predictors of GE in Parkinson’s disease patients using an 13C-octanoic acid breath test and reported that GE is delayed in about 88 and 38% of the patients on solid and liquid meals, respectively. In addition to the effect of age and the disease on the GE times in Parkinson’s disease patients, delayed GE has been associated with treatment with LDOPA as a pharmacological effect even in healthy volunteers (9,10) which leads to secondary peaks in its PK profiles. Dopamine which is a product of LDOPA significantly delayed GE in healthy male volunteers when administered as a continuous intravenous infusion which is consistent with what has been observed with other dopamine-stimulating agents (11,12).
GE is very important for human nutritional health and can affect the rate and extent of drug absorption from the gastrointestinal tract. It is a very complex and continuous process that is carefully regulated by neural and hormonal mechanisms (13). Methods for studying GE can be categorised into direct and indirect methods. Scintigraphy is a direct method because it measures the content of the stomach; it involves administration of a radiolabelled test meal and measurement of radioactivity around the stomach at different time points following ingestion (14). The measurements are expressed as the remaining activity in the stomach at each time point as a percentage of the initial activity, which gives an indication of the rate of GE (14–18). Although this is the gold standard, it requires expensive equipment and is therefore not generally available. Other widely used methods for assessing GE include the paracetamol absorption test and 13C-octanoic acid breath tests. These are indirect methods because GE is assessed through the PK of markers (paracetamol or 13C-octanoic acid).
A number of models have been proposed for modelling multiple peaks in PK profiles, often linked to the mechanisms causing the effect. Variability in absorption and enterohepatic recirculation are the most widely discussed mechanisms in the literature. Models that have been proposed for variability in absorption include the parallel first-order absorption model (19), multisegment absorption model (19), modified two-portion absorption model (2), delay absorption site model (20), multiple sites discontinuous gastrointestinal absorption model (21), double-site absorption window model (22,23) and parallel inputs model (23). Models that have been proposed for enterohepatic recirculation often include a gallbladder compartment, these models describing physiological processes involved in enterohepatic recirculation and biliary excretion. The population PK model proposed by Funaki (24) was based on estimation of gallbladder emptying time as a bolus for the single episode of emptying. The population PK model proposed by Ezzet et al. (25) allowed gallbladder emptying to coincide with food intake and the amount recycled was allowed to vary both within a subject and between subjects, allowing variability in bile secretion. The model developed by Plusquellec and Houin (26) allows for multiple recirculation, gallbladder emptying times and their duration and the number of re-circulations being estimated. Other variants of these models have also been proposed in the literature (27).
Drugs such as alprazolam (20), avitriptan (28), LDOPA (9,10,29), dopamine and other dopamine-stimulating agents (11) have been shown to have effects on gastric emptying and intestinal motility which sometimes can lead to multiple peaks in plasma concentration-time profiles. Despite the information available in the literature on the role of GE as the physiological explanation for multiple peaks in the plasma concentration-time profiles of some drugs, no model has been proposed for these drugs. Attention has been focused mostly on other causes such as variability in absorption and enterohepatic recirculation. This work was therefore focused on the development of models for the double-peak phenomenon in PK which is caused by interruption of GE following single-dose administration of drugs. To the best of our knowledge, this represents the first time in the literature the double-peak phenomenon in PK is modelled using a GE function.
MATERIALS AND METHODS
The Data
The data for this work was obtained from the literature. Robertson et al. (9) defined the effect of LDOPA on GE and established a relationship between patterns of GE and occurrence of multiple peaks. In the study, eight healthy male volunteers (19–22 years) were recruited and studied after an overnight fast on two occasions in random order that were at least 1 week apart. GE was studied in the subjects on both days using scintigraphy and paracetamol absorption tests using a solution containing 12 MBq 99Tc-diethylenetriaminepentaacetic acid and a solution of 1.5 g paracetamol. On one of the study days, subjects received 125 mg LDOPA in suspension. Also, 100 mg carbidopa was administered 1 h before the start of each GE study. Serial samples of measurements from the stomach were used to construct a time-activity curve and plasma concentrations of paracetamol and LDOPA were also obtained from serial blood samples. In the absence of LDOPA, the plasma concentration-time profile for paracetamol showed a single peak in all subjects and when given with LDOPA, a second peak was seen in seven out of eight subjects. Also, there was excellent agreement between LDOPA and paracetamol plasma concentration-time profiles in terms of different phases observed. The focus of this work was on the data obtained from a representative individual when the study was conducted with LDOPA. Time-activity curve (scintigraphy), paracetamol and LDOPA plasma concentration-time profiles were digitized using GetData (30) to obtain data points that were used for the present work. The serial scintigraphy measurements were normalised by extrapolated activity at time zero to obtain a time-fraction of activity (fraction of dose) in the stomach curve. The semi-mechanistic model was also fitted to two individual datasets obtained from Robertson et al. (10).
The Model
Empirical Model
The proposed empirical model for a double-peak in a PK profile due to GE is based on the model proposed for variability of absorption by Godfrey et al. (23) and is shown in Fig. 1a. In this case, the model assumes four compartments for LDOPA and paracetamol, representing stomach, intestine, central and peripheral compartments. In this model, stomach content and central compartment concentration are monitored by scintigraphy and plasma concentration measurements, respectively. It is assumed that all processes of GE, absorption, distribution and elimination are described by first-order rate constants. The GE process is modelled using an input rate kg(t) as a function of time, and the shape is described in Fig. 1a. Following meal ingestion, the content of the stomach is emptied into the intestine at an initial constant rate kg1 for a period of time tend after which emptying is interrupted and the rate of emptying changes to a reduced rate kg2. The second rate of emptying occurs for a period time Δt (Δt = tlag − tend), and after tend, the rate of emptying reverses to the initial rate kg1. The parameters used for describing the GE input function therefore include kg1, kg2, tend and tlag. The disposition parameters include absorption rate constant, ka, elimination rate constant, k, transfer rate constants between central and peripheral compartments, k12 and k21, and volume of distribution for the central compartment, V. The differential equations describing changes in the different compartments are given by Eq. (1) to (4)
| 1 |
| 2 |
| 3 |
| 4 |
where kg = kg1 (t ≤ tend or t > tlag) and kg = kg2 (t > tend and t ≤ tlag), Ast, Aint and Aper represent the amount of drug in stomach, intestine and peripheral compartments, Ccen and t represent the concentration of the drug in the central compartment (plasma) and time, respectively.
Fig 1.
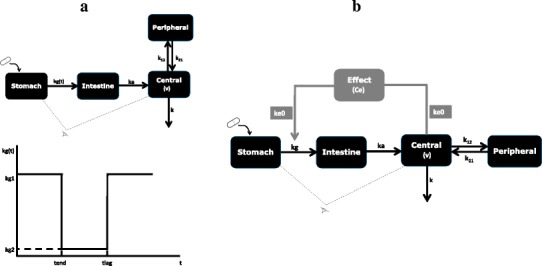
a Schematic representation of empirical gastric emptying compartmental model and its input rate function. b Schematic representation of the semi-mechanistic gastric emptying model showing control of gastric emptying by feedback mechanism (kg(t) = input rate function, kg1, kg2 fast initial and slow gastric emptying rate constants, ka, k absorption and elimination rate constant, k 12, k 21 transfer rate constants between central and peripheral compartments, V volume of distribution of central compartment, tend end of initial gastric emptying, tlag end of gastric emptying interruption, kg gastric emptying rate constant, Ce, k e0 effect compartment concentration and plasma and effect compartments’ equilibration rate constant)
In the case of joint analysis of the scintigraphy and plasma concentration data for both LDOPA and paracetamol, a set of GE parameters and two sets of disposition parameters each for LDOPA and paracetamol were estimated. However, in case of joint analysis of scintigraphy and plasma concentration data for LDOPA only, a set of GE parameters and a set of disposition parameters for LDOPA were estimated. It is also possible to analyse plasma concentration data for LDOPA only in the absence of scintigraphy, and in this case, GE parameters and disposition parameters were estimated. During joint analysis, the data were combined and analysed simultaneously to obtain parameter estimates that describe various aspects of the model.
Semi-Mechanistic Model
The approach for using a semi-mechanistic model to describe double-peaks in PK profiles is based on the evidence available in the literature that suggests that interruption of GE by drugs such as LDOPA when given orally can lead to double-peaks in the plasma concentration-time profiles. This has been attributed to a secondary pharmacological effect of drugs such as LDOPA, dopamine and other dopamine-stimulating agents. The aim of this approach is therefore to link interruption of GE to disposition properties of the drug, in this case LDOPA. The semi-mechanistic model proposed for modelling the double-peak in the PK is shown in Fig. 1b. This model has four compartments for describing the disposition of LDOPA: ka, k, k12, k21 and v similar to the disposition parameters described above under the empirical model using first-order absorption, distribution and elimination processes. In this model, however, kg is modelled as a function of the plasma concentration of LDOPA via an effect compartment using a sigmoidal Emax model. The differential equations describing changes in the compartments of this model are given by Eq. (5) to (9).
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
where kg0, emax, Ce, ec50, ke0 and γ represent baseline emptying, maximum fraction reduction in the emptying rate, effect compartment concentration, effect compartment concentration that produces 50% fraction reduction in the emptying rate, plasma and effect compartments’ equilibration rate constant and slope parameter, respectively. The control of GE by plasma concentration of LDOPA acts via a feedback mechanism on kg. The initial rise in the plasma concentration profile is a consequence of rapid emptying of the stomach content after ingestion. However, when the plasma concentration of LDOPA is high enough, this leads to interruption of GE and a decline in plasma concentration profile. When the plasma concentration of LDOPA becomes sufficiently low, GE resumes at its faster rate, and because the amount of the drug in the stomach is still high, more of the drug is emptied into the intestine, and this produces the second peak and the cycle can continue until the drug in the stomach is completely emptied.
The differential equations that describe the empirical and semi-mechanistic models were implemented in MATLAB (31), and parameter estimation was performed using the lsqnonlin nonlinear least squares optimisation function. In order to improve the efficiency of the fitting process, analytical solutions to the differential equations for the empirical model were derived using Laplace transformation techniques. Model prediction was used to weight the difference between the observed data and model prediction at each time point to calculate a final objective function of the sum of the squared weighted differences which was then minimised. Relative standard errors (SE %) were calculated using the expressions described in Landaw et al. (32).
RESULTS
The parameter estimates and SE % obtained from fitting the empirical model to scintigraphy, LDOPA and paracetamol plasma concentration data simultaneously, joint scintigraphy and LDOPA plasma concentration data and LDOPA plasma concentration data only are presented in Table I. The fitted profiles for simultaneous fitting of scintigraphy, LDOPA and paracetamol plasma concentration data and the data are shown in Fig. 2. The fitted profiles for the simultaneous fitting of scintigraphy and LDOPA plasma concentration data also superimposed with the data are shown in Fig. 3a. The fitted profile of the model to only LDOPA plasma concentration data are shown in Fig. 3b. Also, in Fig. 3b is the simulated profile for the stomach using the fitted model superimposed with the observed scintigraphy data. The fittings were also repeated using the semi-mechanistic model, and the parameter estimates and SE % obtained are presented in Table II. The fitted profiles for simultaneous fitting of scintigraphy, LDOPA and paracetamol plasma concentration data are shown in Fig. 4. The fitted profiles for joint fitting of scintigraphy and LDOPA plasma concentration data also superimposed with the data are shown in Fig. 5a. The fitted profile of the model to only LDOPA plasma concentration data and the data are shown in Fig. 5b. Also, in Fig. 5b is the simulated profile for the stomach using the fitted model superimposed with the observed scintigraphy data.
Table I.
Parameter Estimates (Est) and Percentage Relative Standard Errors (SE%) Obtained by Fitting the Empirical Model to (a) Scintigraphy (Scin), LDOPA and Paracetamol (PCM) Plasma Concentration Data (b) Scin and LDOPA and (c) LDOPA Only
| Parameter | Scin LDOPA PCM | Scin LDOPA | LDOPA | |
|---|---|---|---|---|
| Est (SE%) | Est (SE%) | Est (SE%) | ||
| Gastric Emptying | kg1 (min‐ 1) | 0.100 (9.8) | 0.0958 (8.1) | 0.142 (401) |
| kg2 (min‐ 1) | 0.00889 (23) | 0.00894 (33) | 0.00626 (180) | |
| tend (min) | 10.4 (12) | 11.0 (12) | 9.06 (38) | |
| tlag (min) | 53.1 (2.4) | 52.9 (2.4) | 49.8 (2.7) | |
| LDOPA profile | ka (min‐ 1) | 7.50 (1600) | 290. (1.1E6) | 0.850 (490) |
| k (min‐ 1) | 0.0498 (18) | 0.0507 (31) | 0.0453 (44) | |
| k 12 (min‐ 1) | 0.0285 (21) | 0.0290 (39) | 0.0268 (74) | |
| k 21 (min‐ 1) | 0.0109 (39) | 0.0111 (47) | 0.0149 (37) | |
| v (L) | 15.9 (15) | 15.6 (24) | 18.1 (34) | |
| Paracetamol profile | ka (min‐ 1) | 2580 (7.6E5) | – | – |
| k (min‐ 1) | 0.0170 (44) | – | – | |
| k 12 (min‐ 1) | 0.0768 (26) | – | – | |
| k 21 (min‐ 1) | 0.0163 (43) | – | – | |
| v (L) | 14.4 (26) | – | – |
Fig. 2.
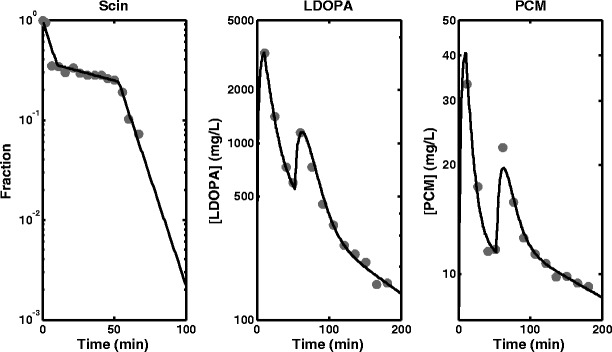
Fitted profiles obtained from the fitting of the empirical model to scintigraphy (Scin) data, levodopa (LDOPA) and paracetamol (PCM) plasma concentration data simultaneously
Fig. 3.
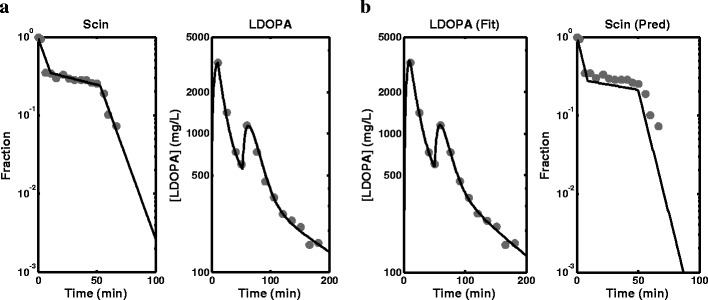
a Fitted profiles obtained from the fitting of the empirical model to scintigraphy (Scin) data and levodopa (LDOPA) plasma concentration data simultaneously. b Fitted profile obtained from the fitting of the empirical model to levodopa (LDOPA) plasma concentration data only and prediction of the stomach profile using the model (observed data overlaid)
Table II.
Parameter Estimates (Est) and Percentage Relative Standard Errors (SE%) Obtained by Fitting the Semi-mechanistic Model to (a) Scintigraphy (Scin), LDOPA and Paracetamol (PCM) Plasma Concentration Data (b) Scin and LDOPA and (c) LDOPA Only
| Parameter | Scin LDOPA PCM | Scin LDOPA | LDOPA | |
|---|---|---|---|---|
| Est (SE%) | Est (SE%) | Est (SE%) | ||
| Gastric emptying | kg0 (min‐ 1) | 0.0116 (12) | 0.0921 (10) | 0.0938 (200) |
| emax | 0.927 (2.3) | 0.900 (4.7) | 0.896 (76) | |
| ec50 (μg/L) | 936 (5.6) | 997 (9.4) | 1010 (80) | |
| gamma | 90.1 (270) | 69.4 (240) | 77.6 (940) | |
| ke0 (min‐ 1) | 0.0605 (16) | 0.0512 (41) | 0.0514 (520) | |
| LDOPA profile | ka (min‐ 1) | 1.06 (88) | 3.05 (1100) | 3.08 (9800) |
| k (min‐ 1) | 0.0409 (31) | 0.0403 (46) | 0.0405 (310) | |
| k 12 (min‐ 1) | 0.0287 (24) | 0.0300 (31) | 0.0305 (290) | |
| k 21 (min‐ 1) | 0.00623 (64) | 0.00669 (79) | 0.00681 (240) | |
| v (L) | 16.8 (15) | 17.0 (25) | 17.1 (230) | |
| Paracetamol profile | ka (min‐ 1) | 7.65 (2500) | – | – |
| k (min‐ 1) | 0.0179 (43) | – | – | |
| k 12 (min‐ 1) | 0.0795 (26) | – | – | |
| k 21 (min‐ 1) | 0.0162 (50) | – | – | |
| v (L) | 13.7 (34) | – | – |
Fig. 4.
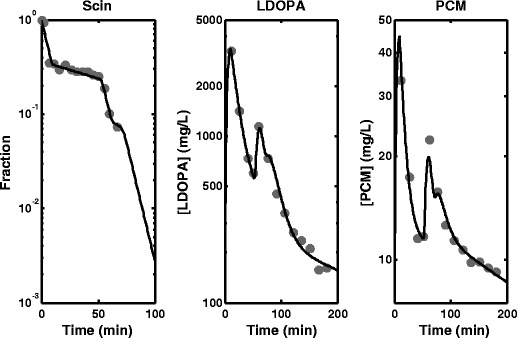
Fitted profiles obtained from the fitting of the semi-mechanistic model to scintigraphy (Scin) data, levodopa (LDOPA) and paracetamol (PCM) plasma concentration data simultaneously
Fig. 5.
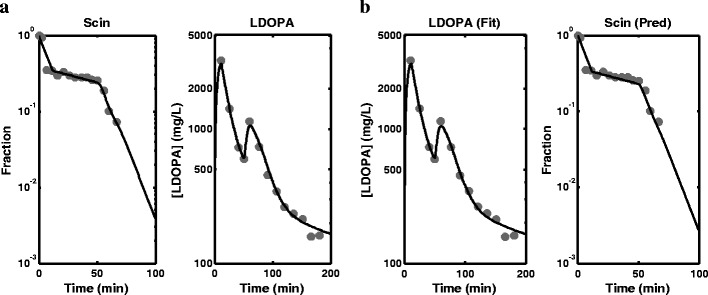
a Fitted profiles obtained from the fitting of the semi-mechanistic model to scintigraphy (Scin) data and levodopa (LDOPA) plasma concentration data simultaneously. b Fitted profile obtained from the fitting of the semi-mechanistic model to levodopa (LDOPA) plasma concentration data only and prediction of the stomach profile using the model (observed data overlaid)
The profiles in Fig. 6 were generated to investigate the behaviour of the model; the parameter estimates used for the simulation were obtained from simultaneous fitting of scintigraphy and LDOPA plasma concentration data (Table II). Figure 6a shows simulated profiles for plasma (Cp) and effect compartment concentration (Ce) against time, Fig. 6b shows the change in value of the GE rate constant, kg, as a function of time, Fig. 6c shows change in kg as a function Ce and Fig. 6d shows change in kg as a function of Cp. The semi-mechanistic model was also fitted to two individual datasets obtained from the literature (10). LDOPA Cp data for two elderly individuals in a study designed to investigate the effect of age on the PK of LDOPA was presented. The dose given was 250 mg, and these individuals also manifest double-peaks in the Cp-time profiles. The data were digitized from the published profiles using GetData (30). The parameter estimates and SE % obtained for these individuals are shown in Table III, and the fitted profiles superimposed with data are shown in Fig. 7.
Fig. 6.
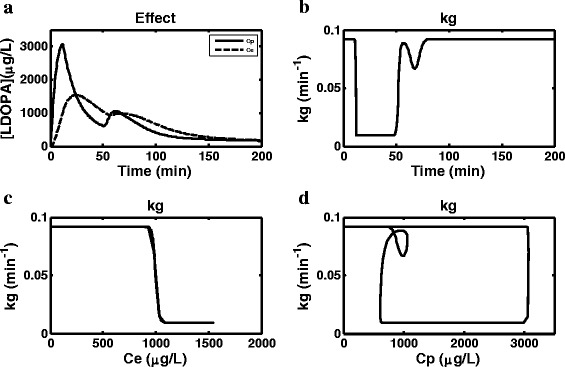
Simulated profiles using the semi-mechanistic model a plasma (Cp) and effect compartment (Ce) concentration versus time b gastric emptying rate constant (kg) versus time c kg versus Ce d kg versus Cp (kg gastric emptying rate constant, Ce effect compartment concentration and Cp central (plasma) compartment concentration)
Table III.
Parameter Estimates (Est) and Percentage Relative Standard Error (SE%) Obtained by Fitting the Semi-mechanistic Model to LDOPA Plasma Concentration Data for Two Individuals
| Parameter | ID 1 | ID 2 | |
|---|---|---|---|
| Est (SE%) | Est (SE%) | ||
| Gastric Emptying | kg0 (min‐ 1) | 0.0492 (92) | 0.0248 (370) |
| emax | 1.00 (37) | 0.951 (150) | |
| ec50 (μg/L) | 984 (14) | 701 (55) | |
| gamma | 80.0 (840) | 39.9 (2.1E3) | |
| k e0 (min‐ 1) | 0.0356 (85) | 0.0258 (310) | |
| LDOPA profile | ka (min‐ 1) | 0.126 (260) | 0.0584 (3.9E4) |
| k (min‐ 1) | 0.0520 (260) | 0.0168 (4.6E4) | |
| k 12 (min‐ 1) | 0.0250 (280) | 0.0417 (3.9E4) | |
| k 21 (min‐ 1) | 0.00554 (38) | 0.000335 (6.6E3) | |
| v (L) | 22.6 (260) | 25.0 (3.9E4) |
Fig. 7.
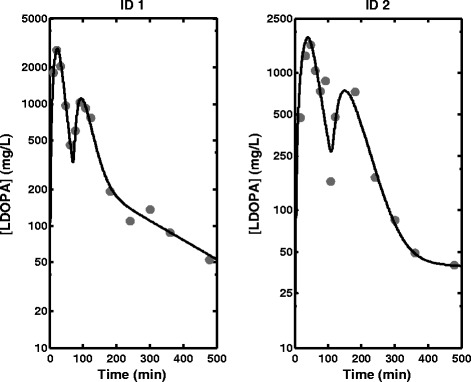
Plasma concentration data and fitted profiles obtained from fitting the semi-mechanistic model to data obtained for two individuals (Robertson et al. (10))
DISCUSSION
Models that have been developed for analysis of plasma concentration-time profiles with a double-peak phenomenon in PK have focused mostly on variability in absorption and enterohepatic recirculation, despite information available in the literature on the effect of some drugs on GE. In this work, two models have been proposed for analysis of the double-peak PK phenomenon which is caused by interruption of GE following administration of some drugs. Data for a typical individual from a study designed to establish a relationship between patterns of GE and occurrence of multiple peaks in PK profiles was used. Both scintigraphy and paracetamol absorption tests were used to monitor GE in the study. It was observed that in the absence of LDOPA, the Cp-time profiles showed single-peaked profiles, but in the presence of LDOPA, secondary peaks were noticeable in almost all subjects. It was concluded that LDOPA is responsible for interruption of GE which leads to the occurrence of secondary peaks in the plasma profiles. The data used for the present analysis came from scintigraphy activity measurement in the stomach, Cp profiles for LDOPA and paracetamol. The analysis was carried out in three ways using the proposed empirical and semi-mechanistic models: simultaneous analysis of scintigraphy data, LDOPA PK data and paracetamol PK data; joint analysis of scintigraphy and LDOPA PK data; and analysis of LDOPA PK data only.
The results of the simultaneous analysis of scintigraphy data, LDOPA PK data and paracetamol PK data in Table I and Fig. 2a show fitting of the empirical model to the data with low SE % for most parameters except ka for LDOPA and paracetamol, which is probably due to the sampling design used for LDOPA and paracetamol plasma sampling: there was no sampling during the rising phases of the profiles for the peaks for both LDOPA and paracetamol where maximum information about absorption is present. The consequence of this is the lack of ability to estimate a reliable ka for both LDOPA and paracetamol and hence the large values for the estimated parameter estimates and their associated SE %. The results of the fitting using the empirical model and the scintigraphy and LDOPA PK data (Fig. 3a) are also consistent with results obtained for simultaneous analysis of the three measurements including paracetamol PK data, and the parameter estimates are also comparable. The fittings are good, and the parameter estimates and SE % are well estimated except LDOPA ka, with a very high parameter estimate and SE %, which again can be linked to the sampling design used for LDOPA blood sampling. The empirical model was also fitted to LDOPA PK only, and the results in Fig. 3b also show adequate fitting of the model to the data. This analysis was included to investigate application of the model when only Cp data is available, which is the case in most situations due to the cost, ethics and other practical problems associated with scintigraphy. The scintigraphy data allows assessment of the model’s capacity to predict the stomach emptying profile. The parameter estimates and SE % obtained using the model in Table I show satisfactory performance of the model. The parameter estimates are comparable to the previous analysis that included scintigraphy measurements: high SE % was obtained for kg2 and ka which is also attributable to the sampling design. The SE %s obtained were generally higher for all parameters compared to the other two previous analyses that included scintigraphy data. This shows the contribution of scintigraphy data to the estimation of these parameters especially the parameters associated with GE. The prediction of the stomach profile in Fig. 3b also shows satisfactory agreement, which shows that although scintigraphy data is very useful, it is still possible to characterise double-peak profile and make adequate prediction of the stomach profile using only Cp data.
Figure 4 shows fitting of the semi-mechanistic model to the scintigraphy data, LDOPA PK data and paracetamol PK data simultaneously, and the SE % in Table II are also generally acceptable except for γ and paracetamol ka. The parameter estimates obtained for joint analysis of scintigraphy data and LDOPA PK data are also comparable to the simultaneous analysis of the three responses that included paracetamol PK. The fitting is shown in Fig. 5a, and the SE %s are generally low except for γ and ka. As with the empirical model fitting, the high SE %s especially for ka can be explained by the sampling designs used for LDOPA and paracetamol blood sampling. Figure 5b shows fitting of the semi-mechanistic model to LDOPA PK data only and good prediction of the stomach profile using the model. The prediction of the stomach profile by this model appears to be better than that of the empirical model. Although the parameter estimates from this fitting are comparable to the other two fittings (analysis of scintigraphy data, LDOPA PK data and paracetamol PK data and analysis of scintigraphy data and LDOPA PK data), the SE %s obtained for most parameters are generally higher than 100%. Again, this is attributable to the sampling design. To improve the estimation of these parameters, more samples have to be collected around the peaks and for a bit longer than 200 min.
Figure 6a shows simulated Cp and Ce profiles. Ce is required to link the LDOPA concentration to changes in GE. A direct link could not be established between Cp and GE and therefore an indirect model via Ce was used. Comparison of the two profiles shows that the times to maximum concentration for the two peaks are longer for Ce compared to Cp, and while the maximum concentration for the first peak is higher for Cp compared to Ce, the maximum concentrations for the second peak are almost equal for the two profiles. Figure 6b–d show changes in kg as a function of time, Ce and Cp, respectively. The profiles show how kg is switching between two values; fast and slow, which are around 0.09 and 0.01 min−1, respectively. The fast kg is equivalent to the baseline physiological GE in healthy subjects under fasting condition. The fast kg obtained in this study translates to a gastric residence time of 11 min compared to 15 min (CV = 38%) which has been described in the literature for an average healthy adult (33). Figure 6b shows that GE starts at the fast, physiological level after ingestion of the test meal and drugs and continues for about 10 min until it switches to the slow rate, and this continues for about 40 min after which it is switched back to the fast baseline level. Figure 6c shows that the switch between fast and slow rate is happening at around 1000 μg/L concentration in Ce. This concentration can be considered a critical concentration above which fast kg operates and below which slow kg operates; the switch between fast and slow is almost instantaneous as shown by the profile and this is due to the large estimate of the slope or Hill coefficient (γ) (Table II). This critical concentration in the effect compartment is not a real physiological concentration; however, due to the way the equation is scaled though, it has the units of plasma equivalence. The high SE % on γ for the semi-mechanistic model can also be linked to the steepness of the kg versus Ce profile in Fig. 6c where it is almost impossible to sample during the change from fast to slow or vice versa. Figure 6d shows how kg changes as a function of Cp, which show a clockwise hysteresis loop.
The fitted Cp profiles for two individuals obtained from another study using the semi-mechanistic model also showed good fitting of the model to the data in Fig. 7. The parameter estimates in Table III are also consistent with the parameter estimates obtained previously when the semi-mechanistic model was fitted to LDOPA data only.
The two models proposed in this work have different properties: while the empirical model is very easy to implement and the estimation is very straightforward, the semi-mechanistic model has a clearer physiological interpretation but can be difficult to implement. Due to the steepness of the kg versus Ce profile, the differential equation system can be stiff and therefore difficult to solve. The empirical model has an analytical solution, making the model easier to implement and use in fittings. In this work, these models have been implemented in MATLAB; however, they can be easily implemented in other software and can also be implemented within a mixed-effect model where variability in the parameters can be introduced to account for differences in exposure between individuals.
CONCLUSION
This work has presented an empirical and a semi-mechanistic model for the analysis of plasma concentration profiles that show a double-peak phenomenon that is due to interruption of GE following single-dose administration of drugs. The models were applied to plasma LDOPA and paracetamol PK data with and without simultaneous analysis of scintigraphy data, in both cases giving a good fit and in the absence of scintigraphy data adequately predicting the stomach profile. The models have potential in PK modelling especially in the development of prokinetic (gastrointestinal motility stimulating) drugs.
Acknowledgment
The authors would like to thank Dr Lakshmi Vasist, Dr George Dukes and Dr Malcolm Young, GlaxoSmithKline, Research Triangle Park, NC, USA for helpful discussions during the course of this work.
Conflict of Interest
The authors declare that they have no conflicts of interest to disclose.
References
- 1.Davies NM, Takemoto JK, Brocks DR, Yanez JA. Multiple peaking phenomena in pharmacokinetic disposition. Clin Pharmacokinet. 2010;49(6):351–377. doi: 10.2165/11319320-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 2.Yin OQ, Tomlinson B, Chow AH, Chow MS. A modified two-portion absorption model to describe double-peak absorption profiles of ranitidine. Clin Pharmacokinet. 2003;42(2):179–192. doi: 10.2165/00003088-200342020-00005. [DOI] [PubMed] [Google Scholar]
- 3.Keranen T, Gordin A, Harjola VP, Karlsson M, Korpela K, Pentikainen PJ, et al. The effect of catechol-O-methyl transferase inhibition by entacapone on the pharmacokinetics and metabolism of levodopa in healthy-volunteers. Clin Neuropharmacol. 1993;16(2):145–156. doi: 10.1097/00002826-199304000-00007. [DOI] [PubMed] [Google Scholar]
- 4.Yamamoto M, Yokochi M, Kuno S, Hattori Y, Tsukamoto Y, Narabayashi H, et al. Effects of tolcapone, a catechol-O-methyltransferase inhibitor, on motor symptoms and pharmacokinetics of levodopa in patients with Parkinson's disease. J Neural Transm. 1997;104(2):229–236. doi: 10.1007/BF01273183. [DOI] [PubMed] [Google Scholar]
- 5.Jorga K, Banken L, Fotteler B, Snell P, Steimer JL. Population pharmacokinetics of levodopa in patients with Parkinson's disease treated with tolcapone. Clin Pharmacol Ther. 2000;67(6):610–620. doi: 10.1067/mcp.2000.106795. [DOI] [PubMed] [Google Scholar]
- 6.Jorga K, Fotteler B, Sedek G, Nielsen T, Aitken J. The effect of tolcapone on levodopa pharmacokinetics is independent of levodopa/carbidopa formulation. J Neurol. 1998;245(4):223–230. doi: 10.1007/s004150050209. [DOI] [PubMed] [Google Scholar]
- 7.Mearrick PT, Wade DN, Birkett DJ, Morris J. Metoclopramide, gastric emptying and L-dopa absorption. Aust N Z J Med. 1974;4(2):144–148. doi: 10.1111/j.1445-5994.1974.tb03163.x. [DOI] [PubMed] [Google Scholar]
- 8.Goetze O, Nikodem AB, Wiezcorek J, Banasch M, Przuntek H, Mueller T, et al. Predictors of gastric emptying in Parkinson's disease. Neurogastroenterol Motil. 2006;18(5):369–375. doi: 10.1111/j.1365-2982.2006.00780.x. [DOI] [PubMed] [Google Scholar]
- 9.Robertson DRC, Renwick AG, Wood ND, Cross N, Macklin BS, Fleming JS, et al. The influence of levodopa on gastric-emptying in man. Br J Clin Pharmacol. 1990;29(1):47–53. doi: 10.1111/j.1365-2125.1990.tb03601.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Robertson DR, Wood ND, Everest H, Monks K, Waller DG, Renwick AG, et al. The effect of age on the pharmacokinetics of levodopa administered alone and in the presence of carbidopa. Br J Clin Pharmacol. 1989;28(1):61–69. doi: 10.1111/j.1365-2125.1989.tb03506.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Levein NG, Thörn SE, Wattwil M. Dopamine delays gastric emptying and prolongs orocaecal transit time in volunteers. Eur J Anaesthesiol. 1999;16(4):246–250. doi: 10.1046/j.1365-2346.1999.00471.x. [DOI] [PubMed] [Google Scholar]
- 12.Soykan I, Sarosiek I, Shifflett J, Wooten GF, McCallum RW. Effect of chronic oral domperidone therapy on gastrointestinal symptoms and gastric emptying in patients with Parkinson's disease. Mov Disord. 1997;12(6):952–7. [DOI] [PubMed]
- 13.Hellström PM, Grybäck P, Jacobsson H. The physiology of gastric emptying. Best Practice & Research Clinical Anaesthesiology. 2006;20(3):397–407. doi: 10.1016/j.bpa.2006.02.002. [DOI] [PubMed] [Google Scholar]
- 14.Verbeke K. Will the 13C-octanoic acid breath test ever replace scintigraphy as the gold standard to assess gastric emptying? Neurogastroenterol Motil. 2009;21(10):1013–1016. doi: 10.1111/j.1365-2982.2009.01388.x. [DOI] [PubMed] [Google Scholar]
- 15.Clements JA, Heading RC, Nimmo WS, Prescott LF. Kinetics of acetaminophen absorption and gastric-emptying in man. Clin Pharmacol Ther. 1978;24(4):420–431. doi: 10.1002/cpt1978244420. [DOI] [PubMed] [Google Scholar]
- 16.Clements JA, Nimmo WS, Heading RC, Prescott LF. Physiologically-Based Pharmacokinetic Model for Absorption of Oral Paracetamol in Man. J Pharm Pharmacol. 1978;30 Supple S:60. [DOI] [PubMed]
- 17.Heading RC. Gastric emptying: a clinical perspective. Clin Sci. 1982;63(3):231–235. doi: 10.1042/cs0630231. [DOI] [PubMed] [Google Scholar]
- 18.Holt S, Reid J, Taylor TV, Tothill P, Heading RC. Gastric emptying of solids in man. Gut. 1982;23(4):292–296. doi: 10.1136/gut.23.4.292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mirfazaelian A, Mahmoudian M. A simple pharmacokinetics subroutine for modeling double peak phenomenon. Biopharm Drug Dispos. 2006;27(3):119–124. doi: 10.1002/bdd.492. [DOI] [PubMed] [Google Scholar]
- 20.Wang Y, Roy A, Sun L, Lau CE. A double-peak phenomenon in the pharmacokinetics of alprazolam after oral administration. Drug Metab Dispos. 1999;27(8):855–859. [PubMed] [Google Scholar]
- 21.Plusquellec Y, Efthymiopoulos C, Duthil P, Houin G. A pharmacokinetic model for multiple sites discontinuous gastrointestinal absorption. Med Eng Phys. 1999;21(8):525–532. doi: 10.1016/S1350-4533(99)00060-0. [DOI] [PubMed] [Google Scholar]
- 22.Plusquellec Y, Campistron G, Staveris S, Barre J, Jung L, Tillement JP, et al. A double-peak phenomenon in the pharmacokinetics of veralipride after oral administration: a double-site model for drug absorption. J Pharmacokinet Pharmacodyn. 1987;15(3):225–239. doi: 10.1007/BF01066319. [DOI] [PubMed] [Google Scholar]
- 23.Godfrey KR, Arundel PA, Dong Z, Bryant R. Modelling the double peak phenomenon in pharmacokinetics. Comput Methods Programs Biomed. 2011;104(2):62–69. doi: 10.1016/j.cmpb.2010.03.007. [DOI] [PubMed] [Google Scholar]
- 24.Funaki T. Enterohepatic circulation model for population pharmacokinetic analysis. J Pharm Pharmacol. 1999;51(10):1143–1148. doi: 10.1211/0022357991776831. [DOI] [PubMed] [Google Scholar]
- 25.Ezzet F, Krishna G, Wexler DB, Statkevich P, Kosoglou T, Batra VK. A population pharmacokinetic model that describes multiple peaks due to enterohepatic recirculation of ezetimibe. Clin Ther. 2001;23(6):871–885. doi: 10.1016/S0149-2918(01)80075-8. [DOI] [PubMed] [Google Scholar]
- 26.Plusquellec Y, Houin G. Drug recirculation model with multiple cycles occurring at unequal time intervals. J Biomed Eng. 1992;14(6):521–526. doi: 10.1016/0141-5425(92)90107-V. [DOI] [PubMed] [Google Scholar]
- 27.Sherwin CMT, Fukuda T, Brunner HI, Goebel J, Vinks AA. The evolution of population pharmacokinetic models to describe the enterohepatic recycling of mycophenolic acid in solid organ transplantation and autoimmune disease. Clin Pharmacokinet. 2011;50(1):1–24. doi: 10.2165/11536640-000000000-00000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Marathe PH, Sandefer EP, Kollia GE, Greene DS, Barbhaiya RH, Lipper RA, et al. In vivo evaluation of the absorption and gastrointestinal transit of avitriptan in fed and fasted subjects using gamma scintigraphy. J Pharmacokinet Biopharm. 1998;26(1):1–20. doi: 10.1023/A:1023236823320. [DOI] [PubMed] [Google Scholar]
- 29.Berkowitz DM, McCallum RW. Interaction of levodopa and metoclopramide on gastric-emptying. Clin Pharmacol Ther. 1980;27(3):414–420. doi: 10.1038/clpt.1980.55. [DOI] [PubMed] [Google Scholar]
- 30.GetData Graph Digitizer, http://getdata-graph-digitizer.com/. 2013.
- 31.MATLAB 8.1.0.604. Natick, Massachusetts: The MathWorks Inc. R2013a.
- 32.Landaw EM, DiStefano JJ., 3rd Multiexponential, multicompartmental, and noncompartmental modeling II data analysis and statistical considerations. Am J Physiol. 1984;246(5 Pt 2):R665–R677. doi: 10.1152/ajpregu.1984.246.5.R665. [DOI] [PubMed] [Google Scholar]
- 33.Jamei M, Turner D, Yang J, Neuhoff S, Polak S, Rostami-Hodjegan A, et al. Population-based mechanistic prediction of oral drug absorption. AAPS J. 2009;11(2):225–237. doi: 10.1208/s12248-009-9099-y. [DOI] [PMC free article] [PubMed] [Google Scholar]


