Performance of Nonlinear Mixed Effects Models in the Presence of Informative Dropout

Abstract

Informative dropout can lead to bias in statistical analyses if not handled appropriately. The objective of this simulation study was to investigate the performance of nonlinear mixed effects models with regard to bias and precision, with and without handling informative dropout. An efficacy variable and dropout depending on that efficacy variable were simulated and model parameters were reestimated, with or without including a dropout model. The Laplace and FOCE-I estimation methods in NONMEM 7, and the stochastic simulations and estimations (SSE) functionality in PsN, were used in the analysis. For the base scenario, bias was low, less than 5% for all fixed effects parameters, when a dropout model was used in the estimations. When a dropout model was not included, bias increased up to 8% for the Laplace method and up to 21% if the FOCE-I estimation method was applied. The bias increased with decreasing number of observations per subject, increasing placebo effect and increasing dropout rate, but was relatively unaffected by the number of subjects in the study. This study illustrates that ignoring informative dropout can lead to biased parameters in nonlinear mixed effects modeling, but even in cases with few observations or high dropout rate, the bias is relatively low and only translates into small effects on predictions of the underlying effect variable. A dropout model is, however, crucial in the presence of informative dropout in order to make realistic simulations of trial outcomes.

INTRODUCTION

In longitudinal studies, it is common that patients withdraw, or drop out, of the study and no further data is collected from that individual. This missing data is a complicating factor in the analysis of the studies, and could have consequences for the interpretation of the results (1). Dropout has in the statistical literature been classified as missing completely at random (MCAR), when the dropout does not depend on observed or unobserved values of the dependent variable, missing at random (MAR) when the dropout is dependent on the observed, but not the unobserved, value of the dependent variable, and missing not at random (MNAR) when the dropout is dependent on unobserved measurements (2–5). Dropout can also be described as ignorable, when the interpretation of the study endpoint is valid even if the dropout is ignored, or nonignorable, when the dropout needs to be taken into account to make valid inference of the drug effects (4). Dropout that is MNAR is nonignorable (3) and can also be referred to as informative dropout (6).

In a dropout analysis, the time of dropout is typically modeled. If a patient has not dropped out at the end of the study period, the dropout in that patient is said to be right-censored, i.e., the time of dropout is greater than the time of the last observation. If a patient drops out between two observations, but the exact time is not known, the dropout time is said to be interval-censored, i.e., occurring any time between two time points.

Missing observations could potentially complicate nonlinear mixed effects modeling. As long as the dropout is at random, it only leads to lower precision because of the reduced information due to the missing observations. However, when the dropout is not at random, it has been suggested that it could lead to biased parameter estimates in nonlinear mixed effects models (7–9). Informative dropout, if not handled appropriately, can also lead to unrealistic simulations, for example, when performing clinical trial simulations, or visual predictive checks (VPC) (6,7,9–11). If informative dropout is ignored in the simulations, the simulated data will include records that would not be present if dropout is accounted for, leading to a discrepancy between simulated and observed data. For example, in a pain trial, simulated without a dropout model, the model may simulate patients that have high pain intensity for a long time, but in reality, these patients would drop out due to lack of efficacy. In order to make realistic simulations in the presence of informative dropout, patients simulated with high pain intensity will need to have a higher probability of dropping out.

There are many different reasons why patients drop out of clinical trials, e.g., due to adverse events or lack of efficacy (1). This simulation study deals only with dropout due to lack of efficacy of the treatment. When the dropout is influenced by the dependent variable, the fact that a subject has or has not dropped out provides some information about the dependent variable. By modeling such informative dropout together with the dependent variable, potential bias may be avoided and imprecision in the parameter estimates could potentially be decreased.

The objectives of this simulation study were to assess the performance of nonlinear mixed effects models with and without taking informative dropout into account and to investigate the influence of sample size, number of assessments, size of the placebo effect and magnitude of dropout on bias and imprecision in parameter estimates, as well as the effect on the underlying efficacy variable. In addition, the effect of dropout that is completely at random, as well as the effect of ignoring informative dropout, on simulations is exemplified by VPCs.

MATERIALS AND METHODS

In this study, simulations of a hypothetical efficacy variable were performed. The model used for the simulations was adapted from a published model on the effect on pain intensity and dropout in dental pain (11). Study dropout, that was dependent on the efficacy variable, was also simulated. The simulated studies were reestimated with and without dropout models, and with different estimation methods, in order to assess bias and imprecision in the parameter estimates and the influence on the underlying efficacy variable. Different design aspects and certain parameters of the simulation model were also altered to investigate their impact on the bias and imprecision.

Simulation Model

The simulation model consisted of a pharmacokinetic (PK) model, a placebo effect model, a drug effect model, and a dropout model. The parameters for the base model are presented in Table I, and the concentrations, efficacy endpoint, and probability of remaining in the study over time for a typical individual in the base scenario (scenario 1) are presented in Fig. 1.

Table I.

Parameter values used in the simulation of the base scenario (scenario 1)

Parameter	Typical value	Interindividual variability (%)a	Explanation
BL	50	30	Efficacy variable at baseline
PLmax (%)	20	120	Maximum placebo effect
k pl (h−1)	0.25	44	Rate constant for onset of placebo effect
EC50 (units/L)	20	122	Concentration leading to 50% of maximum efficacy
CL (L/h)	10	30	Clearance
V (L)	10	30	Volume of distribution
h 0 (h−1)	0.01	-	Baseline hazard
h e	0.05	-	Parameter for relationship between hazard and effect variable
σ (effect units)	7.5	-	Additive residual variability

^aInterindividual variability expressed as coefficient of variation

Fig. 1.

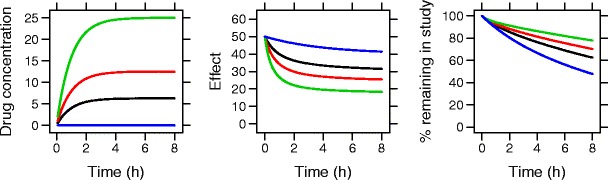
Drug concentrations, effect variable, and probability of remaining in the study for a typical individual based on the true model parameters from the base model. Blue = placebo, black = low dose, red = medium dose, green = high dose

An exponential model was used to describe the placebo effects, including the natural progression of pain in the absence of active treatment, according to:

$$E_{\mathrm{placebo}}={\mathrm{PL}}_{\text{max}}\cdot \left(1-e^{-k_{\mathrm{pl}}\times \mathrm{time}}\right)$$

where PL_max is the maximum placebo effect (restricted to a maximum of 1) and k_pl is describing the rate constant for placebo effect development.

The inhibitory effect of the drug (E_drug) was described by an E_max model, where it was assumed that full effect (E_drug = 1, no pain) can be achieved:

$$E_{\mathrm{drug}}=\frac{C}{{\mathrm{E}\mathrm{C}}_{50}+C}$$

where C is the drug concentration and EC₅₀ is the concentration resulting in 50% reduction in the effect variable. The drug concentration was modeled as a one-compartment model with the PK parameters clearance (CL) and volume of distribution (V). The drug effect model was combined with the placebo model to describe the effect variable according to:

$$\mathrm{Effect}=BL\cdot \left(1-E_{\mathrm{placebo}}\right)\cdot \left(1-E_{\mathrm{drug}}\right)$$

where BL is the effect variable at baseline.

Interindividual variability was log-normally distributed for BL, k_pl, EC₅₀, CL, and V. For PL_max, the interindividual variability was additive, allowing for the placebo effect to be either positive or negative in relation to baseline. An additive model was also used to describe the residual unexplained variability in the effect.

The probability of remaining in the study at time t, S(t), was described by a survival function,

$$S\left(t\right)=exp\left(-{\displaystyle \underset{0}{\overset{t}{\int }}h\left(t\right)dt}\right)$$

where h(t) is the hazard function, modeled as

$$h\left(t\right)=h_0\cdot e^{h_e\mathrm{Effect}\left(t\right)}$$

where h₀ is the background hazard and h_e describes the relationship between the hazard and the effect score at time t (Effect(t)). As the hazard is dependent on the unobserved efficacy variable, the mechanism of dropout is not at random. No other reasons for dropout were included in the model. For interval-censored dropout, the probability of dropping out during an interval equals the difference between the probability of remaining in the study at the beginning of the interval and the probability of remaining in the study at the end of the interval.

As a comparison, simulations were also performed where the mechanism of dropout was completely at random (a constant hazard of 0.065 h⁻¹, giving approximately 40% dropout), or at random, where the hazard was dependent on the previous observation of the efficacy variable (the dependent value simulated with residual error) rather than the underlying predictions.

Study Design

Fourteen different scenarios were constructed to investigate different study designs or model properties. The different simulated scenarios consisted of changes in number of patients per dose group (scenarios 2–4), size of the placebo effect, PL_max, (scenarios 5–7), number of observations per patient (scenarios 8–10), and extent of efficacy-dependent dropout (different h_e, scenarios 12–14). The different scenarios are presented in Table II.

Table II.

Parameters and design variables varied in the different simulation scenarios. For each scenario, the gray cells gives the value of the variable that was changed compared to the base scenario (scenario 1)

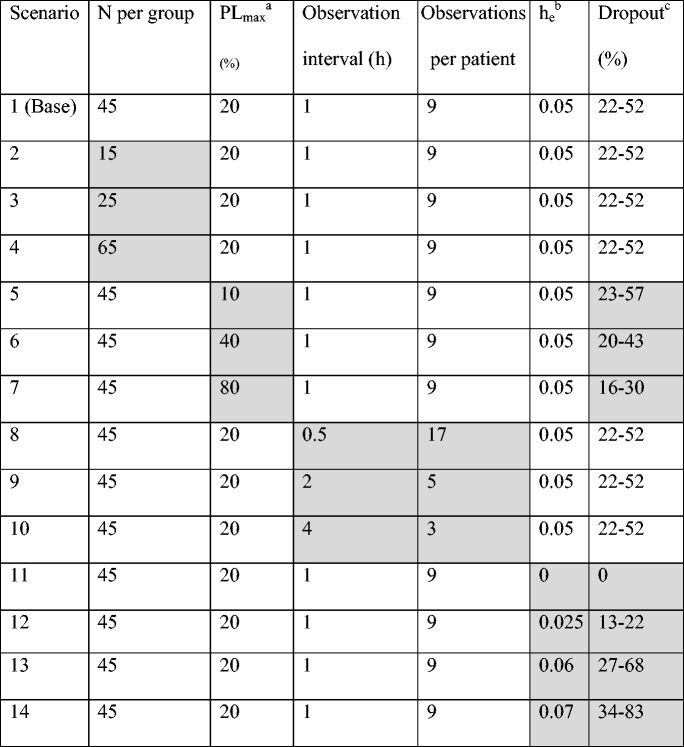
^aMaximum placebo effect

^bParameter relating the hazard to the effect variable. A high value represents a larger probability of dropout

^cThe range of probability of dropout for a typical individual between treatment groups, where the lower number represents the highest dose and the highest number represents placebo

All scenarios consisted of four groups, treated either with active drug, in a 1:2:4 relation between the three dose levels, or placebo. In this simulation study, the drug was administered as a constant infusion over the study duration, 8 h. The base study design included 45 patients per group, and the effect variable was simulated at baseline and at every hour after start of treatment until end of the study. In all scenarios, simulated dropout was allowed to be recorded in the simulated dataset at their actual time of dropout, i.e., also at times when there was no observation of the effect variable. Dropout can only be simulated at prespecified times in the NONMEM dataset, and therefore data records for potential dropout were added at every 5 min. In order to explore the potential benefit of knowing the actual time of dropout, compared to only knowing if a subject has dropped out between two visits (interval censoring), scenarios 1, 8, 9, and 10 (i.e., the base model with different observation interval) were also simulated without recording the exact time of dropout.

Stochastic Simulation and Reestimation

Stochastic simulations and estimations (SSE) were performed using NONMEM 7.2 (ICON Development Solutions, Ellicott City, MD) (12) and PsN version 3.4.2 (13). The F_FLAG option in NONMEM was used to simultaneously model the continuous effect data and the likelihood of the categorical dropout data. For each scenario, 1,000 replicate studies were simulated and each of the simulated studies was analyzed using two different models; the same model as was used for the simulations, i.e., including estimation of the dropout, and the simulation model but ignoring the part of the model describing dropout. When a dropout model was included, the estimation was done with the Laplacian method, whereas both the Laplacian method and the FOCE with interaction (FOCE-I) were used when the analysis was done with a model not including dropout. The bias, expressed as the difference between the means of the estimated and true parameters divided by the true parameter according to

$$\mathrm{Bias}=100\%\cdot \frac{1}{N}\cdot {\displaystyle {\sum }_i\frac{{\mathrm{E}\mathrm{s}\mathrm{t}}_i-{\mathrm{True}}_i}{\mathrm{True}}}$$

and imprecision, expressed as the relative root mean squared error in the parameter estimates, according to

$$\mathrm{RMSE}=100\%\times \sqrt{\frac{1}{N}\cdot {\displaystyle \sum _i\frac{{\left({\mathrm{E}\mathrm{s}\mathrm{t}}_i-{\mathrm{True}}_i\right)}^2}{{\mathrm{True}}_i^2}}}$$

were calculated by PsN for all estimation models and methods. In the estimation models, the simulated PK parameters were fixed for each individual.

In the simulations where the actual time of dropout was not recorded, models using interval censoring were used to analyze the data. The probability of dropping out during an interval was equal to the probability of remaining in the study in the beginning of the interval, minus the probability of remaining in the study at the end of the interval.

Visual Predictive Checks

To illustrate the need for using a dropout model in simulations, VPCs were created in NONMEM using PsN, Xpose (14), and R. An arbitrarily simulated dataset, simulated from the base model, served as the observations. Subjects that were simulated to dropout only had “observations” up to the time of dropout. VPCs were created by simulating both with and without a dropout model. The true parameters were used in the simulations. In addition, an arbitrarily simulated dataset with 40% dropout completely at random (a constant hazard of 0.065 h⁻¹), instead of the informative dropout used in the other simulations, was used to create a VPC. The simulations for this VPC were created without the use of any dropout model.

RESULTS

When dropout was accounted for, i.e., when the simulated data were analyzed with the same model as used for the simulation, bias was less than 5% in all fixed effects parameters in scenario 1 (base model and base study design; Fig. 2). The bias was larger when data were analyzed without including a dropout model, although the bias was still less than 8% in the fixed effects when using the Laplacian method. When dropout was not accounted for and the FOCE-I method was used in the estimation, the bias was more pronounced. In this situation, bias was 21% in EC₅₀ for scenario 1. For the random effect parameters, bias was up to 22% in scenario 1 regardless of estimation model or method. Bias in the interindividual variability was higher when a dropout model was not used for the following parameters and estimation methods: rate constant for placebo when the Laplace method was used (8.1 vs. 4.5 and 4.9% for the model including dropout and the model ignoring dropout using FOCE-I, respectively), and EC₅₀ when FOCE-I was used (14.8 vs. 8.9 and 8.8% for the model including dropout and the model ignoring dropout using Laplace, respectively). For all other estimation models and methods, bias in random effect parameters was rather similar (Fig. 2). When the effect variable was simulated without any dropout at all (scenario 11), bias was less than 1% in all fixed effects parameters except PL_max (8.9%) when the Laplace method was used, and less than 2% in all fixed effects parameters except EC₅₀ (−7.8%) when FOCE-I was used.

Fig. 2.

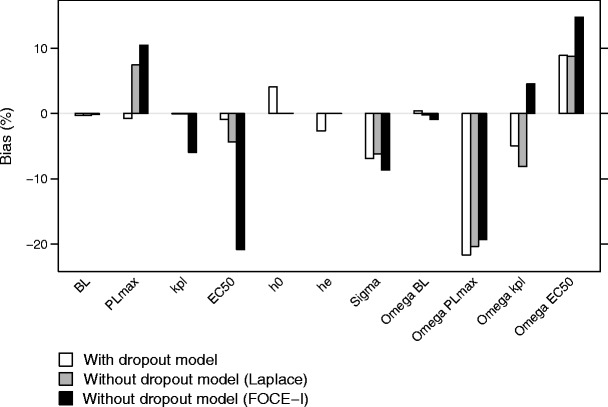
Bias in the parameter estimates for scenario 1, when estimations included a dropout model (white), without including a dropout model, using the Laplace method (gray), and without a dropout model, using the FOCE-I method (black)

For scenario 1, the bias did not, however, result in any major difference in the predictions of effect variable at any time point (Fig. 3, top row). A correlation between the estimated placebo effect parameters was apparent, and the bias in the rate constant of onset of placebo effect was balanced by the bias in the maximum placebo effect, leading to very similar simulated effect profiles over time as for simulations with unbiased parameter estimates. Bias in the baseline value of the effect variable was low in all scenarios and with all different estimation models.

Fig. 3.

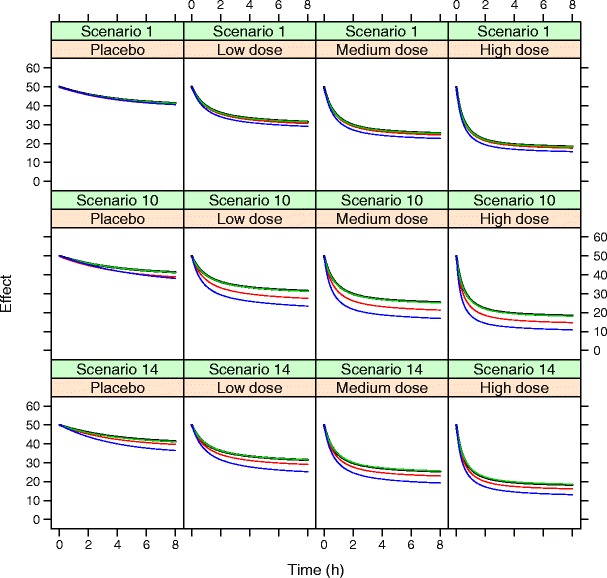
Simulated effect variable for a typical individual in the different dose groups for scenario 1, scenario 10 (observations every 4^th hour only), and scenario 14 (increased dropout rate, on average 57%). Simulations are based on true parameters (black), parameters estimated with dropout model (green), parameters estimated without dropout model using Laplace (red) or FOCE-I (blue)

As expected, the bias in EC₅₀ increased with increasing dropout rate, increasing placebo effect, and decreasing number of observations per subject (Fig. 4). The increase in bias was larger when dropout was ignored, and it was also larger when the FOCE-I method was used compared to the Laplacian method. The largest bias in EC₅₀, 50% for the FOCE-I method, was found when the observation interval was long, with only two post dose assessments of efficacy during the 8-h study period. The impact on the underlying effect variable when only two post dose assessments were used is shown in the middle row of Fig. 3, and the impact when the dropout rate was on average 57% is shown in the bottom row of Fig. 3. Bias in EC₅₀ was relatively unaffected by number of patients per treatment group, although there was a trend toward higher bias with lower number of subjects per group, especially when the FOCE-I method was used (Fig. 4d).

Fig. 4.

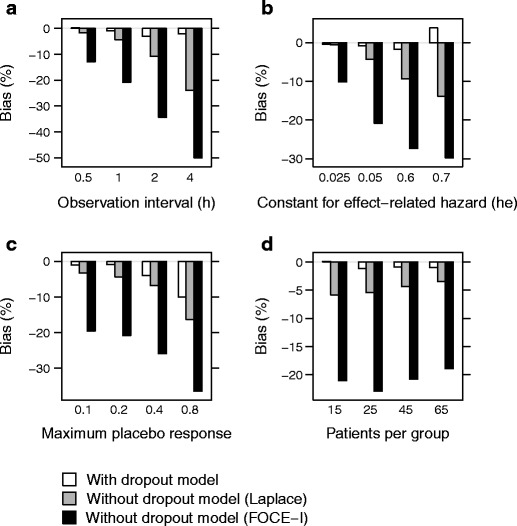
Bias in EC₅₀ when estimating with a dropout model (white), without a dropout model, using the Laplace method (gray), and without a dropout model, using the FOCE-I method (black), when varying observation interval (and hence number of observations) (a), extent of dropout (relation between hazard and effect score, h _e) (b), maximum placebo response (PL_max) (c), and number of patients per group (d)

When simulations were performed without recording the exact time of dropout (interval censoring), bias was, as expected, higher than when the exact time of dropout was recorded. This was especially evident when there were few measurements of the effect variable. When there were only three measurements of the effect variable, bias in EC₅₀ was almost five times higher for interval censoring, compared to when the exact time of dropout was known.

An increased imprecision was seen with increasing dropout rate, increasing placebo effect and decreasing number of observations per subject (Fig. 5). In contrast to the bias, imprecision increased with decreasing number of patients per treatment group. The lowest imprecision was seen when a dropout model was used, although the imprecision was almost as low without a dropout model as long as the Laplacian method was applied. The highest imprecision was seen when the FOCE-I method was used and no dropout model was included (Fig. 6).

Fig. 5.

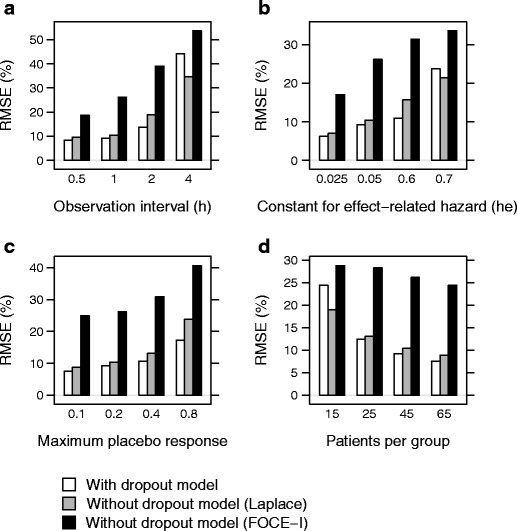
Root mean square errors (RMSE) in EC₅₀ when including a dropout model (white), without a dropout model, using the Laplace method (gray), and without a dropout model, using the FOCE-I method (black), when varying observation interval (a), extent of dropout (relation between hazard and effect score, h _e) (b), maximum placebo response (PL_max) (c), and number of patients per group (d)

Fig. 6.

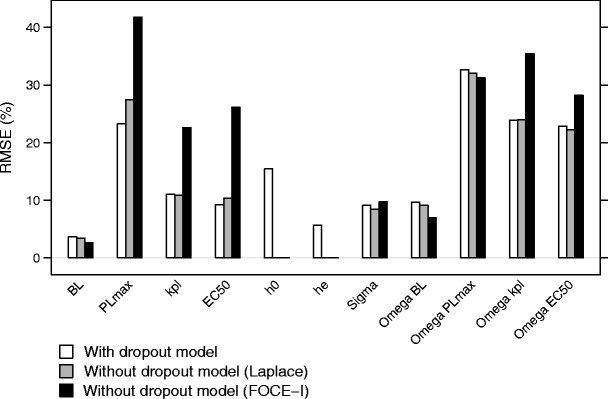
Root mean square error (RMSE) of the parameter estimates for scenario 1, when including a dropout model (white), without a dropout model, using the Laplace method (gray), and without a dropout model, using the FOCE-I method (black)

The mechanism of dropout in the above mentioned simulations is MNAR. As a comparison, simulations were made where the dropout was either MCAR or MAR (dependent on the observed effect variable at the time of the last observation). In the simulations where the dropout was at random, the bias was similar to that found after the base simulations (Fig. 7). Due to dense sampling and a relatively low residual variability the MNAR and MAR mechanisms were relatively similar. For the simulations with dropout completely at random, bias was in general less than for the base model (Fig. 7). The MCAR scenario for efficacy modeling in our work can be viewed as dropout due to toxicity under the assumption that toxicity is unrelated to efficacy.

Fig. 7.

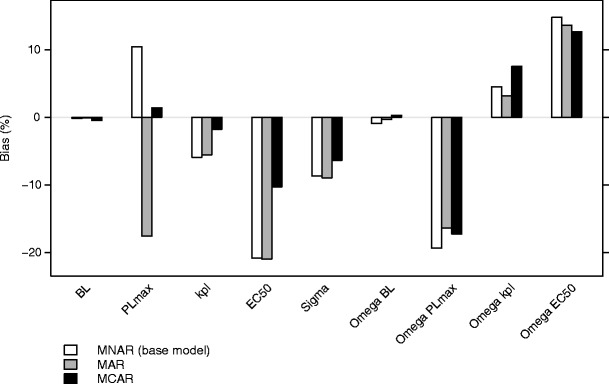
Bias in the parameter estimates for scenario 1, when simulations were performed with dropout not at random (base model), at random, or completely at random. The estimations were performed using the FOCE-I method

The VPCs created when not simulating with a dropout model showed clear differences between the “observed” and simulated medians and percentiles (Fig. 8a). This was most apparent for the placebo group, where the reduction in the effect variable was small and dropout was high, and the “observed” median was lower than the simulated median. For the active treatment groups, it was apparent that the simulated 97.5th percentile was high, while in the “observed” data, most patients with a high effect variable had dropped out. When including a dropout model in the VPC simulations, the resulting VPCs showed a good fit and agreement between “observed” and simulated medians and percentiles (Fig. 8b). This clearly shows that a dropout model is necessary in order to produce realistic simulations in the presence of informative dropout. When the dropout was completely at random, however, a dropout model was not needed in order to produce realistic VPCs (Fig. 8c).

Fig. 8.

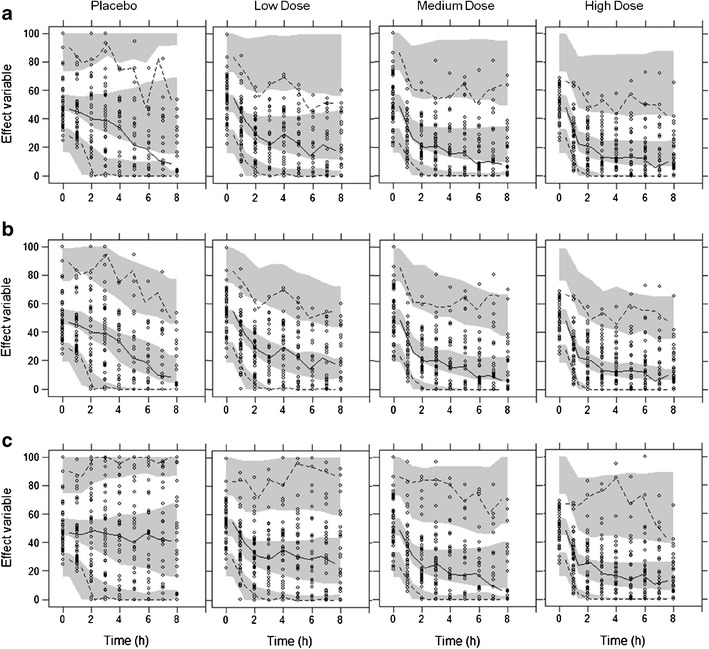
Visual Predictive Checks, without inclusion of dropout model for data containing informative dropout (scenario 1) (a), with dropout model for data containing informative dropout (scenario 1) (b) and without inclusion of dropout model for data with 40% dropout completely at random (c). Circles represent “observations” in an arbitrarily simulated dataset. Solid and dashed lines are the median, 2.5^th and 97.5^th percentiles of the “observations.” Shaded areas represent the 95% confidence interval of the simulated median, 2.5^th and 97.5^th percentiles

DISCUSSION

This work shows that ignoring informative dropout can lead to biased parameter estimates in nonlinear mixed effects modeling. This has previously been suggested by others, based on what is known from linear mixed effects models, but the size or importance of the bias has not been investigated (7–9). The size of the bias, however, does not necessarily need to be large, suggesting that simultaneous modeling of dropout and the variable of interest is not always necessary in nonlinear mixed effects modeling. With increasing dropout rate, the information provided by the dropout data was larger, not only because there was more dropout, but also because the number of observations of the effect variable decreased, leading to more information from dropout in relation to the information provided from effect measurements. The increase in bias with decreasing number of observations per patient was more prominent when a dropout model was not used. As a dropout event may provide information about the efficacy variable between the observations, this information becomes more important the fewer the observations. Naturally, as there is less data available when dropout increases, the imprecision in the parameter estimates also becomes higher. When the magnitude of the placebo effect was increased, bias in EC₅₀ also increased, even though the dropout rate decreased with increased placebo effect. This may be due to that when the drug effect becomes small in relation to the placebo effect, it also becomes more difficult to quantify. The need for simultaneous modeling of the effect variable and informative dropout is hence dependent on the information content remaining in the effect variable data. In many nonlinear mixed effects analyses, it will be sufficient to develop the dropout model separately from the effect variable.

The effect of changing the number of subjects was more pronounced on the imprecision than on the bias in EC₅₀. This is because decreasing the number of patients does not change the structure of the captured data, but rather change the amount of information, and hence a reduced number of patients increase the imprecision. The bias in the efficacy variable at baseline was small in all scenarios. This is not surprising, as the baseline observations were included in all estimations, and the dropout occurred after the baseline visit.

This simulation study was based on a model from a short-duration study design, but the results could potentially be extended to a long-term trial. The constant infusion regimen used in the simulations could be compared to a slow increase to steady-state concentrations after multiple dosing or the slow onset of drug action. In the current study, dropout was recorded at the actual time of dropout. This is generally the case in, for example, acute pain trials, during which the request of rescue medication is the main cause of dropout and the time of rescue medication is typically recorded. In other studies, the exact time of dropout may not be recorded, but rather it is noted that a patient has dropped out between two predefined visits. This interval censoring did in this work lead to less information in the dropout, and a smaller difference in bias between a model that accounts for the dropout and one that does not. In this study, the reason for the dropout was only lack of efficacy, but in reality, a mix of different reasons for dropout, e.g., adverse events and reasons completely at random, may be present.

The simulated data was analyzed using the same models as were used for the simulations, with or without including a dropout model. In some of the simulated studies, other models such as a linear concentration-effect relationship instead of an E_max model might have been more appropriate based on goodness of fit criteria (e.g., objective function value or diagnostic graphics). It is possible that all parameters would not have been identifiable in all scenarios, which might have affected the bias and imprecision. The choice of dropout model could also possibly influence the bias and imprecision in the parameter estimates. Time to event models can have problems with stability if they get more complex, and other methods to model dropout are available, e.g., logistic regression. This method has, however, been shown to introduce more bias than when a time to event model is used, possibly because it assumes that the hazard for dropout is constant between observations.

When a dropout model is used, NONMEM requires the use of the Laplace method, as the dropout is of categorical type data. When a dropout model is not used, the FOCE-I method can be applied on effect variables of continuous type data, but our results indicate that the bias is lower if the Laplace method is used despite not including a dropout model. Typically, the Laplace method is not used for analysis of continuous data, but our results suggest that in the case of informative dropout, the Laplace method could lead to less bias and higher precision than using the FOCE-I method.

In the simulations, the dropout mechanism was not at random, as the hazard was dependent on the unobserved, predicted effect variable. However, as the measurements of efficacy was frequent, the dropout was similar to that simulated at random, where the hazard was dependent on the last observation of the effect variable, and the bias was similar between the two dropout mechanisms. When the dropout was completely at random, or the dropout was related to other drug effects than those measured, bias was in general lower. The comparison between the different mechanisms of dropout is complicated by the fact that the proportion of patients dropping out is not exactly the same, and the distribution of dropout in the different treatment groups is different for the different mechanisms.

Although there was bias in the parameters when dropout was not accounted for in the estimation, the bias was in general not very high. Simulations of the efficacy variable were also in many cases not very different between biased and unbiased parameters, and decisions based on the model would in most cases not be different. It is possible, however, that with a different study design and other properties of the measured variable, nonrandom dropout can be of greater importance. In this case, the true model was always used for the estimations, but in case of sparse or complex data, and a high degree of missing data, it may not be possible to identify the true model, leading to more bias or an erroneous model structure. Even though the bias may be small, and the effect on the underlying efficacy time course may be limited, informative dropout will still affect simulations and goodness of fit plots like VPC, making it difficult to select a good model without adequate handling of the dropout (6,7,9–11). In order to simulate realistic studies, e.g., for clinical trial simulation purposes, a model describing the dropout is needed. VPC in the presence of nonrandom dropout also require special consideration in study designs allowing dose adjustments, as the simulations require assumptions of what the dosing regimen would have been if dropout had not occurred (9). The VPC presented used simulated “observations,” and therefore the presented figures are just one representation of how the VPC may appear. Another simulation, given the same set of parameters, would have given other “observations,” but the general trends of overpredicting the efficacy variable at late time points could on average be expected as similar. The VPC shown should therefore be seen as an illustration rather than a quantitative assessment of the importance of simulating informative dropout.

CONCLUSIONS

Ignoring informative dropout leads to biased parameter estimates in nonlinear mixed effects modeling, although the bias may be small and may not affect the predictions of the efficacy variable. A dropout model is, however, important in order to make realistic simulations. The bias increased with increasing dropout rate, increasing placebo effect and decreasing number of observations per subject. Knowing the exact time of dropout decreased the bias compared to interval-censored data. Using FOCE-I can lead to larger bias than if the Laplace method is used for models ignoring informative dropout.