Efficient Transformation of Parahydrogen Spin Order into Heteronuclear Magnetization

Abstract

Spin order obtained in the strong coupling regime of protons from parahydrogen-induced hyperpolarization (PHIP) is initially captured as an ensemble of singlet states. For biomedical applications of PHIP, locking this spin order on long-lived heteronuclear storage nuclei increases spectral dispersion, reduces background interference from water protons, and eliminates the need to synchronize subsequent detection pulse sequences to accrued singlet-state evolution. A variety of traditional sequences such as INEPT or HMQC are available to interconvert heteronuclear single quantum coherences at high field, but new approaches are required for converting singlet states into heteronuclear single quantum coherences at low field in the strong coupling regime of protons. Described here is a consolidated pulse sequence that achieves this transformation of singlet-state spin order into heteronuclear magnetization across a wide range of scalar couplings in AA′X spin systems. Analytic solutions to the spin evolution are presented, and performance was validated experimentally in the parahydrogen addition product, 2-hydroxyethyl 1-¹³C-propionate-d₃. Hyperpolarized carbon-13 signals were enhanced by a factor of several million relative to Boltzmann polarization in a static magnetic field of 47.5 mT (~13% polarization). We anticipate that this pulse sequence will provide efficient conversion of parahydrogen spin order over a broad range of emerging PHIP agents that feature AA′X spin systems.

INTRODUCTION

Hyperpolarization of nuclear spin ensembles has increased NMR sensitivity to a level that is now enabling detection of metabolism in biological tissue on a time scale of seconds.^1,2 The most developed of these technologies, DNP (dynamic nuclear polarization),^3–5 in particular has already been used to detect, grade, and monitor response to therapy in tumors.^6–8 These encouraging developments have demonstrated the overall viability of NMR-based hyperpolarized methods for the study of in vivo metabolism, and are naturally spurring development in alternative methods of hyperpolarization, such as parahydrogen-induced polarization (PHIP).^9–11 Polarization yields from the less mature PHIP technology are similar to DNP where precursors are available, and accessed at significantly reduced instrumental complexity and expense. An array of complementary advances are still required, however, for PHIP to reach its potential as a diagnostic imaging modality.

In particular, efficient and streamlined methods for transforming the initial parahydrogen spin order into heteronuclear magnetization would improve translation of emerging PHIP contrast agents to biomedical applications. Upon addition of parahydrogen to a perdeuterated and unsaturated backbone containing a spin-active heteronucleus, the initial singlet state of an AA′X spin system will evolve unless J_AX = J_AX′. Transforming these states into longitudinal heteronuclear magnetization maximizes spectral dispersion during subsequent imaging experiments and reduces interference from the intense proton background arising from water in vivo. It has recently been demonstrated that parahydrogen singlet states can themselves be long-lived at Earth’s field,¹² but even in cases where the parahydrogen proton lifetimes are similar to or even more favorable than carbonyl ¹³C for example, locking the initial spin order also eliminates the need to synchronize subsequent imaging with ongoing evolution of the initial parahydrogen singlet state.

Determining the timing, frequency, and magnitude of the applied electromagnetic fields necessary to efficiently transform parahydrogen spin order into heteronuclear magnetization in the strong coupling regime of protons is a challenging problem though, even for small AA′X spin systems. Two prior sequences have been reported for pulsed transformation of parahydrogen spin order into heteronuclear magnetization in this field regime.^13,14 Most recently, Kadlecek and co-workers reported a series of sequences that yield piecewise optimal polarization in three distinct coupling regimes.¹³ The earlier and most frequently cited sequence developed by Goldman and coworkers offers unity efficiency for the targeted molecules and a recursive procedure for pumping polarization yields when outside of those coupling regimes.¹⁴ We sought to build on those earlier works by developing a streamlined sequence that could achieve optimal polarization in a single streamlined implementation across a broad range of scalar couplings without conditional or iterative application.

In this study, we describe a consolidated pulse sequence that transforms parahydrogen spin order into heteronuclear magnetization in AA′X spin systems with a yield near unity and independent of spin couplings. The shorthand hyper-SHIELDED (Singlet to Heteronuclei by Iterative Evolution Locks Dramatic Enhancement for Delivery) was adopted for quick referencing because the sequence effectively locks the spin order of hyperpolarized molecules for subsequent delivery and examination in biological or other systems of interest. The sequence provides near-unity conversion across a broad range of coupling topologies, by flanking a heteronuclear excitation with two asymmetric proton refocusing intervals to provide four unique evolution intervals. These delay intervals are in turn optimized using prior knowledge of the spin couplings to efficiently transform the initial parahydrogen spin order into pure heteronuclear magnetization. We anticipate that the streamlined construction of hyper-SHIELDED will be well suited to multidimensional PHIP experiments and for efficient preparation of existing and emerging PHIP contrast agents.

THEORY

The Hamiltonian of the three-spin system (AA′X = I₁I₂S) formed from the parahydrogen addition product (PASADE-NA)^9,10 and a coupled heteronucleus in the strong proton coupling regime can be written as

$$\mathbf{H}=2\pi [J_{12}({\mathbf{I}}_{\mathbf{1}}·{\mathbf{I}}_{\mathbf{2}})+J_{1\mathrm{S}}{\mathbf{I}}_{\mathbf{1}\mathbf{z}}{\mathbf{S}}_{\mathbf{z}}+J_{2\mathrm{S}}{\mathbf{I}}_{\mathbf{2}\mathbf{z}}{\mathbf{S}}_{\mathbf{z}}]$$ (1)

The initial density matrix of parahydrogen at low field in the strong coupling regime of protons can be written:

$${\mathit{\sigma }}_{\mathbf{0}}=\frac{\mathbf{E}}{4}-{\mathbf{I}}_1·{\mathbf{I}}_2$$ (2)

The I_1zI_2z component of this initial density matrix commutes with all components, and hence does not evolve under the Hamiltonian in eq 1. The remainder of the initial density matrix with hyper-SHIELDED (Figure 1) evolves during the interval t₁ under the influence of the Hamiltonian according to the following expression:

$${\mathit{\sigma }}_{\mathbf{1}}\stackrel{{\mathbf{t}}_{\mathbf{1}}}{\to }[{sin}^2\theta +({cos}^2\theta )cos(2\pi \mathrm{\Omega }{t}_1)]({\mathbf{I}}_{\mathbf{1}\mathbf{x}}{\mathbf{I}}_{\mathbf{2}\mathbf{x}}+{\mathbf{I}}_{\mathbf{1}\mathbf{y}}{\mathbf{I}}_{\mathbf{2}\mathbf{y}})$$ (3a)

$$+(cos\theta )sin(2\pi \mathrm{\Omega }{t}_1)2({\mathbf{I}}_{\mathbf{1}\mathbf{y}}{\mathbf{I}}_{\mathbf{2}\mathbf{x}}-{\mathbf{I}}_{\mathbf{1}\mathbf{x}}{\mathbf{I}}_{\mathbf{2}\mathbf{y}}){\mathbf{S}}_{\mathbf{z}}$$ (3b)

$$+(sin\theta )(cos\theta )[1-cos(2\pi \mathrm{\Omega }{t}_1)]({\mathbf{I}}_{\mathbf{1}\mathbf{z}}-{\mathbf{I}}_{\mathbf{2}\mathbf{z}}){\mathbf{S}}_{\mathbf{z}}$$ (3c)

where cos θ = Δ/(1 + Δ²)^1/2, sin θ = 1/(1 + Δ²)^1/2, Δ = [J_1s − J_2s](2J₁₂)⁻¹, and Ω = J₁₂(1 + Δ²)^1/2. After applying a 180°(+x) pulse on protons, the density operator σ₂ evolves according to

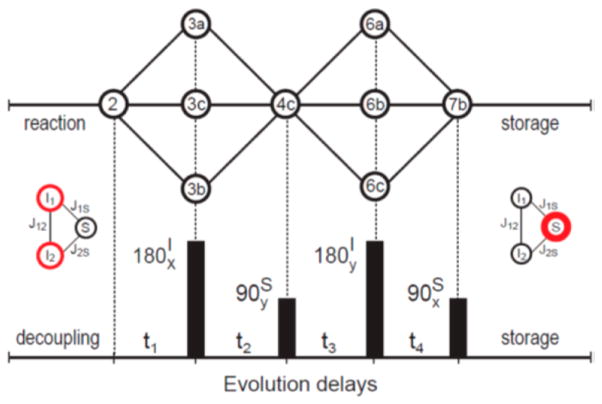
Figure 1.

Graphical depiction of density matrix evolution (upper graph) with the hyper-SHIELDED sequence (lower graph). Para-hydrogen singlet states (represented by bold circles, middle left) are converted into pure heteronuclear magnetization (bold circle, middle right) for strongly coupled spin systems (I₁I₂S or AA′X). Circled symbols in the upper diagram represent density matrix terms and correspond directly with numbered equations (see Theory).

$$\begin{array}{l}{\mathit{\sigma }}_{\mathbf{2}}\stackrel{t_2}{\to }[-cos2\theta ({sin}^2\theta )+(1/2){sin}^{2}2\theta (cos(2\pi \mathrm{\Omega }{t}_1)\\ +cos(2\pi \mathrm{\Omega }{t}_2))+cos2\theta ({cos}^2\theta )cos(2\pi \mathrm{\Omega }{t}_1)\\ cos(2\pi \mathrm{\Omega }{t}_2)+({cos}^2\theta )sin(2\pi \mathrm{\Omega }{t}_1)sin(2\pi \mathrm{\Omega }{t}_2)]\\ ({\mathbf{I}}_{\mathbf{1}\mathbf{x}}{\mathbf{I}}_{\mathbf{2}\mathbf{x}}+{\mathbf{I}}_{\mathbf{1}\mathbf{y}}{\mathbf{I}}_{\mathbf{2}\mathbf{y}})\end{array}$$ (4a)

$$\begin{array}{l}+[sin(2\theta )sin(\theta )sin(2\pi \mathrm{\Omega }{t}_2)+cos(2\theta )cos(\theta )\\ cos(2\pi \mathrm{\Omega }{t}_1)sin(2\pi \mathrm{\Omega }{t}_2)-cos(\theta )sin(2\pi \mathrm{\Omega }{t}_1)\\ cos(2\pi \mathrm{\Omega }{t}_2)]2({\mathbf{I}}_{\mathbf{1}\mathbf{y}}{\mathbf{I}}_{\mathbf{2}\mathbf{x}}-{\mathbf{I}}_{\mathbf{1}\mathbf{x}}{\mathbf{I}}_{\mathbf{2}\mathbf{y}}){\mathbf{S}}_{\mathbf{z}}\end{array}$$ (4b)

$$\begin{array}{l}+[-(1/2)sin(2\theta )(cos(2\theta )+2{sin}^2(\theta )cos(2\pi \mathrm{\Omega }{t}_2)\\ -2{cos}^2(\theta )cos(2\pi \mathrm{\Omega }{t}_1)+cos(2\theta )cos(2\pi \mathrm{\Omega }{t}_1)cos(2\pi \mathrm{\Omega }{t}_2)\\ +sin(2\pi \mathrm{\Omega }{t}_1)sin(2\pi \mathrm{\Omega }{t}_2))]({\mathbf{I}}_{\mathbf{1}\mathbf{z}}-{\mathbf{I}}_{\mathbf{2}\mathbf{z}}){\mathbf{S}}_{\mathbf{z}}\end{array}$$ (4c)

In order to drive the terms in eq 4 exclusively to eq 4c, the intervals t₁ and t₂ are chosen to satisfy eqs 5a and 5b:

$$\begin{array}{l}-cos2\theta {sin}^2\theta +(1/2){sin}^{2}2\theta (cos(2\pi \mathrm{\Omega }{t}_1)\\ +cos(2\pi \mathrm{\Omega }{t}_2))\\ +cos(2\theta ){cos}^2\theta cos(2\pi \mathrm{\Omega }{t}_1)cos(2\pi \mathrm{\Omega }{t}_2)\\ +{cos}^2\theta sin(2\pi \mathrm{\Omega }{t}_1)sin(2\pi \mathrm{\Omega }{t}_2)\\ =0\end{array}$$ (5a)

$$\begin{array}{l}sin(2\theta )sin(\theta )sin(2\pi \mathrm{\Omega }{t}_2)+cos(2\theta )cos(\theta )cos(2\pi \mathrm{\Omega }{t}_1)\\ sin(2\pi \mathrm{\Omega }{t}_2)-cos(\theta )sin(2\pi \mathrm{\Omega }{t}_1)cos(2\pi \mathrm{\Omega }{t}_2)\\ =0\end{array}$$ (5b)

A 90°(+y) pulse on the S spin then converts the state (I_1z − I_2z)S_z into (I_1z − I_2z)S_x. During the subsequent interval t₃, this state evolves into three terms:

$${\mathit{\sigma }}_{\mathbf{3}}=({\mathbf{I}}_{\mathbf{1}\mathbf{z}}-{\mathbf{I}}_{\mathbf{2}\mathbf{z}}){\mathbf{S}}_{\mathbf{x}}\stackrel{t_3}{\to }cos(2\pi \mathrm{\Omega }{t}_3)({\mathbf{I}}_{\mathbf{1}\mathbf{z}}-{\mathbf{I}}_{\mathbf{2}\mathbf{z}}){\mathbf{S}}_{\mathbf{x}}$$ (6a)

$$+cos(\theta )sin(2\pi \mathrm{\Omega }{t}_3)(1/2){\mathbf{S}}_{\mathbf{y}}(\mathbf{E}-4{\mathbf{I}}_{\mathbf{1}\mathbf{z}}{\mathbf{I}}_{\mathbf{2}\mathbf{z}})$$ (6b)

$$-sin(\theta )sin(2\pi \mathrm{\Omega }{t}_3)2({\mathbf{I}}_{\mathbf{1}\mathbf{y}}{\mathbf{I}}_{\mathbf{2}\mathbf{x}}-{\mathbf{I}}_{\mathbf{1}\mathbf{x}}{\mathbf{I}}_{\mathbf{2}\mathbf{y}}){\mathbf{S}}_{\mathbf{x}}$$ (6c)

A proton 180(+x) pulse is then applied, and during the subsequent interval t₄, the density matrix evolves according to the expressions:

$$\begin{array}{l}{\mathit{\sigma }}_{\mathbf{4}}\stackrel{t_4}{\to }[cos(2\pi \mathrm{\Omega }{t}_3)cos(2\pi \mathrm{\Omega }{t}_4)+cos(2\theta )sin(2\pi \mathrm{\Omega }{t}_3)\\ sin(2\pi \mathrm{\Omega }{t}_4)]({\mathbf{I}}_{\mathbf{1}\mathbf{z}}-{\mathbf{I}}_{\mathbf{2}\mathbf{z}}){\mathbf{S}}_{\mathbf{x}}\end{array}$$ (7a)

$$\begin{array}{l}+[cos(\theta )cos(2\pi \mathrm{\Omega }{t}_3)sin(2\pi \mathrm{\Omega }{t}_4)-sin(2\theta )sin(\theta )\\ sin(2\pi \mathrm{\Omega }{t}_3)-cos(\theta )cos(2\theta )sin(2\pi \mathrm{\Omega }{t}_3)cos(2\pi \mathrm{\Omega }{t}_4)]\\ (1/2){\mathbf{S}}_{\mathbf{y}}(\mathbf{E}-4{\mathbf{I}}_{\mathbf{1}\mathbf{z}}{\mathbf{I}}_{\mathbf{2}\mathbf{z}})\end{array}$$ (7b)

$$\begin{array}{l}+[sin(\theta )cos(2\theta )sin(2\pi \mathrm{\Omega }{t}_3)cos(2\pi \mathrm{\Omega }{t}_4)-sin(\theta )\\ cos(2\pi \mathrm{\Omega }{t}_3)sin(2\pi \mathrm{\Omega }{t}_4)-sin(2\theta )cos(\theta )sin(2\pi \mathrm{\Omega }{t}_3)]2\\ ({\mathbf{I}}_{\mathbf{1}\mathbf{y}}{\mathbf{I}}_{\mathbf{2}\mathbf{x}}-{\mathbf{I}}_{\mathbf{1}\mathbf{x}}{\mathbf{I}}_{\mathbf{2}\mathbf{y}}){\mathbf{S}}_{\mathbf{x}}\end{array}$$ (7c)

where E equals the identity operator. The intervals t₃ and t₄ are chosen to satisfy the following set of equations:

$$cos(2\pi \mathrm{\Omega }{t}_3)cos(2\pi \mathrm{\Omega }{t}_4)+cos(2\theta )sin(2\pi \mathrm{\Omega }{t}_3)sin(2\pi \mathrm{\Omega }{t}_4)=0$$ (8a)

$$\begin{array}{l}sin(\theta )cos(2\theta )sin(2\pi \mathrm{\Omega }{t}_3)cos(2\pi \mathrm{\Omega }{t}_4)-sin(\theta )\\ cos(2\pi \mathrm{\Omega }{t}_3)sin(2\pi \mathrm{\Omega }{t}_4)-sin(2\theta )cos(\theta )sin(2\pi \mathrm{\Omega }{t}_3)=0\end{array}$$ (8b)

This condition is satisfied when

$$tan(2\pi \mathrm{\Omega }{t}_3)=-1/\sqrt{1+2cos(2\theta )}$$ (9a)

$$tan(2\pi \mathrm{\Omega }{t}_4)=1/\sqrt{1+2cos(2\theta )}$$ (9b)

Finally, a 90°(+x) pulse converts the term from eq 7b into longitudinal magnetization on the heteronucleus for storage until subsequent detection in vivo. The pulse sequence diagram and schematic of spin evolution represented by eqs 2–7 is illustrated in Figure 1.

EXPERIMENTAL SECTION

Approximately 98% parahydrogen gas was synthesized by pulsing ambient research grade hydrogen gas at 14 bar (200 psi) into a catalyst-filled (iron oxide) copper chamber held at 14 K using a previously described semiautomated parahydrogen generator.¹⁵ Fresh batches of parahydrogen were collected in 10 L aluminum storage tanks (14745-SHF-GNOS, Holley, KY), used without Teflon lining or additional modification.

The preparation of PASADENA^9,10 precursor aqueous solutions was similar to those previously described¹⁶ with the exception that water was used in place of 99.8% D₂O as a solvent. 320 μmol (0.180 g) of the disodium salt of 1,4-bis[(phenyl-3-propanesulfonate)phosphine]butane (#717347, Sigma-Aldrich-Isotec, OH) was combined with 100 mL of H₂O in a 1 L flask. This ambient solution was then degassed with a rotary evaporator (model R-215 equipped with V-710 pump, Buchi, New Castle, DE) fitted with an N₂(g) input, by decrementing the onboard pressure slowly to avoid boiling, from 70 to 25 mbar over approximately 10 min. The rhodium(I) catalyst, bis(norbornadiene) rhodium(I) tetrafluoroborate (0.10 g, 0.27 mmol, 45-0230, CAS 36620-11-8, Strem Chemicals, MA) was dissolved in 7 mL of acetone and was added dropwise to the phosphine ligand solution to limit undesirable precipitation. After the prior degassing procedure was repeated, this catalyst solution was mixed with 2-hydroxyethyl acrylate-1-¹³C,2,3,3-d₃ (HEA, 97% chemical purity, 99 atom % ¹³C, 98 atom % D (20 mg, 0.16 mmol, Sigma-Aldrich, 676071) in a 150 mL square bottle (431430, Corning Life Sciences, NY).

Solutions containing unsaturated precursor molecules with bidentate Rh(I) catalyst prepared as described above were then connected to a previously described automated parahydrogen polarizer,¹⁶ equipped with a dual-tuned ¹H/¹³C coil.¹⁷ Briefly, the chemical reaction was pulse programmed with a commercial NMR console (model KEA2, Magritek, Wellington, New Zealand) to synchronize chemical reaction parameters, decoupling fields, polarization transfer sequences, and detection of NMR signals. PASADENA precursors were sprayed remotely into a plastic (polysulfone) reactor located within a 47.5 mT static magnetic field. The external solution was equilibrated at 65 °C prior to spraying, and 16.5 bar (240 psi) nitrogen gas was used to inject this heated PASADENA precursor solution into a pressurized atmosphere of 7 bar (100 psi) parahydrogen. Immediately following injection, proton continuous wave decoupling was applied at a frequency of 2.02 MHz (B₀ = 47.5 mT) with a magnitude of 5 kHz. This decoupling radio frequency field was maintained for 4 s to freeze the parahydrogen spin ensemble while the hydrogenation reaction went to completion.¹⁴

The pulse sequences for transferring polarization were applied immediately after continuous wave decoupling was turned off (Figure 1). For the HEP molecule, the t₁, t₂, t₃, and t₄ intervals were 9.75, 58.47, 36.20, and 28.28 ms, respectively, calculated by inverting the density matrix expressions above (see Theory) assuming a proton–proton coupling of 7.57 Hz, and a carbon–proton scalar coupling asymmetry of 12.86 Hz.¹⁴ The actual couplings could vary somewhat from these values depending on pH and specific attributes of the polarization process such as temperature and pressure. After parahydrogen spin order was transferred to net magnetization, a single free induction decay was acquired (90–acquire) on the carbon channel with 512 points at a receiver bandwidth of 5 kHz, for a digital resolution of ~10 Hz per point.

RESULTS AND DISCUSSION

Described here is a new pulse sequence (hyper-SHIELDED) for transforming parahydrogen spin order in the strong coupling regime of protons into net heteronuclear magnetization. Hyper-SHIELDED operates at nearly unity efficiency with yields that are approximately independent of scalar coupling topology in three spin systems (AA′X). The AA′X moiety is a widespread and important spin system in PHIP experiments formed for example, by molecular addition of parahydrogen to perdeuterated and unsaturated molecular backbones.

Hyper-SHIELDED flanks two asymmetric proton refocusing intervals about a heteronuclear excitation pulse to generate four unique delays (t₁ − t₄). Optimization of these delays to spin couplings in the molecule of interest sequentially converts the initial parahydrogen singlet state into pure heteronuclear magnetization (see Theory, Figure 1). Density matrix evolution under the influence of hyper-SHIELDED is depicted graphically in Figure 1 and linked directly to equations in the Theory section.

The analysis of spin dynamics under the influence of hyper-SHIELDED assumed strongly coupled protons and weak heteronuclear scalar couplings (eq 1). The initial parahydrogen density operator was retained without truncation and proportional to I₁·I₂ (eq 2). Chemical shifts were not considered because the effects are small compared to homonuclear proton couplings at targeted fields in the vicinity of 47.5 mT or lower, and we note that offsets were refocused with 180° pulses on both channels placed at 1/4 and 3/4 of each evolution interval.¹⁴ Evolution of the strongly coupled parahydrogen density operator of eq 2 is relatively complicated compared to (truncated) high field density operators proportional to I_1zI_2z. While analytical solutions to the spin dynamics are more tedious, heteronuclear magnetization yields from parahydrogen spin order are increased by a factor of 2 at low field in the strong coupling regime of protons.

Hyper-SHIELDED was applied immediately following the hydrogenation reaction. During the fast catalytic hydrogenation,⁹ proton decoupling was used to maintain equivalence of the parahydrogen protons and freeze evolution of the spin density operator until reaction completion (Figure 1).¹⁸ After this period of decoupling and chemical addition, with hyper-SHIELDED the initial density matrix evolved from the parahydrogen singlet state (eq 2) to three terms (eqs 3a–3c, symbols 3a–c in Figure 1) in the Cartesian product basis¹⁹ during the first interval (t₁). A 180°(x) proton pulse then focused these three terms of the density matrix into term 4c during the interval t₂. A 90°(y) pulse on the S-nucleus then allowed term 4c to evolve into an additional three terms (symbols 6a–c, Figure 1) during the interval t₃. Following a proton 180° pulse, these three terms (symbols 6a–c, Figure 1) collapse into a single term during t₄ (symbol 7b, Figure 1).

Note that since I_1zI_2z commutes with the Hamiltonian, I_1zI_2z(t=0) = I_1zI_2z(t). Since I_z1(t=0) + I_z2(t=0) = 0 for the parahydrogen singlet state, 4I_1zI_2z reduces to −E. Therefore, when the evolution intervals are chosen to satisfy eqs 8a and 8b, eq 7b reduces to a pure S_y term. Rotating this heteronuclear magnetization then locks the original parahydrogen spin order along S_z, where it will persist according to relaxation kinetics specific to the storage nucleus. Alternatively, if left unperturbed in the transverse plane this term could be detected directly at the field where the PHIP preparation was performed.¹⁶ Nonselective refocusing pulses were interleaved at 1/4 and 3/4 on both channels in each evolution interval to refocus offsets and mitigate the deleterious impact of static field inhomogeneities.¹⁴

Two prior sequences have been reported to transform parahydrogen spin order into heteronuclear magnetization in the strong proton coupling regime where the process is most efficient.^13,14 Most recently, Kadlecek and co-workers reported a set of sequences that can be selectively applied to yield optimal transfer efficiency in three distinct scalar coupling regimes.¹³ Goldman and co-workers reported the first pulsed transfer method which yields near unity singlet-state transformation efficiency in proximity to the scalar couplings of the design molecule. They also described a recursion procedure to pump polarization yields with GPS toward unity when outside of those targeted coupling regimes.¹⁴ With hyper-SHIELDED, we sought to build on these efficient earlier works by developing a sequence that could achieve optimal conversion efficiency in a single streamlined sequence without recursive application and with minimal sensitivity to scalar coupling.

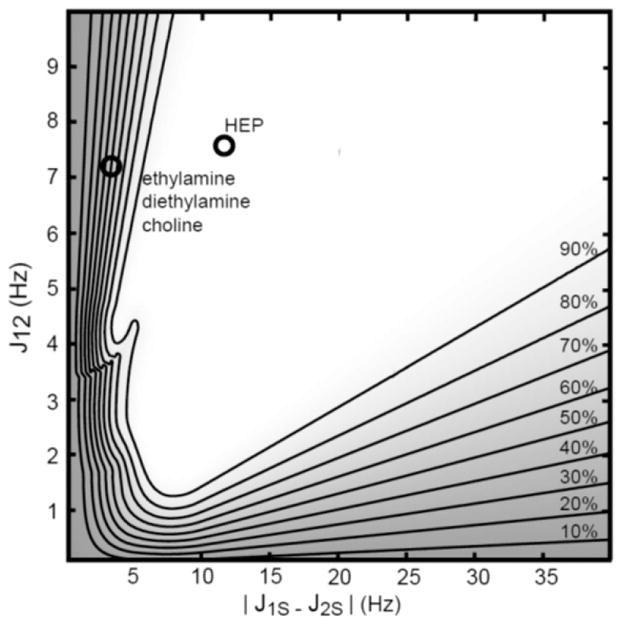
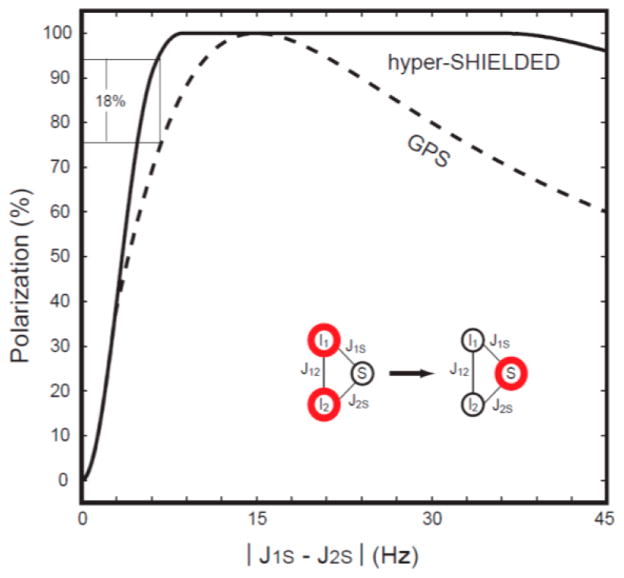
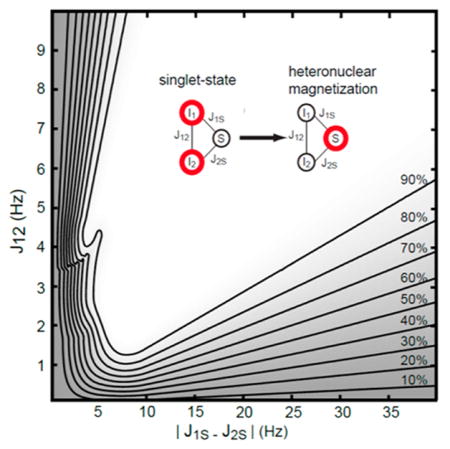
To characterize sensitivity of hyper-SHIELDED to scalar couplings, transfer efficiency was calculated with respect to proton–proton scalar couplings (J₁₂) and coupling asymmetry (|J_1S − J_2S|) over a range spanning known and conceivable PHIP reaction products (Figures 2 and 3). For each unique set of couplings (J₁₂, |J_1S − J_2S|), the set of evolution intervals yielding maximum efficiency was determined by inverting the density matrix equations subject to a 300 ms total sequence duration constraint (see Theory). As illustrated in Figure 3, a broad plateau of unity transformation efficiency was obtained with as little as ~6 Hz heteronuclear coupling asymmetry (|J_1S − J_2S|) and ~2 Hz homonuclear proton coupling (J₁₂). If application warranted and relaxation times were favorable, expanding the total pulse sequence duration constraint beyond 300 ms would enable sharper transitions from valley to plateau.

Figure 2.

Polarization yield as a function of homonuclear proton coupling (J₁₂) and heteronuclear coupling asymmetry (|J_1S − J_2S|) for hyper-SHIELDED. Contour levels are marked at right and superposed onto a gradient map calculated at an isotropic resolution of 0.1 Hz. For each point, the density matrix equations were inverted to find τ intervals (t_i, Figure 1) corresponding to maximum polarization and normalized to the global maximum. Annotated coordinates refer to the test molecule (HEP) and a sample of ¹⁵N parahydrogen addition products with small asymmetries that would be expected to differentially benefit from hyper-SHIELDED.

Figure 3.

Dependence of theoretical polarization transfer efficiency on heteronuclear coupling constant asymmetry |J_1S − J_2S| using the hyper-SHIELDED sequence (solid) versus a nonrecursive implementation of the GPS comparison sequence.¹⁴ The τ intervals were optimized to produce maximum polarization for each sequence at a common value of J₁₂ of 7.5 Hz.

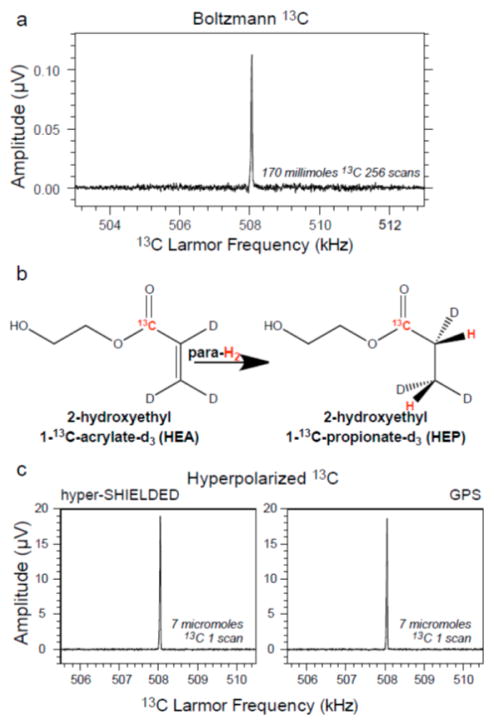
To validate the sequence, experimental heteronuclear ¹³C signals were compared between hyper-SHIELDED and GPS¹⁴ for a PHIP reaction product where both sequences were predicted to perform with identical efficiency (Figures 3 and 4). As shown in Figure 4 and in accord with theoretical expectations, ¹³C magnetization yield in a 7 μmol sample of the PHIP reaction product, 2-hydroxyethyl 1-¹³C-propionate-d₃, was enhanced by a large and equivalent factor of several million with both sequences. Although not yet experimentally demonstrated or implemented on our equipment, the piecewise optimal sequences recently reported by Kadlecek and coworkers would likely offer similarly efficient results.¹³ Whereas the current sequence (hyper-SHIELDED) and earlier sequences all appear to be well-suited to transforming parahydrogen spin order efficiently into net heteronuclear magnetization, we sought to complement the earlier advances^13,14 by creating a single streamlined sequence that could achieve high transfer efficiencies independent of scalar couplings. Implementation of hyper-SHIELDED is experimentally compact and because the sequence does not rely on condition or recursive application for broadband efficiency, it can be readily extended to multidimensional experiments on mixtures containing molecules with a range of couplings.

Figure 4.

Polarization yield of hyper-SHIELDED sequence versus GPS.¹⁴ (a) Boltzmann polarized carbon-13 spectrum acquired from an aqueous solution containing 170 mmol of the reaction product. (b) Reaction schematic for synthesizing parahydrogenated 2-hydroxyethyl 1-¹³C-propionate-d₃ (HEP). (c) Experimentally determined yields for hyper-SHIELDED and GPS comparison sequence were nearly identical and in accord with theory for the coupling arrangement in the test HEP molecule.

Theoretical conversion efficiency was also analyzed at a specific J₁₂ (7.5 Hz) and compared to the nonrecursive application of GPS. As illustrated in Figure 2, the dependence of polarization yield in the small asymmetry regime is relatively insensitive to J₁₂. Polarization yields reach uniform efficiency more rapidly as a function of asymmetry in hyper-SHIELDED versus the nonrecursive application of GPS,¹⁸ and high levels of polarization are sustained across a broad range of asymmetries (Figure 3). Although the calculated data points in Figure 3 were not parsed by sequence duration, hyper-SHIELDED was slightly longer (17.88 ms) at the HEP optimum. For the ¹³C relaxation constants of HEP, the increased duration of the hyper-SHIELDED sequence did not reduce polarization yield (Figure 4). Hyper-SHIELDED should perform particularly well in molecules with small asymmetries such as ethylamine, diethyamine, and choline (Figure 3 inset).^20,21

CONCLUSIONS

A new pulse sequence was presented for transforming singlet-state spin order in the strong coupling regime of protons into heteronuclear magnetization. Conversion efficiency with this sequence (hyper-SHIELDED) is uniform and approximately independent over a broad range of scalar coupling patterns, and these attributes are obtained in a single consolidated sequence without recursion by invoking four independently optimized evolution delays. Analytical solutions to density matrix evolutions were found sequentially for each interval, and performance was validated experimentally with in situ detection of hyperpolarized 2-hydroxyethyl 1-¹³C-propionate-d₃. Locking parahydrogen spin order efficiently in the form of heteronuclear magnetization in a flexible array of scalar coupling topologies is important for translating parahydrogen-based hyperpolarization from basic science to emerging applications in biomedicine, and we anticipate that this sequence will be generally useful for a range of emerging PHIP contrast agents targeted for in vivo metabolism.