Abstract
Nuclear magnetic resonance (NMR) spectroscopy is an important experimental technique that allows one to study protein structure and dynamics in solution. An important bottleneck in NMR protein structure determination is the assignment of NMR peaks to the corresponding nuclei. Structure-based assignment (SBA) aims to solve this problem with the help of a template protein which is homologous to the target and has applications in the study of structure–activity relationship, protein–protein and protein–ligand interactions. We formulate SBA as a linear assignment problem with additional nuclear overhauser effect constraints, which can be solved within nuclear vector replacement’s (NVR) framework (Langmead, C., Yan, A., Lilien, R., Wang, L. and Donald, B. (2003) A Polynomial-Time Nuclear Vector Replacement Algorithm for Automated NMR Resonance Assignments. Proc. the 7th Annual Int. Conf. Research in Computational Molecular Biology (RECOMB), Berlin, Germany, April 10–13, pp. 176–187. ACM Press, New York, NY. J. Comp. Bio., (2004), 11, pp. 277–298; Langmead, C. and Donald, B. (2004) An expectation/maximization nuclear vector replacement algorithm for automated NMR resonance assignments. J. Biomol. NMR, 29, 111–138). Our approach uses NVR’s scoring function and data types and also gives the option of using CH and NH residual dipolar coupling (RDCs), instead of NH RDCs which NVR requires. We test our technique on NVR’s data set as well as on four new proteins. Our results are comparable to NVR’s assignment accuracy on NVR’s test set, but higher on novel proteins. Our approach allows partial assignments. It is also complete and can return the optimum as well as near-optimum assignments. Furthermore, it allows us to analyze the information content of each data type and is easily extendable to accept new forms of input data, such as additional RDCs.
Keywords: binary integer programming, structural bioinformatics, automated NMR assignments
1. INTRODUCTION
The 3D structure of a protein plays a critical role in defining the protein’s function. High-throughput protein structure determination methods are very important to obtain structural information quickly and accurately. The two main experimental techniques for structure determination are X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy. About 85% of the structures in the Protein Data Bank (PDB) were determined using X-ray crystallography, whereas approximately 15% were solved using NMR. Not all proteins can be crystallized and studied by X-ray crystallography. Moreover, NMR allows one to solve protein structure in solution.
In NMR, various experiments are performed on the protein. The protein is excited via radio frequency energy, and the resulting signal (free induction decay) is recorded. This signal is transformed into a spectrum via Fourier transform. In the resulting spectrum, each peak corresponds to a tuple of atomic nuclei. In NMR, the first challenge is to pick the peaks and to separate the real signal from noise. This is largely automated. The second challenge is to find the mapping between the peaks and the atoms. This is called the assignment problem. The assignment problem is not difficult for very small molecules. However, for very large molecules (e.g. proteins), the assignment problem is very difficult, and is one of the primary computational challenges in NMR. Additionally, NMR data is noisy (because of peak crowding, overlap and missing or extra peaks), which makes the problem even more difficult. Once the assignments are made, traditional NMR structure determination proceeds by minimizing a hybrid energy potential, which has terms for the force field, as well as experimentally derived constraints. There is also a new linear time algorithm that determines protein backbone structure accurately by solving, in closed form, systems of low-degree polynomial equations formulated using residual dipolar coupling restraints [1].
Structure-based assignments (SBAs) denote automated assignment given prior information in the form of the putative structure (‘template’) of the protein. By analogy, in X-ray crystallography, the molecular replacement technique allows solution of the crystallographic-phase problem when a ‘close’ or homologous structural model is known, thereby facilitating rapid structure determination [2]. An automated procedure for rapidly determining NMR assignments given a homologous structure will similarly accelerate structure determination. Furthermore, even when the structure has already been determined by crystallography or homology modelling, NMR assignments are valuable to probe protein–protein interactions and protein–ligand binding (via chemical shift (CS) mapping or line-broadening). Previous SBA algorithms include CAP [3, 4], nuclear vector replacement (NVR) [5, 6] and MARS [7]. CAP is an RNA assignment algorithm which performs an exhaustive search over all permutations and which has an exponential time complexity. The approach of Hus et al. [4] applies maximum bipartite matching to one protein (ubiquitin) using three residual dipolar couplings (RDCs) per residue and triple resonance experiments (which correlate three different nuclei through covalent bonds and require double labelling of the protein). MARS [7] also uses triple resonance experiments and can incorporate RDCs as well, if they are available. IPASS [8] is a novel binary integer programming (BIP)-based assignment (not an SBA) method on perfect as well as noisy peak lists. It requires triple resonance experiments which are used for amino-acid typing and sequential connectivity information. A new integer linear programming-based method for SBA finds a solution using heuristics and previous solution computed by IPASS [9]. In contrast, NVR does not require triple resonance experiments and instead relies on data that requires less spectrometer time and is therefore less expensive to acquire; furthermore, it has a polynomial time complexity.
NVR [5, 6] is a molecular replacement-like [2] approach for SBA of resonances and sparse nuclear overhauser effects (NOEs). NVR computes assignments that correlate experimentally measured NMR data types such as HN–15N heteronuclear single quantum coherence spectroscopy (HSQC), HN–15N RDCs (in two media), 3D Nuclear Overhauser Enhancement Spectroscopy (NOESY)-15N-HSQC spectra (dNN’s) and amide exchange rates, to a given backbone structural model. However, in our tests, NVR performed poorly on one new protein and less well than desired on two other proteins. Furthermore, NVR requires a type of backbone RDC (NH RDC) in two aligning media and does not accept CH RDCs, limiting its usability.
In this paper, we develop NVR-BIP, a new tool in NVR framework that accepts a new form of input data and that works well on new proteins using BIP. Specifically, our contributions are as follows:
We enable NVR to use both NH and CH RDCs. This allows NVR to be applied to a wider range of proteins.
We develop a BIP formulation of the SBA problem.
We implement a system that solves the BIP formulation of the assignment problem using CPLEX.
We successfully demonstrate our algorithm on NVR’s test set as well as four additional proteins.
The outline of the rest of the paper is as follows: In Section 2, we give a brief outline of the NVR framework. In Section 3, we describe the BIP formulation. Data preparation is in Section 4. In Section 5, we discuss our implementation of the system using CPLEX to find the solution of the BIP problem and that also accepts CH and NH RDCs in one medium. We report our results in Section 6. We analyze the assignment accuracies using individual components of the scoring function in Section 7 and conclude in Section 8.
2. NVR FRAMEWORK
2.1. NVR-expectation-maximization
NVR-expectation-maximization (NVR-EM) [6] is a polynomial time algorithm that uses maximum bipartite matching in an EM framework to assign a protein using information from a structural homolog. One set of nodes in the bipartite graphs correspond to the peaks and the other corresponds to the residues. The edges carry a weight which corresponds to the probability of assigning that edge. These probabilities form the basis of NVR’s scoring function and are computed by using the difference in the backcomputed and observed NMR data, such as RDCs.
NVR-EM performs the assignments in two stages: In the first phase, the assignments are performed using only CSs. After five unambiguous assignments are made, the alignment tensor is computed and the RDCs are also added to the computation. The alignment tensor is updated as more assignments are made. NVR-EM has been successfully demonstrated on 3 target proteins with 21 protein templates.
2.2. Data used by NVR
NVR uses HN–15N HSQC, NOESY-15N-HSQC (yielding sparse dNN’s, observed between nearby pairs of amide protons), NH RDCs in two media (which provide global orientational restraints on NH amide bond vectors). NVR does not require triple resonance experiments unlike most other assignment programs, but relies on a few cheap key spectra.
RDCs provide global information on the orientation of internuclear vectors. For each RDC r, we have the following RDC equation [10, 11]:
| (1) |
Here Dmax is the dipolar interaction constant, v is the internuclear bond vector orientation relative to an arbitrary molecular frame and S is the 3 × 3 Saupe order matrix which describes the average substructure alignment in the weakly aligned anisotropic phase. When two sets of NH RDCs are available, S is computed for two media separately; whereas when NH and CH RDCs in the same medium are available, S is unique for both sets of RDCs.
NVR framework has been extended to also accept 15N TOCSY (for the sidechain CSs) and amide exchange HSQC (to identify, probabilistically, solvent-exposed amide protons) in [12]. This resulted in improved assignment accuracy for distant templates of target proteins. A recent study [13] used Normal ModeAnalysis to further augment the accuracy of NVR for distant structural templates.
2.3. NVR’s scoring functions
In NVR, each peak-residue pair has a corresponding probability of assignment. This probability is derived from seven sources of information. These correspond to:
CS probabilities as computed from Biological Magnetic Resonance Bank (BMRB) [14] statistics,
probabilities obtained from the difference between observed and predicted CSs (predictions made with SHIFTS [15]),
probabilities obtained from the difference between observed and predicted CSs (predictions made with SHIFTX [16]),
probabilities obtained from sidechain CSs measured by TOCSY,
probabilities obtained from hydrogen–deuterium exchange data,
probabilities obtained by RDCs in one medium and
probabilities obtained by another set of RDCs measured in a different medium.
For the first four items, the probabilities use a precomputed mean and standard deviation of the parameter values and assign a probability for the CSs using a normal distribution assumption. For the fifth item, the solvent exposedness data of the template protein atoms are used to give a binary score to the peak-residue assignment. The last two items also use a normal distribution assumption to assign a probability.
3. PROBLEM FORMULATION
SBA problem can be formulated as a BIP as follows.
Notation:
P set of peaks
A set of amino acids
sij score associated with assigning peak i to amino acid j
N number of peaks to be assigned (N ≤ |P|)
djl distance between amide protons of amino acids j and l
NOE(i) set of peaks that have an NOE with peak i
- NTH distance threshold for an NOE interaction
Decision variables:
Mathematical model:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
In the above model, the objective function (2) minimizes the total score associated with assigning NMR peaks to amino acids. Constraints (3) ensure that each amino acid is matched with at most one NMR peak and constraints (4) make sure that each NMR peak is assigned to at most one amino acid. Constraint (5) determines the number of NMR peaks to be assigned. In general, N is equal to the number of peaks. In this case, constraint (4) can be replaced with ‘=’ sign and constraint (5) can be removed. However, in rare cases, the problem may be infeasible. Thus, N in constraint (5) can be used as a control parameter to obtain a partial assignment.
Constraints (6) are the NOE constraints. For instance, if there is an NOE constraint between the 2nd and 17th NMR peaks, the distance between the protons corresponding to the amino acids that 2nd and 17th peaks are assigned to is expected to be less than a threshold (NTH). If we consider two amino acids, j and l, if the distance between the protons of the amino acids j and l is less than NTH, these two amino acids can be assigned to the 2nd and 17th peaks (or to 17th and 2nd peaks). If the distance between the protons of the amino acids j and l is more than NTH, then only one of these amino acids can be assigned to peaks 17 or 2. The distance between the protons of amino acids j and l is measured between amide protons of these two amino acids.
Constraints (6) are formulated for each NOE relationship and amino-acid pair. In practice, this creates a large number of constraints and the problem may be intractable for large proteins. To remedy this, we reformulated the NOE constraints as follows:
| (8) |
Each constraint in (8) puts together all peaks that have an NOE relationship with peak i, instead of considering each pair of peaks having an NOE relationship separately. This formulation is possible since only one peak can be assigned to an amino acid, as restricted in constraints (3). The new formulation reduces the number of NOE constraints significantly. Finally, constraints (7) define the decision variables as binary. Note that we further reduce the problem size by setting the values of xij variables equal to 0 if the corresponding probability is 0 according to one or more parts of the scoring function in Section 2.3.
The assignments are obtained by solving the above described mathematical model to optimality and determining the optimal xij values. In the first stage, the assignments are made without using the RDCs. An alignment tensor is obtained from these assignments, and then RDC’s are added to the scoring function to determine the values of the xij variables. The determination of this alignment tensor (which involves the recomputation of the backcomputed RDCs) is continued until the assignment accuracies converge and the final assignments are obtained.
4. DATA PREPARATION
We tested our approach on NVR’s test set [6] (consisting of ubiquitin, streptoccal protein G and lysozyme), as well as four additional proteins: human Set2-Rpb1 interacting domain (hSRI), the FF Domain 2 of human transcription elongation factor CA150 (RNA polymerase II C-terminal domain interacting protein) (ff2), the zinc finger domain of the human DNA Y-polymerase Eta (pol η) and B1 domain of streptococcal protein G (GB1). The CSs, RDCs and NOEs for these proteins were collected by Dr. P. Zhou at Duke University except for GB1 for which RDCs were not collected. Since the GB1 structure in the PDB (ID: 3GB1) does not have CH RDCs, we used the CH and NH RDCs from GB3 (PDB ID: 1P7E) which is homologous to the structure of GB1 (The backbone RMSD between 1P7E and 3GB1 is 0.5Å). We obtained CH RDCs for ubiquitin from its .mr file in the PDB (1D3Z). We simulated the TOCSY data for ff2 by predicting its CSs with SHIFTX [16]. We parsed these CSs to extract the sidechain proton CSs. We extracted the sidechain proton CSs for hSRI and pol η from their BMRB [14] entry (bmrb #6834 and #15160, respectively). For GB1, the collected CS data contains the sidechain proton CSs from which we assembled the TOCSY data. We simulated the HD-exchange data from the .mr file for the PDB entry 2A7O for hSRI and PDB entry 2I5O for pol η, following the procedure in [6]. We did not simulate the HD-exchange data for ff2 since the PDB file we used as a template (2E71) does not have a corresponding .mr file. We used the HD-exchange data from [6] for GB1. We extracted the NH- and CH-bond vector coordinates for ubiquitin from the corresponding PDB files listed in Table 3, for hSRI from pdb ID 2A7O, for ff2 from pdb ID 2E71, for pol η from pdb ID 2I5O and for GB1 from pdb ID 3GB1. We extracted the backbone NOEs (NOEs between Hα and amide protons) for hSRI, ff2, ubiquitin, pol η and GB1 from the list of assigned NOEs by HANA [17]. This amounts to 156, 105, 155, 78 and 138 NOEs, respectively. The summary of the RDC data we used is given in Table 1. Table 2 contains information on the HSQC data. The remaining data is from [6].
TABLE 3.
Results on ubiquitin.
| PDB ID | Accuracy without RDCs (%) | Accuracy with RDCs (%) | Accuracy with 4 RDCs/residue (%) |
|---|---|---|---|
| 1UBI | 87 | 97a 100b |
100 |
| 1UBQ | 87 | 97a 100b |
100 |
| 1G6J | 87 | 97a 93b |
96 |
| 1UD7 | 81 | 97a 97b |
97 |
| 1AAR | 79 | 97a 100b |
97 |
With NH RDCs in two media.
With NH and CH RDCs.
TABLE 1.
The number of observed and missing RDCs. For the remaining proteins, we use the same RDC data as in [6].
| Protein | RDCs
|
|||
|---|---|---|---|---|
| Observed #
|
Missing # (%)
|
|||
| NH RDCs |
CH RDCs |
NH RDCs |
CH RDCs |
|
| Ubiquitin | 63 | 57 | 9 (13%) | 15 (21%) |
| hSRI | 60 | 56 | 36 (38%) | 40 (42%) |
| ff2 | 51 | 50 | 29 (36%) | 30 (38%) |
| pol η | 24 | 19 | 7 (23%) | 12 (39%) |
| GB1 | 42 | 44 | 13 (24%) | 11 (20%) |
TABLE 2.
The number of observed and missing HSQC peaks. For the remaining proteins, we use the same data HSQC data as in [6].
| Protein | HSQC peaks
|
|
|---|---|---|
| Observed # | Missing # (%) | |
| ff2 | 55 | 25 (31) |
| hSRI | 95 | 1 (1) |
| pol η | 31 | 0 (0) |
| GB1 | 54 | 1 (2) |
5. IMPLEMENTATION
In NVR framework, only NH RDCs are used and these must be obtained in two separate media. Extending NVR to accept CH and NH RDCs in one medium requires only a single alignment tensor, instead of two separate ones. There is also a simple scaling of the CH RDCs to take into account the differences in the gyromagnetic ratios and the internuclear bond vector lengths. Changing one of the NH RDC components of the scoring function into a CH RDC is then straightforward.
The parameters of the algorithm were set differently for three proteins. For 1AAR, pol η and GB1, the NOE distance threshold was set 0.07, 0.20 and 1.5Å higher; in addition, for pol η the CS maximum deviation from the predicted value by SHIFTX is multiplied by a coefficient of 3.90, and similarly for GB1 the TOCSY probability thresholding is commented out. These changes were done for reporting the results with both NVR-EM and NVR-BIP.
The system that we implemented to solve the BIP problem is ran on Matlab and on IBM ILOG OPL Development Studio v.5.5 with mathematical programming engine CPLEX v.11.0. ILOG CPLEX is a state-of-the-art optimization software that can solve large-scale linear, integer and quadratic programming problems. We use NVR-EM’s source code which is written in Matlab and which we enabled to accept CH RDCs. Using NVR-EM’s source code, we output a scoring matrix which includes the sum of the minus logarithm of the probability of assignments according to each of the first five components of NVR’s scoring function in Section 2.3. We output a very large score for a peak-residue pair if the probability is 0 according to at least one component of the scoring function. If RDCs are also included in the scoring function computation, the corresponding alignment tensor is computed using the assignments obtained from an earlier run for that protein. This alignment tensor is used to compute the RDC scoring matrices (constraints (6) and (7) in Section 2.3) which are also added to the overall scoring matrix. In addition to the scoring matrix, we output a matrix that contains the binary distances between pairs of protons, which is 1 if the corresponding pair of protons is within a threshold distance, and 0 otherwise. We vary the distance threshold for an NOE relationship so that it is smaller for smaller proteins, and large for larger ones. We finally output the list of NOE constraints. These three files provide the necessary data to formulate the BIP problem and find the optimal assignments. We repeat the computation with the RDCs until the assignments converge. It takes maximum of four iterations for the assignments to converge. The solution time of CPLEX in each iteration varies from a few seconds to about 30 min depending on the problem size and structure on an Intel Pentium T2130 1.86 GHz processor with 1 GB of RAM.
In order to find near-optimal assignments, we added a constraint that the score should be above a threshold into ILOG CPLEX. However, we found that generating near-optimal assignments using this method could be very time-consuming as CPLEX reduces the gap between the current score and the optimal to a low value and then continues the search in order to guarantee the optimal solution according to tolerance limits. One solution we implemented is to put a time limit, in which case the returned solutions may not reflect the best k solutions. An alternative method to generate near-optimal assignments faster is Monte Carlo simulation which starts from a given assignment and explores its neighborhood by switching the assignment of the peaks or by assigning a random peak to an unassigned residue, while at each step making sure that the NOE constraints are satisfied and an assignment deemed impossible by one of the scoring sources is not made. We ran the simulation at different (constant) ‘temperatures’ in order to explore the neighborhood of the optimal solution.
6. RESULTS
Our results are given in Tables 3, 4, 5, and 6. The assignment accuracy without the RDCs is provided in the second column and the accuracy with the RDCs is provided in the third column. The addition of RDCs improved the assignment accuracy by 3–26%. We obtained perfect assignments for three proteins (1GB1, 2GB1 and pol η) even without RDCs. Our accuracies are comparable to the accuracies in [6]. However, our assignment accuracies are better than or same as the accuracies obtained by NVR-EM for hSRI, ff2, pol η and GB1, for which NVR-EM results in 16, 73, 100 and 87% assignment accuracy, whereas our implementation results in 89, 93, 100 and 100% assignment accuracy, respectively. We tested both the combination of CH and NH RDCs and only NH RDCs in two different media for ubiquitin (Table 3). Using CH RDCs instead of NH RDCs gave similar results. We also tested combining all four RDCs for ubiquitin in Table 3. Note that 1AAR is an additional template not tested in [6] and for which NVR-EM resulted in 87% assignment accuracy whereas our approach resulted in 97–100% accuracy depending on the set of used RDCs. Note also that for GB1 we have two sets of data (except the HD-exchange data) and the results are very similar.
TABLE 4.
Results on streptococcal protein G.
| PDB ID | Accuracy without RDCs (%) | Accuracy with RDCs (%) |
|---|---|---|
| 1GB1 | 100 | 100 |
| 2GB1 | 100 | 100 |
| 1PGB | 96 | 100 |
TABLE 5.
Results on lysozyme.
| PDB ID | Accuracy without RDCs (%) | Accuracy with RDCs (%) |
|---|---|---|
| 193L | 78 | 100 |
| 1AKI | 78 | 98 |
| 1AZF | 74 | 94 |
| 1BGI | 75 | 97 |
| 1H87 | 77 | 100 |
| 1LSC | 74 | 100 |
| 1LSE | 75 | 98 |
| 1LYZ | 79 | 82a |
| 2LYZ | 75 | 91 |
| 3LYZ | 79 | 90 |
| 4LYZ | 75 | 91 |
| 5LYZ | 75 | 91 |
| 6LYZ | 75 | 96 |
with only one set of RDCs.
TABLE 6.
Results on ff2, hSRI, pol η and GB1.
| Protein name | Accuracy without RDCs (%) | Accuracy with RDCs (%) |
|---|---|---|
| ff2 | 85 | 93 |
| hSRI | 73 | 89 |
| pol η | 100 | 100 |
| GB1 | 96 | 100 |
In Table 5, with 1LYZ as a template, the incorporation of both sets of (NH) RDCs resulted in an infeasible solution, i.e. there is no assignment that satisfies all constraints. This is due to one NH RDC for the residue R14 whose backcomputed RDC is far away from the experimental RDC and the corresponding probability is 0. This makes it impossible to assign the corresponding peak to the residue R14 and causes an infeasibility. Therefore, we assigned 1LYZ using only one set of NH RDCs.
We also studied how close the score corresponding to 100% correct assignment is to the optimal assignment’s score. For the tested proteins which did not result in 100% correct assignments, the 100% correct assignment score was within 5% of the optimal assignment score for 12 cases, between 5 and 10% for two cases and between 10 and 21% for three cases. We also found the best near-optimal assignments for four representative proteins: 1UBI (with NH RDCs), hSRI, ff2 and 1AZF. We found the 100% correct assignment for 1UBI as the seventh best solution. For the other three proteins, the 100% correct assignment was not in the top-10 best solutions.
We then looked at reducing N in the problem formulation and assigning only a subset of the peaks. We found that reducing the number of peaks to be assigned in general lowers the assignment accuracy.
7. CONTRIBUTION OF EACH COMPONENT OF THE SCORING FUNCTION TO THE ASSIGNMENTS
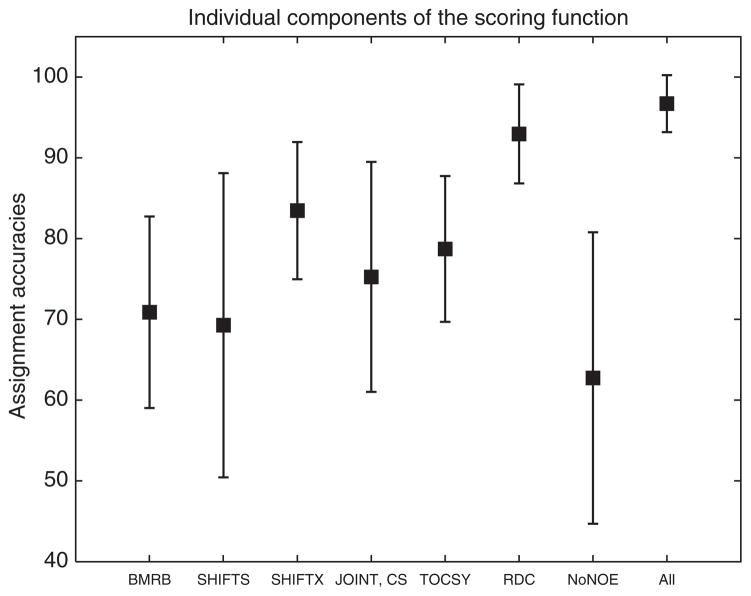
We studied the contribution of each of the components of the scoring function to the assigments. These components are described in Section 2.3 and are used to derive the scoring matrix. We solved the assignments using each of the components of the scoring function combined with NOE constraints. We also considered the effect of using the joint scoring function due to CSs or RDCs, and not using the NOE constraints at all in the assignments. We did this study for the proteins in our data set. The results are in Fig. 1. The results with RDCs were obtained assuming a perfect alignment tensor.
FIGURE 1.
Assignment accuracies with each component of the scoring function separately and NOEs.
It can be seen from Fig. 1 that on average the highest assignment accuracies using an individual scoring function component and NOE constraints are obtained with RDCs, followed by CSs as predicted by SHIFTX, then TOCSY. Joint CS probability is followed by BMRB and CSs as predicted by SHIFTS. The NOE constraints boosted the assignments by 34% on average when all of the terms of the scoring function are present.
8. CONCLUSION AND FUTURE WORK
In this paper, we used the data types and scoring function in NVR framework to develop NVR-BIP, an SBA scheme which returns the resonance assignments corresponding to the optimum of the scoring function subject to the NOE constraints. We also extended NVR’s input data types to accept CH RDCs. Our results are demonstrated on NVR’s test set as well as on four additional proteins. Our assignment accuracies are comparable on NVR’s test set. However, our approach reached 89–100% assignment accuracy on four novel proteins, whereas the performance of NVR-EM was below the desired levels. This reveals that NVR-EM may perform poorly on new proteins and NVR-BIP may remedy this. The reason why NVR-EM may perform poorly is that it includes many built-in constants and involves an assignment algorithm which may not be generalizable. Even though NVR-BIP also has builtin constants, they are fewer and the algorithm consists of a general optimization approach. Since our approach is very simple to implement and our preliminary results are promising, we plan to extend our tests on more proteins in the future. We also plan to reduce the number of built-in constants in NVR-BIP.
A nice feature of this work is that our formulation is independent of the scoring function. As future work, we plan to test other scoring functions such as MARS [18, 19]. One other aspect of this work is that we add each component of the scoring function linearly; this allowed us to study the information content of individual components by testing our algorithm with each of these components separately in Section 7. It is also the case that these components are dependent on each other, such as the probabilities corresponding to CSs obtained using SHIFTS [15] and SHIFTX [16]. As future work, we plan to study optimal ways of combining these data sources, rather than by using simple addition.
One can obtain partial assignments by setting N < |P| in constraint (5) in Section 3. This allows partially assigning a protein whose complete assignment is infeasible due to unsatisfied constraints. However, we found that when a feasible complete assignment exists partial assignments have in general lower assignment accuracy compared with assigning all the peaks. The reason is that as the number of peaks to be assigned is reduced, the NOE constraints become invalidated. For instance, in Section 3, if peak i is not assigned to any residue, constraint (6) is always satisfied for peak k. Therefore, it seems preferable to assign all the peaks when a solution exists. However, in the case where there are extra peaks, assigning a subset of them could improve the assignment accuracy.
One area of future work is to tolerate errors in the data to avoid infeasibilities and to make the program more robust. The reason why the problem is infeasible in certain cases is because we do not allow the assignment of a peak to a residue if any of the data types sets a probability of 0 for that assignment. This helps reduce the number of variables and makes the problem easier to solve. However, if the template is too distant from the target protein, or due to noise, if there is a component of the scoring function which assigns a probability of 0 to a particular assignment, we may want to still allow the corresponding peak/residue assignment. For instance, as discussed in Section 6, the problem is intractable for 1LYZ with both sets of RDCs due to only one noisy RDC value. Similarly, with a distant template or due to noise, a couple of protons which have an NOE between them may be more distant than our distance threshold. A possible solution is to use Bayesian statistics to update the assignment probability with new evidence from the various components of the scoring function, rather than assigning it to 0 if at least one of the components returns 0.
A way to solve the larger problems which CPLEX cannot solve to optimality is to use relaxation/decomposition or metaheuristic approaches such as ant colony optimization or tabu search. While these approaches do not guarantee optimality and usually provide approximate solutions, nevertheless the assignments obtained could be valuable for an otherwise intractable problem.
Our approach handles missing peaks. In fact, as shown in Tables 1 and 2, our approach works with up to 42% missing data. As future work, we plan to extend our approach to handle extra peaks as well. To handle extra peaks and to achieve robustness against noise, one possibility is to use Normal Mode Analysis to obtain an ensemble of protein structures and to combine the assignments for each of these structures using a voting scheme as in [13].
Another area of future work is to incorporate the intensity information of the NOEs into the computation to improve the assignments, as well as to take into account ambiguous NOEs.
Our approach is complete, in the sense that it can return all assignments consistent with the constraints and that are within a delta score of the optimum assignment. Returning near-optimal assignments can be accomplished by iteratively solving the BIP problem with the additional constraint that imposes a lower bound on the objective function value or using Monte Carlo simulation as described in Section 5. The lower bound ensures finding a new assignment with a higher score than the one previously obtained. On the other hand, Monte Carlo simulation does not guarantee returning all near-optimal solutions in the order of increasing score, but is nevertheless useful to quickly explore the neighborhood of the optimal solution. As future work, we plan to investigate the ensemble of near-optimal assignments using an algorithm such as in [20], and also consider using a pair of scoring functions and find those assignments that have the minimum combination of scores according to these functions.
Note that it is possible to determine the alignment tensor using other methods such as a grid search instead of by following a two-stage strategy. However, it has been shown [18] that the alignment tensor obtained with assignments of as low as 50% accuracy has a very similar orientation as the correct alignment tensor.
While doing our experiments with NVR-BIP, we became aware of another approach for resonance assignments (not an SBA approach) using BIP and IPASS [8]. Our approach is complementary to IPASS by the data types and the structural template that we use. For instance, IPASS does not use RDCs. We thus study the amount of information available in few key spectra. There is also a more recent integer linear programming approach for SBA based on IPASS that uses IPASS to bootstrap the assignments and does not guarantee returning the global optimum of the scoring function [9].
It must be mentioned that using CH and NH RDCs in the NVR framework requires us to establish correspondence between CH and NH RDCs, to determine they are in the same residue. This can be achieved using triple resonance experiments [18]. However, it is rather straightforward to obtain assignments with triple resonance data alone using one of many tools that are available, such as MARS [7]. We propose that NVR with CH RDCs is nevertheless a valuable tool that allows to cross-check the assignments obtained using triple-resonance data. Our contribution with CH RDCs is similar to [4] since both approaches require triple resonance experiments, but do not use sequential connectivity information. However, our approach is different from [4] since the assignment algorithm based on maximum bipartite matching proposed in [6] is not successful with NVR’s data as shown in [6]. Furthermore, our approach is tested on multiple proteins. Finally, some of our examples are based solely on NH RDCs, for which triple resonance experiments are not required, offering NVR a distinct advantage in terms of data acquisition time and expense over other assignment programs.
Acknowledgments
We thank Dr. Pei Zhou for providing us with data for novel proteins and Dr. Hakan Erdoğan, Mr. Jianyang (Michael) Zeng and Mr. Chittaranjan Tripathy for useful comments and discussion.
FUNDING
This work was supported by the National Institutes of Health [R01-GM-065982-07 to B.R.D.] and the Scientific and Technical Research Council of Turkey research support program (program code 1001) [109E027 to M.S.A.].
Footnotes
AVAILABILITY
The NVR-BIP software is available upon request and is distributed open source under the GNU General Public License.
References
- 1.Wang L, Mettu R, Donald B. A polynomial-time algorithm for de novo protein backbone structure determination from NMR data. J Comput Biol. 2006;13:1276–1288. doi: 10.1089/cmb.2006.13.1267. [DOI] [PubMed] [Google Scholar]
- 2.Rossman M, Blow D. The detection of subunits within the crystallographic asymmetric unit. Acta Crystallogr (D) 1962;15:24–31. [Google Scholar]
- 3.Al-Hashimi H, Gorin A, Majumdar A, Gosser Y, Patel D. Towards structural genomics of RNA: Rapid NMR resonance assignment and simultaneous RNA tertiary structure determination using residual dipolar couplings. J Mol Biol. 2002;318:637–649. doi: 10.1016/S0022-2836(02)00160-2. [DOI] [PubMed] [Google Scholar]
- 4.Hus J, Prompers J, Brüschweiler R. Assignment strategy for proteins of known structure. J Magn Reson. 2002;157:119–125. doi: 10.1006/jmre.2002.2569. [DOI] [PubMed] [Google Scholar]
- 5.Langmead C, Yan A, Lilien R, Wang L, Donald B. A Polynomial-Time Nuclear Vector Replacement Algorithm for Automated NMR Resonance Assignments. Proc. the 7th Annual Int. Conf. Research in Computational Molecular Biology (RECOMB); Berlin, Germany. April 10–13; New York, NY: ACM Pres; 2003. pp. 176–187. [DOI] [PubMed] [Google Scholar]; J Comp Bio. 2004;11:277–298. [Google Scholar]
- 6.Langmead C, Donald B. An expectation/maximization nuclear vector replacement algorithm for automated NMR resonance assignments. J Biomol NMR. 2004;29:111–138. doi: 10.1023/B:JNMR.0000019247.89110.e6. [DOI] [PubMed] [Google Scholar]
- 7.Jung Y, Zweckstetter M. Mars—robust automatic backbone assignment of proteins. J Biomol NMR. 2004;30:11–23. doi: 10.1023/B:JNMR.0000042954.99056.ad. [DOI] [PubMed] [Google Scholar]
- 8.Alipanahi B, Gao X, Karakoc E, Balbach F, Donaldson L, Arrowsmith C, Li M. Technical Report CS-2009-16. University of Waterloo; 2009. IPASS: Error Tolerant NMR Backbone ResonanceAssignment by Linear Programming. [Google Scholar]
- 9.Jang R, Gao X, Li M. Technical Report CS-2009-32. University of Waterloo; 2009. Integer Programming Model for Automated Structure-Based NMR Assignment. [Google Scholar]
- 10.Tolman JR, Flanagan JM, Kennedy MA, Prestegard JH. Nuclear magnetic dipole interactions in field-oriented proteins: Information for structure determination in solution. Proc Natl Acad Sci USA. 1995;92:9279–9283. doi: 10.1073/pnas.92.20.9279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tjandra N, Bax A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science. 1997;278:1111–1114. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- 12.Langmead C, Donald B. High-Throughput 3D Structural Homology Detection via NMR Resonance Assignment. Proc. IEEE Computational Systems Bioinformatics Conf; Stanford, CA. August; London: Imperial College Press; 2004. pp. 278–89. [PubMed] [Google Scholar]
- 13.Apaydin MS, Conitzer V, Donald BR. Structure-based protein NMR assignments using native structural ensembles. J Biomol NMR. 2008;40:263–276. doi: 10.1007/s10858-008-9230-x. [DOI] [PubMed] [Google Scholar]
- 14.Seavey B, Farr E, Westler W, Markley J. J Biomol NMR. 1991;1:217–236. doi: 10.1007/BF01875516. [DOI] [PubMed] [Google Scholar]
- 15.Xu XP, Case DA. Automated prediction of 15N, 13Cα, 13Cβ and 13C′ chemical shifts in proteins using a density functional database. J Biomol NMR. 2001;21:321–333. doi: 10.1023/a:1013324104681. [DOI] [PubMed] [Google Scholar]
- 16.Neal S, Nip AM, Zhang H, Wishart DS. Rapid and accurate calculation of protein 1H, 13C and 15N chemical shifts. J Biomol NMR. 2003;26:215–240. doi: 10.1023/a:1023812930288. [DOI] [PubMed] [Google Scholar]
- 17.Zeng JM, Tripathy C, Zhou P, Donald BR. A Hausdorff-Based NOE Assignment Algorithm Using Protein Backbone Determined from Residual Dipolar Couplings and Rotamer Patterns. The Computational Systems Bioinformatics Conf. (CSB); Stanford, CA. August 26–29; London: Imperial College Press; 2008. pp. 169–181. [PMC free article] [PubMed] [Google Scholar]
- 18.Jung Y, Zweckstetter M. Backbone assignment of proteins with known structure using residual dipolar couplings. J Biomol NMR. 2004;30:25–35. doi: 10.1023/B:JNMR.0000042955.14647.77. [DOI] [PubMed] [Google Scholar]
- 19.Meiler J, Baker D. Rapid protein fold determination using unassigned NMR data. Proc Natl Acad Sci USA. 2003;100:15404–15409. doi: 10.1073/pnas.2434121100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Danna E, Fenelon M, Gu Z, Wunderling R. Generating multiple solutions for mixed integer programming problems. Integer Program Comb Optim. 2007;4513:280–294. [Google Scholar]