Sensitivity analysis for direct and indirect effects in the presence of exposure-induced mediator-outcome confounders

Abstract

Questions of mediation are often of interest in reasoning about mechanisms, and methods have been developed to address these questions. However, these methods make strong assumptions about the absence of confounding. Even if exposure is randomized, there may be mediator-outcome confounding variables. Inference about direct and indirect effects is particularly challenging if these mediator-outcome confounders are affected by the exposure because in this case these effects are not identified irrespective of whether data is available on these exposure-induced mediator-outcome confounders. In this paper, we provide a sensitivity analysis technique for natural direct and indirect effects that is applicable even if there are mediator-outcome confounders affected by the exposure. We give techniques for both the difference and risk ratio scales and compare the technique to other possible approaches.

1. Introduction

It is often of interest to investigators in the health sciences to examine the extent to which the effect of an exposure on some outcome is mediated by an intermediate variable. The causal inference literature on mediation has been important in extending traditional mediation analysis approaches in the social sciences to settings with interactions and nonlinearities and in clarifying the no-unmeasured-confounding assumptions underlying such mediation analyses. Progress was made by relying on counterfactual-based definitions of direct and indirect effects referred to as “natural direct and indirect effects”. However, Avin et al. (2005; cf. Pearl, 2001) have shown that if the exposure affects a variable that in turn confounds the relationship between the mediator and the outcome, then natural direct and indirect effects are not identified from the data, irrespective of whether data was collected on the post-exposure confounder or not. Natural direct and indirect effects are still theoretically appealing but they cannot be estimated. This essentially has restricted the contemporary methods for causal mediation analysis to settings in which the mediator occurs shortly after the exposure in order to minimize the possibility of such exposure-induced mediator-outcome confounding (VanderWeele and Vansteelandt, 2009). This is a severe limitation. It is not one that is possible to address directly. However, one might still hope to use sensitivity analysis to examine a range of plausible estimates for natural direct and indirect effects even though these effects are not identified. Here, we develop such a sensitivity analysis technique.

Existing work on this problem includes the derivation of bounds for natural direct and indirect effects (Sjölander, 2009; Kaufman et al., 2009; Robins and Richardson, 2011). Bounds, however, are often too wide to be very informative and effectively consider extreme scenarios. Some concurrent work by other authors (Tchetgen Tchetgen and Shpitser, 2012; Imai et al., 2012; Vansteelandt and VanderWeele, 2012) likewise develop a sensitivity analysis technique for direct and indirect effects that is applicable in the presence of an exposure-induced mediator-outcome confounder. Different techniques will likely be advantageous in different settings and later in the paper we will compare the techniques developed here with other techniques that have been proposed. In a number of settings, our technique provides parameters that are easier to specify in practice and are applicable to more general settings. Prior work has shown that sensitivity analysis techniques for natural direct and indirect effects can be very informative in settings without exposure-induced mediator-outcome confounding (VanderWeele, 2010; VanderWeele and Hernández-Diaz, 2011; Ananth and VanderWeele, 2011). We believe the extension of such techniques to the exposure-induced confounding setting will likely shed further insight on an even wider range of settings.

2. Direct and Indirect Effects: Notation, Definitions and Framework

In this section, we introduce the notation, definitions and typical assumptions employed in the causal mediation analysis literature and we provide a brief overview of a regression-based approach that can be used to estimate direct and indirect effects when they are identified.

2.1. Notation and definitions

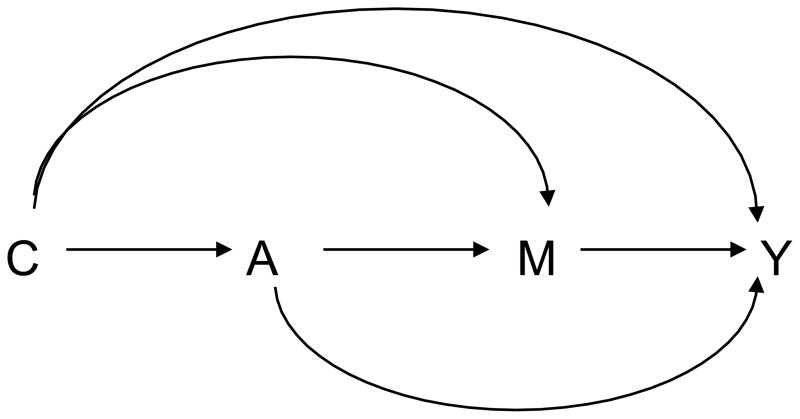
Let A denote the exposure received by an individual, let Y denote some post-exposure outcome, and let M denote some post-exposure intermediate variable that may serve as a mediator for the exposure-outcome relationship. For example, in an application we will consider later, for the treatment of depression, the exposure A might be extensive collaborated care management for depression, the outcome Y might be depression scores during follow-up, and the mediator M might be adherance to the use of an anti-depressant. Let C denote some set of confounding variables that may affect the exposure, mediator and/or outcome. We will assume that the subjects are sampled from a population and thus treat A, M, Y and C as random variables. The relationships between A, M, Y and C are given in Figure 1.

Fig. 1.

Exposure A, mediator M, outcome Y, baseline covariates C.

We now consider counterfactuals or potential outcomes under possible interventions on the variables (Rubin, 1974, 1978). Let Y_a denote a subject’s outcome if exposure A were set, possibly contrary to fact, to a. In the context of mediation, there will also be potential outcomes for the intermediate variable. Let M_a denote a subject’s counterfactual value of the intermediate M if exposure A were set to the value a. Finally, let Y_am denote a subject’s counterfactual value for Y if A were set to a and M were set to m. Some additional technical conditions referred to as consistency and composition are also needed to relate the observed data to counterfactual quantities. The consistency assumption in this context is that when A = a, the counterfactual outcomes Y_a and M_a are, respectively, equal to the observed outcomes Y and M, and that when A = a and M = m, the counterfactual outcome Y_am is equal to Y. The composition assumption is that Y_a = Y_aMa. Further discussion of these assumptions in the context of mediation is given elsewhere (VanderWeele and Vansteelandt, 2009).

Pearl (2001) gave the following definitions for controlled and natural direct and indirect effects based on interventions on the mediator M. Robins and Greenland (1992) provided related definitions. The controlled direct effect of exposure A on outcome Y comparing A = a with A = a^* and setting M to m is defined by Y_am–Y_a^*m and measures the effect of A on Y not mediated through M, i.e. the effect of A on Y after intervening to fix the mediator to some value m. For a binary exposure this would be Y_1m–Y_0m. In the example above, with m = 0, the controlled direct effect Y₁₀–Y₀₀ would indicate whether the collaborated care managed would have any effect on depression symptom outcomes if there were no use of antidepressants. It would capture the effect of the collaborative care management not through antidepressant use. In contrast to controlled direct effects, natural direct effects fix the intermediate variable for each individual to the level it naturally would have been under e.g. the absence of exposure. The natural direct effect of exposure A on outcome Y comparing A = a with A = a^* intervening to set M to what it would have been if exposure had been A = a^* is formally defined by Y_aMa^*–Y_a^*Ma^*. Essentially, the natural direct effect assumes that the intermediate M is set to M_a^*, the level it would have been for each individual had exposure been a^*, and then compares the direct effect of exposure (with the intermediate set to this level M_a^*). Thus, in the example above, the natural direct effect, Y_1M0–Y_0M0 would compare having versus not having collaborated care management with the use of antidepressant in both scenarios fixed to the level it would have been in the absence of collaborated care management. Corresponding to a natural direct effect is a natural indirect effect. The natural indirect effect comparing A = a with A = a^* and intervening to set exposure A to a is formally defined by Y_aMa–Y_aMa^*. The natural indirect effect assumes that exposure is set to some level A = a and then compares what would have happened if the mediator were set to what it would have been if exposure had been a versus what would have happened if the mediator were set to what it would have been if exposure had been a^*. In the example above, the natural indirect effect, Y_1M1–Y_1M0, would compare the effect of having collaborative care management with antidepressant use set to the level it would have been with versus without collaborative care management.

A total effect can be decomposed into a natural direct and indirect effect. For example, with a binary exposure, the total effect Y₁–Y₀ can be written as Y₁–Y₀ = Y_1M1–Y_0M0 =(Y_1M1–Y_1M0)+(Y_1M0–Y_0M0), where the first expression in the sum is the indirect or mediated effect and the second expression is the natural direct effect. An important difference between controlled and natural direct effects is that the effect decomposition above works for natural direct and indirect effects but not for controlled direct effects. If one subtracts a controlled direct effect from a total effect, the resulting quantity cannot in general be interpreted as an indirect effect unless there is no interaction at the individual level between the effects of the exposure and the mediator on the outcome (Robins, 2003; Kaufman et al., 2004) in which case controlled direct effects and natural direct effects are equivalent since Y_am–Y_a^*m will be constant for all values of m and thus Y_am–Y_a^*m = Y_aMa^*–Y_a^*Ma^*. In practice individual effects are not estimable and we therefore focus on population effects conditional on covariates C, which are defined as E(Y₁–Y₀|c), E(Y_1m–Y_0m|c), E(Y_1M0–Y_0M0|c), and E(Y_1M1–Y_1M0|c) for the total, controlled direct, natural direct and natural indirect effects respectively.

2.2. Assumptions for identification

The identification of direct and indirect effects requires various no-unmeasured confounding assumptions. It is well understood that, in order to estimate causal effects in observational studies, data is needed on a set C that contains the variables that confound the relationship between the exposure A and the outcome Y. Formally, we will use the notation A ⫫ B|C to denote that A is independent of B conditional on C. To identify total effects, it is generally assumed that, conditional on some set of measured covariates C, the effect of exposure A on outcome Y is unconfounded given C; in counterfactual notation, this is Y_a ⫫ A|C. In practice, a researcher will attempt to collect data on a sufficiently rich set of covariates C to make the assumption plausible.

For controlled direct effects, one needs not just one no unmeasured confounding condition but two. Controlled direct effects are identified if the set of baseline covariates C suffices to control for confounding of not only the exposure-outcome relationship but also the mediator-outcome relationship. In counterfactual notation, we require that for all a and m (Robins and Greenland, 1992; Pearl, 2001):

$$Y_{am}⫫A\mid C$$ (1)

$$Y_{am}⫫M\mid \{A,C\}.$$ (2)

Assumption (1) can be interpreted as: conditional on C, there is no unmeasured confounding for the exposure-outcome relationship. Assumption (2) can be interpreted as: conditional on {A, C} there is no unmeasured confounding for the mediator-outcome relationship. If assumptions (1) and (2) hold, then average controlled direct effects conditional on C are identified and given by

$$E[Y_{am}\_Y_{a^{\ast }m}\mid c]=E[Y\mid a,m,c]-E[Y\mid a^{\ast },m,c]$$

When attempts are made to estimate direct effects by including the mediator in a regression of the outcome on the exposure, it is often forgotten that one must control not only those variables which confound the exposure-outcome relationship but also those which confound the mediator-outcome relationship. When control is not made for confounders of the mediator-outcome relationship, this leads to biased estimates for the controlled direct effect (Judd and Kenny, 1981; Robins and Greenland, 1992; Cole and Hernán, 2002). Judd and Kenny (1981) had pointed out early on that assumption (2) requiring control for mediator-outcome confounders was needed for direct and indirect effects but unfortunately the point was not noted by Baron and Kenny (1986) and much of the subsequent literature, following Baron and Kenny (1986), has ignored this point.

Natural direct and indirect effects will be identified if four no-unmeasured confounding assumptions hold. Natural direct and indirect effects will be identified if, in addition to assumptions (1) and (2), the following two assumptions hold, that for all a, a^* and m (Pearl, 2001):

$$M_a⫫A\mid C$$ (3)

$$Y_{am}⫫M_{a^{\ast }}\mid C.$$ (4)

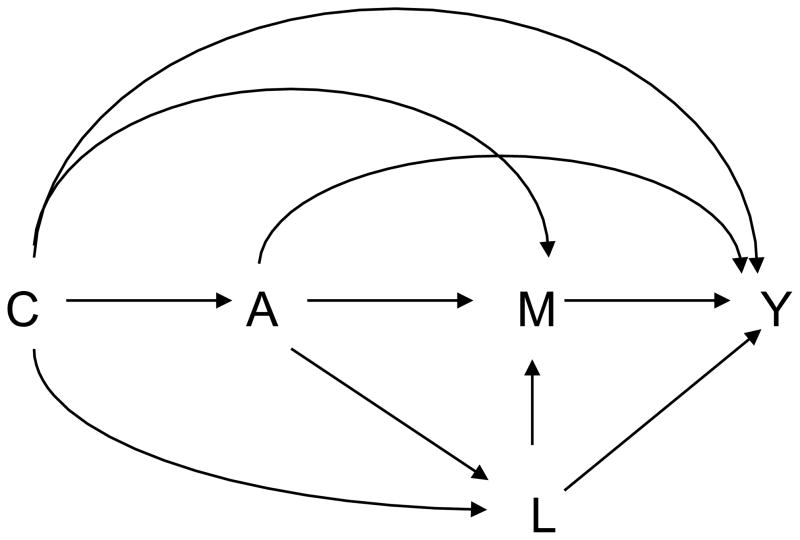
Assumption (3) can be interpreted as: conditional on C, there is no unmeasured confounding of the exposure-mediator relationship. On a causal diagram interpreted as a set of non-parametric structural equations (Pearl, 2009), if assumption (2) holds, then assumption (4) will hold if there is no effect L of exposure A that itself affects both M and Y, i.e. no effects of exposure A that confound the mediator-outcome relationship. If, however, there is an effect of the exposure that confounds the mediator-outcome relationship as in Figure 2, then natural direct and indirect effects will not in general be identified irrespective of whether data is available on L or not (Avin et al., 2005), except under strong assumptions about no interaction between the exposure and the mediator at the individual level (Robins, 2003).

Fig. 2.

Mediation with a mediator-outcome confounder, L, that is affected by the exposure.

In Section 3, we will develop sensitivity analysis techniques for cases in which there is a mediator-outcome confounder L that is affected by the exposure.

If assumptions (1)–(4) hold, then the average natural direct effect conditional on C is identified and is given by (Pearl, 2001):

$$E[Y_{{aM}_{a^{\ast }}}-Y_{a^{\ast }{M}_{a^{\ast }}}\mid c]={\sum }_m\{E[Y\mid a,m,c]-E[Y\mid a^{\ast },m,c]\}P(m\mid a^{\ast },c)$$

and the average natural indirect effect conditional on C is identified and is given by

$$E[Y_{{aM}_a}-Y_{{aM}_{a^{\ast }}}\mid c]={\sum }_{m}E[Y\mid a,m,c]\{P(m\mid a,c)-P(m\mid a^{\ast },c)\}.$$

Note that if exposure A is randomized then assumptions (1) and (3) will hold automatically, but assumptions (2) and (4) may not.

2.3 Overview of a regression-based approach

VanderWeele and Vansteelandt (2009) recently showed how the notions of direct and indirect effects from the causal inference literature presented above could be used to extend the regression approach of Baron and Kenny (1986) to settings in which there were interactions between A and M. In particular, if assumptions (1)–(4) hold and if Y and M are continuous and the following regression models for Y and M are correctly specified:

$$\begin{array}{l}E[Y\mid a,m,c]={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\theta }_{3}am+{\theta }_4^{\prime }c\\ E[M\mid a,c]={\beta }_0+{\beta }_{1}a+{\beta }_2^{\prime }c\end{array}$$

then the average controlled direct effect and the average natural direct and indirect effects are given by

$$\begin{array}{l}E[Y_{am}-Y_{a^{\ast }m}\mid c]=({\theta }_1+{\theta }_{3}m)(a-a^{\ast })\\ E[Y_{{aM}_{a^{\ast }}}-Y_{a^{\ast }{M}_{a^{\ast }}}\mid c]=\{{\theta }_1+{\theta }_3({\beta }_0+{\beta }_1{a}^{\ast }+{\beta }_2^{\prime }c)\}(a-a^{\ast })\\ E[Y_{{aM}_a}-Y_{{aM}_{a^{\ast }}}\mid c]=({\theta }_2{\beta }_1+{\theta }_3{\beta }_{1}a)(a-a^{\ast }).\end{array}$$

If there is no interaction between A and M so that θ₃ = 0, then these expressions reduce to the expressions of Baron and Kenny (1986) employed in the psychology literature. The controlled direct effect and the natural direct effect are then both equal to θ₁(a − a^*) and the natural indirect effect is θ₂β₁(a − a^*).

VanderWeele and Vansteelandt (2009) also derived standard errors for these effects and showed that if Σ_β and Σ_θ are the covariance matrices for the estimators β̂ of $\beta \equiv {({\beta }_0,{\beta }_1,{\beta }_2^{\prime })}^{\prime }$ and θ̂ of $\theta \equiv {({\theta }_0,{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4^{\prime })}^{\prime }$ and we let

$$\mathrm{\sum }\equiv \left(\begin{array}{cc}{\mathrm{\sum }}_{\beta }& 0\\ 0& {\mathrm{\sum }}_{\theta }\end{array}\right),$$

then standard errors of the controlled and natural direct and indirect effects estimators given above then can be obtained using the Delta method as

$$\sqrt{\mathrm{\Gamma }\mathrm{\sum }{\mathrm{\Gamma }}^{\prime }}\mid a-a^{\ast }\mid$$

with Γ ≡ (0, 0, 0′, 0, 1, 0, m, 0′) for the controlled direct effect, $\mathrm{\Gamma }\equiv ({\theta }_3,{\theta }_3{a}^{\ast },{\theta }_3{C}^{\prime },0,1,0,{\beta }_0+{\beta }_1{a}^{\ast }+{\beta }_2^{\prime }C,0^{\prime })$ for the natural direct effect and Γ ≡ (0, θ₂ + θ₃a, 0′, 0, 0, β₁, β₁a, 0′) for the natural indirect effect, where 0′ denotes a row vector of the dimension of C, containing only zeroes.

With a binary outcome, we would likewise define direct and indirect effects on an risk ratio or odds ratio scale (VanderWeele and Vansteelandt, 2010). On a risk ratio scale conditional on C = c, the total effect is given by ${RR}_{a,a^{\ast }\mid c}^{TE}=\frac{P(Y_a=1\mid c)}{P(Y_{a^{\ast }}=1\mid c)}$, the controlled direct effect is given by ${RR}_{a,a^{\ast }\mid c}^{\mathit{CDE}}(m)=\frac{P(Y_{am}=1\mid c)}{P(Y_{a^{\ast }m}=1\mid c)}$, and the natural direct effect is given by ${RR}_{a,a^{\ast }\mid c}^{\mathit{NDE}}=\frac{P(Y_{{aM}_{a^{\ast }}}=1\mid c)}{P(Y_{a^{\ast }{M}_{a^{\ast }}}=1\mid c)}$. The natural indirect effect on the risk ratio scale conditional on C = c is given by ${RR}_{a,a^{\ast }\mid c}^{\mathit{NIE}}=\frac{P(Y_{{aM}_a})=1\mid c}{P(Y_{{aM}_{a^{\ast }}}=1\mid c)}$. The total effect then decomposes into the product of the natural direct and indirect effects on the risk ratio scale: ${RR}_{a,a^{\ast }\mid c}^{TE}={RR}_{a,a^{\ast }\mid c}^{\mathit{NIE}}\times {RR}_{a,a^{\ast }\mid c}^{\mathit{NDE}}$. Effects could likewise be defined on the odds ratio scale.

VanderWeele and Vansteelandt (2010) derived expressions for controlled direct effects and natural direct and indirect effects for a rare binary outcome under a logistic regression model and a normally distributed continuous mediator; these would apply then on the odds ratio scale that also approximates the risk ratio scale for a rare outcome. The expressions obtained in VanderWeele and Vansteelandt (2010) would also hold for a common binary outcome if the logistic model was replaced by a log-linear model and natural direct and indirect effects on the risk ratio scale were used. Valeri and VanderWeele (2012) derived similar expressions for either binary or continuous outcomes when the mediator is binary. Other techniques to estimate natural direct and indirect effects are also available (van der Laan and Petersen, 2008; Imai et al., 2010; Tchetgen Tchetgen and Shpitser, 2012). The approach described here has the advantage that macros are currently available to provide estimates and standard errors in SAS and SPSS (Valeri and VanderWeele, 2012).

3. Sensitivity Analysis in the Presence of an Exposure-Induced Mediator-Outcome Confounder

We introduce sensitivity analysis parameters in Section 3.1, and propose a sensitivity analysis method using the parameters in Section 3.2. The proposed method is compared with other techniques in Section 3.3.

3.1. Sensitivity analysis parameter

Suppose now that exposure is randomized but that no further assumptions are made about confounding so that there may be mediator-outcome confounding variables that are unmeasured or there may be mediator-outcome confounding variables that are affected by exposure. Our covariate set C can either be empty or we can consider analysis conditional on C = c. For each possible value m, consider the following sensitivity analysis parameter:

$${\gamma }_{mc}=E[Y_{1m}\mid A=1,m,c]-E[Y_{1m}\mid A=0,m,c]$$ (5)

In the application already mentioned, the exposure A is a care management intervention and the outcome Y is a depression score; the potential mediator M is an indicator of adherence to antidepressant medication. The sensitivity analysis parameter γ_1c = E[Y₁₁|A = 1, M = 1, c] − E[Y₁₁|A = 0, M = 1, c] would be a contrast of depressive outcome scores for two sub-populations. The two subpopulations would be first those who had in fact received the care management intervention (A = 1) and adhered to the antidepressant (M = 1), and second, those who had not received the care management intervention (A = 0) but had adhered to the antidepressant (M = 1). We would then consider what would have happened to depression scores for these two subpopulations had we intervened to give the care management program and ensure adherence antidepressant (i.e. we would consider Y₁₁); the contrast between the depression scores for these two subpopulations under this particular intervention is our sensitivity analysis parameter γ_1c. If we thought that the second subpopulation was overall healthier or more competent (e.g. because they adhered even though they did not have the care management intervention), then the depression scores might be higher in the first subpopulation and our sensitivity analysis parameter γ_1c would in this case be positive.

The other sensitivity analysis parameter γ_0c = E[Y₁₀|A = 1, M = 0, c] − E[Y₁₀|A = 0, M = 0, c] would also be a contrast of depressive outcome scores for two subpopulations. The two subpopulations in this case would be first those who had in fact received the care management intervention (A = 1) but had not adhered to the antidepressant (M = 0), and second, those who had not received the care management intervention (A = 0) and had not adhered to the antidepressant (M = 0). For these two subpopulations, we would consider what would have happened to depression scores for these two subpopulations had we intervened to give the care management program but had not allowed adherence to the antidepressant (i.e. we would consider Y₁₀); the contrast between the depression scores for these two subpopulations under this particular intervention is our sensitivity analysis parameter γ_0c. Again, if we thought that the second subpopulation were healthier or more competent (e.g. because the first did not adhere even though they had the care management intervention), then the depression scores for the first subpopulation were higher and our sensitivity analysis parameter γ_0c would also be positive.

We have considered sensitivity analysis parameters of the type given above in (5) in other work on inference for principal stratum effects when outcomes have been truncated by death (Chiba and VanderWeele, 2011). Here we will exploit this sensitivity analysis parameter for inference about natural direct and indirect effects in the potential presence of an exposure-induced mediator-outcome confounder.

3.2. Sensitivity analysis method

If the exposure is randomized, we might then proceed to attempt to estimate natural direct and indirect effect using methods, such as those described in Section 2, which will be consistent for natural direct and indirect effects if no-unmeasured-confounding assumptions (1)–(4) hold. Define

$$\begin{array}{l}{Q}_1={\sum }_{m}E[Y\mid A=1,m,c]\{P(m\mid A=1,c)-P(m\mid A=0,c)\}\\ Q_2={\sum }_m\{E[Y\mid A=1,m,c]-E[Y\mid A=0,m,c]\}P(m\mid A=0,c).\end{array}$$

The expressions Q₁ and Q₂ will be consistent for the natural indirect and direct effects, respectively, if assumptions (1)–(4) hold. Suppose that these assumptions do not hold but that exposure is randomized. If we had unmeasured mediator-outcome confounding variables that were not affected by exposure we could use sensitivity analysis techniques in VanderWeele (2010). However, if we have a mediator-outcome confounder that is affected by exposure, then the techniques in VanderWeele (2010) are inapplicable.

Define the bias factor for natural indirect effect, $B_c^{\mathit{NIE}}$, as the difference between Q₁ and the true natural indirect effect; and define the bias factor for natural direct effect, $B_c^{\mathit{NDE}}$, as the difference between Q₂ and the true natural direct effect; i.e.

$$\begin{array}{l}{B}_c^{\mathit{NIE}}=Q_1-E[Y_{1M_1}-Y_{1M_0}\mid c]\\ B_c^{\mathit{NDE}}=Q_2-E[Y_{1M_0}-Y_{0M_0}\mid c].\end{array}$$

We then have the following result. The proof is given in the appendix.

Theorem 1

Suppose that exposure A is randomized. Let γ_mc = E[Y_1m|A = 1, m, c] − E[Y_1m|A = 0, m, c] and let Γ_c = Σ_m γ_mcP(m|A = 0, c), then

$$\begin{array}{l}{B}_c^{\mathit{NIE}}=-{\mathrm{\Gamma }}_c\\ B_c^{\mathit{NDE}}=-{\mathrm{\Gamma }}_c.\end{array}$$

We thus have that

$$\begin{array}{l}E[Y_{1M_1}-Y_{1M_0}\mid c]=Q_1-B_c^{\mathit{NIE}}\\ E[Y_{1M_0}-Y_{0M_0}\mid c]=Q_2-B_c^{\mathit{NDE}}\end{array}$$

where $B_c^{\mathit{NIE}}$ and $B_c^{\mathit{NDE}}$ are given as in Theorem 1. Note that $B_c^{\mathit{NIE}}=-B_c^{\mathit{NDE}}$.

If we estimate Q₁ and Q₂ using methods for natural indirect and direct effects (e.g. van der Laan and Petersen, 2008; VanderWeele and Vansteelandt, 2009; Imai et al., 2010; Valeri and VanderWeele, 2012; Tchetgen Tchetgen and Shpitser, 2012) but if the identification assumptions (1)–(4) do not hold because of unmeasured mediator-outcome confounding or an exposure-induced mediator-outcome confounding variable, then our estimators will not be consistent for the true natural indirect and direct effects. However, we can obtain corrected estimates of the natural indirect and direct effects by specifying the sensitivity analysis parameter γ_mc for each level of m (we will have two such parameters if M is binary as above) and then computing the bias factors from Theorem 1. To obtain corrected estimates for natural indirect and direct effects we then subtract the bias factors, $B_c^{\mathit{NIE}}$ and $B_c^{\mathit{NDE}}$, respectively, from our estimates of the natural indirect and direct effects. The corrected estimators will be consistent for the true natural indirect and direct effects if we have specified the sensitivity analysis parameters γ_mc correctly. Of course, we do not know what the true values of these sensitivity analysis parameters are but we can vary them in a sensitivity analysis to assess the extent to which our conclusions about direct and indirect effects depend on the magnitude of these parameters. We give an example of such a sensitivity analysis in Section 5.

The sensitivity analysis parameters in Theorem 1 depend on the probabilities P(m|A = 0, c) which must be estimated from the data. This can make obtaining corrected confidence intervals for direct and indirect effect estimates more challenging. If γ_mc were constant across strata of m then the bias factors $B_c^{\mathit{NIE}}$ and $B_c^{\mathit{NDE}}$ would no longer depend on P(m|A = 0, c) and we could simply subtract $B_c^{\mathit{NIE}}$ and $B_c^{\mathit{NDE}}$ from both limits of the confidence intervals for Q₁ and Q₂ to obtain corrected confidence intervals for natural indirect and direct effects respectively. Likewise, if the data set is sufficiently large so that estimates of P(m|A = 0, c) are very precise e.g. if the mediator were binary and the covariate set C empty, and the sample size large, then approximate corrected confidence intervals for natural indirect and direct effects could be obtained by simply subtracting $B_c^{\mathit{NIE}}$ and $B_c^{\mathit{NDE}}$ from both limits of the confidence intervals for Q₁ and Q₂. In other contexts, however, in which we must estimate P(m|A = 0, c) from the data and our estimates of P(m|A = 0, c) are themselves subject to sampling variability, then to obtain corrected confidence intervals for natural indirect and direct effects, we could proceed by bootstrapping wherein for each fixed value of the sensitivity analysis parameters γ_mc and with each bootstrapped sample we would obtain both estimates of Q₁ and Q₂ and estimates of P (m|A = 0, c) and subsequently $B_c^{\mathit{NIE}}$ and $B_c^{\mathit{NDE}}$ to derive a corrected estimate of the natural direct and indirect effects. Corrected confidence intervals could then be obtained by using a percentile method over the corrected estimates across the bootstrapped samples.

Theorem 1 has an interesting corollary.

Corollary 1

If γ_mc ≥ 0 for all m, then E[Y_1M1 – Y_1M0|c] ≥ Q₁ and E[Y_1M0 – Y_0M0|c] ≤ Q₂. If γ_mc ≤ 0 for all m, then E[Y_1M1 – Y_1M0|c] ≤ Q₁ and E[Y_1M0 – Y_0M0|c] ≥ Q₂.

Corollary 1 states that if the sensitivity analysis parameter γ_mc is non-negative for all values of m, then using the observed data and estimators that are consistent for Q₁ and Q₂, we will numerically underestimate the true natural indirect effect and numerically overestimate the true natural direct effect. Conversely, if the sensitivity analysis parameter γ_mc is non-positive for all values of m, then using the observed data and estimators that are consistent for Q₁ and Q₂, we will overestimate the true natural indirect effect and underestimate the true natural direct effect. This corollary will also be of interest in the application below.

Here, we have been considering a binary exposure A; however the approach generalizes to non-binary exposures by simply replacing A = 1 and A = 0 with A = a and A = a^*. We have also assumed that the exposure is randomized, but this assumption can be relaxed in observational studies to (Y_am, M_a^*) *#x02AEB; A|C for all a, a^*, and m. This is essentially an assumption of joint unconfoundedness of the exposure-outcome and exposure-mediator relationships. It would hold if exposure is randomized. Technically, it is a slightly stronger than simply Y_am #x02AEB; A|C (i.e. assumption 1) and M_a^* #x02AEB; A|C (i.e. assumption 3), but on any causal diagram defined by non-parametric structural equations (Pearl, 2009), where these two conditions hold the stronger condition (Y_am, M_a^*) #x02AEB; A|C will also hold.

3.3. Comparison with other techniques

Other techniques for sensitivity analysis for direct and indirect effects have also recently been developed that handle the presence of an exposure-induced mediator-outcome confounder.

Imai and Yamamoto (2012) proposed a technique that requires specification of a linear structural equation model with random coefficients. Our technique, in contrast to theirs, is non-parametric. Their technique also assumes that data is available on the exposure-induced mediator outcome confounder L, whereas ours does not.

Tchetgen Tchetgen and Shpitser (2012) proposed a technique that requires specifying as sensitivity analysis parameters the quantities E[Y_1m|A = a, M = m, C = c] – E[Y_1m|A = a, M ≠ m, C = c] for each a and m. For a fixed level of c, their technique thus requires specifying a number of sensitivity analysis parameters equal to dim(A) × dim(M), whereas our technique only requires specifying a number of sensitivity analysis parameters equal to dim(M). Moreover, for the technique of Tchetgen Tchetgen and Shpitser (2012), the parameters E[Y_1m|A = a, M = m, C = c] – E[Y_1m|A = a, M ≠ m, C = c] may be difficult to specify in practice if M is not binary as the parameters are not a simple contrast comparing two values of M, but rather comparing a single value (M = m) to an entire set of values (M ≠ m). Note that when M is not binary, both their technique and ours will require specifying a potentially large number of parameters, making it more difficult to use such techniques in practice.

Finally, Vansteelandt and VanderWeele (2012) also proposed a sensitivity analysis technique for an exposure-induced mediator-outcome confounder. Their technique, like that of Imai and Yamamoto (2012), requires that data is available on the exposure-induced mediator-outcome confounder L, whereas the technique presented here does not. The technique of Vansteelandt and VanderWeele (2012) also involves specifying a selection bias function which can be difficult to interpret in practice, but does have the advantage that it is essentially zero so long as there is no three-way interaction between A, L and M.

4. Sensitivity Analysis for Natural Direct and Indirect Effects on a Ratio Scale

We will now consider how a similar sensitivity analysis technique can be employed when natural direct and indirect effects on the ratio scale are of interest, as for example in the application to perinatal epidemiology considered by Ananth and VanderWeele (2011). Suppose again that exposure is randomized but that no further assumptions are made about confounding. Under assumptions (1)–(4) above, the natural indirect and direct effects on the risk ratio scale would be identified by (VanderWeele and Vansteelandt, 2010):

$$\begin{array}{l}{Q}_3=\frac{{\sum }_{m}E[Y\mid A=1,m,c]P(m\mid A=1,c)}{{\sum }_{m}E[Y\mid A=1,m,c]P(m\mid A=0,c)}\\ Q_4=\frac{{\sum }_{m}E[Y\mid A=1,m,c]P(m\mid A=0,c)}{{\sum }_{m}E[Y\mid A=0,m,c]P(m\mid A=0,c)}.\end{array}$$

However, these expressions will be biased for the true natural indirect and direct effects if there is an unmeasured mediator-outcome confounder or a mediator-outcome confounder affected by the exposure. Define the following bias factors:

$$\begin{array}{l}{B}_c^i=\frac{1}{Q_3}-\frac{1}{\frac{P(Y_{1M_1}=1\mid c)}{P(Y_{1M_0}=1\mid c)}}\\ B_c^d=Q_4-\frac{P(Y_{1M_0}=1\mid c)}{P(Y_{0M_0}=1\mid c)}.\end{array}$$

We then have the following result. The proof is given in the appendix.

Theorem 2

Suppose that exposure A is randomized. Let γ_mc = E[Y_1m|A = 1, m, c] – E[Y_1m|A = 0, m, c] and let Γ_c = Σ_mc γ_mcP(m|A = 0, c), then

$$\begin{array}{l}{B}_c^i=\frac{{\mathrm{\Gamma }}_c}{E[Y\mid A=1,c]}\\ B_c^d=\frac{{\mathrm{\Gamma }}_c}{E[Y\mid A=0,c]}.\end{array}$$

and thus

$$\begin{array}{l}\frac{P(Y_{1M_1}=1\mid c)}{P(Y_{1M_0}=1\mid c)}=\frac{Q_3}{1-Q_3\times B_c^i}\\ \frac{P(Y_{1M_0}=1\mid c)}{P(Y_{0M_0}=1\mid c)}=Q_4-B_c^d.\end{array}$$

If we estimate Q₃ and Q₄ using methods for natural indirect and direct effects on the ratio scale (VanderWeele and Vansteelandt, 2010) but if the identification assumptions (1)–(4) do not hold because of unmeasured mediator-outcome confounding or an exposure-induced mediator-outcome confounding variable, then our estimators will not be consistent for the true natural indirect and direct effects. However, we can use Theorem 2 to obtain corrected natural indirect and direct effect estimates by specifying the sensitivity analysis parameters γ_mc = E[Y_1m|A = 1, m, c] – E[Y_1m|A = 0, m, c], and then using this to obtain the bias factors $B_c^i$ and $B_c^d$ by using also empirical estimates for E[Y|A = 1, c] and E[Y|A = 0, c] and then using these bias factors to obtain corrected natural indirect and direct effect estimates on the ratio scale.

In general, to obtain corrected confidence intervals for natural indirect and direct effect risk ratio, we would have to use bootstrapping, wherein for each fixed value of the sensitivity analysis parameters γ_mc and with each bootstrapped sample, we would obtain both estimates of Q₃ and Q₄ and estimates of P(m|A = 0, c), E[Y|A = 1, c] and E[Y|A = 0, c] from the data, and subsequently $B_c^i$ and $B_c^d$, and use the formulas in Theorem 2 to calculate a corrected estimate of the natural indirect and direct effect risk ratios. Corrected confidence intervals could then be obtained by using a percentile method over the corrected estimates across the bootstrapped samples.

As with the Corollary to Theorem 1, it likewise follows immediately from Theorem 2, that if γ_mc ≥ 0 for all m, then $\frac{P(Y_{1M_1}=1\mid c)}{P(Y_{1M_0}=1\mid c)}\ge Q_3$ and $\frac{P(Y_{1M_0}=1\mid c)}{P(Y_{0M_0}=1\mid c)}\le Q_4$. If γ_mc ≤ 0 for all m, then $\frac{P(Y_{1M_1}=1\mid c)}{P(Y_{1M_0}=1\mid c)}\le Q_3$ and $\frac{P(Y_{1M_0}=1\mid c)}{P(Y_{0M_0}=1\mid c)}\ge Q_4$.

5. Illustration

Emsley et al. (2010) considered mediation in the Prevention of Suicide in Primary Care Elderly: Collaborative Trial (PROSPECT). They assessed whether the effect of randomized exposure (collaborative care management versus care as usual), A, on the score from the Hamilton Depression Scale, Y, was mediated by adherence to antidepressants, M. They assumed no interaction between the effect of A and M on Y, and obtained an estimate of the direct effect, of −2.66 (standard error = 0.93) and an estimate of the indirect effect, of −0.49 (standard error = 0.43) for a total effect of −3.15. A standard deviation for the Hamilton Depression Scale is about four points. If there was indeed no exposure-mediator interaction, and if assumptions (1)–(4) for the mediator M were satisfied, then their estimator of the direct effect would be consistent for the natural direct effect, E[Y_1M0 – Y_0M0] (i.e. the effect of having versus not having collaborated care management, with the use of antidepressant in both scenarios fixed to the level it would have been in the absence of collaborated care management) and their estimator of the indirect effect would be equal to the natural indirect effect, E[Y_1M1 – Y_1M0] (i.e. the effect of having collaborative care management with antidepressant use set to the level it would have been with versus without collaborative care management).

In their analysis, however, it is likely that there are variables that confound the relationship between antidepressant adherence and depression scores. Medical co-mordities might affect both depression scores and also whether a patient is adherent to antidepressant since patient’s medical co-morbidities may deter patients from taking antidepressant medications because of so many other medications necessitated by their medical condition. If these mediator-outcome confounding variables were not affected by exposure, we could potentially use the sensitivity analysis technique in VanderWeele (2010) or Imai et al. (2010). However, it may be the case the medical co-mordities are affected by the collaborative care management intervention. Moreover, there may be other mediator-outcome confounding variables that are affected by the exposure. For example, we might consider whether patients have a regular eating schedule during follow-up. If patients typically take anti-depressant medications with meals, then having a regular eating schedule may affect adherence; regulation of meals and diet may also affect depression scores; and whether there is a regular eating schedule may itself be affected by whether collaborative care management is provided.

We may allow for such mediator-outcome confounding variables affected by exposure and still apply the sensitivity analysis approach in Theorem 1 with C = Ø. As above, our sensitivity analysis parameter γ_1c = E[Y₁₁|A = 1, M = 1, c] – E[Y₁₁|A = 0, M = 1, c] compares what depression scores would have been with care management and adherence for two subpopulations, those who received the care management intervention (A = 1) and adhered to the antidepressant (M = 1), versus those had not received the care management intervention (A = 0) but had adhered to the antidepressant (M = 1). If we thought that the second subpopulation was overall healthier or more competent, we might specify a positive sensitivity analysis parameter, e.g. γ_1c = 1 (roughly a quarter of a standard deviation for the depressive symptom scale). The other sensitivity analysis parameter, γ_0c = E[Y₁₀|A = 1, M = 0, c] – E[Y₁₀|A = 0, M = 0, c], compares what depression scores would have been with care management without adherence for two subpopulations, those who received the care management intervention (A = 1) but had not adhered to the antidepressant (M = 0) versus those who had not received the care management intervention (A = 0) and had not adhered to the antidepressant (M = 0). If we thought that the second subpopulation was healthier or more competent, we might again specify a positive sensitivity analysis parameter, e.g. γ_0c = 0.5.

The probability of the mediator in the control group in their data is 0.45 and we could then calculate Γ_c = Σ_m γ_mcP(m|A = 0, c) = (0.55)(0.5) + (0.45)(1) = 0.725. The corrected estimates for the direct and indirect effects would be −2.66 – 0.725 = −3.39 and −0.49 – (−0.76) = 0.24, respectively. The direct effect would still be quite substantial, but the indirect effect (the effect mediated by antidepressant adherance) would be detrimental (i.e. would increase depression), which does not seem likely. The sensitivity analysis parameters specified may be too extreme. We could of course specify different sensitivity analysis parameters as well. If we thought that the sensitivity analysis parameters were half of what was specified above, we would have Γ_c = 0.36 and corrected direct and indirect estimates of −2.66 – 0.36 =−3.02 and −0.49 – (−0.36) = −0.13, respectively. By Corollary 1, if the sensitivity analysis parameters are positive, then irrespective of their actual values we would have the true direct effect was in fact more negative (more protective) than the initial estimate of −2.66. Moreover, even if the sensitivity analysis parameters took the opposite sign they would have to be fairly substantial in magnitude, e.g. γ_1c = γ_0c = 2.66 (roughly half a standard deviation in depression scores) to explain away the direct effect. The direct effect itself then seems fairly robust to potential unmeasured or exposure-induced mediator-outcome confounding; however, the indirect, as we have seen, is not.

More generally, several different approaches to assessing robustness are possible. One may not believe any specific values of the sensitivity analysis parameters but they can be changed and varied to assess robustness to conclusions under different values, as in the illustration above. A large table could also be presented with many different values. One can also report the parameters that would suffice to explain away an effect, as in the illustration above. Finally, the parameters themselves might also be informed by external data or expert knowledge.

6. Discussion

In this paper, we have developed a method for sensitivity analysis for natural direct and indirect effects that can be used in the presence of unmeasured mediator-outcome confounding or of an exposure-induced mediator-outcome confounder. The latter scenario, of exposure-induced mediator-outcome confounding, has presented a challenge for the causal inference literature on mediation, both in terms of identification (Avin et al., 2005) and also with regard to prior sensitivity analysis techniques (VanderWeele, 2010; Imai et al., 2010). Our technique is applicable for natural direct and indirect effects on both the difference and ratio scales and requires specifying fewer parameters than some alternative techniques. Our technique has the advantage that it is non-parametric and thus applicable irrespective of the method or models used to obtain the initial direct and indirect effects estimates. Moreover, at least on the difference scale, there are some contexts when it is particularly easy to derive not only corrected estimates but corrected confidence intervals as well. The method provided here is, however, subject to some important limitations. First, the sensitivity analysis parameters are not particularly straightforward to interpret. Second, unless the mediator is binary, the technique proposed here will require specifying a relatively large number of parameters which may make it more difficult to assess the robust of one’s conclusions to mediator-outcome confounding. In spite of these limitations, the sensitivity analysis technique given here still does help extend the range of settings in which investigators can reason about direct and indirect effects, and we hope that it will be useful in future applications.

Appendix

Proof of Theorem 1

Under randomization of A, we have:

$$\begin{array}{l}E[Y_{{aM}_a}\mid c]=E[Y_a\mid c]\\ =E[Y_a\mid A=a,c]\\ =E[Y\mid A=a,c]\\ ={\sum }_{m}E[Y\mid A=a,m,c]P(m\mid A=a,c)\end{array}$$

where the first equality follows by composition, the second by randomization, the third by consistency and the fourth by iterated expectations. We also have

$$\begin{array}{l}E[Y_{1M_0}\mid c]={\sum }_{m}E[Y_{1m}\mid M_0=m,c]P(M_0=m\mid c)\\ ={\sum }_{m}E[Y_{1m}\mid A=0,M_0=m,c]P(M_0=m\mid A=0,c)\\ ={\sum }_{m}E[Y_{1m}\mid A=0,M=m,c]P(M=m\mid A=0,c)\\ ={\sum }_m\{E[Y_{1m}\mid A=1,M=m,c]-{\gamma }_{mc}\}P(M=m\mid A=0,c)\\ ={\sum }_{m}E[Y\mid A=1,M=m,c]P(M=m\mid A=0,c)-{\sum }_m{\gamma }_{mc}P(M=m\mid A=0,c)\\ ={\sum }_{m}E[Y\mid A=1,M=m,c]P(M=m\mid A=0,c)-{\mathrm{\Gamma }}_c\end{array}$$

where the first equality follows by iterated expectations, the second by randomization, the third by consistency, the fourth by definition of γ_mc, and the fifth by consistency. From this it follows that

$$\begin{array}{l}{B}_c^{\mathit{NIE}}={\sum }_{m}E[Y\mid A=1,m,c]\{P(m\mid A=1,c)-P(m\mid A=0,c)\}-E[Y_{1M_1}-Y_{1M_0}\mid c]\\ =E[Y_{1M_1}\mid c]-\{E[Y_{1M_0}\mid c]+{\mathrm{\Gamma }}_c\}-E[Y_{1M_1}-Y_{1M_0}\mid c]\\ =-{\mathrm{\Gamma }}_c\end{array}$$

and likewise

$$\begin{array}{l}{B}_c^{\mathit{NDE}}={\sum }_m\{E[Y\mid A=1,m,c]-E[Y\mid A=0,m,c]\}P(m\mid A=0,c)-E[Y_{1M_0}-Y_{0M_0}\mid c]\\ =E[Y_{1M_0}\mid c]+{\mathrm{\Gamma }}_c-E[Y_{0M_0}\mid c]-E[Y_{1M_0}-Y_{0M_0}\mid c]\\ ={\mathrm{\Gamma }}_c.\end{array}$$

This completes the proof.

Proof of Theorem 2

Suppose that exposure A is randomized. As in Theorem 1, we have P(Y_0M0 = 1|c) = Σ_m E[Y|A = 0, m, c]P(m|A = 0, c) = E[Y|A = 0, c] and P(Y_1M0 = 1|c) = Σ_m E[Y|A = 1, M = m, c]P(M = m|A = 0, c) − Γ_c and thus we have

$$\begin{array}{l}{B}_c^d=Q_4-\frac{P(Y_{1M_0}=1\mid c)}{P(Y_{0M_0}=1\mid c)}\\ =\frac{{\sum }_{m}E[Y\mid A=1,m,c]P(m\mid A=0,c)}{{\sum }_{m}E[Y\mid A=0,m,c]P(m\mid A=0,c)}-\frac{P(Y_{1M_0}=1\mid c)}{P(Y_{0M_0}=1\mid c)}\\ =\frac{{\sum }_{m}E[Y\mid A=1,m,c]P(m\mid A=0,c)}{E[Y\mid A=0,c]}-\frac{{\sum }_{m}E[Y\mid A=1,M=m,c]P(M=m\mid A=0,c)-{\mathrm{\Gamma }}_c}{E[Y\mid A=0,c]}\\ =\frac{{\mathrm{\Gamma }}_c}{E[Y\mid A=0,c]}.\end{array}$$

Also as in Theorem 1, we have P(Y_1M1 = 1|c) = Σ_m E[Y|A = 1, m, c]P(m|A = 1, c) = E[Y|A = 1, c] and P(Y_1M0 = 1|c) = Σ_m E[Y|A = 1, M = m, c]P(M = m|A = 0, c) − Γ_c and thus we have

$$\begin{array}{l}{B}_c^i=\frac{1}{Q_3}-\frac{1}{\frac{P(Y_{1M_1}=1\mid c)}{P(Y_{1M_0}=1\mid c)}}\\ =\frac{{\sum }_{m}E[Y\mid A=1,m,c]P(m\mid A=0,c)}{{\sum }_{m}E[Y\mid A=1,m,c]P(m\mid A=1,c)}-\frac{P(Y_{1M_0}=1\mid c)}{P(Y_{1M_1}=1\mid c)}\\ =\frac{{\sum }_{m}E[Y\mid A=1,m,c]P(m\mid A=0,c)}{E[Y\mid A=1,c]}-\frac{{\sum }_{m}E[Y\mid A=1,M=m,c]P(M=m\mid A=0,c)-{\mathrm{\Gamma }}_c}{E[Y\mid A=1,c]}\\ =\frac{{\mathrm{\Gamma }}_c}{E[Y\mid A=1,c]}.\end{array}$$

Since,

$$B_c^i=\frac{1}{Q_3}-\frac{1}{\frac{P(Y_{1M_1}=1\mid c)}{P(Y_{1M_0}=1\mid c)}},$$

solving for $\frac{P(Y_{1M_1}=1\mid c)}{P(Y_{1M_0}=1\mid c)}$ gives:

$$\frac{P(Y_{1M_1}=1\mid c)}{P(Y_{1M_0}=1\mid c)}=\frac{Q_3}{1-Q_3\times B_c^i}.$$

This completes the proof.