Recent progress on countercurrent chromatography modeling

Abstract

As countercurrent chromatography is becoming an established method in chromatography for many kinds of products, it is becoming increasingly important to model the process and to be able to predict the peaks for a given process. The CCC industries are looking for rapid methods to analyze the processes of countercurrent chromatography and select suitable solvent system. In this paper, recent progress is reviewed in the development and demonstration of several types of models of countercurrent chromatography. Literature lists a number of countercurrent chromatography (CCC) models that can predict the retention time and to a certain extent the peak width of a solute eluting from a CCC column, such as cell model, CCD model, CSTRs model, probabilistic model, temperature dependence plate model, physical models, etc.

1. Introduction

Countercurrent chromatography (CCC) is a liquid chromatography (LC) technique with a support-free liquid stationary phase [1]. It has been 40 years since it was first introduced as a separation approach in the late 1970s by Yoichiro Ito. CCC is widely used in separation and purification areas, especially for various natural and synthetic products. The separation of compounds by CCC is based on their distribution between two immiscible liquid phases. In CCC, one phase is mobile phase and the other phase is stationary phase. Since there is no solid support matrix in column, CCC is free from several band-broadening mechanisms caused by the action of random imperfection in the flow stream. As a result, the mathematical description of the separation process of CCC is less complex than the conventional liquid-liquid chromatography, in which the liquid stationary phase is retained on a solid support. The distribution of compounds between two liquid phases is determined by the mass transfer rate through the interface between the phases. The partition coefficient between two phases for organic compounds, K, is an important parameter to model the transport of organic chemicals in the CCC Separation [2–7]. Sample components are distributed between the two phases by mixing and then transferred with the mobile phase, hence the eluting order is determined by the K value. In CCC separation, the retention time of a solute is directly proportional to its K value, so it can be predicted using mathematical method.

CCC models allow chromatograms to be predicted before carrying out a separation process. Virtual separations can be produced when evaluating column dimensions, such as the column length, radius, number of loops and β-value. Besides, CCC models can provide valuable knowledge to optimize time and materials used in CCC operations, while contributing to establish CCC as a more generally applied chromatographic technique. CCC model can be very helpful in the design of new CCC equipment, particularly in scale-up. Furthermore, it will also help users optimize their results from the CCC instruments.

To predict retention time of a solute in a chromatographic column, it is essential for researchers to do quantitative analysis of longitudinal mixing and mass transfer. Besides, dispersion phenomenon must be represented by means of a set of equations. A large number of empirical functions were proposed and used for the description and interpretation of chromatographic peaks Since the parameters of these mathematical models are not directly related to the characteristic features of a real chromatographic process, their practical application in the process simulation and scale up is problematic. Thus simple and clear mathematical models are required.

Several countercurrent chromatography mathematical models can be found in original literatures. Those models can predict retention time from a CCC column. So far, research workers have built several math models of countercurrent chromatography (CCC), such as cell model, eluting countercurrent distribution model, continuous-stirred tank reactors model, probabilistic model and temperature dependence plate model.

2. What are the differences between reported models

2.1. Cell model

Kostanian attempted to apply an approach used in chemical engineering for modeling of mass transfer process, and he developed a cell model that took into account longitudinal mixing in both phases [8]. In conventional chromatography, a solute is usually considered to be longitudinally transported only in the mobile phase, remaining longitudinally motionless in the stationary phase. In counter-current chromatography, both phases undergo intense mixing in the variable force field of a coil planet centrifuge and longitudinal transportation in the stationary phase should not to be excluded. Kostanian assumed the countercurrent distribution system as ideally mixed cells. The CCC column was considered to be a very long extraction column with an extremely high length L to diameter D ratio, operating under special conditions: one of the contacting phases is the stationary phase and mass transfer takes place under unstable state conditions as in the CCC system.

Kostanian came up with two model schemas, one is discrete (staged)-cell model (a cascade of well mixed equal-size vessels) and the other is continuous-diffusion model, as shown in Figs. 1. According to the discrete model, the axial mixing in the chromatographic column is determined by one parameter, the number of perfectly mixed cells n. However, the continuous-diffusion model is characterized by two parameters thaose are took into account separately the rate of mixing in the phases. The two parameters are in the form of effective longitudinal diffusion coefficients (D_axm in mobile phase, and D_axs in stationary phase), which are defined to include the effects of non-uniform velocity profile, turbulence and molecular diffusion. The diffusion model formally relies on the laws of one-dimensional convective diffusion adapted to the flow in the chromatographic column. In the cell model, uniform properties in all parts of the cell are assumed: 1, instantaneous equilibrium between the phases is reached at any cross-section of the continuous model and in any perfectly mixed cell of the staged model; 2, the distribution constant K_D = y/x = constant (here x and y are substance concentrations in mobile and stationary phases, respectively); 3, the retained volume of stationary phase V_s is constant at any cross-section of the column, in other words, S_f = V_s/(V_s + V_m)= V_s/V_c= constant, in which V_m and V_s are the volumes of mobile and stationary phases in the chromatographic column, respectively, and V_c = V_s + V_m is the column volume. The cell model describes the chromatographic column hydrodynamics and unstable state mass transfer process between the two phases. Experiments were carried out to prove the effectiveness of the cell model in predicting partitioning behavior and the chromatographic peak profiles of solutes [9]. The equilibrium cell model can be used for describing CCC chromatographic peaks. Comparing original chromatograms with theoretical curves generated by the established model, it can be seen a good agreement between them. Longitudinal mixing rates in stationary and mobile phases was experimentally determined by using several peaks of a sample, which enabled the prediction of peak shape for a solute with a given distribution constant from experimental data.

Fig. 1.

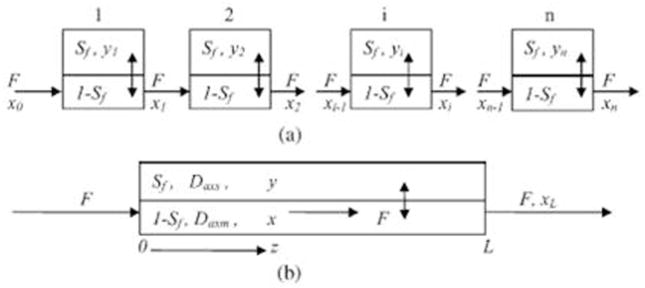
Scheme of diffusion longitudinal mixing (a) and ideally mixed cells (b) models. [8] Cited from Kostanian, A.E. J. Chromatogr. A. 2002, 973, 39–46.

The cell model included a series of complex mathematical equations. The model can be applied for CCC process simulation when the mass transfer rate between the phases is large enough to be ignored. It is applicable to symmetrical chromatographic peaks. However, for low mass transfer, the presented model must be extended to include the mass transfer rate.

For the first generation cell model, model description was strong on concept, but simply handled in mathematics. Given available computing power and choice in mathematical modeling tools, the mass balance equation could have been solved as a differential equation to determine the elution profile. The cell model has improved in recent years, and now it can be applied as a simple method to predict the retention time as well as the retention time. Furthermore, the cell model can also be used in Modelling countercurrent and dual countercurrent chromatography [24].

2.2. CCD model

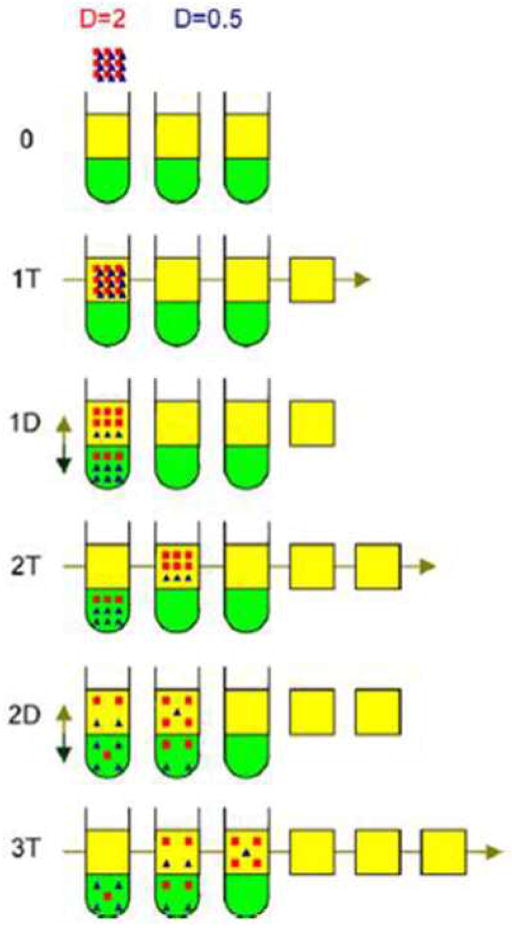
Another approach reported on CCC modeling was an eluting CCD model, which was based on eluting countercurrent distribution theory. Countercurrent chromatography can be considered as a form of column chromatography without a solid support, in other words, as a continuous form of countercurrent distribution (CCD). In the 1950s Craig’s CCD apparatus was extensively used for the purification of natural products [10] based on their distribution ratio or partition coefficient. The distribution ratio is the ratio of sample concentrations in the two immiscible phases. It is an excellent example of a separation system that is completely mathematically predictable if the ratio of solute distribution and the mobile to stationary phase volumes are known. Prof. Sutherland described the theory of CCD model and used the model to predict CCC chromatograms [11]. The CCD model was built using an array of positions representing a chain of test tubes in one dimension, while mixing, settling, and transfer processes in the other. As in Fig. 2, an array of positions, representing test tubes is set up in one dimension, with mixing settling and transfer activities set up in the other. Firstly each tube is filled with a given proportion of each phase, which was defined by the retention of stationary phase (S_f). Then a sample component containing equal amount of two solutes of distribution ratio, D₁ and D₂, dissolved in mobile phase, is transferred to the first tube displacing the mobile phase components of the other test tubes in the chain until a mobile phase volume is eluted from the chain into fraction collector. The whole chain is then mixed and the phases allowed to settling assuming thorough mixing and ideal mass transfer distribution between the two phases. Next, the mobile phase parts of each tube are again transferred to the next tube and so on. After thousands of such steps, the whole chromatograph can be eluted out.

Fig. 2.

Schematic diagram of CCD elution model for two solutes with distribution ratios of 0.5 and 2 undergoing two mixing and settling/transfer steps. [12] Cited from Folter, J. de; Sutherland, I. A. J. Chromatogr. A. 2009, 1216, 4218–4224.

CCD model was very flexible in such a way that it can simulate different CCC modes. It can not only model conventional elution mode, but also be applied in co-current elution mode and dual mode [12]. It was validated successfully in analytical as well as production scales and proved to obtain accurate results for peak retentions. However, peak widths were not predicted precisely. CCD, a discreet process, remains fundamentally different from CCC which is a continuous process. Such adaptation is possible only when fully phase mixing and settling over each rotation has been achieved, which cannot be reached in reality. A drawback of this model is that the number of test tubes in the series was estimated to match with an existing chromatogram and not related to instrument parameters.

The theory and application of the longitudinal mixing cell model and the eluting countercurrent distribution model for the description of CCC and dual CCC processes was compared by A.E. Kostanyan [13]. The cell model represents perfectly mixed, equally sized cells in series. The number of cells characterizes the rates of longitudinal mixing in the stationary and mobile phases. In the eluting countercurrent distribution (CCD) model, the CCC process is considered as a continuous form of Craig’s countercurrent distribution. It is shown that the two models describe two types of separation processes with essential difference: CCC model represents continuous type of process performance, however, the CCD model describes the cyclic performance of separation processes. It is demonstrated that each vessel of the Craig’s CCD chain provides the separation efficiency of more than one theoretical plate which causes an essential difference in CCC modeling by using of both approaches. With decreasing capacity factor k’ the difference between the models increases. In fact, the Craig’s countercurrent distribution and CCC are physically different extraction processes. A simple relationship between the number of theoretical plates and the vessel number in the Craig’s CCD chain is established. Taking this relationship into account the eluting CCD model can be formally applied to analyze the countercurrent chromatography processes.

2.3. CSTR model

Hacer Guzlek [14] modeled the CCC column using a continuous-stirred tank reactors (CSTR) model. In CCC the velocity of a mixing wave (v_mix) is considerably higher than the mobile phase velocity (v_MP), because a mixing wave moves forward the length of one column loop with every column rotation and generally rotational speeds are several hundreds to thousands per minute; but a mobile phase increment usually precedes only several loops per minute. This means by the time a mobile phase increment has moved forward the entire length of the mixing zone, it has experienced tens to hundreds of mixing and settling cycles. TThe CCC column was modeled based on mass balance equations in a series of CSTRs containing two immiscible liquid phases. The following assumptions were made in CSTR model: 1. Mobile phase increment is assumed to be the length of one mixing wave and this segment is assumed to be totally equilibrated. Therefore, the entire length of the column is taken as a series of fully equilibrated CSTRs. 2. As long as stationary phase is retained in the column, the behavior of a solute concentration in the column can be represented by the CSTR model. 3. The volume of every mixing zone was considered equal. 4. Ideal mixing and instantaneous distribution of the solute between the two phases were assumed.

The CSTRs have identical volumes and are filled with stationary and mobile phases while respecting the stationary phase retention for a given solvent system in the CCC column (see Fig. 3). The essential parameters, such as the mobile phase flow rate F, stationary and mobile phase volumes V_SP and V_MP, the solute concentration c_in, and its partition ratio K_D are known. The injection is introduced into the first CSTR in the series; from the second tank onwards the outlet concentration of the previous CSTR (c_{out, n−1}) is the inlet concentration of the next (c_{in, n}). The stationary phase remains in each CSTR, however, the mobile phase is continuously washed through according to the mobile phase flow rate. The solute enters the mixing zone, distributes between the two phases according to partition ratio and leaves this zone with the mobile phase.

Fig. 3.

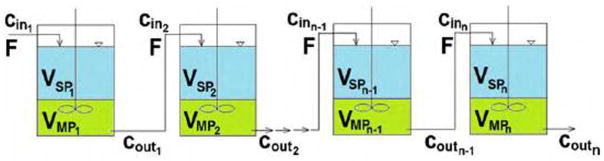
Scheme of CSTR model. [14] Cited from Guzlek, H.; Baptista, I. I. R.; Wood, P. L.; Livingston, A. J. Chromatogr. A 2010, 1217, 2030–2040.

Using the CSTR model, the elution chromatogram of a solute can be calculated as concentration leaving the column over a selected period of time. This was a novel CCC model that can predict the elution profile of a column using instrument and operational parameters only. The model inputs were the column specifications such as column length, internal diameter, β-value, and number of column loops as well as the mobile phase flow rate, stationary phase retention, a solute’s partition ratio, and its mass and volume. Using the instrument specifications the number and volume of CSTRs were calculated, which are specific for each column. The CSTR model was validated using experimental results produced by a wide range of CCC instruments. It is a way to predict the elution profile of a CCC instrument from column dimensions and experimental settings, without inserting empirical calibrations.

However, some of the assumptions were idealized. One segment of CSTRs was assumed to be fully equilibrated, which could not be achieved in real condition. As a result, the prediction of peak shapes may be inaccurate.

2.4. Probabilistic model

A ProMISE (probabilistic model for immiscible phase separations and extractions) model was developed by Joost de Folter [15]. This model was based on simulating probabilistic units. It does not use compartments or cells like in the Craig based model, and it is not based on diffusion theory., so it is not limited to a compartment or cell nature, and it allows for an even greater flexibility. With this model, all the CCC flow modes can be predicted. The main advantage of this model is that it does not require a somewhat arbitrary number of steps or theoretical plates, whereas it uses an efficiency factor.

Bayes’ theorem shows the relationship between two conditional probabilities which are the reverse of each other. The probabilistic model was based on this theorem. Considering a molecule of a particular compound in a two phase system, assuming it is located somewhere in either phases, its behaviour can be described by the probability of its moving to the other phase. An efficiency factor is introduced here by simply multiplying by the efficiency factor for the final probability value. This model consists of simulating many of these representative units, following the probabilistic rules. Each unit represents a very small amount of sample compound. Then, each unit is moved according to the movement of the phase which is located in. A density function with an adaptive Gaussian filter is used to convert the separate unit values into a chromatogram. The nature of this model allows its internal values to be volume or time. This model has been realized using a computer application, interactively visualizing the behaviour of the units in the CCC process, which make it easy to understand the CCC mechanism.

The model was established and calibrated according to the experimental set up. This includes the coil volume, the rotational speed of the CCC apparatus, the stationary phase volume retention, the mobile phase flow rates and the K values of the components.

In spite of all the advantages above, this model also have some shortcomings. This model needs to be calibrated for each experimental condition, using a mixing/settling effective efficiency, which might be complex. All CCC modes could be predicted with this model. Besides, this model introduced a very slight variation in its output, due to its probabilistic nature.

2.5. Temperature dependence plate model

Prof. Wei [16] found that none of the models reported before included the temperature parameter, which may lead to the inaccurate result. In some cases even minor change in temperature can lead to a great difference in the partition coefficient (K) values. In CCC operation, the temperature change is really common if the CCC instrument has no temperature controller. The influence of temperature on the partition coefficient of target compounds in solvent system was discussed. A new temperature dependence plate model was produced. Using the parameter of plate coefficient and temperature, this model solved the resolution problem. In the plate model, it was assumed that the chromatographic column contains a large number of separate layers, which are called theoretical plates. Thorough equilibration of the sample between the stationary and mobile phases occurred in each ‘plate’, and the analyte moved through the column by transfer of equilibrated mobile phase from one plate to another. Plate efficiency is defined as below: the equilibrium produced by an actual plate of a distillation column or countercurrent tower extractor compared with that of a perfect plate, expressed as a ratio. Plate efficiency is related to many factors, such as viscosity, flow rate, rotation speed, etc., which makes it difficult to measure by experimental approach. The plate efficiency was calculated from inverse computation in this model. seen from Fig. 4, this temperature dependence plate model is more accurate in predicting CCC separation and well explain why CCC partition efficiency is not the same in different seasons without temperature controller.

Fig. 4.

Modelling result using temperature dependence plate model. Comparison of simulated results and without considering temperature effect. [16] Cited from Wei, Y.; Wang, F.; Wang, S.; Zhang, Y. J. Chromatogr. B. 2013, 933, 30–36.

2.6. Physical models

In addition to mathematical models in modeling CCC, there are also some physical models. Y.H. Guan established a 3-D physical model for the helical column (termed as the helix model) undergoing type-J synchronous planetary motion, and different types of columns were illustrated in Fig. 5. This model was used for understanding the effect of helix angle on the phase behavior, which is for the most popular multi-layer helical column geometry [17]. All objects with different densities present in the rotating coil are driven toward the head of the coil. This type of forces was termed as the Archimedean screw force. Under the type-J planetary rotation and with β > 0.5, the internal surface of the column exerts a drag force primarily in the head-to-tail (not tail-to-head) direction, irrespective of heavy or light phase. This drag force can be arranged to counteract the liquid-to-liquid drag force which are caused by flowing the mobile phase through the stationary phase. Consequently the liquid stationary phase could be retained throughout the tubular path of the column to a reasonable extent. Furthermore, the Archimedean screw force is monotonically related to the β-value for this device type, especially when β≥0.5. These findings can explain why stationary phase retention reduces when mobile phase flow rate increases and often increases when rotational speed of rotor increases.

Fig. 5.

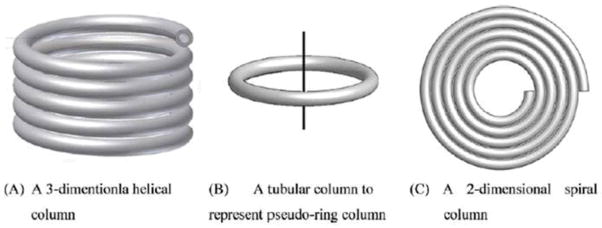
An illustration of (A) the helical column, (B) the pseudo-ring column and (C) the spiral column studied. [17] Cited from Guan, Y.H.; Heuvel, R. J. Chromatogr. A. 2011, 1218, 5108–5114.

The locus of a synchronous type-J planetary motion was described by Ito. The information on the column geometry was required for an improved understanding on physical forces leading to stationary phase retention and the mixing-settling pattern of the two liquid phases. By assuming the CCC column as a pseudo-ring coil, location vector on such a column undergoing the dynamic motion can be quantified in the 3-D Cartesian coordinate system. Then, the initial angle for location on the column was added to the original model for generalization. This generalization was used for distinguishing different locations on the coil.

This pseudo-ring model explains the effects of the rotor’s rotation speed (ω) and the β-value on stationary phase retention and phase mixing intensities. Besides, the pseudo-ring model simplifies the 3-D helical geometry into a 2-D planetary geometry. This model help the understanding of how a liquid stationary phase is retained in the column, and how periodical phase mixing and settling occur.

3. What are the applications of CCC models?

3.1. Multi-dual mode countercurrent chromatography

Dual flow CCC, in which both phases are pumped simultaneously in opposite directions was first suggested for CCD in 1963 [18] and first applied to CCC by Ito [19]. In fact, the dual countercurrent chromatography can be treated as the application of fractional extraction principle to CCC. The dual-mode method was used to reduce the elution time of highly retained compounds [20, 21] or to measure high solute liquid-liquid partition coefficients [22]. Nowadays, the dual-mode method was used to increase the resolution power of a CCC column in the case of two solutes with close partition coefficients.

A universal model is needed to take into account the numerous operating modes and pump out procedures that can be used with CCC. Different models on dual flow have been developed recently [23–25]. Another mode where the phases both move in the same direction, is referred to as co-current CCC [26]. Recently, modelling on this type of CCC has been proposed by Berthod and Hassoun [27].

3.2. Elution–extrusion countercurrent chromatography (EECCC)

This type of CCC mode combines classical chromatographic elution with stationary phase extrusion to save large amounts of solvents and reduce the time of experiments in cases where the retention volumes of solutes are too high [28, 29]. EECCC consists of three steps: the first step is a classical elution, the second is sweeping elution, and the third is extrusion [29]. Theoretical analysis of the three steps of the EECCC providing equations for retention volumes, peak widths, resolution factors, and distribution constants is carried out [29]. The theory of EECCC is based on what can be called as perfect replacement approach: During the sweeping elution period, the “old” mobile phase contained in the column moves and interacts with the “old” stationary phase in the same mode as during the classical elution period. The “new” mobile phase then replaces the old mobile phase in a plug-flow mode.

A math model was used to describe the transport and separation of solutes inside a chromatographic column. Some assumptions were made in the model: After the switch volume V_CM of mobile phase has eluted from the column, sweep elution begins, during which only mobile phase leaves the column. The mobile phase moves and interacts with the “old” stationary phase in the same mode as before. The “new” stationary phase moves and replaces the mobile phase in plug-flow mode that means: (1) the “new” and “old” stationary phases do not mix; (2) after the contacting with the mobile phase the concentration of solutes in the “old” stationary phase in a cell remains constant and this stationary phase volume is simply pushed ahead to the exit of the column. This model can help the choosing of the optimal value of V_CM for conducting elution–extrusion countercurrent chromatography.

3.3. Comparing two models of gradient elution in countercurrent chromatography

There are solutes highly retained in the column in any chromatographic methods. Gradient methods were developed to speed up the retention of slowly eluting compounds. The principle is simple: the elution conditions are gradually modified to increase the elution strength of the mobile phase. This poses little problem in liquid chromatography: the mobile phase composition is changed with no or minimum changes of the solid stationary phase. Some re-equilibration time is needed after the gradient run. Gradients are much more difficult in CCC where the liquid mobile phase is in equilibrium with the liquid stationary phase. Any composition change in one phase may induce a composition change in the other phase [30]. Two different ways to model gradient composition changes in CCC are presented and compared by Shihua Wu [31]. Linear and step gradient elution of a hypothetical mixture of solutes were compared calculating the solute retention volumes. The conclusion is that solutions for the CCC gradient modeling developed independently with two different approaches produced mathematically two very different equations, but both models are truly correct. The popular step-gradient method is also easily modeled and can produce very acceptable separations using an experimental setting simpler than that needed for linear gradient experiments.

4. Conclusion

Since its inception more than two decades ago, the CCC model has grown up to be a matured theory. Concerning the CCC model’s application, it is established that CCC model is a powerful tool for the isolation and purification of natural products. Different models have been developed along the years, which have permitted to predict CCC separations without doing time consuming experiments. Furthermore, the CCC models have proved to be useful for the choosing of proper method to do separations.

Recently, the CCC model has played an important role on the industrial scale-up of countercurrent chromatography. In the near future, a tremendous increase of the CCC utility in the industrial may occur, where CCC model will benefit to all the concerned.