Plasmonic Library Based on Substrate-Supported Gradiential Plasmonic Arrays

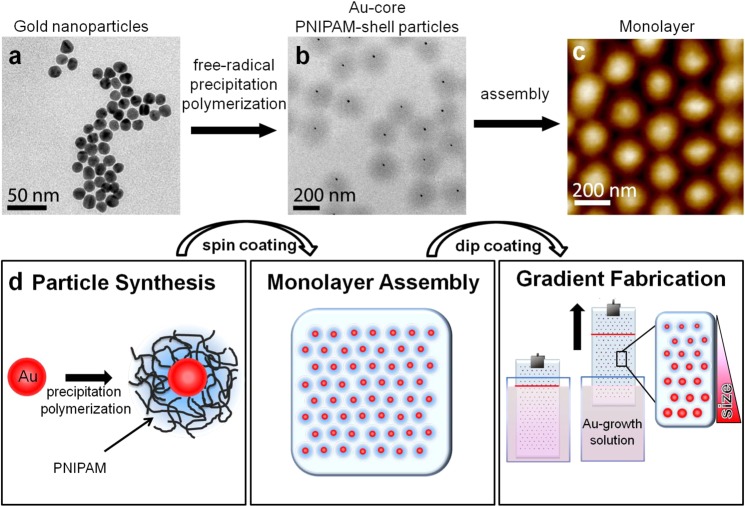
Abstract

We present a versatile approach to produce macroscopic, substrate-supported arrays of plasmonic nanoparticles with well-defined interparticle spacing and a continuous particle size gradient. The arrays thus present a “plasmonic library” of locally noncoupling plasmonic particles of different sizes, which can serve as a platform for future combinatorial screening of size effects. The structures were prepared by substrate assembly of gold-core/poly(N-isopropylacrylamide)-shell particles and subsequent post-modification. Coupling of the localized surface plasmon resonance (LSPR) could be avoided since the polymer shell separates the encapsulated gold cores. To produce a particle array with a broad range of well-defined but laterally distinguishable particle sizes, the substrate was dip-coated in a growth solution, which resulted in an overgrowth of the gold cores controlled by the local exposure time. The kinetics was quantitatively analyzed and found to be diffusion rate controlled, allowing for precise tuning of particle size by adjusting the withdrawal speed. We determined the kinetics of the overgrowth process, investigated the LSPRs along the gradient by UV–vis extinction spectroscopy, and compared the spectroscopic results to the predictions from Mie theory, indicating the absence of local interparticle coupling. We finally discuss potential applications of these substrate-supported plasmonic particle libraries and perspectives toward extending the concept from size to composition variation and screening of plasmonic coupling effects.

The interaction of light with metal nanoparticles leads to the appearance of localized surface plasmon resonances (LSPRs), i.e., the collective oscillation of the conduction electrons at a specific energy. The scattering and absorption cross-section as well as the frequency of the plasmon oscillation depend directly on the particle composition, size, shape, and surrounding effects.^1,2

The fascinating scattering and absorption properties gained metal nanoparticles a broad interest from a fundamental point of view but also for applications in the field of sensing,³⁻⁷ subwavelength optical components,⁸⁻¹² light harvesting in photovoltaic devices,¹³⁻¹⁵ and electrode materials.¹⁶ Such applications require tailored optical properties. Thus, adjusting particle size and shape become essential. Consequently many approaches for the synthesis of size- and shape-controlled metal nanoparticles have been presented in the literature, ranging from procedures of the reduction of the metal salt in solution to seed-mediated growth on a substrate.¹⁷⁻²⁴ Indeed, accurate control of particle growth kinetics was established for a number of synthesis routes, such that size-monodisperse gold and silver nanoparticles are available as building blocks for plasmonic assemblies.^25,26 However, even if well-defined particles can be synthesized, choosing the optimum particle size for the applications mentioned above is a highly challenging task. First, purely theoretical predictions on the ideal particle size for a specific task are difficult. For example surface-enhanced Raman scattering (SERS) from single nanoparticles shows a complex size dependence.²⁷ As another example, the ideal particle size of metal nanoparticles to be used as scattering centers in photovoltaic devices is difficult to estimate due to the strong absorptive losses.²⁸ As well, the catalytic activity of nanoparticles shows a highly complex size and composition dependence. Second, particles are typically used in a substrate-supported form, and hence their optical properties differ from the ones in solution.

Consequently experimental screening studies of substrate-supported nanoparticles of variable size are inevitable for finding the optimal size for particular tasks. For such screening studies, ideally, a library of particles with different size should be immobilized on specific positions of a substrate, such that combinatorial screening of properties under identical conditions is possible. At the same time, interparticle coupling has to be avoided, since coupling results in a complex alteration of LSPR properties.

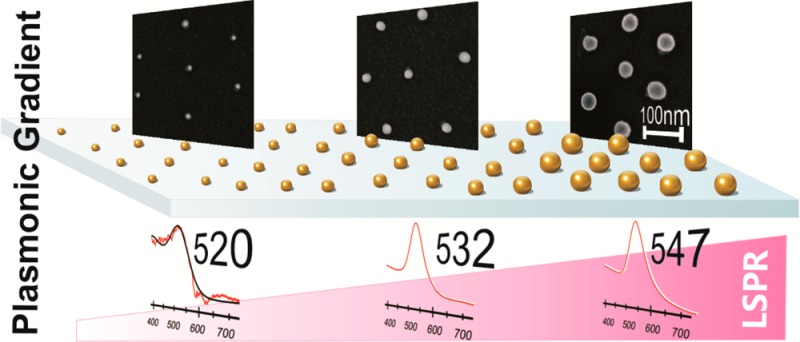
In this work we present the first realization of such a “plasmonic library”. We take advantage of diffusion rate controlled preparation of spherical and highly monodisperse gold particles with distinct particle sizes that are immobilized on a substrate in a way that avoids interparticle plasmonic coupling. Our colloidal building blocks were gold-core/poly(N-isopropylacrylamide)-shell (PNIPAM) particles.²⁹ These particles were deposited on glass substrates by spin-coating in order to prepare a homogeneous monolayer of gold nanoparticles of 9–15 nm in diameter. Due to the polymeric shell, the gold cores were well separated with interparticle distances on the order of 200 nm. Consequently, agglomeration of the particles and hence plasmon resonance coupling are avoided and a constant particle density is ensured. In addition the particles can be fixed to the substrate, which allows for wet-chemical post-treatment. Larger particle sizes were achieved by seeded growth of the adsorbed particles with a growth solution containing surfactant, HAuCl₄, and ascorbic acid. Instead of focusing on a particular particle size, we prepared a uniaxial gradient of particle sizes on substrates with extraordinarily large macroscopic dimensions. The gradient was achieved using a dip-coating procedure. The immersion time of the substrate in the growing solution determined the reaction time. Thus, a direct investigation of particle growth in terms of particle size as a function of time is accessible. Our system shows diffusion-limited growth, which allows the exact size adjustment, but also size predictions become possible. Furthermore, we observe neither Ostwald ripening nor secondary nucleation.

Due to the continuous gradient in particle size, the prepared substrates show a gradient in plasmonic properties, too. The optical properties were investigated by UV–vis spectroscopy, and the results were compared to theoretical predictions from Mie theory.³⁰ Since the particle monolayer has a constant particle density independent of the position on the large substrate, the optical changes along the particle gradient are caused solely by the changes in particle size.

The presented approach is fast, cost-effective, and versatile in terms of accessible particle sizes. Since the interparticle distance is determined by the thickness of the PNIPAM shell, larger or smaller separations are achievable through tuning the polymer thickness.³¹ This will for example allow for single-particle spectroscopy and sensing studies and the effective screening of the particle performance.

Results and Discussion

The basis of our substrate-supported plasmonic arrays are gold-core/poly(N-isopropylacrylamide)-shell particles. These inorganic/organic hybrid particles were synthesized in two steps. First the gold cores were synthesized via the method of Turkevich and Enüstün²⁰ (Figure 1a) and afterward encapsulated in a PNIPAM network by free-radical precipitation polymerization (Figure 1b). The diameter of gold cores (prior encapsulation) was measured with TEM and found to be 15.4 ± 1.6 nm. The corresponding UV–vis extinction spectra can be found in Figure S1 in the Supporting Information.

Figure 1.

TEM images of (a) the Au cores prior to polymer encapsulation and of (b) the Au-core/PNIPAM-shell particles. The shell is visible as the dark gray corona around the gold cores. (c) AFM height image of a monolayer of the core/shell particles deposited on glass by spin-coating. (d) Depiction of the gradient fabrication: First the core/shell particles were synthesized. Second the particles were deposited on glass substrate via spin-coating. In the last step the substrate was mounted on a dip coater and immersed in an Au growth solution and pulled out.

Figure 1d depicts how the surface coatings with a gradient in plasmonic properties were prepared. After the particle synthesis a monolayer of well-separated gold nanoparticles was produced by spin-coating of the gold-core/PNIPAM-shell particles onto glass substrates. This deposition results in a close-packed monolayer of particles, which has locally hexagonally close-packed structures. Due to the PNIPAM shell, a well-defined separation of the gold cores is achieved.³¹ Thus, plasmonic coupling between the gold cores by aggregate formation can be avoided.³² Our self-assembly approach via spin-coating of the gold-core/hydrogel-shell particles differs from recent works reported in the literature, which focus on systems with plasmonic coupling. These assemblies utilize small interparticle distances, which can be achieved by short spacers such as polymer ligands,^33,34 DNA,³⁵ or polymeric spacers combined with Langmuir–Blodgett techniques.^36,37 A representative AFM image of the spin-coated monolayer is presented in Figure 1c and in the Supporting Information, SI 2. The radial distribution function of SI 4 shows five distinct peaks, which emphasizes also the quality of the monolayer. In the last step the gradient in particle size was created by in situ overgrowth of the deposited colloids. Before the overgrowth the particles were physically immobilized on the substrates by short thermal treatment for the following modification. In order to change the gold particle dimensions of the adsorbed Au-PNIPAM particles, a gold growing solution containing CTAB, HAuCl₄, and a weak reducing agent (ascorbic acid) was used. To produce a gradient in core size, and therefore in plasmonic properties, the sample was mounted on a dip-coater. The glass slide with the particle monolayer was fully immersed into the gold growing solution. The substrate was pulled out immediately with decreasing speed.

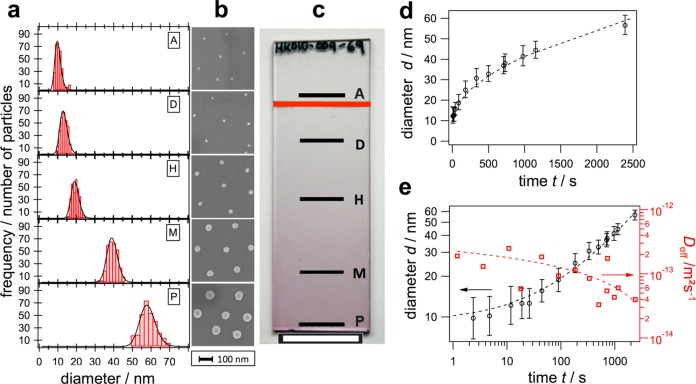
In order to create substrates with a well-defined distribution of nanoparticle sizes and consequently well-defined localized plasmonic properties, the kinetics of nanoparticle growth has to be considered when choosing the dipping protocol. The dipping experiment is performed under a massive excess of gold ions in solution, such that nanoparticle growth is not affected by depletion of the gold ions in the course of the experiment. As well, secondary nucleation is not observed. As a consequence, the number of particles remains constant throughout the experiment, and only the radius of the assembled gold cores increases. The growth kinetics for post-modification of Au-core/PNIPAM-shell particles in solution has not been quantitatively investigated yet. Studies on the catalytic performance of gold nanoparticles encapsulated in cross-linked PNIPAM networks show that diffusion of reactants is hindered inside the PNIPAM network as compared to free diffusion in water.³⁸ The authors have also found that the diffusion rate decreases with increasing cross-linker content. In addition, surpassing the volume phase transition temperature the diffusion becomes significantly slower due to the collapse of the microgel shell. Hence we expect that the growth of gold nanoparticle cores inside PNIPAM should be limited by diffusion and significantly slowed due to the polymer shell as compared to bare nanoparticles in solution. For a diffusion-limited process, we expect nonlinear growth kinetics with a decrease in radial growth with time (in the simplest case a square-root time dependence). Thus, in order to compensate for the expected nonlinear growth kinetics and arrive at a continuous variation of particle diameter across the substrates, we varied the dipping speed of the samples accordingly. The applied dip-coating ramp for withdrawal is depicted in the histogram presented in Figure S3, illustrating a fast withdrawal speed at the beginning and a deceleration throughout the experiment. Following this growth procedure the particles on the top part of the substrate leave the growing solution first, and particles deposited at the bottom have the longest exposure time in the growing solution. The solid red line in the photograph shown in Figure 2c displays the maximum immersion depths. The differences in exposure time lead to a continuous increase of core diameters from top (position A) to bottom (position P).

Figure 2.

Particle size investigation along the gradient: (a) Histograms of the particle size for five different positions on the substrate (details for all 16 spots can be found in Figure 5) with diameter increasing from top to bottom (positions A to P) and (b) corresponding SEM images. (c) Photograph illustrating the macroscopic appearance of the glass slide, where the color gradient is attributed to the increasing particle size from position A (smallest gold cores, not overgrown) to P (largest, overgrown gold cores). The black lines indicate the positions on the substrate. The red line marks the maximum immersion depth. The scale bar is 2 cm. (d) Growth kinetics evaluated by AFM. (e) Effective diffusion coefficient (D_eff) evaluated by incremental regression of the change in size using eq 1. Dashed curves are guides to the eye.

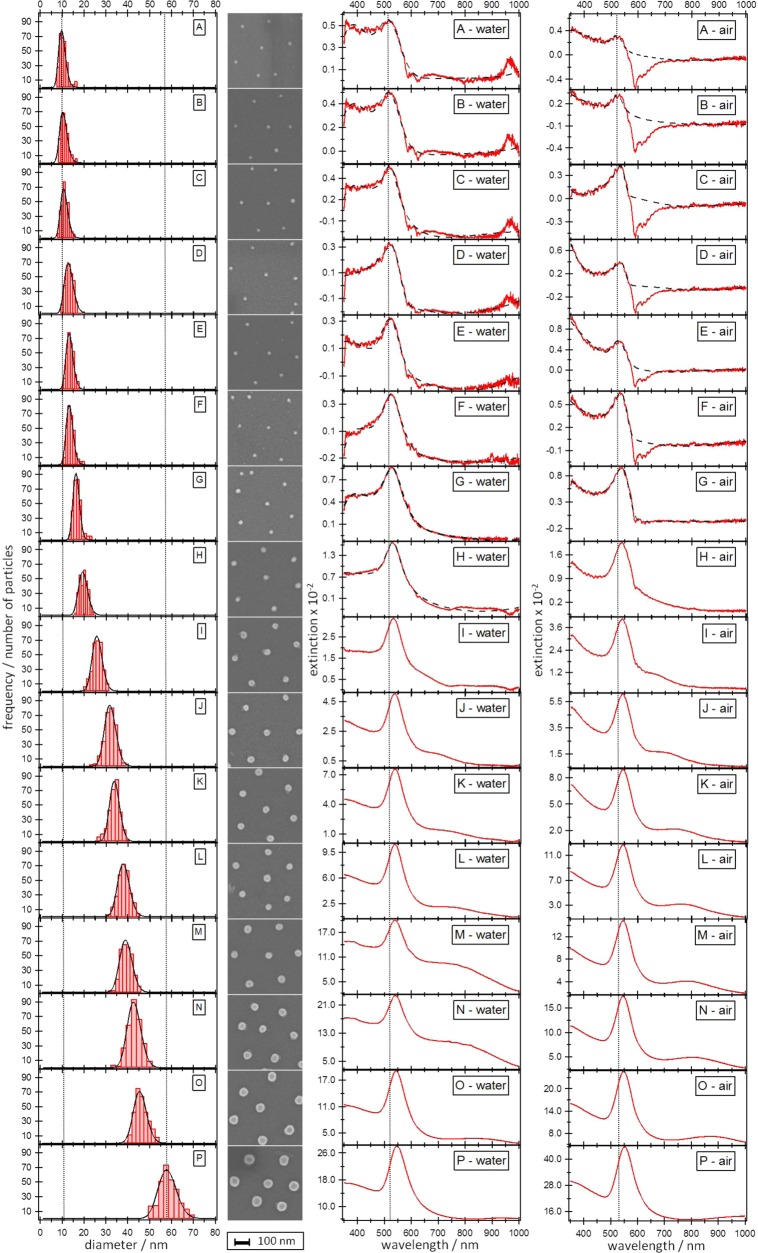
To investigate the gold-core diameter, we performed atomic force microscopy (AFM) at 16 positions on the substrate (see Figure 5 for a complete overview of particle sizes for all positions). The z-resolution of AFM is very reliable from the subnanometer to the micrometer regime and therefore suitable for size investigations of the experimental diameter range.³⁹ Before the AFM images were recorded, the polymer shell was removed by thermal treatment at 550 °C. This is necessary in order to be able to analyze only the dimensions of the gold cores. Since this step influences the spectroscopic properties, it was carried out after the spectroscopic characterization reported later. For each position on the substrate, 300 particle cross sections of particles with a circularity larger than 0.85 were analyzed. The results of five individual positions are shown in Figure 2a (see Figure 5 for a complete data set). In order to determine the mean diameter at each position, we applied log-normal fits to account for slight deviations from normal distributions (see Figures 2a and 5). From the results the increase in diameter from 9.2 (+4.9/–4.5) nm to 56.6 (+3.9/–2.7) nm from position A to P is clearly visible, which results in an average size increase of 0.77 ± 0.05 nm/mm. The diameter obtained from AFM at position A, where no overgrowth happened (not immersed in the growing solution), is slightly smaller than what we obtained from TEM measurements. This was also observed in ref (31). Considering the error for both measurement techniques, AFM and TEM, the particle sizes are in the same range. The SEM pictures presented in Figure 2b show the particles at the corresponding positions without the shell (after thermal treatment). The size increase along the gradient is clearly visible. The images also prove the position stability, because the particles have not aggregated during the overgrowth. They are still assembled in a hexagonal fashion and well separated from each other. The period of the hexagonal arrangement of particles was analyzed by a radial distribution function (RDF), from which the average nearest neighbor distance between the centers of gold cores and the quality of the monolayer can be determined (see Supporting Information SI 4). As expected, the RDF exhibited an average intercore separation of 233 nm, which is in good agreement with the hydrodynamic diameter (253 nm, DLS) of the core–shell particles. Interparticle coupling comes into account when the gap between the two particles is less than 2.5 times the particle diameter.⁴⁰ Consequently, we can neglect the interparticle coupling because the expected minimum gap between the particles is still about 3.2 times the particle diameter when the system reaches its maximum particle size of 56.6 nm. The SEM images also reveal the high quality of our growth procedure, since no additional particles appeared on the substrate, and hence secondary nucleation is completely avoided.

Figure 5.

The first column depicts histograms of all measured spots of the substrate A to P with increasing particle diameter. The second column shows the corresponding SEM images. Columns 3 and 4 show the related UV–vis extinction spectra in water and in air.

The evolution of the particle diameter as a function of the exposure time allowed for a quantitative analysis of the growth kinetics. Figure 2d displays the increase in diameter with time as obtained by AFM. As expected for a diffusion-limited process, the increase in size slows over time.⁴¹ From the evolution of the particle size the effective diffusion coefficient (D_eff) can be evaluated based on Fick’s first law of diffusion: We consider that a known amount of seed particles with initial radius r₀ is introduced into a supersaturated solution containing a concentration c of Au⁺ ions, at t = 0. The seed particles (r₀ = 4.6 nm, AFM) are much larger than the Au⁺ ionic species (r_Au+ = 0.137 nm).⁴² Furthermore, we assume that (a) the seed particles are immobilized on the substrate and thus do not aggregate, (b) no nucleation occurs during the seeded growth process, and (c) particle growth may be viewed in terms of the reduction of the Au⁺ ions to Au⁰ on the surfaces of stationary seed particles. The flux J of Au⁺ ions toward the seed particles is given by Fick’s first law of diffusion: J = −D∂_rc. At steady state, the number of ions per time reaching the seed particle is j = 4πr²|J|. Assuming a linear concentration gradient of Au⁺ between the seed particle surface and the bulk solution, we have j = 4πrDc_∞, where c_∞ is the concentration of Au⁺ ions at infinite distance from the central seed particle of radius r. Assuming that only the Au⁺ ions undergo Brownian motion, characterized by a diffusion coefficient D, then the volume growth of the seed particles is ∂_tV = jV_Au0, i.e., the ion flux j times the partial volume increase per ion (r_Au0 = 0.144 nm),⁴² which yields r dr = V_Au0Dc_∞ dt. If the aqueous phase is of infinite volume, then the bulk concentration of Au⁺ is constant (c_∞ = 0.413 mM) and the equation may be integrated with the initial condition r(t = 0) = r₀ to give the effective diffusion constant D_eff. Thus, the resulting growth law is r² – r₀² = 2 V_Au0D_effc_∞t, which can be solved for D_eff:

1

Considering the complete growth process, we found a mean effective diffusion coefficient of ⟨D_eff⟩ = 6 × 10^–14 m² s^–1, i.e., about 3 orders of magnitude slower than for CTAB-stabilized Au⁺ ions in aqueous solution. The Stokes–Einstein relation predicts a D_Au+@CTAB = 9 × 10^–11 m² s^–1 for Au⁺ species complexed with stabilizing cetylmethylammonium bromide (CTAB) micelles of 6 nm diameter⁴³ in pure water at 30 °C. This deceleration could easily be due to the slower diffusion inside the PNIPAM shell, which acts as a diffusion barrier, and the confined location of the seeds at the surface (not being distributed homogeneously in the bulk solution).

The high data density of our AFM study also allows for an incremental investigation of the diffusion evolution and thus the time-dependent character of D_eff. The time evolution of the effective diffusion coefficient is depicted in Figure 2e for each individual growth step. Apparently, D_eff decreases almost a full order of magnitude throughout the growth process. The double-logarithmic plot in Figure 2e indicates the direct correlation of the diffusion deceleration and the size increase of Au cores inside the PNIPAM shells.

We believe that the deceleration of the diffusion is related to morphological changes of the PNIPAM shell. Upon growth, the expansion of the core particle may induce a compression of the PNIPAM network in close vicinity. Thus, a more compact polymer interphase⁴⁴⁻⁴⁶ would hinder the transport from bulk solution through the shell membrane. A detailed investigation of this rather complex behavior will be addressed in a future study and is not in the scope of the present work.

The impact of the change in core size on the plasmonic properties of the particle monolayer is already visible with the bare eye. In the photograph shown in Figure 2c a pronounced color gradient from nearly transparent to deep purple from the top to the bottom of the substrate is visible. This impression on the macroscopic scale is an indication of the gradient in Au-core size. The increase in color intensity can be attributed to a rise in extinction of the overgrown gold cores. This size gradient leads to position-dependent plasmonic properties.⁴⁷ For the optical characterization we performed UV–vis extinction spectroscopy. The results for five positions along the gradient are presented in Figure 3a and b (for all 16 positions see Figure 5). The measured area was 7 × 1.3 mm² due to the beam size of the UV–vis spectrometer. The rectangular illumination spot was set perpendicular to the dipping direction (indicated by the black lines in the photograph of Figure 2c). Since the measurement averages over a large population of nanoparticles, a local ensemble average of spectroscopic properties is analyzed.

Figure 3.

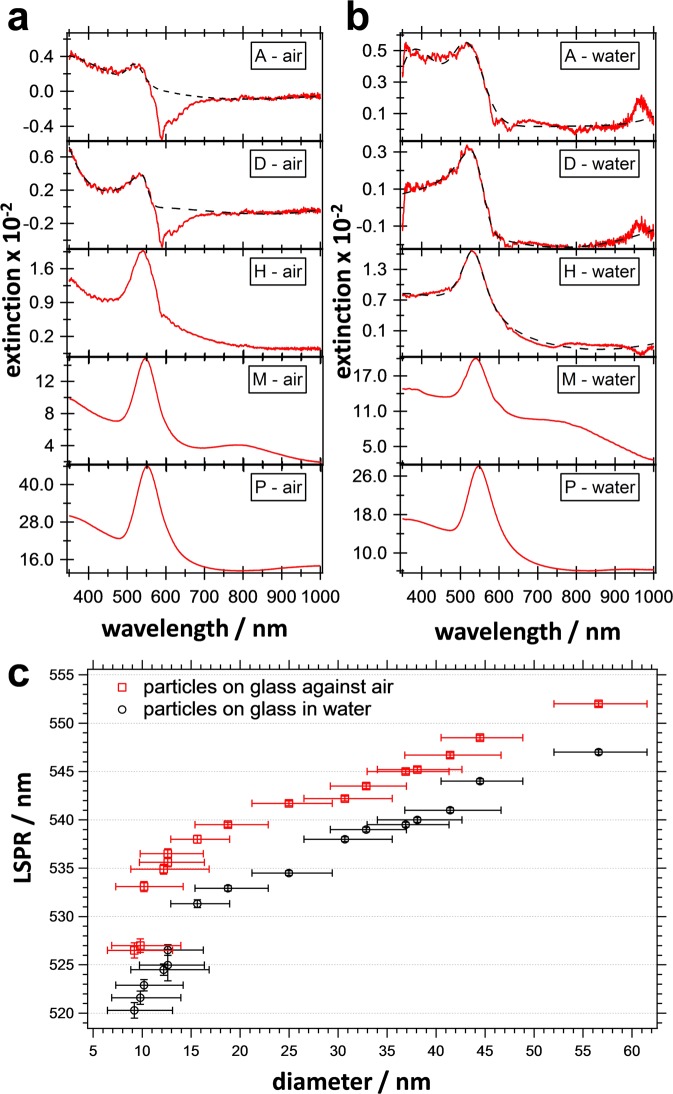
Results from UV–vis extinction spectroscopy of the gradient substrate. Spectra recorded at five different positions measured (a) against air and (b) in water (details for all 16 spots can be found in Figure 5). (c) LSPR positions as a function of core diameter (determined from AFM).

In order to determine the influence of the refractive index of the surrounding medium on the plasmonic properties, we performed extinction measurements against air as well as in water. The spectra were taken in 4 mm steps starting from the original, not overgrown particles, at position A. The extinction spectrum recorded at position A is noisy, and only a week signal was detected. In order to determine the LSPR position, we fitted the spectra with a Lorentzian function (black dotted line). Going from the original particles at position A along the gradient to position P, two effects are visible: On one hand the extinction rises by 2 orders of magnitude, and on the other hand the LSPR position shifts to higher wavelengths. The higher extinction cross-section can be attributed to the increase in gold particle diameter only since the number of particles per area is constant throughout the whole substrate. In other words, the measurement at position A analyzes nearly the same number of gold particles as the measurement at position P. The increase in extinction with increasing particle size can be attributed to an increase in the volume fraction of gold in the plasmonic coating. The volume fraction of the plasmonic particles in a hypothetical layer of gold can be calculated using the gold core diameter as the height of the plasmonic layer and the surface coverage, i.e., the number of gold particles per area. The results are presented in Figure S5A, where the volume fraction is plotted against the logarithm of the immersion time. The volume fraction increases by 2 orders of magnitude from 7.4 × 10^–4 from the original core diameter at position A to 2.6 × 10^–2 at position P. Apart from an increase in extinction along the gradient, the LSPR peak is red-shifted due to the increasing diameter. The red shift of the LSPR with increasing particle size is well known from literature.^48,49 A shoulder at higher wavelength can be observed in the extinction spectra of larger core dimensions shown in Figure 3a and b. This shoulder shifts to higher wavelength for increasing particle diameter (see Figure 5 going from position I to P). We attribute the shoulder to particles with nonspherical morphology such as rods, plates, or triangles.⁵⁰ These morphologies can evolve during the particle growth due to the polycrystallinity of the used seed gold particles. It is well known that the growth velocity of plasmonic nanoparticles is different on different facets, which can lead to anisotropic particles.¹⁷ For larger growing times, also elongation of the rods is supported, which leads to a red shift of the longitudinal peak of the rods—visible as the shoulder—to the near-infrared.⁵¹ In the graph shown in Figure S5B the percentage of nonspherical objects is plotted against the logarithm of the immersion time. For this analysis at least 1400 particles were counted at each position on the substrate. Particles were considered as spherical when the circularity was higher than 0.85. The ratio of nonspherical gold cores is not higher than 12%, and therefore their spectral contribution is not dominating the extinction spectra. The LSPR intensities and positions are mainly influenced by the varying diameter and the refractive index of the surrounding medium.

Since we measured the UV–vis spectra at similar positions as we determined the particle size, we can plot the LSPR position as a function of the core diameter (Figure 3c). With increasing particle diameter the LSPR peak is shifted toward larger wavelengths. An overall LSPR shift of 25.5 nm for measurements against air and 26.7 nm in water is observed when the spectra measured at positions A and P are directly compared. The LSPR could be shifted further toward red upon additional size increases, which was not in our interest. Larger core sizes would inherently result in a broadening of the LSPR extinction peak associated with a loss in absorption and a strong increase in scattering.²⁷ Surprisingly the LSPR at each sample position measured against air is red-shifted compared to the LSPR in water. This behavior is different from that expected for bare gold particles, where a red shift is observed as the refraction index of the surrounding medium changes from n = 1.00 (air) to 1.33 (water).

The presence of the polymer shell, however, explains these findings.^52,53 For measurements against air the PNIPAM shell is in a dried state. The local polymer density in close vicinity of the gold nanoparticle cores is expected to be much higher compared to the swollen state (sample immersed in water). Therefore, the local refractive index is rather high, although the substrate-surrounding medium is air. In contrast, if the substrate is immersed in water, the PNIPAM shell swells for temperatures below the volume phase transition temperature. In this case, the polymer density in the vicinity of the gold cores decreases significantly. Thus, the local refractive index at 25 °C will be close to the value of water due to the rather large degree of swelling. Although the swelling of the polymer shell will not be as high for particles adsorbed on a substrate as compared to a particle dispersed in aqueous solution, the water content in the shell can easily reach 80–90%.⁴⁹ Hence, the PNIPAM shell plays a crucial role in the position of the LSPR peak. Recently Tagliazucchi etal. showed in theoretical studies that the LSPR peak always shifts to higher wavelengths when the solvent for a gold-core/PNIPAM-shell particle is changed from good to bad.⁵⁴ This observation implies that the red shift expected due to increasing polymer density always overcomes the blue shift expected from decreasing layer thickness.

In our case the increase of the local refractive index is triggered by water evaporation during drying and therefore an increase in the polymer fraction in close proximity around the core. Even if a residual water content of 12% is considered in the PNIPAM network for the dried state, which is known in the literature,^55,56 the overall polymer fraction in the dried state has to be higher around the core than for the water-immersed particles. Since the refractive index of the polymer PNIPAM (n = 1.52) is higher than that of water, the red shift in our experimental results can be explained.^54,55

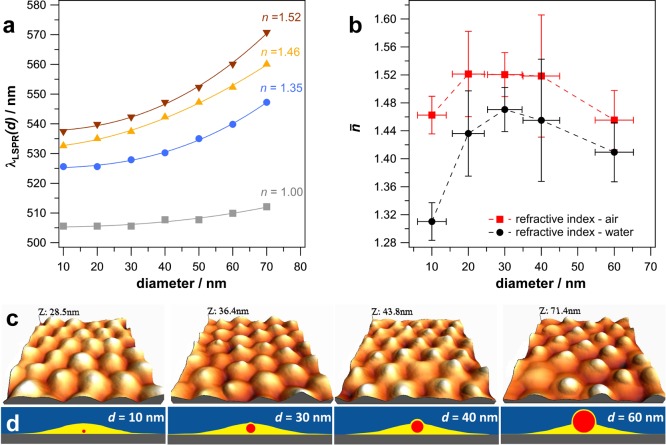
To quantitatively describe the red shift of the plasmon resonance wavelength λ_LSPR with increasing gold nanoparticle diameter d, we used the allometric power law as follows:

2

with k as amplitude, a as scaling exponent, and c as offset constant (for values, see Supporting Information SI 6). To the best of our knowledge, the power law description is a more precise description of the plasmonic red shift compared to an earlier publication, which used an exponential power law with respect to a bulk refractive index change.⁵⁷Figure 4a shows the approximation of the allometric power law to the Mie theory modeling at different surrounding refractive indices.⁵⁸ The plasmon resonance positions for the used particle diameters and four different refractive indices ranging from air (n = 1.00) to glass (n = 1.52) are determined. Consequently, from theoretical modeling we expect a concave shape of the plasmon resonance with increasing diameter (Figure 4a), but our experimental observation shows a convex characteristic (Figure 3c). To discuss this discrepancy, we derived a so-called average surrounding refractive index n̅ from the plasmon resonance position for a specific particle diameter. An intermediate parabola fitting step is necessary to obtain the surrounding refractive index from the plasmon resonance position at a given particle diameter. This intermediate step is described in more detail in the Supporting Information SI 7. The results of the performed analysis are shown in Figure 4b. In the swollen state the refractive index changes between 1.31 ± 0.03 and 1.47 ± 0.03. In the dried state the refractive index lies between 1.45 ± 0.04 and 1.52 ± 0.06 and therefore 0.08 ± 0.04 higher compared to the swollen state. These findings reveal indeed that the increased polymer density in the dried state leads to a larger refractive index in the nanoparticle vicinity as compared to the water-swollen system. However, the calculation of the average refractive index based on the experimental LSPR positions considers a homogeneous refractive index environment. Due to the finite size of the PNIPAM shell, potential density inhomogeneities in the shell, and the presence of the glass substrate (n = 1.52) underneath the adsorbed particles, the real refractive index environment is more complex. This complexity can be seen in the AFM height profiles in Figure 4c and is also illustrated in the scheme in Figure 4d. The AFM images were recorded at four sample positions with different core sizes increasing from left to right. For small-core dimensions (approximately 15 nm) the core is nearly invisible (image on the far left in Figure 4c). On growing the gold particle inside the network (approximately to 60 nm), the core becomes more and more pronounced. Finally, the gold particle is clearly visible and the PNIPAM shell is stretched around the core particle (fried egg shape). The scheme in Figure 4d depicts cross sections of the system and represents the possible structural morphology of the deposited particles. Despite the complex setup, the plasmonic shift can be described sufficiently enough by an average surrounding refractive index model based on Mie theory.^2,30 This simple theoretical model makes the plasmonic array a valuable template for versatile applications (post-treatment) such as reversible tuning of the plasmonic resonances over the full visible spectrum,⁵⁹ high sensitivity sensing,⁶⁰ and precise mapping of the plasmonic hybridization model.^61,62

Figure 4.

(a) Plasmonic resonance (LSPR) modeled by Mie theory for different surroundings and gold-core diameters. (b) Apparent surrounding refractive index as expected from the experimental LSPR position observed against air and in water. (c) 3D representations of AFM height images in air for increasing core diameters of the core/shell particles from left to right. (d) Schematic depictions of the cross sections through gold-core (red)/PNIPAM-shell (yellow) particles for different core diameters deposited on a glass substrate (gray); blue is the surrounding medium.

Figure 5 summarizes the extremely precise control of both particle size and LSPR that can be achieved by the approach. The large size of the gradient on the centimeter scale together with the very sharp local size distributions allow screening sizes and plasmonic properties in 16 equidistant steps between positions A and P indicated in Figure 2c. Thus, the requirements for a plasmonic library are met for the first time.

Conclusion

We have presented a novel approach for the formation of macroscopic, substrate-supported arrays of plasmonic nanoparticles with well-defined interparticle spacing and a continuous particle size gradient. The core/shell nature of the individual particles allowed for creating monolayers with interparticle distances for which local interparticle coupling effects are negligible. At the same time, post-modification of the substrate-supported arrays allowed for a controlled overgrowth of the plasmonic cores, such that the local particle size could be varied in a gradient fashion between 9.2 and 56.6 nm, which allows for spectroscopic analysis of 16 intermediate sizes. The local particle sizes were determined and the kinetics of core growth could be explained by a diffusion-limited growth model. The hydrogel shell resulted in a reduction of effective diffusion coefficients to ⟨D_eff⟩ = 6 × 10^–14 m² s^–1, which allowed for a precise control of particle sizes. Spectroscopic investigations and comparison to generalized Mie theory show that local plasmon resonance frequency and extinction are systematically varying over a broad range, while the single-particle character of the LSPR is maintained. Consequently, the substrates present a “plasmonic library” that can serve as a substrate for screening experiments to find the optimum size for specific applications.

The concept presented here can be generalized in various ways. First, rather than choosing the hydrogel shell such that interparticle coupling is avoided, thinner hydrogel shells will allow for precisely following the onset of interparticle coupling and systematic studies of near-field effects such as hot-spot formation. In this respect the temperature-sensitive character of the PNIPAM shell can also be exploited to achieve temperature-controlled interparticle separations, especially if a cross-linking step and delamination from the substrate are added, as for example realized in 3D superstructures.^63,64 Second, the overgrowth protocol can be expanded toward probing not only size effects but also compositional effects. First experiments demonstrate successful overgrowth of gold cores with a second metal, opening an additional dimension for combinatorial screening. This will be especially of interest for screening catalytic nanoparticle properties as well as the impact of overgrowth on changes in LSPR characteristics.

Experimental Part

Materials

All chemicals were purchased from Sigma-Aldrich unless mentioned differently: Gold(III) chloride, HAuCl₄·3H₂O (≥99.9%), cetylmethylammonium bromide (CTAB; ≥99.9%), ascorbic acid (≥99.9), N-isopropylacrylamide (NIPAM; 97%), N,N′-methylenebis(acrylamide) (BIS; ≥99.5%; Fluka), potassium peroxodisulfate (≥99.0%; Fluka), trisodium citrate dihydrate (≥99%), sodium dodecyl sulfate (SDS; ≥99.0%), and 3-butenylamine hydrochloride (BA; 97.0%) were used as received without any further purification. Water was purified using a Milli-Q system (Millipore). The final resistivity was 18 MΩcm.

Synthesis of Gold-Core/PNIPAM-Shell Particles

Au-core/PNIPAM-shell particles were prepared as previously reported.²⁹ Briefly the core/shell particles were synthesized in two steps: Gold nanoparticles of 9–15 nm in diameter were prepared by the well-known citrate reduction protocol of Turkevich and Enüstün.²⁰ A 500 mL amount of an aqueous solution of HAuCl₄ ([Au³⁺] = 0.5 mM) was heated until heavy boiling. Then 25 mL of a 1 wt % aqueous trisodium citrate dihydrate solution was added quickly during strong stirring with a magnetic stirrer. After 15 min, the deep-red gold nanoparticle dispersion was allowed to cool to room temperature. The gold particles were then functionalized by the dropwise addition of 3 mL of an aqueous SDS solution ([SDS] = 0.624 mM) and 20 min later by the addition of 0.98 mL of an ethanolic BA solution ([BA] = 2.88 mM). The particles were cleaned and concentrated using centrifugation at 1400 rcf. Several centrifugation steps were necessary to separate the majority of particles from the dispersions. The residues were collected and mixed, leading to a gold nanoparticle stock solution with a concentration of [Au⁰] = 0.011 mM. The as-prepared functionalized gold nanoparticles were encapsulated in poly(N-isopropylacrylamide) shells using free-radical precipitation polymerization. A 791 mg amount of the monomer NIPAM and 161 mg of the cross-linker BIS were dissolved in 200 mL of water in a 250 mL three-neck round-bottom flask. The clear solution was heated to 70 °C and purged with nitrogen. After 15 min of equilibration time, 5 mL of the as-prepared functionalized gold nanoparticle stock solution ([Au⁰] = 0.011 mM) was added dropwise. The polymerization was initiated by the rapid addition of 4 mg of potassium peroxodisulfate dissolved in 1 mL of water. The reaction was allowed to proceed for 2 h under continuous stirring with a magnetic stirrer. The core/shell particles were cleaned by repeated centrifugation/redispersion steps. The final residues were collected, redispersed in approximately 15 mL of water, and freeze-dried.

Substrate Preparation

Microscopy glass slides (Fisher Scientific, Premium microscope slides 12-544-4) were cleaned by using an RCA-1 solution of NH₄OH/H₂O₂/H₂O in the ratio 1:1:5 at 80 °C for 20 min.⁶⁵ The cleaned glass slide was placed on the spin-coater (model P6700, Specialty Coating Systems Inc.) and was coated with a 1 wt % solution of Au-PNIPAM particles, which were deposited by using a ramp of 20 s from 0 to 500 rpm, 20 s from 500 to 1000 rpm, and kept at this speed for 90 s. Both sides of the glass slide were coated. To fix the monolayer on the substrate, the slide was heated by a heat gun for 1 min at 200 °C. For the overgrowth of the 15 nm gold cores the substrate was dipped into a growing solution at 100 mm/min and pulled out with decreasing speed (see Figure S3) using a dip-coater (DC/D/LM, KSV Instruments). The growth solution was prepared by slowly adding 416.8 μL of 0.1 M HAuCl₄ under vigorous stirring to 100 mL of 0.1 M CTAB, and after 5 min 588 μL of a fresh solution of 0.1 M ascorbic acid was added dropwise under vigorous stirring. Finally the substrate was washed by immersing it twice in Milli-Q water at 29 °C first for 20 min then for 19 h. The optical properties of the plasmonic substrate were investigated by UV–vis extinction spectroscopy. To investigate the gold-core dimensions, the PNIPAM shell was removed by heat treatment, following the procedure of Jaber etal. under a nitrogen atmosphere.³¹

Simulation

Classical Mie theory³⁰ is an exact solution of Maxwell’s equations that was applied to model the optical response of Au particles in different media. Extinction cross-sections of ideal spherical particles were calculated by a code implementation based on C. Mätzler⁶⁶ following the formulations of Bohren and Huffman.² We modified the code to allow for screening of the LSPR by variation of the optical constants of the surrounding medium. For the optical constants of gold we applied a fitting of the experimental data by Johnson and Christy⁶⁷ (six coefficients, RMS error = 0.211).

Characterization

UV–vis spectra were taken with a Specord 250 Plus from Analytik Jena. To determine the particle diameter, AFM height images were recorded in intermittent contact mode with a Nanoscope V from Bruker. The height of the particles was determined by cross-section analysis using the program WSxM 5.0 from Nanotec Electronica S.L. The SEM pictures were made with a LEO 1530 VP Gemini from Zeiss operating at 2 kV, and the sample was sputtered with 1.3 nm of Pt. The initial gold nanoparticle cores as well as the initial Au-core/PNIPAM-shell particles were analyzed by TEM using a FEI TF 20 transmission electron microscope operated with an acceleration voltage of 200 kV. Samples were prepared by drop-casting of dilute aqueous dispersions on carbon-coated copper grids (400 mesh). The hydrodynamic dimensions of the Au-core/PNIPAM-shell particles were determined by dynamic light scattering (DLS). DLS measurements were conducted with a standard goniometer setup (ALV, Langen, Germany). Measurements were performed at a constant scattering angle of 60°. We used a HeNe laser (JDSU, USA) with 632.8 nm and a maximum output power of 35 mW as the light source. The sample temperature was regulated by a heat-controlled toluene refractive index matching/temperature bath. Multiple intensity–time autocorrelation functions were recorded and analyzed by inverse Laplace transformation using the CONTIN algorithm.

Supporting Information Available

UV/vis spectra of Au cores and core/shell particles; monolayer fabrication; details on withdrawal process; radial distribution function; analysis of volume fraction of Au cores on glass; plasmonic model based on Mie theory. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.