Determination of cable parameters in skeletal muscle fibres during repetitive firing of action potentials

Abstract

Recent studies in rat muscle fibres show that repetitive firing of action potentials causes changes in fibre resting membrane conductance (G_m) that reflect regulation of ClC-1 Cl⁻ and K_ATP K⁺ ion channels. Methodologically, these findings were obtained by inserting two microelectrodes at close proximity in the same fibres enabling measurements of fibre input resistance (R_in) in between action potential trains. Since the fibre length constant (λ) could not be determined, however, the calculation of G_m relied on the assumptions that the specific cytosolic resistivity (R_i) and muscle fibre volume remained constant during the repeated action potential firing. Here we present a three-microelectrode technique that enables determinations of multiple cable parameters in action potential-firing fibres including R_in and λ as well as waveform and conduction velocities of fully propagating action potentials. It is shown that in both rat and mouse extensor digitorum longus (EDL) fibres, action potential firing leads to substantial changes in both muscle fibre volume and R_i. The analysis also showed, however, that regardless of these changes, rat and mouse EDL fibres both exhibited initial decreases in G_m that were eventually followed by a ∼3-fold, fully reversible increase in G_m after the firing of 1450–1800 action potentials. Using this three-electrode method we further show that the latter rise in G_m was closely associated with excitation failures and loss of action potential signal above −20 mV.

Key points

• Current methods for determination of the resting membrane conductance in active, action potential-firing muscle fibres are based on the assumptions that the volume and the cytosolic composition of the fibres remain constant during activity.

• Here, we present a microelectrode-based method that without such assumptions measures a range of cable parameters including the resting membrane conductance together with action potential characteristics of individual fibres during intermittent action potential firing.

• The method can be used to study the role of activity-induced regulation of the resting membrane conductance for action potential excitation and propagation in active muscles.

Introduction

The resting membrane conductance (G_m) of skeletal muscle fibres reflects the function of the K⁺ and Cl⁻ ion channels that are open at the resting membrane potential. Classically, G_m of intact fibres has been assessed using a current clamping technique with two intracellular microelectrodes: one electrode is used for injecting currents (current electrode) while the other electrode records the membrane potential (recording electrode) at two or more inter-electrode distances by consecutively penetrating the fibre at different locations. The fibre input resistance (R_in) and length constant (λ) are then obtained from fits of the cable equation to plots showing steady membrane potential change induced by constant current injection against inter-electrode distances (Hodgkin & Rushton, 1946). From these values, G_m can be calculated assuming a constant that characterizes the cytosolic resistivity (R_i) (Hodgkin & Rushton, 1946; Boyd & Martin, 1959; Pedersen et al. 2005). However, the time needed to perform the multiple, consecutive penetrations of the fibre with the recording microelectrode (minutes) does not allow for determinations of more rapid changes in G_m during ongoing muscle activity. To circumvent this problem, G_m in active muscle fibres has in some studies (Fink & Lüttgau, 1976; Pedersen et al. 2009a,b) been estimated by a method where two microelectrodes were placed in the muscle fibre at close proximity, making it possible to determine R_in from a single current injection lasting just 25 ms. The obtained values for R_in during the experiment could then be used to estimate G_m in the active fibre.

While this approach did reveal novel regulation of the muscle specific Cl⁻ channel (ClC-1) and ATP-sensitive K⁺ (K_ATP) channels in active muscle fibres that is important for normal muscle function, the studies by Pedersen et al. (2009a,b) had three important methodological limitations. First, because the electrodes were placed at close proximity in order to directly measure R_in, λ could not be determined and estimates of G_m during the ongoing muscle activity therefore had to assume that resistance of the intracellular space (r_i) and its constituents of R_i and muscle fibre cross-sectional area (CSA) or, equivalently, muscle fibre volume, remained constant during activity. In conflict with this, several studies report that muscle activity is associated with muscle fibre swelling (Fink & Lüttgau, 1976; Sejersted & Sjøgaard, 2000; Usher-Smith et al. 2006, 2009). If fibre volume was actually increasing during the activity the assumption of constant r_i would have introduced overestimates of G_m. Second, since G_m estimates were solely based on observed R_in changes, absolute values of G_m were not obtained directly. Instead R_in changes during activity had to be multiplied by a G_m value determined in resting fibres under similar experimental conditions in order to obtain absolute values of G_m during activity. Third, due to the close proximity of the electrodes, an evaluation of whether the elicited action potentials propagated and determination of their propagation velocities were excluded.

The present study aimed to develop a method for measuring cable parameters in active muscle fibres that did not have these methodological limitations. Here we introduce a three-microelectrode technique that permits multiple cable parameters to be measured in 200 ms, enabling the measurements to be completed between repeated action potential trains. This method which yields absolute values for R_in, λ, r_i and the membrane conductance per unit length of fibre (g_m) in individual muscle fibres, has previously been applied to effectively resting muscles from frogs and rats (Adrian et al. 1970; Adrian & Marshall, 1977) but here we use the method in fibres firing repeated trains of action potentials. We furthermore present a method for describing to what extent R_i and CSA contribute to observed r_i changes during activity. The three-electrode method then provided measurement of G_m during activity without having to rely on the assumptions of a constant R_i and CSA, or values of G_m from resting fibres. Additionally, the three-electrode technique permitted simultaneous determinations of action potential waveform and conduction velocity during the experiments. This made it possible to examine the action potential excitation, waveform characteristics and velocity of fully propagating action potentials.

Methods

Ethical approval, dissection of muscles and solutions

In all experiments extensor digitorum longus (EDL) muscles from adult C57BL/6 mice (12- to 14-week-old, ∼25 g, males and females) or adult Wistar rats (12- to 14-week-old, ∼230 g, females) were used. EDL contains almost exclusively fast-twitch fibres (Edström et al. 1982; Smith et al. 2013). Animals were fed ad libitum and kept under 12 h light/dark conditions at 21°C. To obtain muscles, the animals were anaesthetized with isoflurane, then killed by cervical dislocation. Such handling, killing and use of animals complied with Danish Animal Welfare regulations. No experiments were performed on live animals. After dissection, muscles were placed in an experimental chamber that was perfused (∼25 ml min⁻¹) with standard Krebs–Ringer bicarbonate solution containing (mm): 122 NaCl, 25 NaHCO₃, 2.8 KCl, 1.2 KH₂PO₄, 1.2 MgSO₄, 1.3 CaCl₂, 5.0 d-glucose. To avoid problems with breakage or dislocation of the microelectrodes used for electrophysiological measurements, the contractile activity of the muscles was in all experiments reduced by addition of 50 μm of the myosin II inhibitor N-benzyl-p-toluene sulphonamide (BTS) to the incubation solutions (Cheung et al. 2002). Other studies have shown that this has minimal effect on muscle excitability (Pedersen et al. 2009a) and, furthermore, only reduces energy consumption during activity by ∼20% (Zhang et al. 2006). All experiments were carried out at 30°C and the re-cycled solution was continuously gassed with a mixture of 95% O₂ and 5% CO₂ (pH ∼7.4) throughout the experiments.

Electrophysiological set-up

Individual muscle fibres in intact EDL muscles and the electrodes used for impalements were visualized on a TV screen using a Nikon DS-Vi1 camera and a Nikon upright microscope (Eclipse FN1, DFA, Glostrup, Denmark). The glass pipettes were filled with 2 m potassium citrate resulting in electrode resistances around 15 MΩ. Two electrodes were connected to a TEC-05X two-electrode clamp system (NPI, Tamm, Germany) and the third electrode was connected to a SEC-05X single electrode amplifier system (NPI, Tamm, Germany). Experimental protocols for current injection and sampling of data (>30 kHz) were performed using Signal 4 or 5 and a Power1401 interface (Cambridge Electronic Design Ltd, Cambridge, UK). Retrieval of data values and fitting of data to the cable equation (eqn (1)) to obtain R_in and λ were done using scripts written in Signal.

Two- and three-electrode-based measurements

When G_m of intact fibres is assessed using current clamping techniques the most common approach is to experimentally determine R_in and λ and then calculate G_m from these parameters assuming a constant R_i. Two electrodes have typically been used to determine the steady membrane potential responses to constant current injections at a minimum of three inter-electrode distances. By dividing the magnitude of the membrane responses (ΔV) with the current injected (I) the transfer resistances at the three inter-electrode distances are obtained. These are then plotted against inter-electrode distance and fitted to the cable equation (eqn (1)) that applies to cells of infinite length with a membrane represented by a parallel resistor–capacitor (RC) circuit (Hodgkin & Rushton, 1946). R_in and λ are then obtained from such fits:

(1)

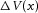represents the steady state change in membrane potential at position x in response to constant current injected at x = 0. From R_in and λ the membrane resistance per unit length of fibre (r_m), r_i and the membrane conductance per unit length of fibre (g_m) can be calculated:

(2)

(3)

G_m can then be calculated by dividing g_m with the surface area per unit length of fibre (FSA). In resting muscle fibres a common approach for estimating FSA is to first determine the cross-sectional area of the fibre (CSA) from r_i assuming a constant value for the specific sarcoplasmic resistivity (R_i), here taken to be 180 Ω cm as determined in resting fibres (Albuquerque & Thesleff, 1968), using eqn (4):

(4)

Next, by assuming the muscle fibre to be a perfect cylinder, FSA can be calculated from CSA as:

(5)

and G_m can then be calculated as:

(6)

The present study introduces a three-electrode method that enables measurements of R_in and λ in between trains of action potentials without having to move electrodes. In these experiments, three electrodes (V₁–V₃) were inserted into the same fibre with inter-electrode distances of around 0.3–0.5 mm (V₁ to V₂) and 1.1–1.8 mm (V₁ to V₃). By switching the current injection between V₁ and V₃ it was then possible to obtain the membrane potential response to the current injections at three inter-electrode distances, because the V₂–V₃ distance was kept at approximately twice the V₁–V₂ distance. Note that, with this approach for alternating the current injections between the V₁ and the V₃ electrodes, the response at the longest distance was determined twice. This allowed for a comparison of the two voltage responses at the longest distances. These were almost identical in all fibres examined, a finding that is compatible with the application of cable theory for infinite cable structures. The current injections that were used for determination of cable parameters were 50 ms long (−20 or –30 nA) and the time between the current injections from V₁ and V₃ was 600 ms. This time between current injections could, however, easily be reduced to allow all the measurements that are required for determination of cable parameters to be performed in less than 200 ms. Trains of action potentials were triggered by injecting large-amplitude currents (300 nA, 1 ms) through V₁. Fibres, in which the resting membrane potential recorded by any of the three electrodes depolarized beyond −60 mV during the experimental protocol, were omitted.

Intracellular water content

Contralateral pairs of rat EDL muscles were dissected out and equilibrated at 4 or 40 mm K⁺ for 90 min in Krebs–Ringer buffer to obtain groups of muscles with normal and increased volume, respectively. To determine the extracellular space of the muscles, the incubation solution contained [¹⁴C]sucrose (0.1 μCi ml^–1 and 1 mm non-labelled sucrose). After incubation, the tendons were cut off and the muscles were blotted, weighed for determination of wet weight and subsequently dried overnight at 60°C. After determination of dry weights, the muscles were soaked in 0.12 m trichloroacetic acid (TCA) for 20 h, after which the content of [¹⁴C]sucrose in the supernatant was determined by scintillation counting. Intracellular water content, expressed per gram dry weight, was calculated from the total water content by subtracting the extracellular water as determined from the muscle content of [¹⁴C]sucrose.

Chemicals and isotopes

All chemicals were of analytical grade. BTS was purchased from Toronto Research Chemicals, isoflurane from Baxter Medical and [¹⁴C]sucrose from Perkin Elmer.

Statistics

Average data are presented as mean ± SEM. Statistical difference between groups was obtained using Student's two-tailed t test.

Results

The experimental approach with the three electrodes is illustrated in Fig. 1: Three electrodes (V₁, V₂, V₃) were inserted in a fibre to give three different inter-electrode distances (X₁, X₂ and X₃) (Fig. 1A). To rapidly determine cable parameters, small-amplitude currents (−30 nA, 50 ms) were injected first through V₁ and then through V₃. This made it possible to obtain the resulting membrane potential responses at the three inter-electrode distances: V₂ recorded the voltage responses at the shortest distance (V₁ to V₂ = X₁) during the V₁ current injection and at the middle distance (V₃ to V₂ = X₂) during the V₃ current injection. The voltage response at the longest distance (between V₁ and V₃ = X₃) was recorded twice, firstly by V₃ when injecting current through V₁ and secondly by V₁ when injecting current through V₃. For each run of current injections, V₁ was additionally used to inject large-amplitude currents for triggering a 3.5 s train of 50 action potentials (300 nA, 1 ms). Figure 1B illustrates the current injections during one run and Fig. 1C and D show typical membrane potential recordings from V₂ and V₃ during such a run of current injections.

Figure 1. Three-electrode technique for determination of cable parameters in between intermittently fired trains of action potentials.

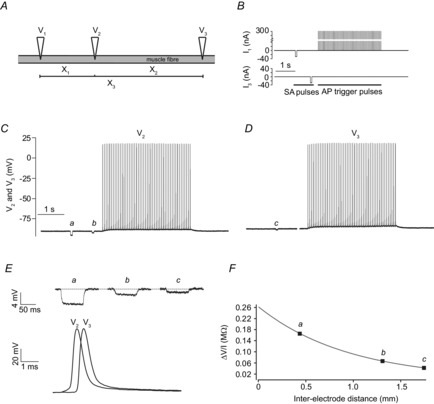
A, illustration of the three microelectrodes (V₁, V₂, V₃) when inserted in the same muscle fibre of an intact muscle. The positions of the inserted electrodes allowed three inter-electrode distances to be identified (X₁, X₂, X₃). Two electrodes were used for current injections (V₁, V₃) and recording of the membrane potential while the third electrode (V₂) only recorded the membrane potential. B shows one run of current injections (I₁, I₃) through the V₁ and V₃ electrodes consisting of small-amplitude hyperpolarizing pulses (−30 nA, 50 ms duration) used for determination of the cable parameters (SA pulses) and a train of large-amplitude depolarizing current pulses (15 Hz, 50 pulses, 1 ms duration, 300 nA) that were used to trigger action potentials (AP trigger pulses). C and D, representative recordings of membrane potential from V₂ and V₃ in a rat EDL muscle fibre during a run of the current injections. Because the voltage recording by electrode V₃ was unreliable during its current injection, the part of the trace in D when current was injected through V₃ has been removed for clarity. E, shows the deflections of the membrane potential (a, b, c) at the three inter-electrodes distances in response to the small hyperpolarizing currents that were injected prior to the train of action potentials. Shown below is an overlay of the first action potential in the trains recorded by V₂ and V₃. F, by dividing the magnitude of the deflections (a, b, c) with the current injected (−30 nA) the transfer resistance was obtained. This was plotted against inter-electrode distance and fitted to the cable equation (eqn (1)) to obtain R_in and λ of the fibre.

It can be seen that the V₂ electrode recorded small deflections in the membrane potential resulting from the small-amplitude currents injected from both V₁ and V₃ (indicated by a and b). The membrane potential response to current injection from V₁ is larger than that observed during current injection by V₃ (a vs. b) reflecting the placing of V₂ at ∼half the distance from V₁ as from V₃. Similarly, the membrane potential response at V₃ to the current injection through V₁ (indicated by c) is smaller than the responses at V₂ reflecting the longest distance between electrodes. Figure 1E shows enlargements of the membrane potential deflections (a, b, c) in response to the small-amplitude current injections (upper panel). It further shows the first action potential of the V₂ and V₃ trains in Fig. 1C and D (lower panel). The action potential was clearly delayed in the V₃ recording when compared to the V₂ recording reflecting the conduction delay between the two electrodes. Also, when comparing the foot of the action potentials at the two electrodes it is clear that the electrotonic membrane potential response to the current through V₁ that triggered the action potential had dissipated almost completely in the V₃ recording confirming that at this electrode the action potential was fully propagating. Figure 1F shows how the membrane potential responses (a, b, c) to the small-amplitude current pulses were used to extract R_in and λ. The magnitudes of the responses were divided by the injected current, and the resulting transfer resistances were plotted against inter-electrode distance and fitted to the steady state cable equation (eqn (1)).

Figure 2 summarizes experiments applying the three-electrode method to determine cable parameters in rat EDL fibres during repeated action potential firing. The experimental protocol consisted of 78 repetitive runs of the current injections shown in Fig. 1B. After this the action potential triggering was stopped allowing the cable parameters to be measured during recovery from the activity. Figure 2A and B shows membrane potential recordings from V₂ and V₃ during the first, the 20^th and the 78^th run. Responses to the small-amplitude current injections were larger in the 20^th run and, contrastingly, smaller in the 78^th run when compared to observations in the first run. This is most clearly seen in the enlarged membrane potential responses from the three runs (upper panel of Fig. 2C). In the lower panel of Fig. 2C the transfer resistances from these three runs have been plotted and fitted to the cable equation (eqn (1)). Compared to the fit from the first run, the fit from the 20^th run yielded a larger ordinate intercept, demonstrating an increased R_in, and its shallower slope reflects an increased λ. In contrast, the 78^th run gave a lower ordinate intercept equivalent to a lower R_in and a steeper slope reflecting a reduced λ. This type of analysis to extract R_in and λ during action potential firing was repeated for all runs of current injection in 14 rat EDL fibres. Figure 2D shows that on average R_in and λ both rose with the onset of action potential firing and remained elevated for around 200–250 s, which corresponds to firing 1450–1800 action potentials (hereafter referred to as Phase 1). With continued action potential firing, R_in and λ both showed marked reductions with the decline in R_in slightly preceding the decline in λ (hereafter referred to as Phase 2). The changes in R_in and λ were reversible with both parameters returning to their respective control levels prior to action potential firing within 100 s after cessation of the activity.

Figure 2. Determination of R_in and λ in action potential-firing rat EDL fibres using the three-electrode technique.

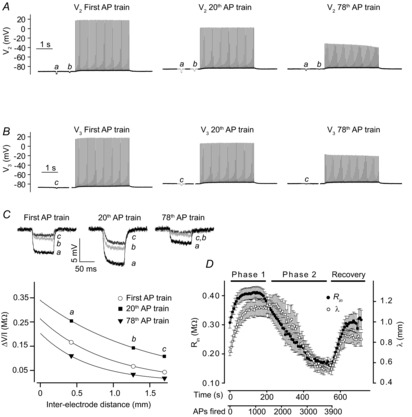
A and B show membrane potential recordings from electrodes V₂ (A) and V₃ (B) during the first, the 20^th and the 78^th run of current injections (see Fig. 1B) in a representative fibre. C, upper panel shows enlargements of the membrane potential deflections from the three runs of current injections in A and B. The lower panel shows plots and fits for the three runs of current injections from which R_in and λ could be obtained. This approach was performed on all 78 runs in the protocol. D shows average R_in and λ from 14 fibres as a function of time and number of action potentials excited. Average data shown as mean ± SEM.

The three-electrode approach for measuring cable parameters during action potential firing also proved useful when studying mouse EDL fibres. As in the rat fibres, the mouse fibres showed initial significant increases in R_in and λ during repeated action potential firing, from 0.30 ± 0.06 MΩ and 0.53 ± 0.03 mm in the first run to 0.35 ± 0.06 MΩ and 0.93 ± 0.04 mm in the 20^th run (Phase 1, P = 0.01 and 0.0002, t test, n = 7 fibres). With continued action potential firing, both R_in and λ decreased significantly, with R_in and λ dropping to 0.19 ± 0.06 MΩ and 0.35 ± 0.04 mm after the 76^th run (Phase 2, P = 0.01 and 0.003, t test, n = 7 fibres). As in rat fibres, the decline in R_in with the onset of Phase 2 slightly preceded the decline in λ. When the action potential firing was ceased, R_in and λ both recovered to their levels prior to action potential firing within 100 s. These data illustrate that action potential firing in mouse fibres also elicited dramatic changes in cable parameters and, furthermore, that the three-electrode method is applicable when studying the smaller mouse fibres.

Determination of g_m and r_i

Since the three-electrode method presented here determines both R_in and λ, it is possible to calculate g_m and r_i using eqns (2) and (3). Figure 3A shows that in fibres from both rat and mouse, the average g_m was roughly halved over the first 200 s of action potential firing (Phase 1) whereas a fully reversible ∼3-fold increase took place at the beginning of Phase 2. While the previous method for determining G_m during muscle activity (Pedersen et al. 2009a,b) assumed a constant r_i throughout the activity, the three-electrode technique revealed that r_i actually underwent clear changes during the action potential activity (Fig. 3B). Since r_i is determined by the specific sarcoplasmic resistivity (R_i) and the cross-sectional area of the muscle fibres (CSA) (see eqn (4)), this shows that either R_i, CSA or both were changing during the activity.

Figure 3. Cable parameters during repeated firing of action potentials in rat and mouse EDL fibres calculated from observations of R_in and λ.

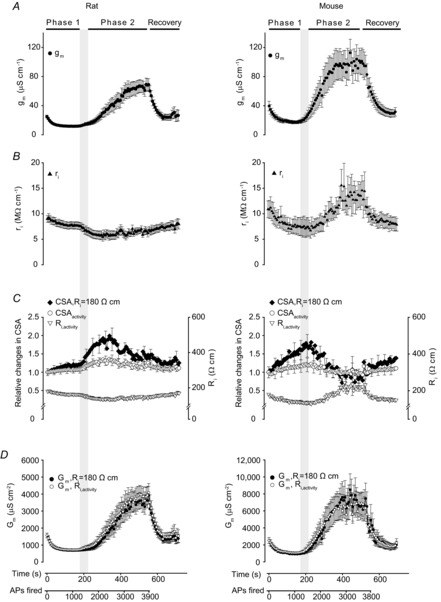
All plots are plotted against the abscissa displayed below D. The shaded vertical bar indicates the time during the experiments when Phase 2 started to develop. A, membrane conductance per centimetre of fibre length, g_m. B, resistance of the intracellular space per unit length, r_i. The observed changes in r_i during the experiments could theoretically be explained from changes in muscle fibre cross-sectional area (CSA), or a combination of changes in CSA and the specific intracellular resistivity (R_i). Thus, C shows both how CSA would change if R_i remained constant at 180 Ω cm (CSA,R_i = 180 Ω cm) and how CSA and R_i would change during the experiments if the increases in CSA represent an additional intracellular cross-sectional area with a resistivity of 65 Ω cm (CSA_activity and R_i,activity; see Results for calculations). For clarity, only every fifth SEM is shown. D, G_m, the resting membrane conductance per square centimetre of surface membrane was calculated either on the assumption of a constant R_i of 180 Ω cm (G_m,R_i = 180 Ω cm) or by using CSA_activity and R_i,activity (G_m,R_i,activity). n = 7 or 14 (mouse and rat, respectively). Average data shown as mean ± SEM.

Determination of G_m

To calculate G_m it was necessary to determine whether the changes in r_i during activity were caused by changes in R_i, CSA or both. Initially, calculating CSA under the assumption of a constant value for R_i of 180 Ω cm (Albuquerque & Thesleff, 1968) using eqn (4) showed that both mouse and rat fibres underwent a marked and reversible increase in CSA of 80–100% with the highest values obtained early in Phase 2 (filled symbols, Fig. 3C). As expected the muscle fibre length remains constant during the experiments, and the increments in CSA during activity would therefore suggest a corresponding 80–100% increase in fibre volume. Although the transient nature of this swelling may to some extent have escaped detection in other studies, where the approaches for measuring fibre swelling had lower temporal resolution, the magnitude of the swelling appeared unreasonably large. However, if swelling-associated water entry caused a decline in R_i then the above CSA calculations would have overestimated the fibre swelling during activity (see eqn (4)). It was therefore possible that the above increments in CSA and volume estimates of up to 100% did at least in part reflect swelling-induced declines in R_i. Prompted by this analysis, an experiment was made to evaluate whether electrophysiological recordings overestimate fibre swelling. Thus, rat EDL muscles were exposed to an elevation in extracellular K⁺ from 4 to 40 mm, an experimental manoeuvre that is known to cause swelling of frog muscle fibres (Usher-Smith et al. 2006). The intracellular water content was then compared between muscles at 4 and 40 mm K⁺ to directly determine muscle swelling and this could then be compared to estimates of swelling obtained in electrophysiological recordings. These experiments showed that while intracellular water content increased by 16.2 ± 0.4% (n = 6 vs. 6) at 40 mm K⁺, the electrophysiological approach relying on a constant R_i of 180 Ω cm suggested a volume increase of 45% (CSA from 2037 ± 108 μm² at 4 mm K⁺ to 2956 ± 123 μm² at 40 mm K⁺, n = 8 vs. 27, P = 0.0005, t test). This confirmed that electrophysiological recordings overestimate fibre swelling, a finding that must reflect a reduction in R_i during swelling. Formalizing this idea, entry of water introduces a lower resistance pathway for intracellular current flow, and the intracellular conductivity at 40 mm K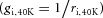⁺ after swelling then becomes:

(7)

where 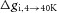reflects the change in intracellular conductivity by fibre swelling and 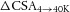represents the actual volume expansion as determined from the water content measurements. From these two parameters the resistivity of the added intracellular volume (R_s) can be calculated to be ∼65 Ω cm using eqn (8):

(8)

This value is close to the resistivity of 300 mm NaCl saline (55 Ω cm, Geddes & Baker, 1967) as might be expected for an isosmotic accumulation of water in the swelling fibres. Having extracted R_s for volume expansion it became possible to give a more realistic determination of CSA during muscle activity. Again the intracellular conductivity is considered to consist of a conductivity from the resting fibre and a conductivity introduced by activity-induced swelling:

(9)

From this the area introduced by swelling (ΔCSA_s) can be isolated to:

(10)

where g_i,activity is the intracellular conductivity during muscle activity, which consist of the conductivity from a resting fibre (g_i,rest) and the conductivity added by swelling (Δg_i,s); adding the area introduced by swelling to the area of the fibre prior to activity (CSA_rest) the cross-sectional area of the fibre during activity (CSA_activity) can be calculated:

(11)

From this the average R_i during activity, R_i,activity, can in turn be calculated using eqn (4):

(12)

This analysis showed that with the lower resistivity of the added intracellular volume, the resistivity of the fibres declined during activity with the largest drop occurring during the transition from Phase 1 to Phase 2 (Fig. 3C, triangles). It further showed that CSA_activity, and therefore the fibre volume, only rose ∼35%.

Having determined R_i and CSA during activity G_m was next calculated (open circles in Fig. 3D). This was compared to the limiting case of calculating G_m under the assumption of a constant R_i of 180 Ω cm during the activity (filled circles in Fig. 3D). Comparison of the two scenarios shows that G_m during activity was largely unaffected by the assumption of constant R_i (compare filled and open circles). Thus, under the assumption of a constant R_i of 180 Ω cm the reduction in G_m during Phase 1 in rats as estimated from the values recorded after 1000 action potentials (APs) was only 4% larger than the values obtained using CSA_activity. Likewise, after 2000 APs corresponding to Phase 2, the assumption of a constant R_i of 180 Ω cm only led to an underestimation of 20%. Figure 3D further demonstrates that very similar magnitudes and timings of G_m changes were observed in rat and mouse fibres. Thus, in both species G_m went through an initial reduction of around 60% during Phase 1, and after firing around 1450–1800 action potentials, it transitioned to its elevated state in Phase 2 of ∼3 times the resting level.

Action potential waveform and conduction velocity during the repetitive action potential firing

The three-electrode technique permitted characterization of the waveform of fully propagating action potentials from the V₃ recording, and, from the latency in the action potential between the V₂ and V₃ recordings, the conduction velocity could be determined. Figure 4A shows overlays of V₂ and V₃ recordings of the first action potential in the first, the 20^th and the 78^th action potential train in a representative rat fibre. Through the protocol, the propagation delay between the V₂ and V₃ recordings rose progressively as indicated by the lengthening of the horizontal lines above the recordings in Fig. 4A that span the gaps between the peaks in the V₂ and V₃ action potentials. From such delays the conduction velocity was calculated for the first action potential in all runs. In both species, this analysis showed that the conduction velocity fell gradually throughout the protocol. In rat fibres it was 2.14 ± 0.19, 1.75 ± 0.10, 1.62 ± 0.11, 1.43 ± 0.15 and 1.24 ± 0.15 m s⁻¹ for the first, the 1001^th, 2001^th, 3001^th and 3801^th action potential, respectively (n = 14 fibres), and in mouse fibres it was 2.02 ± 0.21, 1.50 ± 0.14, 1.10 ± 0.14, 1.02 ± 0.1 and 0.76 ± 0.15 m s⁻¹ for the first, the 1001^th, 2001^th, 3001^th and 3601^th action potential (n = 5 fibres), respectively. When compared to the changes in cable parameters during activity, the conduction velocity appeared to fall gradually during Phase 1 and Phase 2 with only a few fibres showing an accelerated decline in the transition to Phase 2. Contrastingly, Phase 2 was associated with abrupt excitation failure in 5 out of 14 rat fibres and in 2 out of 7 mouse fibres. Excitation failure was categorized as lack of an action potential in both V₂ and V₃ while propagation failure was identified from the presence of an action potential in the V₂ recording but its absence in the V₃ recording. Propagation failure with Phase 2 was observed in 4 of the 14 rat fibres and in 2 of the 7 mouse fibres.

Figure 4. Analysis of action potential waveform and resting membrane potential during activity in rat and mouse fibres.

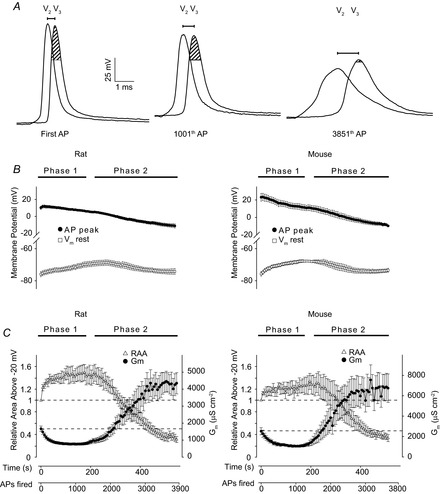
A shows overlays of V₂ and V₃ recordings of the first action potential in the first (First AP), 20^th (1001^th AP) and the 78^th (3851^th AP) run of current injections in a representative rat EDL fibre. The shaded area in the V₃ recording indicates the part of the action potential waveform above −20 mV. B, action potential peak (AP peak) and resting membrane potential (V_m rest) measured by V₃ during the experiments using rat (n = 14) and mouse (n = 7) EDL fibres. C shows the changes in relative waveform area above −20 mV (RAA) of the first action potential recorded by V₃ in each run during the experiments as illustrated in A, together with the calculated G_m. n = 7 or 14 (mouse and rat, respectively). Plots in B and C have been shown on the same time axis displayed below C. Average data shown as mean ± SEM.

Comparing the three pairs of V₂ and V₃ recordings in Fig. 4A, a clear drop in the action potential peak is seen to develop during activity. Also, a slight depolarization of the resting membrane potential is noticed in the middle recordings that contrasts the hyperpolarization/repolarization in the right recordings. The action potential peaks and the resting membrane potential were determined in all fibres and the average observations are shown in Fig. 4B with observations from rat in the left panel and mouse observations in the right panel. In both species a depolarization of around 8 mV occurred during Phase 1. With the transition to Phase 2 the resting membrane potential repolarized to its value prior to activity. Figure 4B further shows that the V₃ action potential peaks declined throughout the protocol. At the transition to Phase 2 the decline in the average recordings of peaks was somewhat accelerated in both species and during this transition the peaks became negative. Importantly, because the onset of Phase 2 occurred with some variation in the different fibres, the averaging tended to smooth the accelerated decline in peaks that was observed in several fibres during transition to Phase 2. Thus, a clear decline in action potential peak during the transition to Phase 2 was observed in 7 out of 11 rat fibres and in 5 out of 7 mouse fibres.

The sarcolemmal action potential triggers the t-system action potential which in turn triggers sarcoplasmic reticulum (SR) Ca²⁺ release by activating voltage sensors in the t-system membrane. Voltage sensor charge movements show that these sensors have a half-activation voltage of around −20 mV (Hollingworth & Marshall, 1981; Chua & Dulhunty, 1988). Provided that the sarcolemmal and t-system action potentials undergo similar changes during repetitive firing, a decline in action potential waveform above −20 mV might reduce SR Ca²⁺ release. The area above −20 mV (illustrated by shaded area in Fig. 4A) of the first action potential in all V₃ trains in the protocol were therefore measured and related to the first V₃ action potential in the first run. Figure 4C shows this relative area of the V₃ action potentials together with G_m during the activity. In both rat and mouse fibres, the area above −20 mV increased during Phase 1 while, contrastingly, during the transition to Phase 2 the area above −20 mV fell precipitously to less than 50% of the value in the first action potential.

Discussion

The present study introduces a three-electrode technique that can be used to determine how a range of cable parameters are affected by repetitive action potential firing. By utilizing this new approach it was possible to test the assumption of a constant r_i that previously had to be made in order to allow G_m changes during muscle activity to be estimated from R_in measurements in active fibres (Pedersen et al. 2009a,b). The method also allowed the determination of whether changes in cable parameters were temporally associated with changes in fibre excitability, action potential waveform and action potential conduction velocity.

Comparison of the three-electrode technique with previous methods for measuring G_m in active fibres

Application of the three-electrode method to measure r_i directly during activity revealed that r_i actually falls during action potential firing in both rat and mouse fibres. The r_i is directly proportional to R_i and inversely related to CSA (see eqn (4)). Since, however, neither R_i nor CSA can be determined directly from electrophysiological measurements of cable parameters, the evaluation of their respective contributions to the recorded changes in r_i required additional information. Here, two different approaches were used to circumvent this problem. In the first approach, G_m was calculated under the assumption that R_i did not change during muscle activity but remained constant at the value of 180 Ω cm determined in resting muscles (Albuquerque & Thesleff, 1968). From this, CSA (eqn (4)) could be calculated, and this could be used to calculate a value for G_m (eqn (6)). In the second approach we reasoned that muscle fibre swelling must reflect the entry of extracellular water to the fibres, and by measuring the increase in water content in muscles swollen at 40 mm K⁺ we estimated that such entry of extracellular water corresponds to adding additional space for intracellular current flow in the form of isosmotic solution. This additional water was determined to have a resistivity of 65 Ω cm approximately corresponding to saline containing 300 mm of NaCl (Geddes & Baker, 1967). Since this resistivity is considerably lower than that of the cytosol in resting fibres (180 Ω cm), an increase in muscle fibre volume during activity will cause a concomitant decrease of R_i (R_i,activity, see eqn (12)). At the same time, the calculated increase in CSA (CSA_activity, see eqn (11)) of the active muscle fibres will be smaller than when calculated from a constant R_i of 180 Ω cm. Thus, if R_i stayed constant at 180 Ω cm throughout the action potential firing activity, the muscle fibre had to swell by around 80–100% to account for the measured decrease in r_i. Contrastingly, given that any increase in cell volume represents additional space for intracellular current flow with a resistivity of 65 Ω cm, the swelling only needed to be around 35% to explain the decrease in r_i. The latter increase in cell volume is in much closer agreement with previous studies employing other methods for volume determination in active muscle. Thus, in a study using XZ-plan confocal scanning of amphibian fibres that allows fast measurements of fibre cross-sectional area during electrical stimulation, it was observed that with prolonged stimulation the fibre volume increased by 20% (Usher-Smith et al. 2006). Using both in vivo and in vitro methods, similar increases in intracellular volume of muscle fibres have been demonstrated in humans during intense exercise (for review, see Usher-Smith et al. 2009). On this basis it seems that the three-electrode technique, with the inclusion of an R_i,activity that depended on cell volume, reliably detects actual changes in muscle volume during repeated action potential firing. An attractive feature of this approach for determination of muscle fibre swelling during activity is the high temporal resolution that the method provides. In addition, because r_i is dependent on both R_i and CSA, and we here demonstrate that R_i falls concomitantly with an increase in CSA, it can be speculated that electrophysiogical determination of volume changes has higher sensitivity than techniques that measure volume directly such as imaging techniques.

Importantly, however, although the calculated volume of the active fibres depended significantly on whether R_i was assumed constant or, more realistically, changed during the experiment (Fig. 3C), the two methods led to almost identical values for G_m (Fig. 3D). Moreover, the observed development in G_m during action potential firing (Fig. 3D) fully confirmed the marked changes in G_m during repeated action potential firing that was originally observed in experiments in rats where the calculations of G_m were based on measurements of R_in using just two electrodes at close proximity and the assumption of constant r_i (Pedersen et al. 2009a,b). This conclusion suggests that the changes in r_i observed in the present study need not preclude the use of R_in measurements to estimate changes in G_m in fibres during activity. Thus, if only G_m is to be measured during action potential firing, the previously presented method, where G_m is evaluated from single measurements of R_in using just two electrodes at close proximity (Pedersen et al. 2009a,b), provides reliable values with very high temporal resolution requiring only around 50–75 ms per measurement. If a more detailed examination of cable parameters is needed together with surface action potential waveforms and conduction velocities, however, the three-electrode method presented here provides a technique for obtaining these measurements with a minimal loss of time resolution requiring around 200 ms per measurement.

Co-temporal changes in cable parameters and propagating action potentials

Analysis of fully propagating action potentials during Phase 1 showed that while the conduction velocity and the peaks of the action potentials tended to drop, there were no observations of excitation or propagation failures. Furthermore, the area of the action potential waveform above −20 mV increased during this part of the activity. These features demonstrate that muscle excitability was well maintained during the first phase of the action potential firing. With continued action potential firing both rat and mouse fibres transitioned into the state of high G_m in Phase 2. The most notable changes in muscle excitability and action potential characteristics that were associated with this transition were the appearance of excitation and propagation failures and marked reduction in the area of the action potential waveform above −20 mV. In contrast, the changes in the conduction velocity during the experiments showed no obvious temporal relation to the changes in G_m.

Since the voltage sensor in the t-system has a half-activation voltage of around −20 mV (Hollingworth & Marshall, 1981; Chua & Dulhunty, 1988), the reduction in action potential waveform area above −20 mV could reduce the efficiency with which action potentials induce SR Ca²⁺ release. Provided that similar changes are induced by the G_m rise on the action potential waveform in the t-system, this would cause failure of voltage sensor activation and, hence, reduced SR Ca²⁺ release. The G_m rise during Phase 2 could represent a cellular mechanism underlying fatigue in fast-twitch fibres by inducing excitation failures and by reducing the action potential waveform in the voltage range that triggers SR Ca²⁺ release.

Conclusion

The three-electrode method presented here allows for detailed electrophysiological measurements of multiple cable parameters including R_in, λ, r_i and g_m together with conduction velocity and waveform characteristics of action potentials with a time resolution of around 200 ms. When combined with inhibitors of the contractile filaments these measurements can be performed repeatedly in action potential-firing muscle fibres. This method makes it possible to study the regulation of ion channels that contributes to the resting membrane conductance and their importance for the excitability of active muscles without the assumptions of a constant volume and constant R_i that were required with previous methods.

Glossary

AP

action potential

BTS

N-benzyl-p-toluene sulphonamide

CSA

muscle fibre cross-sectional area

EDL

extensor digitorum longus

FSA

surface membrane area per unit length of the muscle fibre

g_i

intracellular conductivity

g_m

membrane conductance per unit length of fibre

G_m

membrane conductance per square centimetre of surface membrane

I

injected current

r_i

resistance of the intracellular space per unit length

R_i

specific cytosolic resistivity

R_in

input resistance

r_m

membrane resistance per unit length of fibre

SR

sarcoplasmic reticulum

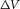
magnitude of the membrane voltage response to constant current injections

λ

length constant

Additional information

Competing interests

None declared.

Author contributions

All authors contributed to the conception and/or design of the experiments. A.R., R.D. and T.H.P. performed the experiments, and they collected and analysed the data. All experiments were carried out at Aarhus University. Data interpretation was done by A.R., R.D., O.B.N., C.L.H. and T.H.P. The article was drafted by A.R., O.B.N and T.H.P. and it was revised critically for important intellectual content by R.D., O.B.N. and C.L.H. All authors approved the final manuscript.

Funding

This work was supported by the Danish Medical Research Council (T.H.P. and O.B.N.), the Lundbeck Foundation (O.B.N.), the Carlsberg Foundation (T.H.P), the A. P. Møller foundation (T.H.P) and the Faculty of Health Science, Aarhus University (A.R.).