Assessment of insulin sensitivity/resistance

Abstract

Insulin resistance is one pretty troublesome entity which very commonly aggravates metabolic syndrome. Many methods and indices are available for the estimation of insulin resistance. It is essential to test and validate their reliability before they can be used as an investigation in patients. At present, hyperinsulinemic euglycemic clamp and intravenous glucose tolerance test are the most reliable methods available for estimating insulin resistance and are being used as a reference standard. Some simple methods, from which indices can be derived, have been validated e.g. homeostasis model assessment (HOMA), quantitative insulin sensitivity check index (QUICKI). For the clinical uses HOMA-insulin resistance, QUIKI, and Matsuda are suitable, while HES, McAuley, Belfiore, Cederholm, Avignon and Stumvoll index are suitable for epidemiological/research purposes. With increasing number of these available indices of IR, it may be difficult for clinicians to select the most appropriate index for their studies. This review provides guidelines that must be considered before performing such studies.

INTRODUCTION

Hyperinsulinemic euglycemic clamp (HEC) is known to be the “gold standard” for the measurement of insulin sensitivity. However, the realization that it is time and money consuming led to the development of a simplified approach in quantification of insulin sensitivity. Various indices of insulin sensitivity/resistance using the data from oral glucose tolerance test (OGTT) were proposed in last 20 years.

There are two groups of insulin sensitivity indices: (1) Indices calculated by using fasting plasma concentrations of insulin, glucose and triglycerides, (2) indices calculated by using plasma concentrations of insulin and glucose obtained during 120 min of a standard (75 g glucose) OGTT [Tables 1 and 2].

Table 1.

The indices for insulin sensitivity/resistance for clinical purpose

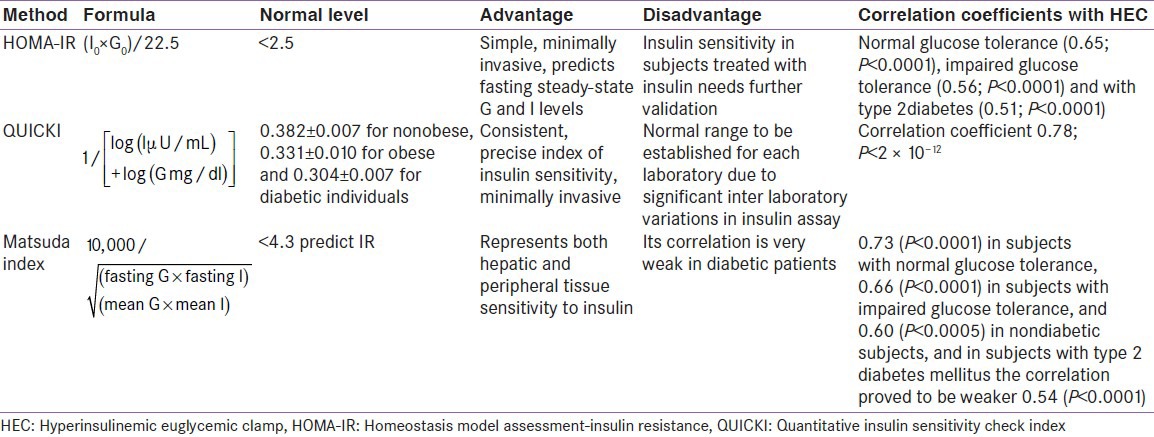
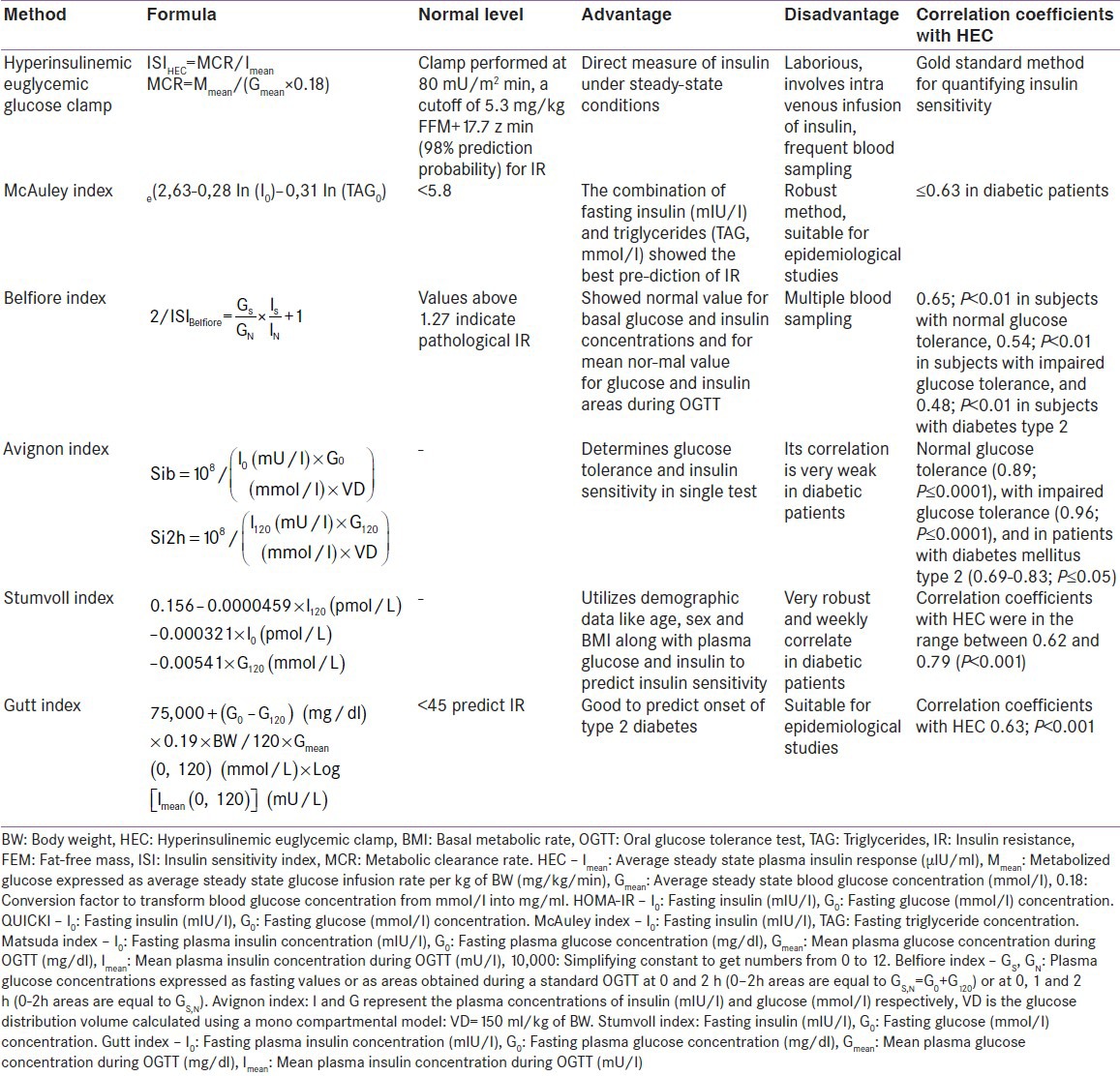
Table 2.

The indices for insulin sensitivity/resistance for epidemiological purpose

Former group include homeostasis model assessment-insulin resistance (HOMA-IR), QUIKI INDEX, and McAuley index while latter include, Matsuda, Belfiore, Cederholm, Avignon and Stumvoll index [Tables 1 and 2].

These indices are conveniently used in epidemiological and clinical studies to predict diabetes development in a non-diabetic population. Their use in clinical practice is limited because of the absence of reference values for normal and impaired insulin sensitivity.

For the clinical uses HOMA-IR, QUIKI, and Matsuda are suitable while HES, McAuley, Belfiore, Cederholm, Avignon and Stumvoll index are suitable for epidemiological/research purposes [Tables 1 and 2].

Insulin resistance is accepted to be a major risk factor in the etiology of type 2 diabetes mellitus, hypertension, dyslipidemia, atherosclerotic vascular disease, and may be a risk factor for coronary heart disease and stroke as well.[1]

Several risk factors (e.g. obesity, physical inactivity, body fat distribution, age and hyperinsulinemia) may be considered markers of insulin resistance. Insulin resistance is a predictor for the development of Type 2 diabetes mellitus even in individuals with normal glucose tolerance. Therefore, it is important to recognize insulin resistance in the pre-disease stage when therapeutic intervention is likely to be more successful than in manifest disease.[2]

Several authors proposed various indices of insulin sensitivity based on the interrelations between the concentration of insulin, glucose and other parameters obtained either in the fasting state or during OGTT and correlated the indices with the data obtained during a HEC.[3]

The HEC-derived index of insulin sensitivity (ISI_HEC, ml/kg/min/μIU ml) is obtained during a steady state period of HEC.

ISI_HEC = MCR/I_mean

where,

I_mean – average steady state plasma insulin response (μIU/ml),

MCR: Metabolic clearance rate of glucose (ml/kg/min).

MCR = M_mean/(G_mean × 0.18), where

M_mean: Metabolized glucose expressed as average steady state glucose infusion rate per kg of body weight (mg/kg/min)

G_mean:Average steady state blood glucose concentration (mmol/l)

0.18 –conversion factor to transform blood glucose concentration from mmol/l into mg/ml.

Correct application of the indices in their proposed form and with the proposed concentration units is of high importance.

Therefore, the aim of this review is to introduce several insulin sensitivity indices, their formulas and units as proposed by their authors, and to evaluate critically the use of some of the suggested indices in insulin sensitivity estimation.

Some of the indices for insulin sensitivity/resistance are given below:

Homeostasis model assessment-insulin resistance

Homeostasis model assessment was first developed in 1985 by Matthews et al. It is a method used to quantify insulin resistance and beta-cell function from basal (fasting) glucose and insulin (or C-peptide) concentrations. HOMA is a model of the relationship of glucose and insulin dynamics that predicts fasting steady-state glucose and insulin concentrations for a wide range of possible combinations of insulin resistance and β-cell function. Insulin levels depend on the pancreatic β-cell response to glucose concentrations while, glucose concentrations are regulated by insulin-mediated glucose production via the liver. Thus, deficient β-cell function will echo a diminished response of β-cell to glucose-stimulated insulin secretion. Similarly, insulin resistance is reflected by the diminished suppressive effect of insulin on hepatic glucose production. The HOMA model has proved to be a robust clinical and epidemiological tool for the assessment of insulin resistance. HOMA describes this glucose-insulin homeostasis by means of a set of simple, mathematically-derived nonlinear equations. The approximating equation for insulin resistance has been simplified; it uses a fasting blood sample. It is derived from the use of the insulin-glucose product, divided by a constant. The product of FPG × FPI is an index of hepatic insulin resistance.[4]

The equation proposed by Matthews et al.:

IR_HOMA = I₀ / (22.5 × e^-In(Go) could be rewritten as:

IR_HOMA = (I₀ × G₀)/ 22.5(mathematically:e^-Inx =1 / x)

It is appropriate to apply this index in large epidemiological studies where only fasting insulin and glucose values are available.

Homeostasis model assessment-IR for Indian children's are: Boys: Normal weight 1.70 ± 1.44 (95%CI: 1.46-1.94) versus overweight 2.67 ± 1.41 (95%CI: 2.40-2.94) versus obese 4.39 ± 2.14 (95%CI: 3.95-4.83), P < 0.0001 between all groups); Girls: Normal weight 1.21 ± 1.10 (95% CI 1.73-2.12) versus overweight 3.19 ± 2.02 (95% CI 2.79-3.60) versus obese 4.19 ± 2.52 (95% CI 3.69-4.69), P < 0.0001 between all groups).

Quantitative insulin sensitivity check index

Quantitative insulin sensitivity check index (QUICKI) is an empirically-derived mathematical transformation of fasting blood glucose and plasma insulin concentrations that provide a consistent and precise ISI with a better positive predictive power. It is simply a variation of HOMA equations, as it transforms the data by taking both the logarithm and the reciprocal of the glucose-insulin product, thus slightly skewing the distribution of fasting insulin values. QUICKI has been seen to have a significantly better linear correlation with glucose clamp determinations of insulin sensitivity than minimal-model estimates, especially in obese and diabetic subjects. It employs the use of fasting values of insulin and glucose as in HOMA calculations. QUICKI is virtually identical to the simple equation form of the HOMA model in all aspects, except that a log transform of the insulin glucose product is employed to calculate QUICKI. The QUICKI can be determined from fasting plasma glucose (mg/dl) and insulin (μIU/ml) concentrations.[5]

QUICKI = 1/(logI₀ + logG₀)

The reported values of QUICKI were 0.382 ± 0.007 for non-obese, 0.331 ± 0.010 for obese and 0.304 ± 0.007 for diabetic individuals.

McAuley index

It is used for predicting insulin resistance in normoglycemic individuals. Regression analysis was used to estimate the cut-off points and the importance of various data for insulin resistance (fasting concentrations of insulin, triglycerides, aspartate aminotransferase, basal metabolic rate (BMI), waist circumference).[6] A bootstrap procedure was used to find an index most strongly correlating with insulin sensitivity index, corrected for fat-free mass obtained by HEC (Mffm/I).

Mffm/I = e (2,63–0,28 ln (I₀) – 0,31 ln (TAG₀)

Matsuda index

Several methods have been described that derive an ISI from the OGTT. In these methods, the ratio of plasma glucose to insulin concentration during the OGTT is used. A novel assessment of insulin sensitivity that is simple to calculate and provides a reasonable approximation of whole-body insulin sensitivity from the OGTT was developed by Matsuda and Defronzo, and is referred to as the Matsuda index. Here the OGTT ISI (composite) was calculated using both the data of the entire 3 h OGTT and the first 2 h of the test. The composite whole-body insulin sensitivity index (WBISI), developed by Matsuda and DeFronzo is based on insulin values given in microunits per milliliter (μU/mL) and those of glucose, in milligrams per deciliter (mg/L) obtained from the OGTT and the corresponding fasting values The index of whole-body insulin sensitivity combines both hepatic and peripheral tissue insulin sensitivity. This index is calculated from plasma glucose (mg/dl) and insulin (mIU/l) concentrations in the fasting state and during OGTT.[7]

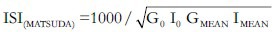
I₀ – Fasting plasma insulin concentration (mIU/l),

G₀ – Fasting plasma glucose concentration (mg/dl),

G_mean – Mean plasma glucose concentration during OGTT (mg/dl),

I_mean – Mean plasma insulin concentration during OGTT (mU/l),

10,000– Simplifying constant to get numbers from 0 to 12.

√– Correction of the nonlinear values distribution.

Belfiore index

The Belfiore index is mainly used for calculation of the Belfiore formulas in defining the normal values for basal glucose and insulin concentrations and mean normal value for glucose and insulin areas during OGTT. The main point of the Belfiore formulas is the comparison of insulin and glucose values measured (fasting, 0-1-2 h areas or 0-2 h areas) with the defined normal reference values.[8]

Cederholm index

The insulin sensitivity index proposed by CEDER-HOLM and Cederholm and Wibell represents mainly peripheral insulin sensitivity and muscular glucose uptake, due to the dominant role of peripheral tissues in glucose disposal after an oral glucose load.[9]

Avignon index

The authors (Avignon et al. 1999) proposed 3 insulin sensitivity indices: Sib (derived from fasting plasma insulin and glucose concentrations), Si2h (derived from plasma insulin and glucose concentrations in the 120^th min of OGTT) and SiM (derived by averaging Sib and Si2h after balancing Sib by a coefficient of 0.137 to give the same weight to both indices).[10]

It was observed that the results obtained by computation of sensitivity indices from glucose and insulin concentrations in the basal state and during a conventional 2 h OGTT were useful for blending both the determination of glucose tolerance and an estimate of insulin sensitivity in a single and simple test.

Stumvoll index

It is possible to calculate insulin sensitivity and insulin release from simple demographic parameters and values obtained during an OGTT with practical precision. Stumvoll and Gerich proposed use of demographic data such as age, sex and BMI in addition to plasma glucose (mmol/L) and insulin (pmol/L) responses during the OGTT to predict insulin sensitivity and beta cell function. The equations were generated using the multiple linear regression analysis and adapted to the availabilities of sampling times during OGTT and of demographic parameters (BMI, age).[11]

EXAMPLE

A 35-year-old male person, weighing 68 kg, with a height of 164 cm, and thus a BMI of 25.28 kg/m². He is non-diabetic, non-hypertensive and has a normal lipid profile. He does not have any family history of coronary artery disease, diabetes mellitus or hypertension. His fasting blood sugar is 100 mg/dl, and fasting insulin level of 4.6 μU/ml. An OGTT was done with 75 g of anhydrous glucose [Table 3]. His blood sugar and insulin levels are as follows.

Table 3.

Comparison of insulin sensitivity through different methods

Using the above values, we calculated various insulin sensitivity indices, the values obtained are as follows:

Parameters derived from above mentioned example: HOMA-IR-1.23 [Normal < 2.5], QUICKI-0.39 [Normal < 0.4], MATSUDA-12.34 [Normal < 4.5].

From the above-derived values, we can conclude that patient does not have insulin resistance as all the three values are within normal limits.

Thus, we see that, there are various tools used for quantifying insulin sensitivity and resistance directly (hyperinsulinemic euglycemic glucose clamping and insulin suppression tests) and indirectly (frequently sampled intravenous glucose tolerance test, OGTT, meal tolerance test, and HOMA-IR). The utility of HOMA-IR in assessment of IR has been validated in children and adolescents. HOMA-IR is a simple method for evaluation of insulin sensitivity and correlates with the results of glucose clamp test in subjects with mild diabetes without significant hyperglycemia. Nevertheless it is difficult to apply to patients with poor glycemic control, those with severe β cell dysfunction or those treated with insulin.[12]

Insulin resistance, earlier thought to be a rare complication of the treatment of diabetes, is now recognized as a component of several disorders, including the following:[13]

• Extreme insulin-resistance syndromes, such as the type B syndrome with autoantibodies against the insulin receptor, and rare inherited disorders, such as Leprechaunism with insulin-receptor mutations and the lipodystrophic states

• Impaired glucose tolerance and type 2 diabetes mellitus.

• Obesity, stress, infection, uremia, acromegaly, glucocorticoid excess, and pregnancy, which cause secondary insulin resistance

• Common disorders such as the metabolic syndrome, hypertension, hyperlipidemia, coronary artery disease, the polycystic ovary syndrome, and ovarian hyperthecosis, in which the mechanism of the associated hyperinsulinemia is unknown.

CONCLUSION

Estimation of impaired insulin sensitivity should be given importance mainly in individuals with risk factors. The importance of the indices lies in their use in large epidemiological studies for assessment of relations between selected variables. For fasting values, insulin resistance is defined by WHO as the highest quartile of the IR_HOMA index in non-diabetic subjects. Insulin resistance is also defined as the lowest decile of insulin sensitivity in the lean subgroup of non-diabetic population. In clinical practice, however, their application is limited due to the lack of exact reference values.