Four dimensional magnetic resonance imaging with retrospective k-space reordering: A feasibility study

Abstract

Purpose:

Current four dimensional magnetic resonance imaging (4D-MRI) techniques lack sufficient temporal/spatial resolution and consistent tumor contrast. To overcome these limitations, this study presents the development and initial evaluation of a new strategy for 4D-MRI which is based on retrospective k-space reordering.

Methods:

We simulated a k-space reordered 4D-MRI on a 4D digital extended cardiac-torso (XCAT) human phantom. A 2D echo planar imaging MRI sequence [frame rate (F) = 0.448 Hz; image resolution (R) = 256 × 256; number of k-space segments (N_KS) = 4] with sequential image acquisition mode was assumed for the simulation. Image quality of the simulated “4D-MRI” acquired from the XCAT phantom was qualitatively evaluated, and tumor motion trajectories were compared to input signals. In particular, mean absolute amplitude differences (D) and cross correlation coefficients (CC) were calculated. Furthermore, to evaluate the data sufficient condition for the new 4D-MRI technique, a comprehensive simulation study was performed using 30 cancer patients’ respiratory profiles to study the relationships between data completeness (C_p) and a number of impacting factors: the number of repeated scans (N_R), number of slices (N_S), number of respiratory phase bins (N_P), N_KS, F, R, and initial respiratory phase at image acquisition (P₀). As a proof-of-concept, we implemented the proposed k-space reordering 4D-MRI technique on a T2-weighted fast spin echo MR sequence and tested it on a healthy volunteer.

Results:

The simulated 4D-MRI acquired from the XCAT phantom matched closely to the original XCAT images. Tumor motion trajectories measured from the simulated 4D-MRI matched well with input signals (D = 0.83 and 0.83 mm, and CC = 0.998 and 0.992 in superior–inferior and anterior–posterior directions, respectively). The relationship between C_p and N_R was found best represented by an exponential function ($C_P=100\left(1-e^{-0.18N_R}\right)$, when N_S = 30, N_P = 6). At a C_P value of 95%, the relative error in tumor volume was 0.66%, indicating that N_R at a C_P value of 95% (N_R,95%) is sufficient. It was found that N_R,95% is approximately linearly proportional to N_P (r = 0.99), and nearly independent of all other factors. The 4D-MRI images of the healthy volunteer clearly demonstrated respiratory motion in the diaphragm region with minimal motion induced noise or aliasing.

Conclusions:

It is feasible to generate respiratory correlated 4D-MRI by retrospectively reordering k-space based on respiratory phase. This new technology may lead to the next generation 4D-MRI with high spatiotemporal resolution and optimal tumor contrast, holding great promises to improve the motion management in radiotherapy of mobile cancers.

1. INTRODUCTION

Respiratory motion can induce errors in target volume delineation and dose delivery in radiation therapy for thoracic and abdominal cancers.¹ Four-dimensional computed tomography (4D-CT) has been widely used to image subject-specific respiratory motion for determining individual safety margins and internal target volumes (ITVs).^2–4 However, its application in abdominal cancers has been largely limited due to low soft-tissue contrast. In addition, 4D-CT involves high imaging radiation dose to the patient.^5–7 Recently, several four-dimensional magnetic resonance imaging (4D-MRI) techniques have been proposed in order to overcome the limitations of 4D-CT. 4D-MRI yields no radiation dose to patients^8,9 and can provide improved tumor and soft-tissue contrast without significantly adding imaging time and cost.^10,11 A detailed review of recent 4D-MRI studies can be found in the literature.¹² In brief, there are two main approaches used in the development of 4D-MRI: prospective and retrospective. The former uses fast 3D MR sequences to acquire real-time volumetric images, while the latter uses fast 2D MR sequences to continuously acquire images from all respiratory phases and all slice locations, followed by retrospectively sorting the images based on respiratory phases. Most recent developments in 4D-MRI have been focused on the retrospective approach mainly because the prospective approach faces significant challenges in achieving both sufficient spatial and temporal resolutions using current available MRI technologies. A prerequisite of retrospective 4D-MRI is the fast 2D MR sequence whose frame rate should be 2 frames/s or greater.¹⁰ Fast 2D MR sequences that can be used for retrospective 4D-MRI include balanced steady state gradient echo (bSSFP or TrueFISP in Siemens and FIESTA in GE),¹² single shot fast spin echo (HASTE in Siemens and SSFSE in GE),^11,13 and fast field echo with echo planar imaging (FFE-EPI).¹⁴

While these fast 2D MR sequences allow 4D-MRI to achieve good temporal resolution, they fall short of adequate spatial resolution and optimal tumor contrast. For example, we have previously demonstrated that a T2^∗/T1-weighted retrospective 4D-MRI technique using a TrueFISP/FIESTA pulse sequence¹⁵ can achieve adequate temporal resolution (∼3 frames/s), acceptable spatial resolution (1.8 × 1.8 × 5 mm), but suffered from suboptimal and inconsistent tumor contrast. In our preliminary patient study, we have observed large degree of intersubject variations in tumor contrast of the 4D-MRI (range: 4.57–45.00; standard deviation: 14.63),¹⁶ presumably due to the admittedly suboptimal T2*/T1 weighting tumor contrast of TrueFISP/FIESTA. On the contrary, some MR sequences can provide better tumor contrast but are not fast enough for retrospective 4D-MRI. For example, T2-weighted fast recovery fast spin echo (FRFSE),^17–19 the clinical standard for hepatic cancer imaging, has excellent tumor contrast for liver cancer but slow imaging speed (frame rate ∼0.5 frames/s), disqualifying it for retrospective 4D-MRI.

In order to overcome the limitations of current retrospective 4D-MRI techniques, and allow MRI sequences with high tumor-tissue contrast but low frame rate to be used for 4D-MRI, we report here a novel strategy which is based on k-space reordering for retrospective 4D-MRI. Unlike previous retrospective 4D-MRI techniques where sorting is performed on images (labeled as image-based sorting in this paper), the new technique reorders the k-space of MR images based on respiratory information, allowing for finer segmentation of data in the time domain. This technique eliminates the necessity of fast 2D MR imaging for retrospective 4D-MRI and enables potential improvement in temporal and spatial resolution of 4D-MRI. Several groups have recently studied motion correction methods. Hansen et al. used a nonrigid registration algorithm to generate deformation maps between different respiratory phases and applied them to each cardiac cycle image to correct respiratory motion.²⁵ Similarly, Odille et al. developed a frequency domain-based reconstruction framework for correcting motion artifacts of MR images. This particular method employed an optical flow-based motion model to determine phase information of k-space data.²⁰ However, this study focused on MR motion correction used in a traditional radiology perspective. It concerns only one respiratory phase and the result is a single 3D MR dataset. The study’s main goal is to achieve high image quality for a single phase, while motion information from other phases is minimized. The reconstruction framework and motion model used are designed for this specific purpose, which is greatly different from respiratory motion management associated with 4D-MRI. Moreover, Hu et al. developed a respiratory amplitude based triggering system that prospectively gates image acquisition to prevent respiratory motion artifacts.²⁶ Akçakaya et al. investigated a k-space-dependent respiratory gating technique where the center of k-space is gated using respiratory navigators to generate 3D flow imaging.²¹ However, both techniques use prospective gating, where image data will only be acquired when the motion reaches a certain phase. The gating requires hardware adjustments on the MR scanner. As presented in the current paper, 4D-MRI requires a systematic approach capable of (a) handling patient breathing irregularities, (b) maximizing MR image quality, and (c) improving motion information accuracy at each phase, while (d) minimizing adverse influence from breathing variation. In our study, we present a retrospective 4D-MRI k-space reordering technique for respiratory motion. Contrary to prospective gating, retrospective sorting methods continually acquire image data and sort them based on synchronized motion signals from a surrogate. In this paper, we explain the principle of k-space reordering and demonstrate its feasibility for 4D-MRI application using digital human phantom and a healthy volunteer.

2. METHODS AND MATERIALS

2.A. Retrospective 4D-MRI with k-space reordering

Similar to image-based retrospective 4D-MRI, k-space sorting 4D-MRI also requires a breathing signal that is synchronously recorded during image acquisition. However, unlike image-based 4D-MRI that assigns a respiratory phase/amplitude to each MR image, the new technique assigns a respiratory phase/amplitude to each k-space line or segment (a group of lines) based on the recorded respiratory signal. The sampling rate of the respiratory signal should be much higher than the MR imaging frame rate to allow for fine segmentation of the k-space. MR image acquisition of the entire scanned volume needs to be repeated for a number of times in order to achieve data sufficient condition of 4D imaging,¹¹ i.e., k-space data of all respiratory phases are acquired. For reconstruction, k-space data will be rebinned based on respiratory phases, and the reordered k-space will be used to generate 4D-MRI.

In principle, the concept of retrospective k-space reordering can be applied to a variety of standard MR sequences, either 2D or 3D, using cine, sequential, or interleave acquisition, given that the respiratory status of k-space lines/segments can be accurately determined. In this paper, we demonstrate this technique on a 4D digital extended cardiac-torso (XCAT) human phantom²³ using a 2D single-shot EPI MRI sequence in sequential 2D image acquisition mode. The sequential 2D image acquisition mode sequentially acquires 2D MRI images for each slice location (slice 1, slice 2, slice 3, …). The k-space acquisition scheme for ky-lines was also sequentially acquired, i.e., ky-lines were acquired from line 1 to line 256 within k-space. Figure 1 shows the schematic plot of k-spacing reordering and image reconstruction based on the EPI sequence. The k-space is divided into only four segments for demonstration purpose. Each k-space segment is assigned to a respiratory phase that is determined from the breathing signal. The k-space is then rebinned based on respiratory phases, and finally the reordered, phase-specific k-space is used to reconstruct 4D-MRI using 2D inverse fast Fourier transform (iFFT).

FIG. 1.

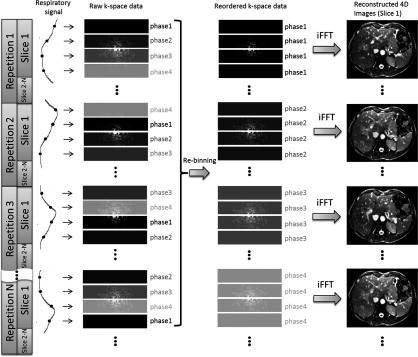
Illustration of the process of retrospective 4D-MRI based on k-space reordering. Respiratory phase of each k-space segment is determined from the breathing signal that is acquired synchronously during image acquisition. K-space reordering is performed so that segments of the same respiratory phases are grouped together. Respiratory correlated 4D MR images are generated by reconstructing each phase-specific k-space using iFFT.

An important challenge of the retrospective k-space reordering technique is the determination of the number of repetitions (N_R) that is needed to satisfy the data sufficient condition²² for 4D-MRI. Due to patients’ breathing variations, the assignment of respiratory phase to k-space segments is rather random, making it difficult to determine if data of all respiratory phases have been collected. To tackle this challenge, we performed computer simulations based on the assumption of a 2D single-shot EPI MRI sequence, with a sequential 2D image acquisition mode, as well as a sequential ky-line acquisition scheme, to systematically study the relationship between N_R and the percentage of data completeness (C_P), and the effects of potential influencing factors: total number of slices (N_S), total number of respiratory phase bins (N_P), the number of k-space segments (N_KS), image frame rate (F), MR image spatial resolution (R), and initial respiratory phase at image acquisition (P₀). A total of 30 cancer patients’ respiratory profiles were used in the simulation study.

2.B. Feasibility study on digital phantom

To demonstrate the feasibility of retrospective 4D-MRI with k-space reordering, we performed a computer simulation study using the XCAT human phantom. The respiratory motion of the XCAT phantom is controlled by two regular motion profiles (period: 5 s): one is diaphragm motion in the superior–inferior (SI) direction (peak-to-peak amplitude: 30 mm), and the other is chest wall motion in the anterior–posterior (AP) direction (peak-to-peak amplitude: 10 mm). There is no input motion signal in the medial–lateral (ML) direction. A hypothesized tumor (diameter: 40 mm) was placed in the middle of the liver and moved with the surrounding tissue (note that the liver is modeled to move as a whole in the XCAT phantom, so the hypothesized liver tumor moves in the same manner as the input diaphragm and chest wall motions). XCAT images were generated using the following parameters: resolution of 256 × 256, pixel size of 2.5 × 2.5 mm, and slice thickness of 3 mm. Organ intensities in the XCAT images were set as in T2-weighted MR images.

Image acquisition and subsequent k-space reordering were mimicked by the computer simulation using a 2D single-shot EPI sequence with sequential acquisition mode. Assuming a frame rate of 0.448 frames/s, it will take 2.23 s to acquire a 2D image, or 8.7 ms to acquire a k-space line (as we assumed 256 × 256 resolution). Based on that, a XCAT volumetric dataset covering the entire liver was generated every 8.7 ms, representing an ultrafast snapshot of the XCAT phantom at a particular respiratory phase. For a 5 s breathing cycle, this resulted in a total of 574 complete XACT volumetric datasets. From each XCAT dataset, a 2D axial slice was extracted, where the location of the slice cycled from top to bottom of the XCAT volume from one XCAT dataset to next. The 2D axial slice underwent FFT to generate its corresponding k-space, which was then evenly divided into 16 segments. Each segment, which contained 16 adjacent k-space lines, was assigned a single respiratory phase based on the breathing curve. The above-described process was repeated for all XCAT datasets, generating a large number of k-space segments at different slice locations and covering different respiratory phases. These k-space segments were then reordered per slice location and per respiratory phase. In case of missing phases, the k-space segment data acquired at the same slice location and nearest respiratory phase will be used as a replacement. Finally, the reordered k-space data were used to reconstruct 4D images using iFFT. In this simulation, the number of respiratory phase bins was set to 10.

Image quality of the simulated “4D-MRI” of the XCAT phantom was qualitatively evaluated. Image noise and SNR were measured for each respiratory phase, and image quality was compared with the simulated 4D-MRI reconstructed from the image-based sorting method.¹³ Tumor motion trajectories were determined from the 4D-MRI and compared with the input signals. Mean absolute amplitude difference (D) and cross correlation coefficient (CC) between the two were calculated.

2.C. A feasibility study with a healthy volunteer

One healthy volunteer was prospectively enrolled in an IRB-approved study. A multishot 2D FSE MR sequence was employed with interleave image acquisition mode (slice 1, slice 3, slice 5, …, and then slice 2, slice 4, slice 6, …) for 4D-MRI reconstruction. All images were acquired in a 3.0 T GE clinical scanner (General Electric, Waukesha WI) with a frame rate of about 7 s/frame. The subject was positioned head-first-supine with arms up. No immobilization device was used, and the patient was instructed to breathe normally during the acquisition. A volume near the diaphragm was chosen as the imaging volume and scans were repeated 20 times in order to ensure sufficient data were collected for each respiratory phase. Imaging parameters were TR/TE, 3750/101 ms; FOV, 400 × 400 mm; slice thickness, 8 mm; matrix, 256 × 256; number of segments, 16; echo train length, 16; bandwidth, 195 Hz/pixel; and number of slices, 9. The Bellows system wrapped around abdomen was used as an external surrogate indicating respiratory motion signal during image acquisition. The respiratory signal was recorded with a sample rate of 25 Hz and synchronized with k-space signal acquisition. Respiratory phases were calculated followed by 4D-MRI reconstruction. A 2D single-shot FSE MR sequence with the same scanning parameters was also employed on this healthy volunteer for the image-based phase sorting.¹³ The image quality of 4D-MRI reconstructed using the k-space reordering and the image-based phase sorting was compared.

3. RESULTS

3.A. Data completion for k-space reordering 4D-MRI

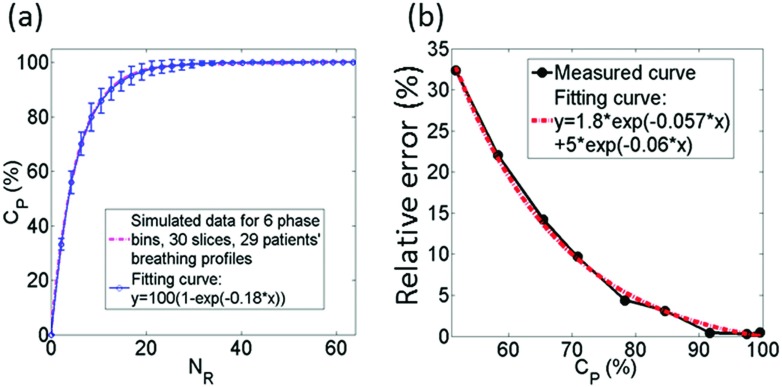
As expected, it was found that the greater the number of repetitions, the more complete the k-space data obtained for 4D-MRI, as shown in Fig. 2(a). In sum of simulations using 30 cancer patients’ breathing profiles, the relationship between the two can be best expressed as an exponential function. When N_S = 30 and N_P = 6, the best fit is

$${\displaystyle C_P=100\left(1-e^{-0.18N_R}\right).}$$ (1)

It can be seen that acquiring 100% of data would require a very large N_R. In practical, missing a very small percentage of data (i.e., C_P is very close to 100%) may not cause any clinically significant differences in the integrity of 4D-MRI. As revealed in Fig. 2(b), the relative error in tumor motion measurement from k-space reordering 4D-MRI decreased as C_P increases and tended to stabilize after 90% of data completion. At C_P of 95%, the relative error was 0.66%, indicating that N_R at C_P of 95%, labeled as N_R,95%, is sufficient for k-space reordering 4D-MRI.

FIG. 2.

Results of study on data competition condition and its relationships with influencing factors for retrospective k-space reordering 4D-MRI: (a) relationship between C_P and N_R, (b) relative error in tumor motion measurement as a function of C_P.

Figure 3 shows the relationships between N_R,95% and the potential influencing factors (N_P, P₀, F, N_S, R, and N_KS). N_R,95% was found to be approximately linearly proportional to N_P (r = 0.99), and nearly independent of all other factors. It should be noted that although F and N_S do not affect N_R, _95%, they will affect the total acquisition time of 4D-MRI (T) in the following manner:

$${\displaystyle T=\frac{N_{R,95\%}\cdot N_S}{F}.}$$ (2)

In addition, spatial resolution and temporal resolution are often constrains to each other in MRI. Increasing spatial resolution will decrease temporal resolution and vice versa. As a result, R will also affect the total acquisition time of 4D-MRI via its effect on F.

FIG. 3.

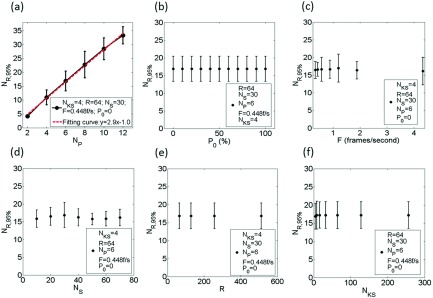
The relationship between N_R,95% and the following: N_P (a), P₀ (b), F (c), N_S (d), R (e), and N_KS (f). N_R,95% was found to be approximately linearly proportional to N_P (r = 0.99) and independent of all other factors.

The derived relationships as shown above can be used to determine the minimum number of repetitions and the imaging time required for k-space reordering 4D-MRI. For example, for a 6-phase EPI-based 4D-MRI with 30 slices, the number of repetitions needs to be 16 or greater in order to achieve at least 95% of the necessary data.

3.B. Feasibility study on digital phantom

Figure 4(a) shows the 10-phase 4D-MRI images of the XCAT phantom using the k-space reordering technique, where the respiratory motion can be readily seen in all three orthogonal views. These 4D-MRI data acquisition completeness reached 100%. On average, image noise is 3.0 ± 1.0 and SNR is 64 ± 27, using ten respiratory phases. Tumor motion trajectories measured from 4D-MRI matched well with the input signals, as shown in Fig. 4(b). D was 0.83 and 0.83 mm, and CC was 0.998 and 0.992 in SI and AP directions, respectively. Fig. 4(c) shows representative coronal images of the original XCAT phantom, the simulated 4D-MRI using image-based phase sorting technique, and the simulated 4D-MRI using the k-space phase reordering technique. The 4D-MRI using the image-based sorting technique showed a discontinuity (zigzag artifacts) on the edges the tumor and organs. The 4D-MRI using the k-space reordering technique demonstrated much smoother edges, but increased background noise (indicated by arrows), presumably because there were some phase variations during k-space reordering and rebinning.

FIG. 4.

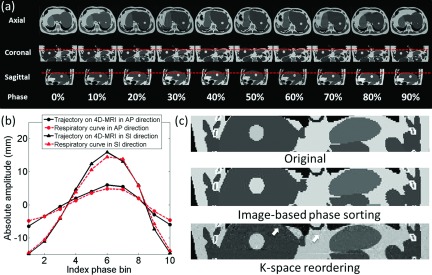
(a) Ten-phase k-space reordering 4D-MRI images of the XCAT phantom. Dashed lines are added to assist the visualization of tumor motion. (b) Comparison of tumor motion trajectories between the 4D-MRI and the input signals. (c) Coronal images of the XCAT phantom illustrating the differences between the k-space reordered 4D-MRI and the original XCAT. Background noise is observed in the k-space reordered 4D-MRI (indicated by arrows).

3.C. A feasibility study with a healthy volunteer

Figure 5 demonstrates the 6-phase 4D-MRI images in orthogonal views of the healthy volunteer. The diaphragm was chosen as the respiratory motion indicator. The slice locations of the sagittal and coronal views were selected to be near the center of liver. The 4D-MRI images successfully revealed the respiratory motion of the healthy volunteer. The most predominant artifacts showed on 4D-MRI images are the aliasing artifacts in the AP direction, induced by the tolerant motion range of each phase bin. This aliasing is minimal in coronal view. The average breathing period of the subject was 8 s, resulting in a data completeness of 96.27% for the 6-phase 4D-MRI.

FIG. 5.

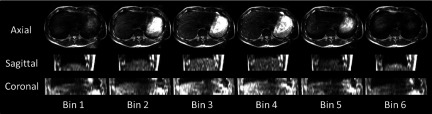
Representative 6-phase 4D-MRI images of the healthy volunteer in the axial, sagittal, and coronal views. All images are anatomically near the center of the liver.

Figure 6 shows coronal and sagittal images of the healthy volunteer using image-based phase sorting technique, and k-space reordering technique from one representative phase bin. Some discontinuity on the dome of the diaphragm (indicated by white arrows) can be observed compared to the 4D-MRI reconstructed with the k-space reordering technique, which demonstrated much smoother edges, but increased background noise. Both edge discontinuities demonstrated on image-based phase sorting 4D-MRI and increased background noise demonstrated on k-space reordering 4D-MRI are presumably induced by breathing variations.

FIG. 6.

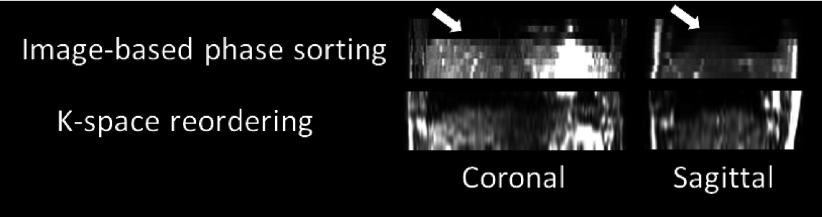
Coronal and sagittal images of the 4D-MRI reconstructed using image-based phase sorting and the k-space reordering methods. Apparent tissue discontinuity on the dome of the diaphragm (indicated by white arrows) are observed on 4D-MRI reconstructed using image-based phase sorting, while 4D-MRI reconstructed using k-space reordering demonstrated much smoother edges.

4. DISCUSSION

In this study, we have demonstrated a novel strategy to generate respiratory correlated 4D-MRI by retrospectively reordering k-space data based on respiratory phase. We have conducted preliminary tests of the new strategy using a 4D digital human phantom. We have also derived important relationships between data completeness and influencing factors, which provide useful information for guiding image acquisition in practice. It should be noted that there are some limitations in the current study. First, the derived relationships were based on a limited number of patients (n = 30). Their characteristics might vary if a larger number of samples were included. Furthermore, we performed only basic analysis of the increased background noise in the reconstructed 4D-MRI. The clinical impact of this noise in regards to tumor volume delineation and motion measurements needs to be carefully evaluated in patient studies.

In principle, the concept of k-space reordering for respiratory correlated 4D-MRI can be applied to a variety of MR sequences. However, some sequences may be more difficult than others in actual implementation, depending upon the level of complexity of its k-space data acquisition and image reconstruction. This study only illustrated an example where both acquisition and reconstruction are relatively straightforward. These processes could be much more complicated in the implementation on other MR sequences.

It is feasible to generate pseudo ultrafast 4D-MRI by combing k-space reordering with some type of phase sharing strategy. For example, using the sliding window technique,²⁴ many pseudo respiratory phases can be generated between actual respiratory phases by sliding the respiratory phase bin along the breathing signal. The final frame rate of the pseudo ultrafast 4D-MRI is determined by the phase bin width and the sliding step size, which are two independent parameters constrained by MR imaging frame rate and patient’s breathing period.

As can be seen from the healthy volunteer study, the aliasing artifacts were the most influential factor affecting image quality. We simulated the MRI image acquisition using the same k-space signal acquisition scheme and 2D image acquisition mode (interleaves) as used in the healthy volunteer on a regular breathing XCAT digital phantom. With the same set of image acquisition parameters, the simulated 4D-MRI images (Fig. 7) clearly demonstrated respiratory motion with aliasing artifacts similar to those observed in the healthy volunteer study. Motion aliasing can be observed in the top row of Fig. 7. Since the volumetric MRI image for each phase bin is composed of 2D MRI images acquired at similar but not exactly the same motion amplitude, the aliasing may be caused by breathing variances in motion amplitude. The corresponding motion ranges in amplitude for each phase bin were shown in Fig. 7 bottom row. It can be seen that the phase bins with larger variances in motion amplitude show more aliasing artifacts, as shown in phase bins 2 and 5; the phase bins with a small variance in motion amplitude demonstrate much better image quality, as shown in phase bins 1, 4, and 6. This simulation result demonstrated that the magnitude of the residual motion at the phase bin is relevant to the aliasing artifact in the 4D-MRI images. Reducing this artifact will be a topic of research in our future investigations.

FIG. 7.

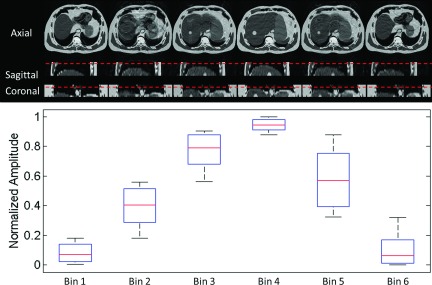
Simulated 6-phase 4D-MRI images (top) using the same k-space acquisition scheme and 2D image acquisition mode (interleaves) as in the healthy volunteer study, along with the corresponding motion ranges in amplitude (bottom) for each phase bin.

5. CONCLUSION

It is feasible to generate respiratory correlated 4D-MRI by retrospectively reordering k-space based on respiratory phase. This new technology may lead to the next generation 4D-MRI with high spatiotemporal resolution and optimal tumor contrast, holding great promises to improve the motion management in radiotherapy of mobile cancers.