Predicting Ambulance Time of Arrival to the Emergency Department Using Global Positioning System and Google Maps

Abstract

Objective

To derive and validate a model that accurately predicts ambulance arrival time that could be implemented as a Google Maps web application.

Methods

This was a retrospective study of all scene transports in Multnomah County, Oregon, from January 1 through December 31, 2008. Scene and destination hospital addresses were converted to coordinates. ArcGIS Network Analyst was used to estimate transport times based on street network speed limits. We then created a linear regression model to improve the accuracy of these street network estimates using weather, patient characteristics, use of lights and sirens, daylight, and rush-hour intervals. The model was derived from a 50% sample and validated on the remainder. Significance of the covariates was determined by p < 0.05 for a t-test of the model coefficients. Accuracy was quantified by the proportion of estimates that were within 5 minutes of the actual transport times recorded by computer-aided dispatch. We then built a Google Maps-based web application to demonstrate application in real-world EMS operations.

Results

There were 48,308 included transports. Street network estimates of transport time were accurate within 5 minutes of actual transport time less than 16% of the time. Actual transport times were longer during daylight and rush-hour intervals and shorter with use of lights and sirens. Age under 18 years, gender, wet weather, and trauma system entry were not significant predictors of transport time. Our model predicted arrival time within 5 minutes 73% of the time. For lights and sirens transports, accuracy was within 5 minutes 77% of the time. Accuracy was identical in the validation dataset. Lights and sirens saved an average of 3.1 minutes for transports under 8.8 minutes, and 5.3 minutes for longer transports.

Conclusions

An estimate of transport time based only on a street network significantly underestimated transport times. A simple model incorporating few variables can predict ambulance time of arrival to the emergency department with good accuracy. This model could be linked to global positioning system data and an automated Google Maps web application to optimize emergency department resource use. Use of lights and sirens had a significant effect on transport times.

Introduction

Accurately predicting ambulance time of arrival to the emergency department (ED) is important for effective resource management, especially for critical patients. Overestimates of arrival time potentially waste resources in the ED as personnel await the ambulance. Underestimates result in unpreparedness when the patient arrives, with potential adverse outcomes in high-acuity patients. Currently, there are no aids available for the EMS crew or ED staff to reliably estimate the ambulance time of arrival.

There are numerous disadvantages to relying on the prehospital provider's estimated time of arrival (ETA). First, providers' perception of elapsed time is often inaccurate, with a prospective study of transport times showing that the prehospital provider's estimate of the duration of the transport at its conclusion was off by an average of 33%.¹ Predictions made at the beginning of the transport were also inaccurate. A study of 6139 trauma patients in Portland, Oregon, showed that prehospital providers were more than 5 minutes outside their ETA 55% of the time and greater than 10 minutes inaccurate in 28% of transports.² Secondly, as the ETA is often reported to the receiving hospital along with the medical report, it may be delayed until the patient is nearly at the hospital, giving little time to prepare. Finally, calling in an ETA by radio or telephone distracts providers from patient care and driving.

Our objective in this study was to derive and validate a model to more accurately predict ambulance time of arrival to the ED based on global positioning system (GPS) location data and other relevant factors. This model was then used to create a Google Maps web application that could provide these predictions in real time to ED providers for all EMS transports. A secondary objective was to assess the influence of lights and sirens on transport time.

Methods

Study Design

This was a retrospective analysis of all scene transports of a single EMS agency in Multnomah County, Oregon, from January 1 through December 31, 2008. A year's data was used to avoid seasonal bias. Scene and destination hospital locations were used along with other significant variables to derive and validate a model to predict arrival time to the ED.

Population and Setting

Multnomah County, Oregon, has a population of 735,000, an area of 435 square miles, and is served by multiple first responding agencies (e.g., fire departments), with one commercial ambulance company transporting all patients.³ All scene ground transports originating with a call to 911 or the county centralized dispatch were included. Interfacility transfers, intermode (e.g., air to ground) transfers, and nonurgent transports, such as those for medical appointments, were excluded. Transports longer than 60 minutes were excluded as outliers in a mostly urban EMS system.

Data Collection

Cases were collected retrospectively from electronic patient care records. EMS personnel completed these reports on a laptop computer during and after the transport. Exact times of scene departure and emergency department arrival and mileage were automatically recorded by the driver pressing a key on the ambulance's automated data terminal, following guidelines for uniform reporting of these intervals.⁴

Scene and hospital addresses were converted into latitude and longitude coordinate pairs (geocoded) using the batchgeo.com web application.⁵ This free, internet-based applet sends large batches of addresses to Google Maps for geocoding. Addresses that could not be geocoded by Google maps (e.g., highway milepost numbers and descriptions of locations) were reviewed by the investigators and manually geocoded using Google Earth.⁶ Scene locations that could not conclusively be identified were excluded. The study was granted a HIPPA waiver of informed consent by the Oregon Health and Science University Institutional Review Board.

Data Analysis

The model was derived on a 50% random sample of the data and validated on the remainder. Randomization was based on the last digit of the EMS agency's sequentially assigned run number. Characteristics of the derivation and validation sets were compared. Mean ages were compared by two-tailed t-tests. Median transport durations and route lengths were compared by the Wilcoxon rank-sum test because of their right-skewed distributions. The dichotomous variables were compared by the chi-squared test.

ArGIS 9.1 Network Analyst (ESRI Corporation, Redlands, CA) was used to generate a route from each scene and destination coordinate pair. Network Analyst uses hierarchical route analysis favoring larger highways and arterials over local roads to determine the fastest possible route and estimates driving time based on the speed limits for each street segment in the route. The street network included in the ArcGIS package was used. Transports in which the actual transport time was less than the raw prediction from ArcGIS were excluded, as this software's algorithm produced very short estimates, so these cases likely represented failure of the ambulance driver to activate the automated data terminal on leaving the scene.

Linear regression was then used to create a model to more accurately predict transport time by refining the street network estimate from ArcGIS using other significant covariates. The outcome of the model was the actual transport time recorded from the ambulance's automated data terminal.

The model was built by stepwise removal of variables found to be insignificant at p < 0.05 from a model containing all variables considered likely to be of a priori importance to the investigators. As the effect of each predictor would increase for longer transports, each of these dichotomous variables was multiplied by the uncorrected street network transport time estimate (interaction terms). These included use of lights and sirens, daylight transport time, transport during rush hour, transport during wet weather, patient age 18 and under, patient sex, and entry into the trauma system. Wet weather conditions were defined as those that began on a calendar day in which 0.01 or more inches of precipitation were recorded at the National Weather Service Portland office. This was based on the minimum precipitation necessary to make the ground wet.⁷ Daylight was a transport beginning between sunrise and sunset.⁸ Rush hour was defined as transports beginning from 7:00 to 9:00 am and 4:00 to 6:30 pm. A transport was considered to use lights and sirens if the patient care record denoted it as such at any time, even if the priority was changed during transport.

We determined that a model without a constant would maximize accuracy as the ambulance neared the hospital, while an equation with a constant would more accurately predict the time of arrival when the ambulance was still farther away. The point at which the model switched from the equation for long versus short transports was determined by trial and error so that there would not be a jump in the predicted ETA as an ambulance driving toward the hospital with lights and sirens crossed that threshold. Accuracy of the model was quantified as the proportion of transports arriving within 5 minutes of the predicted time, a previously used criterion.²

We then developed a Google Maps web application using simulated data to demonstrate how this model might be deployed in EMS operations. Google makes a free set of tools to allow developers with a basic knowledge of JavaScript to embed Google Maps in their web and mobile applications.⁹ In our demonstration application, users go to a website hosted on our server and enter the ambulance location and destination hospital. The application calls upon the Google Maps server to provide a map of the ambulance's current position, projected route, uncorrected street network ETA, and a corrected ETA refined by the predictors that this study found to be significant. This same interface could be fed from real-time GPS data from the ambulance, providing a constantly updated ETA and position data with minimal manual input from the user.

Results

Our dataset consisted of 50,245 scene transports occurring in 2008. A total of 48,248 (96.0%) of scene addresses were successfully geocoded by Google maps without any manual editing. An additional 1997 4.0% were geocoded manually. Charts for 1843 transports were excluded for actual transport times shorter than estimated. Charts for 94 transports were excluded for transport times > 60 minutes. After exclusions, 24,133 transports were used to derive our model and 24,175 for validation. The two datasets showed no significant differences (Table 1). <T1> Figure 1 shows the distribution of actual transport times recorded by computer-aided dispatch terminals on the ambulances. <F1> The median transport interval was 15.8 minutes (interquartile range [IQR] 11.3–21.6 minutes). Transport intervals were reasonably normally distributed, with a Shapiro-Francia statistic of p = 0.50, justifying use of a linear regression model. The median transport interval was similar to the mean at 17.3 minutes, also supporting the assumption of normality.

Table 1. Characteristics of EMS transports in the derivation and validation sets for the model of transport time.

	Derivation (n = 24,133)		Validation (n = 24,175)		P value*
Age, mean years (95% CI)	54.7	54.4–55.0	54.6	54.3–54.9	0.57
Age ≤ 18 years	1,210	5.0%	1,301	5.4%	0.07
Male sex	11,381	47.2%	11,402	47.2%	0.99
Trauma system activation	631	2.6%	587	2.4%	0.19
Lights and sirens	1,653	6.8%	1,601	6.6%	0.32
Daylighta	14,436	59.8%	14,345	59.3%	0.28
Rush hourb	4,972	20.6%	4,988	20.6%	0.93
Wet weatherc	11,242	46.6%	11,196	46.3%	0.55
Transport time, median minutes (IQR)	15.8	(11.3–21.6)	15.8	(11.3–21.6)	0.82
Transport distance, median miles (IQR)d	5	(3–8)	5	(3–8)	0.93

^*P value for the difference between derivation and validation sets.

^aDaylight was defined as sunrise to sunset.

^bRush hour was defined as 7–9 am and 4–6:30 pm.

^cWet weather was defined as ≥0.01 inches measured precipitation.

^dRecorded from vehicle odometer

Figure 1.

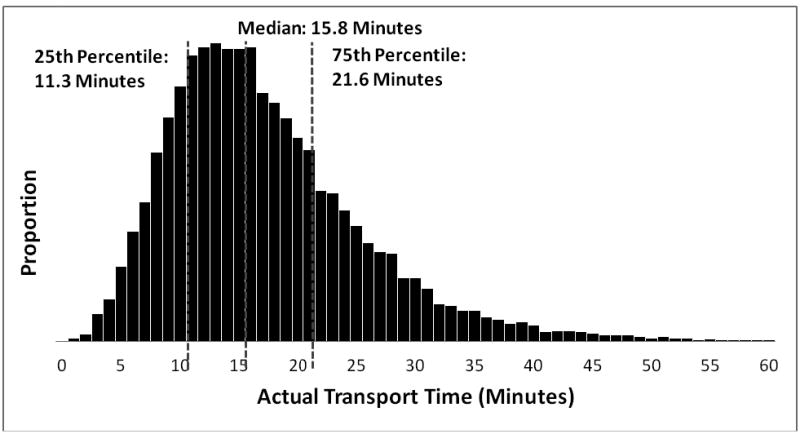
Distribution of actual transport times from scene to emergency department (n = 24,133). From derivation dataset.

Table 2 shows the linear regression models used to refine the estimate of transport time from the ArcGIS street network. <T2> We determined by trial and error that a switch from the equation for long transports (with a constant) to the one for shorter transports (without a constant) at 8.8 minutes of street network predicted transport time would minimize the jump in the estimated time of arrival when an ambulance using lights and sirens crossed that threshold. All predictor variables were multiplied by the street network estimated transport time (interaction terms) to account for the fact that the effect of these variables on transport time would be proportional to the length of the transport (see Table 2 legend for model). In a model containing all variables from Table 1, wet weather significantly increased transport times by 4 seconds per minute of street network estimated transport time; however, it was not significant for transports longer than 8.8 minutes and was therefore omitted from the final model. Patients meeting predefined criteria were considered “trauma activations” and transported to one of two level 1 trauma centers. Trauma activation status decreased transport time by 4 seconds per minute of raw estimated transport time for longer transports, but was not significant for shorter transports. Age 18 and under was not significant. As our goal was to create a web application that would require minimal manual entry of data, it was fortuitous that weather, trauma system entry, and age were not significant and could thus be omitted. Our final model included street network-estimated transport time, daylight, rush hour, and the use of lights and sirens (Table 2). When the models were derived from only lights and sirens transports, daylight and rush hour became insignificant. This suggests that the use of lights and sirens overcame much of the variability associated with time of day and traffic conditions.

Table 2. Multivariable linear models for actual transport time (n = 24,133).

Variable	Coefficient	95% Confidence interval
Street network estimated time <8.8 min
Street network estimated time	2.59	2.58 to–2.61
Lights and sirens	-0.76	-0.83 to -0.69
Rush hour	0.17	0.12 to 0.22
Daylight	0.14	0.10 to 0.18
Street network estimated time ≥8.8 min
Street network estimated time	1.07	1.03 to 1.12
Lights and sirens	-0.40	-0.44 to -0.36
Rush hour	0.16	0.13 to 0.19
Daylight	0.13	0.11 to 0.15
Constant	9.63	9.09 to 10.2

Separate models were used for street network estimated transport times shorter or longer than 8.8 minutes, with the inclusion of a constant in the model for the longer transports. Each term in the model was multiplied by the street network estimated time to account for the increasing effect of each term on transport time. The equation for transports ≥8.8 minutes was Actual transport time = 9.63 + 1.07 * Street network estimated time − 0.40 * Lights and sirens * Street network estimated time + 0.16 * Rush hour * Street network estimated time + 0.13 * Daylight * Street network estimated time.

Figure 2 shows scatterplots of the street network estimated transport times compared with actual transport times recorded from the ambulance's computerized data terminals. <F2> The slope of the lines shows that the street network significantly underestimated actual transport times, especially for transports without the use of lights and sirens.

Figure 2.

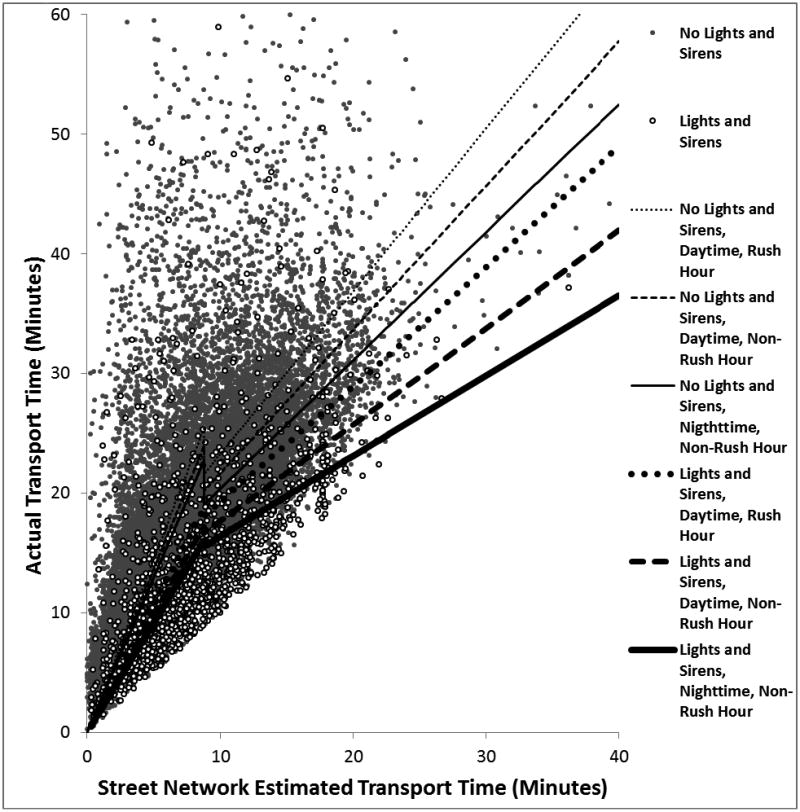
Scatterplot of actual transport times in minutes versus street network estimates in the derivation dataset (n = 24,133). Lines show model predicted times. Lines for nighttime, rush-hour transports represent less than 2 hours a day in the middle of winter and were omitted for clarity.

Figure 3 shows the distribution of model error. <F3> The street network predicted time of arrival within 5 minutes only 15.6% of the time. A two-part model split at 8.8 minutes using just a constant and coefficient but no additional predictors improved accuracy within 5 minutes to 70.6% of the time. Addition of the other significant predictors of rush hour, daylight, and use of lights and sirens further improved prediction of arrival time to within 5 minutes 72.8% of the time (95% CI 72.2–73.3%). The improvement given by the addition of those additional predictors was seen by the slightly higher, narrower error distribution for the full model in Figure 3. Model fit for transports shorter than 8.8 minutes was excellent, with an R-squared statistic of 0.84. For transports longer than 8.8 minutes, the model explained less of the variability, with an R-squared of 0.33. For transports using lights and sirens, the full model was accurate within 5 minutes 76.9% of the time (95% CI 74.9–78.9%). The mean error (mean of absolute value of predicted time-actual time/actual time) was 25.1%. Accuracy was the same in the validation data set.

Figure 3.

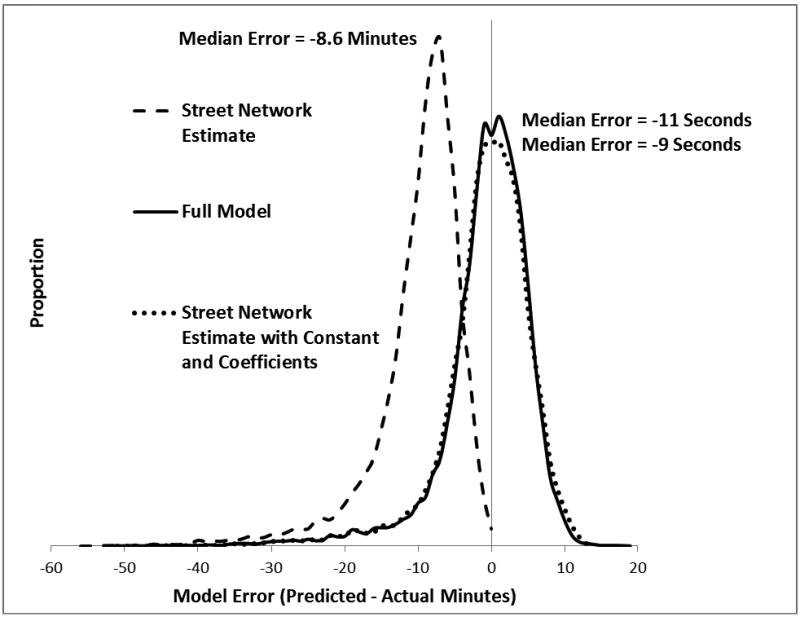
Distribution of error in predicted transport time for three models. Error is shown as predicted minus actual, so negative numbers signify the model underestimating transport time (patient arriving after the predicted time).

The model was then used to create a Google Maps web application that could be implemented in the emergency department to give providers a visual display of ambulance routing and predicted time of arrival (Figure 4, demonstration application at www.emedresearch.net/ems/).

Figure 4.

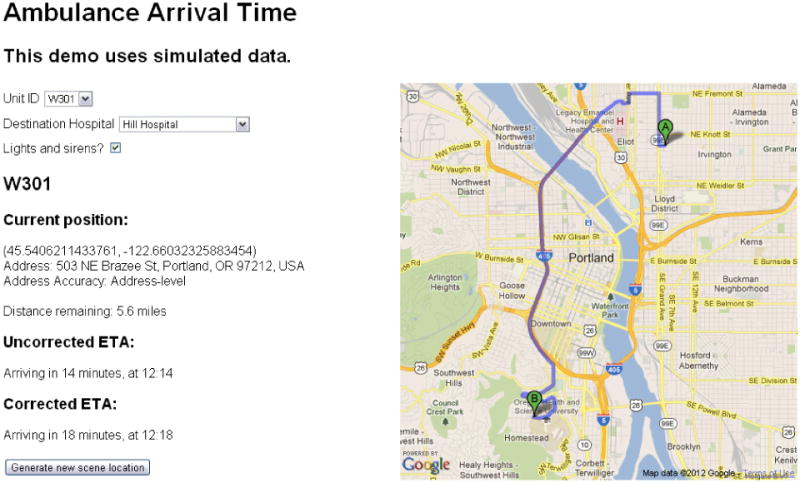
Google Maps web application to display ambulance time of arrival.

For our second objective of determining the influence of lights and sirens on transport time, a model was created using all the predictors in Table 2, but with lights and sirens entered by itself rather than multiplied by the estimated transport duration. In this model, lights and sirens transports averaged 3.1 minutes (47%) shorter than non-lights and sirens transports for those under 8.8 minutes, and 5.3 minutes (28%) shorter for those longer than 8.8 minutes street network estimated time.

Discussion

In this project, we used a large set of transport records from one EMS system to derive and validate a model that accurately predicts ambulance time of arrival to the emergency department. While GPS and mapping technologies are widespread in emergency response, we know of no other studies looking at their accuracy in predicting time of arrival.^10,11 A meta-analysis by Carr et al. showed an average national transport time of 10.8 minutes for urban trauma patients transported by ground ambulance and summarized previous attempts to standardize reporting of prehospital time intervals.^12,13 In a project with practical application to EMS system design somewhat similar to ours, Lerner et al. used observed transport intervals and geographical information system (GIS) technology to identify regions in which air versus ground transport would be faster.¹⁴ Other studies have looked to GIS for other aspects of system planning, such as helipad siting, resource levels, trauma triage, and ambulance deployment locations.^15–19

Our goal in this project was to produce a model that maximized accuracy while requiring a minimum number of predictors. Our findings met this objective since neither age, wet weather, nor trauma system entry was a significant predictor of arrival time. Daylight and rush-hour times were significant but could be looked up automatically by our web application from astronomical tables such as those from the US Naval Observatory. Only the use of lights and sirens and the number of the ambulance would need to be entered manually. Our approach of using a model based on separate equations for short and long transports is supported by Do et al.'s study showing that a quantile regression model found different predictors of ambulance response times for different lengths of transport.¹⁵

While static maps can be used to predict transport times and guide dispatch decisions, they lack the automation of a computer-based model, which can incorporate relevant factors and can be constantly updated as transportation progresses. Other projects have demonstrated the usefulness of live GPS technology in operations.^16,17

Our Google Maps demonstration web application is an example of how rapidly advancing technologies can be applied to improve EMS. GPS-based automated vehicle locators are widely used throughout the country. Most EMS and fire vehicles in our system feed these data live to the communication and online medical control center. Sophisticated computerized routing algorithms informed by real-time traffic condition data are constantly becoming more accessible as consumers demand these technologies in their smartphone and car navigation systems. As we demonstrated, this information can be displayed in an easily accessible format through application programming interfaces (APIs) developed by Google Maps, MapQuest, and others. Another example of applying this technology to EMS is the www.public911.com website, which displays live EMS response information from the Seattle fire department on a Google map.

Our model was significantly more accurate than other estimates of arrival time reported in the literature. In a prospective study of ambulance transport times, Jurkovich et al. showed that the prehospital provider's estimate of the duration of the transport at its conclusion was off by an average of 33% in either direction.¹⁸ Given that these paramedics were asked to estimate their transport time after it had been completed, we would expect estimates given before or during transport to be even less reliable. Our mean error of 25% was better than this. Furthermore, our automated tool has the previously mentioned advantages of being available from the start of the transport rather than at the time the paramedic radios the hospital to give report, and does not interfere with patient care or driving.

A study of 6139 Portland-area trauma patients showed that paramedics were more than 5 minutes outside their ETA 55% of the time and greater than 10 minutes inaccurate in 28% of transports.² Our model's accuracy within 5 minutes 72.8% of the time overall and 76.9% of the time for lights and sirens transport was much better than the medic-reported ETAs in that study. A study of online medical control cases found that the physician's prehospital management would have been altered 8.5% of the time by a more accurate ETA.¹⁹ Given that our model is envisioned to be tied to a web application that constantly updates and improves based on GPS telemetry data coming from the ambulance, our accuracy would continue to improve as the ambulance neared the hospital. Such an application would be extremely easy to use, as ambulance location (via GPS automated vehicle locator), hospital, daylight, and rush-hour information would all be entered automatically, requiring the user only to choose the proper ambulance unit and the use of lights and sirens. In the ED setting, knowledge that the arrival of a critical patient was delayed by even a minute could allow providers to accomplish a few other tasks prior to engaging in an extended period of critical care.

Our findings also supported the value of lights and sirens in shortening transport times. Use of lights and sirens and high-speed driving is associated with an increased risk of accident as well as the disruption of traffic; therefore, the savings in transport times must be weighed against the risks. Two prospective studies have attempted to answer the question of potential time savings using lights and sirens by comparing actual lights and sirens response times to those of an ambulance driving the route at the same time on the same day of a different week while obeying normal traffic laws. Hunt et al. showed that transports using lights and sirens averaged 43.5 seconds faster on a 6-minute transport time than their non-lights and sirens controls.²⁰ Brown demonstrated a greater difference in a similar study investigating time intervals en route to the scene, showing a difference of 106 seconds in transports averaging 4.9 minutes.²¹ Another methodology was to follow each lights and sirens-using ambulance with another non-lights and sirens control. In two studies, Ho et al. found a savings of 3.0 minutes for urban transports using a chase vehicle and 3.6 minutes for rural calls.^22,23 This was closer to our observed benefit, with our model showing that lights and sirens transports were 3.1 minutes shorter when restricted to transports under 8.8 minutes street network estimated time and 5.3 minutes shorter for those between 8.8 and 60 minutes. While our study does not address the clinical importance of this time savings compared with the risk of high-speed driving, it does show that transport intervals are significantly shorter when lights and sirens are used. Our observation that lights and sirens were used in only 6.9% of transports may understate their impact, as a recent study of the National Emergency Medical Services Information System (NEMSIS) database showed that they were used at some point in 78.5% of EMS responses (whether to the scene or in transport).²⁴

Limitations

Given our goal of creating a tool based on Google Maps, it would have been ideal to derive our transport time estimates from Google Maps; however, the Google Maps licensing agreement prohibits submitting large batches of addresses through their website for route generation, requiring us to estimate transport time and distance using the ArcGis Network Analyst. Our demonstration application complies with the Google Maps licensing agreement, as it generates routes one at a time. We expect estimates from Google Maps would be more accurate than those we derived, as Google Maps makes use of live traffic data.

The refinement of technologies that can be marketed to billions and adapted to EMS will far outpace that which is produced exclusively for use by emergency responders. Unfortunately, the rapid progress in consumer mapping guarantees that today's publications report on yesterday's technology. In addition, commercial secrecy limits our understanding of the how these applications work and leaves those who develop end-user applications at the mercy of those who create the underlying technology. Developers of applications that are mission-critical to EMS systems will need to consider the reliability of internet-based technologies. Confidentiality issues are also a concern, as the Google Maps API requires sending location data, which is potentially considered to be protected health information, to Google's servers for processing.

Conclusion

Ambulance location data and a simple web-based application can be used to provide accurate estimates of ambulance time of arrival to the emergency department, which could be applied to improve emergency medical resource use. Use of lights and sirens was related to a greater savings in transport time than previously reported.